基于ABAQUS的钢管轴心受压非线性屈曲分析

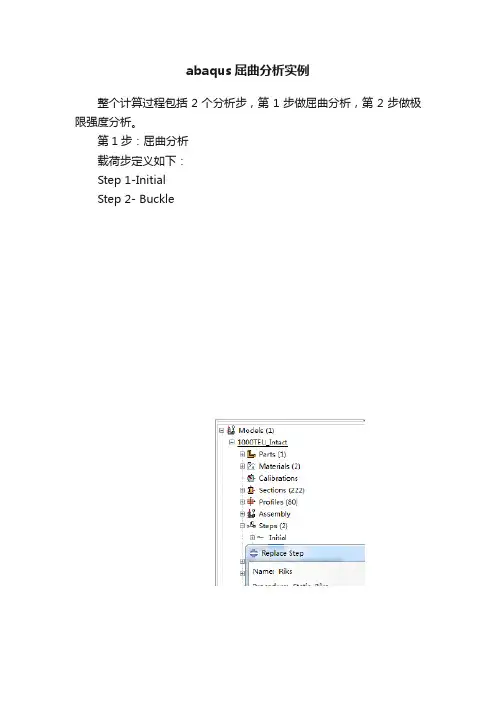
abaqus屈曲分析实例整个计算过程包括2个分析步，第1步做屈曲分析，第2步做极限强度分析。

第1步：屈曲分析载荷步定义如下：Step 1-InitialStep 2- Buckle并在Model-Edit Keywords 的图中位置加入下面的文字，输出屈曲模态 *nodefile, global=yes U,Create job 名称为“Buckling”点击continue，完成第1步的计算。

第2步：极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中，Nlgeom：选择打开在Instrumentation选项卡中，定义如下参数，然后点击OK定义一个新计算工作，输入名称，点击continue在Parallelization选项卡，选择2个CPU，如下所示，点击OK。

在此编辑Model-edit keywords，删除“第1步”加入的文字“*nodefile, global=yes U,”，并在下图位置加入下段文字：*imperfection, file=buckling, step=11, 2.5点击OK，再保存文件。

最后提交计算。

提取计算结果进入visualization Module点击Create XY data选择ODB filed output，点击continue选项卡，选择跨中载荷加载点，最后点击save。

重复上一步操作，Position 选择Unique Nodal ，U ：spatial displacement 选择 U3，再点击elements/nodes 选项卡，选择板格中心点，最后点击save 。

点击Create XY data, 选择operate on XY data，点击continue择保存的Point load曲线，点击最后一行Create XY Data与Save as。

目录：1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4．结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要：钢结构的稳定性能是决定其承载力的一个特别重要的因素，稳定理论和设计方法需要完善。

近几十年以来，在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面，国内外都取得了长足的进步。

例如完善钢结构的弹塑性稳定理论，研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载，用数值法来解决这类问题等都取得了不少研究成果。

在作理论分析的同时进行稳定性能的试验验证，以及将理论研究结果利用图表表示或深化为计算公式，从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。

本文的主要内容是对现有失稳理论进行完善和发展及其总结，利用通用有限元abaqus软件，采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析，文中总共给了10个特征向量，进而得出相应的模态分析变形图，最后把lanczos 方法及子空间迭代法进行了比较，提出一些新的问题。

关键词：有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点，是制造结构物的一种极好的建筑材料。

钢材与在建筑结构中应用广泛的钢筋混凝土结构相比，对于受力功能相同的构件，具有截面轮廓尺寸小、构件细长和板件薄柔的特点。

但是对于因受压、受弯和受剪等存在受压区域的构件和板件，如果技术上处理不当，可能使钢结构出现整体失稳或局部失稳。

目录：1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4．结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要：钢结构的稳定性能是决定其承载力的一个特别重要的因素，稳定理论和设计方法需要完善。

近几十年以来，在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面，国内外都取得了长足的进步。

例如完善钢结构的弹塑性稳定理论，研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载，用数值法来解决这类问题等都取得了不少研究成果。

在作理论分析的同时进行稳定性能的试验验证，以及将理论研究结果利用图表表示或深化为计算公式，从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。

本文的主要内容是对现有失稳理论进行完善和发展及其总结，利用通用有限元abaqus软件，采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析，文中总共给了10个特征向量，进而得出相应的模态分析变形图，最后把lanczos 方法及子空间迭代法进行了比较，提出一些新的问题。

关键词：有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点，是制造结构物的一种极好的建筑材料。

钢材与在建筑结构中应用广泛的钢筋混凝土结构相比，对于受力功能相同的构件，具有截面轮廓尺寸小、构件细长和板件薄柔的特点。

但是对于因受压、受弯和受剪等存在受压区域的构件和板件，如果技术上处理不当，可能使钢结构出现整体失稳或局部失稳。

目录：1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4．结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要：钢结构的稳定性能是决定其承载力的一个特别重要的因素，稳定理论和设计方法需要完善。

近几十年以来，在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面，国内外都取得了长足的进步。

例如完善钢结构的弹塑性稳定理论，研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载，用数值法来解决这类问题等都取得了不少研究成果。

在作理论分析的同时进行稳定性能的试验验证，以及将理论研究结果利用图表表示或深化为计算公式，从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。

本文的主要内容是对现有失稳理论进行完善和发展及其总结，利用通用有限元abaqus软件，采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析，文中总共给了10个特征向量，进而得出相应的模态分析变形图，最后把lanczos 方法及子空间迭代法进行了比较，提出一些新的问题。

关键词：有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点，是制造结构物的一种极好的建筑材料。

钢材与在建筑结构中应用广泛的钢筋混凝土结构相比，对于受力功能相同的构件，具有截面轮廓尺寸小、构件细长和板件薄柔的特点。

但是对于因受压、受弯和受剪等存在受压区域的构件和板件，如果技术上处理不当，可能使钢结构出现整体失稳或局部失稳。

四、ABAQUS钢柱特征值屈曲分析问题描述：利用有限元软件分析咋爱不同特征值下的一个 4.2m高的钢柱的变形情况。

钢柱的截面尺寸如图所示。

钢柱的材料特性：弹性模量E=2.1e11N/m2，泊松比0.3，屈服强度f y=3.45e8 N/m2。

1.创建部件将Modeling Space设为3D，Shape设为shell，Type选择Extrusion，Approximate size项输入1，点击继续开始绘制草图。

以坐标的形式绘制线条，生成三维模型。

2.创建材料点击创建材料按钮，弹出对话框。

名称输入steel，在对话框中点击General(常规特性)-Density，在Mass Density中输入7850；点击Mechanical（力学特性）-Elasticity（弹性）-Elastic，将Young’s Modulus（弹性模量）设为2.0e11，Poisson’s Ratio为0.3。

3.创建截面属性点击创建截面按钮，将Category设为shell，Type设为Homogeneous，其余参数不变，点击继续弹出Edit section对话框，Value后面输入0.01，保持其余参数不变，完成对翼缘截面属性的定义。

同理输入0.006，完成对腹板截面属性的定义。

4.给部件赋予截面属性点击赋予截面属性按钮，分别赋予翼缘和腹板的截面属性。

5.定义装配件6.设置分析步点击创建分析步按钮，在名称后面输入load，procedure type项选择linear perturbation，下拉菜单中选择Buckle。

点击继续，弹出编辑分析步对话框，Eigensolver 项中选择Lanczos，在Number of eigenvalus requested（所需特征值数量）后输入10，即分析10个特征值下的变形情况，剩余参数不变。

7.定义荷载和边界条件●给钢柱施加边界荷载点击Create Load对话框，在名称后面输入load-1，step项中选择load，将出现的Type for Selected Step（所选分析步的荷载类型）设为Shell edge laod(壳体边缘荷载)，保持其他不变，点击继续，提示区显示选择要添加荷载的壳体边缘，选择如图所示的边界，在弹出的对话框的Magnitude（幅值）后面输入1e4，剩余参数不变。

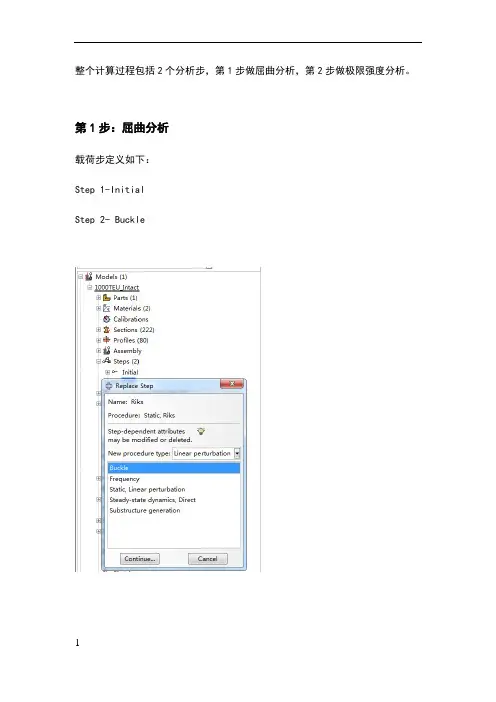
整个计算过程包括2个分析步，第1步做屈曲分析，第2步做极限强度分析。

第1步：屈曲分析载荷步定义如下：Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字，输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue，完成第1步的计算。

第2步：极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中，Nlgeom：选择打开在Instrumentation选项卡中，定义如下参数，然后点击OK定义一个新计算工作，输入名称，点击continue在Parallelization选项卡，选择2个CPU，如下所示，点击OK。

在此编辑Model-edit keywords，删除“第1步”加入的文字“*nodefile, global=yesU,”，并在下图位置加入下段文字：*imperfection, file=buckling, step=11,点击OK，再保存文件。

最后提交计算。

提取计算结果进入visualization Module 点击 Create XY data选择 ODB filed output，点击continuePosition选择 Unique Nodal， CF：point loads选择 CF2，再点击elements/nodes选项卡，选择跨中载荷加载点，最后点击save。

重复上一步操作，Position选择 Unique Nodal， U：spatial displacement 选择 U3，再点击elements/nodes选项卡，选择板格中心点，最后点击save。

点击Create XY data, 选择operate on XY data，点击continue选择Combine（X,X）命令，横坐标选择保存的displacement曲线，纵坐标选择保存的Point load曲线，点击最后一行Create XY Data与Save as。

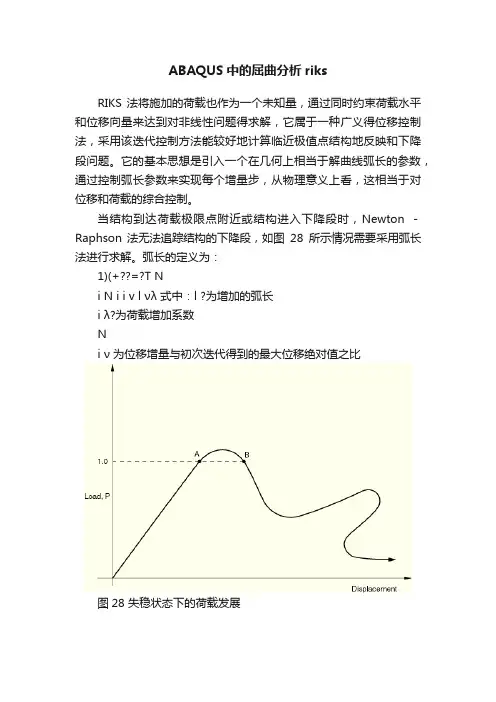
ABAQUS中的屈曲分析riks
RIKS 法将施加的荷载也作为一个未知量，通过同时约束荷载水平和位移向量来达到对非线性问题得求解，它属于一种广义得位移控制法，采用该迭代控制方法能较好地计算临近极值点结构地反映和下降段问题。

它的基本思想是引入一个在几何上相当于解曲线弧长的参数，通过控制弧长参数来实现每个增量步，从物理意义上看，这相当于对位移和荷载的综合控制。

当结构到达荷载极限点附近或结构进入下降段时，Newton －Raphson 法无法追踪结构的下降段，如图28所示情况需要采用弧长法进行求解。

弧长的定义为：
1)(+??=?T N
i N i i v l νλ 式中：l ?为增加的弧长
i λ?为荷载增加系数
N
i ν为位移增量与初次迭代得到的最大位移绝对值之比
图28 失稳状态下的荷载发展
图29 RIKS 法示意图
图29为RIKS 法计算过程中的迭代示意图。

具体计算流程如下所示：
初始情况下：
对于 i=迭代步 (i=1,2,3,etc): a. 形成内部节点应力矩阵I N
b. 检查平衡方程
如果R i N 足够小，则计算收敛，否则求解方程
得到v i N 和c i N
c. 将初始矢量（1,N i v ）加上（N i N i c ρ,）（其中N
N N i i P P R /=ρ），这样解就由点A 1移动到点A 2,如图29所示。

求解等式
得到：
则最终的解为：
d. 更新到下一次迭代
返回到a，进行下一步迭代。

目录：1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4．结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要：钢结构的稳定性能是决定其承载力的一个特别重要的因素，稳定理论和设计方法需要完善。

近几十年以来，在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面，国内外都取得了长足的进步。

例如完善钢结构的弹塑性稳定理论，研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载，用数值法来解决这类问题等都取得了不少研究成果。

在作理论分析的同时进行稳定性能的试验验证，以及将理论研究结果利用图表表示或深化为计算公式，从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。

本文的主要内容是对现有失稳理论进行完善和发展及其总结，利用通用有限元abaqus软件，采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析，文中总共给了10个特征向量，进而得出相应的模态分析变形图，最后把lanczos 方法及子空间迭代法进行了比较，提出一些新的问题。

关键词：有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点，是制造结构物的一种极好的建筑材料。

钢材与在建筑结构中应用广泛的钢筋混凝土结构相比，对于受力功能相同的构件，具有截面轮廓尺寸小、构件细长和板件薄柔的特点。

但是对于因受压、受弯和受剪等存在受压区域的构件和板件，如果技术上处理不当，可能使钢结构出现整体失稳或局部失稳。

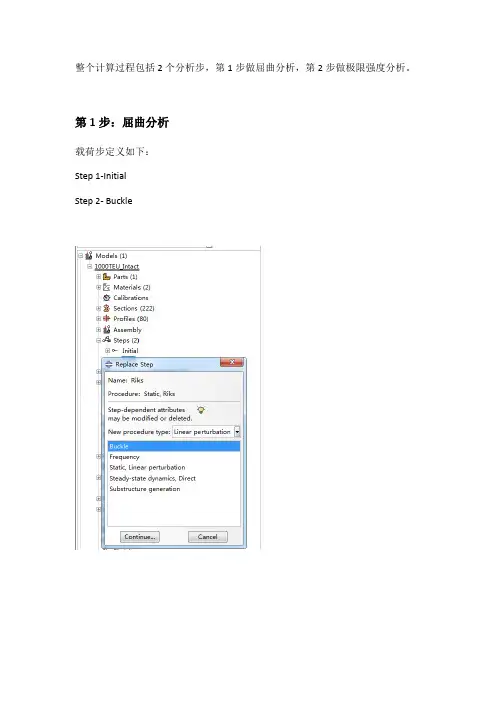
整个计算过程包括2个分析步，第1步做屈曲分析，第2步做极限强度分析。

第1步：屈曲分析载荷步定义如下：Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字，输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue，完成第1步的计算。

第2步：极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中，Nlgeom：选择打开在Instrumentation选项卡中，定义如下参数，然后点击OK定义一个新计算工作，输入名称，点击continue在Parallelization选项卡，选择2个CPU，如下所示，点击OK。

在此编辑Model-edit keywords，删除“第1步”加入的文字“*nodefile, global=yes U,”，并在下图位置加入下段文字：*imperfection, file=buckling, step=11,点击OK，再保存文件。

最后提交计算。

提取计算结果进入visualization Module点击Create XY data选择ODB filed output，点击continuePosition选择Unique Nodal，CF：point loads选择CF2，再点击elements/nodes 选项卡，选择跨中载荷加载点，最后点击save。

重复上一步操作，Position选择Unique Nodal，U：spatial displacement选择U3，再点击elements/nodes选项卡，选择板格中心点，最后点击save。

点击Create XY data, 选择operate on XY data，点击continue选择Combine（X,X）命令，横坐标选择保存的displacement曲线，纵坐标选择保存的Point load曲线，点击最后一行Create XY Data与Save as。

第３３卷第６期２０１９年１１月兰州文理学院学报(自然科学版)J o u r n a l o fL a n z h o uU n i v e r s i t y ofA r t s a n dS c i e n c e (N a t u r a l S c i e n c e s )V o l ．３３N o ．６N o v ．２０１９收稿日期:２０１９Ｇ０９Ｇ１０基金项目:安徽省高校优秀青年人才支持计划项目(g x y q２０１７１７５);安徽省质量工程项目大模在线开放课程(２０１６m o o c ０３８㊁２０１６m o o c ０３５);校级品牌课程(２０１６y j p p k c ３０);安徽省自然科学基金研究项目(K J ２０１７B ００２);教育部创新发展行动计划(X M Ｇ０７ＧS ３４);校级品牌课程(２０１９y j p pk c ０５)作者简介:张传俊(１９７３Ｇ),男,安徽淮南人,讲师,硕士,研究方向:机械设计㊁自动控制㊁工业机器人等．E Ｇm a i l:３５５３８１４７１＠q q．c o m．㊀㊀文章编号:２０９５Ｇ６９９１(２０１９)０６Ｇ００２８Ｇ０４基于A B A Q U S 的筋板件线性与非线性屈曲缺陷分析张传俊１,张春芳１,毕厚煌２(１．安徽工商职业技术学院,安徽合肥２３１１３１;２．芜湖职业技术学院,安徽芜湖２４１００６)摘要:结构的屈曲响应与初始几何缺陷条件密切相关,非线性后屈曲状态彼此之间相互影响．为了研究筋板零件在一定载荷作用下屈曲状态,在A B A Q U S 首先建立零件的三维模型,再对其进行几何的线性与非线性屈曲分析,由此获得对应的各阶特征值及其对应的屈曲形状变化云图．通过对后屈曲状态中的L P F 弧长曲线进行对比分析来研究缺陷敏感性,实验数据表明筋板件受到不同缺陷缩放因子的影响非常明显,分析求解结果为板件形状零件的设计提供参考．关键词:几何缺陷;筋板零件;屈曲分析;缩放因子中图分类号:T H １１３．１㊀㊀㊀文献标志码:A0㊀引言板状零件是汽车车身部件中的重要组成部分,随着汽车车身设计不断复杂化,对车身结构的稳定性㊁可靠性提出了更高的要求．结合板状零件的几何特征,实际装配使用过程中,会在零件表面焊接对应的加强筋,以此来增加零件的力学性能,加强筋的位置分布也对零件的结构强度等有重要影响．本文以某型号车身板材为例,截取一定区域的板材并添加纵向加强筋．对其进行线性屈曲分析和缺陷几何的非线性屈曲分析,研究低阶特征值及其屈曲形状和对缺陷因子的敏感程度．1㊀屈曲分析理论基础屈曲分析在工程应用研究中常用来求解构件或结构的刚度及强度等问题．屈曲分析的类型可按照载荷施加形式㊁材料特性㊁线性与非线性来区分,其中几何线性与否成为屈曲分析分类的重要形式．1.1㊀线性屈曲分析方程与求解该形式的屈曲分析适用于初始缺陷不敏感结构的屈曲模态和临界载荷极值求解,计算得到的结果包含模态分析数据．线性屈曲分析以模态中的特征值为研究对象,同材料力学求解压杆失稳类型问题分析类似,在远低于安全应力状态下就发生屈曲[１Ｇ２],其本质是一种近似线弹性理论的失稳分析法,可以预测结构的理论屈曲强度[３]．在有限元求解线性屈曲特征值时,外部载荷作用导致模型刚度矩阵出现奇异,如式(１)所示存在非无效解[４]．K X Y S X ＝０．(１)式(１)中K X Y 为平衡方程中切向刚度矩阵,S X 为有效位移解．为了获得屈曲临界载荷,需要先求解模型对应特征值λ,对应的求解方程如下:(K X Y ０＋λiK X Y Δ)S X i ＝０．(２)式(２)中K X Y０为系统包含预载荷的初始状态刚度矩阵,X 和Y 为系统构件自由度．S Xi ㊁λi 为第i 阶屈曲响应模态的特征向量和特征值,二者分别对应系统的失稳模态和屈曲载荷安全系数[５]．1.2㊀非线性屈曲分析方程与求解非线性屈曲分析涵盖几何形状㊁边界条件㊁材料特性等非线性问题求解,几何非线性来源于大位移㊁大转动㊁大应变㊁结构失稳等．在有限元软件A B A Q U S 计算时,与线性屈曲问题求解相比,最大的不同在于前者可以查看后屈曲状态．该种形式屈曲分析适用于求解结构弹塑性失稳等稳定性问题,在载荷与位移响应过程中出现负刚度矩阵时,系统需要释放应变能来维持平衡方程．针对一些极限载荷等问题使用R i k s 法(弧长法)进行求解,该方法属于双重目标控制类型[６]．采用改进型R i k s 法计算时,能够保持非稳定时段响应的静力平衡状态．同时可以设定一个载荷变化标量参数和位移的步长量,有利于迭代求解收敛．R i k s 法求解时载荷增量步长Δλ存在一定变化,为此需要补充对初始弧长半径控制及其对应方程[７]．ΔL j ＝ΔL j －１n e n j －１．(u ~iu j －u ~j －１)２＋(λi j －λj )２＝ΔL ２j ．ìîíïïïï(３)式(３)中ΔL j 为收敛圆弧半径;( u j －１,λj－１)为收敛点;n e 为载荷步理想迭代收敛次数;n j－１为第j －１步迭代次数;λj 为迭代计算子步对应的载荷因子系数．2㊀板件的几何线性与非线性屈曲分析2.1㊀线性屈曲分析在C r e o 软件中按照以下材料参数进行建模,具体参数信息如表１所列．选取板件材料长度１２０mm ,宽度７０mm ,加强筋纵向分布在板面上,板材厚度１mm．完成建模后保存为x _t 格式,并导入A B A Q U S 之中．在线性屈曲分析中是以特征值为研究对象,为此需要提取低阶特征值及其屈曲状态．在分析中设置提取６阶的屈曲变形量,选择在板件一端施加均表１㊀板件材料参数材料名称密度弹性模量泊松比屈服应力塑性应变碳素钢７８５０k g/m ３１９８００M P a０．３５５０~９６０M P a０~０．１布载荷１N /mm ,一端施加固定约束,两侧施加水平位移约束．网格划分数量为２４００,网格质量检查错误或警告为零．在分析求解之前,为了输出屈曲形状并导入到后续非线性分析中,需要对I N P文件中关键字进行修改,最后得到具体分析结果,如图１所示．从图１中可以看出,１~６阶特征值之间间隔很小,表明结构的屈曲载荷临界值对初始缺陷较为敏感,因此需要对其进行缺陷几何的非线性屈曲分析．2.2㊀非线性屈曲分析将线性屈曲分析中的模型及其参数整体复制到本分析环节中,改变分析类型为静态弧长分析．在几何非线性中设置停止条件为达到设定的最大载荷比例系数１５,设置初始弧长增量为０ １,最大弧长增量为０．５．在I N P 文件中修改关键字,设定初始几何缺陷条件为满足第一阶的屈曲形状和对应缺陷因子之乘积．同时,为了研究屈曲临界力对缺陷敏感程度,设定缺陷缩放因子分别为１％㊁５％㊁１０％㊁１５％㊁２０％,对计算得到结果中包含的L P F 载荷比例系数曲线图进行对比,结果显示如图２所示．图２为不同缺陷缩放因子条件的L P F 弧长曲线对比展示,以缺陷因子为１％时为例,其１阶临界边载荷约为６x １N /mm ,小于其前面线性屈曲分析时获得的１阶屈曲模态７．１４０５N /mm．当边载荷超过此临界数值后L P F 弧长曲线发生转折,意味着出现了几何缺陷．随着缺陷缩放因子逐渐递增至２０％,L P F 弧长曲线转折逐渐平滑而无显著转折点,表明板件的屈曲临界力对缺陷非常敏感．3㊀结束语本文通过在有限元分析软件A B A Q U S 中对筋板件做了几何的线性屈曲分析和非线性屈曲分析,并将各个求解进行了分析和对比,总结得出以下结论:(１)线性屈曲分析结果显示前６阶特征值彼此间隔很小,数据表明筋板件对初始缺陷极为敏感,因此有必要对其进行缺陷几何的非线性屈曲分析,求解获得的第１阶特征值及其屈曲形状,可作为初始几何缺陷条件引入后续非线性分析之中．(２)在线性屈曲分析时,板件上的加强筋的分布对于其屈曲形状存在一定影响,使得变形方向和幅度大致呈现左右两边对称．由于要输出屈曲变形位移,需在分析之前修改I N P 文件中的关键字．９２第６期张传俊等:基于A B A Q U S 的筋板件线性与非线性屈曲缺陷分析(a)一阶特征值及屈曲形状㊀㊀(b)二阶特征值及屈曲形状(c)三阶特征值及屈曲形状㊀㊀(d)四阶特征值及屈曲形状(e)五阶特征值及屈曲形状㊀㊀(f)六阶特征值及屈曲形状图１㊀前６阶特征值及其屈曲形状云图图２㊀L P F弧长曲线图对比㊀㊀(３)非线性屈曲分析表明缺陷缩放因子对L P F弧长曲线有明显影响,随着其数值的逐渐增大,求解所需时间更短,表明几何缺陷在该条件判断更加迅速．通过不同缩放因子下L P F曲线图对比,显示结构的临界载荷作用对初始条件下几何缺陷非常敏感．参考文献:[１]李元齐,李功文,沈祖炎,等．冷弯厚壁型钢考虑冷弯效应的屈服强度计算方法研究[J]．建筑结构学报,２０１５,３６(５):１Ｇ７．０３㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀兰州文理学院学报(自然科学版)㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第３３卷[２]何保康．轴心压杆局部稳定试验研究[J ]．西安建筑科技大学学报(自然科学版),１９８５,４１(１):２０Ｇ３４．[３]惠川川,张虎山,高永超,等．屈曲分析在提升滑轮稳定性评估中的应用[J ]．机械工程师,２０１９(４):７３Ｇ７５．[４]江丙云,孔祥宏,罗元元．A B A Q U S 工程实例详解[M ]．北京:人民邮电出版社,２０１４．[５]丁欣硕,凌桂龙．A N S Y S W o r k b e n c h１４．５有限元分析案例详解[M ]．北京:清华大学出版社,２０１４．[６]D A S S A U L T S ,S I MU L I A C ．A B A Q U S T h e o r yG u i d e [M ]．P r o v i d e n c e ,R I ,U S A :S c i e n t i f i cR e s e a r c hP u b l i s h i n g,２０１４．[７]佟光军,胡知辉,于莉,等．深水海底管道屈曲扩展非线性有限元分析[J ]．石油工程建设,２０１８,４４(５):１２Ｇ１５．[责任编辑:李岚]T h eL i n e a r a n dN o n l i n e a rB u c k l i n g D e f e c tA n a l y s i s o fR e i n f o r c e dR i b b e dP a r t sB a s e do nA B A QU S Z HA N GC h u a n Ｇj u n １,Z HA N GC h u n Ｇf a n g １,B IH o u Ｇh u a n g２(１．A n h u i B u s i n e s s a n dT e c h n o l o g y C o l l e g e ,H e f e i ２３１１３１,C h i n a ;２．W u h u I n s t i t u t e o fT e c h n o l o g y,W u h u２４１００６,A n h u i ,C h i n a )A b s t r a c t :T h eb u c k l i n g r e s p o n s eo f s t r u c t u r e s i sc l o s e l y r e l a t e dt ot h e i n i t i a l g e o m e t r i c i m p e r f e c t i o n c o n d i t i o n s ,a n dt h en o n Ｇl i n e a r p o s t Ｇb u c k l i n g s t a t e s i n t e r a c tw i t he a c ho t h e r ．I no r d e rt os t u d y th e b u c k l i n g s t a t e o f r i b b e d s t r u c t u r a l pa r t s u n d e r c e r t a i n l o a d s ,t h e t h r e e Ｇd i m e n s i o n a lm o d e l o f t h e p a r t s i s e s t ab l i s h e d i nA B A Q U S ,a n d t h e nt h e g e o m e t r ic l i n e a r a n dn o n Ｇl i n e a rb u c k l i n g a n a l y s i s i s c a r r i ed o u t ,t he r e b y o b t a i n i n g t h e c o r r e s p o n d i n g e i g e n v a l u e s a n d t h e i r c o r r e s p o n d i n g b u c k l i n g s h a pe s ．D ef e c t s e n s i t i v i t y i s s t u d i e db y c o m p a r i ng L P Fa r c l e n g t hc u r v e s i n p o s t Ｇb u c k l i n g st a t e ．T h ed a t a s h o wt h a t t h e r i b b e d p a r t s a r e g r e a t l y a f f e c t e db y d i f f e r e n t d e f e c t s c a l i n g f a c t o r s ．T h e a n a l y s i s a n d s o l u t i o n p r o Ｇv i d e a r e f e r e n c e f o r t h e d e s i g no f s h a pe p a r t s ．K e y wo r d s :g e o m e t r i c i m p e r f e c t i o n s ;r i b b e d p a r t s ;b u c k l i n g a n a l y s i s ;s c a l i n g f a c t o r s (上接第２７页)AP o r t f o l i oM o d e l B a s e do nD u a l E x p e c t e dU t i l i t yL IC h a o Ｇy i ,WA N G X i a o Ｇqi n ,G A OY u e Ｇl i n (N i n g x i aK e y L a b o r a t o r y o f I n t e l l i g e n t I n f o r m a t i o na n dB i g D a t aP r o c e s s i n g ,N o r t h M i n z uU n i v e r s i t y,Y i n c h u a n７５００２１,C h i n a)A b s t r a c t :C o n s i d e r i n g t h e f a c t t h a t t h ec u r r e n tC h i n e s e m a r k e t r e q u i r e ss e c u r i t i e s t r a d i n g tob e f u l l Ｇh a n d t r a d i n g a n d n o t t o a l l o ws h o r t s e l l i n g ,t h e p a p e r i n c r e a s e s t h e b a s e c o n s t r a i n t a n d t h e u p pe r l i m i t of s i ng l e a s s e t i n v e s t m e n t ,a n d a n a l y z e s a p o r t f o l i o p r o b l e mi n c l u d i n gt r a n s a c t i o n c o s t s u n d e r t h e n o n Ｇt r a d i t i o n a l e x p e c t e du t i l i t y t h e o r y ．T a k i n g u t i l i t y r i s k a s t h e r i s ko f p o r t f o l i o ,a n e w p o r t f o l i om o d e l i s e s t a b l i s h e du n d e r t h e c o n d i t i o n t h a t t h e r e t u r n r a t e o f s e c u r i t i e s f o l l o w s a n o r m a l d i s t r i b u t i o n ．T h e n,an e w p o r t f o l i om o d e l i s e s t a b l i s h e d a n d s o l v e db y d i f f e r e n t i a l e v o l u t i o n a l g o r i t h m．N u m e r i c a l e x p e r i Ｇm e n t s s h o wt h e r a t i o n a l i t y o f t h em o d e l a n d t h e v a l i d i t y o f t h e a l go r i t h m．K e y wo r d s :p o r t f o l i oo p t i m i z a t i o n ;d u a l e x p e c t e du t i l i t y ;c a r d i n a l i t y c o n s t r a i n t ;n o n l i n e a r i n t e g e r p r o Ｇg r a mm i n g ;d i f f e r e n t i a l e v o l u t i o na l go r i t h m １３第６期张传俊等:基于A B A Q U S 的筋板件线性与非线性屈曲缺陷分析。

第34卷第1期2012年2月工程抗震与加固改造Earthquake Resistant Engineering and RetrofittingVol. 34 ，No. 1Feb．2012［文章编号］1002-8412（2012）01-0020-06基于ABAQUS 的全钢装配式防屈曲支撑有限元分析张振兴，宁响亮，刘［提军，李文斌，陈彦北（中国南车株洲时代新材料科技股份有限公司，湖南株洲412007）要］防屈曲支撑受拉受压时都可以屈服，抑制了压曲现象，可获得饱满的荷载－位移滞回曲线。

本研究主要探讨一种新型的装配式防屈曲支撑的滞回性能，该装配式防屈曲支撑由一组核心单元与两组约束单元利用螺栓栓接组合而成，具有组便于制作等优点。

基于有限元分析软件ABAQUS ，模拟核心钢与面板在不同间隙下的滞回性能以及各部装和拆解过程简易、给出核心钢与面板分的应力分布，对比分析分别由理论简化计算和有限元分析得到的屈服力与屈服位移之间的差异。

最后，间隙范围的合理化建议。

［关键词］防屈曲支撑；装配式；滞回性能；ABAQUS ［中图分类号］TU 352．1文献标识码］ AFinite Element Analysis of Full Steel Assembled Buckling Restrained Brace Based on ABAQUSZhang Zhen-xing ，Ning Xiang-liang ，Liu Jun ，Li Wen-bin ，Chen Yan-bei(CSR Zhuzhou Times New Material Technology Co．，Ltd ，Zhuzhou 412007，China )Abstract ：Buckling restrained brace is able to yield in both axial tension and compression ，and having the ability to prevent buckling ，the full load-displacement hysteretic curve can be obtaine．d In this paper ，the hysteretic performance of assembled buckling restrained braces is discuss．edThis new type of buckling restrained brace is composed by a set of steel core and some constraints un，itsa nd bolts are employed herein ，which having the advantages of easy to assemble and disassemb，le manufacture．Based on the finite element analysis software ABAQUS，the stress distribution of various parts and hysteretic behavior of the buckling restrained brace with different gap between steel core and panel are simulate，d and the comparisons of the yield force and yield displacement obtained from theoretical value and finite element simulation results are also conducte．d Finally ，reasonable suggestion for the gap range is proposed．Keywords ：BRB (buckling restraied brace) ；assembled；hystereticbehavior ；ABAQUS E-mail ：zhangzhenxing2010@teg．cn1引言防屈曲支撑( Buckling Restrained Brace ，简称BRB )由主受力构件(核心钢)与外围约束单元组成，防屈曲支撑的轴力由主受力元件承受，外围约束元件则提供主受力元件侧向支撑，防止主受力元件受压屈曲，由于主受力元件在轴压力下不产生屈曲，因此可以有效发挥主受力元件的轴向强度及延展性，并充分发挥钢材的耗能容量，是一种优良的结构抗震构件 [ 1]。

一.问题描述在钢结构中，受压杆件一般在其达到极限承载力前就会丧失稳定性，所以失稳是钢结构最为突出的问题。

压杆整体失稳形式可以是弯曲、扭转和弯扭。

钢构件在轴心压力作用下，弯曲失稳是常见的失稳形式。

而影响轴心受压构件整体稳定性的主要因素为纵向残余应力、初始弯曲、荷载初偏心及端部约束条件等。

实际的轴心受压构件往往会存在上述的一种或多种缺陷，导致构件的稳定承载力降低。

本文主要针对任意轴对称的圆形钢管截面，利用ABAQUS有限元非线性分析软件，对其在轴心受压情况下进行特征值屈曲分析和静态及动态的非线性屈曲分析（考虑材料弹塑性和初始缺陷的影响）。

通过考虑材料非线性、几何非线性并引入初弯曲，得出构件发生弯曲失稳的极限荷载,并且由弯曲失稳的临界荷载得出的构件荷载位移曲线。

同时再进行非线性分析时，需要施加初始扰动，以帮助非线性分析时失稳，可以通过特征值屈曲分析得到的初始弯曲模态来定义初始缺陷；最后由可以将特征值屈曲分析得到的临界荷载作为非线性屈曲分析时所施加荷载的参考。

二.结构模型用ABAQUS中的壳单元建立轴心受压模型，采用SI国际单位制（m）。

1.构件的材料特性： E=2.0×1011N m2,μ=0.3, f y=2.35×108N m2，ρ=7800kg m3，钢管半径：60mm，厚度：3mm，长度：2.5m。

2.钢管的截面尺寸及钢管受到的约束和荷载施加的模型图如图2-1及图2-2所示。

图2-1 图2-2三.建模步骤（Buckle分析）（1）创建部件在创建part模块中命名构件的名字为gang guan，创建的模型为三维可变形壳体单元，如图3-1所示。

截面参数见图2-1，构件长度2.5m。

图3-1（2）创建材料特性及截面属性并将其赋予单元。

材料定义为弹塑性，弹性模量E=2.0×1011N m2，泊松比0.3，屈服强度2.35×108N m2，ρ=7800kg m3，材料定义如下图3-2所示。

ABAQUS 6.7 非线性屈曲分析步骤riks法，或者general statics法（加阻尼），或者动力法一共三种方法，【问】在aba中能实现非线性屈曲分析吗？在step中选定line- perturbation下的各项，其Nlgeom 都为Off ，是不是意味着是进行不了啊？【答】line-perturbation 应该是特征值屈曲分析，只能是线性的，要想进行非线性屈曲分析要引入初始缺陷ABAQUS 中非线性屈曲分析采用riks 算法实现，可以考虑材料非线性、几何非线性已经初始缺陷的影响。

其中，初始缺陷可以通过屈曲模态、振型以及一般节点位移来描述。

no.1:利用abaqus进行屈曲分析，一般有两步，首先是特征值屈曲分析，此分析为线性屈曲分析，是在小变形的情况进行的，也即上面提到过的模态，目的是得出临界荷载（一般取一阶模态的eigenvalue乘以所设定的load），且需要在inp 文件中，作如下修改*node file,global=yes*End Step此修改目的在于：在下一步后屈曲分析所需要的初始缺陷的节点输出为.fil 文件。

no.2：其次，就是所谓的后屈曲分析，此步一般定义为非线性，原因在于是在大变形情况进行的，一般采用位移控制加修正的弧长法，可以定义材料非线性，以及几何非线性，加上初始确定，所以也称为非线性屈曲分析。

此步分析，为了得到极限值，需要得出荷载位移曲线的下降段，除了采用位移控制以及弧长法设定外，需在所得到的inp文件中，嵌入no.1中的.fil节点数据。

修改如下：IMPERFECTION （缺陷），FILE=results_file （此文件名为.fil）, STEP=step特征值分析步名）,1 （模态），2e-3（模态的比例因子，此值一般取杆件的1%,壳体厚度1%）此修改一般加在boundary之后step之前。

Re:新手请教非线性屈曲中如何加初始扰动？6.2.4 Unstable collapse and postbuckling analysisRik 法用于跳越失稳问题的研究，也可以用于分支屈曲的后屈曲研究。

压杆屈曲非线性分析专业：结构工程******学号：**********压杆屈曲分析1.问题描述在钢结构中，受压杆件一般在其达到极限承载力前就会丧失稳定性，所以失稳是钢结构最为突出的问题。

压杆整体失稳形式可以是弯曲、扭转和弯扭。

钢构件在轴心压力作用下，弯曲失稳是常见的失稳形式。

影响轴心受压构件整体稳定性的主要因素为纵向残余应力、初始弯曲、荷载初偏心及端部约束条件等。

实际的轴心受压构件往往会存在上述的一种或多种缺陷，导致构件的稳定承载力降低。

本文利用abaqus 对一定截面不同长细比下的H 型钢构件进行屈曲分析，通过考虑材料非线性、几何非线性并引入初弯曲，得出构件发生弯曲失稳的极限荷载。

通过比较不同长细比下的弯曲失稳的临界荷载得出构件荷载位移曲线，并与《规范》中的构件曲线相比较。

钢构件的截面尺寸如图1-1所示。

构件的材料特性： E =2.0×1011 N m 2⁄ ,μ=0.3 , f y =3.45×108N m2⁄图1-1压杆截面尺寸（单位：m）2.长细比计算通过计算截面几何特性，截面绕y轴的回转半径为i y=0.0384m ,长细比取值及杆件长度见表1：表13.模型分析ABAQUS非线性屈曲分析的方法有riks法，general statics法（加阻尼），或者动力法。

非线性屈曲分析采用riks算法实现，可以考虑材料非线性、几何非线性已及初始缺陷的影响。

其中，初始缺陷可以通过屈曲模态、振型以及一般节点位移来描述。

利用abaqus进行屈曲分析，一般有两步，首先是特征值屈曲分析，此分析为线性屈曲分析，是在小变形的情况进行的，也即上面提到过的模态，目的是得出临界荷载（一般取一阶模态的eigenvalue乘以所设定的load）。

其次，就是后屈曲分析，此步一般定义为非线性，原因在于是在大变形情况进行的，一般采用位移控制加修正的弧长法，可以定义材料非线性，以及几何非线性，加上初始缺陷，所以也称为非线性屈曲分析。

压杆屈曲非线性分析专业：结构工程姓名：刘耀荣学号：2110150113压杆屈曲分析1.问题描述在钢结构中，受压杆件一般在其达到极限承载力前就会丧失稳定性，所以失稳是钢结构最为突出的问题。

压杆整体失稳形式可以是弯曲、扭转和弯扭。

钢构件在轴心压力作用下，弯曲失稳是常见的失稳形式。

影响轴心受压构件整体稳定性的主要因素为纵向残余应力、初始弯曲、荷载初偏心及端部约束条件等。

实际的轴心受压构件往往会存在上述的一种或多种缺陷，导致构件的稳定承载力降低。

本文利用abaqus 对一定截面不同长细比下的H 型钢构件进行屈曲分析，通过考虑材料非线性、几何非线性并引入初弯曲，得出构件发生弯曲失稳的极限荷载。

通过比较不同长细比下的弯曲失稳的临界荷载得出构件荷载位移曲线，并与《规范》中的构件曲线相比较。

钢构件的截面尺寸如图1-1所示。

构件的材料特性： E =2.0×1011 N m 2⁄ ,μ=0.3 , f y =3.45×108N m 2⁄图1-1压杆截面尺寸（单位：m）2.长细比计算通过计算截面几何特性，截面绕y轴的回转半径为i y=0.0384m ,长细比取值及杆件长度见表1：表13.模型分析ABAQUS非线性屈曲分析的方法有riks法，general statics法（加阻尼），或者动力法。

非线性屈曲分析采用riks算法实现，可以考虑材料非线性、几何非线性已及初始缺陷的影响。

其中，初始缺陷可以通过屈曲模态、振型以及一般节点位移来描述。

利用abaqus进行屈曲分析，一般有两步，首先是特征值屈曲分析，此分析为线性屈曲分析，是在小变形的情况进行的，也即上面提到过的模态，目的是得出临界荷载（一般取一阶模态的eigenvalue乘以所设定的load）。

其次，就是后屈曲分析，此步一般定义为非线性，原因在于是在大变形情况进行的，一般采用位移控制加修正的弧长法，可以定义材料非线性，以及几何非线性，加上初始缺陷，所以也称为非线性屈曲分析。

目录【摘要】 (2)【关键词】 (2)一．计算方法和模型简介及分析过程 (3)1.1计算方法 (3)1.2模型简介 (3)1.3分析过程 (5)1.3.1特征值屈曲分析 (5)1.3.2非线性屈曲分析 (10)二．计算结果分析 (13)2.1荷载-位移曲线 (13)2.2稳定系数比较 (14)【参考文献】 (16)【摘要】本文是基于Abaqus采用梁单元，对热轧工字钢在轴心受压情况下发生弯曲失稳的非线性屈曲分析。

通过考虑材料非线性、几何非线性并引入初弯曲这一几何初始缺陷，得出构件发生弯曲失稳的极限荷载。

通过保持柱子的截面不变，只改变长度，进而实现得到不同长细比的弯曲失稳的临界荷载，并得到相应的荷载位移曲线以及稳定系数，最后与规范给出的稳定系数做比较验证分析的正确性。

【关键词】特征值屈曲分析弯曲失稳非线性屈曲分析稳定系数一．计算方法和模型简介及分析过程1.1计算方法利用abaqus进行屈曲分析，一般分为两步：首先是特征值屈曲分析，此分析为线性屈曲分析，是在小变形的情况进行的，是用于预测一个理想弹性结构的理论屈曲荷载，并在inp文件里做一定的修改，此修改是在下一步后屈曲分析所需要的初始缺陷的节点输出为.fil文件，作为下一步后屈曲分析所需要的初始缺陷的数据。

其次，就是非线性屈曲分析，此步一般定义为非线性，原因在于是在大变形情况进行的，一般采用位移控制加修正的弧长法（riks法），可以定义材料非线性，几何非线性，以及加上初始缺陷。

此步分析，为了得到极限值，需要得出荷载位移曲线的下降段，除了采用位移控制以及弧长法设定外，需在所得到的inp文件中，嵌入第一步分析中的.fil节点数据。

1.2模型简介本文利用abaqus有限元分析软件时，采用了梁单元，所选取的是热轧工字型截面，截面参数见图一（单位m）：图一热轧工字钢截面参数又，其中的材料本构关系采用双线性塑性材料模型，所选材料为Q345钢材，故弹性模量为：2.1e11Pa，屈服强度取：3.45e8Pa，泊松比取0.3。