当前位置：文档之家 › 第1章 线性规划基本模型资料

第1章 线性规划基本模型资料

  • 格式：pptx
  • 大小：1.22 MB
  • 文档页数：59

下载文档原格式

  / 59

合集下载

运筹学第一章线性规划

运筹学第一章线性规划

0
X1
约束条件所组成的可行 域为空集，无可行解。
《运筹学》 第一章 线性规划
Slide 19
二、线性规划的标准形式
1、目标函数：max z c1x1 c2x2 cnxn
a x11 1 a x12 2 a x1n n b1 a x21 1 a x22 2 a x2n n b2
《运筹学》 第一章 线性规划
Slide 9
方案 根数
ABC
下料
3m 2 3 0
4m 1 0 2
合计 (m)
10
9
8
料头 (m)
0
1
2
P70 习题1－1： 设按这三种方案下料的原材料
根数分别为x1、x2、x3 。 min x1+x2+x3 S.t. 2x1+3x2>=90 x1+2x3>=60 Xi>=0
minz=2X1＋3X2＋5X3
s.t. X1＋X2－X3>=－5 －6X1＋7X2－9X3=15 ︱19X1－7X2＋5X3︱<=13
X1>=0, X2>=0
令X3=X3`－X3`` -X1－X2＋X3 `－X3`` ＋X4=5 －6X1＋7X2－9X3`＋9X3``=15 19X1－7X2＋5X3`－5X3``+X5=13 －19X1＋7X2－5X3 `＋5X3``＋X6=13 maxz=－2X1－3X2－5X3 `＋5X3`` ＋0X4+0X5+0X6 X1,X2,X3`,X3``,X4,X5,X6>=0 三、线性规划的解的概念（参考P12例1.7） 1、可行解和最优解：满足约束条件的解（X1，X2， …，Xn）T称为线性规划的可行解。而使得目标函数达到 最优值的可行解称为最优解。 2、基：（注意课本P15的定义对“基”的定义有误） 设A是约束方程组m×n维的系数矩阵，其秩为m，B是 矩阵A中m×m阶非奇异子矩阵（B的行列式│B│≠0），则 称B是线性规划问题的一个基。

线性规划基本模型

线性规划基本模型
5 x11 x21 x31 6 x12 x22 x32 2 x13 x23 x33
目标函数：总利润=总收益-原料总费用
8 x11 x12 x13 6 x21 x22 x23 3 x31 x32 x33 5 x11 x21 x31 -6 x12 x22 x32 -2 x13 x23 x33
1. 决策变量：
设xij表示机床i每个工作日加工零件j的时间（单位：工作日）i 1, 2,3; j 1, 2；
z为A,B两种零件按3: 5的比例配套的数量（套 日）
2. 约束条件： （1）工时约束
x11 x12 1
x21
x22
1
x31 x32 1
15
山西大学经济与管理学院 范建平
2020年6月18日星期四
11
山西大学经济与管理学院 范建平
2020年6月18日星期四
1、资源分配模型—小结
建立线性规划模型的一般步骤：
1.正确设立决策变量
设 xj（j=1,2,···,n）为项目j的经营数量。
2.恰当建立目标函数
n
n 项经营活动的总利润（或总产值，总收入）为 z c j x j
3. 适度构建约束方程
山西大学经济与管理学院 《运筹学》
第一章 线性规划基本模型
主讲：范建平 博士
1.1 线性规划的实用模型
2
山西大学经济与管理学院 范建平
2020年6月18日星期四
在管理中一些典型的线性规划应用
合理利用线材问题：如何在保证生产的条件下，下料最少 配料问题：在原料供应量的限制下如何获取最大利润 投资问题：从投资项目中选取方案，使投资回报最大 产品生产计划：合理利用人力、物力、财力等，使获利最大 劳动力安排：用最少的劳动力来满足工作的需要 运输问题：如何制定调运方案，使总运费最小

第1章线性规划

第1章线性规划
第1章线性规划
单击此处添加副标题内容
第1章 线性规划
1.1 原始问题 1.2 对偶问题 1.3 敏感分析 1.4 模型讨论
• 数学规划（mathematical programming）是 运筹学的一个主要分支，它是研究在一些 给定的条件下（即约束条件下），求的考 察函数（即目标函数）在某种意义下的极 值（极小或极大）。
表1.1 产品组合问题的数据表
生产单位产品所需时间
生产线
生产线每周可用时间
产品甲 产品乙
一
1
0
4
二
0
2
12
三
3
2
18
单位产品 的利润
3
5
此问题是在生产线可利用时间受到限制 的情形下寻求每周利润最大化的产品组合问 题。
在建立产品组合模型的过程中，以下问 题需要得到回答：
（1）要做出什么决策？ （2）做出的决策会有哪些条件限制？ （3）这些决策的全部评价标准是什么？
在使用单纯形法解决问题中，必须对线 性规划的一般形式进行变形，化为标准形式。
线性规划的标准形式： n
max z = c j x j
j 1
s.t.
n
j 1
aij x j
bi
(i 1,2,m)
xj 0
( j 1,2,n)
①目标函数取极大化， ②约束条件全为等式，
③约束条件右端常数项均为非负值，④变量
令非基变量x1＝x2＝0，解得x3＝4， x4＝12， x5＝18，则x＝(0,0,4,12,18)T是一个基解。因该基解 中所有变量取值为非负，满足线性规划问题的所有 约束条件，故也是基可行解。
1.2 对偶问题
例1.3（委托加工）对于例1.1的产品组合问 题，公司从交易市场上得到另一信息：某中 间商得到一笔生产与公司相同产品的合同。 但该中间商并没有生产这些产品的设备，欲 委托该公司为其加工产品。现在的问题是公 司应该让中间商至少付出多少代价，才能放 弃这两种新产品的生产，为中间商委托生产？

线性规划（1）

线性规划（1）

第一章线性规划一、线性规划的一般模型1、线性规划问题的三个要素•决策变量▪决策问题待定的量值称为决策变量。

▪决策变量的取值要求非负。

•约束条件▪任何问题都是限定在一定的条件下求解，把各种限制条件表示为一组等式或不等式，称之为约束条件。

▪约束条件是决策方案可行的保障。

▪LP的约束条件，都是决策变量的线性函数。

•目标函数▪衡量决策方案优劣的准则，如时间最省、利润最大、成本最低。

▪目标函数是决策变量的线性函数。

▪有的目标要实现极大，有的则要求极小。

2、线性规划模型的构建•例1. 生产计划问题某厂生产甲乙两种产品，各自的零部件分别在A、B车间生产，最后都需在C车间装配，相关数据如表所示：建立模型(1)决策变量。

要决策的问题是甲、乙两种产品的产量，因此有两个决策变量：设x1为甲产品产量，x2为乙产品产量。

(2)约束条件。

生产这两种产品受到现有生产能力的制约，用量不能突破。

▪生产单位甲产品的零部件需耗用A车间的生产能力1工时，▪生产单位乙产品不需耗用A车间的生产能力，▪A车间的能力总量为8工时，则A车间能力约束条件表述为x1≤8▪同理，B和C车间能力约束条件为2x2≤123x1 +4 x2≤36(3)目标函数。

目标是利润最大化，用Z表示利润，则maxZ=3x1 +5 x2(4)非负约束。

甲乙产品的产量不应是负数，否则没有实际意义，这个要求表述为x1≥0，x2≥0•综上所述，该问题的数学模型表示为maxZ=3x1 +5 x2x1≤82x2≤123x1 +4 x2 ≤36x1 ≥0, x2 ≥0例2. 运输问题某名牌饮料在国内有三个生产厂，分布在城市A1、A2、A3,其一级承销商有4个，分布在城市B1、B2、B3、B4，已知各厂的产量、各承销商的销售量及从A i到B j的每吨饮料运费为C ij，为发挥集团优势，公司要统一筹划运销问题，求运费最小的调运方案。

(1)(2)目标函数。

运费最小的目标函数为minZ=6x11+3x12+2x13+5x14+7x21+5x22+8x23+4x24+3x31+2x32+9x33+7x34(3)约束条件。

运筹学第1章-线性规划

运筹学第1章-线性规划
凸集的数学定义:设K为n维欧氏空间的一个点集，若K中任意两个 点X1和X2连线上的所有点都属于K，即“X =αX1+(1-α) X2 ∈ K(0≤a ≤ 1)”，则称K为凸集。设X(x1，x2，…，xn)，X1(u1， u2，...，un)，X2(v1，v2，…，vn)，如图1一5所示，“X =αX1+(1α) X2 ∈ K(0≤a ≤ 1)”的证明思路如下:
下一页 返回
图解法步骤：
（1）建立坐标系； （2）将约束条件在图上表示； （3）确立满足约束条件的解的范围； （4）绘制出目标函数的图形 （5）确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。 生产计划问题是典型的已知资源求利润最大化的问题，对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产 过程的损失忽略不计;③市场需求无限制，即假设生产的产品全部 卖出。
下一页 返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容 器，应如何裁剪，使做成的窗口的容积为最 大？
解：设 x1, x2分别表示从A,B两处采购的原油量（单
位：吨），则所有的采购方案的最优方案为：
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式，其中模型(1-7)较为常用。

第1节线性规划的数学模型

第1节线性规划的数学模型

第1节线性规划的数学模型线性规划(linear programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。

线性规划属于规划论中的静态规划,即单周期决策,是一种重要的优化工具,能够解决有限资源的最佳分配问题。

一、线性规划的三个要素决策变量(decision variable)是决策问题待定的量值。

决策变量应当完全描述出此问题应当作出的决策。

约束条件(constraint conditions)是指决策变量取值时受到的各种资源条件的限制。

目标函数(objective function)是指决策变量的函数表达式,表示决策者希望实现的目标,它是衡量决策优劣的准则。

线性规划的决策目标是单一的;同时,目标函数也是决策变量的线性函数。

目标函数中变量的系数称为价值系数,反映出每个决策变量单位取值对目标的贡献程度。

二、线性规划模型线性规划模型是目标函数和约束条件都是决策变量的线性函数的最优化数学模型。

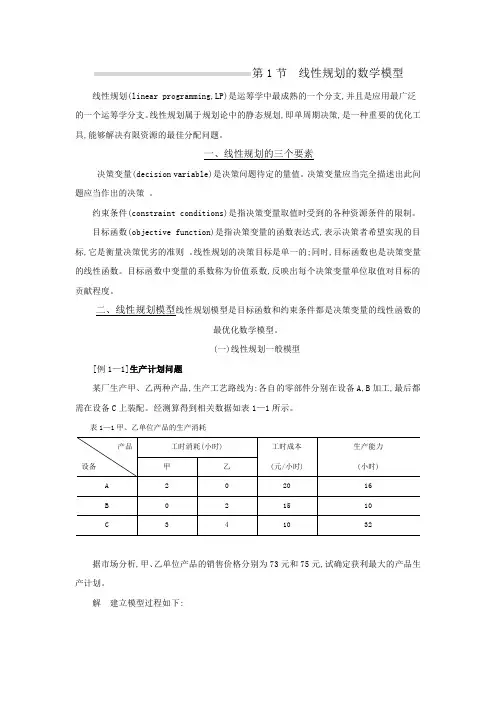
(一)线性规划一般模型[例1—1]生产计划问题某厂生产甲、乙两种产品,生产工艺路线为:各自的零部件分别在设备A,B加工,最后都需在设备C上装配。

经测算得到相关数据如表1—1所示。

表1—1甲、乙单位产品的生产消耗据市场分析,甲、乙单位产品的销售价格分别为73元和75元,试确定获利最大的产品生产计划。

解建立模型过程如下:(1)决策变量:此问题是要确定甲、乙两种产品的产量,这些待定的量值就称为决策变量。

设x1=生产甲产品的产量x2=生产乙产品的产量(2)约束条件:生产产品受到现有设备能力的制约,能力需求量不能突破有效供给量。

如果只考虑目标函数,则随着决策变量x1和x2值的增大,目标函数的值也会很快地增大,但是决策变量x1和x2的值受到三种设备加工能力的限制。

约束条件1:生产单位甲产品需耗2个小时的设备A,设备A加工能力不能超过16个小时,则设备A的约束条件表达为:2x1≤16约束条件2:设备B的加工能力约束条件表达为:2x2≤10约束条件3:设备C的装配能力也有限,其约束条件表达式为:3x1+4x2≤32(3)目标函数:目标是企业利润最大化,用Z表示利润。

第一章 线性规划

第一章 线性规划

常数项bi全为非负。变量xj值非负。
m axz c j x j
j 1
n
s.t.
aij x j bi i 1, , m j 1 x 0 j 1, , n j
n
一般形变成标准形的方法
1、目标函数：求极大值
两边乘以-1，最大变最小。
例
max z x1 2 x2 3x3 3x3 0 x4 0 x5
2 x x x x x 9 1 2 3 3 4 3x x 2 x 2 x x5 4 1 2 3 3 s.t. 3x1 2 x 2 3x3 3x3 6 x1 , x 2 , x3 , x3 , x 4 , x5 0
b
min z 3x1 5 x 2 x3 x1 2 x 2 x3 6 2 x x 3x 16 1 2 3 s.t. x1 x 2 5 x3 10 x1 , x 2 0, x3无约束
1-4线性规划问题的解



1、可行解 2、最优解



一般线性规划的数学模型 线性规划的标准形式 图解法 单纯形法
§ 1、一般线性规划问题的数学模型
1-1 数学模型
例1 用一块边长为a的正 方形铁皮做一个容器， 应如何裁剪，使做成 的容器的容积最大
x
a
v a 2x x，x 0, a 0
2
例2 常山机器厂生产Ⅰ、Ⅱ两种产品。这两 种产品都要分别在A、B、C三种不同设备 上加工.按工艺资料规定，生产每件产品Ⅰ 需占用各设备分别为2h、4h、0h，生产 每件产品Ⅱ，需占用各设备分别为2h、0h、 5h.已知各设备计划期内用于生产这两种 产品的能力分别为12h、16h、15h，又知 每生产一件产品Ⅰ企业能获利2元利润， 每生产一件产品Ⅱ企业能获利3元，问该 企业应安排生产两种产品各多少件，使得 总利润计划期内的产量

第1章_线性规划

第1章_线性规划

2x1 3x2 5x3 300
x1 0，x2 0，x3 0
产品 甲 乙 丙 资源
设备 A 3 1 2 设备 B 2 2 4 材料 C 4 5 1 材料 D 2 3 5 利润（元/件）40 30 50
现有 资源
200 200 360 300
最优解X=(50,30,10)；Z=3400
第1章 线性规划
10
§1.1 线性规划的数学模型 Mathematical Model of LP
小结
1、定义？所谓线性规划就是求一个线性函数在一组线性约 束条件下极值的问题。
2、构成？线性规划的数学模型由决策变量 （Decision variables）、目标函数（Objective function）及约束条 件（Constraints）构成。称为三个要素。
例1.10
max Z=x1+2x2
x1 3x2 6 3x1x1x2x246 x1 0、x2 0
无界解(无最优解)
4
6
x1
第1章 线性规划
20
x2
50 40
30 20
10
§1.2 图解法 The Graphical Method
例1.11
max Z=10x1+4x2
2.线性规划数学模型的组成及其特征 3.线性规划数学模型的一般表达式。
作业：教材P31 T 2，3，4，5，6
下一节：图解法
2020-03-11
第1章 线性规划
14
Chapter1 线性规划
§1.2 图解法
Graphical Method
一、图解法的含义 二、图解法的步骤 三、图解法的几种可能结果 四、图解法的几何意义

第1章 线性规划模型

第1章 线性规划模型
• 区域污染治理的约束——8 即满足环保要求排放工业污水
（区域内河流中任何点检测都7应符合环保标准）。 • 区域污染治理的目标——总治理成本最少。 6
4
1
5
3
管理运筹学
21
河流污染治理规划问题
.
• 模型描述：
• 设第i个化工厂应处理的工业污水量为Xi万9m3，则根据问
题描述的情况以化2工厂1、2、… 、9 加以分析则可得
0.3716X1+0.5125X2+…+0.5020X14=0.4500∑Xj
管理运筹学
• 3、计算结果
.
• 使用单纯形算法（或MATLAB软件），极易求出此模 型的最优解：
•
X*=（X*1，X*2，…，X*14），它们是：
•
X*1 =31.121
X*2 = 7
X*3 =17
•
X*4 =23
X*5 = 3
出矿点，年产量及各矿点矿石的平 均品位（含铁量的百分比）均为已 知（见表1）。 表1 矿点出矿石量及矿石平均品位表
管理运筹学
矿点号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
出矿石量 (万吨)
平均铁品位（%）
70
37.16
7
51.25
17
40.00
23
47.00
3
42.00
9.5
. 此项目所要求的“效益最佳”。作为决策准则有一
定的模糊性。由于配矿后混合矿石将作为后面工序的 原料而产生利润，故在初始阶段，可将目标函数选作 配矿总量，并追求其极大化。
于是，可得出基本（LP）模型如下： （LP） Max Z=∑Xj
s.t. 0≤ X1 ≤70 0≤ X2 ≤ 7 …… 0≤ X14 ≤ 7.2

第1章 线性规划模型

第1章 线性规划模型

第1章线性规划Chapter 1 Linear Programming本章内容提要线性规划是运筹学的重要内容。

本章介绍线性规划数学模型、线性规划的基本概念以及求解线性规划数学模型的专门软件——Lingo。

学习本章要求掌握以下内容：⏹线性规划模型的结构。

包括：决策变量，目标函数，约束条件。

⏹线性规划的标准形式，非标准形式转化为标准形式⏹线性规划的基本概念。

包括：约束直线，可行域，可行解，凸集，极点，目标函数等值线，最优解⏹线性规划的软件求解。

包括：lingo软件简介，lingo软件求解规划问题§1.1 线性规划1.1.1 线性规划线性规划(LinearProgramming，LP)是运筹学中最重要的一种系统优化方法。

它的理论和算法已十分成熟，应用领域十分广泛，通常研究资源的最优利用、设备最佳运行等问题。

例如，当任务或目标确定后，如何统筹兼顾，合理安排，用最少的资源(如资金、设备、原材料、人工、时间等)去完成确定的任务或目标；企业在一定的资源条件限制下，如何组织安排生产获得最好的经济效益(如产品量最多、利润最大)。

还包括生产计划，物资调运，资源优化配置，物料配方，任务分配，经济规划等问题。

随着计算机硬件和软件技术的发展，目前用微型计算机就可以求解大规模的规划问题。

Lingo软件就是其中的代表软件之一。

在本章中，我们将介绍线性规划的基本概念，线性规划在经济分析中的应用。

§1.2 线性规划问题线性规划问题由目标函数、约束条件以及变量的非负约束三部分组成。

根据实际问题的条件和要求，可以建立线性规划问题数学模型。

下面列举五种最常见的线性规划问题的类型。

1.2.1 生产计划问题例1.1某工厂拥有A、B、C三种类型的设备，生产甲、乙、丙、丁四种产品。

每件产品在生产中需要占用的设备机时数，每件产品可以获得的利润以及三种设备可利用的时数如下表所示：表1-1用线性规划制订使总利润最大的生产计划。

设变量x i为第i种产品的生产件数（i＝1，2，3，4），目标函数z为相应的生产计划可以获得的总利润。

管理运筹学讲义 第1 章 线性规划

管理运筹学讲义 第1 章 线性规划

(3)约束条件：产量之和等于销量之和,故要满足：
供应平衡条件
x11+x12+x13+x14=50 x21+x22+x23+x24=20 x31+x32+x33+x34 =30
x11+x21+x31=20 x12+x22+x32=30 x13+x23+x33=10 x14+x24+x34=40
xij≥0 (i=1,2,3；j=1,2,3,4)
决策变量对目标函数和约束方程的影响是独立于其他变量的。 目标函数值是决策变量对目标函数贡献的总和。
（4）连续性假定
决策变量取值连续。
（5）确定性假定
所有参数都是确定的，不包含随机因素。
9 OR:SM
第一节 线性规划的一般模型
三、线性规划模型的特征
2、一般数学模型
• 用一组非负决策变量表示的一个决策问题； • 存在一组等式或不等式的线性约束条件； • 有一个希望达到的目标，可表示成决策变量的极值线性函数。
4 2 6
8
O
2
4
6
8
x1
OR:SM
23
• 当决策变量是三维的，如何求解？ • 当维数再高时，又如何求解？
24
OR:SM
第二节 线性规划的一般模型
一、线性规划的标准型式
1、标准型表达方式
1）代数式
max Z c j x j
j 1 n
2）向量式
max Z CX
i 1,2,, m j 1,2,, n
20
OR:SM
第一节 线性规划的一般模型

01线性规划数学建模

01线性规划数学建模

01-线性规划(数学建模) 线性规划是一种数学建模技术，用于解决一类特定的优化问题。

这些问题通常涉及到在一组线性约束条件下最大化或最小化一个线性目标函数。

线性规划的应用广泛，包括诸如生产计划、货物运输、资源分配等问题。

线性规划的基本模型由以下三个要素组成：1.决策变量：这是我们希望优化的变量。

它们通常是连续的实数变量，可以在问题中自由设定其范围。

2.目标函数：这是我们希望最大化或最小化的函数。

目标函数通常是决策变量的线性函数。

3.约束条件：这些是限制决策变量选择的条件。

它们通常是由决策变量的线性不等式或等式表示。

线性规划问题的一般形式可以表示为：最大化（或最小化）目标函数: c^T x在满足以下条件的情况下：Ax = bx >= lbx <= ub其中，c是目标函数的系数向量，x是决策变量向量，A是约束条件的系数矩阵，b是约束条件的右侧常数向量，lb和ub分别是决策变量的下界和上界。

线性规划问题的求解方法有很多种，其中最常用的方法是使用单纯形法。

单纯形法的基本思想是通过在约束条件下不断迭代，寻找最优解。

在每次迭代中，我们根据目标函数的系数和约束条件，计算出每个约束条件的"优势"，然后选择具有最大优势的约束条件进行扩展，直到找到最优解或确定无解。

线性规划问题在现实世界中的应用非常广泛。

例如，我们可以使用线性规划来安排生产计划，使得总成本最低。

我们也可以使用线性规划来分配资源，使得某种资源的需求总和不超过供应总和。

下面是一个具体的例子：假设我们有一个公司，生产三种产品：A、B和C。

每种产品都有各自的生产成本（单位成本），以及各自的预期销售量（单位售价）。

我们希望确定每种产品的生产量，以使得总生产成本最低，同时总销售收入最高。

这个问题可以通过一个线性规划来解决。

我们可以将生产量作为决策变量，将总生产成本和总销售收入分别作为目标函数和约束条件。

通过求解这个线性规划问题，我们可以得到最优的生产计划。

第一章 线性规划的模型(3)——第一章线性规划资料文档

第一章 线性规划的模型(3)——第一章线性规划资料文档
-9-
4. 线性规划模型的标准形式
（1）变量：所有变量均xj≥0 （2）目标函数：为取“max”形式 （3）约束条件：全部约束方程均为“=”连接 （4）约束右端项：bi≥ 0 非标准形式情况有 变量： xj≤0 ,或xj无约束 目标函数：min 约束条件：“≤”或“≥” 约束右端项： bi<0
-10-
-2-
2.线性规划模型的一般要求
（1）变量：取值为连续的、可控的量； （2）目标函数：线性表达式； （3）约束条件：线性的等式或者不等式。
-3-
线性规划问题的一般形式
max z=c1x1+c2x2+………+cnxn
s.t. a11x1+a12x2+………+a1nxn≤(=, ≥)b1
a21x1+a22x2+………+a2nxn≤b2 ………… ………………… am1x1+am2x2+………+amnxn≤bm
如 x1+x23 x1+x2+ x3=3
当 “”时，引进剩余（surplus） 变量 - xs；
如 x1+2x2 4 x1+2x2－x4=4
（4）约束右端项：当 bi < 0，则不等式 两端同乘（- 1）
zmi
n
z
x z = -
z z
max
-11-
例：将下述LP模型标准化：
obj. Min z=2x1- x2+3x3
st.- 2x2+ x3 = 4 2x1- x2 - 3x3 5 x1 0, x2无符号限制, 解：设 zx3=- 0z, x2= x2 - x2 , x2 0 , x2 0, x3= - x3 , x3 0 ，x40, x50, 则有

第一章---线性规划--第一节

第一章---线性规划--第一节

线性规划问题及数学模型
例1 生产计划问题
Ⅰ Ⅱ 每天可用能力
设备A (h) 0 5
15
设备B (h) 6 2
24
调试工序 (h) 1 1
5
利润 (元)
21
两种家电各生产多少, 可获最大利润?
线性规划问题及数学模型
解:设两种家电产量分别为变量x1 ， x2
max Z= 2x1 +x2 5x2 15
约束条件：
从仓库运出总量不超过可用总量，运入零售点的数
量不低于需求量。
由于总供给量等于总需求量，所以都是等号。即
x x x x a ;i 1,2
i1
i2
i3
i4
i
x x b ; j 1,2,3,4
1j
2j
j
蕴含约束：数量非负 x 0;i 1,2, j 1,2,3,4 ij
非标准形转化为标准形
练习一： 将minZ= 0.15x1 + 0.25x2 + 0.1x3
50x1 + 150x2 + 90 x3 175
100x2 - 50x3 -30
70x1+ 10 x2
200
30x1 + 80x2 + 200 x3 100
xi 0 (i =1,2)
一：标准形为 maxZ=- 0.15x1- 0.25x2 - 0.1x3 + 0.1x4
50x1 + 150x2 + 90 x3 -90 x4+ x5 = 175 -100x2 +50x3 - 50x4-x6=30
70x1+ 10 x2 – x7= 200 30x1 + 80x2 + 200 x3 – 200 x4 – x8= 100 xi 0 (i =1,……,8)

第一章 线性规划模型

第一章 线性规划模型

第一章 线性规划模型一、 线性规划模型的建立例1某工厂A 有生产甲，乙二种产品的能力，且生产一吨甲产品需要3个工日和0.35吨小麦。

生产一吨乙产品需要4个工日和0.25吨小麦。

该厂仅有工人12人，一个月只能出300个工日，小麦一个月只能进21吨，并且还知生产一吨甲产品可盈利80（百元），生产一吨乙产品可盈利90（百元）。

那么，工厂A 在一月中应如何安排这两种产品的生产，使之获得最大的利润？由以上条件可列表如下：问题一的数学模型:设1x ,2x 分别表示一月中生产甲，乙二种产品的数量，称之为决策变量。

所得利润为z ，问题一的目标是使得总利润函数219080x x z +=有最大值。

工日的约束为：3004321≤+x x原料小麦的约束为：2125035021≤+x .x .于是问题一可归结为求目标函数在约束条件下的最大值问题，显然目标函数和约束条件都是决策变量的线性函数，即可建立以下线性规划模型2125035030043908021212121≥≤+≤++=x ,x x .x .x x .t .s x x z max (1.1)1.1 线性规划模型的一般形式()()n,,j x m ,,i b ,x a.t .s x cz minmax j inj j ijni ii2102111=≥==≥≤=∑∑== (1.2)矩阵形式()()0≥=≥≤=X b ,AX .t .s Xc z min max T(1.3) 其中()Tn x ,x ,x X 21=为决策向量，()Tn c c c c ,,21=为目标函数的系数向量，()Tm b ,b ,b b 21=为常数向量，()nm ija A ⨯=为系数矩阵。

1.2 线性规划模型的标准形≥==X b AX .t .s Xc z min T(1.4) 对于例1可取：()90,80=Tc，⎪⎪⎭⎫ ⎝⎛=25035043..A ，⎪⎪⎭⎫ ⎝⎛=21300b 。

01- 线性规划基本模型

01- 线性规划基本模型

a12 a22 am 2

a1n a2 n am 2
A为约束方程组（约束条件）的系数矩阵。
三、线性规划问题的标准形式
1、LP标准型的概念 （1）什麽是LP的标准型？ （2）LP标准型的特点 目标函数约定是极大化Max(或极小化 Min); 约束条件均用等式表示; 决策变量限于取非负值; 右端常数均为非负值 ;
第三节（1） 线性规划问题解的 性质
一、线性规划问题解的概念
（一）可行解、最优解
1.可行解：满足所有约束 条件（包括非负条件） 的解。 可行解的集合称为可行 集，或可行域。 2.最优解：使目标函数达 到极值的解（理应属于 可行解集）。
解：上述问题中令： ⑴ ⑵ ⑶
Z Z
max 得到 Z Z
x1 x1
x3 x3 x3
x4 ( x4 0)
⑷在第一个约束条件的左端加入一个松弛变量
⑸在第二个约束条件是左端减去一个剩余变量 ⑹将第三个约束条件两端同乘“-1”
x5 ( x5 0)
该问题的标准形式为：
Max z c j x j
j 1
n
2．右端项bi<0
只需将等式或不等式两端同乘(-1)，则等式右端项必大于零。 3．约束条件为不等式： 当约束条件为“≤”时，需将约束条件左端加松弛变量； 当约束条件为“≥”时，需将约束条件左端减去剩余变量。 4．取值无约束的变量 可令x＝x’-x”，其中x’≥0，x”≥0 5．对x≤0的情况 令x’＝-x，显然x’≥0
假定线性规划问题中含有n个决策变量xj(j＝1，…，n)，在目标函数中xj的系 数为cj(cj通常称为价值系数)；有m种资源的限制，每种资源数量用bi(i=1,...m)表 示；用aij表示变量xj取值为1个单位时所消耗或含有的第i种资源的数量，通常称aij 为技术系数或消耗系数。

01线性规划模型

01线性规划模型
1.6 算法复杂性简介
2
莫 莉
一、线性规划模型 1.1 线性规划模型
一、 线性规划模型
1、线性规划问题
在生产管理和经营活动中经常需要解决：如 何合理利用有限的资源，以得到最大的效益。
莫 莉
3
一、线性规划模型
例1 某工厂可生产甲、乙两种产品，需消耗煤、 电、油三种资源。现将有关数据列表如下：
试拟订使总收入最大的生产计划方案。
1）典范型转化成标准型 加入剩余（松弛）变量。 2）标准型转化成典范型 等式可用两不等式表示。
3）一般型转化为典范型和标准型
无限制的变量可用两非负变量的差表示，或由某 一等式解出该无限制的变量。
2品，已知生产单位产 品所需设备台时及A、B两种原材料的消耗如下表：
（4）右端项 bi 0 ，仅需等式或不等式两端同乘（-1）；
令x ' x 即可。 （5）对 x 0，
30
莫 莉
8
莫 莉
第一章 线性规划
9
莫 莉
一、线性规划模型
例3 污水处理问题。环保要求河水含污低于2‰， 河水可自身净化20%。问：化工厂1、2每天各处理 多少污水总费用最少？
10
莫 莉
一、线性规划模型
建模型之前的分析和计算，设：
化工厂1每天处理的污水量为x1万立方米；
化工厂2每天处理的污水量为x2万立方米。
其中X称为决策变量向量，C 称为价格系数向量，
A称为技术系数矩阵，b 称为资源限制向量。
？思考：为什么将A称为技术系数矩阵？
20
莫 莉
二、型式相互转换
3、一般线性规划转化为标准型线性规划
(1) 若要求目标函数实现最小化，即min z =CX，则只需 将目标函数最小化变换求目标函数最大化，即令z′= −z，于是得到max z′= −CX。 (2) 约束条件为不等式。分两种情况讨论： 若约束条件为“≤”型不等式，则可在不等式左端加 入非负松弛变量，把原“≤”型不等式变为等式约束； 莫 莉
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

所需人数 60 70 60 50 20 30
设司机和乘务人员分别在各时间段一开始时上班，并 连续工作八小时，问该公交线路怎样安排司机和乘务人员， 既能满足工作需要，又配备最少司机和乘务人员?
2020/9/9
管 理 运9 筹 学
解：设 xi 表示第i班次时开始上班的司机和乘务人员
数, 这样我们建立如下的数学模型。
2020/9/9
管 理 运6 筹 学
资源分配模型
例1-1. 某工厂要安排甲、乙两种产品分别在车间A、B生 产，然后都在C车间装配。生产数据如下表：
车间
产品
A B C 单位产品获利(元)
单耗(工时/件)
甲
乙
1
0
0
2
2
3
300 200
最大生产能力 （工时/周）
6 8 18
问题：工厂应分别生产多少单位甲、乙产品？
2020/9/9
管 理 1运2 筹 学
甲 乙 丙 资源限制 铸造工时(小时/件) 5 10 7 8000 机加工工时(小时/件) 6 4 8 12000 装配工时(小时/件) 3 2 2 10000 自产铸件成本(元/件) 3 5 4 外协铸件成本(元/件) 5 6 -机加工成本(元/件) 2 1 3 装配成本(元/件) 3 2 2 产品售价(元/件) 23 18 16
资源限制 300 台时 400 千克 250 千克
问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利 最多？
2020/9/9
管 理 运4 筹 学
线性规划模型：
max f = 50 x1 + 100 x2
s.t.
x1 + x2 ≤ 300
2 x1 + x2 ≤ 400
x2 ≤ 250
x1 , x2 ≥ 0
6x1 + 4x2 + 8x3 + 6x4 + 4x5 ≤ 12000
3x1 + 2x2 + 2x3 + 3x4 + 2x5 ≤ 10000
x1,x2,x3,x4,x5 ≥ 0
2020/9/9
管 理 1运4 筹 学
例1.3 永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品，均要经过A、B 两道工序加工。假设有两种规格的设备A1、A2能完成 A 工 序；有三种规格的设备B1、B2、B3能完成 B 工序。Ⅰ可在A、 B的任何规格的设备上加工；Ⅱ 可在任意规格的A设备上加 工，但对B工序，只能在B1设备上加工；Ⅲ只能在A2与B2设 备上加工；数据如下表。问：为使该厂获得最大利润，应 如何制定产品加工方案？
资源分配模型 产品配套模型 下料模型 配料模型
2020/9/9
管 理 运3 筹 学
例1.0 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产，
已知生产单位产品所需的设备台时及A、B两种原材料的消
耗、资源的限制，如下表：
设备 原料 A 原料 B 单位产品获利
Ⅰ 1 2 0 50 元
Ⅱ 1 1 1 100 元
2020/9/9
管 理 1运3 筹 学
解：设 x1,x2,x3 分别为三道工序都由本公司加工的甲、乙、 丙三种产品的件数，x4,x5 分别为由外协铸造再由本公司
加工和装配的甲、乙两种产品的件数。
max 15x1 + 10x2 + 7x3 + 13x4 + 9x5
s.t.
5x1 + 10x2 + 7x3 ≤ 8000
2020/9/9
管 理 1运5 筹 学
设备
A1 A2 B1 B2 B3 原料（元/件） 售价（元/件）
产品单件工时
Ⅰ
Ⅱ
Ⅲ
5
10
2020/9/9
管 理 运7 筹 学
解：设 变量（单位）
max z 3x1 2x2
x1
6
s.t.
2
x1
2x2 3x2
8 18
x1, x2 0
ቤተ መጻሕፍቲ ባይዱ
2020/9/9
管 理 运8 筹 学
例1.1 某昼夜服务的公交线路每天各时间段内所需司机 和乘务人员数如下：
班次 1 2 3 4 5 6
时间 6：00 —— 10：00 10：00 —— 14：00 14：00 —— 18：00 18：00 —— 22：00 22：00 —— 2：00 2：00 —— 6：00
另解：设 xi ( i = 1,2,…,6)表示第1班次至第6班次开始
休息的人数,这样我们建立如下的数学模型。
min x1 + x2 + x3 + x4 + x5 + x6 s.t. x2 + x3 ≥ 60
x3 + x4 ≥ 70 x4 + x5 ≥ 60 x5 + x6 ≥ 50 x6 + x1 ≥ 20 x1 + x2 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0
min x1 + x2 + x3 + x4 + x5 + x6 s.t. x1 + x6 ≥ 60
x1 + x2 ≥ 70 x2 + x3 ≥ 60 x3 + x4 ≥ 50 x4 + x5 ≥ 20 x5 + x6 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0
2020/9/9
管 理 1运0 筹 学
管理运筹学
——模型与方法
赵明霞 山西大学经济与管理学院
管理运筹学
第1章 线性规划基本模型
1.1 线性规划的实用模型 1.2 线性规划的一般模型 1.3 线性规划的图解法 1.4 标准形线性规划的解
2020/9/9
管 理 运2 筹 学
1.1 线性规划的实用模型
线性规划(LP, Linear Programming)的组成： •目标函数 opt（optimize） max z (f) 或 min z(f) •约束条件 s.t. (subject to) 满足于 •决策变量 用符号来表示可控制的因素
2020/9/9
管 理 1运1 筹 学
例1.2 某公司面临一个是外包协作还是自行生产的问题。 该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工 和装配三个车间。甲、乙两种产品的铸件可以外包协作，亦 可以自行生产，但产品丙必须本厂铸造才能保证质量。数据 如表。问：公司为了获得最大利润，甲、乙、丙三种产品各 生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由 外包协作各应多少件？
2020/9/9
管 理 运5 筹 学
线性规划建模过程
1.理解要解决的问题，明确目标和条件；
2.定义决策变量（ x1 ，x2 ，… ，xn ），每一组值表示一个方 案；
3.用决策变量的线性函数形式写出目标函数，确定最大化或最 小化目标；
4.用一组决策变量的等式或不等式表示解决问题过程中必须遵 循的约束条件