数学：新人教A版必修五 1.2应用举例(同步练习)

第一章 1.2 应用举例第二课时 高度、角度问题课时分层训练‖层级一‖|学业水平达标|1.如图，在湖面上高为10 m 处测得天空中一朵云的仰角为30°，测得湖中之影的俯角为45°，则云距湖面的高度为(精确到0.1 m)( )A ．2.7 mB ．17.3 mC ．37.3 mD ．373 m解析：选C 根据题图，由题意知CM ＝DM . ∴CM －10tan 30°＝CM ＋10tan 45°，∴CM ＝tan 45°＋tan 30°tan 45°－tan 30°×10≈37.3(m)，故选C. 2．渡轮以15 km/h 的速度沿与水流方向成120°角的方向行驶，水流速度为4 km/h ，则渡轮实际航行的速度为(精确到0.1 km/h)( )A ．14.5 km/hB ．15.6 km/hC ．13.5 km/hD ．11.3 km/h解析：选C 由物理学知识，画出示意图如图．AB ＝15，AD＝4，∠BAD ＝120°.在▱ABCD 中，D ＝60°.在△ADC 中，由余弦定理，得AC ＝AD 2＋CD 2－2AD ·CD cos D ＝16＋225－4×15＝181≈13.5(km/h)．故选C.3．某人在C 点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10米到D ，测得塔顶A 的仰角为30°，则塔高为( )A ．15米B ．5米C ．10米D ．12米解析：选C如图，设塔高为h ，在Rt △AOC 中，∠ACO ＝45°，则OC ＝OA ＝h .在Rt △AOD 中，∠ADO ＝30°，则OD ＝3h ， 在△OCD 中，∠OCD ＝120°，CD ＝10，由余弦定理，得OD 2＝OC 2＋CD 2－2OC ·CD cos ∠OCD ，即(3h )2＝h 2＋102－2h ×10×cos 120°，∴h 2－5h －50＝0，解得h ＝10或h ＝－5(舍去)．4．甲船在B 岛的正南A 处，AB ＝10 km ，甲船以4 km/h 的速度向正北航行，同时，乙船自B 岛出发以6 km/h 的速度向北偏东60°的方向驶去，当甲、乙两船相距最近时，它们航行的时间是( )A.1507 minB ．157 hC ．21.5 minD ．2.15 h 解析：选A 设经过x 小时时距离为s ，则在△BPQ 中，由余弦定理知PQ 2＝B P 2＋BQ 2－2BP ·BQ ·cos 120°，即s 2＝(10－4x )2＋(6x )2－2(10－4x )·6x ·⎝ ⎛⎭⎪⎫－12＝28x 2－20x ＋100，∴当x ＝514 h 时，s 2最小，即当航行时间为514 h ＝1507 min 时，s 最小．5.如图所示，在地面上共线的三点A ，B ，C 处测得一建筑物的仰角分别为30°，45°，60°，且AB ＝BC ＝60 m ，则建筑物的高度为( )A ．15 6 mB ．20 6 mC ．25 6 mD ．30 6 m解析：选D 设建筑物的高度为h ，由题图知，P A ＝2h ，PB ＝2h ，PC ＝233h ，∴在△PBA 和△PBC 中，分别由余弦定理，得cos ∠PBA ＝602＋2h 2－4h 22×60×2h，① cos ∠PBC ＝602＋2h 2－43h 22×60×2h.② ∵∠PBA ＋∠PBC ＝180°，∴cos ∠PBA ＋cos ∠PBC ＝0.③由①②③，解得h ＝306或h ＝－306(舍去)，即建筑物的高度为30 6 m.6．学校里有一棵树，甲同学在A 地测得树尖的仰角为45°，乙同学在B 地测得树尖的仰角为30°，量得AB ＝AC ＝10 m 树根部为C (A 、B 、C 在同一水平面上)，则∠ACB ＝ .解析：如图，AC ＝10，∠DAC ＝45°，∴DC ＝10.∵∠DBC ＝30°，∴BC ＝103， cos ∠ACB ＝102＋(103)2－1022×10×103＝32， ∴∠ACB ＝30°.答案：30°7.如图，为测量山高MN ，选择A 和另一座山的山顶C为测量观测点．从A 点测得M 点的仰角∠MAN ＝60°，C 点的仰角∠CAB ＝45°以及∠MAC ＝75°；从C 点测得∠MCA＝60°.已知山高BC ＝100 m ，则山高MN ＝ m.解析：根据题图所示，AC ＝100 2.在△MAC 中，∠CMA ＝180°－75°－60°＝45°.由正弦定理得AC sin 45°＝AM sin 60°⇒AM ＝100 3.在△AMN 中，MN AM ＝sin 60°，∴MN ＝1003×32＝150(m)．答案：1508．海上一观测站测得方位角240°的方向上有一艘停止航行待修的商船，在商船的正东方有一艘海盗船正以每小时90海里的速度向它靠近，此时海盗船距观测站107海里，20分钟后测得海盗船距观测站20海里，再过 分钟，海盗船到达商船．解析：如图，设观测站、商船、分别位于A，B处，开始时，海盗船位于C处，20分钟后，海盗船到达D处．在△ADC中，AC＝107，AD＝20，CD＝30，由余弦定理，得cos∠ADC＝AD2＋CD2－AC2 2AD·CD＝400＋900－7002×20×30＝12，则∠ADC＝60°.在△ABD中，由已知，得∠ABD＝30°，∠BAD＝60°－30°＝30°，所以BD＝AD＝20，2090×60＝403(分)．答案：40 39.在社会实践中，小明观察一棵桃树．他在点A处发现桃树顶端点C的仰角大小为45°，往正前方走4米后，在点B处发现桃树顶端点C的仰角大小为75°.(1)求BC的长；(2)若小明身高为1.70米，求这棵桃树顶端点C离地面的高度(精确到0.01米，其中3≈1.732)．解：(1)∠CAB＝45°，∠DBC＝75°，则∠ACB＝75°－45°＝30°，AB＝4，由正弦定理得BCsin 45°＝4sin 30°，解得BC＝42(米)，即BC的长为4 2 米．(2)在△CBD中，∠CDB＝90°，BC＝42，∴DC＝42sin 75°.∵sin 75°＝sin(45°＋30°)＝sin 45°cos 30°＋cos 45°sin 30°＝6＋24，则DC ＝2＋23，∴CE ＝ED ＋DC ＝1.70＋2＋23≈3.70＋3.464≈7.16(米)，即这棵桃树顶端点C 离地面的高度约为7.16米．10．碧波万顷的大海上，“蓝天号”渔轮在A 处进行海上作业，“白云号”货轮在“蓝天号”正南方向距“蓝天号”20海里的B 处．现在“白云号”以每小时10海里的速度向正北方向行驶，而“蓝天号”同时以每小时8海里的速度由A 处向南偏西60°方向行驶，经过多少小时后，“蓝天号”和“白云号”两船相距最近．解：如图，设经过t 小时，“蓝天号”渔轮行驶到C 处，“白云号”货轮行驶到D 处，此时“蓝天号”和“白云号”两船的距离为CD .根据题意，知在△ADC 中，AC ＝8t ，AD ＝20－10t ，∠CAD＝60°.由余弦定理，知CD 2＝AC 2＋AD 2－2×AC ×AD cos 60°＝(8t )2＋(20－10t )2－2×8t ×(20－10t )×cos 60°＝244t 2－560t ＋400＝244⎝ ⎛⎭⎪⎫t －70612＋400－244×⎝ ⎛⎭⎪⎫70612， ∴当t ＝7061时，CD 2取得最小值，即“蓝天号”和“白云号”两船相距最近．‖层级二‖|应试能力达标|1．在一座20 m 高的观测台台顶测得对面一水塔塔顶仰角为60°，塔底俯角为45°，那么这座塔的高为( )A ．20⎝⎛⎭⎪⎫1＋33m B ．20(1＋3)m C ．10(6＋2)m D ．20(6＋2)m解析：选B 如图所示，AB 为观测台，CD 为水塔，AM 为水平线．依题意得AB ＝20，∠DAM ＝45°，∠CAM ＝60°，从而可知MD ＝20，AM ＝20，CM ＝203， ∴CD ＝20(1＋3)(m)． 2．在静水中划船的速度是每分钟40 m ，水流的速度是每分钟20 m ，如果船从岸边A 处出发，沿着与水流垂直的航线到达对岸，那么船前进的方向指向河流的上游并与河岸垂直的方向所成的角为( )A.π4B ．π3 C.π6 D ．512π解析：选C 设水流速度与船速的合速度为v ，方向指向对岸．则由题意知，sin α＝v 水v 船＝2040＝12， 又α∈⎝ ⎛⎭⎪⎫0，π2，∴α＝π6.故选C. 3.某工程中要将一长为100 m 倾斜角为75°的斜坡，改造成倾斜角为30°的斜坡，并保持坡高不变，则坡底需加长( )A ．100 2 mB ．100 3 mC ．50(2＋6)mD ．200 m解析：选A ∠BAC ＝75°－30°＝45°.在△ABC 中，AC ＝100 m ，由正弦定理，得BC sin ∠BAC＝AC sin B ，∴BC ＝AC sin ∠BAC sin B ＝100×sin 45°sin 30°＝1002(m)．故选A.4．如图，在O 点测量到远处有一物体做匀速直线运动，开始时物体位于P 点，1分钟后，其位置在Q 点，且∠POQ ＝90°，再过1分钟，该物体位于R 点，且∠QOR ＝30°，则tan ∠OPQ 的值为( )A.12 B ．22 C.32 D ．3解析：选C 由题意知，PQ ＝QR ，设其长为1，则PR ＝2.在△OPR 中，由正弦定理，得2sin 120°＝OP sin R .在△OQR 中，由正弦定理，得1sin 30°＝OQ sin R ，则tan ∠OPQ ＝OQ OP ＝sin 120°2sin 30°＝32.故选C.5．江岸边有一炮台高30 m ，江中有两条船，船与炮台底部在同一水平面上，由炮台顶部测得俯角分别为45°和30°，而且两条船与炮台底部连线成30°角，则两条船相距 m.解析：设两条船所在位置分别为A ，B 两点，炮台底部所在位置为C 点，在△ABC 中，由题意可知AC ＝30tan 30°＝303(m)，BC ＝30tan 45°＝30(m)，C ＝30°，AB 2＝(303)2＋302－2×303×30×cos 30°＝900，所以AB ＝30(m)．答案：306．某海岛周围38海里有暗礁，一轮船由西向东航行，初测此岛在北偏东60°方向，航行30海里后测得此岛在东北方向，若不改变航向，则此船 (填“有”或“无”)触礁的危险．解析：如图所示，暗礁位于C 处，开始时，轮船在A 处，航行30海里后，轮船在B 处．由题意在△ABC 中，AB ＝30，∠BAC ＝30°，∠ABC ＝135°，则∠ACB ＝15°.由正弦定理，得BC＝AB sin ∠BAC sin ∠ACB ＝30sin 30°sin 15°＝156－24＝15(6＋2)． 在Rt △BDC 中，CD ＝22BC ＝15(3＋1)>38.所以，此船无触礁的危险．答案：无7．如图，小明同学在山顶A 处观测到，一辆汽车在一条水平的公路上沿直线匀速行驶，小明在A 处测得公路上B ，C 两点的俯角分别为30°，45°，且∠BAC＝135°.若山高AD ＝100 m ，汽车从C 点到B 点历时14 s ，则这辆汽车的速度为 m/s(精确到0.1，参数数据：2≈1.414，5≈2.236)．解析：由题意，AB ＝200 m ，AC ＝100 2 m ，在△ABC 中，由余弦定理可得BC ＝40 000＋20 000－2×200×1002×⎝ ⎛⎭⎪⎫－22≈ 316．17 m ，这辆汽车的速度为316.17÷14≈22.6 m/s.答案：22.68.如图所示，A ，B 是海面上位于东西方向相距5(3＋3)n mile 的两个观测点．现位于A 点北偏东45°方向、B 点北偏西60°方向的D 点有一艘轮船发出求救信号，位于B 点南偏西60°且与B点相距20 3 n mile的C点的救援船立即前往营救，其航行速度为30 n mile/h，则该救援船到达D点需要多长时间？解：由题意，知AB＝5(3＋3)，∠DBA＝90°－60°＝30°，∠DAB＝90°－45°＝45°，∴∠ADB＝180°－(45°＋30°)＝105°.在△DAB中，由正弦定理得BDsin∠DAB ＝ABsin∠ADB，即BD＝AB sin∠DABsin∠ADB＝5(3＋3)sin 45°sin 105°＝5(3＋3)sin 45°sin 45°cos 60°＋cos 45°sin 60°＝10 3 n mile.又∠DBC＝∠DBA＋∠ABC＝60°，BC＝20 3 n mile，∴在△DBC中，由余弦定理，得CD＝BD2＋BC2－2BD·BC cos∠DBC＝300＋1 200－2×103×203×1 2＝30 n mile，则救援船到达D点需要的时间为3030＝1 (h)．。

精品“正版”资料系列，由本公司独创。

旨在将“人教版”、”苏教版“、”北师 大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和 检测题分享给需要的朋友。

本资源创作于2020年8月，是当前最新版本的教材资源。

包含本课对应 内容，是您备课、上课、课后练习以及寒暑假预习的最佳选择。

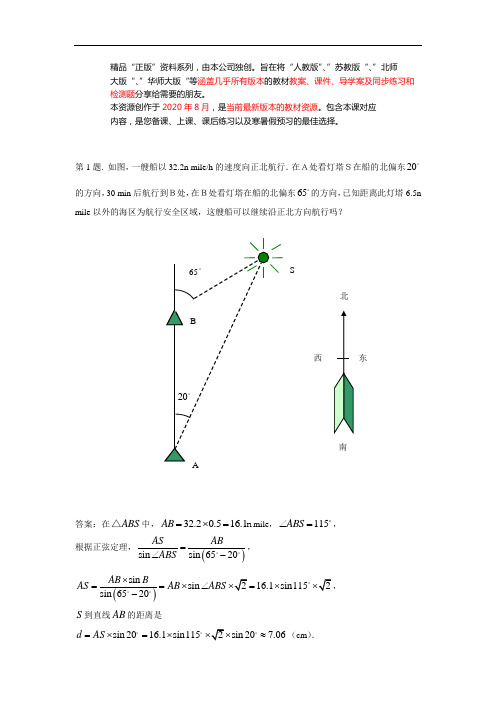
第1题. 如图，一艘船以32.2n mile/h 的速度向正北航行．在Ａ处看灯塔Ｓ在船的北偏东20的方向，30 min 后航行到Ｂ处，在Ｂ处看灯塔在船的北偏东65的方向，已知距离此灯塔6.5n mile 以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？答案：在ABS △中，32.20.516.1AB =⨯=n mile ，115ABS ∠=， 根据正弦定理，()sin sin 6520AS ABABS =∠-， ()sin sin 16.1sin1152sin 6520AB B AS AB ABS ⨯==⨯∠=⨯⨯-，S 到直线AB 的距离是sin 2016.1sin1152sin 207.06d AS =⨯=⨯⨯⨯≈（cm ）．南 6520所以这艘船可以继续沿正北方向航行．第2题. 如图，在山脚A 测得出山顶P 的仰角为a ，沿倾斜角为β的斜坡向上走a 米到B ，在B 处测得山顶P 的仰角为γ，求证：山高()()sin sin sin -a a h a γβγ-=．答案：在ABP △中，180+ABP γβ∠=-，()()()180- 180-180+ =-BPA ABPαβαβγβγα∠=--∠=---．在ABP △中，根据正弦定理，()()()()sin sin sin -sin 180+αsin -sin -AP ABABP APBAP AP αγαγβγβγα=∠∠=-⨯=ＡＱ αβaBγＣ所以山高为()()sin sin -sin sin -h AP ααγβαγα==．第3题. 测山上石油钻井的井架BC 的高，从山脚A 测得65.3AC =m ，塔顶B 的仰角α是2525'．已知山坡的倾斜角是1738'，求井架的高BC ．答案：在ABC △中，65.3AC =m ，=25251738747BAC αβ'''∠=--=，90=9017387222ABC β''∠=--=，根据正弦定理，sin sin AC BCABC BAC=∠∠()sin 65.3sin 7479.3m sin sin 7222AC BAC BC ABC '∠==≈'∠井架的高约为9.3m ．Ａ βα DＢＣ(6739)第4题. 如图，货轮在海上以35n mile / h 的速度沿着方位角（从指北方向顺时针转到目标方向线的水平角）为148的方向航行．为了确定船位，在B 点观察灯塔A 的方位角是126，航行半小时后到达Ｃ点，观察灯塔A 的方位角是78．求货轮到达Ｃ点时与灯塔A 的距离（精确到１ n mile ）．答案：在ABC △中，BC ＝350.517.5⨯=n mile ，14812612ABC ∠=-=，()78180148110ACB ∠=+-=，1801101258BAC ∠=--=，根据正弦定理，sin sin AC BCABC BAC=∠∠， sin 17.5sin124.29sin sin 58BC ABC AC BAC ∠==≈∠（nmile ）．货轮到达Ｃ点时与灯塔的距离是约4.29n mile ．第5题. 轮船A 和轮船B 在中午12时离开海港C ，两艘轮船的航行方向之间的夹角为120，轮船A 的航行速度是25 n mile/h ，轮船B 的航行速度是15 n mile/h ，下午2时两船之间的距离是多少？答案：70 n mile ．第6题. 如图，已知一艘船从30 n mile/h 的速度往北偏东10的A 岛行驶，计划到达A 岛后停留10 min 后继续驶往B 岛，B 岛在A 岛的北偏西60的方向上．船到达Ｃ处时是上午10时整，此时测得B 岛在北偏西30的方向，经过20 min 到达Ｄ处，测得B 岛在北偏西45的方向，如果一切正常的话，此船何时能到达B 岛？78126BA3045 60BA20 min答案：在BCD △中，301040,BCD ∠=+=1801804510125BDC ADB ∠=-∠=--=，130103CD =⨯=（n mile ）， 根据正弦定理，sin sin CD BD CBD BCD =∠∠，()10sin 40sin 18040125BD=∠--， 10sin 40sin15BD ⨯=．在ABD △中，451055ADB ∠=+=，1806010110BAD ∠=--=， 1801105515ABD ∠=--=．根据正弦定理， sin sin sin AD BD ABABD BAD ADB==∠∠∠， 就是sin15sin110sin 55AD BD AB==， sin1510sin 406.84sin 70sin110BD AD ==≈（n mile ）．sin 5510sin 40sin 5521.65sin110sin15sin 70BD AB ==≈(n mile)．如果这一切正常，此船从Ｃ开始到Ｂ所需要的时间为：6.8421.65206010306086.983030AD AB +++⨯+≈+⨯≈（min ） 即约１小时26分59秒．所以此船约在11时27分到达Ｂ岛．第7题. 一架飞机在海拔8000m 的高度飞行，在空中测出前下方海岛两侧海岸俯角分别是2739和，计算这个海岛的宽度．答案：约5821.71m ．第8题. 一架飞机从A 地飞到B 到，两地相距700km ．飞行员为了避开某一区域的雷雨云层，从机场起飞后，就沿与原来的飞行方向成21角的方向飞行，飞行到中途，再沿与原来的飞行方向成35夹角的方向继续飞行直到终点．这样飞机的飞行路程比原来路程700km 远了多少？答案：在ABC △中，700AB =km ，1802135124ACB ∠=--=， 根据正弦定理，700sin124sin 35sin 21AC BC==， 700sin 35sin124AC =，700sin 21sin124BC =，700sin 35700sin 21786.89sin124sin124AC BC +=+≈（km ），所以路程比原来远了约86.89km ．8000m27 39P 700km21BC35第9题. 为测量某塔的高度，在A ，B 两点进行测量的数据如图所示，求塔的高度．答案：在21.418.6 2.8ABT ATB ∠=-=△中，，9018.6ABT ∠=+，15AB =（m ）．根据正弦定理，sin 2.8cos18.6AB AT=，15cos18.6sin 2.8AT ⨯=． 塔的高度为15cos18.6tan 21.4tan 21.4114.05sin 2.8AT =≈（m ）．第10题. A ，B 两地相距2558m ，从A ，B 两处发出的 两束探照灯光照射在上方一架飞机的机身上（如图），飞机离 两个探照灯的距离是多少？飞机的高度是多少？答案：飞机离A 处控照灯的距离是4801.53m ， 飞机离B 处探照灯的距离是4704.21m ， 飞机的高度是约4574.23m ．A72.3 76.5B第11题. 一架飞以326km/h 的速度，沿北偏东75的航向从城市A 出发向城市B 飞行，18min 以后，飞机由于天气原因按命令改飞另一个城市C ，问收到命令时飞机应该沿什么航向飞行，此时离城市C 的距离是多少？答案：AE =3261897.860⨯=km ， 在ACD △中，根据余弦定理：222cos66AC AD CD AD CD =+- 2257110257110cos66=+-⨯⨯ 101.235=根据正弦定理：sin sin AD ACACD ADC=∠∠， sin 57sin 66sin 0.5144101.235AD ADC ACD AC ∠∠==≈，30.96ACD ∠≈，13330.96102.04ACB ∠≈-=．在ABC △中，根据余弦定理：222cos AB AC BC AC BC ACB =+-∠22101.2352042101.235204cos102.04=+-⨯⨯245.93≈，222cos 2AB AC BC BAC AB AC +-∠=222245.93101.2352042245.93101.235+-=⨯⨯0.5847≈，54.21BAC ∠=．在ACE △中，根据余弦定理：222cos CE AC AE AC AE EAC +-∠22101.23597.82101.23597.80.5487=+-⨯⨯⨯90.75≈，222cos 2AE EC AC AEC AE EC +-∠=．22297.890.75101.2350.4254297.890.75+-≈≈⨯⨯，64.82AEC ∠=，()180180757564.8210.18AEC -∠--=-=．所以，飞机应该以南偏西10.18的方向飞行，飞行距离约90.75km ．第12题. 飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔20250m ，速度为1000km/h ，飞行员先看到山顶的俯角为1830'，经过150s 后又看到山顶的俯角为81，求山顶的海拔高度（精确到1m ）．答案：飞行在150秒内飞行的距离是150100010003600d =⨯⨯m ， 根据正弦定理，()sin18.5sin 8118.5d x=-，这里x 是飞机看到山顶的俯角为81时飞机与山顶的距离．飞机与山顶的海拔的差是：C DB A E1830'81()sin18.5tan81tan8114721.64sin 8118.5d x =≈-(m)，山顶的海拔是2025014721.645528-≈m ．第13题. 一个人在建筑物的正西A 点，测得建筑物顶的仰角是α，这个人再从A 点向南走到B 点，再测得建筑物顶的仰角是β，设A，B 间的距离是a ． ．答案：设建筑物的同度是h ，建筑物的底部是C ， 则tan tan h h AC BC αβ==，． ABC △是直角三角形，BC 是斜边，所以222tan tan b h a αβ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，222211tan tan a h βα⎡⎤⎛⎫⎛⎫=-⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦， 222222tan tan tan tan a h αβαβ=-2222222sin sin sin cos cos sin a αβαβαβ=- ()()222sin sin sin sin a αβαβαβ=--． 所以，h =．α ABDCβah。

《海伦——秦九韶公式》教案【教学内容】人教A版普通高中课程标准试验教科书必修5 第一章“阅读与思考”海伦与秦九韶.【教学对象】高一学生.【教材分析】本节内容选自高中数学必修五的第一章，是阅读与思考部分的内容，在《高中数学新课程标准》中并没有做要求，教材中只占用一篇幅叙述了海伦公式与秦九韶公式（“三斜求积”公式）的记载历史，并未给出证明和应用.本节内容之前学生已经学习了解三角形，从而这节课是三角形面积公式的延续与拓展.本节课的主要设计对象为数学学习程度较好的学生——在完成《高中数学新课程标准》中要求的学习之后仍有余力的学生，意在引领学生了解数学文化史，同时启发学生运用所学知识由“三斜求积”公推导海伦公式，并让学生从中体会数学之美.【学情分析】高一学生在进入本节课的学习之前，需要熟悉前面已学过的三角形面积公式，余弦定理的推论，同角三角函数的平方关系以及平方差公式和完全平方公式.【教学目标】∙知识与技能：（1）会推导秦九韶公式与海伦公式，并理解海伦公式的本质；（2）理解秦九韶公式与海伦公式的本质相同.（3）会用海伦公式解决简单的涉及到三角形三边与面积之间关系的问题.∙过程与方法：（1）经历推导秦九韶公式与海伦公式的全过程，培养学生严谨的的数学逻辑思维；（2）提高学生会应用海伦公式解决涉及到三角形三边与面积之间关系问题的能力.∙情感态度与价值观：（1）体会公式书写的简洁美；（2）体会数学以不变应万变的魅力.【教学重点】秦九韶公式与海伦公式的推导及其应用.【教学难点】秦九韶公式与海伦公式的本质.【教学方法】引导探究、实力应用.【教学过程】（一）旧知回顾1.三角形的面积公式：（1）ah S ABC 21=∆（h 为边a 上的高）； （2）==∆C ab S ABC sin 21 = . 2.余弦定理的推论：bca cb A 2cos 222-+=；=B cos ；=C cos . 3.同角三角函数的平方关系：+α2sin 1=.[师生活动]通过提问，让学生回答出本节课涉及到的已经学习过的公式.(二)新课引入【引例】问沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里。

1．2 应用举例(二)[学习目标] 1.能够运用正弦定理、余弦定理等学问和方法解决一些有关底部不行到达的物体高度测量的问题.2.巩固深化解三角形实际问题的一般方法，养成良好的争辩、探究习惯.3.进一步培育同学学习数学、应用数学的意识及观看、归纳、类比、概括的力量．[学问链接] 现实生活中，人们是怎样测量底部不行到达的建筑物高度呢？又怎样在水平飞行的飞机上测量飞机下方山顶的海拔高度呢？要点一 测量仰角求高度问题例1 如图所示，A 、B 是水平面上的两个点，相距800 m ，在A 点测得山顶C 的仰角为45°，∠BAD ＝120°，又在B 点测得∠ABD ＝45°，其中D 点是点C 到水平面的垂足，求山高CD .解 由于CD ⊥平面ABD ，∠CAD ＝45°，所以CD ＝AD . 因此只需在△ABD 中求出AD 即可，在△ABD 中，∠BDA ＝180°－45°－120°＝15°， 由AB sin 15°＝ADsin 45°， 得AD ＝AB ·sin 45°sin 15°＝800×226－24＝800(3＋1) (m)．即山的高度为800(3＋1) m.规律方法 在运用正弦定理、余弦定理解决实际问题时，通常都依据题意，从实际问题中抽象出一个或几个三角形，然后通过解这些三角形，得出实际问题的解．和高度有关的问题往往涉及直角三角形的求解． 跟踪演练1 如图，地平面上有一旗杆OP ，为了测得它的高度h ，在地面上选一基线AB ，AB ＝20 m ，在A 点处测得P 点仰角∠OAP ＝30°，在B 点处测得P 点的仰角∠OBP ＝45°，又测得∠AOB ＝60°，求旗杆的高度h .(结果保留两个有效数字)解 在Rt △AOP 中，∠OAP ＝30°，OP ＝h ， ∴OA ＝OP ·1tan 30°＝3h .在Rt △BOP 中，∠OBP ＝45°，∴OB ＝OP ·1tan 45°＝h .在△AOB 中，AB ＝20，∠AOB ＝60°，由余弦定理得AB 2＝OA 2＋OB 2－2×OA ×OB ·cos 60°， 即202＝(3h )2＋h 2－2·3h ·h ·12，解得h 2＝4004－3≈176.4，∴h ≈13(m)．答 旗杆高度约为13 m. 要点二 测量俯角求高度问题例2 如图所示，在山顶铁塔上B 处测得地面上一点A 的俯角为α，在塔底C 处测得A 处的俯角为β.已知铁塔BC 部分的高为h ，求出山高CD . 解 在△ABC 中， ∠BCA ＝90°＋β， ∠ABC ＝90°－α， ∠BAC ＝α－β，∠CAD ＝β. 依据正弦定理得AC sin ∠ABC ＝BCsin ∠BAC，即AC sin (90°－α)＝BCsin (α－β)，∴AC ＝BC cos αsin (α－β)＝h cos αsin (α－β).在Rt △ACD 中，CD ＝AC sin ∠CAD ＝AC sin β ＝h cos αsin βsin (α－β).答 山的高度为h cos αsin βsin (α－β).规律方法 利用正弦定理和余弦定理来解题时，要学会审题及依据题意画示意图，要懂得从所给的背景资料中进行加工、抽取主要因素，进行适当的简化．跟踪演练2 江岸边有一炮台高30 m ，江中有两条船，船与炮台底部在同一水平面上，由炮台顶部测得俯角分别为45°和30°，而且两条船与炮台底部连线成30°角，则两条船相距________m. 答案 30解析 设两条船所在位置分别为A 、B 两点，炮台底部所在位置为C 点，在△ABC 中，由题意可知AC ＝30tan 30°＝303，BC ＝30tan 45°＝30，C ＝30°， AB 2＝(303)2＋302－2×303×30×cos 30°＝900，所以AB ＝30. 要点三 测量方位角求高度问题例3 如图，为测得河对岸塔AB 的高，先在河岸上选一点C ，使C 在塔底B 的正东方向上，测得点A 的仰角为60°，再由点C 沿北偏东15°方向走10 m 到位置D ，测得∠BDC ＝45°，求塔AB 的高度．解 在△BCD 中，CD ＝10，∠BDC ＝45°，∠BCD ＝15°＋90°＝105°，∠DBC ＝30°， 由正弦定理，得BC sin 45°＝CDsin 30°， BC ＝CD sin 45°sin 30°＝10 2.在Rt △ABC 中，tan 60°＝ABBC，AB ＝BC tan 60°＝10 6. 答 塔AB 的高度为10 6 m.规律方法 利用正弦定理和余弦定理来解题时，要学会审题及依据题意画方位图，要懂得从所给的背景资料中进行加工、抽取主要因素，进行适当的简化．跟踪演练3 一船以每小时15 km 的速度向东航行，船在A 处看到一个灯塔B 在北偏东60°方向，行驶4 h 后，船到达C 处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为________ km.答案 30 2解析 如图，由已知条件， 得AC ＝60 km ，∠BAC ＝30°， ∠ACB ＝105°，∠ABC ＝45°.由正弦定理得BC ＝AC sin ∠BAC sin B＝302(km)1．已知两座灯塔A ，B 与海洋观看站C 的距离相等，灯塔A 在观看站C 的北偏东40°，灯塔B 在观看站C 的南偏东60°，则灯塔A 在灯塔B 的( ) A ．北偏东10° B ．北偏西10°C ．南偏东10°D ．南偏西10°答案 B解析 如右图，因△ABC 为等腰三角形，所以∠CBA ＝12(180°－80°)＝50°，60°－50°＝10°，故选B.2．从高出海平面h 米的小岛看正东方向有一只船俯角为30°，看正南方向有一只船俯角为45°，则此时两船间的距离为( ) A ．2h 米 B.2h 米 C.3h 米D ．22h 米答案 A解析 如图所示， BC ＝3h ， AC ＝h ， ∴AB ＝3h 2＋h 2＝2h (米)．3．甲、乙两楼相距20 m ，从乙楼底望甲楼顶的仰角为60°，从甲楼顶望乙楼顶的俯角为30°，则甲、乙两楼的高分别是________________. 答案 20 3 m ，4033 m 解析 甲楼的高为20tan 60°＝20×3＝203； 乙楼的高为203－20tan 30°＝203－20×33＝4033.1.在争辩三角形时，机敏依据两个定理可以查找到多种解决问题的方案，但有些过程较烦琐，如何找到最优的方法，最主要的还是分析两个定理的特点，结合题目条件来选择最佳的计算方式．2．测量底部不行到达的建筑物的高度问题．由于底部不行到达，这类问题不能直接用解直角三角形的方法解决，但常用正弦定理和余弦定理，计算出建筑物顶部到一个可到达的点之间的距离，然后转化为解直角三角形的问题．一、基础达标1．为了测某塔AB 的高度，在一幢与塔AB 相距20 m 的楼顶处测得塔顶的仰角为30°，塔基的俯角为45°，那么塔AB 的高为( ) A ．20⎝⎛⎭⎫1＋33 mB ．20⎝⎛⎭⎫1＋32 mC ．20(1＋3) mD ．30 m答案 A解析 如图，h ＝20tan 30°＋20tan 45°＝20⎝⎛⎭⎫1＋33(m)，故选A.2．在某个位置测得某山峰仰角为θ，对着山峰在地面上前进600 m 后测得仰角为2θ，连续在地面上前进200 3 m 以后测得山峰的仰角为4θ，则该山峰的高度为( ) A ．200 m B ．300 m C ．400 m D ．100 3 m 答案 B解析 法一 如图，△BED ，△BDC 为等腰三角形，BD ＝ED ＝600，BC ＝DC ＝200 3.在△BCD 中，由余弦定理可得cos 2θ＝6002＋(2003)2－(2003)22×600×2003＝32，∴2θ＝30°，4θ＝60°.在Rt △ABC 中，AB ＝BC ·sin 4θ＝2003×32＝300，故选B. 法二 由于△BCD 是等腰三角形，12BD ＝DC cos 2θ，即300＝2003cos 2θ.cos 2θ＝32，2θ＝30°，4θ＝60°. 在Rt △ABC 中，AB ＝BC ·sin 4θ＝2003×32＝300，故选B.3．一架飞机在海拔8 000 m 的高度飞行，在空中测出前下方海岛两侧海岸俯角分别是30°和45°，则这个海岛的宽度为________m. 答案 5 856.4 解析 宽＝8 000tan 30°－8 000tan 45°＝5 856.4(m)． 4．为测量某塔的高度，在A ，B 两点进行测量的数据如图所示，求塔的高度．解 在△ABT 中，∠ATB ＝21.4°－18.6°＝2.8°，∠ABT ＝90°＋18.6°，AB ＝15(m)． 依据正弦定理，AB sin 2.8°＝ATcos 18.6°，AT ＝15×cos 18.6°sin 2.8°.塔的高度为AT ·sin 21.4°＝15·cos 18.6°sin 2.8°sin 21.4°≈106.19(m)．所以塔的高度为106.19 m.5．如图，某货轮在A 处看灯塔B 在货轮的北偏东75°，距离为12 6 n mile ，在A 处看灯塔C 在货轮的北偏西30°，距离为8 3 n mile ，货轮由A 处向正北航行到D处时，再看灯塔B 在货轮的南偏东60°. 求：(1)A 处与D 处的距离； (2)灯塔C 与D 处的距离．解 (1)在△ABD 中，∠ADB ＝60°，B ＝45°，由正弦定理得AD ＝AB sin Bsin ∠ADB ＝126×2232＝24 (n mile)．所以A 处与D 处的距离为24 n mile. (2)在△ADC 中，由余弦定理得CD 2＝AD 2＋AC 2－2AD ·AC cos 30°＝192， 解得CD ＝8 3 n mile.即灯塔C 与D 处的距离为8 3 n mile. 二、力量提升6．某人在C 点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10 m 到D ，测得塔顶A 的仰角为30°，则塔高为( )A ．15 mB ．5 mC ．10 mD ．12 m答案 C解析 如图，设塔高为h ，在Rt △AOC 中，∠ACO ＝45°，则OC ＝OA ＝h .在Rt △AOD 中，∠ADO ＝30°，则OD ＝3h . 在△OCD 中，∠OCD ＝120°，CD ＝10，由余弦定理得OD 2＝OC 2＋CD 2－2OC ·CD cos ∠OCD ， 即(3h )2＝h 2＋102－2h ×10×cos 120°， ∴h 2－5h －50＝0，解得h ＝10或h ＝－5(舍)．7．要测量底部不能到达的东方明珠电视塔的高度，在黄浦江西岸选择甲、乙两观测点，在甲、乙两点分别测得塔顶的仰角分别为45°，30°，在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°，甲、乙两地相距500 m ，则电视塔在这次测量中的高度是( )A ．100 2 mB ．400 mC ．200 3 mD ．500 m 答案 D解析 由题意画出示意图，设高AB ＝h ，在Rt △ABC 中，由已知BC ＝h ， 在Rt △ABD 中，由已知BD ＝3h ，在△BCD 中，由余弦定理BD 2＝BC 2＋CD 2－2BC ·CD ·cos ∠BCD 得，3h 2＝h 2＋5002＋h ·500，解之得h ＝500 m ．故选D. 8．如图，在山脚A 测得山顶P 的仰角为α，沿倾斜角为β的斜坡向上走a 米到B ，在B 处测得山顶P 的仰角为γ，求证：山高h ＝a sin αsin (γ－β)sin (γ－α).解 在△ABP 中，∠ABP ＝180°－γ＋β，∠BP A ＝180°－(α－β)－∠ABP ＝180°－(α－β)－(180°－γ＋β)＝γ－α. 在△ABP 中，依据正弦定理，AP sin ∠ABP ＝AB sin ∠APB ，AP sin (180°－γ＋β)＝αsin (γ－α)，AP ＝a ×sin (γ－β)sin (γ－α)所以山高h ＝AP sin α＝a sin αsin (γ－β)sin (γ－α).9．如图，A 、B 、C 、D 都在同一个与水平面垂直的平面内，B 、D为两岛上的两座灯塔的塔顶．测量船于水面A 处测得B 点和D 点的仰角分别为75°，30°，于水面C 处测得B 点和D 点的仰角均为60°，AC ＝0.1 km.摸索究图中B 、D 间距离 km ，2≈1.414，与另外哪两点间距离相等，然后求B 、D 的距离(计算结果精确到0.01 6≈2.449).解 在△ACD 中，∠DAC ＝30°，∠ADC ＝60°－∠DAC ＝30°，∴CD ＝AC ＝0.1，又∠BCD ＝180°－60°－60°＝60°，故CB 是△CAD 底边AD 的中垂线，∴BD ＝BA ，在△ABC 中，AB sin ∠BCA ＝AC sin ∠ABC ，所以AB ＝AC sin 60°sin 15°＝32＋620.因此，BD ＝32＋620≈0.33 km ，故B 、D 的距离约为0.33 km.三、探究与创新10．为保障高考的公正性，高考时每个考点都要安装手机屏蔽仪，要求在考点四周1千米处不能收到手机信号，检查员抽查青岛市一考点，在考点正西约1.732千米有一条北偏东60°方向的大路，在此处检查员用手机接通电话，以每小时12千米的速度沿大路行驶，问最长需要多少分钟检查员开头收不到信号，并至少持续多长时间该考点才算合格？解 如图所示，考点为A ，检查开头处为B ， 设大路上C ，D 两点到考点的距离为1千米． 在△ABC 中，AB ＝3≈1.732(千米)，AC ＝1(千米)， ∠ABC ＝ 30°，由正弦定理sin ∠ACB ＝sin 30°AC ·AB ＝32，∴∠ACB ＝120°(∠ACB ＝60°不合题意)， ∴∠BAC ＝30°， ∴BC ＝AC ＝1(千米)，在△ACD 中，AC ＝AD ，∠ACD ＝60°，∴△ACD 为等边三角形，∴CD ＝1(千米)．∵BC12×60＝5，∴在BC上需5分钟，CD上需5分钟．所以最长需要5分钟检查员开头收不到信号，并持续至少5分钟才算合格．。

A 级 基础巩固一、选择题1．已知A 、B 两地的距离为10 km ，B 、C 两地的距离为20 km ，现测得∠ABC ＝120°，则A 、C 两地的距离为( D )A ．10 kmB ． 3 kmC ．10 5 kmD ．107 km[解析] 在△ABC 中，AB ＝10，BC ＝20，∠ABC ＝120°，则由余弦定理，得 AC 2＝AB 2＋BC 2－2AB ·BC cos ∠ABC ＝100＋400－2×10×20cos120° ＝100＋400－2×10×20×(－12)＝700，∴AC ＝107，即A 、C 两地的距离为107 km ．2．如图，在河岸AC 测量河的宽度BC ，测量下列四组数据，较适宜的是( D )A ．γ，c ，αB ．b ，c ，αC ．c ，α，βD ．b ，α，γ[解析] 本题中a 、c 、β这三个量不易直接测量，故选D ．3．一船向正北航行，看见正西方向有相距10 n mlie 的两个灯塔恰好与它在一条直线上，继续航行半小时后，看见一灯塔在船的南偏西60°方向上，另一灯塔在船的南偏西75°方向上，则这艘船的速度是每小时( C )A ．5 n mlieB ．5 3 n mlieC ．10 n mlieD ．10 3 n mlie[解析] 如图，依题意有∠BAC ＝60°，∠BAD ＝75°，∴∠CAD ＝∠CDA ＝15°，从而CD ＝CA ＝10， 在Rt △ABC 中，求得AB ＝5， ∴这艘船的速度是50.5＝10(n mlie/h)．4．某观察站C 与两灯塔A 、B 的距离分别为300 m 和500 m ，测得灯塔A 在观察站C 北偏东30°，灯塔B 在观察站C 正西方向，则两灯塔A 、B 间的距离为( C )A ．500 mB ．600 mC ．700 mD ．800 m[解析] 根据题意画出图形如图．在△ABC 中，BC ＝500，AC ＝300，∠ACB ＝120°， 由余弦定理得，AB 2＝AC 2＋BC 2－2AC ·BC cos120° ＝3002＋5002－2×300×500×(－12)＝490 000，∴AB ＝700(m)．5．要直接测量河岸之间的距离(河的两岸可视为平行)，由于受地理条件和测量工具的限制，可采用如下办法：如图所示，在河的一岸边选取A 、B 两点，观察对岸的点C ，测得∠CAB ＝45°，∠CBA ＝75°，且AB ＝120 m 由此可得河宽为(精确到1m)( C )A ．170 mB ．98 mC ．95 mD ．86 m[解析] 在△ABC 中，AB ＝120，∠CAB ＝45°，∠CBA ＝75°，则∠ACB ＝60°，由正弦定理，得BC ＝120sin45°sin60°＝406．设△ABC 中，AB 边上的高为h ，则h 即为河宽， ∴h ＝BC ·sin ∠CBA ＝406×sin75°≈95(m)．6．甲船在湖中B 岛的正南A 处，AB ＝3 km ，甲船以8 km/h 的速度向正北方向航行，同时乙船从B 岛出发，以12 km/h 的速度向北偏东60°方向驶去，则行驶15 min 时，两船的距离是( B )A ．7 kmB ．13 kmC ．19 kmD ．10－3 3 km[解析] 由题意知AM ＝8×1560＝2，BN ＝12×1560＝3，MB ＝AB －AM ＝3－2＝1，所以由余弦定理，得MN 2＝MB 2＋BN 2－2MB ·BN cos120°＝1＋9－2×1×3×(－12)＝13，所以MN ＝13 km ．二、填空题7．在相距2km 的A ，B 两点处测量目标点C ，若∠CAB ＝75°，∠CBA ＝60°，则A ，C 两点之间的距离是__6__km ．[解析] 如图所示，由题意易知C ＝45°，由正弦定理得AC sin60°＝2sin45°，从而AC ＝222·32＝6(km)．8．一只蜘蛛沿东北方向爬行x cm 捕捉到一只小虫，然后向右转105°，爬行10 cm 捕捉到另一只小虫，这时它向右转135°爬行回它的出发点，则x ＝__1063__cm ．[解析] 如图，由题意知，∠BAC ＝75°，∠ACB ＝45°.∠B ＝60°， 由正弦定理，得x sin ∠ACB ＝10sin B ，∴x ＝10sin ∠ACB sin B ＝10×sin45°sin60°＝1063．三、解答题9．如图，我炮兵阵地位于地面A 处，两观察所分别位于地面点C 和D 处，已知CD ＝6 000 m ．∠ACD ＝45°，∠ADC ＝75°，目标出现于地面B 处时测得∠BCD ＝30°，∠BDC ＝15°.求炮兵阵地到目标的距离．(结果保留根号)[解析] 在△ACD 中，∠CAD ＝60°， AD ＝CD ·sin45°sin60°＝63CD ．在△BCD 中，∠CBD ＝135°，BD ＝CD ·sin30°sin135°＝22CD ，∠ADB ＝90°．在Rt △ABD 中，AB ＝AD 2＋BD 2＝426CD ＝1 00042(m)．10．一艘船以32.2 n mile/h 的速度向正北航行．在A 处看灯塔S 在船的北偏东20°的方向，30 min 后航行到B 处，在B 处看灯塔在船的北偏东65°的方向，已知距离此灯塔6.5 n mile 以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？[解析] 在△ASB 中，∠SBA ＝115°，∠S ＝45°.由正弦定理，得SB ＝AB sin20°sin45°＝16.1sin20°sin45°≈7.787(n mile)．设点S 到直线AB 的距离为h ，则h ＝SB sin65°≈7.06(n mile)．∵h >6.5 n mile ，∴此船可以继续沿正北方向航行．B 级 素养提升一、选择题1．已知船A 在灯塔C 北偏东85°且到C 的距离为2 km ，船B 在灯塔C 西偏北25°且到C 的距离为 3 km ，则A 、B 两船的距离为( D )A ．2 3 kmB ．3 2 kmC ．15 kmD ．13 km[解析] 如图可知∠ACB ＝85°＋(90°－25°)＝150°，AC ＝2，BC ＝3，∴AB 2＝AC 2＋BC 2－2AC ·BC ·cos150°＝13， ∴AB ＝13．2．一船自西向东匀速航行，上午10时到达一座灯塔P 的南偏西75°距塔68 n mile 的M 处，下午2时到达这座灯塔的东南方向的N 处，则这只船的航行速度为( A )A ．1762 n mile/hB ．34 6 n mile/hC ．1722n mile/hD ．34 2 n mile/h[解析] 如图所示，在△PMN 中，PM sin45°＝MNsin120°，∴MN ＝68×3222＝346，∴v ＝MN 4＝1762(n mile/h)．3．如图，货轮在海上以40 km/h 的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为140°的方向航行．为了确定船的位置，船在B 点观测灯塔A 的方位角为110°，航行12 h 到达C 点，观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是( B )A ．10 kmB ．10 2 kmC ．15 kmD ．15 2 km[解析] 在△ABC 中，BC ＝40×12＝20( km)，∠ABC ＝140°－110°＝30°，∠ACB ＝(180°－140°)＋65°＝105°，则A ＝180°－(30°＋105°)＝45°． 由正弦定理，得AC ＝BC ·sin ∠ABC sin A ＝20·sin30°sin45°＝102( km)．二、填空题4．海上一观测站测得方位角240°的方向上有一艘停止航行待修的商船，在商船的正东方有一艘海盗船正向它靠近，速度为每小时90 n mile.此时海盗船距观测站107 n mile ，20 min 后测得海盗船距观测站20 n mlie ，再过__403__min ，海盗船到达商船．[解析] 如下图，设开始时观测站、商船、海盗船分别位于A 、B 、C 处，20 min 后，海盗船到达D 处，在△ADC 中，AC ＝107，AD ＝20，CD ＝30，由余弦定理，得cos ∠ADC ＝AD 2＋CD 2－AC 22AD ·CD ＝400＋900－7002×20×30＝12．∴∠ADC ＝60°，在△ABD 中，由已知得∠ABD ＝30°， ∠BAD ＝60°－30°＝30°， ∴BD ＝AD ＝20，2090×60＝403(min)．5．如图，一艘船上午8∶00在A 处测得灯塔S 在它的北偏东30°处，之后它继续沿正北方向匀速航行，上午8∶30到达B 处，此时又测得灯塔S 在它的北偏东75°处，且与它相距4 2 n mile ，则此船的航行速度是__16__n mile/h ．[解析] 在△ABS 中，∠A ＝30°，∠ABS ＝105°， ∴∠ASB ＝45°，∵BS ＝42，BS sin A ＝ABsin ∠ASB ，∴AB ＝BS ·sin ∠ASBsin A ＝42×2212＝8，∵上午8∶00在A 地，8∶30在B 地， ∴航行0.5小时的路程为8 n mile ， ∴此船的航速为16 n mile/h ． 三、解答题6．如图，为了解某海域海底构造，在海平面内一条直线上的A 、B 、C 三点进行测量，已知AB ＝50 m ，BC ＝120 m ，于A 处测得水深AD ＝80 m ，于B 处测得水深BE ＝200 m ，于C 处测得水深CF ＝110 m ，求∠DEF 的余弦值．[解析] 由题意可得DE 2＝502＋1202＝1302， DF 2＝1702＋302＝29 800， EF 2＝1202＋902＝1502， 由余弦定理，得cos ∠DEF ＝1665．C 级 能力拔高1．为了测量两山顶M 、N 间的距离，飞机沿水平方向在A 、B 两点进行测量，A 、B 、M 、N 在同一个铅垂平面内(如图)．能够测量的数据有俯角和A 、B 间的距离．请设计一个方案，包括：①指出需要测量的数据(用字母表示，并在图中标出)；②用文字和公式写出计算M 、N 间的距离的步骤．[解析] 方案一：①需要测量的数据有：点A 到点M 、N 的俯角α1、β1；点B 到点M 、N 的俯角α2、β2；A 、B 间的距离d (如图)．②第一步：计算AM ，由正弦定理，得AM ＝d sin α2sin α1＋α2；第二步：计算AN ，由正弦定理，得AN ＝d sin β2sin β2－β1；第三步：计算MN ，由余弦定理，得 MN ＝AM 2＋AN 2－2AM ·AN cos α1－β1．方案二：①需要测量的数据有：点A 到点M 、N 的俯角α1、β1；点B 到点M 、N 的俯角α2、β2；A 、B 间的距离d (如图)．②第一步：计算BM ，由正弦定理，得BM ＝d sin α1sin α1＋α2；第二步：计算BN ，由正弦定理，得BN ＝d sin β1sin β2－β1；第三步：计算MN ，由余弦定理，得 MN ＝BM 2＋BN 2＋2BM ·BN cos β2＋α2．2．已知海岛B 在海岛A 的北偏东45°方向上，A 、B 相距10 n mile ，小船甲从海岛B 以2 n mile/h的速度沿直线向海岛A 移动，同时小船乙从海岛A 出发沿北偏西15°方向也以2 n mile/h 的速度移动．(1)经过1 h 后，甲、乙两小船相距多少海里？(2)在航行过程中，小船甲是否可能处于小船乙的正东方向？若可能，请求出所需时间，若不可能，请说明理由．[解析] 经过1 h 后，甲船到达M 点，乙船到达N 点， AM ＝10－2＝8，AN ＝2，∠MAN ＝60°，所以MN 2＝AM 2＋AN 2－2AM ·AN cos60°＝64＋4－2×8×2×12＝52．所以MN ＝213．所以经过1 h 后，甲、乙两小船相距213海里．(2)设经过t (0<t <5)h 小船甲处于小船乙的正东方向，则甲船与A 距离为AE ＝(10－2t )n mile ，乙船与A 距离为AF ＝2t n mile ，∠EAF ＝60°，∠EF A ＝75°，则由正弦定理，得AF sin45°＝AE sin75°，即2tsin45°＝10－2t sin75°，则t ＝10sin45°2sin75°＋2sin45°＝103＋3＝53－33<5．答：经过53－33小时小船甲处于小船乙的正东方向．。

我国南宋著名数学家秦九韶也发现了与海伦公式等价的从三角形三边求面积的公式，他把这种方法称为“三斜求积”. 在他的著作《数书九章》里有一个题目：“问有沙田一段，有三斜，其小斜一十二里，中斜一十四里，大斜一十五里. 里法三百步. 欲知为田几何？ 答曰：田积三百一十五顷.” 这道题实际上是已知三角形的三边长，求三角形面积. 《数书九章》中的求法是：“以小斜幂并大斜幂减中斜幂 ，余半之，自乘于上. 以小斜幂乘大斜幂减上，余四约之，为实，一为从隅，开平方，得积.” 译成现代式子是])2([41222222b a c a c S -+-= 这个式子称为秦九韶“三斜求积”公式.通过上述证明可以看出：秦九韶公式与海伦公式的本质是一样的! 从中充分说明我国古代已具有很高的数学水平.秦九韶 (约公元 1 2 0 2～ 1 2 61年 ) ，字道古，字道古,祖籍为鲁郡(今山东兖州)，与李冶、杨辉、朱世杰并称宋元数学四大家，是我国古代数学家杰出代表之一. 著有《数书九章》，全书为十八卷，共 81题，分九大类. 系统总结和发展了高次方程的数值解法（在必修三《算法初步》中有“秦九韶算法”）和一次同余问题的解法，提出了相当完备的“正负开方术”和“大衍求一术”，对数学发展产生了广泛的影响，奠定了其时人难以望其项背的数学地位.他被外国科学史家赞誉为“他那个民族，那个时代，并且确实也是所有时代最伟大的数学家之一”. 如果将秦九韶和意大利文艺复兴时期的风云人物相比,竟有几分相似:他多才多艺,懂得星占、数学、音乐、建筑,还擅长诗文,会骑术、剑术、踢球等.4. 海伦公式的应用示例海伦公式除了可以解决“已知三角形三边长求面积”的问题外，还有什么应用呢？例1 三边长a ，b ，c 的三角形，满足c>a>b ，2a=b+c ，且它的周长是12，面积是6，试判断这个三角形的形状.分析：由已知得，a=4，b+c=8，p=6，于是。