应用多元统计分析:主成分分析共110页
- 格式:ppt
- 大小:12.05 MB
- 文档页数:110


主成分分析6.1 试述主成分分析的基本思想。
答:我们处理的问题多是多指标变量问题,由于多个变量之间往往存在着一定程度的相关性,人们希望能通过线性组合的方式从这些指标中尽可能快的提取信息。
当第一个组合不能提取止。
这就是主成分分析的基本思想。
6.2 主成分分析的作用体现在何处?答:一般说来,在主成分分析适用的场合,用较少的主成分就可以得到较多的信息量。
以各个主成分为分量,就得到一个更低维的随机向量;主成分分析的作用就是在降低数据“维数”6.3 简述主成分分析中累积贡献率的具体含义。
答:主成分分析把p 个原始变量12,,,p X X X 的总方差()tr Σ分解成了p 个相互独立的变量p 个主成分的,忽略一些带有较小方差的主成分将不会给总方差带来太大的影响。
这里我们()m p <个主成分,则称11pmm kkk k ψλλ===∑∑ 为主成分1,,m Y Y 的累计贡献率,累计贡献率表明1,,m Y Y 综合12,,,p X X X 的能力。
通常取m ,使得累计贡献率达到一个较高的百分数(如85%以上)。
答:这个说法是正确的。
即原变量方差之和等于新的变量的方差之和6.5 试述根据协差阵进行主成分分析和根据相关阵进行主成分分析的区别。
答:从相关阵求得的主成分与协差阵求得的主成分一般情况是不相同的。
从协方差矩阵出发的,其结果受变量单位的影响。
主成分倾向于多归纳方差大的变量的信息,对于方差小的变量就可能体现得不够,也存在“大数吃小数”的问题。
实际表明,这种差异有时很大。
我6.6 已知X =()’的协差阵为 试进行主成分分析。
解:=0计算得当时,同理,计算得时,易知相互正交单位化向量得,,综上所述,第一主成分为第二主成分为第三主成分为6.7 设X=()’的协方差阵(p为, 0<p<1证明:为最大特征根,其对应的主成分为。
证明:==,为最大特征根当时,=所以,6.8利用主成分分析法,综合评价六个工业行业的经济效益指标。
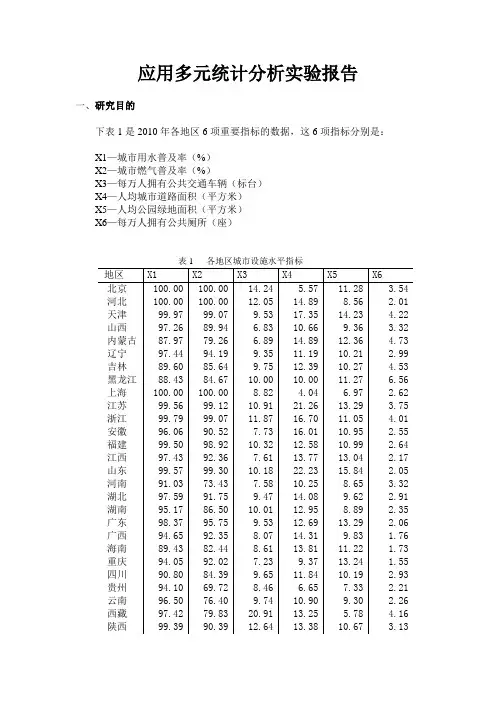
应用多元统计分析实验报告一、研究目的下表1是2010年各地区6项重要指标的数据,这6项指标分别是:X1—城市用水普及率(%)X2—城市燃气普及率(%)X3—每万人拥有公共交通车辆(标台)X4—人均城市道路面积(平方米)X5—人均公园绿地面积(平方米)X6—每万人拥有公共厕所(座)表1 各地区城市设施水平指标本次实验的研究目的是根据这些指标用主成分分析法对各地区城市设施水平进行综合评价和排序,得出结论并提出建议。
二、研究过程从标准化数据出发,首先计算这些指标的主成分,然后通过主成分的大小进行排序。
1.利用SPSS进行因子分析表2和表3分别是特征根(方差贡献率)和因子载荷阵的信息。
表3 因子载荷阵2.利用因子分析结果进行主成分分析 ⑴.表4是特征向量的信息表4 特征向量矩阵 z1 z2 z3 z4 z5 z6 x1 0.52 0.35 (0.31) (0.00) 0.08 0.70 x2 0.58 0.09 (0.19) 0.45 (0.37) (0.53) x3 0.17 0.67 0.26 (0.36) 0.41 (0.39) x4 0.43 (0.32) 0.32 (0.66) (0.41) 0.03 x5 0.41 (0.51) 0.25 0.21 0.68 (0.01) x6 (0.01) 0.23 0.79 0.43 (0.24) 0.28⑵.利用主成分得分进行综合评价时,从特征向量可以写出所有6个主成分的具体形式:Y1=0.52X1+0.68X2+0.17X3+0.43X4+0.41X5-0.01X6Y2=0.35X1+0.09X2+0.67X3-0.32X4-0.51X5+0.23X6 Y3=-0.31X1-0.19X2+0.26X3+0.32X4+0.25X5+0.79X6 Y4=0.00X1+0.45X2-0.36X3-0.66X4+0.21X5+0.43X6 Y5=0.08X1-0.37X2+0.41X3-0.41X4+0.68X5-0.24X6 Y6=0.70X1-0.53X2-0.39X3+0.03X4-0.01X5+0.28X6⑶.以特征根为权,对6个主成分进行加权综合,得出各地区的综合得分及排序,具体数据见表5.综合得分的计算公式是6161Y Y Y ii ∑∑+⋯+=λλλλ三、结果说明从表5可以看出,北京、天津。



多元统计分析与主成分分析的关系与应用多元统计分析和主成分分析是统计学中两个重要的技术手段,它们在数据分析和统计建模中具有广泛的应用。
本文将探讨多元统计分析与主成分分析的关系以及它们在实际问题中的应用。
一、多元统计分析与主成分分析的关系多元统计分析是一种综合运用多种统计学方法和技术,研究多个变量之间关系的分析方法。
它旨在通过对大量的数据进行整合和分析,揭示不同变量之间的潜在结构和规律。
而主成分分析则是多元统计分析中常用的技术之一。
主成分分析(Principal Component Analysis,简称PCA)是一种通过降维的方法来简化数据集的技术。
它的基本思想是通过线性组合将原始数据变换为一组新的变量,这些新变量称为主成分,它们能够尽量保留原始数据的信息。
主成分分析通过将原始数据投影到主成分上,实现数据维度的压缩和去除冗余信息。
在多元统计分析中,主成分分析被广泛应用于数据预处理、变量选择和模型建立等环节。
通过主成分分析,可以将原始的高维数据转化为少数几个主成分,从而降低数据的维度,减少模型的复杂度,同时保留了原始数据中的主要信息,有助于提取数据的潜在结构和进行更有效的数据分析。
二、主成分分析的应用1. 数据可视化主成分分析可以帮助我们对高维数据进行可视化分析。
通过将数据投影到低维的主成分上,我们可以将原始数据在二维或三维空间中进行可视化展示。
这样可以更直观地观察数据之间的关系,发现异常值和聚类结构,为后续的模型建立提供重要的参考。
2. 数据预处理在建立统计模型之前,通常需要对数据进行预处理。
主成分分析可以作为一种预处理方法,通过去除原始数据中的冗余信息和噪声,减少数据维度,提高模型的建模效率和精度。
主成分分析还可以用于数据的标准化和归一化,使得不同变量之间具有可比性,更好地满足模型的要求。
3. 变量选择在众多的变量中选择对目标变量具有显著影响的变量是建立高效模型的关键一步。
主成分分析可以通过计算各个主成分的贡献率或者变量的负荷量,来评估每个变量对数据的影响程度。

应用多元统计分析作业(一)——主成分分析 8‐1:用主成分分析方法探讨城市工业主体结构。
解:执行SAS程序代码:data dxiti81;input number x1-x8;cards;1 90342 52455 101091 19272 82 16.1 197435 0.1722 4903 1973 2035 10313 34.2 7.1 592077 0.0033 6735 21139 3767 1780 36.1 8.2 726396 0.0034 49454 36241 81557 22504 98.1 25.9 348226 0.9855 139190 203505 215898 10609 93.2 12.6 139572 0.6286 12215 16219 10351 6382 62.5 8.7 145818 0.0667 2372 6572 8103 12329 184.4 22.2 20921 0.1528 11062 23078 54935 23804 370.4 41 65486 0.2639 17111 23907 52108 21796 221.5 21.5 63806 0.27610 1206 3930 6126 15586 330.4 29.5 1840 0.43711 2150 5704 6200 10870 184.2 12 8913 0.27412 5251 6155 10383 16875 146.4 27.5 78796 0.15113 14341 13203 19396 14691 94.6 17.8 6354 1.574;proc princomp data=dxiti81 out=oxiti81;var x1-x8;run;proc sort data=oxiti81;by prin1;proc print;id number;var prin1;run;proc sort data=oxiti81;by prin2;proc print;id number;var prin2;run;proc sort data=oxiti81;by prin3;proc print;id number;var prin3;run;proc plot;plot prin2*prin1=number;run;proc cluster data=oxiti81 method=ave pseudo ccc outtree=tr81;var x1-x8;id number;proc tree data=tr81 horizontal graphics;run;结果分析:◆我们使用原始数据的相关系数矩阵计算特征根矩阵。


多元应用分析第七章主成分分析1.对全国30个省市自治区经济发展基本情况的八项指标作主成分分析。
Spss-分析-描述统计-描述对变量进行标准化如下图分析-降维-因子分析将标准化后的变量添加进变量框在描述中勾选相关矩阵—系数、球形度检验1.在抽取—勾选碎石图以及协方差矩阵2.在抽取—勾选碎石图以及相关性矩阵两个作对比在得分中勾选显示因子得分系数矩阵在选项中系数显示按大小排序其他保持默认状态,点击确定输出结果相关系数矩阵可以看出许多变量存在较强的相关关系,有必要进行因子分析,且相关系数的检验值多数较小。
球面结构检验结果KMO 和 Bartlett 的检验取样足够度的 Kaiser-Meyer-Olkin 度量。
.585Bartlett 的球形度检验近似卡方203.134 df 28 Sig. .000从下图看,除X2、X4外,如下变量共同度都大于0.8,即三个因子较好的解释了八个变量公因子方差初始提取Zscore<GDP_X1> 1.000 .954Zscore<居民消费水平X2> 1.000 .609Zscore<固定资产投入x3> 1.000 .912Zscore<职工平均工资x4> 1.000 .785Zscore<货物周转量x5> 1.000 .825Zscore<居民消费价格指数X6>1.000 .906Zscore<商品零售价格指数X7>1.000 .907Zscore<工业总产值X8> 1.000 .893提取方法:主成份分析。
提取的三个主成分是:固定资产投入X3、商品零售价格指数X7、居民消费价格Zscore<固定资产投入x3> .923 -.031 .243 .923 -.031 .243 Zscore<工业总产值X8> .868 .295 .228 .868 .295 .228 Zscore<货物周转量x5> .629 .618 -.217 .629 .618 -.217 Zscore<职工平均工资x4> .302 -.772 .314 .302 -.772 .314-.510 .737 .323 -.510 .737 .323 Zscore<商品零售价格指数X7>-.491 .392 .715 -.491 .392 .715 Zscore<居民消费价格指数X6>Zscore<居民消费水平X2> -.028 -.327 .708 -.028 -.327 .708 提取方法 :主成份。

