下载文档原格式
请打双面习题与综合训练 第一章2-1 一单层房屋结构可简化为题2-1图所示的模型，房顶质量为m ，视为一刚性杆；柱子高h ，视为无质量的弹性杆，其抗弯刚度为EJ 。
求该房屋作水平方向振动时的固有频率。
解：由于两根杆都是弹性的，可以看作是两根相同的弹簧的并联。
等效弹簧系数为k则其中为两根杆的静形变量，由材料力学易知=则 =设静平衡位置水平向右为正方向，则有所以固有频率2-2 一均质等直杆，长为 l ，重量为W ，用两根长h 的相同的铅垂线悬挂成水平位置，如题2-2图所示。
试写出此杆绕通过重心的铅垂轴作微摆动的振动微分方程，并求出振动固有周期。
解：给杆一个微转角θθ＝h α2F ＝mg由动量矩定理： 其中2-3 求题2-3图中系统的固有频率，悬臂梁端点的刚度分别是和，悬臂梁的质量忽略不计。
解：悬臂梁可看成刚度分别为k 1和k 3的弹簧，因此，k 1与k 2串联，设总刚度为k 1ˊ。
k 1ˊ与k 3并联，设总刚度为k 2ˊ。
k 2ˊ与k 4串联，设总刚度为k 。
即为，，2-4 求题2-4图所示的阶梯轴一圆盘系统扭转振动的固有频率。
其中、和是mg k δ=δδ324mgh EJ =k 324EJ h "m x kx =-3n 24mh EJ p =2aah a mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ12cossin ≈≈θααh l ga p ha mg ml n 22222304121==⋅+θθg h a l ga h l p T n 3π23π2π222===1k 3k 21211k k k k k+='212132k k kk k k ++='4241213231421432421k k k k k k k k k k k k k k k k k k k k ++++++=)(42412132314214324212k k k k k k k k k k m k k k k k k k k k p ++++++=1J 2J 3J θF sin α2θαFhmgθF三个轴段截面的极惯性矩，I 是圆盘的转动惯量，各个轴段的转动惯量不计，材料剪切弹性模量为G 。
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。
求系统的固有频率。
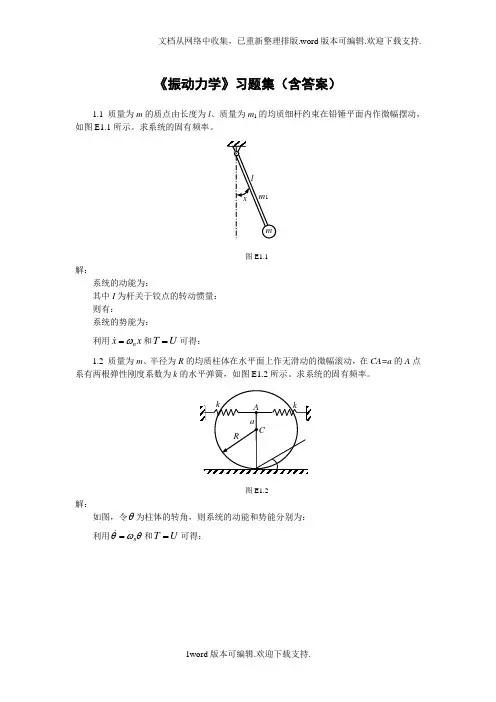
图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。
求系统的固有频率。
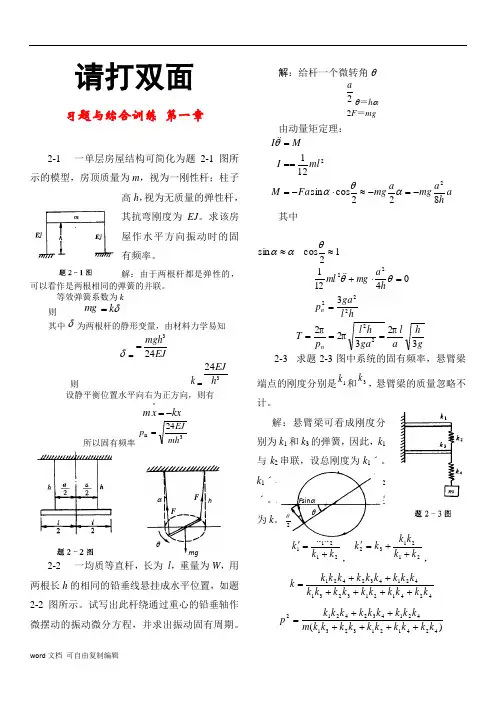
图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。
求系统的固有频率。
图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。
《振动力学》习题集（含答案）1.1质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动， 如图E1.1所示。
求系统的固有频率。
lxm 1 m 图E1.1解：系统的动能为： T 1 2 m x l 2 1 2I x2 其中I 为杆关于铰点的转动惯量： I l 0 m 1 l dx 2 x l 0 m 1 lx 2 dx 1 3 ml 1 2 则有： T 1 2 ml 11 22223 xmlx1 66m m 1 l 2 2 x 系统的势能为： Umgl1cosx mg 1 l 21 cos x1 2mglx 2 1 4 mglx 1 21 42m m 1 glx2 n 和TU 可得： 利用xx 32m m 1 gn23mm 1l1.2质量为m、半径为R的均质柱体在水平面上作无滑动的微幅滚动，在CA=a的A点系有两根弹性刚度系数为k的水平弹簧，如图E1.2所示。
求系统的固有频率。
kAaCR图E1.2解：如图，令为柱体的转角，则系统的动能和势能分别为：T 12I B212mR212mR2234mR22U122kRakRa222利用n和TU可得：24kRaRa4kn23mRR3m1.3转动惯量为J 的圆盘由三段抗扭刚度分别为 k ，k 和 12k 的轴约束，如图E1.3所示。
3 求系统的固有频率。
Jk1k2k3图E1.3解：系统的动能为：1 2TJ2k 和k 3相当于串联，则有： 22,kk32233 以上两式联立可得：k 3 2,kk 233k 2 k 2 k 3系统的势能为：U 1 2 k 1 2 1 2 k 2 2 2 1 2 k 3 2 3 1 2 k 1 k 2 k 2 k 3 k3k k 2 3 2 利用n 和TU 可得： kk 23 k 1 k 2 k 3nJ k 2 k 31.4在图E1.4所示的系统中，已知kimab i1,2,3,,和，横杆质量不计。
求固有 频率。
《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示，重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置，另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
解：222221v gW h W =，gh v 22=动量守恒：122122v gW W v g W +=，gh W W W v 221212+=平衡位置：11kx W =，kW x 11=1221kx W W =+，kW W x 2112+=故：kW x x x 21120=-= ()2121W W kgg W W k n +=+=ω故：tv t x txt x x n nn n nn ωωωωωωsin cos sin cos 12000+-=+-=xx 0x 1x 12平衡位置2-2 一均质等直杆，长为l ，重量为w ，用两根长h 的相同的铅垂线悬挂成水平位置，如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程，并求出振动固有周期。
解：给杆一个微转角θ2aθ＝h α2F ＝mg由动量矩定理：ah a mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ其中12cossin ≈≈θααh l ga p ha mg ml n 22222304121==⋅+θθ g h a l ga h l p T n 3π23π2π222===2-3 一半圆薄壁筒，平均半径为R , 置于粗糙平面上做微幅摆动，如图2-3所示。
试求其摆动的固有频率。
图2-3 图2-42-4 如图2-4 所示，一质量m连接在一刚性杆上，杆的质量忽略不计，试求下列情况系统作垂直振动的固有频率：（1）振动过程中杆被约束保持水平位置；（2）杆可以在铅垂平面内微幅转动；（3）比较上述两种情况中哪种的固有频率较高，并说明理由。
图T 2-9 答案图T 2-9解：（1）保持水平位置：m kk n 21+=ω（2）微幅转动：mglllF2112+=mgl1l2xx2xx'mglll2121+=k2k1ml1l2()()()()()()()()()mgk k l l k l k l mgk k l l k l l k l l l k l mg k k l l k l k l l l l k l l mg l mgk l l l k l l l l l l k l l mg l l l l x x k F x x x 2122122212121221221121212221212211211121212122211211121221112111 ++=+-++=+-⋅+++=⎥⎦⎤⎢⎣⎡+-++++=+-+='+=故：()22212121221k l k l k k l l k e++=mk en =ω 2-5 试求图2-5所示系统中均质刚性杆AB 在A 点的等效质量。
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。
求系统的固有频率。
图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。
求系统的固有频率。
图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。
求系统的固有频率。
图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。
第7章 弹性体振动7-3 一端受弹簧支承的均质杆,试导出其频率方程。
解: 左端边界条件(0,)0u t =， 右端边界条件：(,)(,)x l x lu x t EAku x t x ==∂=-∂。
则关于固有振型的边界条件为()(0)0,()x ld x EAk l dx =ΦΦ==-Φ代入振型函数，得到频率方程：cot ξξη=，其中：kl EAξω==-当依次计算出正根i ξ(i ＝1，2，…)后，即可计算出固有频率和相应的固有振型i ω=，()()sini i i x x A lξΦ= ，(i ＝1，2，…)。
7-7 求如图所示均质杆纵向振动u (x 、t )的稳态响应。
解: （1）边界条件(0,)0u t =，(,)0x lu x t EAx =∂=∂。
关于固有振型的边界条件(0)0,()0l 'Φ=Φ=，代入振型函数，得到频率方程： cos 0l aω=，固有频率与相应的固有振型为i ω=，()(21)()sin2i i i xx A lπ-Φ= ，(i ＝1，2，…)。
（2）由正规化条件1li i A dx ρ=⎰ΦΦ确定系数A i后得到(21)()2i i xx lπ-=Φ。
（3）标准标准下的响应方程211()()()sin i i i i i q q x F t x F t ωω+==ΦΦ，由单自由度谐和激励下的响应公式得：22()(21)()sin sin (1)2i i i i l Fi q t t t t πωωωωω+-===--Φ （4）广义坐标响应122112(21)(,)()()(1)sin sin 2i i i i i i F i xu x t x q t t Al lπωρωω∞∞+==-==--∑∑Φ。
7-8 一简支梁在中间受荷载作用下挠曲10mm ，若激振力加在同一位置且ω/ω1=1/2，其中ω1为梁的基频，求其稳态响应。
解: （1）由边界条件得出简支梁的频率方程为sin 0l β=，固有频率和固有振型为2i ia ωβ=()()sini i xx C lπΦ=（i ＝1，2，……） （2）由正规化条件1li i A dx ρ=⎰ΦΦ确定系数A i后得到()()i i x x lπΦ=。
题 7-3 图t )Fsinωt题 7-7 图（3）标准标准下的响应方程211()()()sin i i i i i q q x F t x F t ωω+==ΦΦ， 由题意知31048Fl EI =，3480EI F l =，212122EIl πωωρ==由单自由度谐和激励下的响应公式得：2222(/2)2()sin sin sin 2i i i i l FF i q t t t l πωωωωρωω==--Φ（4）广义坐标响应22112(,)()()sin sin sin 2iii i i F i i x u x t x q t t l l ππωρωω∞∞====-∑∑Φ。
【说明：以下习题中，各均质杆、弦或梁的部分参数都相同，长度为l ，横截面积为A ，弹性模量为E ，截面惯性矩为I ，单位体积的质量为ρ ，单位长度的质量为l ρ】7-12 均质简支梁若受如图所示突加分布载荷()cxp x t l=、的作用求其动响应。
解: （1）由边界条件得出简支梁的频率方程为sin 0l β=，固有频率和固有振型为2222i ii EIa lπωβρ==，()()sini i xx C lπΦ=（i ＝1，2，……） （2）由正规化条件1li i A dx ρ=⎰ΦΦ确定系数A i 后得到()2()sin i i x x l lπρΦ=。
（3）由杜哈美积分计算广义坐标响应。
1(,)(,)sin[()]ltii i i iu x t f x t d dx τωττω∞==-∑⎰⎰ΦΦ00121sin sin sin[()]l t i i ii x i x cxt d dx l l l l ππωττρω∞==-∑⎰⎰=…… 7.13 一根两端固定的弦，在弦线上作用着均匀分布的横向力f （x ，t ），方向铅垂向上。
证明弦的振动微分方程为：22(,)(,)()(,)()()y x t y x t F x f x t x A x x x t ρ∂∂∂⎡⎤+=⎢⎥∂∂∂⎣⎦证明：F 为张力。
研究长度为d x 的微元体有 22sin sin y F Adx F dx dx F fdx t x x θρθθ∂∂∂⎛⎫⎛⎫=++-+ ⎪ ⎪∂∂∂⎝⎭⎝⎭xlc题 7-12 图f d xFF dx x∂+∂微振动时展开sin dx x θθ∂⎛⎫+ ⎪∂⎝⎭得sin sin dx dx x x θθθθ∂∂⎛⎫+≈+ ⎪∂∂⎝⎭ 代入前式忽略高价微量且yxθ∂=∂得 22sin y FAdx F dx dx fdx t x x θρθ∂∂∂=++∂∂∂()F dx fdx xθ∂=+∂ 即22(,)(,)()(,)()()y x t y x t F x f x t x A x x x t ρ∂∂∂⎡⎤+=⎢⎥∂∂∂⎣⎦。
7.14 设弦振动的振型()sinn n n xU x C l π=中，C n为待定常数，用正规化方法证明n C = 证明：将()sinn n n xU x C lπ=代入由正规化条件01ln n U AU dx ρ=⎰即可求得n C =7.15左端固定的杆，右端连接一刚度为k 的弹簧，试导出杆纵向振动的主振型相对于刚度的正交条件为：0()()()()0li j i j EA U x U x dx kU l U l ''+=⎰。
解: 求出频率方程：cot ξξη=，其中：klEAξωη==-。
当依次计算出正根n ξ(n ＝1，2，…)后，即可计算出固有频率和相应的固有振型n ω=()sinn n n x U x A lξ= ，(n ＝1，2，…)。
将分离变量解代入波动方程得2221()1()()()()()d q t d dU x EA x q t dt A x U x dx dx ωρ⎛⎫==- ⎪⎝⎭则第i ，j 阶振型函数满足2i i i d dU EA AU dx dx ωρ⎛⎫=- ⎪⎝⎭，2j j j dU d EA AU dx dx ωρ⎛⎫=- ⎪⎝⎭分别用U j ，U i 乘上两式两端，并积分()20000[]ll l l j i j i i j i j i d U EAU dx EAU U EAU U dx U AU dx dx ωρ''''=-=-⎰⎰⎰ ()20000[]l l l l i j j i i j j j i d U EAU dx EAU U EAU U dx U AU dx dx ωρ''''=-=-⎰⎰⎰ 根据边界条件()(0)0,()x ldU x U EAkU l dx ===-，上两式变为20()()ll i j i j i j i kU l U l EAU U dx U AU dx ωρ''--=-⎰⎰20()()lli j i j jjikU l U l EAU U dx U AU dx ωρ''--=-⎰⎰两式相减22()0li j j i U AU dx ωωρ-=⎰，即得两个正交条件0lj i U AU dx ρ=⎰，0()()()()0li j i j EA U x U x dx kU l U l ''+=⎰。
7.16 左端固定右端自由的杆，已知左端支承相当于地面的纵向运动为200(/)s u u t t =，在初瞬时杆静止。
试确定支承运动引起杆纵向振动的响应。
解: （1）同题7.7，固有频率与相应的固有振型为i ω=，(21)()2i i xx lπ-=Φ，(i ＝1，2，…)。
（2）相对基础的响应22001(,)sin[()]l tisr i i i id u u x t A t d dx dt ρωττω∞==--∑⎰⎰ΦΦ02102sin[()]ltii i i i u At d dx t ρωττω∞==--∑⎰⎰ΦΦ 02201022(21)(21)(1cos )sin sin 22l i i i u A i x i xt dx t Al l l ρππωωρ∞=--=--∑⎰ 022108(21)(1cos )sin (21)2i i i u i x t t i lπωωπ∞=-=---∑221,3,5081sin 2i i u i xt i lπωπ∞=⎛=-- ⎝∑响应：200221,3,5008(,)(,)(12s r i i t u i xu x t u u x t u t t i lπωπ∞=⎛⎫=+=-- ⎪⎝⎭∑。
7.20 一杆左端固定，左端自由，假设杆的右半部分在t ＝0时具有沿轴向的初速度v 0，试求杆纵向振动的响应。
解: （1）同题7.7，固有频率与相应的固有振型为i ω=，(21)()2i i xx lπ-=Φ，(i ＝1，2，…)。
（2）初始条件：000()0,()(/2)u x u x v l x l ==≤≤变换到标准坐标下000()0li i q A u x dx ρ==⎰Φ，0000/2(21)()2lli i l i x q A u x dx v dx l πρρ-==⎰⎰Φ(21)4i π-= （3）响应011(,)()()()sin i ii i i i i iq u x t x q t x t ωω∞∞===Φ=Φ∑∑1(21)1(21)cos sin 2(21)4i ii x i t l i ππωω∞=--=- 21,3,51cos sin 42i i x i l ππ∞==∑。
