6-5、6第五节 宇宙航行

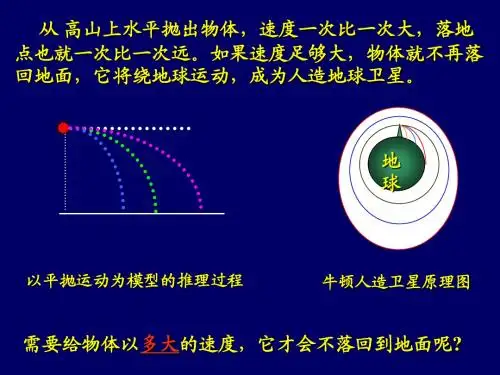
6-5 宇宙航行一宇宙速度1.第一宇宙速度（1）第一宇宙速度的推导第一宇宙速度也叫环绕速度，是人造卫星在地面附近绕地球做匀速圆周运动的速度。

推导地球的第一宇宙速度的方法：【推导1】设地球的质量为M，半径为R，近地卫星质量为m，环绕速度为v1，由万有引力定律和牛顿第二定律有 G MmR2=m v12R，把R＝6400 km 和M＝6×1024kg 代入计算得地球的环绕速度v1=√GMR=7.9km/s 。

【推导2】在地面附近，万有引力近似等于重力。

设g为地球表面重力加速度，g＝9.8m/s2。

由人造地球卫星的重力为其环绕地球运动提供向心力，有mg=m v12R，所以v1=√gR=7.9km/s 。

每个星球都有自己的宇宙速度，并且不同星球上的宇宙速度并不相同。

上述两种推导地球第一宇宙速度的方法，也可以推广应用到其他星球上去，即知道了某个星球的质量M和半径R，或该星球的半径R及星球表面的重力加速度g，可以用同样的方法，求得该星球上的第一宇宙速度。

（2）第一宇宙速度的深层含义【含义1】第一宇宙速度是人造地球卫星的最大环绕速度如图所示，一质量为m的卫星在距地心r（r大于地球半径）的圆轨道上做匀速圆周运动。

由上述第一宇宙速度推导相同的方法可得运行速度 v2=√GMr，由于r＞R，所以v2＜v1，即v1=7.9km/s 是人造地球卫星的最大环绕速度。

【含义2】第一宇宙速度是人造地球卫星的最小发射速度如图所示，一质量为m的卫星在地面被发射入轨，设发射速度为v3，若v3=v1，则G MmR2=m v32R，即卫星恰在地面附近环绕地球做匀速圆周运动。

若v3＜v1，则G MmR2＞m v32R，此时万有引力大于卫星所需的向心力，卫星将做靠近地心的运动而落回地面。

可见，要将卫星送入轨道，需v3≥v1＝7.9km/s ，即人造地球卫星的最小地面发射速度为v1=7.9km/s 。

2.第二宇宙速度（脱离速度）在地面上发射物体，使之能够脱离地球的引力作用，成为绕太阳运行的人造卫星或飞到其他行星上所必需的最小发射速度，成为第二宇宙速度，其大小为v2=11.2km/s 。

《宇宙航行》说课稿尊敬的各位领导，各位老师，大家好。

今天我说课的题目选自人教版高中物理必修二第六章第五节《宇宙航行》。

下面我将从教材分析、学情分析，教学目标、教学重难点、教学方法、教学程序、作业设计与板书设计几个的方面进行阐述。

一、教材分析《宇宙航行》是新课程人教版必修二第六章第五节的内容，本节课是以学生前面已掌握的平抛运动、圆周运动和向心力等知识以及万有引力定律为基础，重点推导了第一宇宙速度，介绍了第二、第三宇宙速度。

通过对人造卫星、宇宙速度的介绍，使学生对航天科学产生兴趣，增强民族自信心和自豪感。

是学生进一步学习研究天体物理问题的基础。

二、学情分析从学生年龄特征来看，大多是00后出生，他们已经对本节知识有一定的接受能力，但是对知识体系条理性掌握，对易混淆知识的辨别能力还欠缺。

从学生的知识基础来看，本节与第五章息息相关，不同水平的学生学起来认知程度不一样。

从认知特点及思维规律来看，学生容易接收表象、浅显的知识，不易接收推理性强、易混淆的知识。

因此在教学过程中教师要作合理的引导。

三、教学目标1、知识与技能（1）知道三个宇宙速度的含义和数值，会推导第一宇宙速度。

（2）会解决涉及人造地球卫星运动的较简单的问题。

（3）理解卫星的运行速度、角速度、周期、向心加速度与轨道半径的关系。

2、过程与方法(1)在学习牛顿对卫星发射猜想的同时，培养学生科学探索能力；(2)培养学生在处理实际问题时，如何构建物理模型的能力。

3、情感态度与价值观（1）通过展示人类在宇宙航行领域中的伟大成就，激发学生学习物理知识的热情。

（2）通过介绍我国在航天方面的成就，激发学生的爱国热情，增强民族自信心和自豪感。

（3）感知人类探索宇宙的梦想，促使学生树立献身科学的人生观和价值观。

四、教学重点依据课程标准要求和本节教材实际，并结合课后习题，确定本节的教学重点为：宇宙第一速度的推导过程和方法，了解第一宇宙速度的应用领域。

因为高一学生思维还不够敏捷，很难做到大跨度的思维跳跃，对于人造卫星、宇宙飞船等高科技产品，学生在学习时往往存在一定的心里障碍。

第六章 第五、六节1．关于第一宇宙速度，下列说法正确的是( ) A ．它是人造地球卫星绕地球飞行的最小速度 B ．它是近地圆轨道上人造地球卫星的运行速度 C ．它是使卫星进入近地圆轨道的最小发射速度 D ．它是卫星在椭圆轨道上运行时在远地点的速度解析：第一宇宙速度是卫星的最小发射速度、最大绕行速度．故选B 、C. 答案：BC2．现有两颗绕地球做匀速圆周运动的人造地球卫星A 和B ，它们的轨道半径分别为r A 和r B 如果r A ＞r B ，则( )A ．卫星A 的运动周期比卫星B 的运动周期大 B ．卫星A 的线速度比卫星B 的线速度大C ．卫星A 的角速度比卫星B 的角速度大D ．卫星A 的加速度比卫星B 的加速度大 解析：由G Mmr 2＝m v 2r ＝m ω2r得v ＝GMr，ω＝ GMr 3又T ＝2πω＝2πr 3GM由此分析A 正确． 答案：A3．土卫十和土卫十一是土星的两颗卫星，都沿近似为圆周的轨道绕土星运动，其参数如表：A ．受土星的万有引力较大B ．绕土星做圆周运动的周期较大C ．绕土星做圆周运动的向心加速度较大D ．动能较大解析：设土星质量为M ，其卫星质量为m ，卫星轨道半径为r ，土星对卫星的万有引力F引＝G Mmr 2，M 不变，r 相同，则m 大的受到的引力大，故A 正确．再由G Mm r 2＝ma n ＝m 4π2T 2r ＝m v 2r可知：T ＝2πr 3GM ，a n ＝GMr2，因轨道半径相同，则两卫星的周期、向心加速度都相同，故B 、C 错．卫星的动能E k ＝12m v 2＝G Mm2r ，则m 大的E k 大，故D 正确．答案：AD4．探测器绕月球做匀速圆周运动，变轨后在周期较小的轨道上仍做匀速圆周运动，则变轨后与变轨前相比( )A ．轨道半径变小B ．向心加速度变小C ．线速度变小D ．角速度变小解析：探测器做匀速圆周运动由万有引力提供向心力，则：G Mm r 2＝m 4π2T 2r ，整理得T ＝2πr 3GM，可知周期T 较小的轨道，其半径r 也小，A 正确； 由G Mm r 2＝ma n ＝m v 2r ＝mrω2，整理得：a n ＝G Mr2，v ＝GMr，ω＝GMr 3，可知半径变小，向心加速度变大，线速度变大，角速度变大，故B 、C 、D 错误．答案：A5．在地球上发射一颗近地卫星需7.9 km/s 的速度，在月球上发射的近月卫星需要多大速度？(已知地球和月球质量之比M 地∶M 月＝81∶1，半径之比R 地∶R 月＝4∶1)解析：设卫星的环绕速度为v ，则由G MmR 2＝m v 2R ，得v ＝GMR ，所以v 月v 地＝ M 月R 地M 地R 月＝ 1×481×1＝29， 解得v 月＝29v 地＝1.76 km/s.答案：1.76 km/s(时间：45分钟满分：60分)1.如图所示中的圆a、b、c，其圆心均在地球的自转轴线上．b、c的圆心与地心重合，对卫星环绕地球做匀速圆周运动而言()A．卫星的轨道可能为aB．卫星的轨道可能为bC．卫星的轨道可能为cD．同步卫星的轨道只可能为b解析：卫星轨道的中心与地球中心重合，这样的卫星轨道才可能存在．故可能为B、C.同步卫星轨道只能与赤道是共面同心圆．故D对．答案：BCD2．人造地球卫星的轨道半径越大，则()A．速度越小，周期越小B．速度越小，加速度越小C．加速度越小，周期越大D．角速度越小，加速度越大解析：由v＝GMr，ω＝GMr3，T＝4π2r3GM，a＝GMr2，可得出B、C选项正确．答案：BC3．在轨道上运行的人造地球卫星，若卫星上的天线突然折断，则天线将() A．做自由落体运动B．做平抛运动C．和卫星一起绕地球在同一轨道上运行D．由于惯性沿轨道切线方向做直线运动解析：折断的天线由于惯性而具有卫星原来的速度，在地球引力作用下继续在原轨道上运行，故选C.明确折断的天线与卫星具有相同的运动情况和受力情况是解题的关键．答案：C4．甲、乙为两颗地球卫星，其中甲为地球同步卫星，乙的运行高度低于甲的运行高度，两卫星轨道均可视为圆轨道．以下判断正确的是( )A ．甲的周期大于乙的周期B ．乙的速度大于第一宇宙速度C ．甲的加速度小于乙的加速度D ．甲在运行时能经过北极的正上方解析：地球卫星绕地球做圆周运动时，万有引力提供向心力，由牛顿第二定律知G Mm r 2＝m 4π2rT2，得T ＝2π r 3GM .r 甲>r 乙，故T 甲>T 乙，选项A 正确；贴近地球表面运行的卫星的速度称为第一宇宙速度，由G Mm r 2＝m v2r 知v ＝GMr，r 乙>R 地，故v 乙比第一宇宙速度小，选项B 错误；由G Mm r 2＝ma ，知a ＝GMr 2，r 甲>r 乙，故a 甲<a 乙，选项C 正确；同步卫星在赤道正上方运行，故不能通过北极正上方，选项D 错误．答案：AC5．若取地球的第一宇宙速度为8 km/s ，某行星质量是地球的6倍，半径是地球的1.5倍，此行星的第一宇宙速度约为( )A ．16 km/sB ．32 km/sC ．4 km/sD ．2 km/s解析：第一宇宙速度是近地卫星的环绕速度，对于近地卫星其轨道半径近似等于星球半径，所受万有引力提供其做匀速圆周运动的向心力，根据万有引力定律和牛顿第二定律得：G Mmr 2＝m v 2r，解得：v ＝ GMr .因为行星的质量M ′是地球质量M 的6倍，半径R ′是地球半径R 的1.5倍，故v ′v ＝GM ′R ′GM R＝ M ′RMR ′＝2， 即v ′＝2v ＝2×8 km/s ＝16 km/s ，A 对．答案：A6．1989年10月18日，人类发射的“伽利略”号木星探测器进入太空，于1995年12月7日到达木星附近，然后绕木星运转并不断发回拍摄到的照片，人类发射该探测器的发射速度应为( )A ．等于7.9 km/sB ．大于7.9 km/s 而小于11.2 km/sC ．大于11.2 km/s 而小于16.7 km/sD ．大于16.7 km/s解析：要到达木星，发射速度应介于第二宇宙速度与第三宇宙速度之间，故选C. 答案：C7．关于人造地球卫星及其中物体的超重、失重问题，下列说法中正确的是( ) A ．在发射过程中向上加速时产生超重现象 B ．在降落过程中向下减速时产生超重现象 C ．进入轨道时做匀速圆周运动，产生失重现象D ．失重是由于地球对卫星内物体的作用力减小而引起的解析：超、失重是一种表象，是从重力和弹力的大小关系而定义的．当向上加速时超重，向下减速时(a 方向向上)也超重，故A 、B 正确．卫星做匀速圆周运动时，万有引力完全提供向心力，卫星及卫星内的物体皆处于完全失重状态，故C 正确．失重的原因是重力(或万有引力)使物体产生了向心加速度，故D 错．答案：ABC8．某同学设想驾驶一辆“陆地—太空”两用汽车，沿地球赤道行驶并且汽车相对于地球速度可以增加到足够大．当汽车速度增加到某一值时，它将成为脱离地面绕地球做圆周运动的“航天汽车”．不计空气阻力，已知地球的半径R ＝6 400 km.下列说法正确的是( )A ．汽车在地面上速度增加时，它对地面的压力增大B ．当汽车速度增加到7.9 km/s ，将离开地面绕地球做圆周运动C ．此“航天汽车”环绕地球做圆周运动的最小周期为1 hD ．在此“航天汽车”上可以用弹簧测力计测量物体的重力解析：由mg －N ＝m v 2R 得N ＝mg －m v 2R ，可知A 错；7.9 km/s 是最小的发射速度，也是最大的环绕速度，B 对；由mg ＝m ⎝⎛⎭⎫2πT 2R 知T ＝84分钟，C 错；“航天汽车”上处于完全失重状态，任何与重力有关的实验都无法进行，D 错．答案：B二、非选择题(共2个小题，每题10分，共20分)9．一颗人造地球卫星在离地面高度等于地球半径的圆形轨道上运行，已知地球的第一宇宙速度是v 1＝7.9 km/s ，问：(1)这颗卫星运行的线速度多大？ (2)它绕地球运动的向心加速度多大？(3)质量为1 kg 的仪器放在卫星内的平台上，仪器的重力多大？它对平台的压力多大？ 解析：(1)卫星近地运行时，有：G Mm R 2＝m v 21R 卫星离地高度为R 时，有：G Mm 4R 2＝m v 222R ，从而可得v 2＝5.6 km/s.(2)卫星离地高度为R 时，有：G Mm 4R 2＝ma ；靠近地面时，有：G MmR 2＝mg ，从而可得a ＝g /4＝2.45 m/s 2.(3)在卫星内，仪器的重力就是地球对它的吸引力，则：G ′＝mg ′＝ma ＝2.45 N ；由于卫星内仪器的重力充当向心力，仪器处于完全失重状态，所以仪器对平台的压力为零．答案：(1)5.6 km/s (2)2.45 m/s 2 (3)2.45 N 010．已知地球的半径为R ＝6 400 km ，地球表面附近的重力加速度g ＝9.8 m/s 2，若发射一颗地球的同步卫星，使它在赤道上空运转，其高度和速度应为多大？解析：设同步卫星的质量为m ，离地面的高度为h ，速度为v ，周期为T ，地球的质量为M ，同步卫星的周期等于地球自转的周期．G MmR2＝mg① G Mm (R ＋h )2＝m (R ＋h )⎝⎛⎭⎫2πT 2②由①②式得h ＝3R 2T 2g 4π2－R＝3(6 400×103)2×(24×3 600)2×9.84×3.142 m－6 400×103 m ≈3.6×107 m. 又因为G Mm(R ＋h )2＝m v 2R ＋h③由①③式得v＝R2g R＋h＝(6 400×103)2×9.86 400×103＋3.6×107m/s≈3.1×103 m/s.答案：3.6×107 m 3.1×103 m/s。