1傅里叶分析解析

1的傅里叶反变换过程1. 任务介绍本文将深入探讨1的傅里叶反变换过程。

我们将介绍傅里叶变换的基本概念，并通过示例逐步演示1的傅里叶反变换过程。

傅里叶变换是一种将时域信号转换为频域信号的数学工具，而傅里叶反变换则将频域信号转换回时域信号。

2. 傅里叶变换基础知识傅里叶变换的核心思想是将一个信号分解为一系列复杂振幅和相位的正弦和余弦波。

这些正弦和余弦波的频率范围从低频到高频，并且每个正弦和余弦波都有不同的振幅和相位。

傅里叶变换通过将信号从时间域转换为频域，使我们能够分析信号的频率成分。

傅里叶变换的数学表达式如下：F(ω) = ∫[f(t) * e^(-iωt)] dt其中，F(ω)表示频域中的信号，f(t)表示时域中的信号，ω表示角频率，e^(-iωt)为欧拉公式。

3. 傅里叶反变换的定义傅里叶反变换是傅里叶变换的逆过程，它将频域中的信号转换回时域。

傅里叶反变换的数学表达式如下：f(t) = 1/(2π) * ∫[F(ω) * e^(iωt)] dω其中，f(t)表示时域中的信号，F(ω)表示频域中的信号，e^(iωt)为欧拉公式。

4. 1的傅里叶反变换示例为了更好地理解1的傅里叶反变换过程，我们将通过一个示例来演示每个步骤。

假设我们有一个频域信号F(ω)，它的值如下：F(ω) = {1, 2, 3, 4, 5, 4, 3, 2, 1}步骤1：求解反变换的积分根据傅里叶反变换的数学表达式，我们需要计算积分：f(t) = 1/(2π) * ∫[F(ω) * e^(iωt)] dω在这个例子中，我们需要计算频域信号F(ω)与函数e^(iωt)的乘积并进行积分。

步骤2：计算傅里叶反变换将频域信号F(ω)与函数e^(iωt)相乘并进行积分计算，得到1的傅里叶反变换f(t)。

计算的结果如下：f(t) = 1/(2π) * [1 * e^(iωt) + 2 * e^(2iωt) + 3 * e^(3iωt) + 4 * e^(4iωt)+ 5 * e^(5iωt) + 4 * e^(4iωt) + 3 * e^(3iωt) + 2 * e^(2iωt) + 1 * e^(iωt)]整理化简上述表达式得到：f(t) = 1/(2π) * [e^(iωt) + 2 * e^(2iωt) + 3 * e^(3iωt) + 4 * (e^(4iωt) +e^(-4iωt)) + 5 * e^(5iωt)]步骤3：化简傅里叶反变换为了使傅里叶反变换结果更简洁，我们可以进一步对傅里叶反变换表达式进行化简。

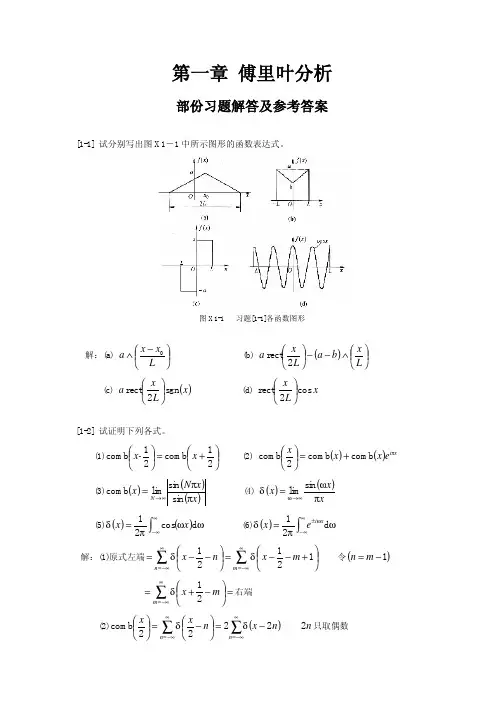
第一章 傅里叶分析部份习题解答及参考答案[1-1] 试分别写出图X1－1中所示图形的函数表达式。

图X1-1 习题[1-1]各函数图形解：(a)−∧L x x a 0 (b) () ∧−−L x b a L x a 2rect(c) ()x L x a sgn 2rect (d) x L x cos 2rect[1-2] 试证明下列各式。

(1) += 21comb 21comb x x- (2) ()()x i e x x x πcomb comb 2comb +=(3)()()()x x N x N ππsin sin lim comb ∞→= (4) ()()xx x πωδωsin lim ∞→=(5)()()∫∞∞−=ωωπδd cos 21x x (6)()ωπδωd 21∫∞∞−±=x i e x解：(1)原式左端∑∑∞−∞=∞−∞=+−−=−−=m n m x n x 12121δδ 令()1−=m n=−+=∑∞−∞=m m x 21δ右端 (2)()∑∑∞−∞=∞−∞=−=−= n n n x n x x 2222comb δδ n 2只取偶数()()∑∞−∞=−=m m x x δcomb()()πδδππm m x e m x e x m im m x i cos 2comb ∑∑∞−∞=∞−∞=−=−=当=m 奇数时，()()0comb comb =+xi ex x π；当=m 偶数时，令n m 2=，则12 cos =x π，并且有： ()()()∑∞−∞=−=+n n x x x 22e comb comb xi δπ 得证。

(3)由公式(1-8-7)知：()∑∞−∞=−=n nxex π2i comb上式可视为等比级数求和，其前N 项之和为：()()()()()x Nx e e e e e e e e q q a S x i x i x i Nx i Nx i Nx i x i Nx i N N ππππππππππsin sin 1111221=−−=−−=−−=−−−−−− 所以 ()()()x Nx S x N N N ππsin sin limlim comb ∞→∞→==得证。

1傅里叶分析解析傅里叶分析是一种重要的数学工具，用于分析和描述周期性信号及其频谱。

在物理学、工程学和数学等领域中都有广泛的应用。

本文将介绍傅里叶分析的基本原理和方法，并探讨其在不同领域的具体应用。

傅里叶分析的基本原理是基于傅里叶级数展开定理，即任意周期信号都可以表示为一组正弦和余弦信号的叠加。

根据傅里叶级数展开定理，一个周期为T的连续信号f(t)可以表示为：f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中，a0、an和bn是待定系数，ω=2π/T是信号的角频率。

为了求解这些系数，需要利用傅里叶变换的方法，将连续信号f(t)转化为连续频率域的表示。

傅里叶变换将时域信号转换为频域信号，通过将信号分解为不同频率的正弦和余弦信号，得到信号在频域的幅度和相位信息。

在连续傅里叶变换中，信号f(t)的傅里叶变换F(ω)给出了信号在频率域的表示，其中：F(ω) = ∫[f(t)*exp(-jωt)]dt其中，j是虚数单位。

类似地，对于离散信号，可以使用离散傅里叶变换和离散傅里叶级数展开来进行分析。

离散傅里叶变换是对信号采样后的离散版本进行频域分析，而离散傅里叶级数展开则将离散信号表示为一组离散频率上的正弦和余弦波的叠加。

傅里叶分析的应用广泛，下面将介绍一些具体的应用。

1.信号处理：傅里叶分析在信号处理中有广泛的应用，例如，可以通过傅里叶变换将时域上的声音信号转换为频域上的频谱图，用于音频压缩、滤波和降噪等处理。

2.图像处理：傅里叶变换也可以应用于图像处理，将二维图像转换为频域上的频谱图，用于图像增强、去噪和特征提取等。

3.通信系统：傅里叶分析在通信系统中起到重要作用，例如，信号可以通过傅里叶变换转换为频谱图后，可以对信号进行调制、解调和信道编码等操作。

4.物理学：傅里叶分析在物理学中也有广泛的应用，例如，可以用于分析光谱、原子和分子结构以及量子力学等问题。

5.工程学：在工程学中，傅里叶分析可以用于分析和处理信号和系统的特性，包括控制系统、电路和通信系统等。

1的傅里叶反变换过程
傅里叶分析不仅在物理学、数学和工程学等领域发挥着重要作用，也在计算机科学、通信系统、图像处理和音频处理等现代科技领域得
到广泛应用。

其中，傅里叶反变换，作为傅里叶分析的基本操作之一，可将频域信号转化为时域信号，为我们理解信号的本质提供了有力支持。

傅里叶反变换是一种将频域信号转换为时域信号的数学技术。

因
为频域信号是由各种频率和幅度的正弦波组成的，傅里叶反变换通过
这些正弦波的合成，将频域信号还原成原始的时域信号。

在实际应用中，傅里叶反变换的过程通常是由计算机程序完成的，而程序中需要
用到傅里叶变换和离散傅里叶变换的知识。

在进行傅里叶反变换时，我们需要先对频域信号进行采样和量化，将其转化为离散的频域信号。

然后，我们需要使用离散傅里叶反变换
算法，将离散频域信号转化为时域信号。

在实际应用中，常用的离散
傅里叶反变换算法有快速傅里叶反变换（FFT）算法和蝶形算法。

值得注意的是，傅里叶反变换过程中可能会出现谐波失真和量化
误差等问题，因此在实际应用中需要采取相应的措施进行处理。

例如，在音频处理中，常会对采样率进行调整和滤波处理，以提高还原信号
的质量和准确度。

总之，傅里叶反变换作为一种重要的信号处理技术，在现代科技
领域发挥着越来越重要的作用。

深入理解其基本原理和计算方法，对
于实现各种信号处理任务、解决实际问题以及推动科技进步具有重要的指导意义。

傅里叶变换详细解释
傅里叶变换是数学中的一种重要分析工具，用于将一个函数表示为一系列复指数的加权和。

它得名于法国数学家约瑟夫·傅
里叶。

简单来说，傅里叶变换可以将一个函数或信号从时域（即时间域）转换到频域（即频率域），从而揭示出了信号中不同频率分量的强弱情况。

傅里叶变换的数学表示如下：
F(ω) = ∫[−∞,+∞] f(t) e^(−jωt) dt
其中，F(ω)表示频率为ω的复指数分量的权重，f(t)表示输入
函数或信号，e^(−jωt)表示复指数函数。

傅里叶变换将输入函
数或信号f(t)与复指数函数相乘，并对结果进行积分，得到频
率域的表示。

傅里叶变换可以将任意复数函数f(t)分解为多个复指数函数的
加权和，每个复指数函数的频率和权重由变换结果F(ω)确定。

所以，傅里叶变换可以将时域的函数转换为频域的复数表示。

傅里叶变换的应用非常广泛，尤其在信号处理、图像处理和通信领域中发挥着重要作用。

它可以帮助我们理解和分析信号的频域特性，如频率分量的强度、相位关系和频谱形状。

此外，傅里叶变换还可以用于信号滤波、频率分析、谱估计、图像压缩等方面。

总之，傅里叶变换通过将函数或信号从时域转换到频域，使我
们能够更好地理解和处理信号的频率特性，并在许多应用中发挥着重要的作用。

傅里叶分析傅里叶分析是一项重要的数学方法，它从数学的角度解释了任何周期性现象的原理。

这个方法得名于法国数学家约瑟夫·傅里叶，他在1807年首次提出了这个理论。

傅里叶分析的核心思想是将一个周期性函数分解成一系列具有不同频率的正弦和余弦函数的和。

通过分析这些分量的振幅、频率和相位，可以获得原始周期性函数的详细特征。

这个方法的应用非常广泛，涵盖了许多领域，包括物理学、工程学、信号处理和图像处理等等。

在物理学中，傅里叶分析被用于研究波动现象，如声音和光线的传播。

在工程学中，它被应用于电路设计和通信系统的优化。

在信号处理中，傅里叶分析被用于音频和视频的压缩和解压缩。

在图像处理中，它被用于图像的滤波和增强。

傅里叶分析的基本原理是将一个周期性函数表示为周期为T的正弦和余弦函数的和。

数学公式可以表达为：f(t) = a0 + ∑(an*cos(nωt) + bn*sin(nωt))其中，f(t)是周期性函数，n是一个正整数，an和bn是系数，ω是角频率，通过关系ω = 2π/T与周期T相联系。

a0是直流分量，表示函数在周期内的平均值。

这个公式中的每一项都表示一个谐波分量。

高频的分量对应着函数的细节，低频的分量对应着函数的整体变化。

为了计算这些系数，可以利用傅里叶级数展开的性质，通过积分计算得到。

具体的计算方法可以参考数学相关的教材和资料。

傅里叶分析的强大之处在于，几乎任何周期性函数都可以通过将其展开成傅里叶级数来近似表示。

这使得我们可以更好地理解周期性现象的本质和特征。

傅里叶分析在现代科学和工程中的应用非常广泛。

在物理学中，它被用于研究波动现象，如声音和光线的传播。

通过分解波动信号，可以获得频谱信息，进而了解波动信号的频率分布和强度。

这对于研究和解释各种波动现象具有重要意义。

在工程领域，傅里叶分析被广泛应用于电路设计和通信系统的优化。

通过分析信号的频谱特征，可以得到电路和系统的频率响应，从而设计出更好的电路和系统。

傅里叶变换空间域运算本身在信号处理方面有许多不足之处，如无法显而易见地表示出信号的能量分布状况，而频域为我们提供了不同的视角，使得信号可以通过某些变换（傅里叶变换、离散余弦变换、沃尔什-哈达码变换以及小波变换等）进行分析和处理。

三角级数由三角函数组成函数项级数，即所谓的三角级数，着重研究如何把函数展开成三角函数。

1.三角级数 三角函数系的正交性周期函数反映了客观世界中周期性运动，正弦函数反映了客观世界中周期运动，简谐振动的函数：y = Asin(ωt+ϕ) 就是以ωπ2为周期的正弦函数，其中y 表示动点的位置，t 表示时间，A 表示振幅，ω表示角频率，ϕ为初相。

实际问题中，除了正弦波外，还会遇到非正弦函数的周期函数，反映了较复杂的周期运动，如周期为T 的矩形波，就是一个非正弦函数的例子，所以，可以将周期函数展开成由 简单的周期函数例如三角函数组成的级数，具体就是说，将周期为T = ωπ2的函数用一系列以T 为周期的正弦函成的级数来表示，即为：()()∑∞=++=10sin n n n t n A A t f ϕω（1）其中，A0、A1和n ϕ（n = 0,1,2...）都是常数。

周期函数按上述方式展开，它的物理意义是很明确的，就是把一个比较复杂的周期运动看成由许多不同频率的简谐震动的叠加。

在电工上，这种展开称为谐波分析。

其中A0称为f(t)的直流分量；)sin(11ϕω+t A 称为一次谐波；)2sin(21ϕω+t A 称为二次谐波，等等。

当然，也可以将正弦函数)sin(n n t n A ϕω+按三角公式变形，得：t n A t n A t n A n n n n n n ωϕωϕϕωsin cos cos sin )sin(+=+并且令002A a =，n n n A a ϕsin =，n n n A b ϕcos =，lπω=（T=2l ），则（1）式的右端可以改写成：∑∞=⎪⎭⎫ ⎝⎛++10sin cos 2n n n l t n b l t n a a ππ（2） 形同（2）式的级数称为三角级数，其中0a 、n a 、n b （n = 0,1,2...）都是常数。

1对应的傅里叶变换1. 傅里叶变换的基本概念和原理傅里叶变换是一种将一个函数变换到另一个函数的数学工具，它可以将一个函数在时域上的表达转换为频域上的表达。

傅里叶变换的基本原理是将一个函数分解成一系列正弦和余弦函数的和，这些正弦和余弦函数的频率不同，振幅也不同，通过对这些正弦和余弦函数的分析，我们可以得到函数在频域上的表示。

2. 傅里叶变换在信号处理中的应用傅里叶变换在信号处理中有着广泛的应用。

首先，傅里叶变换可以将时域上的信号转换为频域上的信号，从而可以对信号的频谱进行分析。

通过分析信号的频谱，我们可以得到信号的频率成分，从而可以了解信号中包含的各种频率的信息。

这对于音频、图像等信号的处理非常重要。

3. 傅里叶变换在图像处理中的应用傅里叶变换在图像处理中也有着重要的应用。

图像可以看作是一个二维函数，通过对图像进行傅里叶变换，我们可以将图像从空域转换到频域。

在频域中，我们可以分析图像中不同频率的成分，从而可以进行图像增强、滤波等操作。

例如，通过对图像进行高通滤波，可以提取图像中的边缘信息；通过对图像进行低通滤波，则可以平滑图像的细节。

4. 傅里叶变换在音频处理中的应用傅里叶变换在音频处理中也有着重要的应用。

音频信号可以看作是一个一维函数，通过对音频信号进行傅里叶变换，我们可以将音频信号从时域转换到频域。

在频域中，我们可以分析音频信号中不同频率的成分，从而可以进行音频增强、降噪等操作。

例如，通过对音频信号进行低通滤波，可以去除高频噪声；通过对音频信号进行频谱分析，可以提取音频信号中的音调和音色信息。

5. 傅里叶变换在通信中的应用傅里叶变换在通信中也有着重要的应用。

通信信号可以看作是一个连续的函数，通过对通信信号进行傅里叶变换，我们可以将通信信号从时域转换到频域。

在频域中，我们可以分析通信信号中不同频率的成分，从而可以进行信号调制、解调、编码、解码等操作。

例如，通过对通信信号进行频谱分析，可以确定信号的带宽需求；通过对通信信号进行频率域滤波，可以去除信号中的噪声。

电子信息工程系实验报告课程名称：数字信号处理成绩：实验项目名称：实验1 离散时间信号与系统的傅里叶分析时间：指导教师（签名）：班级：电信092 姓名：XXX 学号：910706201实验目的:用傅里叶变换对离散时间信号和系统进行频域分析。

实验环境:计算机、MATLAB软件实验原理：对信号进行频域分析即对信号进行傅里叶变换。

对系统进行频域分析即对其单位脉冲响应进行傅里叶变换，得到系统的传输函数；也可由差分方程经过傅里叶变换直接求其传输函数，传输函数代表的就是频率响应特性。

而传输函数是w的连续函数，计算机只能计算出有限个离散频率点的传输函数值，故可在0～2∏之间取许多点，计算这些点的传输函数的值，并取它们的包络，所得包络即所需的频率特性。

实验内容和步骤:1、已知系统用下面差分方程描述：y(n)=x(n)+ay(n-1)，试在a=0.95和a=0.5 两种情况下用傅立叶变换分析系统的频率特性。

要求写出系统的传输函数，并打印|H(e jω)|~ω曲线。

解：B=1;A=[1,-0.95]; [H,w]=freqz(B,A,'whole');subplot(1,3,1);plot(w/pi,abs(H),'linewidth',2);grid on;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');title('幅频响应特性');axis([0,2,0,2.5]);B=1;A=[1,-0.5];[H,w]=freqz(B,A,'whole');subplot(1,3,3);plot(w/pi,abs(H),'linewidth',2);grid on;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');title('幅频响应特性');axis([0,2,0,2.5]);图形如下图1、2所示：图1 a=0.95时的幅频响应特性图2 a=0.5时的幅频响应特性2、已知两系统分别用下面差分方程描述: y1(n)=x(n)+x(n-1) y2(n)=x(n)-x(n-1)试分别写出它们的传输函数，并分别打印|H(e jω)| ~ω曲线。