小学数学_和差的变化规律
- 格式:doc
- 大小:29.50 KB
- 文档页数:2

四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。



和差的变化规律教案7篇编写教案时,要注重培养学生的思维能力和创新意识,优秀教案的编写过程可以促使教师更加注重学生的综合素质培养,以下是作者精心为您推荐的和差的变化规律教案7篇,供大家参考。
和差的变化规律教案篇1说教材我讲的是人教版小学数学四年级上册第五单元“商的变化规律”,这是一节新授课,“商不变的规律”是一个新的数学规律。
在小学数学中占有很重要的地位,它是进行除法简便运算的依据,也是今后学习小数乘、除法、分数、比的基本性质等的基础。
在学习本节课前学生已经掌握了除数是两位数的除法法则,为本节课的学习提供了知识铺垫和思想孕伏。
通过计算比较,提出问题,引导学生思考发现商的变化规律,这部分内容不但可以巩固所学的计算知识,同时培养了学生初步的抽象,概括能力,以及善于观察、勤于思考,勇于探索的良好习惯。
通过本节课的教学,使学生理解掌握商不变的性质,会用商不变的性质对口算除法进行简便运算。
学生在参与,观察,比较,猜想,概括,验证等学习过程中体验成功,同时渗透初步的辩证唯物主义思想启蒙教育。
说教学目标根据课程标准要求:小学数学教学要达到知识与技能,过程与方法,情感态度与价值观三维目标的有机结合,由此我定了一下教学目标:通过计算,观察,比较,探索,使学生发现商随除数(或被除数)的变化而变化的规律。
培养学生初步抽象和概括的能力。
培养学生善于观察,勤于思考,勇于探索的良好习惯,激发学生对数学学习的兴趣。
教学重点难点:通过观察比较,探讨发现商的变化规律,掌握规律。
教学方法:探究法,合作法,观察法,比较法。
教具准备:实物投影,题卡、小黑板我们的`校本研修主题是:在数学课堂中如何使用激励性语言。
我在本节课中的每一个教学环节,都要抓住适当的时机,适时,适当,适量的对学生进行激励性评价,建立评价目标多元,评价方法多样的评价体系,以达到全面了解学生的数学学习历程,激励学生学习热情,促进学生全面发展的目的。
说教法学法本节课我根据教学内容的编排特点和儿童的认知发展规律,引导学生用眼睛观察,比较相关算式的内在联系;动脑去想,抽象出“变”的规律;动口去说,概括出商的变化规律,让学生在多种感官的协同活动中主动获取知识。

小学数学公式大全:和差问题、数量关系式和差问题的公式
(和+差)÷2=大数
(和-差)÷2=小数
和倍问题
和÷(倍数-1)=小数
小数×倍数=大数
(或者和-小数=大数)
差倍问题
差÷(倍数+1)=大数
小数×倍数=大数
(或小数+差=大数)
平均数问题公式
总数量÷总份数=平均数。
数量关系式:
1,每份数×份数=总数总数÷每份数=份数总数÷份数=每份数
2,1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数
3,速度×时间=路程路程÷速度=时间路程÷时间=速度
4,单价×数量=总价总价÷单价=数量总价÷数量=单价
5,工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率
6,加数+加数=和和-一个加数=另一个加数
7,被减数-减数=差被减数-差=减数差+减数=被减数8,因数×因数=积积÷一个因数=另一个因数
9,被除数÷除数=商被除数÷商=除数商×除数=被除数。

小学数学知识点:和差、和倍与差倍问题详解今天小编给大家带来小学数学知识点:和差、和倍与差倍问题详解,希望可以帮助到大家。
和差问题已知两个数量的和与差,求这两个数量各是多少,这类应用题叫和差问题。
其实,解和差问题,还有一段顺口溜:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
和差问题的解题公式:大数=(和+差)÷2小数=(和-差)÷2例1、甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2、长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
和倍问题已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
例1、果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解(1)杏树有多少棵?248÷(3+1)=62(棵)(2)桃树有多少棵?62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2、东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解(1)西库存粮数=480÷(1.4+1)=200(吨)(2)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
例3、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?解:160÷(3+1)=40本乙40×3=120本甲答:甲班120本,已班40本。


小学数学和倍问题、和差问题的解题技巧
和倍问题
和倍问题:已知两个数的和及它们之间的倍数关系,求两个数各是多少的应用题,叫做和倍问题。
解题关键:找准标准数(即1倍数)一般说来,题中说是“谁”的几倍,把谁就确定为标准数。
求出倍数和之后,再求出标准的数量是多少。
根据另一个数(也可能是几个数)与标准数的倍数关系,再去求另一个数(或几个数)的数量。
解题规律:和÷倍数和=标准数标准数×倍数=另一个数
例:汽车运输场有大小货车115 辆,大货车比小货车的 5 倍多7 辆,运输场有大货车和小汽车各有多少辆?
分析:大货车比小货车的 5 倍还多7 辆,这7 辆也在总数115 辆内,为了使总数与(5+1 )倍对应,总车辆数应(115-7 )辆。
列式为(115-7 )÷(5+1 )=18 (辆),18 × 5+7=97 (辆)
差倍问题
差倍问题:已知两个数的差,及两个数的倍数关系,求两个数各是多少的应用题。
解题规律:两个数的差÷(倍数-1 )= 标准数标准数×倍数=另一个数。
例:甲乙两根绳子,甲绳长63 米,乙绳长29 米,两根绳剪去同样的长度,结果甲所剩的长度是乙绳长的3 倍,甲乙两绳所剩长度各多少米?各减去多少米?
分析:两根绳子剪去相同的一段,长度差没变,甲绳所剩的长度是乙绳的 3 倍,实比乙绳多(3-1 )倍,以乙绳的长度为标准数。
列式(63-29 )÷(3-1 )=17 (米)…乙绳剩下的长度,17 × 3=51 (米)…甲绳剩下的长度,29-17=12 (米)…剪去的长度。
1 / 11 / 1。

小学数学“和差,和倍,差倍,倍比”一、和差问题已知两个数的和与差,求出这两个数各是多少的应用题,叫做和差应用题。
基本数量关系是:(和+差)÷2=大数(和-差)÷2=小数和差问题:相加一半是大数、相减一半是小数和差问题,就是已知两数之和、两数之差,求两数。
例题:小红的班级一共有41名同学,其中男生比女生多5人,请问班级里男生和女生各有多少人?这是典型的和差问题,题目中只有两个数字信息,一个是“和=41”,一个是“差=5”,下面我们运用口诀“相加一半是大数、相减一半是小数”对问题进行解答。
注意口诀中的相加、相减,指的是题目中的“和”和“差”。
根据口诀列式:较大数=(和+ 差)÷2 =(41 + 5)÷2 = 23 (人)较小数=(和- 差)÷2 =(41 - 5)÷2 = 18 (人)答:男生有23人,女生有18人。
验证:23+18=41,23-18=5二、和倍问题和倍问题,是指已知两数之和,并且知道其中一数是另一数几倍,求两数。
已知两个数的和,又知两个数的倍数关系,求这两个数分别是多少,这类问题称为和倍问题。
解决和倍问题的基本方法:将小数看成1份,大数是小数的n倍,大数就是n份,两个数一共是n+1份。
基本数量关系:小数=和÷(n+1)大数=小数×倍数或和-小数=大数和倍问题:小数和除倍加一例题:小刚和小明玩拍球游戏,两人一共拍了84下,小刚拍球数是小明的2倍,求两人各拍了多少下?在这道题目中,已知两个数的和是84,一数是另一数的2倍,一个“和”一个“倍”,这就要用和倍口诀来解题了。
小数和除倍加一,列出算式就是:较小数= 和÷(倍数+ 1)= 84 ÷(2 + 1)= 28 (下)求出其中的较小数,再求另一数就十分简单了,根据题意,可以使用减法或乘法求解:较大数= 和- 较小数= 84 - 28 = 56(下)较大数= 较小数×倍数= 28 ×2 = 56(下)答:小刚拍了56下,小明拍了28下。

小学数学解题方法:和差问题已知两数的和及它们的差,求这两个数各是多少的应用题,叫做和差应用题,简称和差问题。
和差问题的解题规律为:两数和加上两数差便是大数的2倍;两数和减去两数差是小数的2倍。
因此,用两数和加上两数差,再除以2,就可求出其中的大数;用两数和减去两数差,再除以2,就可求出小数。
为了解答这种应用题,首先要弄清两个数相差多少的不同叙述方式.有些题目明确给了两个数的差,而有些应用题把两个数的差“暗藏”起来,我们管暗藏的差叫“暗差”。
解答的关键在于找出这两个数的和与差,若题目中没有直接告诉两数的和与差,需先求出两数的和或差,然后根据公式求出这两个数.1:学会运用画图线的方法表示倍关系中两个量,以更方便的找到解题的思路。
2:更熟练掌握解答差倍问题的方法,理解差倍问题中各个量之间的关系。
和差问题(和+差)÷2=大数(和-差)÷2=小数一、和差问题例题例1:两筐水果共重150千克,第一筐比第二筐多8千克,两筐水果各多少千克?分析与解答:我们可以这样想:假设第二筐和第一筐重量相等时,两筐共重150+8=158(千克);假设第一筐重量和第二筐相等时,两筐共重150-8=142(千克).解法1:①第二筐重多少千克?(150-8)÷2=71(千克)②第一筐重多少千克?71+8=79(千克)或150-71=79(千克)解法2:①第一筐重多少千克?(150+8)÷2=79(千克)②第二筐重多少千克?79-8=71(千克)或150-79=71(千克)答:第一筐重79千克,第二筐重71千克。
例2:今年小强7岁,爸爸35岁,当两人年龄和是58岁时,两人年龄各多少岁?分析与解答:题中没有给出小强和爸爸年龄之差,但是已知两人今年的年龄,那么今年两人的年龄差是35-7=28(岁).不论过多少年,两人的年龄差是保持不变的.所以,当两人年龄和为58岁时他们年龄差仍是28岁.根据和差问题的解题思路就能解此题。
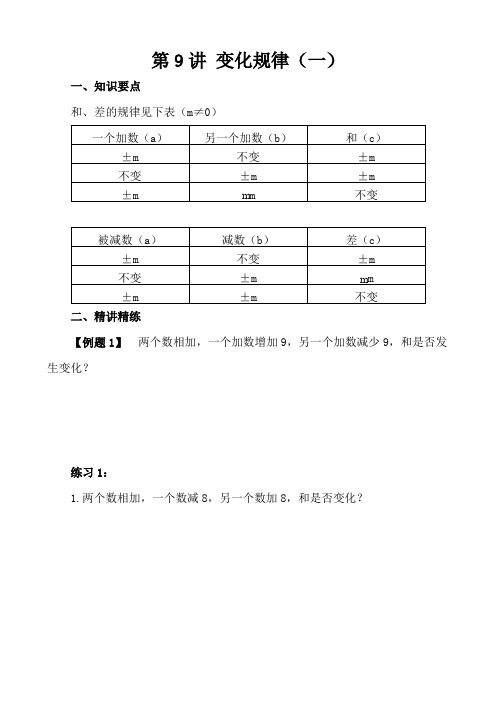
第9讲变化规律(一)一、知识要点和、差的规律见下表(m≠0)二、精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?练习1:1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?练习2:1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?练习3:1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?练习4:1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,积是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?练习5:1.两数相除,被除数扩大30倍,除数缩小5倍,商将怎样变化?2.两数相除,被除数缩小12倍,除数缩小2倍,商将怎样变化?三、课后作业1.两个数相加,一个数减6,另一个数减2.和起什么变化?2.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?3.两数相减,被减数减少10,减数增加10,差起什么变化?4.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?5.两数相除,除数扩大6倍,要使商扩大3倍,被除数应怎样变化?。


和、差、积、商的变化规律学生姓名年级学科授课教师日期时段核心内容和、差、积、商的变化规律课型一对一/一对N教学目标1.掌握和、差、积、商的变化规律2.学会根据规律进行速算重、难点根据积、商的变化规律速算课首沟通1、上讲回顾(错题管理);检查作业;2、询问学生加减乘除的运算公式知识导图课首小测1.两个数相加,一个加数增加25,另一个加数也增加15,和()。
2.两数相减,如果被减数减少18,减数减少8,差()。
3.两个因数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积()。
4.根据每组第一个算式的结果,直接写出第二、第三个算式的得数。
(1)18÷6=3(18×2)÷(6×2)= (18×3)÷(6×3)= (2)480÷10=48(480÷2)÷(10÷2)= (480÷5)÷(10÷5)= (3)420÷6=70(420×2)÷(6÷2)= (420÷5)÷(6×2)=知识梳理导学一:和的变化规律例 1. 按题目要求解答下列各题。
(1)两个数相加,一个数减8,另一个数加8,和是否变化?(2)两个数相加,一个数加3,另一个数也加3,和有什么变化?(3)两个数相加,一个数减6,另一个数减2,和有什么变化?例 2. 按要求解答下列各题。
(1)两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?(2)两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?例 3. 小华在计算两个数相加时,把一个加数个位上的1错误地写成7,把另一个加数十位上的3错误地写成8,所得的和是1996。
原来两个数相加的正确答案是多少?例 4. 两个加数都扩大了8倍,则和扩大()倍。
【学有所获】两个加数都乘以(或除以)同一个数(零除外),和也乘以(或除以)同一个数。

【例1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?一个加数增加(或减少)几,另一个加数减少(或增加)相同的数,和不变。
练习1.两个数相加,一个加数减少8,另一个加数增加8。
和是否变化?2.两个数相加,一个加数增加3,另一个加数减少3。
和有什么变化?【例2】(1)两个数相加,如果一个加数增加10,要使和增加16,那么另一个加数应有什么变化?【例2】(2)两个数相加,如果一个加数减少13,要使和增加10,那么另一个加数应有什么变化?练习1.两个数相加:(1)如果一个加数增加8,要使和增加15,另一个加数应有什么变化?(2)如果一个加数减少9,要使和增加18,另一个加数应有什么变化?2.两个数相加:(1)如果一个加数减少16,要使和增加10,那么另一个加数应有什么变化?(2)如果一个加数减少20,要使和减少10,那么另一个加数应有什么变化?【例3】两个数相减,如果被减数增加8,减数不变,差有什么变化?减数不变,被减数增加(或减少)几,差也随之增加(或减少)几。
练习1.两相减,被减数增加6,减数不变。
差有什么变化?2.两数相减,被减数减少12,减数不变。
差有什么变化?【例4】两个数相减,如果被减数不变,减数减少5,差有什么变化?被减数不变,减数增加(或减少)几,差减少(或增加)几。
练习1.两数相减,被减数不变,减数减少18。
差有什么变化?2.两数相减,被减数不变,减数增加11。
差有什么变化?【例5】两个数相减,如果被减数增加13,减数也增加13,差有什么变化?被减数和减数同时增加(或减少)相同的数,差不变。
练习1.两数相减,被减数增加17,减数增加17。
差有什么变化?2.两数相减,被减数减少14,减数减少14。
差有什么变化?【例6】两个数相减,被减数增加18,要使差减少9,减数应有什么变化?被减数和减数都发生变化,要整体考虑。
练习1.两数相减,被减数增加10,要使差减少15,减数应有什么变化?2.两个数相减,减数减少12,要使差增加8,被减数应有什么变化?总结★1.一个加数增加一个数,另一个加数减少同一个数,和不变。

一、选择题1. 一个加法算式里,一个加数增加5,另一个加数也增加5,它们的和()A.减少5 B.减少10 C.增加10 D.增加52. 被减数增加50,减数减少50,差是()。
A.增加50 B.减少50 C.增加100 D.不变3. 当被减数减少5,减数增加5,它们的差会()。
A.增加5 B.减少5 C.减少10 D.增加104. 马小虎用计算器计算34.86-5.21时,错误地输入了34.8-5.21,要修正这个错误,下面哪个说法是正确的?()A.加0.06 B.减0.06 C.减0.6 D.加0.65. 303-☆=330-○,比较☆与○的大小,是()。
A.☆=○B.☆>○C.☆<○二、填空题6. 两个数的和是86,如果一个加数增加7.18,另一个加数减少5.39,和是( )。
7. 两个数相减,被减数增加15,要使差增加29,减数应( )。
8. 小华在用计算器输入“a- 3.26+5.4”时,错输成“a- 3.26+54”,这样算得结果和正确结果相差( )。
9. 被减数不变,减数增加5,它们的差( )。
10. 三个数的和是579,将这三个数的小数点都向左移动一位,这三个数的和是( )。
三、解答题11. 两个数相加,一个加数增加9,另一个加数增加18,和怎么变化?12. 小巧在做加法计算时,错把一个加数个位上的0看成了6,把十位上的2看成了5,这样得到的和是156,正确的答案是多少?13. 小马虎在做一道小数加法题时,把一个加数个位上的3看成了8,把十分位上的6看成了9,结果得到的和是15.你知道正确的答案是多少吗?14. 两个数的差是32.8,如果被减数减少3.2,减数增加3.2,差变成了多少?。


分析小学数学和差问题考点有哪些:小学数学和差问题讲解【1】南京长江大桥共分两层,上层是公路桥,下层是铁路桥。
铁路桥和公路桥共长11270米,铁路桥比公路桥长2270米,问南京长江大桥的公路和铁路桥各长多少米?【考点分析】典型的和差问题,大数=(和+差)/2,小数=(和-差)/2,(三年级)【分析与解】铁路桥=(11270+2270)÷2=6770米公路桥=11270-6770=4500米【2】三个小组共有180人,一、二两个小组人数之和比第三小组多20人,第一小组比第二小组少2人,求第一小组的人数。
【考点分析】典型的和差问题,,整体法或打包思想的考查,(三年级,四年级)【分析与解】先把第一、二小组看成一个整体,他们与第三小组和为180,差为20,第三小组人数=(180-20)÷2=80一二小组合起来为180-80=100人,一小组与二小组的差为2,一小组人数=(100-2)÷2=49,二小组人数=100-49=51【3】甲、乙两筐苹果,甲筐比乙筐多19千克,从甲筐取出多少千克放入乙筐,就可以使乙筐中的苹果比甲筐的多3千克?【考点分析】正负效应的理解,,(三年级,四年级)【分析与解】(方法1)因为甲乙现在筐里的苹果数量未知,所以可以直接设数,就设甲筐有19千克苹果,那么乙筐有0千克苹果。
此时甲乙和为19千克。
变动后,和仍然为19千克,此时乙筐与甲筐的差为3,则乙筐=(19+3)÷2=11千克,乙筐的11千克都是甲筐给的,所以从甲筐取出11千克给乙筐。
(方法2)主动推荐方法。
甲给乙1千克,甲少1千克,乙多1千克,甲比乙多的数量减少了2甲给乙2千克,甲少2千克,乙多2千克,甲比乙多的数量减少了4所以可用19+3=22,22÷2=11【4】一个减法算式中,被减数、减数与差的和等于120,而减数是差的3倍,那么差等于多少?【考点分析】和倍问题,减法算式的考查,,(三年级,四年级)【分析与解】突破口在被减数、减数、差这三者的关系上。
和差的变化规律
姓名
1、两个数相加,一个加数减少29,另一个加数不变,和将有什么
变化?
2、两个数相加,一个加数增加21,另一个加数增加19,和有什么
变化?
3、两个数相加,一个加数减少20,另一个加数增加20,和怎么样?
4、两个数相加,一个加数增加34,另一个加数减少26,和有什么
变化?
5、两个数相减,被减数不变,减数120,差将有怎样的变化?
6、两个数相减,被减数增加38,减数增加38,差将有怎样的变化?
7、两个数相减,被减数增加42,减数减少24,差将有怎样的变化?
8、两个数相减,被减数增加42,减数增加15,差将有怎样的变化?
9、两个数相加,一个加数减少39,要使和减少18,那么另一个加数将怎么样变化?
10、两个数相加,和是100,一个加数减少48,另一个加数不变,
现在和是多少?
11、两个数相减,如果减数增加72,要使差不变,那么被减数将怎
么样变化?
12、两个数相减,如果被减数增加32,要使差减少52,减数将怎么
样变化?
13、两个数相减,如果被减数减少11,要使差增加20,减数将怎么
样变化?
14、两个数相减,如果被减数增加17,减少增加32,差将有怎么样
变化?
15、小丽在做一道加法题,一个加数十位上的4看作了7,个位上
的5看作了2,算得的和是87。
正确的和是多少?
16、小丽在做一道减法题,把被减数十位上的7看作了9,个位上
的3看作了8,算得的差是76。
正确的差是多少?。