岩体力学 几种常见岩石哒弹性模量 推导公式

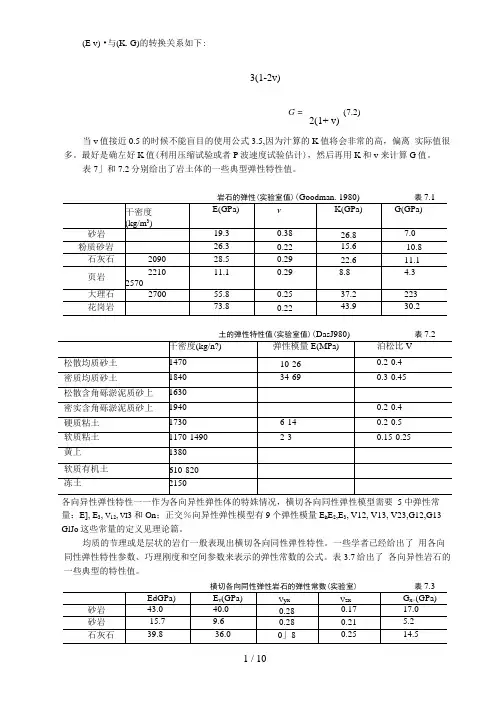
(E v) •与(K. G)的转换关系如下:3(1-2v)G = ------------ (7.2)2(1+ v)当v 值接近0.5的时候不能盲目的使用公式3.5,因为汁算的K 值将会非常的高，偏离 实际值很多。

最好是确左好K 值(利用压缩试验或者P 波速度试验估计)，然后再用K 和v 来计算G 值。

表7」和7.2分别给出了岩土体的一些典型弹性特性值。

各向异性弹性特性一一作为各向异性弹性体的特姝情况，横切各向同性弹性模型需要 5中弹性常量：E], E 3, V 12, VI 3和On ；正交％向异性弹性模型有9个弹性模量E h E 2,E 3, V12, V13, V23,G12,G13 GlJo 这些常量的定义见理论篇。

均质的节理或是层状的岩仃一般表现出横切各向同性弹性特性。

一些学者已经给出了 用各向同性弹性特性参数、巧理刚度和空间参数来表示的弹性常数的公式。

表3.7给出了 各向异性岩石的一些典型的特性值。

1 / 10页岩66.849.50」70.2125.3大理石6&650.20.060.2226.6花岗岩10.7 5.20.200.41 1.2流体弹性特性一一用于地F水分析的模型涉及到不可压缩的土粒时用到水的体积模量K…如果土粒是可压缩的，则要用到比奥模量M o纯净水在室温情况下的K「值是2 Gpa Q 其取值依赖于分析的目的。

分析稳态流动或是求初始孔隙压力的分布状态（见理论篇第三章流体■固体相互作用分析），则尽量要用比较低的Kr,不用折减。

这是由于对于大的K（流动时间步长很小，并且，力学收敛性也较差。

在FLAC3D中用到的流动时间步长,△"与孔隙度m渗透系数k以及心有如下关系：(7.3)对于可变形流体（多数课本中都是将流体设左为不可压缩的）我们可以通过获得的固结系数C,来决定改变&的结果。

(7.4)英中1m|z = -------------K + 4G/3 k = k /f其中，k—一FLAC3D使用的渗透系数k一一渗透系数，单位和速度单位一样（如米/秒）r r——水的单位重量考虑到固结时间常量与G，成比例，我么可以将K（的值从英实际值（2xlOSd）减少，利用上面得表达式看看其产生的误差。

岩体力学参数确定的方法岩体力学参数的确定方法在岩石工程实践中，首先需要了解作为研究对象的工程岩体的力学性质，并确定其特征参数。

岩石力学参数的合理确定一直是岩石力学研究和发展的难点之一。

在应用工程力学领域，如果完整地使用经典理论力学的连续性假设和定义，就会存在理解上的问题。

必须考虑假设的合理使用范围和每个物理量的适用定义。

本文讨论了地下岩体工程中根据不同的重点确定岩体参数的方法。

1、确定岩体参数的传统方法地下巷道、硐室开挖后，围岩产生应力重分异作用,径向应力减少,切向应力增加,并且随着工程不断推进,岩体应力状态不断改变。

巷道、硐室围岩处于“三高一扰动”条件下,岩体表现的力学特性是破坏条件下的稳定失稳再平衡过程。

围岩体处于一种拉压相间出现的复杂应力状态。

该类工程岩体的力学参数的确定要进行岩体的卸荷试验研究,且要依据现场工程实际条件进行卸荷条件下的应力、渗流与温度三场耦合试验研究。

需要进行循环加卸载条件下的岩体力学特性研究,进而获得岩体的力学参数特征。

地下巷道和硐室工程岩体力学参数的确定方法如下：(1)三轴应力状态下的卸荷三场耦合力学试验,获得有关参数;(2)进行岩体流变特性试验研究,获得有关岩体的流变参数。

目前在该领域要进行大量的工作,包括设备仪器的研制等,同时还要利用新的计算机技术才会实现。

二．建立力学模型确定岩体力学参数建立工程岩体力学参数模型主要是解决复杂岩体力学参数的确定问题。

为了确定复杂岩体的力学参数，需要将工程岩体视为一个连续模型。

采用确定岩体力学参数的新方法，建立了层状斜节理岩体的力学模型，并进行了力学试验，确定了岩体的基本力学参数。

1．工程岩体力学参数模型目前，关于岩石的力学性质和划分基本上有两种观点：一种观点认为岩石本身是一种连续的非各向异性材料，另一种观点认为岩石是由多晶系统组成的，存在空洞和裂缝等缺陷，这使得岩石本身的结构表现出各向异性和不连续性。

岩体一般被视为不连续介质，但在一定条件下仍满足连续介质力学的基本假设。

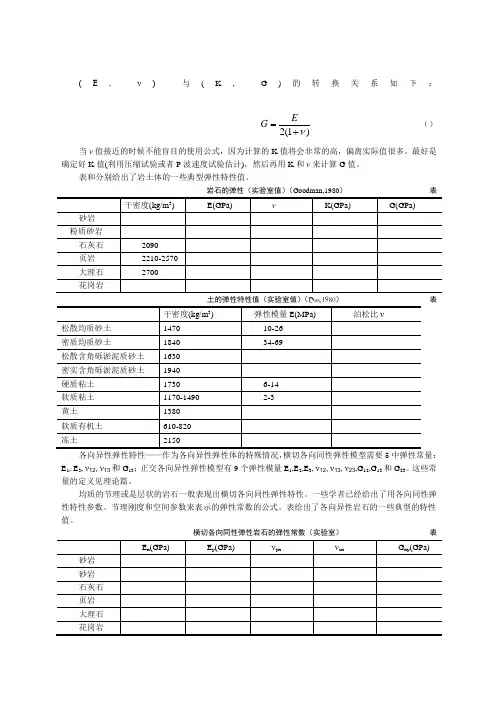
(E , ν) 与(K , G )的转换关系如下：)1(2ν+=EG （）当ν值接近的时候不能盲目的使用公式，因为计算的K 值将会非常的高，偏离实际值很多。

最好是确定好K 值(利用压缩试验或者P 波速度试验估计)，然后再用K 和ν来计算G 值。

表和分别给出了岩土体的一些典型弹性特性值。

岩石的弹性（实验室值）（Goodman,1980） 表土的弹性特性值（实验室值）（Das,1980） 表各向异性弹性特性——作为各向异性弹性体的特殊情况，横切各向同性弹性模型需要5中弹性常量：E 1, E 3, ν12,ν13和G 13；正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。

这些常量的定义见理论篇。

均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。

一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。

表给出了各向异性岩石的一些典型的特性值。

横切各向同性弹性岩石的弹性常数（实验室） 表流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ，如果土粒是可压缩的，则要用到比奥模量M 。

纯净水在室温情况下的K f 值是2 Gpa 。

其取值依赖于分析的目的。

分析稳态流动或是求初始孔隙压力的分布状态（见理论篇第三章流体-固体相互作用分析），则尽量要用比较低的K f ，不用折减。

这是由于对于大的K f 流动时间步长很小，并且，力学收敛性也较差。

在FLAC 3D 中用到的流动时间步长,? tf 与孔隙度n ，渗透系数k 以及K f 有如下关系：'f f k K nt ∝∆ （） 对于可变形流体（多数课本中都是将流体设定为不可压缩的）我们可以通过获得的固结系数νC 来决定改变K f 的结果。

f'K n m k C +=νν （）其中其中，'k ——FLAC 3D 使用的渗透系数k ——渗透系数，单位和速度单位一样（如米/秒） f γ——水的单位重量考虑到固结时间常量与νC 成比例，我么可以将K f 的值从其实际值（Pa 9102⨯）减少，利用上面得表达式看看其产生的误差。

常用的岩土和岩石物理力学参数(E, ν) 与(K, G)的转换关系如下：)21(3ν-=EK)1(2ν+=EG （7.2）当ν值接近0.5的时候不能盲目的使用公式3.5，因为计算的K 值将会非常的高，偏离实际值很多。

最好是确定好K 值(利用压缩试验或者P 波速度试验估计)，然后再用K 和ν来计算G 值。

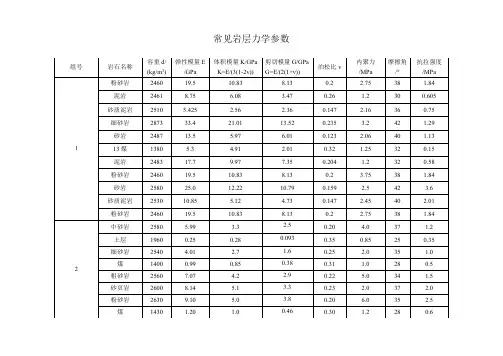
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。

岩石的弹性（实验室值）（Goodman,1980）表7.1干密度(kg/m 3)E(GPa) ν K(GPa) G(GPa) 砂岩19.3 0.38 26.8 7.0 粉质砂岩26.3 0.22 15.6 10.8 石灰石2090 28.5 0.29 22.6 11.1 页岩2210-257011.1 0.29 8.8 4.3大理石2700 55.8 0.25 37.2 22.3 花岗岩73.8 0.22 43.9 30.2土的弹性特性值（实验室值）（Das,1980）表7.2干密度(kg/m 3) 弹性模量E(MPa) 泊松比ν 松散均质砂土1470 10-26 0.2-0.4 密质均质砂土 1840 34-69 0.3-0.45 松散含角砾淤泥质砂土 1630 密实含角砾淤泥质砂土 1940 0.2-0.4 硬质粘土 1730 6-14 0.2-0.5 软质粘土1170-1490 2-3 0.15-0.25 黄土1380 软质有机土610-820 冻土2150各向异性弹性特性——作为各向异性弹性体的特殊情况，横切各向同性弹性模型需要5中弹性常量：E 1, E 3, ν12,ν13和G 13；正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。

这些常量的定义见理论篇。

均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。

一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。

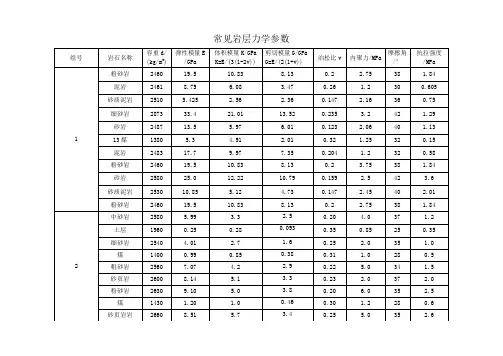
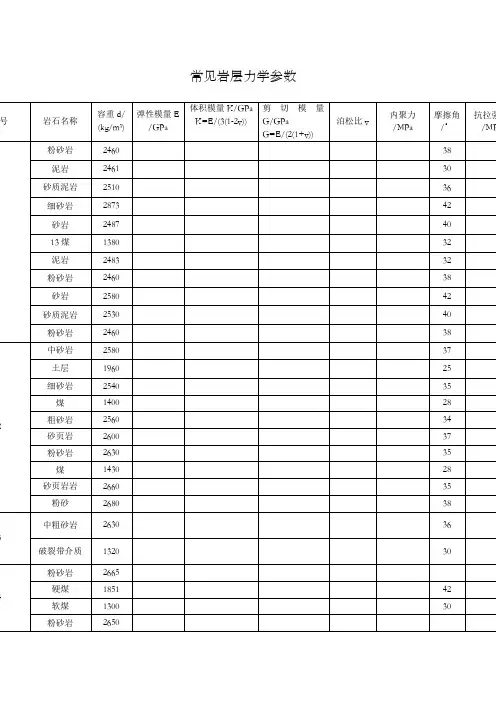
常见岩石力学参数岩石力学参数是指描述岩石在外力作用下的力学行为的物理性质，包括弹性模量、剪切模量、泊松比、抗压强度、抗拉强度、抗剪强度等。

这些参数对于岩石的力学性质和工程应用具有重要意义。

本文将详细介绍这些常见的岩石力学参数。

1. 弹性模量（Young's modulus）：弹性模量是衡量岩石弹性性质的一个重要参数，表示岩石在外力作用下产生弹性变形的能力。

弹性模量越大，岩石的刚度越大，抗弯和抗变形能力越强。

2. 剪切模量（Shear modulus）：剪切模量是衡量岩石抗剪切性质的参数，表示岩石在剪切应力作用下产生剪切变形的能力。

剪切模量越大，岩石的抗剪强度越高，稳定性越好。

3. 泊松比（Poisson's ratio）：泊松比是衡量岩石体积变形性质的参数，表示岩石在受到压缩应力时，横向收缩的程度。

泊松比一般介于0.1到0.4之间，数值越大，岩石的蠕变性越强。

5. 抗拉强度（Tensile strength）：抗拉强度是衡量岩石抗拉性质的参数，表示岩石在受到拉伸应力时的最大承载能力。

抗拉强度一般比抗压强度要小，岩石在受到拉伸时易发生断裂。

6. 抗剪强度（Shear strength）：抗剪强度是衡量岩石抗剪切性质的参数，表示岩石在受到剪切应力时的最大承载能力。

抗剪强度主要与岩石内部的粘聚力和内摩擦角有关。

除了上述常见的岩石力学参数外，还有一些与岩石稳定性有关的参数：7. 断裂韧性（Fracture toughness）：断裂韧性是衡量岩石抗断裂性质的参数，表示岩石在受到裂纹扩展时的抵抗能力，能够反映岩石的破坏扩展能力。

8. 孔隙度（Porosity）：孔隙度是衡量岩石孔隙结构的参数，表示岩石内部的孔隙空间占总体积的比例。

孔隙度能够影响岩石的密实程度和渗透性，对工程建筑的渗流和稳定性有重要影响。

9. 饱和度（Saturation）：饱和度是衡量岩石孔隙中被水、气体或其他流体填充的程度。

弹性模量计算公式图文解析弹性模量是描述材料在受力作用下产生形变的能力的物理量，是衡量材料抗弹性变形能力的重要参数。

弹性模量的计算公式是材料力学性质的基础，通过这个公式可以计算出材料在受力作用下的变形程度，从而为工程设计和材料选择提供重要参考。

弹性模量的计算公式是一个基本的力学公式，它描述了材料在受力作用下的形变情况。

弹性模量的计算公式通常表示为E=σ/ε，其中E表示弹性模量，σ表示应力，ε表示应变。

弹性模量的单位通常是帕斯卡（Pa），1Pa=1N/m^2。

应力是单位面积上的力，是描述材料受力情况的物理量。

应变是材料单位长度上的形变量，是描述材料变形情况的物理量。

弹性模量的计算公式中的应力和应变是描述材料在受力作用下的基本物理量，通过这个公式可以计算出材料在受力作用下的形变情况，从而为工程设计和材料选择提供重要参考。

弹性模量的计算公式中，应力和应变的计算通常是通过材料的拉伸试验或压缩试验得到的。

在拉伸试验中，材料受到拉力，产生的应变称为拉伸应变；在压缩试验中，材料受到压力，产生的应变称为压缩应变。

通过测量拉伸或压缩试验中的应力和应变，可以得到材料的弹性模量。

弹性模量的计算公式中，应力和应变的计算通常是通过材料的拉伸试验或压缩试验得到的。

在拉伸试验中，材料受到拉力，产生的应变称为拉伸应变；在压缩试验中，材料受到压力，产生的应变称为压缩应变。

通过测量拉伸或压缩试验中的应力和应变，可以得到材料的弹性模量。

弹性模量的计算公式是材料力学性质的基础，通过这个公式可以计算出材料在受力作用下的变形程度，从而为工程设计和材料选择提供重要参考。

在工程设计中，根据不同材料的弹性模量，可以选择合适的材料，从而保证工程结构的稳定性和安全性。

在材料选择中，弹性模量也是一个重要的参考指标，不同材料的弹性模量不同，选择合适的材料可以提高工程结构的性能和使用寿命。

总之，弹性模量的计算公式是描述材料在受力作用下产生形变的能力的基本公式，通过这个公式可以计算出材料在受力作用下的变形程度，从而为工程设计和材料选择提供重要参考。

弹性模量计算公式图文并茂弹性模量是材料力学性能的重要指标，它反映了材料在受力时的变形能力。

在工程设计和材料科学领域中，弹性模量的计算是非常重要的。

本文将介绍弹性模量的计算公式，并通过图文并茂的方式进行详细解析。

弹性模量的定义是材料在受力时的应力与应变之比，通常用E表示。

弹性模量的计算公式如下：E = σ / ε。

其中，E表示弹性模量，σ表示应力，ε表示应变。

应力是单位面积上的力，通常用MPa或N/m²表示；应变是材料的变形程度，通常是无单位的。

根据这个公式，我们可以通过已知的应力和应变来计算材料的弹性模量。

下面我们通过图文并茂的方式来详细解析弹性模量的计算公式。

首先，我们需要了解什么是应力和应变。

应力是单位面积上的力，可以用一个简单的图示来表示。

假设有一个正方形的材料样品，上面受到了一个力F，那么应力σ就可以用力F除以正方形的面积A来表示。

这样，我们就可以得到应力σ = F / A。

接下来，我们来看一下应变的计算。

应变是材料在受力时的变形程度，可以用一个简单的图示来表示。

同样假设有一个正方形的材料样品，受到了一个力F，导致了变形。

此时，我们可以用变形后的长度L减去原始的长度L0，再除以原始长度L0来表示应变ε。

这样，我们就可以得到应变ε = (L L0) / L0。

有了应力和应变的计算方法，我们就可以用弹性模量的计算公式来计算材料的弹性模量了。

假设我们已经知道了材料的应力σ和应变ε，那么根据公式E = σ / ε，我们就可以得到材料的弹性模量E了。

通过上面的图文并茂的解析，我们可以清晰地了解了弹性模量的计算公式以及应力和应变的计算方法。

弹性模量是材料力学性能的重要指标，它直接影响着材料在受力时的变形能力。

因此，对于工程设计和材料科学领域的研究人员来说，掌握弹性模量的计算方法是非常重要的。

希望本文的介绍能够帮助大家更好地理解弹性模量的计算公式。

(E, ν) 与(K, G)的转换关系如下：)21(3ν-=EK)1(2ν+=EG （） 当ν值接近的时候不能盲目的使用公式，因为计算的K 值将会非常的高，偏离实际值很多。

最好是确定好K 值(利用压缩试验或者P 波速度试验估计)，然后再用K 和ν来计算G 值。

表和分别给出了岩土体的一些典型弹性特性值。

岩石的弹性（实验室值）（Goodman,1980） 表,土的弹性特性值（实验室值）（Das,1980）表各向异性弹性特性——作为各向异性弹性体的特殊情况，横切各向同性弹性模型需要5中弹性常量：E1, E3,ν12,ν13和G13；正交各向异性弹性模型有9个弹性模量E1,E2,E3,ν12,ν13,ν23,G12,G13和G23。

这些常量的定义见理论篇。

均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。

一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。

表给出了各向异性岩石的一些典型的特性值。

横切各向同性弹性岩石的弹性常数（实验室）表} 花岗岩流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ，如果土粒是可压缩的，则要用到比奥模量M 。

纯净水在室温情况下的K f 值是2 Gpa 。

其取值依赖于分析的目的。

分析稳态流动或是求初始孔隙压力的分布状态（见理论篇第三章流体-固体相互作用分析），则尽量要用比较低的K f ，不用折减。

这是由于对于大的K f 流动时间步长很小，并且，力学收敛性也较差。

在FLAC 3D 中用到的流动时间步长, tf与孔隙度n ，渗透系数k 以及K f 有如下关系：'f f k K nt ∝∆ （） 对于可变形流体（多数课本中都是将流体设定为不可压缩的）我们可以通过获得的固结系数νC 来决定改变K f 的结果。

|f'K nm k C +=νν （）其中3/4G K 1m +=νf 'k k γ=其中，'k ——FLAC 3D 使用的渗透系数k ——渗透系数，单位和速度单位一样（如米/秒） f γ——水的单位重量考虑到固结时间常量与νC 成比例，我么可以将K f 的值从其实际值（Pa 9102⨯）减少，利用上面得表达式看看其产生的误差。

弹性模量计算公式弹性模量是描述材料抵抗外力变形的能力的物理量。

它是一个材料特性常数，用来表征材料在接受外力作用后能否恢复到原来的形状和大小。

弹性模量的计算公式如下：弹性模量（E）=应变（σ）/应力（ε）其中，弹性模量E的单位是帕斯卡（Pa），应变σ和应力ε的单位都是牛顿/平方米（N/m²），即帕斯卡。

应变是指材料在外力作用下变形的程度，它是一个相对值，计算公式为：应变（σ）=ΔL/L0其中，ΔL是材料受力后长度变化的数值，L0是材料受力前的长度。

应力是指材料受到单位面积的外力作用后产生的内部阻力，它是一个绝对值，计算公式为：应力（ε）=F/A其中，F是施加在材料上的力的数值，A是材料的受力面积。

需要注意的是，弹性模量只适用于线弹性材料，即应力和应变之间呈线性关系的材料。

在实际计算中，弹性模量可以通过不同的方法得到。

其中比较常用的方法有：1.静态拉伸法：通过对材料进行拉伸实验，测得应力和应变的值，然后代入弹性模量的计算公式求得。

2.动态弹性应变仪法：通过将材料加在弹性应变仪上，在不同载荷下测得应变的变化值，然后代入弹性模量的计算公式求得。

3.悬臂梁法：通过在材料上施加一个力矩，测得材料的挠度，再代入弹性模量的计算公式求得。

此外，有一些特殊材料的弹性模量可以通过其他方式计算，如杨氏模量、剪切模量等，它们采用的计算公式与传统的弹性模量略有不同，但都遵循材料的弹性恢复性质。

总之，弹性模量是材料力学性质的重要指标之一，通过计算公式可以得到，可以通过不同的实验方法进行测量。

不同的计算方法适用于不同的材料和实验条件，选择合适的方法进行实验计算能够提高计算结果的准确性。

岩石力学参数手册第一章绪论本手册旨在为岩石力学领域的研究人员和工程师提供岩石力学参数的参考。

本手册主要包括岩石力学常用参数的定义和计算公式，以及它们在不同力学实验和工程应用中的应用范围和限制。

第二章岩石力学常用参数1. 弹性模量弹性模量是描述岩石本身抵抗变形能力的参数，也是岩石变形受力学响应的基础。

其定义为应力和应变之比，通常用“E”来表示，单位为千帕。

2. 泊松比泊松比是描述岩石沿某一方向的压缩（或伸长）应变与其在与该方向垂直的方向上相应的膨胀（或收缩）应变之比。

其定义为侧向应变和轴向应变之比，通常用“ν”来表示，无单位。

3. 抗拉强度抗拉强度是指岩石在拉伸状态下最大额外应力强度。

其计算公式为：σt = F/Aσt为抗拉强度，F为最小应变强度，A为岩石断面积。

5. 黏聚力黏聚力是指岩石在未承受分开应力的情况下的最小阻抗力。

其计算公式为：C = 2F/πDC为黏聚力，F为最小阻抗力，D为岩石的直径。

弹性模量试验是通过施加单轴应力或三轴应力来测定岩石的弹性模量。

单轴应力试验主要是通过塑性直线版或岩石试件测定岩石的应力-应变关系，然后确定弹性模量；而三轴应力试验则是通过在三个轴向上施加正、负应力，测定岩石的应力-应变关系，并计算弹性模量。

拉压强度试验是通过塑性直线版或岩石试件施加拉伸或压缩应力来测定岩石的抗拉强度和抗压强度。

拉伸试验通常使用高精度万能试验机，测定点状试件的应变和应力，然后计算抗拉强度；而压缩试验则是将岩石试件置于弹塑料中，测量其最小阻抗力，并计算抗压强度。

4. 断裂韧性试验断裂韧性试验是通过岩石试件施加脆性、韧性和折断初始应力来测定其断裂韧性。

该试验通常通过在岩石试件上使用弯曲粘着板，以爆破等方式施加应力，获得岩石试件的断裂韧性。

岩石力学参数的应用主要分为两个方向：一是在岩石力学基础研究方面，如岩石变形特性、岩石破裂机制研究等；二是在岩石工程实践中的应用，如隧道开挖稳定性评估、堆石坝安全分析等。

岩石物理力学性质指标经验数据在岩石物理学中，岩石的物理力学性质指标是评估岩石力学行为的重要参数，包括岩石的强度、变形性质、破裂特性等。

这些指标的经验数据非常重要，能够为岩石物理学的研究和实际工程应用提供有效的参考。

下面将介绍一些常见的岩石物理力学性质指标的经验数据。

岩石的抗压强度是指在垂直于施加力的方向上，岩石能够抵抗的最大压缩应力。

不同类型的岩石具有不同的抗压强度。

常见的岩石抗压强度经验数据如下：-砂岩：5-25MPa-灰岩：25-100MPa-花岗岩：100-250MPa-片麻岩：50-150MPa-麻岩：50-200MPa2. 抗张强度（Tensile strength）：岩石在拉伸条件下能够承受的最大应力称为抗张强度。

由于岩石的抗拉强度较低，因此常常使用岩石抗压强度的一半作为岩石的抗拉强度估计值。

常见的岩石抗张强度经验数据如下：-砂岩：1-5MPa-灰岩：5-20MPa-花岗岩：20-100MPa-片麻岩：10-50MPa-麻岩：10-50MPa3. 剪切强度（Shear strength）：岩石的剪切强度是指岩石在剪切应力作用下能够抵抗剪切破坏的最大强度。

常见的岩石剪切强度经验数据如下：-砂岩：3-15MPa-灰岩：15-30MPa-花岗岩：30-100MPa-片麻岩：15-50MPa-麻岩：20-60MPa4. 弹性模量（Young modulus）：弹性模量是岩石在弹性变形范围内的刚度指标，表示岩石在受力时变形程度的大小。

常见的岩石弹性模量经验数据如下：-砂岩：1-30GPa-灰岩：10-100GPa-花岗岩：50-200GPa-片麻岩：10-50GPa-麻岩：5-50GPa5. 泊松比（Poisson's ratio）：泊松比表示材料体积收缩时的径向收缩与轴向延伸之比，常用来表征岩石的变形特性。

-砂岩：0.1-0.4-灰岩：0.1-0.35-花岗岩：0.2-0.35-片麻岩：0.1-0.4-麻岩：0.2-0.4需要注意的是，以上数据仅为经验值，实际岩石的物理力学性质受多种因素的影响，包括岩石类型、成分、结构、孔隙度等。