当前位置：文档之家 › 拉压超静定

拉压超静定

  • 格式：pptx
  • 大小：696.72 KB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

第六章 拉压超静定问题

第六章 拉压超静定问题
FN1
B' C' A' x
Δl1
FN1l EA
FN3 l e F N3 Δl 3 E 3 A3
(4)补充方程
FN2
FN3 l e FN1l Δe E 3 A3 E A
联立平衡方程与补充方程求解,即可得装配内力，进而求出装配 应力.
§6-4 简单超静定梁
Ⅰ.超静定梁的解法 q A 例：求解图示超静定梁 的支座反力，并画剪力 图和弯矩图。 分析：可以铰支座B为 “多余”约束，解除 “多余”约束后的基本 静定系为A端固定的悬 臂梁。
1
2 A
3
F
工程中很多建筑结构的力学模型并不是 静定结构，而是超静定结构。
第六章 力法
“鸟巢”国家体育场 杆件结构中大量采用超静定结构
土木工程中常见的简单超静定结构？
B
大型承重桁架
多跨连续梁
既然静定结构可以承担荷载，为什么工程中还 要使用超静定结构呢？ 原因：采用超静定结构要比静定结构更经济，更安全。 例如 (1)通过给静定梁增加支座，降低梁的最大弯矩。

原结构
相当系统
例：求三杆桁架内力,杆长 L1=L2，L3 =L ,面积 A1=A2=A， A3 ,弹性模量 E1=E2=E，E3
B
3 1
D
C
2 N1 N3

A P

A P
N2
解: (1) 列静力平衡方程 X 0 N1 sin N 2 sin 0
Y 0
(3) 利用物理关系(参见教材中的附录Ⅳ)所得的 补充方程为
ql 4 FB l 3 0 8 EI 3 EI
3 从而解得“多余”未知力 FB ql 8

拉压超静定

拉压超静定

1 2
F
FN 1 FN 2 FN 3
y
A
x
列出变形几何关系 将A点的位移分量向各杆投 影.得
l1 y sin x cos
y
x
A x
整理得
l2 x l3 y sin x cos
变形关系为 l3 l1 2l2 cos
l1
l2
l3
4、补充方程
FN 1l FN 3l cos EA cos EA
FN 1 FN 3 cos 2
5、求解方程组得 F F cos 2 F FN 1 FN 2 N3 1 2 cos 3 1 2 cos 3 3
拉、压超静定问题
木制短柱的4个角用4个40mm×40mm×4mm的等边角钢加固， 已知角钢的许用应力[σst]=160MPa，Est=200GPa；木材的许 用应力[σW]=12MPa，EW=10GPa，求许可载荷F。 F 解： 平衡方程: F FW Fst （1） F 变形协调关系: l st l w FW l FW 物理关系: lW EW AW Fst Fst l lst Est Ast 补充方程:
2
拉、压超静定问题
超静定结构的求解方法： 1、列出独立的平衡方程 Fx 0 FN1 FN 2
y
F
0 2FN1 cos FN 3 F
2、变形几何关系 l1 l2 l3 cos 3、物理关系
FN 1l FN 3l l1 l3 EA cos EA
F
根据角钢许用应力，确定F
0.283F st st F 698 kN Ast 根据木柱许用应力，确定F 0.717F W W AW

拉压超静定问题

拉压超静定问题
L FN L EA
4、联立静力方程与力的补充方程求出所有的未知力。
三、注意的问题 拉力——伸长变形相对应；压力——缩短变形相对应。
例 设 1、2、3三杆用铰链连接如图，已知：各杆长为：
l1=l2、 l3=l；各杆面积为 A1=A2、 A3 ；各杆弹性模量为： E1=E2、E3。外力沿铅垂方向，求各杆的内力。
B
DC
1
3
2
l
A G
(a)
B
DC
解：、平衡方程:
1 32
l3
A
l1
E
A
(c)
Fx 0 FN1 sin FN 2 sin 0 Fy 0 FN1 cos FN 2 cos FN3 G 0
、几何方程——变形协调方程：
L1 L3 cos
补充方程：由力与变形的物理条件得：
FN1 FN 3
工程力学
拉压超静定问题
一、概念
1、静定：结构或杆件的未知力个数等于有效静力方程的个数， 只利用有效静力方程就可以求出所有的未知力。
2、超静定：结构或杆件的未知力个数大于有效静力方程的个数， 只利用有效静力方程不能求出所有的未知力。
3、多余约束：在超静定系统中多余维 持结构几何不变性所需要的杆或支座。
4、多余约束反力：多余约束对应的反力。
BDC
1
3
2
A G
5、超静定的分类（按超静定次数划分）： 超静定次数=多余约束个数=未知力个数-有效静力方程个数。 二、求解超静定（关键——变形几何关系的确定） 步骤：1、根据平衡条件列出平衡方程（确定超静定的次数）。
2、根据变形协调条件列出变形几何方程。 3、根据力与变形的物理条件，列出力的补充方程。
FN 2

6.1拉压超静定问题

6.1拉压超静定问题

A 简图 N A
C P
P 为什么画轴力图? 应注意什么? + x
轴力的简便求法: 轴力的简便求法: 以x点左侧部分为对象,x点的内力N(x)由下式计算:
N ( x ) = ∑ P (←) − ∑ P (→)
其中“ΣP( )”与“ΣP( )”均为x点左侧与右侧部分的 所有外力。
例11 设1、2、3三杆用铰链连接如图，已知：各杆长为： L1=L2、 L3 =L ；各杆面积为A1=A2=A、 A3 ；各杆弹性模量 为：E1=E2=E、E3。外力沿铅垂方向，求各杆的内力。 解： 、平衡方程: B 3 1 D C 2 N3
∑X
= N 1 sin α − N 2 sin α = 0
[σ ] 1 A1 N1 ≤ P= 0 .07 0 .07
160× 308.6 = 705.4kN = 0.07
另外：若将钢的面积增大 倍 怎样？ 另外：若将钢的面积增大5倍，怎样？ 若将木的边长变为25mm，又怎样？ 若将木的边长变为 边长变为 ， 怎样？ 结构的最大载荷永远由钢控制着。 结构的最大载荷永远由钢控制着。
Α1=5cm2 ， Α2=10cm2，当温度升至T2
=25℃时,求各杆的温度应力。 a (线膨胀系数α =12.5× 10 −6 / oC N1 a 弹性模量E=200GPa) 解： 、平衡方程： ；
∑Y = N − N
1
2
=0
、几何方程： a
∆L = ∆LT − ∆LN = 0
N2
、物理方程
∆ LT = 2 a ∆ Tα ;
1 A 3 D
2
B 1
α α
C 2
∑ ∑Y = N1 cosα + N2 cosα − N3 = 0

拉压超静定

拉压超静定

A 1 B 2

FN1
D

FN2 F
D


3 C h
FN3
F
平衡方程为
( FN1 FN3 ) cos FN2 F cos 0 FN1 sin FN3 sin F sin 0
这是一次超静定问题
A 1 B 2

1 D

E
l3
D3
l2
( FN1 FN3 ) cos FN2 F cos 0 FN1 sin FN3 sin F sin 0 l1 l3 2 l2 cos
A 1 B 2

D

物理方程为
FN1l1 FN1h l1 EA EA cos FN2l2 FN2h l2 EA EA FN3l3 FN3h l3 EA EA cos
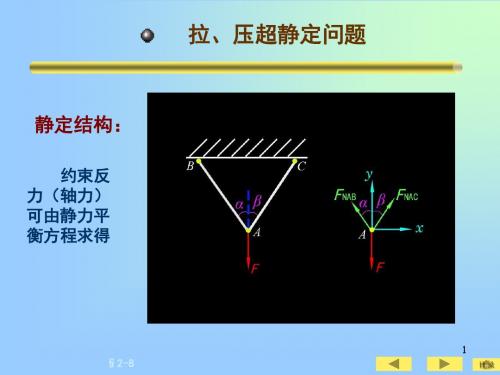
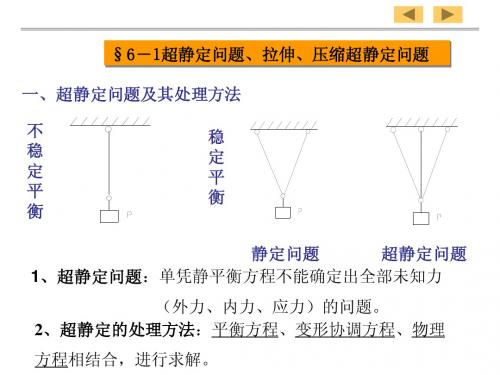
2.10 拉伸、压缩超静定问题 一、超静定问题及求解方法 静定问题: 杆件的轴力可以用静力平衡条件求出, 这种情况称作静定问题。 超静定问题: 只凭静力平衡方程已不能解出全部 未知力, 这种情况称做超静定问题。
超静定的次数: 未知力数超过独立平衡方程数 的数目, 称作超静定的次数。
2.10 拉伸、压缩超静定问题 变形协调方程: 在静不定问题中, 各部分变形之 间必存在相互制约的条件, 这种条件称为变形相 容条件(变形协调方程)。
2 FN1 3 FN2 6 F
这是一次超静定问题
(2) 画变形几何关系图 建立变形几何方程
变形协调条件为： 梁 ABCD 绕 铰 链 A 转 动 , ①、② 两杆仍与其铰接
d C 2d B
②
A a
60º B

工程力学(马浩)拉压超静定问题

工程力学(马浩)拉压超静定问题

解超静定问题的步骤： 解超静定问题的步骤：
根椐变形相容条件建立变形几何方程。变形几何方程的个 根椐变形相容条件建立变形几何方程。 数与超静定次数相等。 数与超静定次数相等。 将变形与力之间的关系（胡克定律） 将变形与力之间的关系（胡克定律）代入变形几何方程得 补充方程。 补充方程。 联立补充方程与静力平衡方程求解。 联立补充方程与静力平衡方程求解。
α
F
几何方程为
∆l1 +∆l3 = 2 l2cosα ∆
A
α
1
1
∆l3
B 2
α α
D
β
E
α α
D
∆l2
C
D1
3
2
P
H
∆l1
3
G
D
'
N 1 l1 N1 H = ∆ l1 = EA EA cosα
α
N 2l2 N 2 H = ∆ l2 = EA EA
N 3 l3 N3 H = ∆ l3 = EA EA cosα
3 3 2 1
2
1
l
B
a C
a A
C
B
A
∆l 3
C′
∆l 2
B′
∆l1
A′
G (4) 联立平衡方程与补充方程求解
N1+ N2 + N3 −G=0 N1⋅ 2a + N2⋅a =0 N1+ N3 = 2N2
x =0
G N1 = − 6 G = N2 3 5 G N3 = 6
思考题 刚性梁 ABC 由抗拉刚度相等的三根杆悬挂着。 由抗拉刚度相等的三根杆悬挂着。
F
A
N 1 l1 N1 H = ∆ l1 = EA EA cosα

轴向拉伸与压缩超静定结构

求各杆的变形量△Li ，如图1；
变形图近似画法，图中弧之切线。
小变形放大图与位移的求法。
A
B
C
L1
L2
P
C"
写出图2中B点位移与两杆变形间的关系 L2 B' P
解：变形图如图2， B点位移至B'点，由图知：
C
图 2
A
L1
B
一、拉、压超静定问题
试判断下图结构是静定的还是超静定的？若是超静定，则为几次超静定？
角钢截面面积由型钢表查得: A1=3.086cm2
[例3] 图示桁架，3根杆材料均相同，AB杆横截面面积为200mm2，AC杆横截面面积为300 mm2，AD杆横截面面积为400 mm2，若F=30kN，试计算各杆的应力。
列出平衡方程：
即：
列出变形几何关系
，则AB、AD杆长为
解：设AC杆杆长为
、物理方程
解平衡方程和补充方程，得: 、补充方程 、温度应力
F
F
F
F
F
F
二、装配应力——预应力
§2-9 装配应力和温度应力
装配应力： 超静定结构中才有装配应力 1、列出独立的平衡方程 2、变形几何关系 3、物理关系 4、补充方程 5、求解方程
、几何方程
解：、平衡方程:
2、静不定结构存在装配应力。
如图，3号杆的尺寸误差为，求各杆的装配内力。
A
B
C
1
2
A
B
C
1
2
D
A1
3
、物理方程及补充方程：
、解平衡方程和补充方程，得:
d
A1
N1
N2
N3
A
A1

工程力学第12讲 拉压：超静定问题


(a)
FN2 l2 ( FBx )l2 lCB EA EA
4. 建立补充方程 5. 支反力计算
FAx l1 FBx l2 0
(b)
联立求解平衡方程(a)与补充方程(b)
FAx Fl2 l1 l2 Fl1 FBx l1 l2
例 8-2 已知：F = 50 kN，[st ] = 160 MPa，[sc ] = 120 Mpa ，A1= A2。试问：A1=? A2=?
§8 应变能概念
应变能与功能原理 外力功与应变能计算 例题
应变能与功能原理
应变能与外力功 弹性体因变形而储存的能量－应变能 Ve
外力在变形过程中所作之功－外力功 W
弹性体功能原理 根据能量守恒定律，弹性体因变形所储 存的应变能 ，数值上等于外力所作的功
Vε W
功能原理Байду номын сангаас立条件：载荷由零逐渐缓慢 增大，弹性体处于准静态，以致动能与热能 等的变化，均可忽略不计。
提问
塑性材料和脆性材料按照什么指标区分？ 塑性材料的失效是指什么？ 脆性材料的失效是指什么？ 拉压杆件的强度条件是什么？ 什么叫作许用应力？ 强度计算有哪几种类型？

§8 简单拉压静不定问题
静不定问题与静不定度 静不定问题分析 例题
静不定问题与静不定度
静定问题 仅由平衡方程即可确定全部未知力（约束反 力与内力）的问题 静不定问题 仅由平衡方程不能确定全部未知力的问题
表面aa－积压, 截面cd－拉应力最大, 截面ab－剪切
2. 强度校核
挤压强度：
Fbs F 2
s bs
F 2
Fbs F 9.0 MPa[s bs ] Abs 2b

2-3 拉压变形、超静定


§2--6 拉压杆的弹性应变能
一、弹性应变能：杆件发生弹性变形，外力功转变为变形能贮存
与杆内，这种能成为应变能（Strain Energy）用“U”表示。 二、 拉压杆的应变能计算： 不计能量损耗时，外力功等于应变能。
N（ x） F N(x)
1 d U = d W = FN ( x ) • ∆ d x 2
A
B
60C ° 60° D ∆1 ∆ C ∆
2
3）变形图如左图 ,
B'
C点的垂直位移为：
∆ LC = BB′ + DD ′ 2 ∆ 1 sin 60 + ∆ 2 sin 60 = 2
D'
A 800
B
60° 60° D C 400 P 400
∆L 1.36 = = 2 sin 60 2 sin 60o = 0.79 mm
FN 2 = 0.72 P = A2 [σ 2 ]
∴[P2 ] = A2 [σ 2 ] / 0.72 = 2502 × 12 / 0.72 = 1042kN
r求结构的许可载荷： 方法2:
[∆1 ] = L[σ 1 ]/ E1 = 0.8mm [∆ 2 ] = L[σ 2 ]/ E2 = 1.2mm
4N 1
FN 1 = 0.07 P ; FN 2 = 0.72 P
r求结构的许可载荷： 方法1: FN 1 = 0.07 P = A1 [σ 1 ]
1m
250
角钢面积由型钢表查得: A1=3.086cm2
∴[P1 ] = A1 [σ 1 ] / 0.07 = 308 .6 × 160 / 0.07 = 705 .4 kN
∑X
= FN 1 sin α − N 2 sin α = 0

26拉压超静定问题


3）物理方程lT Tl Nhomakorabeal RBl EA
T l R l
EA
T

R T
A
E
对于钢杆，
1.21051/C
E210103M P a
当△T= 40°C时:
T 100MPa
2.6 超静定问题
超静定问题的概念
静定问题:
超静定问题: 超静定次数:
2.6.1 拉（压）杆超静定问题解法
1）解除“多余”约束，使超静定结构变 为静定结构（称基本结构），建立静力 平衡方程。
2）根据“多余”约束性质，建立变形协 调方程。
3）建立物理方程（如胡克定律，热膨胀 规律等）。
4）联解静力平衡方程以及2）和3）所建 立的补充方程，求出未知力（约束力或 内力）。
lAClCB0
（3）物理方程 由胡克定律
lAC
NACaRAa EA EA
lBC
NBCbRBb EA EA
得补充方程 RAaRBb
（4）求解得
Pa RB a b
Pb RA a b
1）由静力平衡方程
(FF NN 11F F NN 22)cosFN3F0
求各杆的装配应力。
1）由静力平衡方程
FN1 FN2

FN3 (FN1 FN2 )0
2）变形协调方程 3）物理方程
l1 l3

l2 e


l1

l1

l2

FN1l EA
l3

FN 3l E 3A3
得补充方程 FN3l e FN1l
E3 A3
EA
2．温度应力
1．装配应力
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
内容提要
简单的拉、压超静定问题
第1页/共38页
§7—7 简单的 拉、压超静定问题
一、静定与超静定问题 1、静定问题: 杆件的轴力可以用静力平衡条件求出，这种情况 称作静定问题。 2、超静定问题: 只凭静力平衡方程已不能解出全部未知力， 这种情况称做超静定问题。
3、超静定的次数: 未知力个数与独立平衡方程的数目之差, 称作超静定的次数。
F
A F N 3(l cos )
E3 A3
第15页/共38页
D
A
A
FN3
3、补充方程
B
D
C
3
1
FN3
2
A A
F
(F F N 3)l
2 EA cos 2
F
N 3(l cos )
E3 A3
第16页/共38页
D
B
D
C
3
1
FN3
2
A
A
A A
F
FN3
FN3 1 2
F EA
cos3
E3 A3
第17页/共38页
二、超静定问题的基本解法
例题1：两端固定的等直杆AB横截面积为A，弹性模量为E，在C
点处承受轴力 F 的作用，如图 所示 。计算约束反力。
A a
C
F
B
第4页/共38页
A a
C
F
B
FA
A
C
F
B
FB
这是一次超静定问题
第5页/共38页
A a
C
F
B
A
A
C
F
B
基本系统
C
F
B
FB
相当系统
1、解除多余约束（如选 B 端的约束为多余约束 )， 代以反力FB，得超静定系统的 相当系统。
例题2另解： 设1、2、3三杆用铰链连结，L1 = L2 = L， A1 = A2 = A , E1 = E2 =E ,3 杆的长度 L3,横截面积 A3,弹性模量 E3,试求在 沿铅垂方向的外力P作用下各杆的轴力。
分析：
这是一次超静定问 题，必须建立一个 补充方程。
B
DC
1
3
2
A P
y
FN1 FN 3
FN 2
αα
x
A P
第23页/共38页
B
DC
1
3
2
A P
y
FN1 FN 3
FN 2
αα
x
A P
解： 1、静力方面由平衡方程：
Fx 0 FN1 sin FN 2 sin 0
(1)
Fy 0 FN1 cos FN 2 cos FN 3 P 0 (2)
第24页/共38页
B
DC
1
A1
A'
3、物理方面：
l1
FN 1l EA
l3
FN 3l3 E3 A3
FN 3l cos
E3 A3
代入 Δl1 Δl3 cosα
补充方程：
FN 1
FN 3
EA E3 A3
cos2
(3)
第26页/共38页
B
DC
1
3
2
A P
y
N3 N2 N1
αα
A P
13 2
B
Fa l
第9页/共38页
BF BFB 0
A a
C
F
B
A
C
F
B
FB
C
(F
F B)a EA
Fab lEA
第10页/共38页
例题2：设 1、2、3 三杆用铰链连结，l1 = l2 = l， A1 = A2 = A, E1 = E2 = E ,3 杆的长度 l3 ,横截面积 A3 ,弹性模量 E3 。 试求在沿铅垂方向的外力 F 作用下各杆的轴力。
A C
P B
a
y
(b)
RA
A
C P
解：杆的受力情况如 图 b所示。
Y 0 RA RB P 0
这是一次超静定问题。
B
RB第19页/共38页
(a) A C
P B
a
y RA (b)
A A
C
C
C1
P
B
B
(c)
lAC cc1 lCB cc1 lAC lCB
RB 1、变形方面：变形相容条件是：杆的总长度不变
第6页/共38页
A a
C
F
B
A
C
F
B
FB
2、位移条件：相当系统多余未知力作用处位移与原超静定系统
的相同。
B 0
第7页/共38页
A C
F
B
3、几何条件
A a
C
F
B
FB
BF BFB 0
第8页/共38页
B 0
A C
F
B
4、补充方程 解得
A a
C
F
B
FB
Fa F B l 0 EA EA
F
FN1
FN3
FN2
αα
A
P
FN3 1 2
F EA
cos3
E3 A3
F ( EA )cos2
F
N1
F
N
2
1
E3 A3 2 EA
cos2
E3 A3
第18页/共38页
例题1另解：两端固定的等直杆AB横截面积为A，弹性模
量为E，在C点处承受轴力P的作用，如图 a 所示 。求A处和 B处的约束反力。
(a)
l AC
RAa EA
B
lCB
RBb EA
RA
Pb l
RB
Pa l
第21页/共38页
一、静力方面：列出静力平衡方程。 二、变形几何方面：根椐变形几何相容条件建立变形几何方 程。变形几何方程的个数与超静定次数相等。 三、物理方面：将变形与力之间的关系（胡克定律）代入 变形几何方程得补充方程。
第22页/共38页
变形几何方程为： lAC lCB
2、物理方面：根据胡克定律
l Pl EA
lACRAaຫໍສະໝຸດ EAlCBRBb EA
第20页/共38页
(a) A C
P B
补充方程为
3、静力方面 由平衡方程
a
y RA (b)
A
C
P B
RB
RAa RBb EA EA
RA RB P 0
(c)
A
lAC lCB
C
C1
B
D
C
3 1
2
A
F
第11页/共38页
B
D
C
3 1
2
A
FN1
FN3
FN2
αα
A
F
F
这是一次超静定问题。
第12页/共38页
B
D
C
B
D
C
3
1
FN1
2
A
FN3
αα
A
3
FN2
1
FN3
2
A
F
P
F
1、解除多余约束（如选 3 杆为多余约束 )，代以反力 FN3， 得超静定系统的 基本（相当）系统。
第13页/共38页
D
B
D
C
3
1
FN3
2
A
A
A A
F FN3
2、位移条件：由杆 1 和杆 2 构成的杆系在 ( F - FN3 )作用下节 点 A 的位移 A ，应等于杆 3 在 FN3 作用下节点 A 的位移 ‘A
A A
第14页/共38页
D
A
A
FN3
A
(F 2EA
F N 3)l
cos2
B
D
C
3
1
FN3
2
A A
3
2
B
DC
1
3 2
13 2
A Δl1
y
A FN1 FN 3
FN 2
A
P
αα
x
A'
A
Δl3
A2
A1
A'
P
2、变形几何方面： 变形的几何相容条件是：变形后三杆仍铰结在一起
变形几何方程为： l1 l3 cos
第25页/共38页
B
DC
1
3
2
A P
y
N3 N2 N1
αα
A P
13 2
A Δl1
x Δl3 A2
第2页/共38页
4、多余约束：多于维持平衡所必需的支座或杆件。 5、多余未知力 : 与多余约束相应的支反力或内力。
B
C
D
E
2 1
3 4
A F
FN2 FN1
A
B
FN3 FN4
F
C
D
E
2 1
3 4
A F
这是二次超静定问题 可将 AC，AD 杆看作多余约束 FN2 ， FN3 为相应的多余未知力
第3页/共38页