霍尔实验与热特性实验 讲义请实验前复习
- 格式:doc
- 大小:1.11 MB
- 文档页数:34

霍尔效应实验简介在磁场中的载流导体上出现横向电势差的现象是24岁的研究生霍尔(Edwin H. Hall)在1879年发现的,现在称之为霍尔效应。
随着半导体物理学的迅猛发展,霍尔系数和电导率的测量已经成为研究半导体材料的主要方法之一。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。
若能测得霍尔系数和电导率随温度变化的关系,还可以求出半导体材料的杂质电离能和材料的禁带宽度。
在霍尔效应发现约100年后,德国物理学家克利青(Klaus von Klitzing)等研究半导体在极低温度和强磁场中发现了量子霍尔效应,它不仅可作为一种新型电阻标准,还可以改进一些基本量的精确测定,是当代凝聚态物理学和磁学令人惊异的进展之一,克利青为此发现获得1985年诺贝尔物理学奖。
其后美籍华裔物理学家崔琦(D. C. Tsui)和施特默在更强磁场下研究量子霍尔效应时发现了分数量子霍尔效应。
它的发现使人们对宏观量子现象的认识更深入一步,他们为此发现获得了1998年诺贝尔物理学奖。
用霍尔效应制备的各种传感器,已广泛应用于工业自动化技术、检测技术和信息处理各个方面。
本实验的目的是通过用霍尔元件测量磁场,判断霍尔元件载流子类型,计算载流子的浓度和迁移速度,以及了解霍尔效应测试中的各种副效应及消除方法。
实验原理通过霍尔效应测量磁场霍尔效应装置如图2.3.1-1和图2.3.1-2所示。
将一个半导体薄片放在垂直于它的磁场中(B 的方向沿z轴方向),当沿y方向的电极C、D上施加电流I时,薄片内定向移动的载流子(设平均= q u B (1)速率为u)受到洛伦兹力F B的作用,FB无论载流子是负电荷还是正电荷,F B 的方向均沿着x 方向,在磁力的作用下,载流子发生偏移,产生电荷积累,从而在薄片B 、B’两侧产生一个电位差V BB ’,形成一个电场E 。
电场使载流子又受到一个与F B 方向相反的电场力F E ,F E =q E = q V BB’ / b(2)其中b 为薄片宽度,F E 随着电荷累积而增大,当达到稳定状态时F E =F B ,即q uB = q V BB’ / b(3)这时在B 、B’两侧建立的电场称为霍尔电场,相应的电压称为霍尔电压,电极B 、B’称为霍尔电极。


1. 了解霍尔效应的基本原理和实验方法;2. 掌握霍尔效应测量磁场的方法和技巧;3. 熟悉霍尔元件的结构和特性;4. 通过实验验证霍尔效应的规律。
二、实验仪器1. 霍尔效应实验仪;2. 直流稳流电源;3. 毫伏电压表;4. 电流表;5. 样品支架;6. 霍尔元件;7. 磁场发生器。
三、实验原理霍尔效应是指当电流通过导体或半导体时,在垂直于电流和磁场方向的两侧会产生电压差,这种现象称为霍尔效应。
根据霍尔效应,霍尔电压UH与电流I、磁感应强度B和导体厚度d的关系为:UH = RHBd其中,RH为霍尔系数,它与材料的性质有关。
四、实验步骤1. 连接电路:将霍尔效应实验仪、直流稳流电源、毫伏电压表、电流表等仪器按照实验电路图连接好。
2. 调节样品支架:将霍尔元件放置在样品支架上,调整支架使其位于磁场中间。
3. 调节电流:打开直流稳流电源,调节电流表,使通过霍尔元件的电流为I1。
4. 测量霍尔电压:观察毫伏电压表,记录此时霍尔电压U1。
5. 调节磁场:调整磁场发生器,改变磁感应强度B,保持电流I1不变。
6. 重复步骤3和4,记录不同磁场强度下的霍尔电压U2、U3、U4。
7. 改变电流方向:将霍尔元件的电流方向调反,重复步骤3、4和5,记录不同磁场强度下的霍尔电压U5、U6、U7。
8. 测量样品厚度:使用游标卡尺测量霍尔元件的厚度d。
9. 计算霍尔系数:根据霍尔电压U1、U2、U3、U4、U5、U6、U7和样品厚度d,计算霍尔系数RH。
10. 分析实验数据:根据实验数据,分析霍尔效应的规律,验证实验原理。
五、实验注意事项1. 在实验过程中,注意安全操作,防止触电、电火花等事故发生。
2. 调节电流和磁场时,动作要轻柔,避免对霍尔元件造成损伤。
3. 保持实验环境的稳定,避免外界因素对实验结果的影响。
4. 记录实验数据时,注意数据的准确性和完整性。
六、实验报告撰写1. 实验报告应包括实验目的、实验原理、实验仪器、实验步骤、实验数据、实验结果和分析等内容。

霍尔效应实验原理引言:在研究电磁学和物理学等相关领域时,霍尔效应是一个重要的实验现象。
该效应由爱德华·霍尔在1879年首次观察到,并被广泛应用于传感器、开关和计量设备等领域。
本文将介绍霍尔效应实验的原理及相关实验装置,以及实验中需要注意的要点。
一、实验目的霍尔效应实验的主要目的是研究当一个电流通过载流子数量、方向及速度不同的导体时产生的霍尔电压效应。
通过实验,我们可以进一步了解霍尔效应的物理本质以及相关参数的测量方法。
二、实验原理霍尔效应是指在一个垂直于电流流向的磁场中,当电流从导体中流过时,会产生一种垂直于电流和磁场方向的电势差,这就是所谓的霍尔电压。
霍尔电压(VH)与电流(I)、磁感应强度(B)以及材料本征霍尔系数(RH)之间存在关系。
根据该关系可以得到公式:VH = RH * I * B因此,通过测量霍尔电压,可以推导出材料的霍尔系数,从而了解导体情况。
三、实验装置1. 电源:用于提供所需的电流,确保实验安全、稳定运行。
2. 磁铁:产生一个恒定的磁场,可以使用永磁铁或电磁铁。
3. 引线和导线:将电流引入实验装置,连接各个实验部分。
4. 载流子材料:通常使用金属导体作为载流子材料,如铜线或硅片。
5. 电压测量仪:用于测量霍尔电压,可以是数字电压表或示波器等。
四、实验步骤1. 将磁铁放置在所需位置,确保磁场垂直于电流方向。
2. 通过电源将恒定电流注入载流子材料中。
3. 使用电压测量仪测量载流子材料两侧的电压差,即霍尔电压。
4. 改变电流强度或磁感应强度,观察霍尔电压的变化。
5. 根据实验数据,计算材料的霍尔系数。
五、注意事项1. 实验过程中,一定要注意电流的安全,避免触电或短路等意外情况的发生。
2. 磁场应保持稳定,不应有较大的波动。
3. 测量电压时,确保测量仪器的准确性和灵敏度,避免由于仪器误差导致结果不准确。
4. 多组数据的采集可以提高实验结果的准确性与可靠性。
5. 在实验完成后,及时关闭电源和处理实验装置,保持实验环境整洁。

【⼤学物理实验】霍尔效应与应⽤讲义霍尔效应与应⽤1879年,年仅24岁的霍尔在导师罗兰教授的⽀持下,设计了⼀个根据运动载流⼦在外磁场中的偏转来确定在导体或半导体中占主导地位的载流⼦类型的实验,霍尔的发现在当时震动了科学界,这种效应被称为霍尔效应。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流⼦浓度、载流⼦迁移率等主要参数。
通过测量霍尔系数和电导率随温度变化的关系,还可以求出半导体材科的杂质电离能和材料的禁带宽度。
如今常规霍尔效应不但是测定半导体材料电学参数的主要⼿段,利⽤该效应制成的霍尔器件已⼴泛⽤于⾮电量的电测量、⾃动控制和信息处理等各个研究领域。
该实验要求学⽣了解霍尔效应的基本原理、霍尔元件的基本结构,测试霍尔元件特性的⽅法,并对测量结果给出正确分析和结论。
⿎励学⽣运⽤霍尔效应的基本原理和霍尔元件的特性,设计⼀些测量磁场,或各种⾮磁性和⾮电性物理量的测量的实验⽅案,例如:磁场分布、位置、位移、⾓度、⾓速度等。
让学⽣更好的运⽤霍尔效应来解决⼀些实际问题。
⼀、预备问题1.霍尔效应在基础研究和应⽤研究⽅⾯有什么价值?2.如何利⽤实验室提供的仪器测量半导体材料的霍尔系数?3.怎样判断霍尔元件载流⼦的类型,计算载流⼦的浓度和迁移速率?4.伴随霍尔效应有那些副效应?如何消除?5.如何利⽤霍尔效应和元件测量磁场?6.如何利⽤霍尔元件进⾏⾮电磁的物理量的测量?7.若磁场的法线不恰好与霍尔元件⽚的法线⼀致,对测量结果会有何影响?如何⽤实验的⽅法判断B与元件法线是否⼀致?8.能否⽤霍尔元件⽚测量交变磁场?⼆、引⾔霍尔效应发现⼀百多年来,在基础和应⽤研究范围不断扩展壮⼤,反常霍尔效应、整数霍尔效应、分数霍尔效应、⾃旋霍尔效应和轨道霍尔效应等相继被发现,并构成了⼀个庞⼤的霍尔效应家族。
1985年克利青、多尔达和派波尔因发现整数量⼦霍尔效应,荣获诺贝尔奖;1998年诺贝尔物学理奖授予苏克林、施特默和崔琦,以表彰他们发现了分数量⼦霍尔效应。

高中物理面试霍尔效应教案
教学目标:
1. 了解霍尔效应的基本原理和应用
2. 能够描述霍尔效应在实际中的应用,并能够解决相关问题
3. 实验验证霍尔效应,并能够分析实验结果并得出结论
教学步骤:
一、导入(5分钟)
通过提问引入霍尔效应的基本概念,让学生思考并提出自己对于霍尔效应的理解。
二、讲授霍尔效应(15分钟)
1. 介绍霍尔效应的基本原理和现象
2. 讲解霍尔效应的公式以及相关参数的定义
3. 分析霍尔效应在实际中的应用,如测量电流、磁场强度等
三、实验演示(20分钟)
1. 老师进行霍尔效应的实验演示,让学生观察实验现象
2. 学生根据实验数据进行相关计算,并分析实验结果
四、小组讨论(15分钟)
1. 学生分组讨论实验结果和结论
2. 学生自由发言,分享对于霍尔效应的理解和应用
五、总结与评价(5分钟)
1. 总结本节课的内容,强调霍尔效应的重要性和应用
2. 回顾学生对于霍尔效应的理解,并对学生的表现进行评价
六、作业布置(5分钟)
布置相关作业,让学生对霍尔效应进行更进一步的了解和思考
教学资源:
1. 实验器材:霍尔元件、电源、磁铁等
2. 讲义和实验报告模板
教学评估:
1. 学生的发言和讨论情况
2. 学生实验数据的准确性和分析能力
3. 学生对于霍尔效应的理解和应用能力
教学反思:
1. 霍尔效应是一个较为抽象和复杂的概念,需要通过实验演示和互动讨论来加深学生的理解和应用能力
2. 需要鼓励学生积极参与讨论,提高他们的学习兴趣和主动性。

【实验名称】霍尔效应及其应用 【实验目的】1 •了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。
2•学习用“对称测量法”消除副效应的影响,测量并绘制试样的 线。
3 •确定试样的导电类型、载流子浓度以及迁移率。
【实验原理】霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中, 这种偏转就导致在垂直电流和磁场的方向上产 生正负电荷的聚积,从而形成附加的横向电场,即霍尔电场。
对于图(1) (a )所示的N 型半导体试样,若在 X 方向的电极D 、E 上通以电流Is ,在Z 方向加磁场B ,试样中载流子 (电子)将受洛仑兹力:F g =ev B(1) 其中e 为载流子(电子)电量, V 为载流子在电流方向上的平均定向漂移速率,B 为磁感应强度。
无论载流子是正电荷还是负电荷, F g 的方向均沿Y 方向,在此力的作用下,载流子发 生便移,则在 Y 方向即试样A 、A'电极两侧就开始聚积异号电荷而在试样A 、A'两侧产生一个电位差V H ,形成相应的附加电场 E —霍尔电场,相应的电压V H 称为霍尔电压,电极A 、 A'称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P型半导体的多数载流子为空穴。
对N 型试样,霍尔电场逆 Y 方向,P 型试样则沿Y 方向,有其中E H 为霍尔电场强度。
V H _ I S 和 V H — I M 曲Is (X)、B (Z )E H (Y) ::: 0 E H (Y) 0(N型)(P显然,该电场是阻止载流子继续向侧面偏移,试样中载流子将受一个与F g 方向相反的横向电场力: F E =eE H(2)F E随电荷积累增多而增大,当达到稳恒状态时,两个力平衡,即载流子所受的横向电场力e E H 与洛仑兹VB 相等,样品两侧电荷的积累就达到平衡,故有eE H =eVB(3)3.结合电导率的测量,求载流子的迁移率□设试样的宽度为b ,厚度为d ,载流子浓度为n ,则电流强度I s 与的V 关系为Is = n evbd(4)由(3)、(4)两式可得1VH= E H b=ISB 二 R H ! 1SBned dd(5)即霍尔电压 VH (A 、A '电极之间的电压)与IsB 乘积成正比与试样厚度 d 成反比。

霍尔实验与热特性实验讲义请实验前复习实验讲义请实验前复习实验三半导体材料霍尔效应测量分析(⼀)实验⽬的:掌握⽤霍尔效应测量仪测量半导体材料样品的霍尔系数和电阻率(电导率)的基本原理和⽅法,由测量数据确定半导体样品中载流⼦类型,求出载流⼦浓度及霍尔迁移率。
(⼆)教学基本要求:掌握半导体材料的电阻率、电导率、霍尔系数、衬底浓度、迁移率等理论概念;了解霍尔效应测试系统的⼯作原理及测试⽅法。
掌握产⽣霍尔效应原理以及消除由于样品置于磁场中产⽣的⼏中副效应的测量⽅法。
熟悉霍尔效应测量仪装置的使⽤⽅法,测出样品的电阻率和霍尔系数,判断样品导电类型,计算出霍尔样品的载流⼦浓度及霍尔迁移率,对结果和误差进⾏分析。
(三)半导体材料霍尔效应的物理基础掌握要点:1、半导体材料的霍尔效应霍尔效应从本质上讲是运动的带电粒⼦在磁场中受洛仑兹⼒作⽤⽽引起的偏转。
当带电粒⼦(电⼦或空⽳)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的⽅向上产⽣正负电荷的聚积,从⽽形成横向电场。
下图显⽰了半导体材料中的霍尔效应。
半导体霍尔效应⽰意图 a. N型半导体 b. P型半导体若在X⽅向通以电流Is,在Y⽅向加磁场B,则在Z⽅向,即试样A、A`电极两侧就开始聚积异号电荷,从⽽产⽣相应的附加电场。
电场的指向取决于试样的导电类型。
显然,该电场阻⽌载流⼦继续向侧⾯偏移。
当载流⼦所受的横向电场⼒FE 与洛仑兹⼒FB 相等时,样品两侧电荷的积累就达到平衡,故有:H eE =e Bν其中EH 为霍⽿电场,ν是载流⼦在电流⽅向上的平均漂移速度。
设试样的长为l ,宽为b ,厚度为d ,载流⼦浓度为n ,则:S I ne bdν=//H H S H S V E b I B ned R I b d===即霍尔电压VH (A ,A`电极之间的电压)与ISB 乘积成正⽐,与试样厚度d 成反⽐。
⽐例系数RH=1/ne 称为霍尔系数,它是反映材料霍尔效应强弱的重要参数。


霍尔效应霍尔效应是导电材料中的电流与磁场相互作用而产生电动势的效应。
从本质上讲,霍尔效应是电流的一种磁效应。
1879年,美国霍普金斯大学24岁的研究生霍耳在研究载流导体在磁场中受力性质时发现了这一电磁现象——霍尔效应。
随后人们在半导体、导电流体中也发现了霍耳效应,且半导体的霍耳效应比金属强得多。
霍耳效应发现约100年后,1980年由德国科学家克利青等人又发现了整数量子霍耳效应(IQHE),并于1985年获得了诺贝尔物理学奖。
1982年,崔琦、施特默和劳夫林又发现了分数量子霍耳效应(FQHE),获得了1998年诺贝尔物理学奖。
随着科学技术的发展,霍耳效应已在测量、自动控制、计算机和信息技术等方面得到了广泛的应用,主要用途有以下几个方面:(1)测量磁场;(2)测量直流或交流电路中的电流强度和功率;(3)转换信号,如把直流电流转换成交流电流并对它进行调制,放大直流和交流信号;(4)对各种物理量(可转换成电信号的物理量)进行四则运算和乘方开方运算。
由霍耳效应制成的霍耳元件具有结构简单而牢靠、使用方便、成本低廉等优点,在生产和科研实际中得到越来越普遍的应用。
【实验目的】1.了解霍尔效应的原理;2.掌握霍尔电压的测量方法,学会用霍尔器件测量磁场;3.测量霍尔器件的输出特性。
【实验仪器】DH4512系列霍尔效应实验仪【实验原理】一、霍尔效应的基本原理与应用霍尔效应从本质上讲,是运动的带电粒子在磁场中受洛仑兹力的作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积,从而形成附加的横向电场。
对于(图10-1)所示的半导体试样,若在X方向通以电流I,在Z方向加磁场B,则在Y方向即试样A、A 电极两侧就开始聚积异号电荷而产生相应的附加电场。
电场的指向取决于试样的导电类型。
显然,该电场是阻止载流子继续向侧面偏移,当载流子所受的横向电场力H eE 与洛仑兹力eVB 相等时,样品两侧电荷的积累就达到平衡,故有:H eE eVB = (10-1)其中,H E 为霍尔电场,V 是载流子在电流方向上的平均漂移速度。

变温霍尔效应对通电的导体或半导体施加一与电流方向垂直的磁场,则在垂直于电流和磁场方向上有一横向电位差出现,这个现象于1879年为物理学家霍尔所发现,故称为霍尔效应。
在20世纪的前半个世纪,霍尔系数及电阻率的测量一直推动着固体导电理论的发展,特别是在半导体纯度以及杂质种类的一种有力手段,也可用于研究半导体材料电输运特征,至今仍然是半导体材料研制工作中必不可少的一种常备测试手法。
在本实验中,采用范德堡测试方法,测量样品霍尔系数随温度的变化。
1.实验原理1.1霍尔效应霍尔效应是一种电流磁效应,如图1所示:图1霍耳效应示意图当样品通以电流I,并加一磁场垂直于电流,则在样品的两侧产生一个霍尔电位差:H H IBU Rd,H U 与样品厚度d 成反比,与磁感应强度B 和电流I 成正比。
比例系数H R 叫做霍尔系数。
霍尔电位差是洛伦兹力和电场力对载流子共同作用产生的结果。
1.2一种载流子导电的霍尔系数P 型半导体:1HH pR pq μμ⎛⎫= ⎪ ⎪⎝⎭, N 型半导体:1H H n R pq μμ⎛⎫=- ⎪⎝⎭, 式中n 和p 分别表示电子和空穴的浓度,q 为电子电荷,n μ和p μ分别是电子和空穴的电导迁移率,H μ为霍尔迁移率,H H R μσ=(σ为电导率)。
1.3两种载流子导电的霍尔系数假设载流子服从经典的统计规律,在球形等能面上,只考虑晶体散射及弱磁场(410Bμ,μ为迁移率,单位为)2cmV S ,B 的单位为T )的条件下,对于电子和空穴混合导电的半导体,可以证明:()2238H p nb R p nb π-=+(1)其中n p b μμ=。
2.1实验方法本实验采用范德堡法测量单晶样品的霍耳系数,其作用是尽可能地消除各种副效应。
考虑各种副效应,每一次测量的电压是霍耳电压与各种副效应附加电压的叠加,即1H E N RL H U U E E E E=++++∆实其中,H U 实表示实际的霍耳电压,E E 、N E 和RL E 分别表示爱廷豪森效应、能斯特效应、和里纪-勒杜克效应产生的附加电位差,E ∆表示四个电极偏离正交对称分布产生的附加电位差。

霍尔效应测试㈠霍尔效应的组成,功能及性能,工作原理.组成: HMS测试系统主要由恒电流源、范德堡法则终端转换器、电压测量计,低温管道系统及磁场强度系统组成.功能及性能:工作原理:范德堡法则1 、电阻率测量测量电阻率时,依次在一对相邻的电极通电流,另一对电极之间测电位差,得到电阻R,代入公式得到电阻率ρ。
这种方法对于样品形状没有特殊的要求,但是要求薄膜样品的厚度均匀,电阻率均匀,表面是单连通的,即没有孔洞。
此外,A,B,C,D四个接触点要尽可能小(远远小于样品尺寸),并且这四个接触点必须位于薄膜的边缘。
为了简化测量和计算,常常要求待测薄膜为正方形,这是由于正方形具有很高的对称性,正方形材料的四个顶点从几何上是完全等效,因而可推知电阻值R AB,CD和R BC,AD在理论上也应该是相等。
查表可知当R AB,CD/R BC,AD=1时,f=1。
因此,最终电阻率的公式即可简化为:2、霍尔系数和迁移率测量测量霍尔系数时,在一对不相邻的电极通上电流,并在垂直样品方向上加一磁场,在另一对不相邻的电极上测量电压的变化,可得霍尔系数及其载流子浓度.其中d为样品厚度,B为磁场强度,q为电子电荷。
由电阻率和霍尔系数的测量,同时还可以得到电子的霍尔迁移率。
㈡软件菜单使用说明1. 先打开电脑主机,再打开设备开关。
2. 左手拿磁极的上盖(N朝上),将待测得薄膜样品放入弹簧夹内,此时弹簧夹应正面朝上(如果放反,会将样品烧坏),放好后盖好上盖。
3. 开始界面4. 进入霍尔测试界面需要输入数据的只有左上角的INPUT VALUE栏,别的都不用改动。
INPUT VALUE的菜单说明如下所示。
DATE:测试日期;USER NAME:用户名称;SAMPLE NAME:样品名称;(前三项自己正确填写);COMPORT:通信端口(已设置好不用重新输入);TEMP:测试温度(室温下测选择300K,液氮的环境中测选择77K);I: 测试电流(根据试验需求输入);DELAY:更换测试点测试延时(一般无需改动,0.100s);D:样品厚度(根据自己的样品输入);B:测量磁场(根据磁铁上的数据输入);Measurement Number:测量次数(一般选择1000)。



霍尔效应及其相关测量引言:1879年,霍尔(E.H.Hall)在研究通有电流的导体在磁场中受力的情况时,发现在垂直于磁场和电流的方向上产生了电动势,这个电磁效应称为霍尔效应。
在半导体材料中,霍尔效应比在金属中大几个数量级,引起人们对它的深入研究。
霍尔效应的研究在半导体理论的发展中起了重要的推动作用,直到现在,霍尔效应的测量仍是研究半导体性质的重要实验方法。
利用霍尔效应,可以确定半导体的导电类型和载流子浓度,利用霍尔系数和电导率的联合测量,可以用来研究半导体的导电机构(本征导电和杂质导电)和散射机构(晶格散射和杂质散射),进一步确定半导体的迁移率、禁带宽度、杂质电离能等基本参数。
测量霍尔系数随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的温度特性。
根据霍尔效应原理制成的霍尔器件,可用于磁场和功率测量,也可制成开关元件,在自动控制和信息处理等方面有着广泛的应用。
一、实验目的1、掌握霍尔效应原理与测电阻率的范德堡法2、掌握霍尔效应测试仪的测量原理与使用方法3、用霍尔效应测试仪测量半导体材料的霍尔系数、载流子浓度、电阻率、迁移率4、测量样品霍耳系数及电导率随温度的变化二、实验原理1、霍尔效应霍尔效应是电磁效应的一种,这一现象是美国物理学家霍尔(E.H.Hall,1855—1938)于1879年在研究金属的导电机制时发现的。
当电流垂直于外磁场通过导体时,载流子发生偏转,垂直于电流和磁场的方向会产生一附加电场,从而在导体的两端产生电势差,这一现象就是霍尔效应,这个电势差也被称为霍尔电势差。
霍尔电场应使用左手定则判断。
图1 霍尔效应原理图在半导体上外加与电流方向垂直的磁场,会使得半导体中的电子与空穴受到相同方向的洛伦兹力而在相同方向上聚集(见图二),由于载流子的聚集,会产生一个与磁场方向和电流方向都垂直的电场,电场力与洛伦兹力产生平衡之后,载流子将不再聚集,于是与电场相垂直的两极板间将具有一个电势差,这就是半导体的霍尔效应。

霍尔效应的实验研究与解释霍尔效应(Hall Effect)是指当一块导电材料处于垂直于外磁场方向的电流流动时,在材料的宽度方向会产生与电流方向垂直的电场。
这个现象最早由美国物理学家霍尔(Hall)于1879年发现并解释。
霍尔效应不仅在科学研究中有重要的应用,而且在电子器件的设计中也有着广泛的应用。
为了研究霍尔效应,我们可以进行一项简单的实验。
实验所需材料包括一块导电板、一台电源、一块磁铁和一台电压表。
首先,将导电板固定在一块平整的支架上,然后将电源的正极连接到导电板的一侧,负极连接到另一侧,使电流在导电板上产生一定的流动。
接下来,将磁铁放置在导电板下方并靠近导电板。
最后,用电压表测量导电板两侧产生的电势差。
实验结果显示,在材料的宽度方向,电流通过后会产生一个与电流方向垂直的电场。
这样的话,电子在导电板上运动时会受到这个电场的作用,导致电子的运动受到偏折。
由于磁场的存在使电子发生在垂直于磁场方向上的偏折, 偏转直至两个力平衡。
能达到平衡的电子数量受到偏折作用的强度和电子在材料中的浓度的影响。
实验解释霍尔效应的机理。
根据洛伦兹力的原理,电子在磁场作用下会受到一个由以下公式给出的力的作用:F = q * (v x B)其中,F为力,q为电子的电荷,v为电子的速度矢量,B为磁场的磁感应强度矢量。
可以看出,力的方向与速度和磁场的方向垂直。
当电子在导电板上运动时,电场引起的力将与洛伦兹力相抵消,形成一个平衡。
根据霍尔效应的定义,我们可以得到霍尔电压(VH)与电流(I)、磁感应强度(B)和导电板材料特性(例如载流子浓度)之间的关系。
具体来说,霍尔电压由以下公式给出:VH = R * IH * B / d其中,R为导电板的霍尔系数,IH为电流强度,B为磁感应强度,d为导电板的宽度。
从这个公式可以看出,霍尔电压与电流和磁场的乘积成正比,与导电板的宽度成反比。
因此,通过对实验数据的分析,我们可以确定导电板材料的特性。
变温霍尔效应实验霍尔效应的测量是研究半导体性质的重要实验方法。
利用霍尔系数和电导率的联合测量,可以用来确定半导体的导电类型和 载流子浓度。
通过测量霍尔系数与电导率随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的温度系数等基本参数。
本仪器采用现代电子技术和计算机数据采集系统,对霍尔样品在弱场条件下进行变温霍尔系数和电导率的测量,来确定半导体材料的各种性质。
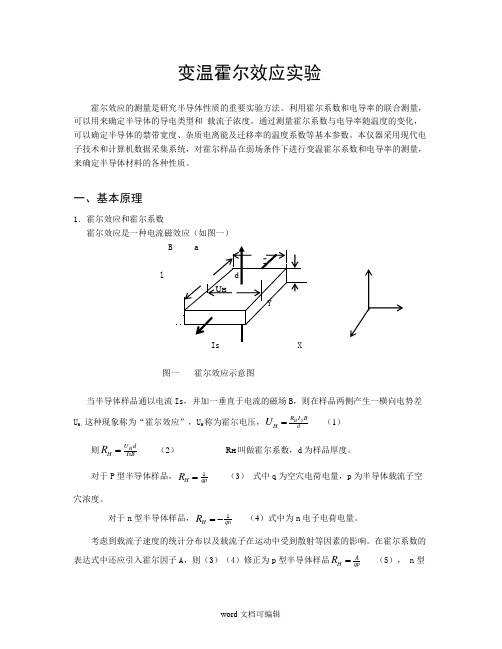
一、基本原理1.霍尔效应和霍尔系数霍尔效应是一种电流磁效应(如图一)图一 霍尔效应示意图当半导体样品通以电流Is ,并加一垂直于电流的磁场B ,则在样品两侧产生一横向电势差U H ,这种现象称为“霍尔效应”,U H 称为霍尔电压,d B I R H S H U =(1) 则IsB dU H H R = (2) R H 叫做霍尔系数,d 为样品厚度。
对于P 型半导体样品,qp H R 1=(3) 式中q 为空穴电荷电量,p 为半导体载流子空穴浓度。
对于n 型半导体样品,qn H R 1-= (4)式中为n 电子电荷电量。
考虑到载流子速度的统计分布以及载流子在运动中受到散射等因素的影响。
在霍尔系数的表达式中还应引入霍尔因子A ,则(3)(4)修正为p 型半导体样品qp AH R = (5), n 型半导体样品,qn A H R -= (6)。
A 的大小与散射机理及能带结构有关。
在弱磁场(一般为200mT )条件下,对球形等能面的非简并半导体,在较高温度(晶格散射起主要作用)情况下,A=1.18,在较低的温度(电离杂质散射起主要作用)情况下,A=1.93,对于高载流子浓度的简并半导体以及强磁场条件A=1。
对于电子、空穴混合导电的情况,在计算RH 时应同时考虑两种载流子在磁场偏转下偏转的效果。
对于球形等能面的半导体材料,可以证明:22)()(nb p q nb p A R H +-= (7) 式中 Up Un b = ,Up 、Un 分别为电子和空穴的迁移率,A 为霍尔因子,A 的大小与散射机理及能带结构有关。
实验讲义请实验前复习实验三半导体材料霍尔效应测量分析(一)实验目的:掌握用霍尔效应测量仪测量半导体材料样品的霍尔系数和电阻率(电导率)的基本原理和方法,由测量数据确定半导体样品中载流子类型,求出载流子浓度及霍尔迁移率。
(二)教学基本要求:掌握半导体材料的电阻率、电导率、霍尔系数、衬底浓度、迁移率等理论概念;了解霍尔效应测试系统的工作原理及测试方法。
掌握产生霍尔效应原理以及消除由于样品置于磁场中产生的几中副效应的测量方法。
熟悉霍尔效应测量仪装置的使用方法,测出样品的电阻率和霍尔系数,判断样品导电类型,计算出霍尔样品的载流子浓度及霍尔迁移率,对结果和误差进行分析。
(三)半导体材料霍尔效应的物理基础掌握要点:1、半导体材料的霍尔效应霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积,从而形成横向电场。
下图显示了半导体材料中的霍尔效应。
半导体霍尔效应示意图 a. N型半导体 b. P型半导体若在X方向通以电流Is,在Y方向加磁场B,则在Z方向,即试样A、A`电极两侧就开始聚积异号电荷,从而产生相应的附加电场。
电场的指向取决于试样的导电类型。
显然,该电场阻止载流子继续向侧面偏移。
当载流子所受的横向电场力FE 与洛仑兹力FB 相等时,样品两侧电荷的积累就达到平衡,故有: H eE =e B ν其中EH 为霍耳电场,ν是载流子在电流方向上的平均漂移速度。
设试样的长为l ,宽为b ,厚度为d ,载流子浓度为n ,则:S I ne bd ν= //H H S H S V E b I B ned R I b d ===即霍尔电压VH (A ,A`电极之间的电压)与ISB 乘积成正比,与试样厚度d 成反比。
比例系数RH=1/ne 称为霍尔系数,它是反映材料霍尔效应强弱的重要参数。
只要测出VH (伏)以及知道Is (安),B (高斯)和d (厘米),可按下式计算RH (3厘米/库仑)。
810H H S V d R I B =⨯ 上式中的810是由于单位换算而引入的。
当霍尔元件的材料和厚度确定时,令KH=RH/d ,称为霍尔灵敏度。
它表示霍尔元件在单位磁感应强度和单位控制电流下的霍尔电势大小。
根据H K 的定义,可以把霍尔电压改写为: H H S V K I B =为了获得明显的霍尔电压,要求H K 越大越好,因此制作霍尔样品时,往往采用减少d 的办法来增加灵敏度。
但不能认为d 越薄越好,因为此时元件的输入和输出电阻将会显著增加,这是不希望发生的。
同时我们还会看到,当工作电流S I 或磁感应强度B 两者之一改变方向时。
霍尔电势H V 方向随之改变,若两者方向同时改变,则霍尔电势不变。
应当注意:如果磁感应强度B 和元件法线成一个角度时,作用在元件上的有效磁场是其法线上的分量cos B θ,此时cos H H S V K I B θ=,所以一般在使用时应调整元件两平面方位,使H V 达到最大,即0θ= 。
2、霍尔效应的测量是研究半导体性质的重要实验方法实验表明,在磁场不太强的情况下,霍耳电场与电流密度和磁感应强度成正比,即Z x H y B j R E =,比例系数H R 称为霍耳系数,可以通过实验间接测量。
在实验中通常用霍耳电压和电流强度代替霍耳电场和电流密度,即z x H H B I d V R =,式中d 为磁场方向上样品的厚度。
理论分析表明,对于不同的材料,若不考虑载流子速度的统计分布,弱磁场下的霍耳系数:n 型半导体: nq R H 1-=p 型半导体: pq R H 1=由上两式看出,只有一种载流子时,n 型和p 型半导体的霍耳系数的符号是相反的,原因是它们的霍耳电场方向相反。
如果计入载流子速度的统计分布,上两式右端均乘以因子μμ/H ,H μ称为霍耳迁移率。
如果半导体中有两种载流子即电子和空穴,不计入载流子速度的统计分布时,霍耳系数为:)()(122nb p nb p q R H +-= (式中 p n b μμ=) 如果计入载流子速度的统计分布,设μμμμμμH p Hp nHn ==,在这种情况下,上式右端乘以n H μμ/。
所以利用霍耳电压的正负可以判断半导体的导电类型。
利用霍耳效应制成的电子器件称为霍耳器件。
为了使霍耳效应比较大,常选用迁移率高的半导体材料,因为迁移率高在同样电场作用下,漂移速度大,因而加磁场后载流子受到的洛仑兹力就大,霍耳效应就明显。
利用霍尔系数和电导率的联合测量,可以用来确定半导体的导电类型和 载流子浓度。
通过测量霍尔系数与电导率随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的温度系数等基本参数。
a.由H R 的符号(或霍尔电压的正负)判断样品的导电类型:判别的方法是按图所示Is 和B 的方向:若测得0H V <,(即点A`的电位低于点A 的电位),则H R 为负,样品为N 型半导体。
反之则为P 型。
b.由H R 求载流子浓度n :由H R =1/ne 可得,n=1/(|H R |e)。
应该指出,这个关系式是假定所有载流子都具有相同的漂移速度得到的,严格一点,考虑载流子的速度统计分布,需引入3/8π修正因子。
所以实际的计算公式是:318H n R e π=c.结合电导率的测量,求载流子的迁移率μ:由于电导率σ,载流子浓度n ,迁移率μ之间有如下关系:ne σμ=于是可得H R μσ=。
因此测出σ值,就可以求出μ。
从以上可以看出,利用霍尔效应,我们可以测得半导体材料如:判断霍尔样品的导电类型、计算室温下的霍尔系数及电导率,计算样品的载流子浓度,霍尔迁移率等诸多重要的特性参数。
3、相关理论知识根据H R 可进一步确定以下参数。
由H R 求载流子浓度n 。
由公式n=1/e|H R |可得。
应该指出,这个关系式是假定所有载流子都具有相同的漂流速度,严格说来,考虑载流子的速度统计分布,需引入3π/8的修正因子。
结合电导率的测量,求载流子的迁移率μ。
电导率σ与载流子浓度n 以及迁移率μ之间的关系为:σ= ne μ。
即μ=|H R |σ,测出σ值即可求μ。
根据上述可知,要得到大的霍尔电压,关键是选择霍尔系数的(即迁移率高、电阻率ρ亦高)的材料。
因|H R |=μρ,就金属导体而言,μ和ρ均很低;而不良导体ρ虽高,但μ极小。
因而这两种材料的霍尔系数都很小,不能用于制造霍尔器件,半导体μ高,ρ适中,是制造霍尔元件较理想的材料。
由于电子的迁移率比空穴迁移率大,所以,霍尔元件多采用N 型半导体材料。
另外,由霍尔灵敏度H K 定义式可知霍尔电压与材料的厚度成反比,因此薄膜型的霍尔元件的输出电压较片状的要高得多。
就霍尔器件而言,其厚度是一定的,实际上常采用霍尔灵敏度来表示器件的灵敏度。
1)霍尔电压: )(414321H H H H H V V V V V +++=实验中通过测量厚度d 、宽度b 、长度L 的矩形样品的霍尔电压H V 就可以求出霍尔系数H R , 霍尔电场 εy =z X H B J R =b V H /电流密度 bd I J X X /= 霍尔系数 Z X H H B I d V R /=霍尔电压d B I R V z X H H 1⨯= 由H V 的符号判断样品的导电类型:判断的方法是若测得的H V 的值是正值,样品属N 型,否则,为P 型。
判断时一定要注意到电流、磁场和霍尔电压的值必同时为正时才成立。
若正、反向测出样品的霍尔系数为正,可以判断样品为P 型,霍尔系数为负可以判断样品为N 型.2)霍尔系数:B I d V R S H H =式中:H V 是霍尔电压,单位为伏特;d 是样品厚度,单位为米; Is 是通过样品的电流,单位为安培; B 是磁通密度,单位为韦伯/米2;霍尔系数的单位是:q m /3 (3米 / 库仑 )。
根据霍尔系数H R 的正负可判断样品的导电类型已知d B I Z X 测出H V 可以求霍尔系数 Z X H H B I d V R /=,P 型半导体01>=Pq R H 、N 型半导体 10H R nq =-< 从霍尔系数的值可以求出载流子的浓度P 或者n,对于单一载流子导电情况:载流子浓度为: )(6.110319-=m R n H霍尔片载流子浓度 bq U IBn H =(其中q 为载流子电量,C q 19106.1-⨯±=,电子电量取负,空穴电量取正)。
霍尔灵敏度 1H K nqb ==3)电阻率: 标准样品的电阻率: ).(m IL dbV Ω=σρ 其中:V σ为电导电压(正反向电流后测得的平均值),单位为伏特;d 是样品厚度,单位为米;b 是样品宽度,单位为米;L 是样品长度单位为米;而I 是通过样品的电流,单位为安培。
4)电导率: 根据样品的霍尔系数和电导率,可以求得样品的霍尔迁移率p H p H R σμ=)( n H n H R σμ=)(5)霍尔迁移率: ρμ/H R = 迁移率:S V l I S σμ=电导率:μσne = 霍尔迁移率 H H H R σ⋅=μ4、半导体霍尔效应的副效应a 、 不等势电压0V 由于测量霍尔电压的电极A 和A`位置难以做到在一个理想的等势面上,因此当有电流S I 通过时,即使不加磁场也会产生附加的电压0S V I r =,其中r 为A 、A`所在的两个等势面之间的电阻(如图所示)。
不等位电势产生的原因主要有:工艺误差如电极定位误差,杂质扩散不均匀引起的误差,外界机械压力通过压阻效应造成的偏差等。
简述为:由于霍尔样品在制作时,两个霍尔电势的电极引线既不可能绝对对称的焊在霍尔片两侧、霍尔片电阻率不均匀、控制电流极的端面接触不良都可能造成两个电极不处在同一等位面上,此时虽未加磁场,但两个电极间存在电势差V0,此称不等位电势。
不等位电压0V 示意图:b 、爱廷豪森效应从微观来看,当霍尔电压达到一个稳定值VH时,速度为v的载流子的运动达到动态平衡。
但从统计的观点看,元件中速度大于v和小于v的载流子还是存在的。
因速度大的载流子所受的洛仑兹力大于电场力,而速度小的载流子所受的洛仑兹力小于电场力,因而速度大的载流子会聚集在元件的一侧,而速度小的载流子聚集在另一侧。
又因速度大的载流子的能量大,所以有快速粒子聚集的一侧温度高于另一侧。
由于霍耳电极和霍耳元件两者材料不同,电极和元件之间形成温差电偶,这一温差产生温差电动势E V。
这种由于温差而产生电势差的现象称为爱廷豪森效应。
如图所示。
E V的大小和正负号与S I、B的大小和方向有关,V与S I、B的关系相同,所以不能在测量中消除。
简述为:当样品X方向通跟H以工作电流Is,Z方向加磁场B时,由于霍尔片内的载流子速度服从统计分布,有快有慢。