高中理科椭圆的典型例题
- 格式:doc
- 大小:1.02 MB
- 文档页数:19

《椭圆》方程典型例题20例典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程.分析:题目没有指出焦点的位置,要考虑两种位置.解:(1)当()02,A 为长轴端点时,2=a ,1=b , 椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a , 椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三 例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112a a x x x M +=+=,2111a x y M M +=-=,4112===ax y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k . 证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:ac x ca AF =-12, ∴ 11545x ex a AF -=-=. 同理 2545x CF -=.∵ BF CF AF 2=+,且59=BF , ∴ 51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即 821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得 ()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上,∴ ()212125259x y -=()222225259x y -= ∴ ()()21212221259x x x x y y -+-=-.将此式代入①,并利用821=+x x 的结论得 253640-=-x ∴ 4540590=--=x k BT.典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M 到左准线l 的距离MN 是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=. 又由焦半径公式知:111212x ex a MF -=-=, 112212x ex a MF +=+=.∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x .整理得048325121=++x x .解之得41-=x 或5121-=x . ① 另一方面221≤≤-x . ②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122k kk x x +-=+.∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --. 解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x . ⑤ 将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-. 所求直线方程为0342=-+y x .说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,; (2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y . 解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=. ①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba . ② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y . (2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x . 说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 解:由已知:4=a ,2=c .所以21=e ,右准线8=x l :.过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然MF AM 2+的最小值为AQ ,即M 为所求点,因此3=M y ,且M 在椭圆上.故32=M x .所以()332,M .说明:本题关键在于未知式MF AM 2+中的“2”的处理.事实上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九 例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十 例10设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫ ⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫⎝⎛230,P 的距离是7.解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫⎝⎛-=-==a b a b a a c e 可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49sin 3sin 34222+--=θθb b b 3421sin 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值.由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,.典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点.设m x y x =++222,则 ()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化,120≠∠APB .(2)如果椭圆上存在一个点Q ,使 120=∠A Q B ,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+a y x ay ,将22222y ba a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2.∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠ ∵22c a > ∴2tan -<∠APB故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x ya x y AQB -+=-++--=∠∵ 120=∠AQB , ∴32222-=-+ay x ay整理得()023222=+-+ay a y x∵22222y ba a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a∵0≠y , ∴2232c ab y = ∵b y ≤, ∴b c ab ≤2232 232c ab ≤,()222234c c a a ≤-∴04444224≥-+a c a c ,044324≥-+e e ∴232≥e 或22-≤e (舍),∴136<≤e .典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k .当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=. 由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅. ∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解.解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α, ∴P 点坐标为)5154,554(.典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=. 分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,ca x PQ 20+=,由椭圆第二定义,e PQPF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA +的最大值、最小值及对应的点P 坐标;(2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQ PF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(. 说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1) ⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九 例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F .(1)求椭圆离心率的取值范围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+b y a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值范围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF ∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+b y a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取范围是)1,21[∈e .(2)将2222134ea c x -=代入12222=+b y a x 得 24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆. 即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12FPF ,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα,∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值范围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+=∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=. ∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+by a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos b a b -=θ,∵1cos 1<<-θ ∴1cos =θ(舍去),11222<-<-ba b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。

高三数学理科椭圆典型例题 本周教学重难点: 掌握椭圆的定义、标准方程和椭圆的简单几何性质,了解椭圆的参数方程,了解椭圆的初步应用。
【典型例题】 [例1] 已知A 、B 是椭圆12592222=+a y a x 上的点,2F 是右焦点且a BF AF 58||||22=+,AB 的中点N 到左准线的距离等于23,求此椭圆方程。
解:如图,设1F 为左焦点,连结1AF 、1BF ,则根据椭圆定义有||2||2||||2211BF a AF a BF AF -+-=+|)||(|422BF AF a +-=a a a 512584=-= 再设A 、B 、N 三点到左准线距离分别为1d 、2d 、3d由梯形中位线定理,有32321==+d d d而已知22259a b =∴22222516a b a c =-= ∴ 得离心率54=e ∵11||ed AF =,21||ed BF =∴512)(512||||2111=+==+d d e a BF AF ∴1=a ,则椭圆方程为125922=+y x[例2] 设椭圆12222=+by a x )0(>>b a 的两焦点为1F 、2F ,若在椭圆上存在一点P ,使021=⋅PF PF ,求椭圆的离心率e 的取值X 围。
解:方法一:如图所示,设)0,(1c F -、)0,(2c F 、),(00y x P则01||ex a PF +=,02||ex a PF -=,c F F 2||21=∵021=⋅PF PF ∴21PF PF ⊥∴2212221||||||F F PF PF =+即222022202024)()(a c x e c ex a ex a -=⇒=-++ 据题意,知P 点在椭圆上,但不在x 轴上∴2200a x <≤∴22020c x e <≤于是22220c a c <-≤,即1222222<≤⇒<≤a c a c a ∴)1,22[∈e方法二:设)sin ,cos (θθb a P )20(πθ≤< ∵021=⋅PF PF ∴21PF PF ⊥又O 为21F F 的中点 ∴c F F PO ==||21||21 ∴22222sin cos c b a =+θθ222222sin )(cos c c a a =-+⇒θθ即)sin 1(222θ+=c a ∴θ2sin 11+==a c e ∵20πθ≤<∴1sin 02≤<θ∴)1,22[∈e 方法三:∵021=⋅PF PF ∴21PF PF ⊥∴ P 点在以21F F 为直径的圆上,又P 点在椭圆上∴ 圆222c y x =+与椭圆12222=+b y a x 有公共点 由图知,222a c b a c b <≤⇒<≤ 即2222a c c a <≤-∴1222222<≤⇒<≤a c a c a ∴)1,22[∈e[例3] 已知A 、B 、D 三点不在一条直线上,且)0,2(-A ,)0,2(B ,2||=AD ,)(21AD AB AE +=, (1)求E 点的轨迹方程;(2)过A 作直线交以A 、B 为焦点的椭圆于M 、N 两点,线段MN 的中点到y 轴的距离为54,且直线MN 与E 点的轨迹相切,求椭圆的方程。
![《椭圆》方程典型例题20例(含标准答案解析]](https://uimg.taocdn.com/bd84dbd3f705cc1755270984.webp)
《椭圆》方程典型例题20例典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程. 分析:题目没有指出焦点的位置,要考虑两种位置. 解:(1)当()02,A 为长轴端点时,2=a ,1=b ,椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a ,椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三 例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112aa x x x M +=+=,2111a x y M M +=-=,4112===a x y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k . 证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:ac x ca AF =-12, ∴ 11545x ex a AF -=-=. 同理 2545x CF -=. ∵ BF CF AF 2=+,且59=BF , ∴ 51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即 821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上,∴ ()212125259x y -=()222225259x y -= ∴ ()()21212221259x x x x y y -+-=-. 将此式代入①,并利用821=+x x 的结论得 253640-=-x ∴ 4540590=--=x k BT.典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M到左准线l 的距离MN 是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=. 又由焦半径公式知:111212x ex a MF -=-=,112212x ex a MF +=+=.∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x .整理得048325121=++x x .解之得41-=x 或5121-=x . ① 另一方面221≤≤-x . ②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122k kk x x +-=+.∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --. 解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x . ⑤ 将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-.所求直线方程为0342=-+y x .说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,;(2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y . 解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=. ①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba . ② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y . (2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x . 说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 解:由已知:4=a ,2=c .所以21=e ,右准线8=x l :.过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然MF AM 2+的最小值为AQ ,即M 为所求点,因此3=M y ,且M 在椭圆上.故32=M x .所以()332,M .说明:本题关键在于未知式MF AM 2+中的“2”的处理.事实上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九 例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十 例10设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫ ⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b ,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫⎝⎛230,P 的距离是7.解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫⎝⎛-=-==a b a b a a c e 可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49sin 3sin 34222+--=θθb b b3421sin 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值.由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b ,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,.典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点.设m x y x =++222,则 ()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化,120≠∠APB .(2)如果椭圆上存在一个点Q ,使 120=∠AQB ,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+ay x ay ,将22222y b a a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2.∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠ ∵22c a > ∴2tan -<∠APB故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x ya x y AQB -+=-++--=∠∵ 120=∠AQB , ∴32222-=-+ay x ay整理得()023222=+-+ay a y x∵22222y ba a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a∵0≠y , ∴2232c ab y = ∵b y ≤, ∴b cab ≤2232 232c ab ≤,()222234c c a a ≤-∴04444224≥-+a c a c ,044324≥-+e e ∴232≥e 或22-≤e (舍),∴136<≤e .典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k .当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=. 由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅.∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解.解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α, ∴P 点坐标为)5154,554(.典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=. 分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,ca x PQ 20+=,由椭圆第二定义,e PQPF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA +的最大值、最小值及对应的点P 坐标; (2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQ PF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(. 说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1) ⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F .(1)求椭圆离心率的取值范围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+b y a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值范围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+by a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取范围是)1,21[∈e .(2)将2222134ea c x -=代入12222=+b y a x 得 24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆. 即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12F PF,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα ∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα, ∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值范围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+= ∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=. ∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+b y a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos b a b -=θ,∵1cos 1<<-θ ∴1cos =θ(舍去),11222<-<-ba b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。

典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程. 分析:题目没有指出焦点的位置,要考虑两种位置.解:(1)当()02,A 为长轴端点时,2=a ,1=b , 椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a , 椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112a a x x x M +=+=,2111a x y M M +=-=, 4112===ax y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k .证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:a c x ca AF =-12,∴ 11545x ex a AF -=-=. 同理 2545x CF -=.∵ BF CF AF 2=+,且59=BF ,∴ 51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即 821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得 ()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上,∴ ()212125259x y -=()222225259x y -= ∴ ()()21212221259x x x x y y -+-=-.将此式代入①,并利用821=+x x 的结论得253640-=-x ∴ 4540590=--=x k BT .典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M 到左准线l 的距离MN是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=.又由焦半径公式知:111212x ex a MF -=-=,112212x ex a MF +=+=. ∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x . 整理得048325121=++x x . 解之得41-=x 或5121-=x . ① 另一方面221≤≤-x . ②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得 ()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122kkk x x +-=+. ∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --.解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x . ⑤ 将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-.所求直线方程为0342=-+y x . 说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率. (3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,; (2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y . 解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=. ①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba . ② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y . (2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x .说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 解:由已知:4=a ,2=c .所以21=e ,右准线8=x l :. 过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然3=M y ,且M 在MF AM 2+的最小值为AQ ,即M 为所求点,因此椭圆上.故32=M x .所以()332,M .说明:本题关键在于未知式MF AM 2+中的“2”的处理.事实上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十例10 设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫ ⎝⎛230,P 的距离是7. 解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫ ⎝⎛-=-==a b a b a a c e 可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49sin 3sin 34222+--=θθb b b 3421sin 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b 成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,. 典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点. 设m x y x =++222,则 ()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化, 120≠∠APB . (2)如果椭圆上存在一个点Q ,使 120=∠AQB ,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+a y x ay ,将22222y ba a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2. ∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠ ∵22c a >∴2tan -<∠APB 故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x y a x y AQB -+=-++--=∠∵ 120=∠AQB , ∴32222-=-+ay x ay整理得()023222=+-+ay a y x ∵22222y b a a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a ∵0≠y , ∴2232c ab y = ∵b y ≤, ∴b c ab ≤2232 232c ab ≤,()222234c c a a ≤- ∴04444224≥-+a c a c ,044324≥-+e e∴232≥e 或22-≤e (舍),∴136<≤e . 典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k . 当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=. 由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅. ∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解. 解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α,∴P 点坐标为)5154,554(. 典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=.分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,c a x PQ 20+=,由椭圆第二定义,e PQPF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA +的最大值、最小值及对应的点P 坐标;(2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQPF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(.说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1) ⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y 轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F . (1)求椭圆离心率的取值范围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+by a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值范围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF ∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+by a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取范围是)1,21[∈e .(2)将2222134e a c x -=代入12222=+by a x 得 24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆.即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12FPF ,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα,∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值范围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+=∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=. ∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+by a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos ba b -=θ, ∵1cos 1<<-θ ∴1cos =θ(舍去),11222<-<-b a b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。

《椭圆》方程典型例题20例典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程.分析:题目没有指出焦点的位置,要考虑两种位置.解:(1)当()02,A 为长轴端点时,2=a ,1=b , 椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a , 椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三 例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112a a x x x M +=+=,2111a x y M M +=-=,4112===ax y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k . 证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:ac x ca AF =-12, ∴ 11545x ex a AF -=-=. 同理 2545x CF -=.∵ BF CF AF 2=+,且59=BF , ∴ 51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即 821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得 ()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上,∴ ()212125259x y -=()222225259x y -= ∴ ()()21212221259x x x x y y -+-=-.将此式代入①,并利用821=+x x 的结论得 253640-=-x ∴ 4540590=--=x k BT.典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M 到左准线l 的距离MN 是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=. 又由焦半径公式知:111212x ex a MF -=-=, 112212x ex a MF +=+=.∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x .整理得048325121=++x x .解之得41-=x 或5121-=x . ① 另一方面221≤≤-x . ②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122k kk x x +-=+.∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --. 解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x . ⑤ 将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-. 所求直线方程为0342=-+y x .说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,; (2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y . 解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=. ①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba . ② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y . (2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x . 说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 解:由已知:4=a ,2=c .所以21=e ,右准线8=x l :.过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然MF AM 2+的最小值为AQ ,即M 为所求点,因此3=M y ,且M 在椭圆上.故32=M x .所以()332,M .说明:本题关键在于未知式MF AM 2+中的“2”的处理.事实上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九 例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十 例10设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫ ⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫⎝⎛230,P 的距离是7.解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫⎝⎛-=-==a b a b a a c e 可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49sin 3sin 34222+--=θθb b b 3421sin 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值.由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,.典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点.设m x y x =++222,则 ()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化,120≠∠APB .(2)如果椭圆上存在一个点Q ,使 120=∠AQB ,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+a y x ay ,将22222y ba a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2.∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠ ∵22c a > ∴2tan -<∠APB故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x ya x y AQB -+=-++--=∠∵ 120=∠AQB , ∴32222-=-+ay x ay整理得()023222=+-+ay a y x∵22222y ba a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a∵0≠y , ∴2232c ab y = ∵b y ≤, ∴b c ab ≤2232 232c ab ≤,()222234c c a a ≤-∴04444224≥-+a c a c ,044324≥-+e e ∴232≥e 或22-≤e (舍),∴136<≤e .典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k .当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=. 由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅. ∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解.解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α, ∴P 点坐标为)5154,554(.典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=. 分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,ca x PQ 20+=,由椭圆第二定义,e PQPF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA +的最大值、最小值及对应的点P 坐标;(2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQ PF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(. 说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1) ⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九 例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F .(1)求椭圆离心率的取值范围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+b y a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值范围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF ∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+by a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取范围是)1,21[∈e .(2)将2222134ea c x -=代入12222=+b y a x 得 24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆. 即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12FPF ,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα,∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值范围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+=∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=. ∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+by a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos b a b -=θ,∵1cos 1<<-θ ∴1cos =θ(舍去),11222<-<-ba b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。

椭圆的经典例题1.已知点A(2,5)、B(3,一1),则线段AB 的方程是( ).(A)6x+y-17=0(B)6x+y-17=0(x ≥3)(C)6x+y-17=0(x ≤3)(D)6x+y-17=0(2≤x ≤3)2.(直接法)已知一条直线l 和它上方的一个点F ,点F 到l 的距离是2,一条曲线也在直线l 的上方,它上面的每一个点到F 的距离减去到l 的距离的差都是2,建立适当的坐标系,求曲线的方程.3.(相关点法) 动点M 在曲线x 2+y 2=1上移动,M 和定点B(3,O)连线的中点为P ,求P 点的轨迹方程,并指出点P 的轨迹.4.已知方程13522-=-+-ky k x 表示椭圆,求k 的取值范围.5. 已知椭圆06322=-+m y mx 的一个焦点为(0,2)求m 的值.6.已知椭圆的中心在原点,且经过点()03,P ,b a 3=,求椭圆的标准方程.7.已知M 是椭圆14922=+y x 上的一点,21,F F 是椭圆的焦点,则||||21MF MF ⋅的最大值是( ) A 、4 B 、6 C 、9 D 、128.点P 为椭圆22154x y +=上一点,以点P 以及焦点F 1, F 2为顶点的三角形的面积为1,则点P 的坐标是(A )(±2, 1) (B )(2, ±1) (C )(2, 1) (D )(±2, ±1) 9.已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为354和352,过P 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.10.求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.11.已知椭圆方程()012222>>=+b a by a x ,长轴端点为1A ,2A ,焦点为1F ,2F ,P 是椭圆上一点, α=∠21PF F .求:21PF F ∆的面积(用a 、b 、α表示).12.已知动圆P 过定点()03,-A ,且在定圆()64322=+-y x B :的内部与其相内切,求动圆圆心P 的轨迹方程.13.已知椭圆1422=+y x 及直线m x y +=.(1)当m 为何值时,直线与椭圆有公共点?(2)若直线被椭圆截得的弦长为5102,求直线的方程.14.如果椭圆221369x y +=弦被点A (4,2)平分,那么这条弦所在的直线方程是。

椭圆高中练习题及讲解椭圆是圆锥曲线的一种,其定义为平面上所有到两个固定点(焦点)距离之和为常数的点的集合。
这个常数称为椭圆的长轴长度,而长轴长度的一半称为椭圆的长半轴。
椭圆的另一个重要参数是短半轴,它的长度是长半轴的一半乘以椭圆的离心率的倒数。
### 练习题1. 椭圆的基本性质给定一个椭圆,其长半轴为6,短半轴为4,求椭圆的离心率。
2. 椭圆的方程已知椭圆的中心在原点,焦点在x轴上,求椭圆的方程,其中长半轴a=5,短半轴b=3。
3. 椭圆的切线若点P(2,3)在椭圆x²/16 + y²/9 = 1上,求过点P的椭圆切线的方程。
4. 椭圆与直线的位置关系直线y=2x+4与椭圆x²/25 + y²/16 = 1相交于两点,求这两点的坐标。
5. 椭圆的面积求椭圆x²/100 + y²/64 = 1的面积。
### 讲解1. 椭圆的基本性质离心率e定义为焦点到椭圆上任意一点的距离与长半轴的比值。
由于椭圆上任意一点到两个焦点的距离之和等于长轴长度,设长轴长度为2a,那么离心率e = √(1 - (b²/a²))。
对于本题,a=6,b=4,所以e = √(1 - (4²/6²)) = √(1 - 4/9) = √(5/9)。
2. 椭圆的方程当椭圆的中心在原点,焦点在x轴上时,椭圆的方程为x²/a² + y²/b² = 1。
代入a=5,b=3,得到椭圆的方程为x²/25 + y²/9 = 1。
3. 椭圆的切线对于椭圆上的点P(2,3),切线斜率可以通过椭圆的梯度求得。
首先求椭圆在点P处的梯度,然后切线的斜率是梯度的负倒数。
具体计算过程涉及到求导和使用点斜式方程。
4. 椭圆与直线的位置关系将直线方程代入椭圆方程,得到一个关于x的二次方程,解此方程可得x的值,再代回直线方程求得y的值,从而得到交点的坐标。

《椭圆》方程典型例题20例典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程.分析:题目没有指出焦点的位置,要考虑两种位置.解:(1)当()02,A 为长轴端点时,2=a ,1=b , 椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a , 椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三 例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112a a x x x M +=+=,2111a x y M M +=-=,4112===ax y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k . 证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:ac x ca AF =-12, ∴ 11545x ex a AF -=-=.同理 2545x CF -=.∵ BF CF AF 2=+,且59=BF , ∴ 51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即 821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得 ()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上,∴ ()212125259x y -=()222225259x y -= ∴ ()()21212221259x x x x y y -+-=-.将此式代入①,并利用821=+x x 的结论得 253640-=-x ∴ 4540590=--=x k BT.典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M 到左准线l 的距离MN 是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=. 又由焦半径公式知:111212x ex a MF -=-=, 112212x ex a MF +=+=.∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x .整理得048325121=++x x .解之得41-=x 或5121-=x . ① 另一方面221≤≤-x . ②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122k kk x x +-=+.∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --. 解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x . ⑤ 将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-. 所求直线方程为0342=-+y x .说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,; (2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y .解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=. ①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba . ② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y .(2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x . 说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 解:由已知:4=a ,2=c .所以21=e ,右准线8=x l :.过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然MF AM 2+的最小值为AQ ,即M 为所求点,因此3=M y ,且M 在椭圆上.故32=M x .所以()332,M .说明:本题关键在于未知式MF AM 2+中的“2”的处理.事实上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九 例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十 例10设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫ ⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫⎝⎛230,P 的距离是7.解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫⎝⎛-=-==a b a b a a c e 可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49sin 3sin 34222+--=θθb b b 3421sin 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值.由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,.典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点.设m x y x =++222,则 ()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化,120≠∠APB .(2)如果椭圆上存在一个点Q ,使 120=∠A Q B ,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+a y x ay ,将22222y ba a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2.∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠ ∵22c a > ∴2tan -<∠APB故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x ya x y AQB -+=-++--=∠∵ 120=∠AQB , ∴32222-=-+ay x ay整理得()023222=+-+ay a y x∵22222y ba a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a∵0≠y , ∴2232c ab y = ∵b y ≤, ∴b c ab ≤2232 232c ab ≤,()222234c c a a ≤-∴04444224≥-+a c a c ,044324≥-+e e ∴232≥e 或22-≤e (舍),∴136<≤e .典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k .当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=. 由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅. ∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解.解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α, ∴P 点坐标为)5154,554(.典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=. 分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,ca x PQ 20+=,由椭圆第二定义,e PQPF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA +的最大值、最小值及对应的点P 坐标;(2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQ PF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(. 说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1) ⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九 例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F .(1)求椭圆离心率的取值范围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+b y a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值范围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF ∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+by a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取范围是)1,21[∈e .(2)将2222134ea c x -=代入12222=+b y a x 得 24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆. 即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12FPF ,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα,∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值范围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+=∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=.∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+by a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos b a b -=θ,∵1cos 1<<-θ ∴1cos =θ(舍去),11222<-<-b a b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。

椭圆标准方程典型例题(参考答案)例1 已知椭圆06322=-+m y mx 的一个焦点为(0,2)求m 的值.解:方程变形为12622=+my x .因为焦点在y 轴上,所以62>m ,解得3>m . 又2=c ,所以2262=-m ,5=m 适合.故5=m .例2 已知椭圆的中心在原点,且经过点()03,P ,b a 3=,求椭圆的标准方程. 解:当焦点在x 轴上时,设其方程为()012222>>=+b a by a x .由椭圆过点()03,P ,知10922=+b a .又b a 3=,代入得12=b ,92=a ,故椭圆的方程为1922=+y x . 当焦点在y 轴上时,设其方程为()012222>>=+b a bx a y .由椭圆过点()03,P ,知10922=+ba .又b a 3=,联立解得812=a ,92=b ,故椭圆的方程为198122=+x y . 例3 ABC ∆的底边16=BC ,AC 和AB 两边上中线长之和为30,求此三角形重心G 的轨迹和顶点A 的轨迹.解: (1)以BC 所在的直线为x 轴,BC 中点为原点建立直角坐标系.设G 点坐标为()y x ,,由20=+GB GC ,知G 点的轨迹是以B 、C 为焦点的椭圆,且除去轴上两点.因10=a ,8=c ,有6=b ,故其方程为()013610022≠=+y y x . (2)设()y x A ,,()y x G '',,则()013610022≠'='+'y y x . ① 由题意有⎪⎪⎩⎪⎪⎨⎧='='33y y x x ,代入①,得A 的轨迹方程为()0132490022≠=+y y x ,其轨迹是椭圆(除去x 轴上两点).例4 已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为354和352,过P 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程. 解:设两焦点为1F 、2F ,且3541=PF ,3522=PF .从椭圆定义知52221=+=PF PF a .即5=a . 从21PF PF >知2PF 垂直焦点所在的对称轴,所以在12FPF Rt ∆中,21sin 1221==∠PF PF F PF ,可求出621π=∠F PF ,3526cos21=⋅=πPF c ,从而310222=-=c a b .∴所求椭圆方程为1103522=+y x 或1510322=+y x . 例5 已知椭圆方程()012222>>=+b a by a x ,长轴端点为1A ,2A ,焦点为1F ,2F ,P 是椭圆上一点,θ=∠21PA A ,α=∠21PF F .求:21PF F ∆的面积(用a 、b 、α表示).解:如图,设()y x P ,,由椭圆的对称性,不妨设()y x P ,,由椭圆的对称性,不妨设P 在第一象限.由余弦定理知: 221F F 2221PF PF +=12PF -·224cos c PF =α.①由椭圆定义知: a PF PF 221=+ ②,则-①②2得 αcos 12221+=⋅b PF PF . 故αsin 212121PF PF S PF F ⋅=∆ ααsin cos 12212+=b 2tan 2αb =. 例6 已知动圆P 过定点()03,-A ,且在定圆()64322=+-y x B :的内部与其相内切,求动圆圆心P 的轨迹方程. 解:如图所示,设动圆P 和定圆B 内切于点M .动点P 到两定点,即定点()03,-A 和定圆圆心()03,B 距离之和恰好等于定圆半径, 即8==+=+BM PB PM PB PA .∴点P 的轨迹是以A ,B 为两焦点,半长轴为4,半短轴长为73422=-=b 的椭圆的方程:171622=+y x . 例7 已知椭圆1222=+y x ,(1)求过点⎪⎭⎫ ⎝⎛2121,P 且被P 平分的弦所在直线的方程; (2)求斜率为2的平行弦的中点轨迹方程; (3)过()12,A 引椭圆的割线,求截得的弦的中点的轨迹方程; (4)椭圆上有两点P 、Q ,O 为原点,且有直线OP 、OQ 斜率满足21-=⋅OQ OP k k , 求线段PQ 中点M 的轨迹方程.解:设弦两端点分别为()11y x M ,,()22y x N ,,线段MN 的中点()y x R ,,则⎪⎪⎩⎪⎪⎨⎧=+=+=+=+④,③,②,①,y y y x x x y x y x 222222212122222121①-②得()()()()022*******=-++-+y y y y x x x x . 由题意知21x x ≠,则上式两端同除以21x x -,有()()0221212121=-+++x x y y y y x x ,将③④代入得022121=--+x x y y yx .⑤(1)将21=x ,21=y 代入⑤,得212121-=--x x y y ,故所求直线方程为: 0342=-+y x . ⑥ 将⑥代入椭圆方程2222=+y x 得041662=--y y ,0416436>⨯⨯-=∆符合题意,0342=-+y x 为所求. (2)将22121=--x x y y 代入⑤得所求轨迹方程为: 04=+y x .(椭圆内部分)(3)将212121--=--x y x x y y 代入⑤得所求轨迹方程为: 022222=--+y x y x .(椭圆内部分)(4)由①+②得 :()2222212221=+++y y x x , ⑦, 将③④平方并整理得 212222124x x x x x -=+, ⑧, 212222124y y y y y -=+, ⑨将⑧⑨代入⑦得:()224424212212=-+-y y y x x x , ⑩ 再将212121x x y y -=代入⑩式得: 221242212212=⎪⎭⎫ ⎝⎛--+-x x y x x x , 即 12122=+y x . 例8 已知椭圆1422=+y x 及直线m x y +=.(1)当m 为何值时,直线与椭圆有公共点?(2)若直线被椭圆截得的弦长为5102,求直线的方程. 解:(1)把直线方程m x y +=代入椭圆方程1422=+y x 得 ()1422=++m x x , 即012522=-++m mx x .()()020*********≥+-=-⨯⨯-=∆m m m ,解得2525≤≤-m . (2)设直线与椭圆的两个交点的横坐标为1x ,2x ,由(1)得5221m x x -=+,51221-=m x x .根据弦长公式得 :51025145211222=-⨯-⎪⎭⎫⎝⎛-⋅+m m .解得0=m .方程为x y =. 例9 以椭圆131222=+y x 的焦点为焦点,过直线09=+-y x l :上一点M 作椭圆,要使所作椭圆的长轴最短,点M 应在何处?并求出此时的椭圆方程.解:如图所示,椭圆131222=+y x 的焦点为()031,-F ,()032,F . 点1F 关于直线09=+-y x l :的对称点F 的坐标为(-9,6),直线2FF 的方程为032=-+y x . 解方程组⎩⎨⎧=+-=-+09032y x y x 得交点M 的坐标为(-5,4).此时21MF MF +最小.所求椭圆的长轴:562221==+=FF MF MF a ,∴53=a ,又3=c ,∴()3635322222=-=-=c a b .因此,所求椭圆的方程为1364522=+y x . 例10 已知方程13522-=-+-ky k x 表示椭圆,求k 的取值范围. 解:由⎪⎩⎪⎨⎧-≠-<-<-,35,03,05k k k k 得53<<k ,且4≠k .∴满足条件的k 的取值范围是53<<k ,且4≠k .例11 已知1cos sin 22=-ααy x )0(πα≤≤表示焦点在y 轴上的椭圆,求α的取值范围.解:方程可化为1cos 1sin 122=+ααy x .因为焦点在y 轴上,所以0sin 1cos 1>>-αα. 因此0sin >α且1tan -<α从而)43,2(ππα∈. 例12 求中心在原点,对称轴为坐标轴,且经过)2,3(-A 和)1,32(-B 两点的椭圆方程.解:设所求椭圆方程为122=+ny mx (0>m ,0>n ).由)2,3(-A 和)1,32(-B 两点在椭圆上可得⎪⎩⎪⎨⎧=⋅+-⋅=-⋅+⋅,11)32(,1)2()3(2222n m n m 即⎩⎨⎧=+=+,112,143n m n m 所以151=m ,51=n .故所求的椭圆方程为151522=+y x . 例13 知圆122=+y x ,从这个圆上任意一点P 向y 轴作垂线段,求线段中点M 的轨迹. 解:设点M 的坐标为),(y x ,点P 的坐标为),(00y x ,则2x x =,0y y =. 因为),(00y x P 在圆122=+y x 上,所以12020=+y x .将x x 20=,y y =0代入方程12020=+y x 得1422=+y x .所以点M 的轨迹是一个椭圆1422=+y x . 例14 已知长轴为12,短轴长为6,焦点在x 轴上的椭圆,过它对的左焦点1F 作倾斜解为3π的直线交椭圆于A ,B 两点,求弦AB 的长.解:(法1)利用直线与椭圆相交的弦长公式求解.2121x x k AB -+=]4))[(1(212212x x x x k -++=.因为6=a ,3=b ,所以33=c .因为焦点在x 轴上,所以椭圆方程为193622=+y x ,左焦点)0,33(-F ,从而直线方程为93+=x y . 由直线方程与椭圆方程联立得:0836372132=⨯++x x .设1x ,2x 为方程两根,所以1337221-=+x x ,1383621⨯=x x ,3=k , 从而1348]4))[(1(1212212212=-++=-+=x x x x k x x k AB . (法2)利用椭圆的定义及余弦定理求解.由题意可知椭圆方程为193622=+y x ,设m AF =1,n BF =1,则m AF -=122,n BF -=122. 在21F AF ∆中,3cos22112212122πF F AF F F AF AF -+=,即21362336)12(22⋅⋅⋅-⋅+=-m m m ; 所以346-=m .同理在21F BF ∆中,用余弦定理得346+=n ,所以1348=+=n m AB .(法3)利用焦半径求解.先根据直线与椭圆联立的方程0836372132=⨯++x x 求出方程的两根1x ,2x ,它们分别是A ,B 的横坐标. 再根据焦半径11ex a AF +=,21ex a BF +=,从而求出11BF AF AB +=.例15 椭圆192522=+y x 上的点M 到焦点1F 的距离为2,N 为1MF 的中点,则ON (O 为坐标原点)的值为A .4 B .2 C .8 D .23解:如图所示,设椭圆的另一个焦点为2F ,由椭圆第一定义得10221==+a MF MF ,所以82101012=-=-=MF MF ,又因为ON 为21F MF ∆的中位线,所以4212==MF ON ,故答案为A . 例16 在面积为1的PMN ∆中,21tan =M ,2tan -=N ,建立适当的坐标系,求出以M 、N 为焦点且过P 点的椭圆方程.解:以MN 的中点为原点,MN 所在直线为x 轴建立直角坐标系,设),(y x P .则⎪⎪⎪⎩⎪⎪⎪⎨⎧==+-=-.1,21,2cy c x yc x y∴⎪⎪⎩⎪⎪⎨⎧===233435c c y cx 且即)32,325(P ∴⎪⎪⎩⎪⎪⎨⎧=-=+,43,134********b a b a 得⎪⎩⎪⎨⎧==.3,41522b a∴所求椭圆方程为1315422=+y x例17 已知)2,4(P 是直线l 被椭圆193622=+y x 所截得的线段的中点,求直线l 的方程. 解:方法一:设所求直线方程为)4(2-=-x k y .代入椭圆方程,整理得036)24(4)24(8)14(222=--+--+k x k k x k ①设直线与椭圆的交点为),(11y x A ,),(22y x B ,则1x 、2x 是①的两根,∴14)24(8221+-=+k k k x x∵)2,4(P 为AB 中点,∴14)24(424221+-=+=k k k x x ,21-=k .∴所求直线方程为082=-+y x . 方法二:设直线与椭圆交点),(11y x A ,),(22y x B .∵)2,4(P 为AB 中点,∴821=+x x ,421=+y y . 又∵A ,B 在椭圆上,∴3642121=+y x ,3642222=+y x 两式相减得0)(4)(22212221=-+-y y x x , 即0))((4))((21212121=-++-+y y y y x x x x .∴21)(4)(21212121-=++-=--y y x x x x y y .∴直线方程为082=-+y x .方法三:设所求直线与椭圆的一个交点为),(y x A ,另一个交点)4,8(y x B --.∵A 、B 在椭圆上,∴36422=+y x ①。
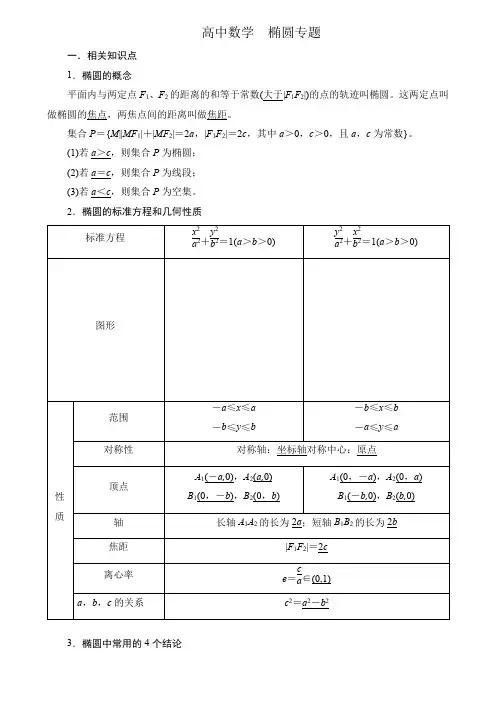
高中数学椭圆专题一.相关知识点1.椭圆的概念平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆。
这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
集合P={M||MF1|+|MF2|=2a,|F1F2|=2c,其中a>0,c>0,且a,c为常数}。
(1)若a>c,则集合P为椭圆;(2)若a=c,则集合P为线段;(3)若a<c,则集合P为空集。
2.椭圆的标准方程和几何性质3.椭圆中常用的4个结论(1)设椭圆x2a2+y2b2=1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最小值b,这时P在短轴端点处;当x=±a时,|OP|有最大值a,这时P在长轴端点处。
(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a是斜边长,a2=b2+c2。
(3)已知过焦点F1的弦AB,则△ABF2的周长为4a。
(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c。
一、细品教材1.(选修1-1P34例1改编)若F1(3,0),F2(-3,0),点P到F1,F2距离之和为10,则P点的轨迹方程是()A.x225+y216=1 B.x2100+y29=1 C.y225+x216=1 D.x225+y216=1或y225+x216=12.(选修1-1P42A组T6改编)设椭圆的两个焦点分别为F1,F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是()A.22 B.2-12C.2- 2 D.2-1走进教材答案1.A; 2.D 二、双基查验1.设P是椭圆x24+y29=1上的点,若F1,F2是椭圆的两个焦点,则|PF1|+|PF2|等于()A.4B.8 C.6 D.182.方程x25-m+y2m+3=1表示椭圆,则m的范围是()A.(-3,5) B.(-5,3) C.(-3,1)∪(1,5) D.(-5,1)∪(1,3)3.椭圆x 29+y 24+k =1的离心率为45,则k 的值为( )A .-21B .21C .-1925或21 D.1925或214.已知椭圆的一个焦点为F (1,0),离心率为12,则椭圆的标准方程为________。

例1 已知椭圆06322=-+m y mx 的一个焦点为(0,2)求m 的值.分析:把椭圆的方程化为标准方程,由2=c ,根据关系222c b a +=可求出m 的值. 解:方程变形为12622=+my x .因为焦点在y 轴上,所以62>m ,解得3>m . 又2=c ,所以2262=-m ,5=m 适合.故5=m .例2 已知椭圆的中心在原点,且经过点()03,P ,b a 3=,求椭圆的标准方程. 分析:因椭圆的中心在原点,故其标准方程有两种情况.根据题设条件,运用待定系数法,求出参数a 和b (或2a 和2b )的值,即可求得椭圆的标准方程. 解:当焦点在x 轴上时,设其方程为()012222>>=+b a by a x . 由椭圆过点()03,P ,知10922=+ba .又b a 3=,代入得12=b ,92=a ,故椭圆的方程为1922=+y x . 当焦点在y 轴上时,设其方程为()012222>>=+b a bx a y . 由椭圆过点()03,P ,知10922=+ba .又b a 3=,联立解得812=a ,92=b ,故椭圆的方程为198122=+x y . 例3 已知方程13522-=-+-ky k x 表示椭圆,求k 的取值范围. 解:由⎪⎩⎪⎨⎧-≠-<-<-,35,03,05k k k k 得53<<k ,且4≠k .∴满足条件的k 的取值范围是53<<k ,且4≠k .例4 已知1cos sin 22=-ααy x )0(πα≤≤表示焦点在y 轴上的椭圆,求α的取值范围.分析:依据已知条件确定α的三角函数的大小关系.再根据三角函数的单调性,求出α的取值范围. 解:方程可化为1cos 1sin 122=+ααy x .因为焦点在y 轴上,所以0sin 1cos 1>>-αα. 因此0sin >α且1tan -<α从而)43,2(ππα∈.例5 已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为354和352,过P 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.解:设两焦点为1F 、2F ,且3541=PF ,3522=PF .从椭圆定义知52221=+=PF PF a .即5=a . 从21PF PF >知2PF 垂直焦点所在的对称轴,所以在12F PF Rt ∆中,21sin 1221==∠PF PF F PF , 可求出621π=∠F PF ,3526cos 21=⋅=πPF c ,从而310222=-=c a b . ∴所求椭圆方程为1103522=+y x 或1510322=+y x . 例6 求中心在原点,对称轴为坐标轴,且经过)2,3(-A 和)1,32(-B 两点的椭圆方程.分析:由题设条件焦点在哪个轴上不明确,椭圆标准方程有两种情形,为了计算简便起见,可设其方程为122=+ny mx (0>m ,0>n ),且不必去考虑焦点在哪个坐标轴上,直接可求出方程.解:设所求椭圆方程为122=+ny mx (0>m ,0>n ).由)2,3(-A 和)1,32(-B 两点在椭圆上可得 ⎪⎩⎪⎨⎧=⋅+-⋅=-⋅+⋅,11)32(,1)2()3(2222n m n m 即⎩⎨⎧=+=+,112,143n m n m 所以151=m ,51=n .故所求的椭圆方程为151522=+y x .例7 椭圆192522=+y x 上的点M 到焦点1F 的距离为2,N 为1MF 的中点,则ON (O 为坐标原点)的值为A .4 B .2 C .8 D .23例8 已知)2,4(P 是直线l 被椭圆193622=+y x 所截得的线段的中点,求直线l 的方程. 分析:本题考查直线与椭圆的位置关系问题.通常将直线方程与椭圆方程联立消去y (或x ),得到关于x (或y )的一元二次方程,再由根与系数的关系,直接求出21x x +,21x x (或21y y +,21y y )的值代入计算即得. 并不需要求出直线与椭圆的交点坐标,这种“设而不求”的方法,在解析几何中是经常采用的.解:方法一:设所求直线方程为)4(2-=-x k y .代入椭圆方程,整理得036)24(4)24(8)14(222=--+--+k x k k x k ①设直线与椭圆的交点为),(11y x A ,),(22y x B ,则1x 、2x 是①的两根,∴14)24(8221+-=+k k k x x ∵)2,4(P 为AB 中点,∴14)24(424221+-=+=k k k x x ,21-=k .∴所求直线方程为082=-+y x . 方法二:设直线与椭圆交点),(11y x A ,),(22y x B .∵)2,4(P 为AB 中点,∴821=+x x ,421=+y y . 又∵A ,B 在椭圆上,∴3642121=+y x ,3642222=+y x 两式相减得0)(4)(22212221=-+-y y x x , 即0))((4))((21212121=-++-+y y y y x x x x .∴21)(4)(21212121-=++-=--y y x x x x y y .∴直线方程为082=-+y x . 方法三:设所求直线与椭圆的一个交点为),(y x A ,另一个交点)4,8(y x B --.∵A 、B 在椭圆上,∴36422=+y x ①。
《椭圆》方程典型例题20例典型例题一例1椭圆的一个顶点为02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程.分析:题目没有指出焦点的位置,要考虑两种位置.解:(1)当02,A 为长轴端点时,2a ,1b ,椭圆的标准方程为:11422yx;(2)当02,A 为短轴端点时,2b ,4a,椭圆的标准方程为:116422yx;说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222cac∴223a c,∴3331e.说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三例3 已知中心在原点,焦点在x 轴上的椭圆与直线01y x交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222yax ,由101222yaxy x ,得021222xa x a ,∴222112a a x x x M,2111ax y MM ,4112ax y k MM OM,∴42a,∴1422yx为所求.说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522y x上不同三点11y x A ,,594,B ,22y x C ,与焦点04,F 的距离成等差数列.(1)求证821x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k .证明:(1)由椭圆方程知5a ,3b ,4c .由圆锥曲线的统一定义知:ac x caAF 12,∴ 11545x ex a AF .同理2545x CF .∵ BF CFAF2,且59BF,∴ 51854554521x x ,即821x x .(2)因为线段AC 的中点为2421y y ,,所以它的垂直平分线方程为42212121xy y x x y y y.又∵点T 在x 轴上,设其坐标为00,x ,代入上式,得21222124x x y y x 又∵点11y x A ,,22y x B ,都在椭圆上,∴ 212125259x y 222225259x y ∴ 21212221259x x x x y y.将此式代入①,并利用821x x 的结论得25364x ∴ 454059x k BT.典型例题五例5已知椭圆13422y x,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M 到左准线l 的距离MN 是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设11y x M ,,由已知条件得2a,3b,∴1c,21e .∵左准线l 的方程是4x,∴14x MN.又由焦半径公式知:111212x ex a MF ,112212x ex a MF .∵212MF MF MN ,∴11212122124x x x .整理得048325121x x .解之得41x 或5121x .①另一方面221x .②则①与②矛盾,所以满足条件的点M 不存在.说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设sin3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222yx,求过点2121,P且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k .解法一:设所求直线的斜率为k ,则直线方程为2121xk y .代入椭圆方程,并整理得0232122212222kkxk kxk .由韦达定理得22212122kkkx x .∵P 是弦中点,∴121x x .故得21k .所以所求直线方程为0342y x .分析二:设弦两端坐标为11y x ,、22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y .解法二:设过2121,P 的直线与椭圆交于11y x A ,、22y x B ,,则由题意得④1.③1②12①12212122222121y y x x y x yx ,,,①-②得0222212221yyxx.⑤将③、④代入⑤得212121x x y y ,即直线的斜率为21.所求直线方程为0342y x .说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点62,;(2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222by ax 求出1482a ,372b ,在得方程13714822yx 后,不能依此写出另一方程13714822xy .解:(1)设椭圆的标准方程为12222by ax 或12222bx ay .由已知b a2.①又过点62,,因此有1622222ba或1262222ba.②由①、②,得1482a,372b或522a,132b.故所求的方程为13714822yx或1135222xy .(2)设方程为12222by ax .由已知,3c ,3c b ,所以182a.故所求方程为191822yx .说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222by ax 或12222bx ay .典型例题八例8椭圆1121622yx的右焦点为F ,过点31,A ,点M 在椭圆上,当MF AM 2为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM1均可用此法.解:由已知:4a,2c.所以21e,右准线8xl :.过A 作l AQ ,垂足为Q ,交椭圆于M ,故MF MQ 2.显然MF AM 2的最小值为AQ ,即M 为所求点,因此3My ,且M 在椭圆上.故32M x .所以332,M .说明:本题关键在于未知式MF AM 2中的“2”的处理.事实上,如图,21e,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九例9 求椭圆1322yx上的点到直线06yx的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为.sin cos 3yx ,设椭圆上的点的坐标为sincos 3,,则点到直线的距离为263sin226sin cos3d.当13sin时,22最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十例10设椭圆的中心是坐标原点,长轴在x 轴上,离心率23e,已知点230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值范围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222by ax ,其中0b a 待定.由222222221ab ab a ac e 可得2143112eab ,即b a 2.设椭圆上的点y x ,到点P 的距离是d ,则4931232222222yyby a yxd34213493342222byyyb其中b yb.如果21b,则当b y 时,2d (从而d )有最大值.由题设得22237b,由此得21237b,与21b矛盾.因此必有21b 成立,于是当21y 时,2d (从而d )有最大值.由题设得34722b ,可得1b ,2a.∴所求椭圆方程是11422yx.由21y及求得的椭圆方程可得,椭圆上的点213,,点213,到点230,P 的距离是7.解法二:根据题设条件,可取椭圆的参数方程是sincos b ya x ,其中0b a ,待定,20,为参数.由22222221ab ab aac e可得2143112eab ,即b a 2.设椭圆上的点y x ,到点230,P 的距离为d ,则22222223sin cos23b a yxd49sin3sin34222b b b 3421sin3222bbb 如果121b ,即21b,则当1sin 时,2d (从而d )有最大值.由题设得22237b,由此得21237b ,与21b矛盾,因此必有121b成立.于是当b 21sin 时2d (从而d )有最大值.由题设知34722b,∴1b ,2a.∴所求椭圆的参数方程是sincos 2yx .由21sin,23cos ,可得椭圆上的是213,,213,.典型例题十一例11设x ,R y,x y x 63222,求x yx 222的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222与椭圆方程的结构一致.设m xyx222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222,得123492322y x可见它表示一个椭圆,其中心在023,点,焦点在x 轴上,且过(0,0)点和(3,0)点.设m x y x 222,则1122m yx 它表示一个圆,其圆心为(-1,0)半径为11mm .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11m ,此时0m ;当圆过(3,0)点时,半径最大,即41m ,∴15m .∴x yx222的最小值为0,最大值为15.典型例题十二例12已知椭圆012222baby axC :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ,求证:不论a 、b 如何变化,120APB .(2)如果椭圆上存在一个点Q ,使120AQB,求C 的离心率e 的取值范围.分析:本题从已知条件出发,两问都应从APB 和AQB 的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x,b y,根据120AQB得到32222ayxay ,将22222y ba ax代入,消去x ,用a 、b 、c 表示y ,以便利用b y列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设0,c F ,0,a A ,0,a B .abc P b a ya xb cx 2222222,于是a c a bk AP 2,aca b k BP2.∵APB 是AP 到BP 的角.∴2222242221tan ca ac a ba c ab ac a bAPB∵22ca∴2tan APB 故3tanAPB∴120APB .(2)设y x Q ,,则ax y k QA ,ax y k QB.由于对称性,不妨设0y,于是AQB 是QA 到QB 的角.∴22222221tan ayxay ax y a x yax yAQB∵120AQB ,∴32222ayxay 整理得023222ay ayx∵22222yba ax∴0213222ay yba ∵0y ,∴2232caby∵b y ,∴bcab 2232232c ab,222234cca a ∴04444224a c a c,044324e e ∴232e或22e (舍),∴136e .典型例题十三例13已知椭圆19822y kx 的离心率21e,求k 的值.分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82ka,92b ,得12k c.由21e,得4k .当椭圆的焦点在y 轴上时,92a ,82kb ,得k c12.由21e,得4191k,即45k .∴满足条件的4k 或45k .说明:本题易出现漏解.排除错误的办法是:因为8k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222by bx上一点P 到右焦点2F 的距离为b )1(b,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222by bx,得b a 2,b c 3,23e.由椭圆定义,b a PF PF 4221,得b b b PF bPF 34421.由椭圆第二定义,e d PF 11,1d 为P 到左准线的距离,∴b ePF d 3211,即P 到左准线的距离为b 32.解法二:∵e d PF 22,2d 为P 到右准线的距离,23ac e,∴b ePF d 33222.又椭圆两准线的距离为b c a 33822.∴P 到左准线的距离为b bb32332338.说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆.sin 32,cos 4yx (为参数)上一点P 与x 轴正向所成角3POx,求P 点坐标.分析:利用参数与POx 之间的关系求解.解:设)sin 32,cos 4(P ,由P 与x 轴正向所成角为3,∴cos4sin 323tan,即2tan .而0sin ,0cos,由此得到55cos,552sin ,∴P 点坐标为)5154,554(.典型例题十六例16设),(00y x P 是离心率为e 的椭圆12222by a x )0(ba 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex ar ,02ex ar .分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线caxl 2:的距离,cax PQ 2,由椭圆第二定义,e PQPF 1,∴01ex a PQe r ,由椭圆第一定义,0122ex ar ar .说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17已知椭圆15922yx内有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点.(1) 求1PF PA 的最大值、最小值及对应的点P 坐标;(2)求223PF PA的最小值及对应的点P 的坐标.分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62a ,)0,2(2F ,22AF ,设P 是椭圆上任一点,由6221aPF PF ,22AF PF PA ,∴26222211AF aAF PF PF PF PA,等号仅当22AF PF PA时成立,此时P 、A 、2F 共线.由22AF PF PA ,∴26222211AF aAF PF PF PF PA,等号仅当22AF PF PA时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02y x,解方程组4595,0222yxy x 得两交点)2141575,2141579(1P 、)2141575,2141579(2P .综上所述,P 点与1P 重合时,1PF PA取最小值26,P 点与2P 重合时,2PF PA取最大值26.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3a,2c ,∴32e.由椭圆第二定义知322ePQPF ,∴223PF PQ,∴PQ PAPF PA223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29x.∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(.说明:求21PF ePA的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18(1)写出椭圆14922yx的参数方程;(2)求椭圆内接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1)sin2cos 3y x )(R .(2)设椭圆内接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y 轴,设)sin 2,cos 3(为矩形在第一象限的顶点,)2(,则122sin 12sin 2cos 34S 故椭圆内接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九例19已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且6021PF F .(1)求椭圆离心率的取值范围;(2)求证21F PF 的面积与椭圆短轴长有关.分析:不失一般性,可以设椭圆方程为12222by ax (0ba ),),(11y x P (01y ).思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212PFPF PFPFK K K K ,设),(11y x P ,)0,(1c F ,)0,(2c F ,化简可得03233212121ccy y x .又1221221by ax ,两方程联立消去21x 得0323412212bcy b y c ,由],0(1b y ,可以确定离心率的取值范围;解出1y 可以求出21F PF 的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF ,12ex a PF ,在21F PF 中运用余弦定理,求1x ,再利用],[1a a x ,可以确定离心率e 的取值范围,将1x 代入椭圆方程中求1y ,便可求出21F PF 的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221求解.解:(法1)设椭圆方程为12222by ax (0ba),),(11y x P ,)0,(1c F ,)0,(2c F ,0c,则11ex a PF ,12ex a PF .在21F PF 中,由余弦定理得))((24)()(2160cos 1122121ex a ex a cex a ex a ,解得2222134eacx.(1)∵],0(221a x ,∴2222340a eac ,即0422ac.∴21a c e.故椭圆离心率的取范围是)1,21[e .(2)将2222134eacx 代入12222by ax 得24213cby ,即cby 321.∴22213332212121b cbcy F F S FPF .即21F PF 的面积只与椭圆的短轴长有关.(法2)设m PF 1,n PF 2,12F PF ,21F PF ,则120.(1)在21F PF 中,由正弦定理得60sin 2sin sinc n m .∴60sin 2sinsinc n m ∵a n m 2,∴60sin 2sinsin2c a ,∴2cos2sin260sin sinsin 60sin a c e212cos 21.当且仅当时等号成立.故椭圆离心率的取值范围是)1,21[e .(2)在21F PF 中,由余弦定理得:60cos 2)2(222mn n m c mnnm22mnn m 3)(2∵a nm 2,∴mn a c 34422,即22234)(34b c a mn.∴23360sin 2121b mn SF PF .即21F PF 的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题中通过变形,使之出现21PF PF 的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20椭圆12222by ax )0(ba与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP(O 为坐标原点),求其离心率e 的取值范围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ,转化为P 点坐标的一个等量关系,再利用坐标的范围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是sincos b ya x )0(ba,则椭圆上的点)sin ,cos (b a P ,)0,(a A ,∵AP OP,∴1cossin cossin aa b a b ,即0coscos)(22222ba b a,解得1cos或222cosb ab ,∵1cos1∴1cos (舍去),11222bab,又222cab∴2022ca ,∴22e,又10e ,∴122e .说明:若已知椭圆离心率范围)1,22(,求证在椭圆上总存在点P 使AP OP.如何证明?。
椭圆标准方程典型例题及练习题椭圆标准方程典型例题4525例1已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为3和3,过P 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.解:设两焦点为F 1、F 2,且PF 1=452PF 2=1+PF 2=25.即a =5.3,3.从椭圆定义知2a =PF从PF 1>PF 2知PF 2垂直焦点所在的对称轴,所以在Rt ∆PF 2F 1中,sin ∠PF 1F 2=PF 2PF 1=12,可求出∠PF 1F 2=π6,2c =PF 1⋅cosπ6=2510b 2=a 2-c 2=,从而3.x 23y 23x 2y 2+=1+=1105∴所求椭圆方程为5或10.x 2y 2+2=1(a >b >0)2∠A 1PA 2=θ,F 2,P 是椭圆上一点,a b 例2 已知椭圆方程,长轴端点为A 1,A 2,焦点为F 1,∠F 1PF 2=α.求:∆F 1PF 2的面积(用a 、b 、α表示).S ∆=1ab sin C 2求面积.分析:求面积要结合余弦定理及定义求角α的两邻边,从而利用解:如图,设P (x ,y ),由椭圆的对称性,不妨设P (x ,y ),由椭圆的对称性,不妨设P 在第一象限.由余弦定理知:F 1F 2=PF 1+PF 2-2PF PF 2cos α=4c 21222.①2b 2PF 1⋅PF 2=2PF ②-①1+PF 2=2a 1+cos α.由椭圆定义知:②,则得S ∆F 1PF 21α12b 2=PF 1⋅PF 2sin α=sin α=b 2tan 22.21+cos α2故2()A -3,0()B :x -3+y =64的内部与其相内切,P 例3 已知动圆过定点,且在定圆求动圆圆心P 的轨迹方程.分析:关键是根据题意,列出点P 满足的关系式.解:如图所示,设动圆P 和定圆B 内切于点M .动点P 到两定点,0)和定圆圆心B (3,0)距离之和恰好等于定圆半径,即定点A (-3,即+=PM +=BM =8.∴点P 的轨迹是以A ,B 为两焦点,x 2y 2+=122半长轴为4,半短轴长为b =4-3=的椭圆的方程:167.说明:本题是先根据椭圆的定义,判定轨迹是椭圆,然后根据椭圆的标准方程,求轨迹的方程.这是求轨迹方程的一种重要思想方法.⎛11⎛x 22P ⎛+y =1例4 已知椭圆2,(1)求过点⎛22⎛且被P 平分的弦所在直线的方程;(2)求斜率为2的平行弦的中点轨迹方程;1)引椭圆的割线,求截得的弦的中点的轨迹方程;(3)过A (2,(4)椭圆上有两点P 、Q ,O 为原点,且有直线OP 、OQ 斜率满足求线段PQ 中点M 的轨迹方程.分析:此题中四问都跟弦中点有关,因此可考虑设弦端坐标的方法.解:设弦两端点分别为M (x 1,y 1),N (x 2,y 2),线段MN 的中点R (x ,y ),则k OP ⋅k OQ =-12,⎛x 12+2y 12=2,⎛22⎛x 2+2y 2=2,⎛⎛x 1+x 2=2x ,⎛y +y =2y ,⎛12①②③④①-②得(x 1+x 2)(x 1-x 2)+2(y 1+y 2)(y 1-y 2)=0.由题意知x 1≠x 2,则上式两端同除以x 1-x 2,有(x 1+x 2)2(y 1+y 2)y 1+y 2x 1-x 2=0,x +2y将③④代入得y 1-y 2=0x 1-x 2.⑤y 1-y 2111=-x =y =2,故所求直线方程为: 2x +4y -3=0.⑥ 2,2代入⑤,得x 1-x 2(1)将 22x +2y =2得将⑥代入椭圆方程6y 2-6y -11=0∆=36-4⨯6⨯>044,符合题意,2x +4y -3=0为所求.y 1-y 2=2x -x 2(2)将1代入⑤得所求轨迹方程为: x +4y =0.(椭圆内部分) y 1-y 2y -1=22x -x x -2x +2y -2x -2y =0.12(3)将代入⑤得所求轨迹方程为:(椭圆内部分) 2x 12+x 22+y 12+y 2=22(4)由①+②得:,⑦,()将③④平方并整理得2x 12+x 2=4x 2-2x 1x 2,⑧,2y 12+y 2=4y 2-2y 1y 2,⑨将⑧⑨代入⑦得:4x 2-2x 1x 2+4y 2-2y 1y 2=24,⑩()y 2x +=1⎛1⎛11222x -x 1x 2+4y -2 -x 1x 2⎛=2y 1y 2=-x 1x 2⎛2⎛22再将代入⑩式得:,即.2此即为所求轨迹方程.当然,此题除了设弦端坐标的方法,还可用其它方法解决.22例5 已知椭圆4x +y =1及直线y =x +m .(1)当m 为何值时,直线与椭圆有公共点?2(2)若直线被椭圆截得的弦长为5,求直线的方程.222y =x +m 4x +y =14x +(x +m )=1,解:(1)把直线方程代入椭圆方程得222即5x +2mx +m -1=0.∆=(2m )-4⨯5⨯m -1=-16m +20≥0,解得2(2)2-5≤m ≤22.2m m 2-1x 1+x 2=-x 1x 2=x x 55.(2)设直线与椭圆的两个交点的横坐标为1,2,由(1)得,m 2-12⎛2m ⎛2+1⋅ -=⎛-4⨯555.解得m =0.方程为y =x .⎛⎛根据弦长公式得:说明:处理有关直线与椭圆的位置关系问题及有关弦长问题,采用的方法与处理直线和圆的有所区别.这里解决直线与椭圆的交点问题,一般考虑判别式∆;解决弦长问题,一般应用弦长公式.用弦长公式,若能合理运用韦达定理(即根与系数的关系),可大大简化运算过程.2x 2y 2+=1例6 以椭圆123的焦点为焦点,过直线l :x -y +9=0上一点M 作椭圆,要使所作椭圆的长轴最短,点M 应在何处?并求出此时的椭圆方程.x 2y 2+=10),F 2(3,0).解:如图所示,椭圆123的焦点为F 1(-3,点F 1关于直线l :x -y +9=0的对称点F 的坐标为(-9,6),直线FF 2的方程为x +2y -3=0.⎛x +2y -3=0⎛MF 1+MF 2x -y +9=0得交点M 的坐标为(-5,4)解方程组⎛.此时最小.所求椭圆的长轴:2a =MF 1+MF 2=FF 2=6,∴a =3,又c =3,22x y 2+=12222b =a -c =3-3=364536∴.因此,所求椭圆的方程为.()例7 求中心在原点,对称轴为坐标轴,且经过A (, -2) 和B (-23, 1) 两点的椭圆方程.22mx +ny =1(m >0,n >0) .由A (3, -2) 和B (-23, 1) 两点在椭圆上可得解:设所求椭圆方程为22⎛22⎛m ⋅(3) +n ⋅(-2) =1, ⎛3m +4n =1, 11x y ⎛⎛m =n =+=122⎛⎛m ⋅(-23) +n ⋅1=1, 即⎛12m +n =1, 所以15,5.故所求的椭圆方程为155.π例8 已知长轴为12,短轴长为6,焦点在x 轴上的椭圆,过它对的左焦点F 1作倾斜解为3的直线交椭圆于A ,B 两点,求弦AB 的长.分析:可以利用弦长公式AB =+k 2x 1-x 2=(1+k 2)[(x 1+x 2) 2-4x 1x 2]求得,也可以利用椭圆定义及余弦定理,还可以利用焦点半径来求.解:(法1) 利用直线与椭圆相交的弦长公式求解.AB =+k 2x 1-x 2=(1+k 2)[(x 1+x 2) 2-4x 1x 2].因为a =6,b =3,所以c =.因为焦点在x 轴上,x 2y 2+=1所以椭圆方程为369,左焦点F (-33, 0) ,从而直线方程为y =3x +9.213x +x +36⨯8=0.设x 1,x 2为方程两根,所以由直线方程与椭圆方程联立得:x 1+x 2=-72313,x 1x 2=36⨯848AB =+k 2x 1-x 2=(1+k 2)[(x 1+x 2) 2-4x 1x 2]=13,k =,从而13(法2) 利用椭圆的定义及余弦定理求解.x 2y 2+=1AF AF 2=12-m BF 2=12-n BF 1=m 1=n 369由题意可知椭圆方程为,设,,则,.1F 2中,在∆AFAF 2=AF 1+F 1F 2-2AF 1F 1F 2cos222π3,即(12-m ) 2=m 2+36⋅3-2⋅m ⋅63⋅12;m =所以6648n =AB =m +n =4+,所以4-.同理在∆BF 13. 1F 2中,用余弦定理得(法3) 利用焦半径求解.先根据直线与椭圆联立的方程13x +x +36⨯8=0求出方程的两根x 1,x 2,它们分别是A ,B 的横坐标.再根据焦半径2AF 1=a +ex 1,BF 1=a +ex 2,从而求出=AF 1+BF 1.x 2y 2+=1ON O 2591的中点,例9 椭圆上的点M 到焦点F 1的距离为2,N 为MF 则为坐标原点)的值为A .43B .2 C .8 D .2说明:(1)椭圆定义:平面内与两定点的距离之和等于常数(大于(2)椭圆上的点必定适合椭圆的这一定义,即关距离F 1F 2)的点的轨迹叫做椭圆.MF 1+MF 2=2a,利用这个等式可以解决椭圆上的点与焦点的有x 2y 2C +=143例10 已知椭圆,试确定m 的取值范围,使得对于直线l :y =4x +m ,椭圆C 上有不同的两点关于该直线对称.M (x 0, y 0) 点.解:设椭圆上A (x 1, y 1) ,B (x 2, y 2) 两点关于直线l 对称,直线AB 与l 交于1⎛y =-x +n , ⎛⎛4⎛221⎛x +y =1, y =-x +nk =4,∴设直线AB 的方程为⎛y 43∵l 的斜率l .由方程组⎛4消去得13x 2-8nx +16n 2-48=0 ①。
1. 已知椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$($a>b>0$),若C关于x轴对称,则下列哪个选项是正确的?A. $a>b$B. $a<b$C. $a=b$D. 无法确定答案:A解析:由于椭圆C关于x轴对称,所以其方程中$x^2$的系数大于$y^2$的系数,即$a>b$。
2. 椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$($a>b>0$),若点P (x0,y0)在椭圆C上,则下列哪个选项是正确的?A. $x_0^2+y_0^2=a^2$B. $x_0^2+y_0^2=b^2$C. $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$D. $\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1$答案:C解析:点P在椭圆C上,所以满足椭圆的方程,即$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$。
3. 椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$($a>b>0$),若直线l的方程为$y=kx+b$,且l与椭圆C相切,则下列哪个选项是正确的?A. $k^2=\frac{a^2}{b^2}$B. $k^2=\frac{b^2}{a^2}$C. $k^2=\frac{a^2+b^2}{a^2b^2}$D. $k^2=\frac{a^2-b^2}{a^2b^2}$答案:A解析:由于直线l与椭圆C相切,所以它们只有一个交点,即判别式$\Delta=0$。
根据直线与椭圆的位置关系,可得$\Delta=\frac{b^2k^2-a^2b^2}{a^2}=0$,解得$k^2=\frac{a^2}{b^2}$。
4. 椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$($a>b>0$),若椭圆C的离心率e满足$e^2=\frac{c^2}{a^2}$,则下列哪个选项是正确的?A. $e^2=\frac{a^2-b^2}{a^2}$B. $e^2=\frac{a^2+b^2}{a^2}$C. $e^2=\frac{b^2}{a^2}$D. $e^2=\frac{a^2}{b^2}$答案:A解析:椭圆的离心率e定义为$\frac{c}{a}$,其中c是焦点到中心的距离。
高二椭圆练习题及答案椭圆是高中数学中的一个重要的几何概念,它在解析几何和微积分等数学分支中有着广泛的应用。
为了帮助高二学生巩固和提高对椭圆的理解和应用能力,以下提供一些高二椭圆练习题及其答案。
练习题一:1. 椭圆的离心率等于0的特殊情况是什么?该椭圆的形状如何?2. 某椭圆的焦点坐标为(2,0)和(-2,0),长轴长度为8. 求该椭圆的方程。
3. 某椭圆的长轴长度为10,短轴长度为8. 如果该椭圆的焦点到椭圆上任意点的距离之和为15,求该椭圆的方程。
4. 某椭圆的方程为(x-1)²/25 + y²/16 = 1,求该椭圆的焦点坐标及离心率。
5. 某椭圆的离心率为1/2,焦点为(0,-4)和(0,4)。
求该椭圆的方程。
答案一:1. 当椭圆的离心率等于0时,它的焦点和中心重合,长轴和短轴相等,椭圆变为一个圆。
2. 根据焦点坐标和长轴的长度,我们可以确定椭圆的中心坐标和短轴的长度。
所以该椭圆的方程为(x-2)²/16 + y²/4 = 1。
3. 根据题目信息,我们可以利用椭圆的定义来求解。
假设该椭圆的焦点为(c, 0),根据定义可得2a = 10,2ae = 15。
解方程组得a = 5/2,c = 3/2。
所以该椭圆的方程为(x-3/2)²/25 + y²/16 = 1。
4. 根据方程的形式,我们可以直接确定椭圆的中心坐标和长短轴长度。
所以该椭圆的焦点坐标为(1±√9, 0),离心率为√(1-16/25) = 3/5。
5. 根据焦点坐标和离心率的信息,我们可以利用椭圆的定义来求解。
假设该椭圆的焦点为(c, 0),根据定义可得2a = 2e,a = 4,c = 2。
所以该椭圆的方程为(x-2)²/16 + y²/9 = 1。
练习题二:1. 已知椭圆的离心率为2/3,焦点坐标为(±4,0),求该椭圆的方程。
椭圆》方程典型例题20例(含标准答案)典型例题一已知椭圆的一个顶点为A(2.0),其长轴长是短轴长的2倍,求椭圆的标准方程。
分析:题目没有指出焦点的位置,要考虑两种位置。
解:(1)当A(2.0)为长轴端点时,a=2,b=1,椭圆的标准方程为:x^2/4+y^2/1=1;(2)当A(2.0)为短轴端点时,b=2,a=4,椭圆的标准方程为:x^2/16+y^2/4=1.说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况。
典型例题二一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率。
解:设椭圆长轴长为2a,焦点到准线的距离为c,则2c/3=a,即c=3a/2.由椭圆定义可得c^2=a^2-b^2,代入c=3a/2中得到9a^2/4=a^2-b^2,化简得b^2=3a^2/4.再由离心率的定义e=c/a得到e=√(1-b^2/a^2)=√(1-3/4)=√(1/4)=1/2.说明:求椭圆的离心率问题,通常有两种处理方法,一是求a,求c,再求比。
二是列含a和c的齐次方程,再化含e的方程,解方程即可。
典型例题三已知中心在原点,焦点在x轴上的椭圆与直线x+y-1=0交于A、B两点,M为AB中点,OM的斜率为0.25,椭圆的短轴长为2,求椭圆的方程。
解:由题意,设椭圆方程为x^2/4+y^2/a^2=1,直线方程为y=1-x。
将直线方程代入椭圆方程得到x^2/4+(1-x)^2/a^2=1,化简得到(4+a^2)x^2-8ax+(4-a^2)=0.设AB的中点为M(x1.y1),则M的坐标为[(x1+x2)/2.(y1+y2)/2],其中x2为方程(4+a^2)x^2-8ax+(4-a^2)=0的另一个解。
由OM的斜率为0.25可得到y1=0.25x1.又因为M在直线x+y-1=0上,所以有y1=1-x1.解以上两个方程可得到M的坐标为(4/5.1/5)。
典型例题一例1 椭圆的一个顶点为()02,A ,其长轴长是短轴长的2倍,求椭圆的标准方程. 分析:题目没有指出焦点的位置,要考虑两种位置.解:(1)当()02,A 为长轴端点时,2=a ,1=b , 椭圆的标准方程为:11422=+y x ; (2)当()02,A 为短轴端点时,2=b ,4=a , 椭圆的标准方程为:116422=+y x ; 说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.典型例题二例2 一个椭圆的焦点将其准线间的距离三等分,求椭圆的离心率.解:31222⨯⨯=c a c ∴223a c =, ∴3331-=e . 说明:求椭圆的离心率问题,通常有两种处理方法,一是求a ,求c ,再求比.二是列含a 和c 的齐次方程,再化含e 的方程,解方程即可.典型例题三例3 已知中心在原点,焦点在x 轴上的椭圆与直线01=-+y x 交于A 、B 两点,M 为AB 中点,OM 的斜率为0.25,椭圆的短轴长为2,求椭圆的方程.解:由题意,设椭圆方程为1222=+y ax ,由⎪⎩⎪⎨⎧=+=-+101222y ax y x ,得()021222=-+x a x a , ∴222112a a x x x M +=+=,2111a x y M M +=-=, 4112===ax y k M M OM ,∴42=a , ∴1422=+y x 为所求. 说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.典型例题四例4椭圆192522=+y x 上不同三点()11y x A ,,⎪⎭⎫⎝⎛594,B ,()22y x C ,与焦点()04,F 的距离成等差数列.(1)求证821=+x x ;(2)若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k . 证明:(1)由椭圆方程知5=a ,3=b ,4=c . 由圆锥曲线的统一定义知:a c x ca AF =-12,∴11545x ex a AF -=-=. 同理2545x CF -=.∵BF CF AF 2=+,且59=BF ,∴51854554521=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x x ,即821=+x x .(2)因为线段AC 的中点为⎪⎭⎫⎝⎛+2421y y ,,所以它的垂直平分线方程为()42212121---=+-x y y x x y y y . 又∵点T 在x 轴上,设其坐标为()00,x ,代入上式,得()212221024x x y y x --=-又∵点()11y x A ,,()22y x B ,都在椭圆上, ∴()212125259x y -=()222225259x y -=∴()()21212221259x x x x y y -+-=-.将此式代入①,并利用821=+x x 的结论得253640-=-x ∴4540590=--=x k BT .典型例题五例5 已知椭圆13422=+yx ,1F 、2F 为两焦点,问能否在椭圆上找一点M ,使M 到左准线l 的距离MN是1MF 与2MF 的等比中项?若存在,则求出点M 的坐标;若不存在,请说明理由.解:假设M 存在,设()11y x M ,,由已知条件得2=a ,3=b ,∴1=c ,21=e . ∵左准线l 的方程是4-=x , ∴14x MN +=. 又由焦半径公式知:111212x ex a MF -=-=,112212x ex a MF +=+=. ∵212MF MF MN ⋅=,∴()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=+11212122124x x x . 整理得048325121=++x x . 解之得41-=x 或5121-=x .① 另一方面221≤≤-x .②则①与②矛盾,所以满足条件的点M 不存在. 说明:(1)利用焦半径公式解常可简化解题过程.(2)本例是存在性问题,解决存在性问题,一般用分析法,即假设存在,根据已知条件进行推理和运算.进而根据推理得到的结果,再作判断.(3)本例也可设()θθsin 3cos 2,M 存在,推出矛盾结论(读者自己完成).典型例题六例6 已知椭圆1222=+y x ,求过点⎪⎭⎫⎝⎛2121,P 且被P 平分的弦所在的直线方程.分析一:已知一点求直线,关键是求斜率,故设斜率为k ,利用条件求k . 解法一:设所求直线的斜率为k ,则直线方程为⎪⎭⎫ ⎝⎛-=-2121x k y .代入椭圆方程,并整理得 ()()0232122212222=+-+--+k k x k kx k .由韦达定理得22212122kkk x x +-=+. ∵P 是弦中点,∴121=+x x .故得21-=k .所以所求直线方程为0342=-+y x .分析二:设弦两端坐标为()11y x ,、()22y x ,,列关于1x 、2x 、1y 、2y 的方程组,从而求斜率:2121x x y y --.解法二:设过⎪⎭⎫⎝⎛2121,P 的直线与椭圆交于()11y x A ,、()22y x B ,,则由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+=+④1.③1②12①12212122222121y y x x y x y x ,,, ①-②得0222212221=-+-y y x x .⑤将③、④代入⑤得212121-=--x x y y ,即直线的斜率为21-.所求直线方程为0342=-+y x . 说明:(1)有关弦中点的问题,主要有三种类型:过定点且被定点平分的弦;平行弦的中点轨迹;过定点的弦中点轨迹.(2)解法二是“点差法”,解决有关弦中点问题的题较方便,要点是巧代斜率.(3)有关弦及弦中点问题常用的方法是:“韦达定理应用”及“点差法”.有关二次曲线问题也适用.典型例题七例7 求适合条件的椭圆的标准方程.(1)长轴长是短轴长的2倍,且过点()62-,; (2)在x 轴上的一个焦点与短轴两端点的联机互相垂直,且焦距为6.分析:当方程有两种形式时,应分别求解,如(1)题中由12222=+b y a x 求出1482=a ,372=b ,在得方程13714822=+y x 后,不能依此写出另一方程13714822=+x y . 解:(1)设椭圆的标准方程为12222=+b y a x 或12222=+bx a y .由已知b a 2=.①又过点()62-,,因此有 ()1622222=-+b a 或()1262222=+-ba .② 由①、②,得1482=a ,372=b 或522=a ,132=b .故所求的方程为13714822=+y x 或1135222=+x y .(2)设方程为12222=+b y a x .由已知,3=c ,3==c b ,所以182=a .故所求方程为191822=+y x .说明:根据条件求椭圆的标准方程的思路是“选标准,定参数”.关键在于焦点的位置是否确定,若不能确定,应设方程12222=+b y a x 或12222=+bx a y .典型例题八例8 椭圆1121622=+y x 的右焦点为F ,过点()31,A ,点M 在椭圆上,当MF AM 2+为最小值时,求点M 的坐标.分析:本题的关键是求出离心率21=e ,把MF 2转化为M 到右准线的距离,从而得最小值.一般地,求MF eAM 1+均可用此法. 8=x l :. 解:由已知:4=a ,2=c .所以21=e ,右准线过A 作l AQ ⊥,垂足为Q ,交椭圆于M ,故MF MQ 2=.显然3=M y ,且M 在MF AM 2+的最小值为AQ ,即M 为所求点,因此椭圆上.故32=M x .所以()332,M .“2”的处理.事实说明:本题关键在于未知式MF AM 2+中的上,如图,21=e ,即MF 是M 到右准线的距离的一半,即图中的MQ ,问题转化为求椭圆上一点M ,使M 到A 的距离与到右准线距离之和取最小值.典型例题九例9 求椭圆1322=+y x 上的点到直线06=+-y x 的距离的最小值.分析:先写出椭圆的参数方程,由点到直线的距离建立三角函数关系式,求出距离的最小值.解:椭圆的参数方程为⎩⎨⎧==.sin cos 3θθy x ,设椭圆上的点的坐标为()θθsin cos 3,,则点到直线的距离为263sin 226sin cos 3+⎪⎭⎫ ⎝⎛-=+-=θπθθd . 当13sin -=⎪⎭⎫⎝⎛-θπ时,22=最小值d .说明:当直接设点的坐标不易解决问题时,可建立曲线的参数方程.典型例题十例10 设椭圆的中心是坐标原点,长轴在x 轴上,离心率23=e ,已知点⎪⎭⎫⎝⎛230,P 到这个椭圆上的点的最远距离是7,求这个椭圆的方程,并求椭圆上的点P 的距离等于7的点的坐标.分析:本题考查椭圆的性质、距离公式、最大值以及分析问题的能力,在求d 的最大值时,要注意讨论b 的取值围.此题可以用椭圆的标准方程,也可用椭圆的参数方程,要善于应用不等式、平面几何、三角等知识解决一些综合性问题,从而加强等价转换、形数结合的思想,提高逻辑推理能力.解法一:设所求椭圆的直角坐标方程是12222=+b y a x ,其中0>>b a 待定.由222222221ab a b a ac e -=-==可得 2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点P 的距离是d ,则4931232222222+-+⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+=y y b y a y x d 34213493342222++⎪⎭⎫ ⎝⎛+-=+--=b y y y b其中b y b ≤≤-. 如果21<b ,则当b y -=时,2d (从而d )有最大值.由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾.因此必有21≥b 成立,于是当21-=y 时,2d (从而d )有最大值. 由题设得()34722+=b,可得1=b ,2=a .∴所求椭圆方程是11422=+y x . 由21-=y 及求得的椭圆方程可得,椭圆上的点⎪⎭⎫ ⎝⎛--213,,点⎪⎭⎫ ⎝⎛-213,到点⎪⎭⎫⎝⎛230,P 的距离是7. 解法二:根据题设条件,可取椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x ,其中0>>b a ,待定,πθ20≤≤,θ为参数.由22222221⎪⎭⎫ ⎝⎛-=-==a b a b a a c e 可得2143112=-=-=e a b ,即b a 2=. 设椭圆上的点()y x ,到点⎪⎭⎫⎝⎛230,P 的距离为d ,则22222223sin cos 23⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=θθb a y x d49sin 3sin 34222+--=θθb b b 3421sin 3222++⎪⎭⎫ ⎝⎛+-=b b b θ如果121>b ,即21<b ,则当1sin -=θ时,2d (从而d )有最大值. 由题设得()22237⎪⎭⎫ ⎝⎛+=b ,由此得21237>-=b ,与21<b 矛盾,因此必有121≤b 成立. 于是当b21sin -=θ时2d (从而d )有最大值. 由题设知()34722+=b,∴1=b ,2=a .∴所求椭圆的参数方程是⎩⎨⎧==θθsin cos 2y x .由21sin -=θ,23cos ±=θ,可得椭圆上的是⎪⎭⎫ ⎝⎛--213,,⎪⎭⎫ ⎝⎛-213,. 典型例题十一例11 设x ,R ∈y ,x y x 63222=+,求x y x 222++的最大值和最小值.分析:本题的关键是利用形数结合,观察方程x y x 63222=+与椭圆方程的结构一致.设m x y x =++222,显然它表示一个圆,由此可以画出图形,考虑椭圆及圆的位置关系求得最值.解:由x y x 63222=+,得123492322=+⎪⎪⎪⎪⎭⎫ ⎝⎛-y x 可见它表示一个椭圆,其中心在⎪⎭⎫⎝⎛023,点,焦点在x 轴上,且过(0,0)点和(3,0)点. 设m x y x =++222,则()1122+=++m y x它表示一个圆,其圆心为(-1,0)半径为()11->+m m .在同一坐标系中作出椭圆及圆,如图所示.观察图形可知,当圆过(0,0)点时,半径最小,即11=+m ,此时0=m ;当圆过(3,0)点时,半径最大,即41=+m ,∴15=m .∴x y x 222++的最小值为0,最大值为15.典型例题十二例12 已知椭圆()012222>>=+b a by a x C :,A 、B 是其长轴的两个端点.(1)过一个焦点F 作垂直于长轴的弦P P ',求证:不论a 、b 如何变化, 120≠∠APB . (2)如果椭圆上存在一个点Q ,使 120=∠AQB ,求C 的离心率e 的取值围.分析:本题从已知条件出发,两问都应从APB ∠和AQB ∠的正切值出发做出估计,因此要从点的坐标、斜率入手.本题的第(2)问中,其关键是根据什么去列出离心率e 满足的不等式,只能是椭圆的固有性质:a x ≤,b y ≤,根据120=∠AQB 得到32222-=-+a y x ay ,将22222y ba a x -=代入,消去x ,用a 、b 、c 表示y ,以便利用b y ≤列出不等式.这里要求思路清楚,计算准确,一气呵成.解:(1)设()0,c F ,()0,a A -,()0,a B . ⎪⎪⎭⎫⎝⎛⇒⎩⎨⎧=+=a b c P b a y a x b c x 2222222, 于是()a c a b k AP+=2,()a c ab k BP -=2. ∵APB ∠是AP 到BP 的角.∴()()()2222242221tan ca a c ab ac a b a c a b APB -=-++--=∠∵22c a >∴2tan -<∠APB 故3tan -≠∠APB ∴ 120≠∠APB . (2)设()y x Q ,,则a x y k QA +=,ax y k QB -=. 由于对称性,不妨设0>y ,于是AQB ∠是QA 到QB 的角.∴22222221tan a y x ay a x y a x ya x y AQB -+=-++--=∠ ∵ 120=∠AQB , ∴32222-=-+a y x ay整理得()023222=+-+ay a y x ∵22222y b a a x -=∴0213222=+⎪⎪⎭⎫ ⎝⎛-ay y b a ∵0≠y , ∴2232c ab y =∵b y ≤, ∴b c ab ≤2232 232c ab ≤,()222234c c a a ≤-∴04444224≥-+a c a c ,044324≥-+e e∴232≥e 或22-≤e (舍),∴136<≤e . 典型例题十三例13 已知椭圆19822=++y k x 的离心率21=e ,求k 的值. 分析:分两种情况进行讨论.解:当椭圆的焦点在x 轴上时,82+=k a ,92=b ,得12-=k c .由21=e ,得4=k . 当椭圆的焦点在y 轴上时,92=a ,82+=k b ,得k c -=12.由21=e ,得4191=-k ,即45-=k . ∴满足条件的4=k 或45-=k .说明:本题易出现漏解.排除错误的办法是:因为8+k 与9的大小关系不定,所以椭圆的焦点可能在x 轴上,也可能在y 轴上.故必须进行讨论.典型例题十四例14 已知椭圆142222=+by b x 上一点P 到右焦点2F 的距离为b )1(>b ,求P 到左准线的距离.分析:利用椭圆的两个定义,或利用第二定义和椭圆两准线的距离求解.解法一:由142222=+by b x ,得b a 2=,b c 3=,23=e .由椭圆定义,b a PF PF 4221==+,得b b b PF b PF 34421=-=-=.由椭圆第二定义,e d PF =11,1d 为P 到左准线的距离,∴b ePF d 3211==,即P 到左准线的距离为b 32. 解法二:∵e d PF =22,2d 为P 到右准线的距离,23==a c e , ∴b ePF d 33222==.又椭圆两准线的距离为b c a 33822=⋅. ∴P 到左准线的距离为b b b 32332338=-. 说明:运用椭圆的第二定义时,要注意焦点和准线的同侧性.否则就会产生误解.椭圆有两个定义,是从不同的角度反映椭圆的特征,解题时要灵活选择,运用自如.一般地,如遇到动点到两个定点的问题,用椭圆第一定义;如果遇到动点到定直线的距离问题,则用椭圆的第二定义.典型例题十五例15 设椭圆⎩⎨⎧==.sin 32,cos 4ααy x (α为参数)上一点P 与x 轴正向所成角3π=∠POx ,求P 点坐标.分析:利用参数α与POx ∠之间的关系求解. 解:设)sin 32,cos 4(ααP ,由P 与x 轴正向所成角为3π, ∴ααπcos 4sin 323tan=,即2tan =α.而0sin >α,0cos >α,由此得到55cos =α,552sin =α,∴P 点坐标为)5154,554(. 典型例题十六例16 设),(00y x P 是离心率为e 的椭圆12222=+by a x )0(>>b a 上的一点,P 到左焦点1F 和右焦点2F 的距离分别为1r 和2r ,求证:01ex a r +=,02ex a r -=.分析:本题考查椭圆的两个定义,利用椭圆第二定义,可将椭圆上点到焦点的距离转化为点到相应准线距离.解:P 点到椭圆的左准线c a x l 2-=:的距离,c a x PQ 20+=,由椭圆第二定义,e PQ PF =1,∴01ex a PQ e r +==,由椭圆第一定义,0122ex a r a r -=-=.说明:本题求证的是椭圆的焦半径公式,在解决与椭圆的焦半径(或焦点弦)的有关问题时,有着广泛的应用.请写出椭圆焦点在y 轴上的焦半径公式.典型例题十七例17 已知椭圆15922=+y x 有一点)1,1(A ,1F 、2F 分别是椭圆的左、右焦点,点P 是椭圆上一点. (1) 求1PF PA +的最大值、最小值及对应的点P 坐标; (2) 求223PF PA +的最小值及对应的点P 的坐标. 分析:本题考查椭圆中的最值问题,通常探求变量的最值有两种方法:一是目标函数当,即代数方法.二是数形结合,即几何方法.本题若按先建立目标函数,再求最值,则不易解决;若抓住椭圆的定义,转化目标,运用数形结合,就能简捷求解.解:(1)如上图,62=a ,)0,2(2F ,22=AF ,设P 是椭圆上任一点,由6221==+a PF PF ,22AF PF PA -≥,∴26222211-=-=-+≥+AF a AF PF PF PF PA ,等号仅当22AF PF PA -=时成立,此时P 、A 、2F 共线.由22AF PF PA +≤,∴26222211+=+=++≤+AF a AF PF PF PF PA ,等号仅当22AF PF PA +=时成立,此时P 、A 、2F 共线.建立A 、2F 的直线方程02=-+y x ,解方程组⎩⎨⎧=+=-+4595,0222y x y x 得两交点 )2141575,2141579(1+-P 、)2141575,2141579(2-+P . 综上所述,P 点与1P 重合时,1PF PA +取最小值26-,P 点与2P 重合时,2PF PA +取最大值26+.(2)如下图,设P 是椭圆上任一点,作PQ 垂直椭圆右准线,Q 为垂足,由3=a ,2=c ,∴32=e .由椭圆第二定义知322==e PQPF ,∴223PF PQ =,∴PQ PA PF PA +=+223,要使其和最小需有A 、P 、Q 共线,即求A 到右准线距离.右准线方程为29=x .∴A 到右准线距离为27.此时P 点纵坐标与A 点纵坐标相同为1,代入椭圆得满足条件的点P 坐标)1,556(.说明:求21PF ePA +的最小值,就是用第二定义转化后,过A 向相应准线作垂线段.巧用焦点半径2PF 与点准距PQ 互化是解决有关问题的重要手段.典型例题十八例18 (1)写出椭圆14922=+y x 的参数方程; (2)求椭圆接矩形的最大面积.分析:本题考查椭圆的参数方程及其应用.为简化运算和减少未知数的个数,常用椭圆的参数方程表示曲线上一点坐标,所求问题便化归为三角问题.解:(1)⎩⎨⎧==θθsin 2cos 3y x )(R ∈θ.(2)设椭圆接矩形面积为S ,由对称性知,矩形的邻边分别平行于x 轴和y 轴,设)sin 2,cos 3(θθ为矩形在第一象限的顶点,)20(π<θ<,则122sin 12sin 2cos 34≤=⨯⨯=θθθS 故椭圆接矩形的最大面积为12.说明:通过椭圆参数方程,转化为三角函数的最值问题,一般地,与圆锥曲线有关的最值问题,用参数方程形式较简便.典型例题十九例19 已知1F ,2F 是椭圆的两个焦点,P 是椭圆上一点,且︒=∠6021PF F . (1)求椭圆离心率的取值围;(2)求证21F PF ∆的面积与椭圆短轴长有关. 分析:不失一般性,可以设椭圆方程为12222=+by a x (0>>b a ),),(11y x P (01>y ). 思路一:根据题设容易想到两条直线的夹角公式,即3160tan 1212=+-=︒PF PF PF PF K K K K ,设),(11y x P ,)0,(1c F -,)0,(2c F ,化简可得03233212121=--+c cy y x .又1221221=+by a x ,两方程联立消去21x 得0323412212=-+b cy b y c ,由],0(1b y ∈,可以确定离心率的取值围;解出1y 可以求出21F PF ∆的面积,但这一过程很繁.思路二:利用焦半径公式11ex a PF +=,12ex a PF -=,在21F PF ∆中运用余弦定理,求1x ,再利用],[1a a x -∈,可以确定离心率e 的取值围,将1x 代入椭圆方程中求1y ,便可求出21F PF ∆的面积.思路三:利用正弦定理、余弦定理,结合a PF PF 221=+求解.解:(法1)设椭圆方程为12222=+by a x (0>>b a ),),(11y x P ,)0,(1c F -,)0,(2c F ,0>c ,则11ex a PF +=,12ex a PF -=. 在21F PF ∆中,由余弦定理得))((24)()(2160cos 1122121ex a ex a c ex a ex a -+--++==︒, 解得2222134ea c x -=. (1)∵],0(221a x ∈,∴2222340a ea c <-≤,即0422≥-a c . ∴21≥=a c e . 故椭圆离心率的取围是)1,21[∈e .(2)将2222134e a c x -=代入12222=+by a x 得24213c b y =,即cb y 321=.∴22213332212121b cb c y F F S F PF =⋅⋅=⋅=∆. 即21F PF ∆的面积只与椭圆的短轴长有关.(法2)设m PF =1,n PF =2,α=∠12FPF ,β=∠21F PF , 则︒=+120βα.(1)在21F PF ∆中,由正弦定理得︒==60sin 2sin sin cn m βα. ∴︒=++60sin 2sin sin cn m βα∵a n m 2=+, ∴︒=+60sin 2sin sin 2ca βα,∴2cos 2sin 260sin sin sin 60sin βαβαβα-+︒=+︒==a c e 212cos21≥-=βα.当且仅当βα=时等号成立.故椭圆离心率的取值围是)1,21[∈e .(2)在21F PF ∆中,由余弦定理得:︒-+=60cos 2)2(222mn n m cmn n m -+=22 mn n m 3)(2-+=∵a n m 2=+,∴mn a c 34422-=,即22234)(34b c a mn =-=. ∴23360sin 2121b mn S F PF =︒=∆. 即21F PF ∆的面积与椭圆短轴长有关.说明:椭圆上的一点P 与两个焦点1F ,2F 构成的三角形为椭圆的焦点三角形,涉及有关焦点三角形问题,通常运用三角形的边角关系定理.解题过变形,使之出现21PF PF +的结构,这样就可以应用椭圆的定义,从而可得到有关a ,c 的关系式,使问题找到解决思路.典型例题二十例20 椭圆12222=+by a x )0(>>b a 与x 轴正向交于点A ,若这个椭圆上总存在点P ,使AP OP ⊥(O 为坐标原点),求其离心率e 的取值围.分析:∵O 、A 为定点,P 为动点,可以P 点坐标作为参数,把AP OP ⊥,转化为P 点坐标的一个等量关系,再利用坐标的围建立关于a 、b 、c 的一个不等式,转化为关于e 的不等式.为减少参数,易考虑运用椭圆参数方程.解:设椭圆的参数方程是⎩⎨⎧==θθsin cos b y a x )0(>>b a ,则椭圆上的点)sin ,cos (θθb a P ,)0,(a A , ∵AP OP ⊥,∴1cos sin cos sin -=-⋅aa b a b θθθθ,即0cos cos )(22222=+--b a b a θθ,解得1cos =θ或222cos ba b -=θ, ∵1cos 1<<-θ∴1cos =θ(舍去),11222<-<-b a b ,又222c a b -= ∴2022<<ca ,∴22>e ,又10<<e ,∴122<<e . 说明:若已知椭圆离心率围)1,22(,求证在椭圆上总存在点P 使AP OP ⊥.如何证明?。