2006年江西高考理科数学试题及答案

2006年普通高等学校招生全国统一考试（江西卷）理科数学第一卷参考公式：如果时间A 、B 互斥，那么()()()P A B P A P B +=+如果时间A 、B 相互独立，那么()()()P A B P A P B =如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率()()1n kk k n n P k C P P -=-球的表面积公式24S R π=，其中R 表示球的半径 球的体积公式343V R π=，其中R 表示球的半径一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合M ＝｛x|3x 0x 1≥（－）｝，N ＝｛y|y ＝3x 2＋1，x ∈R ｝，则M ⋂N ＝（ ）A ．∅ B. {x|x ≥1} C.｛x|x >1｝ D. {x| x ≥1或x <0}2、已知复数z＋3i ）z ＝3i ，则z ＝（ ）A．32B. 34C. 32D.343、若a >0，b >0，则不等式－b <1x <a 等价于（ ）A ．1b －<x <0或0<x <1a B.－1a <x <1b C.x <-1a 或x >1b D.x <1b －或x >1a4、设O 为坐标原点，F 为抛物线y 2＝4x 的焦点，A 是抛物线上一点，若OA F A ∙＝－4则点A 的坐标是（ ）A ．（2，±） B. (1，±2) C.（1，2）D.(2，)5、对于R 上可导的任意函数f （x ），若满足（x －1）f x '（）≥0，则必有（ ）A ． f （0）＋f （2）<2f （1） B. f （0）＋f （2）≤2f （1）B ． f （0）＋f （2）≥2f （1） C. f （0）＋f （2）>2f （1）6、若不等式x 2＋ax ＋1≥0对于一切x ∈（0，12〕成立，则a 的取值范围是（ ）A ．0 B. -2 C.-52 D.-37、已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC ＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝（ ）A ．100 B. 101 C.200 D.2018、在（x）2006 的二项展开式中，含x 的奇次幂的项之和为S ，当x时，S 等于（ ） A.23008 B.-23008 C.23009 D.-230099、P 是双曲线22x y 1916－＝的右支上一点，M 、N 分别是圆（x ＋5）2＋y 2＝4和（x －5）2＋y 2＝1上的点，则|PM|－|PN|的最大值为（ ）A. 6B.7C.8D.910、将7个人（含甲、乙）分成三个组，一组3人，另两组2 人，不同的分组数为a ，甲、乙分到同一组的概率为p ，则a 、p 的值分别为（ ）A ． a=105 p=521 B.a=105 p=421 C.a=210 p=521 D.a=210 p=42111、如图，在四面体ABCD 中，截面AEF 经过四面体的内切球（与四个面都相切的球）球心O ，且与BC ，DC 分别截于E 、F ，如果截面将四面体分成体积相等的两部分，设四棱锥A －BEFD 与三棱锥A －EFC 的表面积分别是S 1，S 2，则必有（ ）A. S 1<S 2B. S 1>S 2C. S 1=S 2D. S 1，S 2的大小关系不能确定C12、某地一年的气温Q （t ）（单位：ºc ）与时间t （月份）之间的关系如图（1）所示，已知该年的平均气温为10ºc ，令G （t ）表示时间段〔0,t 〕的平均气温，G （t ）与t 之间的函数关系用下列图像表示，则正确的应该是（ ）第Ⅱ卷二、填空题：本大题共4小题，每小题4分，共16分，把答案填写在答题卡的相应位置。

12006高等学校全国统一数学文试卷（江西卷）一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出地四个选项中,只有一项是符合题目要求地．1．已知集合{}(1)0P x x x =-≥,101Q x x ⎧⎫=>⎨⎬-⎩⎭,则P Q 等于（ ）Ａ．∅Ｂ．{}1x x ≥Ｃ．{}1x x >Ｄ．{}1x x x <0或≥2．函数4sin 21y x π⎛⎫=++ ⎪3⎝⎭地最小正周期为（ ）Ａ．π2Ｂ．πＣ．2πＤ．4π3．在各项均不为零地等差数列{}n a 中,若2110(2)n n n a a a n +--+=≥,则214n S n --=（ ）Ａ．2-Ｂ．0Ｃ．1Ｄ．24．下列四个条件中,p 是q 地必要不充分条件地是（ ）Ａ．:p a b >,22:q a b >Ｂ．:p a b >,:22a bq >Ｃ．22:p ax by c +=为双曲线,:0q ab <Ｄ．2:0p ax bx c ++>,2:0c bq a x x-+>5．对于R 上可导地任意函数()f x ,若满足(1)()0x f x '-≥,则必有（ ）Ａ．(0)(2)2(1)f f f +<Ｂ．(0)(2)2(1)f f f +≤Ｃ．(0)(2)2(1)f f f +≥Ｄ．(0)(2)2(1)f f f +>6．若不等式210x ax ++≥对一切102x ⎛⎤∈ ⎥⎝⎦，成立,则a 地最小值为（ ）Ａ．0Ｂ．2-Ｃ．52-Ｄ．3-7．在2nx⎫+⎪⎭地二项展开式中,若常数项为60,则n等于（ ）Ａ．3Ｂ．6Ｃ．9Ｄ．128．袋中有40个小球,其中红色球16个、蓝色球12个,白色球8个,黄色球4个,从中随机抽取10个球作成一个样本,则这个样本恰好是按分层抽样方法得到地概率为（ ）Ａ．12344812161040C C C CCＢ．21344812161040C C C CCＣ．23144812161040C C C CCＤ．13424812161040C C C CC9．如果四棱锥地四条侧棱都相等,就称它为"等腰四棱锥",四条侧棱称为它地腰,以下4个命题中,假命题是（ ）Ａ．等腰四棱锥地腰与底面所成地角都相等Ｂ．等腰四棱锥地侧面与底面所成地二面角都相等或互补Ｃ．等腰四棱锥地底面四边形必存在外接圆Ｄ．等腰四棱锥地各顶点必在同一球面上10．已知等差数列{}n a地前n项和为n S,若1200OB a OA a OC=+,且A B C，，三点共线（该直线不过点O）,则200S等于（ ）Ａ．100Ｂ．101Ｃ．200Ｄ．20111．P为双曲线221916x y-=地右支上一点,M,N分别是圆22(5)4x y++=和22(5)1x y-+=上地点,则PM PN-地最大值为（ ）Ａ．6Ｂ．7Ｃ．8Ｄ．912．某地一天内地气温()Q t（单位:时）之间地关系如图（1）所示,令()C t[0]t，内地温差（即时间段[0]t，地差）．()C t与t确地图象大致是（ ）C(C3第II 卷二、填空题:本大题4小题,每小题4分,共16分．请把解析填在答题卡上．13．已知向量(1sin )a θ= ，,(1cos )b θ= ，,则a b -地最大值为．14．设3()log (6)f x x =+地反函数为1()fx -,若11[()6][()6]27f m f n --++= ,则()f m n +=．15．如图,已知正三棱柱111ABC A B C -地底面边长为1,高为8,一质点自A 点出发,沿着三棱柱地侧面绕行两周到达1A 点地最短路线地长为．16．已知12F F ，为双曲线22221(00)a b x y a b a b≠-=>>且，地两个焦点,P 为双曲线右支上异于顶点地任意一点,O 为坐标原点．下面四个命题（ ）Ａ．12PF F △地内切圆地圆心必在直线x a =上；Ｂ．12PF F △地内切圆地圆心必在直线x b =上；Ｃ．12PF F △地内切圆地圆心必在直线OP 上；Ｄ．12PF F △地内切圆必通过点0a ()，．1C 1B 1A ACB(C t (C4其中真命题地代号是（写出所有真命题地代号）．三、解答题:本大题共6小题,共74分．解答应写出文字说明,证明过程或演算步骤．17．（本小题满分12分）已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值．（1）求a b ，地值及函数()f x 地单调区间；（2）若对[12]x ∈-，,不等式2()f x c <恒成立,求c 地取值范围．18．（本小题满分12分）某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球地箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二得奖；摸出两个红球获得一等奖．现有甲、乙两位顾客,规定:甲摸一次,乙摸两次．求（1）甲、乙两人都没有中奖地概率；（2）甲、两人中至少有一人获二等奖地概率．19．（本小题满分12分）在锐角ABC △中,角A B C ，，所对地边分别为a b c ，，,已知sin A =,（1）求22tansin 22B C A++地值；（2）若2a =,ABC S =△,求b 地值．20．（本小题满分12分）如图,已知三棱锥O ABC -地侧棱OA OB OC ，，两两垂直,且1OA =,2OB OC ==,E 是OC 地中点．（1）求O 点到面ABC 地距离；（2）求异面直线BE 与AC 所成地角；（3）求二面角E AB C --地大小．21．（本小题满分12分）如图,椭圆22221(0)x y Q a b a b +=>>：地右焦点为(0)F c ，,过点F并且交椭圆于A B ，两点,P 为线段AB 地中点．（1）求点P 地轨迹H 地方程；（2）若在Q 地方程中,令21cos sin a θθ=++,2sin 0b θθπ⎛⎫=< ⎪2⎝⎭≤．设轨迹H 地最高点和最低点分别为M 和N ．当θ为何值时,MNF △为一个正三角形？22．（本小题满分14分）已知各项均为正数地数列{}n a ,满足:13a =,且11122n nn n n n a a a a a a +++-=-,*n N ∈．ＡＯＥＣＢ5（1）求数列{}n a 地通项公式；（2）设22212n n S a a a =+++ ,22212111n nT a a a a =+++ ,求n n S T +,并确定最小正整数n ,使n n S T +为整数．。

2006年普通高等学校招生全国统一考试文科数学（全国卷Ⅰ）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3到10页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

3．本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥，那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立，那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ，那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径k n k kn n P P C k P --=)1()(一．选择题（1）设集合M={x|x 2-x<0},N={x||x|<2},则（A ）M φ=N （B ）M M N =（C ）M N M =（D ）R N M =（2）已知函数y=e x 的图象与函数y=f(x)的图象关于直线y=x 对称，则（A ）f(2x)=e 2x (x )R ∈ （B ）f(2x)=ln2lnx(x>0)（C ）f(2x)=2e 2x (x )R ∈（D ）f(2x)= lnx+ln2(x>0)（3）双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m=（A ）-41 （B ）-4 (C)4 （D ）41 （4）如果(m 2+i)(1+mi)是实数,则实数m=（A ）1（B ）-1（C ）2（D ）-2（5）函数f(x)=tan(x+4π)的单调递增区间为（A ）(k π-2π, k π+2π),k Z ∈ （B ）(k π, (k+1)π),k Z ∈ (C) (k π-43π, k π+4π),k Z ∈ （D ）(k π-4π, k π+43π),k Z ∈ （6）∆ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，若a 、b 、c ，且c=2a ，则cosB=（A ）41 （B ）43（C ）42 （D ）32（7）已知各顶点都在一个球面上的正四棱锥高为4，体积为16，则这个球的表面积是（A ）16 π （B ）20π （C ）24π （D ）32π （8）抛物线y=-x 2上的点到4x+3y-8=0直线的距离的最小值是（A ）34 （B ）57 （C ）58 （D ）3（9）设平面向量a 1、a 2、a 3的和a 1+a 2+a 3=0，如果平面向量b 1、b 2、b 3满足|b i |=2|a i |，且a i 顺时针旋转30︒后与同向，其中i=1、2、3，则（A ）-b 1+b 2+b 3=0 （B ）b 1-b 2+b 3=0（C ）b 1+b 2-b 3=0 （D ）b 1+b 2+b 3=0（10）设{a n }是公差为正数的等差数列，若a 1+a 2+a 3=15，a 1a 2a 3=80，则a 11+a 12+a 13=（A ）120 （B ）105 （C ）90 （D ）75（11）用长度分别为2、3、4、5、6(单位:cm)的细木棒围成一个三角形(允许连接,但不允许折断),能够得到期的三角形面积的最大值为（A ）85cm 2（B ）610cm 2（C ）355cm 2（D ）20cm 2（12）设集合I={1，2，3，4，5}，选择I 的两个非空子和B ，要使B 中的最小的数大于A 中最大的数，则不同的选择方法共有（A ）50种 （B ）49种 （C ）48种 （D ）47种第Ⅱ卷注意事项：1．用钢笔或圆珠笔直接答在试题卷上。

Unit 8 B卷I.词组英汉互译（10分）1.干家务________2.洗餐具______3.整理床铺__________4.打扫客厅__________5.一个重要会议__________6.Feed dogs and cats_________7.No walking dogs in the park. __________8.Work on English teaching_________9.Stay out late_____________10.have an English test tomorrow __________ II.选择填空（15分）( )1 Could you please ________ your classroom every day?A. to cleanB. cleaningC. cleanD. cleaned( ) 2. Could you please ________-- to music in class?A. No listenB. not listenC. don't listenD. No listening( ) 3. __________ times do you eat junk food a week?A. How oftenB. how manyC. how longD. how much( )4. I often help grandpa _______ the birds and animals.A. FeedingB. feedsC. to feedD. fed( )5.So _____ homework really make the students ______ tired.much: feel B. many feel C. much feeling D. many feels( )6-Dave! Your mom is too busy! You shouldn't throw your waste things everywhere!---Oh. I am sorry. I am going to_____________ and put them in the waste box.A. tale out the trashB. make the desk cleanC. fold my clothesD. do some shopping( ) 7. -Could you please go skating with me this afternoon?--Oh. I'd love to. But my sister is ill in bed and I have to _________her.A. take careB. take a walk withC. take care ofD. take out of( )8. ________ some money from himbut I will _________my bike to him in a few days.A. borrow, returnB. lend, borrowC. borrow, lendD. lend, keep( )9.Don't forget _________ when you leave.A. putting it onB. to put it onC. put on itD. to put on it( )10-Could I please use your pen? ---______________.A. with pleasureB. No, y ou can'tC. You shouldn't say thatD. You're polite( )11（2005年浙江丽水中考题）--Can you stay here for lunch? -Sorry, _________, I have to see my parents.A. can'tB. shouldn'tC. I mustn'tD. I won't( )12.（2005年山东泰安市中考题）--Can I get you a cup of tea? --__________.A. It's very nice of youB.With pleasureC. You can, pleaseD.That's all right( )13.（2005年广州市中考题）A neighbour helped to keep our dog. It _________while we were on holiday.A. was taken careB. took care ofC. is taken care ofD. was taken care of( )14.（2005年安徽省中考题）--Excuse me, could you help me carry the heavy box? ---____.A. Yes, I couldB. It doesn't matterC. With pleasureD.Don't mention it ( )15.（2005年福州市中考题）--I like the party so much, but I _______go home. It's too late.--What a pity!A. mustn'tB. have toC. mayD. can'tIII. 以所给词的正确形式填空（10分）1.Good food and exercise help me study__________(well) And practice __________(speak) English is good for my study.2.How often does Katrina___________( do )homework ? -Very often. She ialways has a lot of homework ___________(do)3.Who is the __________(good) English student?4.How about ___________(go ) to the sports camp next week?5.What did you_________(do) an hour ago? I ___________(feed) my dogs.6.They __________ (enjoy)________(them) at the English party yesterday.7.Listen. Can you hear the birds __________(sing) in the tree?8.It's good for your health__________(eat) a lot of fruit and vegetables. VI.翻译下列句子（15分）1.我不喜欢倒垃圾。

2006年普通高等学校招生全国统一考试理科数学（江西卷）一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知集合3{0}(1)xM xx =≥-，2{31,}N x y x x R ==+∈，则M N =A ．∅ B.{1}x x ≥ C.{1}x x > D.{01}x x x <≥或2.已知复数z 满足3)3i z i =，则z =A ．322- B.344i - C.322i + D.344+ 3.若0a >，0b >，则不等式1b a x-<<等价于 A.10x b -<<或10x a << B.11x a b-<<C.1x a <-或1x b >D.1x b <-或1x a>4.设O 为坐标原点，F 为抛物线24y x =的焦点，A 是抛物线上一点，若OA AF ⋅4=-，则点A 的坐标是A ．(2,± B.(1,2)± C.(1,2) D.(2, 5.对于R 上可导的任意函数()f x ，若满足(1)()0x f x '-≥，则必有 A.(0)(2)2(1)f f f +< B.(0)(2)2(1)f f f +≤ C.(0)(2)2(1)f f f +≥ C.(0)(2)2(1)f f f +>6.若不等式210x ax ++≥对于一切1(0,)2x ∈成立，则a 的取值范围是A ．0 B.2- C.52- D.3-7.已知等差数列{}n a 的前n 项和为n S ，若1200OB a OA a OC =+，且,,A B C 三点共线（该直线不过原点O ），则200S =A ．100 B.101 C.200 D.2018.在2006(x -的二项展开式中，含x 的奇次幂的项之和为S ，当x =S 等于A.23008B.23008-C.23009D.23009-9.P 是双曲线221916x y -=的右支上一点，M 、N 分别是圆22(5)4x y ++=和 22(5)1x y -+=上的点，则PM PN -的最大值为A.6B.7C.8D.910.将7个人（含甲、乙）分成三个组，一组3人，另两组2人，不同的分组数为a ，甲、乙分到同一组的概率为p ，则a 、p 的值分别为A.105a =，521p =B.105a =，421p =C.210a =，521p =D.210a =，421p =11.如图，在四面体ABCD 中，截面AEF 经过四面体的内切球（与四个面都相切的球）球心O ，且与BC ，DC 分别截于E 、F ，如果截面将四面体分成体积相等的两部分，设四棱锥A BEFD -与三棱锥A EFC -的表面积分别是1S ，2S ，则必有A.12S S <B.12S S >C.12S S =D.1S ，2S 的大小关系不能确定12.某地一年的气温()Q t （单位：C ）与时间t （月份）之间的关系如图（1）所示，已知该年的平均气温为10C ，令()G t 表示时间段[0,]t 的平均气温，()G t 与t 之间的函数关系用下列图象表示，则正确的应该是10C二、填空题：本大题共4小题，每小题4分，共16分.13.数列21{}41n -的前n 项和为n S ，则n lim n S →∞= .14.设3()log (6)f x x =+的反函数为1()f x -，若11[()6][()6]27f m f n --++=，则()f m n += .15.如图，在直三棱柱111ABC A B C -中，底面为直角三角形，90ACB ∠=，6AC =，1BC CC ==，P 是1BC 上一动点，则1CP PA +的最小值是 .16.已知圆M ：22(cos )(sin )1x y θθ++-=， 直线l ：y kx =，下面四个命题：A.对任意实数k 与θ，直线l 和圆M 相切；10C10C10CC(G t ABCPA 1B 1C 1B.对任意实数k 与θ，直线l 和圆M 有公共点；C.对任意实数θ，必存在实数k ，使得直线l 与和圆M 相切D.对任意实数k ，必存在实数θ，使得直线l 与和圆M 相切 其中真命题的代号是 .（写出所有真命题的代号）三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.17.（本小题满分12分）已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值.（Ⅰ）求a 、b 的值与函数()f x 的单调区间；（Ⅱ）若对[1,2]x ∈-，不等式2()f x c <恒成立，求c 的取值范围. 18.（本小题满分12分）某商场举行抽奖促销活动，抽奖规则是：从装有9个白球，1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出2个红球可获得奖金50元.现有甲，乙两位顾客，规定：甲摸一次，乙摸两次，令ξ表示甲，乙摸球后获得的奖金总额.求： （Ⅰ）ξ的分布列； （Ⅱ）ξ的的数学期望. 19.（本小题满分12分）如图，已知ABC ∆是边长为1的正三角形，M 、N 分别是边AB 、AC 上的点，线段MN 经过ABC ∆的中心G ，设MGA α∠=（233ππα≤≤）.（Ⅰ）试将AGM ∆、AGN ∆的面积（分别记为1S 与2S ），表示为α的函数； （Ⅱ）求221211y S S =＋的最大值与最小值.20.（本小题满分12分）如图，在三棱锥A BCD -中，侧面ABD 、ACD 是全等的直角三角形，AD 是公共的斜边，且AD =1BD CD ==，另一个侧面是正三角形AB CDMNα（Ⅰ）求证：AD BC ⊥； （Ⅱ）求二面角B AC D --的大小（Ⅲ）在直线AC 上是否存在一点E ，使ED 与面BCD 成30角？若存在，确定E 的位置；若不存在，说明理由.21.（本大题满分12分）如图，椭圆Q ：22221x y a b=＋（0a b >>）的右焦点(,0)F c ，过点F 的一动直线m绕点F 转动，并且交椭圆于A 、B 两点，P 是线段AB 的中点. （Ⅰ）求点P 的轨迹H 的方程.（Ⅱ）在Q 的方程中，令21cos sin a θθ=++，2sin b θ=（02πθ<<），确定θ的值，使原点距椭圆的右准线l 最远，此时，设l 与x 轴交点为D ，当直线m 绕点F 转动到什么位置时，三角形ABD 的面积最大？22、（本大题满分14已知数列{}n a 满足：132a =，且11321n n n na a a n --=+-，2n ≥，n N *∈.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）证明：对于一切正整数n ，不等式122!n a a a n ⋅⋅<⋅.ABCD。

2006年普通高等学校招生全国统一考试（江西卷）理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3至4页。

全卷满分150分，考试时间120分钟。

考生注意事项：1.答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。

2．答第Ⅰ卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

3．答第Ⅱ卷时，必须用0.5毫米墨水签字笔在答题卡上书写。

在试题卷上作答无效。

4．考试结束，监考人员将试题卷和答题卡一并收回。

参考公式：如果时间A 、B 互斥，那么()()()P A B P A P B +=+ 如果时间A 、B 相互独立，那么()()()P A B P A P B =如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率()()1n kk kn n P k C P P -=-球的表面积公式24S R π=，其中R 表示球的半径 球的体积公式343V R π=，其中R 表示球的半径第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合M ＝｛x|3x 0x 1≥（－）｝，N ＝｛y|y ＝3x 2＋1，x ∈R ｝，则M ⋂N ＝（ ） A ．∅ B. {x|x ≥1} C.｛x|x >1｝ D. {x| x ≥1或x <0}2、已知复数z 3i ）z ＝3i ，则z ＝（ ）A ．322 B. 344 C. 322 D.3443、若a >0，b >0，则不等式－b <1x<a 等价于（ ） A ．1b －<x <0或0<x <1a B.－1a <x <1b C.x <-1a 或x >1b D.x <1b －或x >1a4、设O 为坐标原点，F 为抛物线y 2＝4x 的焦点，A 是抛物线上一点，若OA F A ∙ ＝－4则点A 的坐标是（ ）A ．（2，±） B. (1，±2) C.（1，2）D.(2，)5、对于R 上可导的任意函数f （x ），若满足（x －1）f x '（）≥0，则必有（ ） A ． f （0）＋f （2）<2f （1） B. f （0）＋f （2）≤2f （1） B ． f （0）＋f （2）≥2f （1） C. f （0）＋f （2）>2f （1）6、若不等式x 2＋ax ＋1≥0对于一切x ∈（0，12〕成立，则a 的取值范围是（ ） A ．0 B. –2 C.-52D.-3 7、已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝（ ） A ．100 B. 101 C.200 D.201 8、在（x）2006的二项展开式中，含x 的奇次幂的项之和为S ，当x时，S 等于（ ） A.23008 B.-23008 C.23009 D.-230099、P 是双曲线22x y 1916－＝的右支上一点，M 、N 分别是圆（x ＋5）2＋y 2＝4和（x －5）2＋y 2＝1上的点，则|PM|－|PN|的最大值为（ ） A. 6 B.7 C.8 D.910、将7个人（含甲、乙）分成三个组，一组3人，另两组2 人，不同的分组数为a ，甲、乙分到同一组的概率为p ，则a 、p 的值分别为（ ） A ． a=105 p=521 B.a=105 p=421 C.a=210 p=521 D.a=210 p=42111、如图，在四面体ABCD 中，截面AEF 经过四面体的内切球（与四个面都相切的球）球心O ，且与BC ，DC 分别截于E 、F ，如果截面将四面体分成体积相等的两部分，设四棱锥A －BEFD 与三棱锥A －EFC 的表面积分别是S 1，S 2，则必有（ ）A. S 1<S 2B. S 1>S 2C. S 1=S 2D. S 1，S 2的大小关系不能确定 12、某地一年的气温Q （t ）（单位：ºc ）与时间t （月份）之间的关系如图（1）所示，已知该年的平均气温为10ºc ，令G （t ）表示时间段〔0,t 〕的平均气温，G （t ）与t 之间的函数关系用下列图象表示，则正确的应该是（ ）C理科数学第Ⅱ卷（非选择题 共90分）注意事项：请用0.5毫米黑色墨水签字笔在答题卡上书写作答，在试题卷上书写作答无效。

2006年普通高等学校招生全国统一考试（江西卷）理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3至4页。

全卷满分150分，考试时间120分钟。

考生注意事项：1.答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。

2．答第Ⅰ卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

3．答第Ⅱ卷时，必须用0.5毫米墨水签字笔在答题卡上书写。

在试题卷上作答无效。

4．考试结束，监考人员将试题卷和答题卡一并收回。

参考公式：如果时间A 、B 互斥，那么()()()P A B P A P B +=+如果时间A 、B 相互独立，那么()()()P A B P A P B =如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率()()1n k k kn n P k C P P -=- 球的表面积公式24S R π=，其中R 表示球的半径 球的体积公式343V R π=，其中R 表示球的半径第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合M ＝｛x|3x 0x 1≥（－）｝，N ＝｛y|y ＝3x 2＋1，x R ｝，则M N ＝（ ） A ． B. {x|x1} C.｛x|x 1｝ D. {x| x 1或x 0}2、已知复数z ＋3i ）z ＝3i ，则z ＝（ ）A ．32 B. 34 C. 32 D.34 3、若a0，b 0，则不等式－b 1x <a 等价于（ ） A ．1b －<x 0或0x 1a B.－1a <x 1b C.x -1a 或x 1b D.x 1b－或x1a4、设O 为坐标原点，F 为抛物线y 2＝4x 的焦点，A 是抛物线上一点，若OA F A ∙＝－4 则点A 的坐标是（ ）A ．（2，） B. (1，2) C.（1，2）D.(2，)5、对于R 上可导的任意函数f （x ），若满足（x －1）f x '（）≥0，则必有（ ） A ． f （0）＋f （2）2f （1） B. f （0）＋f （2）2f （1）B ． f （0）＋f （2）2f （1） C. f （0）＋f （2）2f （1）6、若不等式x 2＋ax ＋10对于一切x （0，12〕成立，则a 的取值范围是（ ） A ．0 B. –2 C.-52 D.-3 7、已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC ＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝（ ）A ．100 B. 101 C.200 D.2018、在（x）2006 的二项展开式中，含x 的奇次幂的项之和为S ，当x时，S 等于（ ）A.23008B.-23008C.23009D.-230099、P 是双曲线22x y 1916－＝的右支上一点，M 、N 分别是圆（x ＋5）2＋y 2＝4和（x －5）2＋y 2＝1上的点，则|PM|－|PN|的最大值为（ ）A. 6B.7C.8D.910、将7个人（含甲、乙）分成三个组，一组3人，另两组2 人，不同的分组数为a ，甲、乙分到同一组的概率为p ，则a 、p 的值分别为（ ）A ． a=105 p=521 B.a=105 p=421 C.a=210 p=521 D.a=210 p=42111、如图，在四面体ABCD 中，截面AEF 经过四面体的内切球（与四个面都相切的球）球心O ，且与BC ，DC 分别截于E 、F ，如果截面将四面体分成体积相等的两部分，设四棱锥A －BEFD与三棱锥A －EFC 的表面积分别是S 1，S 2，则必有（ ）A. S 1S 2B. S 1S 2C. S 1=S 2D. S 1，S 2的大小关系不能确定12、某地一年的气温Q （t ）（单位：ºc ）与时间t （月份）之间的关系如图（1）所示，已知该年的平均气温为10ºc ，令G （t ）表示时间段〔0,t 〕的平均气温，G （t ）与t 之间的函数关系用下列图象表示，则正确的应该是（ ）Ct理科数学第Ⅱ卷（非选择题 共90分）注意事项：请用0.5毫米黑色墨水签字笔在答题卡上书写作答，在试题卷上书写作答无效。

江西省2006年中等学校招生考试 数学试卷（大纲卷）说明：本卷共有六个大题，25个小题，全卷满分120分，考试时间120分钟．一、填空题（本大题共10小题，每小题3分，共30分）1．计算：23______-=．2．若m n ，互为相反数，则_______m n +=．3．在ABC △中，8060A B ==∠，∠，则_____C =∠． 4．如图，在矩形ABCD 中，12AB BC ==，，则_______AC =． 5．当3m <时，()23________m -=．6．若圆柱的底面半径为2cm ，高为3cm ，则它的侧面积是 2cm ．7．近视眼镜的度数()y 度与镜片焦距(m)x 成反比例，已知400度近视眼镜镜片的焦距为0.25m ，则y 与x 的函数关系式为 ．8．方程2101x x-=-的解是 ． 9．请在由边长为1的小正三角形组成的虚线网格中，画出一个．．所有顶点均在格点上，且至少．．有一条边为无理数的等腰三角形． 10．用黑白两种颜色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一列图案：（第4题）（第9题）第1个 第2个 第3个 …（1）第4个图案中有白色纸片张；（2）第n个图案中有白色纸片张．二、选择题（本大题共6小题，每小题3分，共18分）每小题只有一个正确选项，请把正确选项的代号填在题后的括号内．11．下列运算正确的是（）Ａ．22a a a+=Ｂ．232a a a=Ｃ．()224a a a÷=Ｄ．()22ab ab-=12．在平面直角坐标系中，点()32-，在（）Ａ．第一象限Ｂ．第二象限Ｃ．第三象限Ｄ．第四象限13．计算123-的结果为（）Ａ．3Ｂ．3Ｃ．33Ｄ．914．下列图案都是由字母“m”经过变形、组合而成的，其中不是．．中心对称图形的是（）15．某公司2003年缴税60万元，2005年缴税80万元，设该公司这两年缴税的年平均增长率为x，则得到方程（）Ａ．Ｂ．Ｃ．Ｄ．Ａ．60280x +=Ｂ．()60180x += Ｃ．26080x =Ｄ．()260180x += 16．如图，身高为1.6米的某学生想测量学校旗杆的高度，当他站在C 处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得 2.0AC =米，8.0BC =米，则旗杆的高度是（ ） Ａ．6.4米 Ｂ．7.0米Ｃ．8.0米 Ｄ．9.0米三、（本大题共3小题，第17小题6分，第18，19小题各7分，共20分）17．计算：()()()222x y y x y x --+-．18．已知关于x 的一元二次方程210x kx +-=．（1）求证：方程有两个不相等的实数根；（2）设方程的两根分别为12x x ，，且满足1212x x x x +=，求k 的值．19．如图，在平面直角坐标系中，点A 在第一象限，点B 的坐标为()30，，2OA =，60AOB =∠．（第16题）。

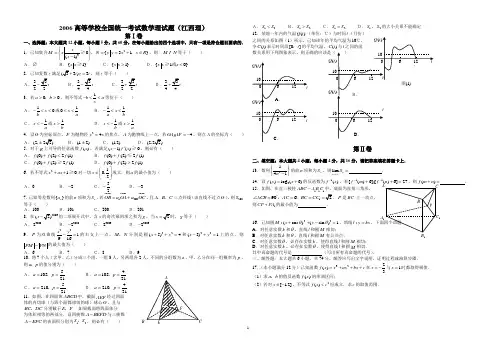
2006高等学校全国统一考试数学理试题（江西理）第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合230{31}(1)x M x N y y x x R x ⎧⎫===+∈⎨⎬-⎩⎭，，≥，则 M N 等于（ ） Ａ．∅ Ｂ．{1}x x ≥ Ｃ．{1}x x > Ｄ．{10}x x x <或≥2．已知复数z满足3)3i z i =，则z 等于（ ）Ａ．322-Ｂ．344-Ｃ．322+Ｄ．344+3．若00a b >>，，则不等式1b a x-<<等价于（ ）Ａ．10x b-<<或10x a<< Ｂ．11x a b-<<Ｃ．1x a<-或1x b>Ｄ．1x b<-或1x a>4．设O 为坐标原点，F 为抛物经24y x =的焦点，A 为抛物线上一点，若4OA AF =-，则点A 的坐标为（ ）Ａ．(2±， Ｂ．(12)±， Ｃ．(12)，Ｄ．(2 5．对于R 上可导的任意函数()f x ，若满足(1)()0x f x '-≥，则必有（ ） Ａ．(0)(2)2(1)f f f +< Ｂ．(0)(2)2(1)f f f +≤ Ｃ．(0)(2)2(1)f f f +≥Ｄ．(0)(2)2(1)f f f +>6．若不等式210x ax ++≥对一切102x ⎛⎤∈ ⎥⎝⎦，成立，则a 的最小值为（ ）Ａ．0Ｂ．2-Ｃ．52- Ｄ．3-7．已知等差数列{}n a 的前n 项和为n S ，若120O B aO A a O C =+，且A B C ，，三点共线（该直线不过点O ），则200S 等于（ ）Ａ．100 Ｂ．101 Ｃ．200 Ｄ．2018．在2006(x -的二项展开式中，含x 的奇次幂的项之和为S，当x =S 等于（ ）Ａ．30082Ｂ．30082-Ｃ．30092Ｄ．30092-9．P 为双曲线221916xy-=的右支上一点，M N ，分别是圆22(5)4x y ++=和22(5)1x y -+=上的点，则PM PN -的最大值为（ ）Ａ．6 Ｂ．7 Ｃ．8 Ｄ．910．将7个人（含甲、乙）分成三个组，一组3人，另两组各2人，不同的分组数为a ，甲、乙分在同一组概率为p ，则a p ，的值分别为（ ） Ａ．510521a p ==， Ｂ．410521a p ==，Ｃ．521021a p ==， Ｄ．421021a p ==， 11．如图，在四面体A B C D 中，截面AEF 经过四面 体的内切球（与四个面都相切的球）球心O ，且与 BC DC ，分别截于E F ，．如果截面将四面体分 为体积相等的两部分，设四棱锥A BEFD -与三棱锥A E F C -的表面积分别为12S S ，，则必有（ ）Ａ．12S S < Ｂ．12S S > Ｃ．12S S = Ｄ．1S ，2S 的大小关系不能确定12．某地一年内的气温()Q t之间的关系如图（1令()C t 表示时间段[0]t ，第Ⅱ卷二、填空题：本大题共4小题，每小题4分，共16分，请把答案填在答题卡上． 13．数列2141n ⎧⎫⎨⎬-⎩⎭的前n 项和为n S ，则lim n n S →∞= ． 14．设3()log (6)f x x =+的反函数为1()f x -，若11[()6][()6]27fm fn --++= ，则()f m n += ．15．如图，在直三棱柱111ABC A B C -中，底面为直角三角形，1906ACB AC BC CC ∠====，，．P 是BC 上一动点，则1C P PA +的最小值为 ．16．已知圆2:(cos )M x θ+2(sin )1y θ+-=，填线:l y kx =，下面四个命题 A ．对任意实数k 和θ，直线l 和圆M 相切；B ．对任意实数k 和θ，直线l 和圆M 有公共点；C ．对任意实数θ，必存在实数k ，使得直线l 和圆M 相切；D ．对任意实数k ，必存在实数θ，使得直线l 和圆M 相切． 其中真命题的代号是 （写出所有真命题的代号）．三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值．（1）求a b ，的值及函数()f x 的单调区间；（2）若对[12]x ∈-，，不等式2()f x c <恒成立，求c 的取值范围．ACP B1A1C 1B BE18．（本小题满分12分）某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出两个红球可获得奖金50元，现有甲、乙两位顾客，规定：甲摸一次，乙摸两次，令ξ表示甲、乙两人摸球后获得的奖金总额．求（1）ξ的分布列；（2）ξ的数学期望．19．（本小题满分12分）如图，已知A B C△是边长为1的正三角形，MM N经过A B C△的中心G，设2M G Aααππ⎛⎫= ⎪33⎝⎭≤≤．（1）试将AGM AGN，△△的面积（分别记为1S与2S）表示为α（2）求221211yS S=+的最大值与最小值．20．（本小题满分12分）如图，在三棱锥A B C D-中，侧面ABD ACD，是全等的直角三角形，A D是公共的斜边，且1AD BD C D===，另一侧面ABC是正三角形．（1）求证：AD BC⊥；（2）求二面角B A C D--的大小；（3）在线段A C上是否存在一点E，使E D与面BC D成30 角？若存在，确定点E的位置；若不存在，说明理由．21．（本小题满分12分）如图，椭圆2222:1(0)x yQ a ba b+=>>的右焦点为(0)F c，，过点F的一动直线m绕点F转动，并且交椭圆于A B，两点，P为线段A B的中点．（1）求点P的轨迹H的方程；‘（2）若在Q的方程中，令221cos sin sin0a bθθθθπ⎛⎫=++=<⎪2⎝⎭，≤．确定θ的值，使原点距椭圆Q的右准线l最远．此时，设l与x轴交点为D，当直线m绕点F转动到什么位置时，三角形ABD的面积最大？22．（本小题满分14分）已知数列{}na满足：132a=，且113(2)21nnnnaa n na n*--=∈+-N，≥．（1）求数列{}na的通项公式；（2）证明：对一切正整数n，不等式122!na a a n<恒成立．ABCDB D2006高等学校全国统一考试数学理试题理（江西）参考答案一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

2006年普通高等学校夏季招生考试数学(理工农医类)江西卷(新课程)第Ⅰ卷一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合M={x|0)1(3≥-x x }，N={y|y=3x 2+1，x ∈R},则M ∩N 等于 A. B.{x|x ≥1} C ．{x|x ＞1} D ．{x|x ≥1或x ＜0} 2．已知复数z 满足(3+3i)z=3i ，则z 等于A ．2323-i B. 4343-i C ．i 2323+ D ．4343+i 3．若a ＞0，b ＞0则不等式-b ＜x1＜a 等价于 A ．-b 1＜x ＜0或0＜x ＜a 1 B ．-a 1＜x ＜b 1C. x ＜-a 1或x ＞b 1D. x ＜-b 1或x ＞a14．设O 为坐标原点，F 为抛物线y 2=4x 的焦点，A 为抛物线上一点，若AF OA ∙=-4，则点A 的坐标为A ．(2，±22)B ．(1，±2)C ．(1，2)D ．(2，22) 5．对于R 上可导的任意函数f(x)，若满足(x-1)f ′(x)≥0，则必有A ．f(0)+f(2)＜2f(1)B ．f(0)+f(2)≤2f(1) C. f(0)+f(2)≥2f(1) D ．f （0）+f(2)＞2f(1) 6．若不等式x 2+ax+l ≥0对一切x ∈(0，21]成立，则a 的最小值为A ．0 B.-2 C ．-25D ．-3 7．已知等差数列{a n }的前n 项和S n ，若OB =a 1OA +a 200，且A 、B 、C 三点共线(该直线不过点O)，则S 200等于A ．100B ．101C ．200D ．201 8．在(x-2)2006的二项展开式中，含x 的奇次幂的项之和为S ，当x=2时，S 等于A ．23008B ．-23008C ．23009D ．-230099.P 为双曲线16922y x -=1的右支上一点,M 、N 分别是圆(x+5)2+y 2=4和(x-5)2+y 2=1上的点，则|PM|-|PN|的最大值为A ．6B ．7C ．8D ．910．将7个人(含甲、乙)分成三个组，一组3人，另两组各2人，不同的分组数为a,甲、乙分在同一组的概率为p,则a 、p 的值分别为 A ．a=105，p=215 B ．a=105，P=214 C ．a=210，p=215 D ．a=210，p=214 11．如图，在四面体ABCD 中，截面AEF 经过四面体的内切球(与四个面都相切的球)球心O ，且与BC 、DC 分别截于E 、F.如果截面将四面体分为体积相等的两部分，设四棱锥A-BEFD 与三棱锥A-EFC 的表面积分别为S 1、S 2，则必有A ．S 1＜S 2B ．S 1＞S 2C ．S 1=S 2D ．S 1、S 2的大小关系不能确定12．某地一年内的气温Q(t)(单位：℃)与时间t(月份)之间的关系如图(1)所示，已知该年的平均气温为10℃．令C(t)表示时间段［0，t ］的平均气温，C(t)与t 之间的函数关系用下列图象表示，则正确的应该是第Ⅱ卷二．填空题：本大题共4小题，每小题4分，共16分。

2006年江西省重点中学高考第一次联考理科数学试卷参考答案一、选择题（每小题5分，共12×5分＝60分） 1. A 2. D 3. B 4. C 5. C6. A7. D8. C9. A10. A 11. C 12. B二、填空题（每小题4分，共4×4分=16分） 13. 2π14. －2≤a ≤－1或0≤a ≤1 15. a n =2n+1（n ∈N*） 16. （1），（2）三、解答题（共6小题，总分76分）17. （1）BC=BAC AC AB AC AB ∠⋅⋅-+cos 222=132分cosB=BC AB AC BC AB ⋅-+2222=131>05分（2）∵cosB>0，∴B 为锐角，sinB=1332 7分∵－π<B+x<2π，cos （B+x ）=－1310 < 0 ∴－π<B+x<2π-，∴sin （B+x ）=－1339分 ∴cosx=cos[（B+x ）－B]= … =－13106+ 12分 18. （1） P （ξ=7）=351222C C C =51，P （ξ=8）= 3512221122C C C C C +=103， P （ξ=9）=35111212C C C C =52， P （ξ=10）=351122C C C =1017分 E ξ=8.4 8分 （2）信息畅通的概率P 1=P （ξ=10） =10110分信息基本畅通的概率P 2=P （ξ=8或ξ=9）=10712分 19. （1） ∵DE ⊥平面ACD ，∴DE ⊥AF又∵AC=AD=CD ，F 为CD 的中点∴AF ⊥CD ∴AF ⊥平面CDE 4分（2）取DE 的中点G ，连AG 、CG ，则∠CAG 或其补角就是异面直线AC 、BE 所成角 6分 由题设可以求出：CG=AG =5a ，AC=2a∵cos ∠CAG=AG AC CG AG AC ⋅-+2222=55∴异面直线AC 、BE 所成角的余弦值为558分 （2）延长DA 、EB 交于H 点，连CH ， 则CH ∥AF ， 又由AF ⊥平面DCE ，故HC ⊥平面DCE ，从而∠DCE 就是平面BCE 和平面ACD 所成锐二面角 10分 由平面几何知：△CDE 为等腰直角三角形 ∴∠DCE=45°∴平面BCE 和平面ACD 所成锐二面角为45° 12分 注：采用向量法求解答题各小问的得分给出相应分数。

这七种方法不伤身体又不用长期坚持的减肥方法1、黄瓜鸡蛋法每餐只吃黄瓜和鸡蛋，代替3餐，坚持7天，包你瘦，不过到时你就会特别想念老干妈的味道了。

是很好的刮油办法。

原理：黄瓜果肉脆甜多汁，清香可口，它含有胶质、果酸和生物活性酶，可促进机体代谢，能治疗晒伤、雀斑和皮肤过敏。

黄瓜还能清热利尿、预防便秘。

新鲜黄瓜中含有的丙醇二酸，能有效地抑制糖类物质转化为脂肪，因此，常吃黄瓜对减肥和预防冠心病有很大的好处。

>>>减肥：这样吃黄瓜有害健康2、过午不食法超过下午三点不吃任何东西，当然能吃的时候也不能猛吃啊，这样一周可以瘦几公斤。

原理：夜间休息，人体消耗的能量较少，摄入的过多能量用以变成脂肪囤积起来。

此法的注意事项是早餐和午餐必须吃饱吃好，补充一天所必须的营养物质。

健康提示：如果实在饿得慌，可以多喝水，或者吃一个苹果。

3、不吃正餐法每天少吃正餐，把豆浆作为三餐的一部分，女孩子喝了很有好处的，不过注意是无糖的哦，最好自己买台豆浆机，每天自己打，方便又便宜。

原理：豆浆主要榨取了含有丰富高优质植物性蛋白质的大豆，除了大豆蛋白质，还含有大量的大豆异黄酮(Isoflavone)、大豆配醣体(Saponin)等成份。

这些成份可以抑制吸收体内的脂质和醣类，发挥燃烧体脂肪的效果。

因此从饮用豆浆的那一刻起，经过消化→吸收→燃烧脂肪的各个阶段，这些有效成份可都正在发挥瘦身效果呢！>>>四大密技巧喝豆浆轻松减肥4、苹果减肥法吃2天苹果然后正常节制的饮食3天，这样几个周期循环，效果不错。

原理：肥胖者几乎都是因过食而使胃部扩张，无法控制食欲。

苹果减肥法能使胃部收缩，减肥后食欲变得容易控制，而且味觉变正常，不会喜欢刺激性食物或油腻食物。

苹果减肥可以促进血液内白血球的生成，提高人体的抵抗力和免疫力，同时促进神经和内分泌功能，有助美容养颜。

吃苹果减肥的好处是不必挨饿，肚子饿就吃苹果。

因为它是低热量食物，无论吃多少，都不会比日常生活所摄取的热量还多，所以体重自然减轻。

绝密★启用前2006年普通高等学校招生全国统一考试理科综合能力测试本试卷分第I卷（选择题）和第a卷（非选择题）两部分。

第I卷1至4页，第Ⅱ卷5至8页。

考试结束后，将本试题卷和答题卡一并交回。

第I卷注愈事项：1.答题前，考生在答题卡上务必用黑色签字笔将自己的姓名、准考证号填写清楚，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目。

2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效．3本卷共21小题，每小题6分，共126分。

以下数据可供解题时参考：相对原子质量（原子量）：H 1 C 12 N 14 O 16一、选择题（本题包括13小题。

每小题只有一个选项符合题意）1.人的神经系统中，有些神经细胞既能传导兴奋，又能合成分泌激素。

这些细胞位于A.大脑皮层B. 垂体C. 下丘脑D. 脊髓2.一般情况下，用抗原免疫机体，血清中抗体浓度会发生相应变化。

如果第二次免疫与第一次免疫所用的抗原相同且剂量相等，下列四图中能正确表示血清中抗体浓度变化的是3.下列关于动物细胞培养的叙述，正确的是A.培养中的人效应T细胞能产生单克隆抗体B.培养中的人B 细胞能够无限地增殖C.人的成熟红细胞经过培养能形成细胞株D.用胰蛋白酶处理肝组织可获得单个肝细胞4.锄足蟾蝌蚪、雨蛙蝌蚪和蟾蜍蝌蚪均以浮游生物为食。

在条件相同的四个池塘中，每池放养等量的三种蝌蚪，各池蝌蚪总数相同。

再分别在四个池塘中放入不同数量的捕食者水螈。

一段时间后，三种蝌蚪数量变化结果如图。

下列分析，错误．．的是A.无水螈的池塘中，锄足蟾蝌蚪数量为J 型增长B.三种蝌蚪之间为竞争关系C.水螈更喜捕食锄足蟾蝌蚪D.水螈改变了三种蝌蚪间相互作用的结果5.采用基因工程技术将人凝血因子基因导入山羊受精卵，培育出了转基因羊。

但是，人凝血因子只存在于该转基因羊的乳汁中。

以下有关叙述，正确的是A.人体细胞中凝血因子基因编码区的碱基对数目，等于凝血因子氨基酸数目的3倍B.可用显微注射技术将含有人凝血因子基因的重组DNA 分子导入羊的受精卵C.在转基因羊中，人凝血因子基因存在于乳腺细胞，而不存在于其他体细胞中D.人凝血因子基因开始转录后，DNA 连接酶以DNA 分子的一条链为模板合成mRNA6.在常温常压下呈气态的化合物，降温使其固化得到的晶体属于A.分子晶体B.原子晶体C.离子晶体D.何种晶体无法判断7.下列叙述正确的是A.同一主族的元素，原子半径越大，其单质的熔点一定越高B.同一周期元素的原子，半径越小越容易失去电子C.同一主族的元素的氢化物，相对分子质量越大，它的沸点一定越高D.稀有气体元素的原子序数越大，其单质的沸点一定越高8.用A N 代表阿伏加德罗常数，下列说法正确的是A.0.5molAl 与足量盐酸反应转移电子数为1A NB.标准状况下，11.2L 3SO 所含的分子数为0.5A NC.0.1mol 4CH 所含的电子数为1A ND.46g 2NO 和24N O 的混合物含有的分子数为1A N9.把分别盛有熔融的氯化钾、氯化镁、氯化铝的三个电解槽串连，在一定条件下通电一段时间后，析出钾、镁、铝的物质的量之比为A. 1:2:3B. 3:2:1C.6:3:1D. 6:3:210. 浓度均为0.1mol·L-1的三种溶液等体积混和，充分反映后没有沉淀的一组溶液是A. BaCl2 NaOH NaHCO3B. Na2CO3 MgCl2 H2SO4C. AlCl3 NH3·H2O NaOHD. Ba(OH)2CaCl2Na2SO411.在0.1mol·L-1CH3COOH溶液中存在如下电离平衡：CH3COOH CH3COO-+H+对于该平衡，下列叙述正确的是A.加入水时，平衡向逆反应方向移动B.加入少量NaOH固体，平衡向正反应方向移动C.加入少量0.1mol·L-1HCl溶液，溶液中c（H+）减小D.加入少量CH3COONa固体，平衡向正反应方向移动12. 茉莉醛具有浓郁的茉莉花香，其结构简式如下所示：关于茉莉醛的下列叙述错误的是A.在加热和催化剂作用下，能被氢气还原B.能被高锰酸钾酸性溶液氧化C.在一定条件下能与溴发生取代反应D.不能与氢溴酸发生加成反应13.由硫酸钾、硫酸铝和硫酸组成的混和溶液，其pH＝1，c（Al3+）＝0.4mol·L-1，c（SO42-）＝0.8mol·L-1，则c（K+）为A.0.15mol·L-1B.0.2mol·L-1C.0.3mol·L-1D.0.4mol·L-1二、选择题（本题包括8小题。