CFD网格及其生成方法概述

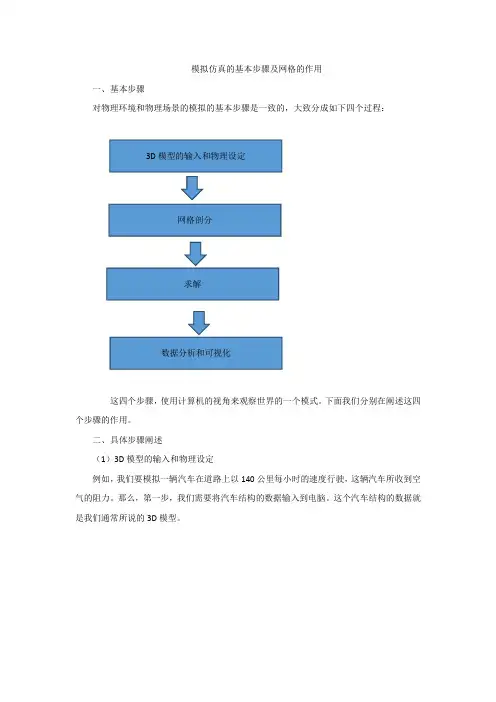
模拟仿真的基本步骤及网格的作用一、基本步骤对物理环境和物理场景的模拟的基本步骤是一致的，大致分成如下四个过程：3D模型的输入和物理设定网格剖分求解数据分析和可视化这四个步骤，使用计算机的视角来观察世界的一个模式。

下面我们分别在阐述这四个步骤的作用。

二、具体步骤阐述（1）3D模型的输入和物理设定例如，我们要模拟一辆汽车在道路上以140公里每小时的速度行驶，这辆汽车所收到空气的阻力。

那么，第一步，我们需要将汽车结构的数据输入到电脑。

这个汽车结构的数据就是我们通常所说的3D模型。

同时，我们还需要给这个汽车一个形式的空间。

通常，由于模拟数据是和风洞试验对比的，我们仍然称这个空间为风洞，只是为了区分，我们称之为数值风洞。

因为它是虚拟的。

风洞的形状通常会是一个方形的。

这样就准备好了我们需要的在结构上的数据。

但是如何和实际的汽车行驶对应起来呢？我们还需要告诉计算机哪个模型是汽车，哪个模型是风洞，他们对应现实中的什么物理特性？例如汽车的轮子是旋转的，汽车的表面会阻碍风的流动等等。

这个步骤称为物理设定。

（2）网格剖分刚才我们已经在计算机里输入了3D模型，并且做了物理属性的设定。

实际上在风洞内包含了风洞的墙，汽车的表面，还有空气。

这些物质的运动是我们需要模拟的。

为了模拟出这些物质的运动，我们需要把这个空间拆分成数千万的小多面体。

每个多面体对应这些物质的一部分，然后进行计算。

将这个空间拆分成数千万小多面体并与物质对应起来的过程，称为网格剖分。

而剖分出来的表征空间和物质的千万个小多面体整体称为网格。

（3）求解有了3D模型，有了物理特性，有了网格剖分，我们就可以建立数学模型实际上是一个方程，进行求解。

这个过程，我们也称为求解。

求解之后，我们就可以获得这个方程的一个解。

这个解，我们可以理解成一个通俗的说法，就是答案。

因为我们希望通过计算的计算来得到汽车在公路上行驶的时候，它的气流分布的答案。

（4）数据分析与可视化经过求解之后，我们获得的答案是一堆数据。

网格生成及修正技巧1引言网格是CFD 模型的几何表达形式，也是模拟与分析的载体。

网格质量对CFD 计算精度和计算效率有着重要的影响。

对于复杂的CFD 问题，网格的生成极为耗时，并且极易出错，生成网格所需的时间常常大于实际CFD 计算的时间。

因此，有必要对网格生成以及修正方法进行足够的研究。

考虑到目前的CFD 计算多是通过专用的网格生成软件来划分所需要的网格，因此，本文就如何利用专用前处理软件GAMBIT 来介绍网格的生成和修正技巧。

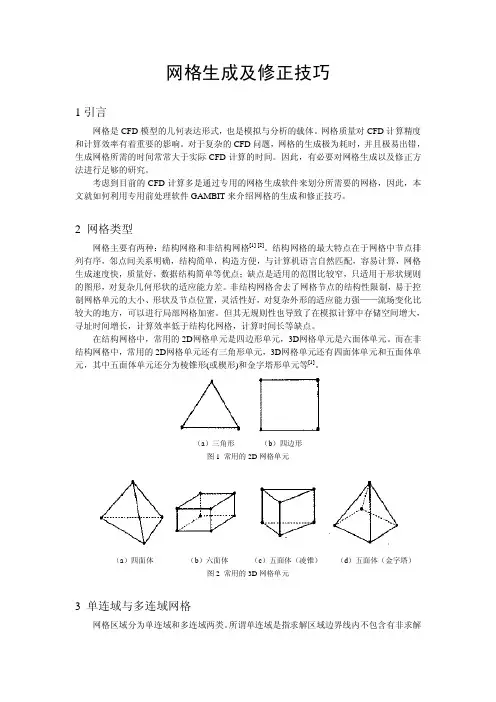
2 网格类型网格主要有两种：结构网格和非结构网格[1] [2]在结构网格中，常用的2D 网格单元是四边形单元，3D 网格单元是六面体单元。

而在非结构网格中，常用的2D 网格单元还有三角形单元，3D 网格单元还有四面体单元和五面体单元，其中五面体单元还分为棱锥形(或楔形)和金字塔形单元等。

结构网格的最大特点在于网格中节点排列有序，邻点间关系明确，结构简单，构造方便，与计算机语言自然匹配，容易计算，网格生成速度快，质量好，数据结构简单等优点；缺点是适用的范围比较窄，只适用于形状规则的图形，对复杂几何形状的适应能力差。

非结构网格舍去了网格节点的结构性限制，易于控制网格单元的大小、形状及节点位置，灵活性好，对复杂外形的适应能力强——流场变化比较大的地方，可以进行局部网格加密。

但其无规则性也导致了在模拟计算中存储空间增大，寻址时间增长，计算效率低于结构化网格，计算时间长等缺点。

[1]。

（a ）三角形 （b ）四边形图1 常用的2D网格单元（a ）四面体 （b ）六面体 （c ）五面体（凌锥） （d ）五面体（金字塔）图2 常用的3D 网格单元3 单连域与多连域网格网格区域分为单连域和多连域两类。

所谓单连域是指求解区域边界线内不包含有非求解区域的情形。

如果在求解区域内包含求解区域，则称该求解区域为多连域。

所有的绕流流动，都属于典型的多连域问题，其网格主要有O 型和C 型两种[1]。

cfd仿真过程的主要步骤CFD（Computational Fluid Dynamics）仿真是一种通过计算流体的数值模拟方法来研究流体力学问题的技术。

它能够精确地预测流体的物理行为，并在实际应用中发挥重要作用。

本文将介绍CFD仿真过程的主要步骤，以帮助读者了解该技术的基本原理和应用。

第一步：建立几何模型CFD仿真的第一步是建立几何模型。

在进行仿真前，需要收集实际问题的相关数据，并据此创建一个三维几何模型。

这可以通过计算机辅助设计（CAD）软件或其他三维建模软件完成。

建立几何模型时需要考虑问题的尺寸、形状和边界条件等因素。

第二步：离散网格生成离散化是CFD仿真的关键步骤之一。

在此步骤中，需要将连续流体域分割成离散网格。

这些网格通常是由简单的几何形状（如立方体或六面体）构成的。

离散网格的精度和分辨率将直接影响到仿真结果的准确性。

第三步：物理建模与边界条件设定在进行CFD仿真之前，需要选择适当的物理模型和设定边界条件。

物理模型可以是基于连续介质力学的Navier-Stokes方程，也可以是基于稀薄气体动力学的Boltzmann方程等。

边界条件包括入口和出口条件、壁面条件、对称条件等。

物理建模和边界条件的选择将决定仿真的结果和准确性。

第四步：数值求解在CFD仿真中，需要使用数值方法对所选的物理模型进行求解。

常用的数值方法包括有限差分法、有限元法和有限体积法等。

这些方法将选择的物理模型转化为离散形式的数值模型，并使用迭代算法来求解流体问题。

第五步：边界条件调整和预处理在进行数值求解之前，通常需要对网格进行预处理，以提高计算效率和准确性。

此外，边界条件和物理模型也需要进行调整和验证，以确保仿真结果的合理性。

第六步：数值模拟和结果分析在对CFD仿真进行数值求解之后，可以开始进行数值模拟和结果分析。

通过对仿真结果的可视化和定量分析，可以了解流体的流动特性、压力分布、速度场等信息。

这对于解决实际问题、优化设计和改进工艺具有重要意义。

CFD网格的分类,如果按照构成形式分,可以分为结构化和非结构化结构化:只能有六面体一种网格单元,六面体顾名思义,也就是有六个面,但这里要区分一下六面体和长方体。

长方体(也就是所有边都是两两正交的六面体)是最理想完美的六面体网格。

但如果边边不是正交,一般就说网格单元有扭曲(skewed).但绝大多数情况下,是不可能得到完全没有扭曲的六面体网格的。

一般用skewness 来评估网格的质量, sknewness=V/(a*b*c).这里V是网格的体积,a,b,c是六面体长,宽和斜边。

sknewness越接近1,网格质量就越好。

很明显对于长方体,sknewness=1.那些扭曲很厉害的网格, sknewness很小。

一般说如果所有网格sknewness>0.1也就可以了。

结构化网格是有分区的。

简单说就是每一个六面体单元是有它的坐标的,这些坐标用,分区号码(B),I,J,K四个数字代表的。

区和区之间有数据交换。

比如一个单元,它的属性是B=1, I=2,J=3,K=4。

其实整个结构化单元的概念就是CFD计算从物理空间到计算空间mapping的概念。

I,J,K可以认为是空间x,y,z 在结构化网格结构中的变量。

三维网技术论坛! p9 T0 u2 z+ @, i6 c非机构化:可以是多种形状,四面体(也就三角的形状),六面体,棱形。

对任何网格,都是希望网格单元越规则越好,比如六面体希望是长方形,对于四面体,高质量的四面体网格就是正四面体。

sknewness的概念这里同样适用,sknewness越小,网格形状相比正方形或者正四面体就越扭曲。

越接近1就越好。

很明显非结构化网格也可以是六面体,但非结构化六面体网格没有什么B,IJK 的概念,他们就是充满整个空间。

对于复杂形状,结构化网格比较难以生成。

主要是生成时候要建立拓扑,拓扑是个外来词,英语是topology,所以不要试图从字面上来理解它的意思。

其实拓扑就是指一种有点和线组成的结构。

CFD是什么技术2008-09-10 09:42【CFD是什么技术】CFD是英文Computational Fluid Dynamics（计算流体动力学）的简称。

它是伴随着计算机技术、数值计算技术的发展而发展的。

简单地说，CFD相当于"虚拟"地在计算机做实验，用以模拟仿真实际的流体流动情况。

而其基本原理则是数值求解控制流体流动的微分方程，得出流体流动的流场在连续区域上的离散分布，从而近似模拟流体流动情况。

即CFD=流体力学+热学+数值分析+计算机科学。

流体力学研究流体（气体与液体）的宏观运动与平衡，它以流体宏观模型作为基本假说。

流体的运动取决于每个粒子的运动，但若求解每个粒子的运动即不可能也无必要。

计算流体动力学概述1 什么是计算流体动力学计算流体动力学（Computational Fluid Dynamics，简称CFD）是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析。

CFD的基本思想可以归结为：把原来在时间域及空间域上连续的物理量的场，如速度场和压力场，用一系列有限个离散点上的变量值的集合来代替，通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组，然后求解代数方程组获得场变量的近似值CFD可以看做是在流动基本方程（质量守恒方程飞动量守恒方程、能量守恒方程）控制下对流动的数值模拟。

通过这种数值模拟，我们可以得到极其复杂问题的流场内各个位置上的基本物理量（如速度、压力、温度、浓度等）的分布，以及这些物理量随时间的变化情况，确定旋涡分布特性、空化特性及脱流区等。

还可据此算出相关的其他物理量，如旋转式流体机械的转矩、水力损失和效率等。

此外，与CAD联合，还可进行结构优化设计等。

CFD方法与传统的理论分析方法、实验测量方法组成了研究流体流动问题的完整体系，图1给出了表征三者之间关系的“三维”流体力学示意图理论分析方法的优点在于所得结果具有普遍性，各种影响因素清晰可见，是指导实验研究和验证新的数值计算方法的理论基础。

文章编号: 1005 0329(2010)04 0032 06技术进展流体机械CFD中的网格生成方法进展刘厚林,董 亮,王 勇,王 凯,路明臻(江苏大学,江苏镇江 212013)摘 要: 网格生成技术是流体机械内部流动数值模拟中的关键技术之一,直接影响数值计算的收敛性,决定着数值计算结果最终的精度及计算过程的效率;本文在分析大量文献的基础上,首先,对流体机械CFD中的网格生成方法即结构化网格、非结构化网格、混合网格进行了比较全面的总结,系统地分析这些网格划分方法的机理、特点及其适用范围;其次,对特殊的网格生成技术,如曲面网格生成技术、动网格技术、重叠网格生成技术、自适应网格技术进行了阐述;再次,指出了良好的网格生成方法应具备的特点;最后提出了网格生成技术的发展趋势。

关键词: 流体机械;网格生成;计算流体动力学;动网格;自适应网格中图分类号: TH311 文献标识码: A do:i10.3969/.j i ssn.1005-0329.2010.04.008Overvie w onM esh Generati o n M et hods i n CF D of F lui d M achineryL IU H ou-lin,DONG L iang,W ANG Y ong,W ANG K a,i LU M i ng-zhen(Jiangsu U n i v ers it y,Zhenji ang212013,Ch i na)Abstrac t: M esh genera ti on techno logy i s one of the cr iti ca l technology f o r fl u i d m ach i nery fl ow nume rica l s i m u l at-i on,and d-i rectly i nfl uence t he astr i ngency o f nume rical si m u l a ti on,wh ich has an i m portan t e ffect on the nu m er ica l s i m u l a tion results,fi na l precision and the effi c i ency o f compu tati onal process.O n the bas i s o f analyzi ng a great dea l litera t ures,firstl y,m esh genera ti on m ethods and t heory of fluid m ach i nery are comprehens i ve l y su mm ar i zed such as structured mesh,unstructured mesh,hybrid gr i d and respecti ve re lati ve m erits and the pr i nciple,charac teristcs and scopes of t hese m ethods we re sy stema ti ca lly ana l ysed.Second-ly,Spec i a lm esh generation m ethod w ere su mm ar i zed,such as surface m eshi ng,m ov ing gr i d,adapti ve gr i d and especiall y i ntro-duced the pr i nci p le and app licati on areao f adapti ve g ri d.T h irdly,the character i sti c o f m esh g enerati on m e t hod w ere pion ted out.F i na lly,t he trends of mesh generati on are presen ted,and the tre m endous d ifference i s analyzed i n mesh au t om atic gene ra tion at a-broad and the necessary o f exp l o iti ng CFD soft w are and resea rchi ng the m esh auto m atic gene ration techn i que i n our country are put forwa rd.K ey word s: fl uids m achi nery;m esh g enerati on;co m puta ti ona l fl u i d dyna m ics;mov i ng gr i d;adaptive gr i d1 前言计算流体动力学(CFD)中,按一定规律分布于流场中的离散点的集合叫网格,产生这些节点的过程叫网格生成。

CFD网格及其生成方法概述网格是CFD模型的几何表达形式，也是模拟与分析的载体。

网格质量对CFD计算精度和计算效率有重要影响。

对于复杂的CFD问题，网格生成极为耗时，且极易出错，生成网格所需时间常常大于实际CFD计算的时间。

因此，有必要对网格生成方式给以足够的关注。

1 网格类型网格（grid）分为结构网格和非结构网格两大类。

结构网格即网格中节点排列有序、邻点间的关系明确。

对一于复杂的儿何区域，结构网格是分块构造的，这就形成了块结构网格（block-structured grids）。

与结构网格不同，在非结构网格（unstructured grid）中，节点的位置无法用一个固定的法则予以有序地命名。

这种网格虽然生成过程比较复杂，但却有着极好的适应性，尤其对具有复杂边界的流场计算问题特别有效。

非结构网格一般通过专门的程序或软件来生成。

2 网格单元的分类单元（cell）是构成网格的基本元素。

在结构网格中，常用的ZD网格单元是四边形单元，3D网格单元是六面体单元。

而在非结构网格中，常用的2D网格单元还有三角形单元，3D网格单元还有四面体单元和五面体单元，其中五面体单元还可分为棱锥形（或楔形）和金字塔形单元等。

3 单连域与多连域网格网格区域（cell zone）分为单连域和多连域两类。

所谓单连域是指求解区域边界线内不包含有非求解区域的情形。

单连域内的任何封闭曲线都能连续地收缩至点而不越过其边界。

如果在求解区域内包含有非求解区域，则称该求解区域为多连域。

所有的绕流流动，都属于典型的多连域问题，如机翼的绕流，水轮机或水泵内单个叶片或一组叶片的绕流等。

均是多连域的例子。

对于绕流问题的多连域内的网格，有O型和C型两种。

O型网格像一个变形的圆，一圈一圈地包围着翼型，最外层网格线上可以取来流的条件，如图6所示。

C型网格则像一个变形的C字，围在翼型的外面，如图7所示。

这两种网格部属于结构网格。

4 生成网格的过程无论是结构网格还是非结构网格，都需要按下列过程生成网格：（1）均建立几何模型。

cfd fluent处理流程CFD Fluent是一种流体力学仿真软件，具有广泛的应用领域，包括空气动力学，热传递，生物医学，化学反应和水力学等方面。

它被广泛地用于有效的流体力学仿真，可以用于设计和优化任何流场，从而提高产品的效率和性能。

在本文中，我们将讨论一个完整的CFD Fluent处理流程，以帮助您更好地了解这个强大的工具的操作和应用。

第一步：准备模型在处理流程中的第一步是准备需要仿真的模型。

这个步骤可以从CAD格式等其他格式导入。

在引进我们将要仿真的物体之后，需要对CAD图形进行优化。

这包括清理冗余网格及小细节，从而减少网格数量，以更好地优化仿真结果。

第二步：生成网格生成网格是流体力学仿真的最关键部分之一。

在此步骤中，需要将模型分割成小网格，以便能够对流体力学进行精细分析。

简单来说，CFD Fluent处理流程中，网格分成小菱形，由大量相互排列的三角形组成，来构建网格。

第三步：定义流体和边界条件之后是定义流体和边界条件，确定流体将如何运动和处理。

在此步骤中，我们需要定义模拟的流体，包括温度，密度，黏性等参数。

同时，我们还需要设置边界条件，主要包括流体入口和出口，墙壁，旋转部件等。

这有助于我们了解流体临界参数、流量、速度、压力等等。

第四步：运行仿真完成准备工作之后，我们可以开始运行仿真。

在CFD Fluent处理流程中，仿真运行需要耗费大量时间，因此需要运用高性能的计算器。

随着仿真的运行，可以查看CFD Fluent中不同的仿真参数，包括曲线图，等值图以及动画。

通过这些图形，可以迅速了解流体在不同时间和空间位置的变化。

第五步：结果分析最后一步是结果分析。

根据仿真的结果，可以调整流体力学细节，在不同的参数下对结果进行分析并比较，明确出最优结果。

CFD Fluent处理流程的步骤已经介绍完了，从以上可看出CFD Fluent需要专业的知识和技能。

总的来说，了解整个流程可以使我们更好地掌握CFD Fluent的操作，从而更好地应用于实际问题的解决。

汽车CFD分析中空间网格的生成作者：湖南大学吴军谷正气钟志华摘要：本文详细叙述了运用椭圆型方程构造三维空间结构化网格的方法，并采用其为汽车CFD （computer fluid dynamic）分析生成了结构化的贴体正交网格。

关键词：CFD 贴体正交网格椭圆型方程1 引言在汽车空气动力学中对于外流场计算时，其空间求解域数值网格的构造品质无疑对其计算速度、精度及收缩性都有着十分重要的意义。

1966 年，Winslow 首先采用Laplace 方程来构造网格，用这种方法构造的网格具有分布均匀，适应性强的特点。

1970 年，Barfield W.D 提出了用变分法来构造网格的思想，即给出某种度量网格性质的泛函，通过求泛函极小构造网格。

1971 年，由W.H.Chu提出，F.Thomas首次应用贴体坐标的概念。

1974 年，Thompson 提出数值求解微分方程生成网格的方法，近年来这种方法也得到了广泛应用。

1982 年，Brackbill J.U.和Saltzman J.S.给出了多种描述网格性质(正交性、光滑性、体积)的泛函文献。

1988 年，Antonios E.G.提出了一种带方向控制的泛函来控制网格线走向的方法。

2 数值网格生成的理论基础数值网格生成就是用数值方法在物理区域内建立一个适当的曲线坐标系，以坐标线相交形成计算网格，网格线光滑分布并与物理边界一致，在边界上网格线正交，并且网格线分布能自动适应物理解变化情况。

实质上网格生成可视为一种坐标变换，即寻求笛卡尔坐标(X,Y,Z)和曲线坐标(x,h,z)之间的变化关系，把物理区域变换为计算域内一个或多个矩形(或长方体)区域。

对于具有复杂形状的区域，可以采用曲线坐标系，并使物面与坐标系内某一坐标线(或面)相吻合，该坐标系可正交，也可非正交，网格的分布是否均匀，应视问题的需要而定。

此外网格还可以设计为自动调节的，即所谓自适应网格。

目前常用的数值网格生成的方法主要有三种：即代数法、微分方程法和保角变换法，其中又以代数法中的超限插值法和微分方程法中的椭圆型方程方法应用最为广泛。

CFD分析的结构化网格自动生成方法在CFD分析的全自动优化过程中，一个关键任务就是如何实现模型、网格的自动生成以及CFD流场分析的自动运行。

最近，我们在的一个名为“GAMMA”研究项目中，遇到这样一个难题——要求自动的生成一个结构化网格。

为什么要结构化网格与非结构化网格相比，结构化网格可以极大地加快流场分析，并且能得到一个精度较好的结果。

在大型设计研究中进行高质量的分析时，两者都可以很好的应用。

然而，在优化研究中，非结构化网格的自动化生成会更加容易实现——只需几何模型就可以实现。

结构画网格却不是这么简单。

结构网格的挑战关键问题在于结构化网格如何去填充一个任意几何的全部特征？举个我们研究的例子，例如涡轮增压器的蜗壳，它就存在一个虽然很小，但却很难处理的几何特征——蜗舌。

如下图所示：整体结构图——造成结构网格困难的区域蜗舌区域是蜗管体和出口段之间的过渡区域。

这对于结构网格来说有点复杂。

对于蜗管主体，可以很好划分结构化网格，一般这部分的结构化网格方式比较明确。

但是在蜗壳存在蜗舌结构，如何对蜗舌处划分结构化网格？在这里就有一些用户迷茫了。

几何框架考虑在这样的蜗壳几何生成结构化网格，那么就需要要为网格系统提取一些有用的信息。

对于各类复杂几何，是不可能只以一种方式来自动生成结构化网格。

我们所做的不仅是生成出新设计的网格，还基于CAESES软件建立一套基于模型参数化的几何框架（能引导生成结构化网格），它在某种逻辑上展示了网格是如何划分的，然后用该几何框架生成结构画网格。

下图展示了几何框架是如何布置的。

CAESES中自动结构化网格的参数化几何案例通过这些几何信息，实现了对这个复杂几何结构的结构化网格划分。

由于这些内部曲线是模型本身的一部分，所以当修改蜗壳的设计变量时，它们也会自动调整。

对于无界面使用者，也可以在优化过程中通过脚本形式创建几何，实现相同的效果，例如通过外部优化工具控制。

这也使得该方法能直接适用于HPC环境。

一、题目二、方法介绍本次作业网格生成主要分为两个部分，第一部分生成代数网格，第二部分使用拉普拉斯方程求解来优化节点分布。

代数网格的生成方法如下：以整个计算域的左下角点作为原点建立笛卡尔坐标系，将计算域的边界曲线解析式求解出来，分别将最下边界、上边界、左边界和右边界表示成首先在边界线上等间距分布101个节点，然后沿着x和y方向，逐层平均分配101个节点。

如，y=0边界上的第一层节点分布为类似地，可以求出左右边界和上边界的网格分布，这样就有了、、、、和。

可以求出沿着y方向平行于下边界的第二行网格节点的横坐标为类似地可以求出每一行网格节点的x坐标。

可以求出沿着y方向平行于左边界的第二列网格节点的纵坐标为：类似地可以求出每一列网格节点的y坐标。

这样就得到了初始的代数网格。

使用拉普拉斯方程优化网格节点坐标的方法如下：在物理平面上，边值问题的拉普拉斯方程为：使用坐标转换，将上式变为将上式中、定义为结构化网格节点的行数和列数，那么解第二个方程组即可解得满足拉普拉斯方程的结构化网格节点坐标。

通过查询相关资料，本次作业采用的差分格式为五点差分格式：求解上述方程组使用高斯赛德尔迭代法，具体迭代公式可见数值分析教材。

收敛条件为迭代步上限为10000步。

三、结果展示1.代数网格可以看到代数网格的正交性和光顺性都很差，所以使用拉普拉斯方程来优化网格节点的分布。

2.优化结果及收敛历史使用拉普拉斯方程优化后的网格如下可以看到优化后的网格正交性和光顺性都得到了很大的改善。

对残差进行分析可以看到残差在开始计算后很快就下降了，因此选取50步、100步的结果进行查看50步的优化结果100步的优化结果可以看到100步时结果已经比较良好，可见这种有优化方法非常适合这种情况下的网格划分。

四、源代码#include <stdio.h>#include <stdlib.h>#include <math.h>#define MALLOC(type,n) (type *)malloc((n)*sizeof(type))const int dot_row=101,dot_col=101,max_ste=100; //定义行节点和列节点数、优化迭代最大步数const double cir_cho=1.5,cir_rad=0.4,lin_sho=0.25,lin_lon=1.25,lin_all=3; //定义图形的形状double max(double a,double b);int main(){double **mesh_x,**mesh_x0;//x0、y0是优化网格时候保存上一步网格节点的数组double **mesh_y,**mesh_y0;double rad=0,deltX=0,deltY=0;int i=0,j=0;/*使用malloc分配动态数组可以分配任意大小的数组*/mesh_x=MALLOC(double *,dot_row);mesh_x0=MALLOC(double *,dot_row);mesh_y=MALLOC(double *,dot_row);mesh_y0=MALLOC(double *,dot_row);for(i=0;i<dot_col;i++){mesh_x[i]=MALLOC(double, dot_col);mesh_x0[i]=MALLOC(double, dot_col);mesh_y[i]=MALLOC(double, dot_col);mesh_y0[i]=MALLOC(double, dot_col);}rad=cir_rad/2+pow(cir_cho,2)/(8*cir_rad);//求圆弧对应的半径/*求解代数法得到的初始网格*//*求解边界上节点的坐标第0、100行、列的网格节点坐标*/deltX=lin_all/(dot_row-1);deltY=lin_all/(dot_col-1);for(i=0;i<dot_col;i++){mesh_x[0][i]=i*deltX;if(mesh_x[0][i]>=lin_sho&&mesh_x[0][i]<=lin_sho+cir_cho){mesh_y[0][i]=sqrt(rad*rad-pow((mesh_x[0][i]-cir_cho/2-lin_sho),2))-rad+cir_rad;}else{mesh_y[0][i]=0;}}for(i=0;i<dot_col;i++){mesh_x[dot_row-1][i]=i*deltX;if(mesh_x[dot_row-1][i]>=lin_lon&&mesh_x[dot_row-1][i]<=lin_lon+cir_cho){mesh_y[dot_row-1][i]=-sqrt(rad*rad-pow((mesh_x[dot_row-1][i]-lin_lon-cir_cho/2),2))+(lin _all-cir_rad+rad);}else{mesh_y[dot_row-1][i]=lin_all;}}for(i=0;i<dot_row;i++){mesh_y[i][0]=i*deltY;if(mesh_y[i][0]>=lin_lon&&mesh_y[i][0]<=lin_lon+cir_cho){mesh_x[i][0]=sqrt(rad*rad-pow((mesh_y[i][0])-lin_lon-cir_cho/2,2))-rad+cir_rad;}else{mesh_x[i][0]=0;}}for(i=0;i<dot_row;i++){mesh_y[i][dot_col-1]=i*deltY;if(mesh_y[i][dot_col-1]>=lin_sho&&mesh_y[i][dot_col-1]<=lin_sho+cir_cho){mesh_x[i][dot_col-1]=-sqrt(rad*rad-pow((mesh_y[i][dot_col-1]-(lin_sho+cir_cho/2)),2))+(li n_all+rad-cir_rad);}else{mesh_x[i][dot_col-1]=lin_all;}}printf("边界网格生成完毕");/*生成内部网格节点坐标*/for(i=1;i<dot_row-1;i++){for(j=1;j<dot_col-1;j++){mesh_x[i][j]=mesh_x[i][0]+j*(mesh_x[i][dot_col-1]-mesh_x[i][0])/100;mesh_y[i][j]=mesh_y[0][j]+i*(mesh_y[dot_row-1][j]-mesh_y[0][j])/100;}}FILE* fp_ini=fopen("data_ini.txt","w");if(fp_ini==NULL){printf("Can't open the file data_ini\n");}else{fprintf(fp_ini,"Title=\"mesh\"\nVariables=\"x\",\"y\"\nZone I=101,j=101,f=point\n");for(i=0;i<dot_row;i++){for(j=0;j<dot_col;j++){fprintf(fp_ini,"%lf " ,mesh_x[i][j]);fprintf(fp_ini,"%lf\n",mesh_y[i][j]);}}fclose(fp_ini);}/*网格优化*/int step=0;//迭代步数double res=1; //残差double a=0,b=0,c=0;//迭代过程中的中间变量FILE* fp_res=fopen("data_res.txt","w");FILE* fp_tec=fopen("data_tecplot.txt","w");while(res>1e-6&&step<=max_ste){res=0;for(i=0;i<dot_row;i++){for(j=0;j<dot_col;j++){mesh_x0[i][j]=mesh_x[i][j];mesh_y0[i][j]=mesh_y[i][j];}}for(i=1;i<dot_row-1;i++){for(j=1;j<dot_col-1;j++){a=((mesh_x0[i][j+1]-mesh_x0[i][j-1])/2)*((mesh_x0[i][j+1]-mesh_x0[i][j-1])/2)+((mesh_y0[ i][j+1]-mesh_y0[i][j-1])/2)*((mesh_y0[i][j+1]-mesh_y0[i][j-1])/2);b=((mesh_x0[i+1][j]-mesh_x0[i-1][j])/2)*((mesh_x0[i][j+1]-mesh_x0[i][j-1])/2)+((mesh_y0[ i+1][j]-mesh_y0[i-1][j])/2)*((mesh_y0[i][j+1]-mesh_y0[i][j-1])/2);c=((mesh_x0[i+1][j]-mesh_x0[i-1][j])/2)*((mesh_x0[i+1][j]-mesh_x0[i-1][j])/2)+((mesh_y0[ i+1][j]-mesh_y0[i-1][j])/2)*((mesh_y0[i+1][j]-mesh_y0[i-1][j])/2);mesh_x[i][j]=(2*a*(mesh_x[i+1][j]+mesh_x[i-1][j])-b*(mesh_x[i+1][j+1]-mesh_x[i-1][j+1]-mesh_x[i+1][j-1]+mesh_x[i-1][j-1])+2*c*(mesh_x[i][j+1]+mesh_x[i][j-1]))/(4*a+4*c);mesh_y[i][j]=(2*a*(mesh_y[i+1][j]+mesh_y[i-1][j])-b*(mesh_y[i+1][j+1]-mesh_y[i-1][j+1]-mesh_y[i+1][j-1]+mesh_y[i-1][j-1])+2*c*(mesh_y[i][j+1]+mesh_y[i][j-1]))/(4*a+4*c);res=max(res,(fabs(mesh_x[i][j]-mesh_x0[i][j])+fabs(mesh_y[i][j]-mesh_y0[i][j])));}}if(fp_res==NULL){printf("Can't open the file data_res\n");}else{fprintf(fp_res,"%lf\n",res);}step++;if(step==max_ste||res<1e-6){if(fp_tec==NULL){printf("Can't open the file fp_tec\n");}fprintf(fp_tec,"Title=\"mesh\"\nVariables=\"x\",\"y\"\nZone I=101,j=101,f=point\n");for(i=0;i<dot_row;i++){for(j=0;j<dot_col;j++){fprintf(fp_tec,"%lf " ,mesh_x[i][j]);fprintf(fp_tec,"%lf\n",mesh_y[i][j]);}}}}fclose(fp_res);fclose(fp_tec);for(i=0;i<dot_row;i++){free(mesh_x[i]);free(mesh_y[i]);}free(mesh_x);free(mesh_y);return 0;}double max(double a,double b){if(a>b){return a;}else{return b;}}。

ICEM CFD网格文件导入FLUENT及生成CFD边界条件方法ICEM CFD软件具有强大的流体网格生成能力，这是一个业内普遍的认识。

但ICEM CFD 创建网格的基本理念与大多数软件不一样，比如说ICEM CFD中基本上没有几何体的概念，又比如说网格不直接依赖于几何模型而是更依赖于Block，这和PA TRAN、ANSYS等常用软件的几何模型+网格模型、网格依赖于几何模型等的普遍概念完全不同。

因此，对于初学ICEM CFD的人来说，这个软件入门很难，这也是作者这半年学习ICEM CFD的深切体会。

在这篇短文中，作者主要想介绍一下比较困扰新手的2个问题：1）怎么将ICEM CFD网格导入Fluent中？2）怎么在ICEM CFD中生成出入口、耦合面等边界条件？1将ICEM CFD网格导入FLUENTICEM CFD默认输出网格文件的后缀是.uds，不是FLUENT能够读入的.msh格式。

设置方法如下：1）点击output > 点击select solver，在Output Solver选项中选择Fluent_V6，Common Structural Solver通常默认为NASTRAN，不用理它。

2）点击Write input →弹出Save current project first对话框→单击Y es（保存uns网格文件）→然后弹出Fluent V6对话框，其他选项都可不改动，可在Output file这一项中改一个你想要的文件名称→最后点Done选项就好了→输出的是mesh文件，可以直接读入Fluent中。

2在ICEM CFD中生成CFD边界条件迄今为止，作者总共摸索出了2种在ICEM CFD中生成CFD边界条件生成CFD边界条件的方法。

在介绍之前，先说明2个基本提示：1）ICEM输出的mesh文件只是包含了节点坐标、节点之间的连接信息以组成网格和表面（faces）、所有表面的区域类型（zone type）和数量，并不包含几何信息。

CFD网格的分类，如果按照构成形式分，可以分为结构化和非结构化结构化：只能有六面体一种网格单元，六面体顾名思义，也就是有六个面，但这里要区分一下六面体和长方体。

长方体(也就是所有边都是两两正交的六面体)是最理想完美的六面体网格。

但如果边边不是正交，一般就说网格单元有扭曲(skewed).但绝大多数情况下，是不可能得到完全没有扭曲的六面体网格的。

一般用skewness来评估网格的质量，sknewness=V/(a*b*c).这里V是网格的体积，a，b，c是六面体长，宽和斜边。

sknewness越接近1，网格质量就越好。

很明显对于长方体，sknewness=1.那些扭曲很厉害的网格，sknewness很小。

一般说如果所有网格sknewness>0.1也就可以了。

结构化网格是有分区的。

简单说就是每一个六面体单元是有它的坐标的，这些坐标用,分区号码(B),I,J,K四个数字代表的。

区和区之间有数据交换。

比如一个单元，它的属性是B=1, I=2,J=3,K=4。

其实整个结构化单元的概念就是CFD计算从物理空间到计算空间mapping的概念。

I,J,K可以认为是空间x,y,z 在结构化网格结构中的变量。

三维网技术论坛! p9 T0 u2 z+ @, i6 c非机构化：可以是多种形状，四面体（也就三角的形状），六面体，棱形。

对任何网格，都是希望网格单元越规则越好，比如六面体希望是长方形，对于四面体，高质量的四面体网格就是正四面体。

sknewness的概念这里同样适用，sknewness越小，网格形状相比正方形或者正四面体就越扭曲。

越接近1就越好。

很明显非结构化网格也可以是六面体，但非结构化六面体网格没有什么B,IJK的概念，他们就是充满整个空间。

对于复杂形状，结构化网格比较难以生成。

主要是生成时候要建立拓扑，拓扑是个外来词，英语是topology，所以不要试图从字面上来理解它的意思。

其实拓扑就是指一种有点和线组成的结构。

计算流体力学模拟中的网格生成方法及优化概述:计算流体力学（CFD）模拟是一种通过数值计算方法来模拟流体力学问题的技术。

在进行CFD模拟时，一个重要的步骤是生成适合模拟的网格。

网格的质量和适应性对CFD模拟的准确性和计算效率具有重要影响。

本文将介绍计算流体力学模拟中常用的网格生成方法以及优化措施。

一、网格生成方法:1. 结构化网格生成方法:结构化网格生成方法是一种将空间分割成规则拓扑结构的网格生成方法。

它的主要优点是适用于几何较简单的模型，计算速度较快。

常见的结构化网格生成方法包括直线加密法、均匀加密法、双曲型加密法等。

2. 非结构化网格生成方法:非结构化网格生成方法是一种将空间划分成不规则形状的网格的生成方法。

它适用于几何较复杂的模型，并且在处理流动现象中的复杂几何和边界条件时更具优势。

在非结构化网格生成中，常用的方法包括三角形剖分法、四面体剖分法和网格点移动法等。

3. 自适应网格生成方法:自适应网格生成方法是一种根据计算区域中流场的变化来调整网格的分布和密度的方法。

通过自适应网格生成方法，可以将网格精细化于流场变化较大的区域，从而提高模拟的准确性和精度。

常用的自适应网格生成方法包括几何适应方法和解适应方法等。

二、网格优化措施:1. 网格质量优化:网格质量对CFD模拟的准确性和计算效率具有重要影响。

因此，在网格生成后，通常需要进行网格质量优化。

常见的网格质量指标包括网格形状、网格扭曲度、网格尺寸、网格变形等。

通过调整网格节点的位置或调整连接节点的几何关系，可以优化网格的质量。

2. 网格适应性优化:为了更好地模拟流场中的局部细节，对于具有复杂边界条件的CFD模拟，网格适应性优化非常重要。

通过根据流场的局部变化来调整网格的分布和密度，可以提高模拟的准确性和计算效率。

常见的网格适应性优化方法包括加密区域网格划分方法、最大垫片法和自适应加密方法等。

3. 网格更新优化:在进行CFD模拟过程中，流场可能会有较大的变化，因此，为了保证模拟的精度和计算效率，需要进行网格更新优化。

1009 CFD 基础和网格计算I0、计算流体力学（CFD）基础计算流体动力学（Computational Fluid Dynamics, CFD ）是近代流体力学、数值数学和计算机科学相结合的产物，是一门具有强大生命力的边缘科学。

CFD方法是对流场的控制方程用计算数学的方法将其离散到一系列网格节点上求其离散的数值解的一种方法。

控制所有流体流动的基本定律是：质量守恒定律、动量守恒定律和能量守恒定律。

由它们分别导出连续性方程、动量方程（N-S方程）和能量方程。

应用CFD方法进行平台内部空气流场模拟计算时，首先需要选择或者建立过程的基本方程和理论模型，依据的基本原理是流体力学、热力学、传热传质等平衡或守恒定律。

由基本原理出发可以建立质量、动量、能量、湍流特性等守恒方程组，如连续性方程、扩散方程等。

这些方程构成非线性偏微分方程组，不能用经典的解析法，只能用数值方法求解。

求解上述方程必须首先给定模型的几何形状和尺寸，确定计算区域并给出恰当的进出口、壁面以及自由面的边界条件。

而且还需要适宜的数学模型及包括相应的初值在内的过程方程的完整数学描述。

求解的数值方法主要有有限差分法（FDM）、有限元法（FEM）以及有限分析法（FAM），应用这些方法可以将计算域离散为一系列的网格并建立离散方程组，离散方程的求解是由一组给定的猜测值出发迭代推进，直至满足收敛标准。

常用的迭代方法有Gauss-Seidel 迭代法、TDMA 方法、SIP法及LSORC法等。

利用上述差分方程及求解方法即可以编写计算程序或选用现有的软件实施过程的CFD模拟。

1、CFD求解力学问题的过程2、网格计算网格，即在计算区域内一些列离散的点。

计算流体力学通过将控制方程离散，使用数值方法得到网格节点上的数据（如速度、温度、压力等），即数值解。

控制方程的离散方法主要由有限控制体积法、有限差分方法和有限元方法。

网格主要分为结构化网格和非结构化网格。

结构化网格，可以用一个固定的法则予以命名，非结构化网格的节点位置不能用一个固定的法则予以有序的命名。