第八章 B 电力系统各元件的参数及等值电路B

3电力系统元件参数及等值电路电力系统的元件参数和等值电路是电力系统中至关重要的部分，它们决定了电力系统的性能和运行稳定性。

在电力系统中，主要的元件包括变压器、发电机、电力线路、开关设备等，这些元件各自具有不同的参数和等值电路模型。

下面将介绍电力系统中常见的元件参数以及它们的等值电路模型。

1.变压器变压器是电力系统中常见的元件之一，它主要用于改变电压的大小。

变压器的参数包括变比、额定功率、绕组电阻、绕组电感等。

变压器的等值电路模型通常包括两个绕组，每个绕组都包含一个电阻和一个电感。

变压器的等值电路模型可以用来计算电流、功率损耗等。

2.发电机发电机是用来将机械能转化为电能的设备，它的参数包括额定功率、功率因数、电压、电流等。

发电机的等值电路模型通常包括一个电动势、一个串联阻抗和一个并联电导。

发电机的等值电路模型可以用来计算电压、电流、功率输出等。

3.电力线路电力线路是电力系统中用来传输电能的设备，它的参数包括线路长度、线路电阻、线路电抗等。

电力线路的等值电路模型通常包括一个串联电阻和一个并联电抗。

电力线路的等值电路模型可以用来计算电压降、损耗功率等。

4.开关设备开关设备是电力系统中用来控制电路通断的设备，它的参数包括额定电流、额定电压、动作特性等。

开关设备的等值电路模型通常包括一个串联电阻和一个并联电容。

开关设备的等值电路模型可以用来计算电流、电压、功率损耗等。

总结来说，电力系统中的元件参数和等值电路是电力系统设计和运行的基础。

了解各个元件的参数和等值电路模型，可以帮助工程师设计和分析电力系统，确保其正常运行和稳定性。

同时，不同元件之间的参数和等值电路模型之间也需要考虑其相互影响，以确保整个电力系统的协调运行。

因此，对电力系统中的元件参数和等值电路模型有深入的了解是非常重要的。

电力系统与分析第八章的答案【篇一：电力系统分析习题集及答案(杨淑英)】集华北电力大学前言本书是在高等学校教材《电力系统稳态分析》和《电力系统暂态分析》多次修改之后而编写的与之相适应的习题集。

电力系统课程是各高等院校、电气工程专业的必修专业课，学好这门课程非常重要，但有很大的难度。

根据国家教委关于国家重点教材的编写要求，为更好地满足目前的教学需要，为培养出大量高质量的电力事业的建设人材，我们编写了这本《电力系统分析习题集》。

力求使该书具有较强的系统性、针对性和可操作性，以便能够使学生扎实的掌握电力系统基本理论知识，同时也能够为广大电力工程技术人员提供必要的基础理论、计算方法，从而更准确地掌握电力系统的运行情况，保证电力系统运行的可靠、优质和经济。

全书内容共分十五章，第一至第六章是《电力系统稳态分析》的习题，第七至第十四章是《电力系统暂态分析》的习题，第十五章是研究生入学考试试题。

本书适用于高等院校的师生、广大电力工程技术人员使用，同时也可作为报考研究生的学习资料。

由于编写的时间短，内容较多，书中难免有缺点、错误，诚恳地希望读者提出批评指正。

目录第一部分电力系统稳态分析第一章第二章第三章第四章第五章第六章电力系统的基本概念电力系统的元件参数及等值电路简单电力系统的计算和分析电力系统潮流的计算机算法电力系统的有功功率和频率调整电力系统的无功功率和电压调整第二部分电力系统暂态分析第七章电力系统故障分析的基本知识第八章同步发电机突然三相短路分析第九章电力系统三相短路的实用计算第十章对称分量法及元件的各序参数和等值电路第十一章不对称故障的分析、计算第十二章电力系统各元件的机电特性第十三章电力系统静态稳定第十四章电力系统暂态稳定第十五章研究生入学考试试题附录第一部分电力系统稳态分析电力系统稳态分析，研究的内容分为两类，一类是电力系统稳态运行状况下的分析与潮流分布计算，另一类是电力系统稳态运行状况的优化和调整。

第二章 电力系统各元件的特性参数和等值电路 主要内容提示：本章主要内容包括：电力系统各主要元件的参数和等值电路，以及电力系统的等值网络。

§2-1电力系统各主要元件的参数和等值电路一、发电机的参数和等值电路一般情况下，发电机厂家提供参数为：N S 、N P 、N ϕcos 、N U 及电抗百分值G X %，由此，便可确定发电机的电抗G X 。

按百分值定义有100100%2⨯=⨯=*NNGG G U S X X X 因此 NNG G S U X X 2100%⋅= （2—1） 求出电抗以后，就可求电势G E •)(G G G G X I j U E •••+=，并绘制等值电路如图2-1所示。

二、电力线路的参数和等值电路电力线路等值电路的参数有电阻、电抗、电导和电纳。

在同一种材料的导线上，其单位长度的参数是相同的，随导线长度的不同，有不同的电阻、电抗、电导和电纳。

⒈电力线路单位长度的参数电力线路每一相导线单位长度参数的计算公式如下。

⑴电阻：()[]201201-+=t r r α（Ω/km ） （2—2） ⑵电抗：0157.0lg1445.01+=rD x m（Ω/km ） （2—3） 采用分裂导线时，使导线周围的电场和磁场分布发生了变化，等效地增大了导线半径，从而减小了导线电抗。

此时，电抗为nr D x eq m 0157.0lg1445.01+=（Ω/km ） 式中m D ——三相导线的几何均距；（a ） G ·（b ）G ·图2-1 发电机的等值电路（a ）电压源形式 （b ）电流源形式eq r ——分裂导线的等效半径；n ——每相导线的分裂根数。

⑶电纳：6110lg 58.7-⨯=rD b m（S/km ） （2—4）采用分裂导线时，将上式中的r 换为eq r 即可。

⑷电导：32110-⨯=UP g g∆（S/km ） （2—5）式中g g ∆——实测的三相线路的泄漏和电晕消耗的总功率， kW/km ； U ——实测时线路的工作电压。

电力系统分析习题集华北电力大学前言本书是在高等学校教材《电力系统稳态分析》和《电力系统暂态分析》多次修改之后而编写的与之相适应的习题集。

电力系统课程是各高等院校、电气工程专业的必修专业课，学好这门课程非常重要，但有很大的难度。

根据国家教委关于国家重点教材的编写要求，为更好地满足目前的教学需要，为培养出大量高质量的电力事业的建设人材，我们编写了这本《电力系统分析习题集》。

力求使该书具有较强的系统性、针对性和可操作性，以便能够使学生扎实的掌握电力系统基本理论知识，同时也能够为广大电力工程技术人员提供必要的基础理论、计算方法，从而更准确地掌握电力系统的运行情况，保证电力系统运行的可靠、优质和经济。

全书内容共分十五章，第一至第六章是《电力系统稳态分析》的习题，第七至第十四章是《电力系统暂态分析》的习题，第十五章是研究生入学考试试题。

本书适用于高等院校的师生、广大电力工程技术人员使用，同时也可作为报考研究生的学习资料。

由于编写的时间短，内容较多，书中难免有缺点、错误，诚恳地希望读者提出批评指正。

目录第一部分电力系统稳态分析第一章电力系统的基本概念第二章电力系统的元件参数及等值电路第三章简单电力系统的计算和分析第四章电力系统潮流的计算机算法第五章电力系统的有功功率和频率调整第六章电力系统的无功功率和电压调整第二部分电力系统暂态分析第七章电力系统故障分析的基本知识第八章同步发电机突然三相短路分析第九章电力系统三相短路的实用计算第十章对称分量法及元件的各序参数和等值电路第十一章不对称故障的分析、计算第十二章电力系统各元件的机电特性第十三章电力系统静态稳定第十四章电力系统暂态稳定第十五章研究生入学考试试题附录第一部分电力系统稳态分析电力系统稳态分析，研究的内容分为两类，一类是电力系统稳态运行状况下的分析与潮流分布计算，另一类是电力系统稳态运行状况的优化和调整。

第一章电力系统的基本概念1-1 什么叫电力系统、电力网及动力系统？电力系统为什么要采用高压输电？ 1-2 为什么要规定额定电压？电力线、发电机、变压器和用电设备的额定电压是如何确定的？ 1-3 我国电网的电压等级有哪些？1-4 标出图1-4电力系统中各元件的额定电压。

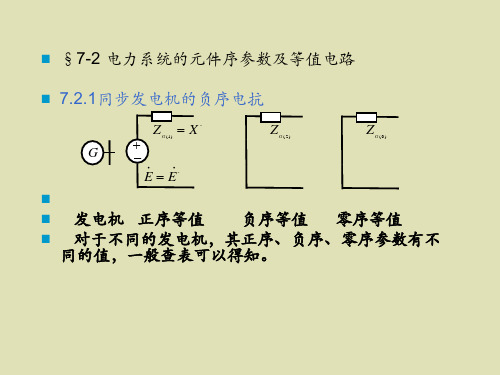
第八章 电力系统不对称故障的分析计算主要内容提示：电力系统中发生的故障分为两类：短路和断路故障。

短路故障包括：单相接地短路、两相短路、三相短路和两相接地短路；断路故障包括：一相断线和两相断线。

除三相短路外，均属于不对称故障，系统中发生不对称故障时，网络中将出现三相不对称的电压和电流，三相电路变成不对称电路。

直接解这种不对称电路相当复杂，这里引用120对称分量法，把不对称的三相电路转换成对称的电路，使解决电力系统中各种不对称故障的计算问题较为方便。

本章主要内容包括：对称分量法，电力系统中主要元件的各序参数及各种不对称故障的分析与计算。

§8—1 对称分量法及其应用利用120对称分量法可将一组不对称的三相量分解为三组对称的三序分量（正序分量、负序分量、零序分量）之和。

设c b a F F F ∙∙∙为三相系统中任意一组不对称的三相量、可分解为三组对称的三序分量如下：()()()()()()()()()021021021c c c c b b b b a a a a F F F F F F F F F F F F ∙∙∙∙∙∙∙∙∙∙∙∙++=++=++= 三组序分量如图8-1所示。

正序分量： ()1a F ∙、()1b F ∙、()1c F ∙三相的正序分量大小相等，彼此相位互差120°，与系统正常对称运行方式下的相序相同，达到最大值的顺序a →b →c ，在电机内部产生正转磁场，这就是正序分量。

此正序分量为一平衡的三相系统，因此有：()()()111c b a F F F ∙∙∙++=0。

负序分量：()2a F ∙、()2b F ∙、()2c F ∙三相的负序分量大小相等，彼此相位互差120°，与系图 8-1 三序分量Fc(0) ·零序F b(0) ·F a(0) ·120°120° 120° 正序F b(1)·F a(1)·F c(1) ·ω120°120°120°负序 F a(2)·F c(2)·F b(2)·ω统正常对称运行方式下的相序相反，达到最大值的顺序a →c →b ，在电机内部产生反转磁场，这就是负序分量。

例1．如图所示电力系统，试分别计算发电机保持不变时的功率特性和功率极限。

已知各元件参数如下：发电机：S GN ＝352.5MV A ，V GN ＝10.5kV ，x d ＝1.0，x q ＝0.6，25.0'=d x ，2.02=x ，T JN =8s 。

变压器：T-1 S T1N =360MV A ，14%1=ST V ，242/5.101=T k T-2 S T2N ＝360MV A ，14%2=ST V ，121/2202=T k 线路：kV V x x km x km l N L L L 220,5,/41.0,2500==Ω== 运行条件：95.0cos ,250,115000===ϕMW P kV V解：（1）网络参数及运行参数计算取()kV V MVA S III B B 115,250==。

为使变压器不出现非标准变比，各段基准电压为()()()()kVkV k V V kV kV k V V T II B I B T III B II B 07.92425.101.2091.20912122011512=⨯=⨯==⨯=⨯=各元件参数归算后的标么值为()()()()()()769.0531.0238.0101.1531.057.0481.1531.095.0531.0108.0586.02113.021586.01.20925025041.0108.01.20925036022014.0100%13.01.20925036024214.0100%238.007.92505.3525.1025.057.007.92505.3525.106.095.007.92505.3525.101''2122122222222222121112222''22222222=+=+==+=+==+=+==+⨯+=++==⨯⨯=⋅==⨯⨯=⨯⨯==⨯⨯=⨯⨯==⨯⨯=⨯⨯==⨯⨯=⨯⨯==⨯⨯=⨯⨯=∑∑∑TL d d TL q q TL d d T L T TL II B B l T II B B N T N T ST T II B B N T N T ST T I B B GN GN ddI B B GN GN q q I B B GN GN d d X X X X X X X X X X X X X V S lx X V S S V V X V S S V V X V S S V x X V S S V x X V S S V x X运行参数计算();0.111511500===III B V V V 0019.1895.0arccos ==ϕ ;0.125025000===B S P P 329.019.18tan 1tan 000=⨯==ϕP Q ()()458.195.38cos 1481.1769.01481.1769.0088.2cos 1088.295.38cos 1101.1481.11101.1481.1752.1cos 195.38101.1329.01101.11arctan 752.1101.11101.1329.00.1000''0'000000002220020000=⨯⨯⎪⎭⎫ ⎝⎛-+⨯=⎪⎪⎭⎫ ⎝⎛-+==⨯⨯⎪⎭⎫ ⎝⎛-+⨯=⎪⎪⎭⎫ ⎝⎛-+==⨯+⨯==⨯+⨯+=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=∑∑∑∑∑∑∑∑∑∑δδδV X X X X E E V X X X X E E V X P V X Q V E d d d d q q q d q d Q q q q Q ()()47.1769.01769.0329.012220'020'00'0=⨯+⨯+=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=∑∑V X P V X Q V E d d 0'054.31769.0329.01769.01arctan =⨯+⨯=δ（2）当保持==0q q E E 常数时，δδδδδδ2sin 117.0sin 41.12sin 101.1481.1101.1481.121sin 481.1088.22sin 2sin 2000+=⎪⎭⎫ ⎝⎛⨯-+=⎪⎪⎭⎫ ⎝⎛-+=∑∑∑∑∑q d q d d q E X X X X V X V E P q 02cos 117.02cos 41.1=⨯+=δδδd dP q E()0234.0cos 41.1cos 468.01cos 2234.0cos 41.122=-+=-+δδδδ 468.02234.0468.0441.141.1cos 2⨯⨯⨯+±-=δ 取正号得093.80=q mEδ。

第8章电力系统短路的基本知识一、填空题1.电力系统的短路故障可分为对称短路和不对称短路两大类型。

2.电力系统发生短路时，若短路处是导体间或导体与地间的直接连接，称为金属性短路；若是通过电弧电阻连接，称为非金属性短路。

3.短路电流计算前，在建立等值电路时，只计及各元件的电抗。

4.为了设计变电所而计算短路电流时，将系统中距离变电所较远的部分看作一个等值系统。

5.当等值系统的短路容量无法得到时，可用断路器的遮断容量替代，这样使短路电流的计算结果偏大（填“大”或“小”）。

6.若等值系统的短路容量为200MVA，取基准功率为100MVA，U B=U av，则等值电抗的标幺值为0.5。

二、选择题1.各种短路故障类型中，危害最大的是（A）A.三相短路B.两相短路C.两相短路接地D.单相接地2.各种短路故障类型中，发生概率最大的是（D）A.三相短路B.两相短路C.两相短路接地D.单相接地3.各种短路故障类型中，发生概率最小的是（A）A.三相短路B.两相短路C.两相短路接地D.单相接地4.短路计算时，以下那些假设条件使短路电流计算结果偏大，趋于保守（C）（1）认为所有发电机电动势相位相同（2）不计及各元件的电阻，只计及电抗（3）变压器的变比取平均额定电压之比（4）认为短路前发电机处于空载运行状态A.（1）（2）（3）B.（2）（3）（4）C.（1）（2）（4）D.（1）（3）（4）三、简答题1.什么是短路？短路有哪些基本类型？2.电力系统发生短路有哪些原因？3.短路故障对电力系统的运行有哪些危害？4.短路计算的目的有哪些？5.短路电流计算有哪些假设条件？6.短路电流的计算步骤有哪些？7.何为转移电抗？何为输入电抗？它们分别是如何得到的？四、计算题1.在下图所示的网络中，A、B为电源点，f为短路点，已知各支路电抗的标幺值，试求各电源点对短路点的转移电抗及输入电抗。

A（如果将图8.4中x2、x3、x7组成的三角形化为星形，能达到网络化简的目的吗？不妨一试！）x7、x10、x13属并联关系，将其简化为一个电抗x14，其值为0.192（并联电抗会算吗？），如下图所示：将x 8、x 11、x 14组成的星形化为三角形（即下图中的x 15、x 16、x 17），如下图所示：x 9、x 16属并联关系，将其简化为一个电抗x 18，其值为0.41；x 12、x 17属并联关系，将其简化为一个电抗x 19，其值为0.89；x 15是两个电源点A 、B 间的联系电抗，无作用，将其去掉，如下图所示：则电源点A 到短路点f 的转移电抗为：x 1f =x 18=0.41电源点B 到短路点f 的转移电抗为：x 2f =x 19=0.89输入电抗为两个转移电抗的并联值，为：28.0//212121=+==∑f f ff f f x x x x x x x 2.下图所示的电力系统中，已知：G 1、G 2为无限大容量电源；L 1=44km ，L 2=34km ，单位长度电抗均为0.4Ω/km ；T 1、T 2同型号：S N =5.0MVA ；短路电压为：u k12%=10.5，u k13%=17，u k23%=6。

一、电力系统的基本概念1、电力系统：发电、变电、输电、配电、用电电网：变电、输电、配电2、电力系统的基本特点：（1）电能的生产与消费具有同时性。

（2）电能与国民经济各部门和人民日常生活密切相关。

（3）电能的过渡过程十分短暂。

3、电力系统运行的基本要求（1）保证安全可靠供电。

（2）保证良好的供电质量（电能质量的指标是：频率、电压、交流电的波形）。

（3）保证电力系统运行的经济性。

（4）保持生态环境良好。

4、电力系统的额定电压（1）用电设备（kV）：3、6、10、35、60、110、220、330、500、750、1000 （2）电力线路的额定电压与用电设备相等。

（3）发电机的额定电压比网络额定电压高5%。

（4）①变压器一次侧绕组的额定电压与网络额定电压相等，直接与发电机相连时，其额定电压等于发电机额定电压。

②变压器二次绕组的额定电压为空载时的电压。

（a）直接接线路（10%）：变压器满载时内部阻抗上约有5%的电压损耗，为使变压器在额定负荷下工作时二次侧的电压比网络额定电压高5%，变压器二次绕组额定电压应比网络额定电压高10%。

（b）内阻抗小于7.5%（5%）：变压器内部损耗可忽略。

（c）直配负荷（5%）：没有线路损耗。

5、电力系统的接线方式按供电可靠性不同可分为：无备用接线（开式网）和有备用接线（闭式网）。

二、电力网络各元件的参数和等值电路1、单位长度参数：电阻r0（线路热效应）、电抗x0（磁效应）、电导g0（反映由泄漏电流和电晕所引起的有功损耗）、电纳b0（对地电场效应）2、采用分裂式导线的目的：增大导线半径，减小线路的电晕损耗以及线路电抗。

3、（1）①短路实验：低压侧短路，在高压侧加电压使绕组通过电流的电流达到额定值，测出高压侧所加电压值和回路所消耗的有功功率。

②空载实验：低压侧开路，高压侧加额定电压测出变压器的空载电流和空载损耗。

（2）变压器参数计算：短路损耗∆P s→R T、短路电压百分数U s%→X T、空载损耗∆P0→G T、空载电流百分数I0→B T。

电力系统暂态分析部分习题答案(参考)第一章 电力系统故障分析的基本知识1-2、发电机F1和F2具有相同的容量，它们的额定电压分别为6.3kV 和10.5kV ，若以它们的额定值为基本条件的发电机电抗的标么值是相同的，问这两个发电机电抗的欧姆值的比值是多少？ 解：X G1*(N)＝X G1*S N1/U N12 X G2*(N)＝X G2*S N2/U N22∵X G1*(N)＝X G2*(N) ∴X G1*S N1/U N12＝X G2*S N2/U N22 故：X G1/ X G2＝U N12/ U N22＝6.32/10.52＝0.36 1-4、求：①准确计算各元件电抗的标么值，基本段取I 段U BI ＝10.5kV 。

②工程近似计算各元件电抗的标么值，S B ＝100MVA 。

解：① 精确计算法U BI ＝10.5kV S B ＝100MVA U BII ＝5.101215.10⨯＝10.5kV U BIII ＝1106.65.101215.10⨯⨯＝7.26kV T50MV A 10.5kV X d ’’=0.1560MV A 10.5kV/121kV U k %=10.5 0.4Ω/km 100km30MV A110kV/6.6kV U k %=10.53.05010015.0''*=⨯=d X 175.05.10100605.101005.1022*1=⨯⨯=T X 273.01211001004.02*=⨯⨯=L X 289.0121100301101005.1022*2=⨯⨯=T X ② 近似计算法U B ＝U av S B ＝100MVA3.05010015.0''*=⨯=d X 175.0601001005.10*1=⨯=T X 302.01151001004.02*=⨯⨯=L X 35.0301001005.10*2=⨯=T X 1-5、某一线路上安装一台Xk%＝5的电抗器，其额定电流为150A ，额定电压为6kV ，若另一台额定电流为300A 、额定电压为10kV 的电抗器来代替它，并要求保持线路的电抗欧姆值不变，问这台电抗器的电抗百分数值应是多少？解：∵2221113100%3100%N N R N N R R I UX I U X X ⨯=⨯=∴61503001065%%122112=⨯⨯=⨯⨯=N N N N R R I I U U X X1-12、 (1) 若短路前空载，计算短路电流的周期分量及短路电流最大有效值；(2) 若A 相非周期分量电流的初值为零及最大时，计算相应的B 、C 相非周期分量电流的初始值；(3) 若短路前变压器满负荷运行，功率因数为0.9（低压侧），计算最大非周期分量电流的初始值，并与空载时短路比较。