物理常数单位制

初中物理基本物理量单位公式常数
基本物理量是指不能通过其他物理量表示的物理量。

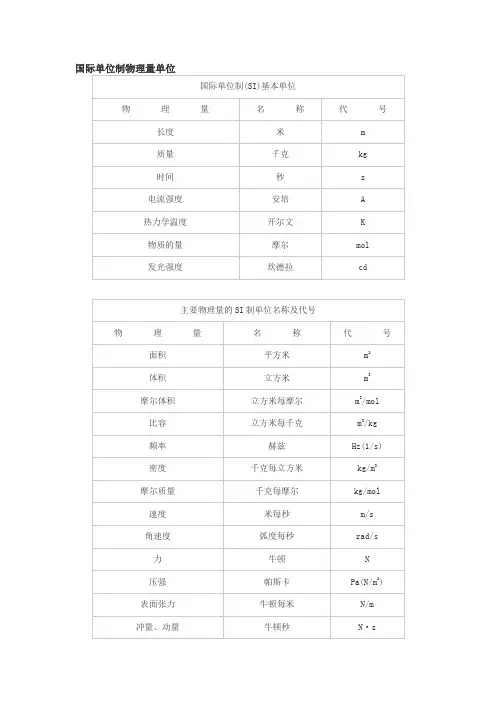
国际单位制（SI
单位制）是国际通用的物理量单位制，它包括七个基本物理量：长度（米，m）、质量（千克，kg）、时间（秒，s）、电流（安培，A）、热力学温
度（开尔文，K）、物质的量（摩尔，mol）和光强度（坎德拉，cd）。

基本物理量单位公式常数如下：
1.长度：
单位：米（m）
2.质量：
单位：千克（kg）
公式常数：一定的铂-钇合金的质量
3.时间：
单位：秒（s）
4.电流：
单位：安培（A）
公式常数：两根平行导线，互相静止时，单位长度上产生的相互作用
力等于2.0×10^−7N的电流
5.热力学温度：
单位：开尔文（K）
公式常数：绝对零度时气体氧气（O2）对应的热运动动能。

6.物质的量：
单位：摩尔（mol）
公式常数：12克的^12C的核在电子静止且处于其基态时包含的粒子数。

7.光强度：
单位：坎德拉（cd）
公式常数：等于1/683瓦特每球面弧度的单色光源的光通量。

此外，还有一些其他常用的物理量单位和公式常数，如：
1.速度：
单位：米每秒（m/s）
公式常数：速度等于位移与时间的比值。

2.加速度：
单位：米每秒平方（m/s²）
公式常数：加速度等于速度的变化率。

3.力：
单位：牛顿（N）
公式常数：力等于质量与加速度的乘积。

4.功：
单位：焦耳（J）
公式常数：功等于力与位移的乘积。

5.功率：
单位：瓦特（W）
公式常数：功率等于功与时间的比值。

七大基本物理量单位常数表示物理量单位常数是指在国际单位制中，用来确定七大基本物理量的单位的常数。

这些常数包括：光速、元电荷、普朗克常数、玻尔兹曼常数、阿伏伽德罗常数、气体常数和亚佛加德罗常数。

下面将逐一介绍这些常数的含义和作用。

1. 光速 (c)光速是物理学中最重要的常数之一，它表示光在真空中传播的速度。

光速的数值约为299,792,458米/秒，它在相对论和电磁学等领域有着重要的应用。

光速的存在使得我们能够测量时间和距离，也为其他物理量的测量提供了基准。

2. 元电荷 (e)元电荷是电荷的基本单位，描述了带电粒子的最小电量。

元电荷的数值约为1.602176634×10^-19库仑，它对于电磁学和粒子物理学的研究具有重要意义。

通过元电荷的概念，我们可以对电子、质子等带电粒子的电量进行精确测量。

3. 普朗克常数 (h)普朗克常数是量子力学中的基本常数，用来描述微观世界的行为。

普朗克常数的数值约为6.62607015×10^-34焦耳秒，它与能量的量子化和粒子的波粒二象性密切相关。

普朗克常数在量子力学的各个领域中都有广泛的应用，如原子物理学、固体物理学和核物理学等。

4. 玻尔兹曼常数 (k)玻尔兹曼常数是描述热力学系统中粒子运动的常数。

它的数值约为1.380649×10^-23焦耳/开尔文，它与温度、熵和能量等热力学量的关系有着重要的作用。

玻尔兹曼常数被广泛应用于理论物理学、统计物理学和热力学等领域，它帮助我们理解和描述宏观和微观系统的行为。

5. 阿伏伽德罗常数 (NA)阿伏伽德罗常数是描述化学反应和粒子物理学中粒子数量的常数。

它的数值约为6.02214076×10^23/mol，它表示在摩尔中的粒子数目。

阿伏伽德罗常数的存在使得我们能够在化学反应和粒子物理学中精确计量和比较不同物质的粒子数量。

6. 气体常数 (R)气体常数是描述理想气体行为的常数，它用来关联气体的压力、体积和温度等物理量。

三大物理常数三大物理常数是指光速、普朗克常数和元电荷。

这三个常数在物理学中起到了重要的作用，对于研究电磁学、量子力学等领域具有重要意义。

光速是指光在真空中传播的速度，它是一个物理学上的基本常数。

根据国际单位制的定义，光速的数值为299,792,458米/秒。

光速的重要性体现在很多方面，例如，在相对论中，光速是一个不变的上限，任何物质都无法超过光速。

光速的大小也影响了天文学中的测量，例如，我们能够通过测量光的传播时间来计算天体之间的距离。

普朗克常数是量子力学中的基本常数之一，记作h。

它的数值约为6.62607015×10^-34焦耳·秒。

普朗克常数与能量的量子化密切相关，它描述了微观世界中粒子的行为。

根据普朗克常数，我们可以计算出光的能量与频率之间的关系，即E=hf，其中E表示能量，f 表示频率。

普朗克常数的大小决定了微观世界的量子效应，例如，原子能级的跃迁、电子的行为等都与普朗克常数有关。

元电荷是指电荷的基本单位，用e表示。

它的数值约为1.602176634×10^-19库仑。

元电荷是指电子或质子所携带的最小电荷量。

在电磁学中，电荷是一个基本的物理量，元电荷的大小决定了电荷的离散性质，即电荷是量子化的。

元电荷的存在使得电子和质子的电荷都是整数倍的元电荷，这也是化学元素周期表中电子数和质子数的整数性质的根源。

光速、普朗克常数和元电荷是三大物理常数。

它们在物理学中有着重要的地位和作用。

光速决定了光的传播速度，普朗克常数描述了微观世界的量子效应，元电荷是电荷的最小单位。

这三个常数的存在和数值为我们揭示了自然界的奥秘，推动了科学的发展。

对于物理学家和研究者来说，深入理解和应用这些常数，将有助于更好地解释和探索自然现象，推动科学的进步。

高斯单位制中的常数高斯单位制是一种物理单位制，其特点是基本单位的选择非常巧妙，能够简化物理公式的形式和计算的精度，因此在电磁学和天文学等领域得到了广泛的应用。

为了方便使用高斯单位制，我们需要了解其所用的常数，包括基本常数、电磁学常数和自然单位制常数。

一、基本常数1、光速：c = 299792458 米/秒光速是真空中电磁波的传播速度，是一个极为重要的参考常数，也是高精度计量的基础。

在高斯单位制中，光速的数值被定义为1，即c = 1。

2、元电荷：e = 1.602176634 × 10^-19 库仑元电荷是电荷量的基本单位，是电子或质子所带电荷的大小。

在高斯单位制中，忽略真空介电常数的影响，元电荷的大小被定义为1，即e = 1。

3、玻尔兹曼常数：k = 1.380649 × 10^-23 焦耳/开尔文玻尔兹曼常数是描述温度与能量之间关系的基本常数，被广泛应用于统计物理学和热力学等领域。

在高斯单位制中，玻尔兹曼常数的数值被定义为1，即k = 1。

磁通量子是描述磁通量与磁通量子数之间关系的常数，是超导电性和量子计量的基础。

在高斯单位制中，磁通量子的大小被定义为1，即Φ0 = 1。

二、电磁学常数3、电荷密度：ρe = ε0^-1 / （4π）4、电位移矢量：D = ε0 E电位移矢量描述了电场（E）与极化电荷之间的关系，单位是库仑/米²。

在高斯单位制中，电位移矢量的大小被定义为1，即D = 1。

5、磁感应强度矢量：B = μ0 H三、自然单位制常数自然单位制是另一种物理单位制，以光速、元电荷和普朗克常数为基本单位，其常数与高斯单位制相比更为简单。

下面列出几个自然单位制常数的高斯单位制数值。

3、电子电荷质量比：me/mp = 5.48579909070 × 10^-4以上常数仅是高斯单位制中的部分常数，还有很多常数在实际计算中也是必不可少的。

因此，熟练掌握高斯单位制中的常数，对于深入理解电磁学和微观物理学等领域的计算方法和理论研究都非常重要。

基本物理常数表单位换算基本物理常数表（单位换算）为了方便在物理学的研究与应用过程中进行单位的换算与计算，科学家们约定了一套国际单位制（SI，International System of Units）来统一物理量的测量与表示方法。

其中，物理常数是一些在物理学中扮演重要角色的恒定数值。

本文将给出一些基本的物理常数以及它们的单位换算关系。

一、长度单位换算常数：1、1米（m）= 100厘米（cm）= 1000毫米（mm）= 1000000微米（μm）= 1000000000纳米（nm）2、1微米（μm）= 10-6米（m）3、1纳米（nm）= 10-9米（m）二、质量单位换算常数：1、1千克（kg）= 1000克（g）= 1000000毫克（mg）2、1克（g）= 0.001千克（kg）三、时间单位换算常数：1、1秒（s）= 1000毫秒（ms）2、1分钟（min）= 60秒（s）3、1小时（h）= 60分钟（min）= 3600秒（s）4、1天（day）= 24小时（h）= 1440分钟（min）= 86400秒（s）四、速度单位换算常数：1、1米每秒（m/s）= 3600米每小时（m/h）= 2.237英里每小时（mph）五、加速度单位换算常数：1、1米每平方秒（m/s^2）= 3.281英尺每平方秒（fps^2）六、力单位换算常数：1、1牛顿（N）= 1000克力（kgf）2、1克力（kgf）= 9.80665牛顿（N）七、压强单位换算常数：1、1帕斯卡（Pa）= 0.000145038磅力每平方英寸（psi）2、1标准大气压（atm）= 760毫米汞柱（mmHg）= 101325帕斯卡（Pa）= 14.6959磅力每平方英寸（psi）八、功、能单位换算常数：1、1焦耳（J）= 0.238846卡路里（kcal）2、1卡路里（kcal）= 4186焦耳（J）九、功率单位换算常数：1、1瓦特（W）= 1牛顿米每秒（N·m/s）= 0.001千瓦（kW）十、电荷单位换算常数：1、1库仑（C）= 10^6微库仑（μC）= 10^9毫库仑（mC）十一、电压单位换算常数：1、1伏特（V）= 1000毫伏特（mV）= 1000000微伏特（μV）以上只是一部分常见的单位换算关系，物理学涉及的常数还有很多。

25个物理常数篇一：标题: 25个物理常数(创建与标题相符的正文并拓展)正文:物理学是研究自然现象的科学,其基础是一些基本常数。

这些常数是通过对自然界的观察和实验得出的,它们对物理学的理论和实践具有至关重要的影响。

本文将介绍25个基本的物理学常数,包括它们的值、定义和意义。

1. 开尔文(k)开尔文(k)是一个常量,它的值为1.19264×10-19J/(K·K)。

它是电离常数,用于描述电解质的电离程度。

2. 普朗克常数(h)普朗克常数(h)是一个基本的物理学常数,它的值为6.626176×10-35J/(K·s)。

它是热力学中的基本常数,用于描述能量和热量之间的关系。

3. 光速(c)光速(c)是一个基本的物理学常数,它的值为299,792,458米/秒。

它是真空中光的速度,也是宇宙中最基本的速度。

4. 磁感应强度(B)磁感应强度(B)是一个物理学常数,用于描述磁场的强度。

它的值通常在0到1000特斯拉之间,磁感应强度越大,磁场越强。

5. 电容(C)电容(C)是一个物理学常数,用于描述电容器的电容值。

它的值通常在0到1特斯拉之间,电容器的电容值越大,电容器的储存电能的能力越强。

6. 电阻(R)电阻(R)是一个物理学常数,用于描述导体的电阻值。

它的值通常在0到无穷大之间,电阻值越大,导体的电阻能力越强。

7. 温度(T)温度(T)是物理学中的基本常数,用于描述物体的状态。

它的值通常在0到开尔文之间,温度越高,物体的状态越热。

8. 引力(G)引力(G)是物理学中的基本常数,用于描述物体之间的引力大小。

它的值通常在6.6743×10-11N·(m/kg)^2。

9. 电磁场频率(E)电磁场频率(E)是物理学常数,用于描述电磁场的传播速度。

它的值通常在真空中约为3×10^10米/秒。

10. 质能关系(E=mc2)质能关系(E=mc2)是物理学中的一个重要公式,用于描述质量和能量之间的关系。

普朗克常数和玻尔兹曼常数是描述微观世界物理现象的两个重要常数。

它们在量子力学和统计物理中有着重要的作用，是研究微观粒子运动和能量转换的基本参量。

由于量子力学和统计物理中常常涉及到单位的换算，因此掌握普朗克常数和玻尔兹曼常数的单位换算表可以帮助我们更好地理解和应用这两个常数。

下面是普朗克常数和玻尔兹曼常数的单位换算表：普朗克常数：1. 普朗克常数的国际单位制（SI单位制）表示为 h，其数值为6.xxx × 10^-34 J·s。

2. 普朗克常数的厘米-克-秒单位制（cgs单位制）表示为 h，其数值为6.xxx × 10^-27 erg·s。

3. 普朗克常数的电子伏特单位制（eV单位制）表示为ℏ，其数值为4.xxx × 10^-15 eV·s。

玻尔兹曼常数：1. 玻尔兹曼常数的国际单位制（SI单位制）表示为 k，其数值为 1.xxx × 10^-23 J/K。

2. 玻尔兹曼常数的厘米-克-秒单位制（cgs单位制）表示为 k，其数值为1.xxx × 10^-16 erg/K。

3. 玻尔兹曼常数的电子伏特单位制（eV单位制）表示为 k，其数值为8.xxx × 10^-5 eV/K。

通过以上的单位换算表，我们可以看出普朗克常数和玻尔兹曼常数在不同的单位制下的具体数值，这有助于我们在实际计算和研究中的应用。

在量子力学和统计物理的研究中，常常需要根据实际问题的不同，选择合适的单位进行计算和描述，因此熟练掌握常数的单位换算表是非常重要的。

普朗克常数和玻尔兹曼常数在科学研究和工程技术领域中有着广泛的应用。

比如在半导体物理中，玻尔兹曼常数常常用于描述半导体中电子的能级分布；在纳米材料的研究中，普朗克常数常常用于描述纳米材料的量子效应。

掌握好普朗克常数和玻尔兹曼常数的单位换算表，对于开展相关领域的研究工作具有重要的指导意义。

普朗克常数和玻尔兹曼常数作为描述微观世界物理现象的重要常数，其在量子力学和统计物理中有着重要的作用。

各个物理量的国际单位制国际单位制(SI)(SI是国际单位制的简称）是在“基本物理常数”基础上确定基本单位的国际组织。

基本物理常数指一个物体的质量占它在整个质量库中储存的总质量的百分比。

国际单位制(SI)由光速单位 m/s、千克基本单位千克、开尔文基本单位开尔文、安培、开尔文电流温度等组成，在地球自转产生的磁场中保持不变（除非地球自转极快),其定义通过直接测量定义和通过量子基准进行复现后得到。

该单位根据普朗克常数对物质“量”作为质量单位。

国际单位制(SI)由基本物理常数来定义物体的质量。

一、基本物理常数对质量的影响SI (SI)定义了一个物体的质量，其定义可以采用物理常数或量子力学的普朗克常数来定义。

普朗克常数是物理常数 Ni的一个系数。

在一条连续平行线上，两个物质处于相对静止状态。

一条直线上的两个点分别有1/2的质量和1/3的能量。

在同一个平面上，两个点都有一个不变的质量单位 Ni,那么两个不变的质量单位就都等于1/2这两个点之间那点质量的乘积就叫做 Ni。

如果用普朗克常数 Ni来定义一个物体的质量时，首先要确定它是不是稳定地不变的。

二、物理常数定义的变化与基本物理常数对质量的影响。

物理常数在 SI中被分为“基本物理常数”和“质量”两个部分，前者定义为：光速 ms/s 和质量 g的单位，后者定义为：质量 mg的10倍。

两个物理常数在国际单位制中保持不变。

根据这个定义方法，可以得到一系列物理量所对应的质量为：其中是1和1的乘积(n);0=ms-1;1=ms2;0=ms3;1=ms4;1=ms5;1=ms2;1=ms3;1=ms5。

为了更好地描述物质是如何相互作用的过程，因此在基本物理常数定义中加入了质量常数的定义。

三、常用质量定义方法对比在定义中，由于物质的质量的不确定性，常采用将物体定义为基本物理常数的方法。

测量方法有：直接测量法、量子测量法和量子基准法。

其中前三种方法可以直接测量出质量的参量。

物理常数引力常数G= 6.672×10-11牛顿·米2/千克2单元电荷e= 1.602189×10-19库仑阿伏加德罗常数N0= 6.02204×1023个粒子数/摩尔法拉第常数F= 96484.6库仑/摩尔斯忒藩―玻尔兹曼常数σ= 5.6703×10-8瓦·米2/K4气体常数R=8.3144焦耳/摩尔·K真空的电容率库仑/焦耳·米光速c= 2.99792458 ×108米/秒真空的磁导率牛顿/安2精细结构常数α=7.297351×10-3=1/137电子康普顿波长米里德伯常数R∞=1.096737318×107米-1质子康普顿波长米里德伯频率cR∞=3.2898420×1015赫兹质子电子质量比值里德伯能量hcR∞=13.60580电子伏玻尔兹曼常数k= 1.38066×10-23焦耳/K = 8.6174×10-5电子伏/K库仑常数k = 1/ (4πε0) = 8.98755179×109牛顿·米2/库仑2电子静质量m e=9.10953×10-31千克=5.485802×10-4u（原子单位）=0.511003兆电子伏/c2质子静质量m p=1.672648×10-27千克= 1.00727674u = 938.280兆电子伏/c2中子静质量m n=1.674954×10-27千克= 1.00866501u = 939.573兆电子伏/c2统一质量单位（原子单位）u =1.660566×10-27千克=931.502兆电子伏/c2玻尔半径a0=5.291771×10-11米玻尔磁子焦耳/特斯拉 = 5.788378×10-9电子伏/高斯核磁子焦耳/特斯拉= 3.152452×10-12电子伏/高斯普朗克常数h= 6.62818×10-34 焦耳·秒= 4.13570×10-15 电子伏·秒焦耳·秒= 6.58217×10-16 电子伏·秒。

物理教案－力学单位制1. 引言力学是物理学的一个分支，研究物体的运动和力的作用。

在力学中，单位制是非常重要的概念。

本教案将重点介绍力学单位制的内容，包括常用的国际单位制（SI单位制）和一些其他的常用单位制。

2. 国际单位制（SI单位制）国际单位制（SI）是用于科学国际交流的标准单位制。

在力学中，有三个基本单位，分别是米（m）、千克（kg）和秒（s）。

其他一些重要的力学量的单位也可以通过基本单位来定义。

•速度：速度是物体在单位时间内所运动的距离。

速度的单位是米每秒（m/s）。

•加速度：加速度是物体单位时间内速度的变化率。

加速度的单位是米每秒平方（m/s^2）。

•力：力是物体之间相互作用的结果，用于改变物体的运动状态。

力的单位是牛顿（N），1N等于1kg*m/s^2。

•质量：质量是物体所具有的惯性特性，不受外力作用时物体的抵抗改变其运动状态。

质量的单位是千克（kg）。

3. 其他常用力学单位制除了国际单位制外，还有一些其他常用的力学单位制。

•厘米－克－秒单位制（CGS单位制）：在CGS单位制中，长度的单位是厘米（cm），质量的单位是克（g），时间的单位是秒（s）。

•托勒密单位制：托勒密单位制是一个古老的单位制，它以托勒密为基础。

在托勒密单位制中，长度的单位是米（m），质量的单位是托勒密（Tol），时间的单位是秒（s）。

•自然单位制：自然单位制是一种使用物理常数的单位制。

在自然单位制中，长度的单位是电子伏特（eV-1），质量的单位是电子伏特秒（eV-1s），时间的单位是电子伏特秒（eV^-1s）。

4. 单位换算在学习力学时，我们经常需要进行不同单位之间的换算。

下面是一些常见的单位换算公式：•米与厘米的换算：1m = 100cm•厘米与米的换算：1cm = 0.01m•千克与克的换算：1kg = 1000g•克与千克的换算：1g = 0.001kg•米与毫米的换算：1m = 1000mm•毫米与米的换算：1mm = 0.001m通过这些单位换算，我们可以将不同单位的物理量统一到同一个单位制下，方便进行计算和比较。

理伯德常数 cgs单位制（原创版）目录1.理伯德常数的定义和含义2.CGS 单位制的概念和特点3.理伯德常数在 CGS 单位制中的应用和重要性4.结论正文1.理伯德常数的定义和含义理伯德常数，又称为理查兹常数，是一个在物理学和工程学中经常用到的常数，表示为 R。

它用于描述电荷在电场中的受力情况，是静电力的单位，即 1 库仑力。

在国际单位制（SI）中，理伯德常数的值为 1.380649×10^-23J·C^-1。

2.CGS 单位制的概念和特点CGS 单位制，即厘米 - 克-秒单位制，是一种物理量的计量单位制度。

它源于 19 世纪，主要用于科学研究领域。

CGS 单位制的主要特点是：长度单位为厘米，质量单位为克，时间单位为秒，能量的单位为尔格（erg），力的单位为达因（dyn）。

3.理伯德常数在 CGS 单位制中的应用和重要性在 CGS 单位制中，理伯德常数的值为 8.9875517923e9 C/N m，是一个非常重要的物理常数。

它在 CGS 单位制中的应用主要体现在以下几个方面：首先，理伯德常数用于表示电场强度。

在 CGS 单位制中，电场强度的单位是达因/库仑，而 1 库仑等于 10^5 C/m，因此，1达因等于10^5 N/C。

这样，我们就可以通过理伯德常数来计算电场强度。

其次，理伯德常数在电势能和电荷量的计算中也有重要应用。

在 CGS 单位制中，电势能的单位是尔格，电荷量的单位是库仑。

通过理伯德常数，我们可以将电势能和电荷量之间的关系联系起来，从而更好地理解和描述电场和电荷的运动。

4.结论理伯德常数在 CGS 单位制中具有重要作用，它帮助我们更好地理解和描述电场和电荷的运动。

虽然现在国际单位制已经成为主流，但 CGS 单位制在某些特定领域仍然具有重要意义。

理伯德常数 cgs单位制理伯德常数是一个重要的物理常数，在物理学中起着举足轻重的作用。

它在cgs单位制下的数值约为6.67430×10^-8 cm³⋅g⁻¹⋅s⁻²，通常用符号G表示。

理伯德常数描述了万有引力定律的强度，它体现了引力的基本特征和物质之间相互作用的重要性。

引力是自然界中最基本的力之一。

从苹果掉落，到地球围绕太阳旋转，无不受到引力的作用。

而理伯德常数则是衡量引力强弱的重要标准。

正因如此，理伯德常数对于研究天体物理学、宇宙学、力学等领域具有重要意义。

理伯德常数的cgs单位制下的数值虽然看起来很小，但在宇宙尺度下的影响却是极其巨大的。

我们以地球和太阳为例，它们之间的引力正是由理伯德常数所描述。

地球围绕太阳运转时，太阳的质量和地球的质量之间的比值即为重要的计算参数。

理伯德常数的具体数值使得地球和太阳之间的引力足够巨大，以保持地球的运动轨道稳定，从而维持了生命的存在。

除了作用于星际天体之间，理伯德常数还在微观领域中发挥着重要作用。

例如，在原子物理学中，理伯德常数是计算电子轨道和原子核之间作用力的关键因素之一。

它决定了原子的化学性质、分子的稳定性以及化学反应的速率等。

可以说，没有理伯德常数的存在，我们很难想象宇宙和物质会如何运作。

除了在物理学研究中的重要性，理伯德常数还对科学教育具有指导意义。

通过学习关于理伯德常数的知识，我们能更好地了解自然界的规律，并能开阔自己对于宇宙的认知。

由于理伯德常数体现了物质之间的相互作用，通过深入研究理伯德常数，我们可以更好地理解许多自然现象，从而提高科学素养和科学研究水平。

总之，理伯德常数是一个重要的物理常数，它在万有引力定律的描述中起着关键作用。

无论是在天体物理学还是微观领域，理伯德常数都具有举足轻重的地位。

通过对于理伯德常数的研究和应用，我们能更好地了解自然界的运作规律，并提高自己的科学素养。

因此，理解并研究理伯德常数对于我们每个人来说都具有重要的指导意义。

国际单位制常数化计算公式国际单位制是世界上通用的计量单位制度，它的基本单位包括米、千克、秒、安培、开尔文、摩尔和坎德拉等。

为了能够更准确地进行科学计量和测量，国际单位制常数化计算公式被广泛应用于各种科学领域，包括物理学、化学、工程学等。

国际单位制常数化计算公式的核心在于将物理常数与计量单位相结合，从而使得计量单位可以通过物理常数的测量来确定。

这种方法在实际应用中具有很高的精度和可靠性，因此被广泛应用于科学研究和工程实践中。

在国际单位制常数化计算公式中，最常用的物理常数包括普朗克常数、元电荷、波尔兹曼常数、阿伏伽德罗常数等。

这些常数与计量单位的定义相关联，通过测量这些物理常数的数值，可以确定计量单位的大小。

以普朗克常数为例，它是量子力学中的一个重要常数，通常用h来表示。

根据国际单位制常数化计算公式，普朗克常数与计量单位之间的关系可以表示为：h = 6.62607015 × 10^-34 J·s。

这个公式表明，普朗克常数的数值可以通过测量来确定，从而确定焦耳和秒的定义。

这种常数化计算公式的方法，使得计量单位的定义更加准确和可靠。

在化学领域，国际单位制常数化计算公式也被广泛应用。

例如，波尔兹曼常数k是描述热力学系统中粒子运动的一个重要常数，它与温度的关系可以表示为：k = 1.380649 × 10^-23 J/K。

通过测量波尔兹曼常数的数值，可以确定开尔文的定义，从而使得温度的测量更加准确和可靠。

除了普朗克常数和波尔兹曼常数，国际单位制常数化计算公式还涉及到其他一些重要的物理常数，包括光速、电荷量、阿伏伽德罗常数等。

通过测量这些物理常数的数值，可以确定米、安培、摩尔等计量单位的定义，从而使得科学计量更加准确和可靠。

在工程领域，国际单位制常数化计算公式也具有重要的应用价值。

例如，光速是一个重要的物理常数，它与米的定义相关联，通过测量光速的数值，可以确定米的定义，从而使得长度的测量更加准确和可靠。