命题符号化

11.1 命题及其符号化[教学重点] 命题的概念和六个联结词的定义[教学目的]1：使学生了解逻辑的框架，命题逻辑的基本要素是命题。

2：通过示例理解命题的概念。

3：通过示例理解合取、析取、异或、蕴涵、等价的含义，了解逻辑语言的精确性，为学习逻辑学打好基础。

4：学会命题符号化的方法。

[教学准备][教学方法]讲述法[课时安排]二课时。

[教学过程]讲述：逻辑是解决推理方法的学科，中心是推理，基本要素是命题，称为命题逻辑。

数理逻辑则是用数学方法研究推理；首先要理解命题是什么，然后了解怎样用数学方法描述命题，甚至逻辑推理。

后者式命题符号化的问题。

板书：第一章命题基本概念1.1 命题及其符号化讲述：首先讨论命题。

板书：一命题A) 概念：在二值逻辑中，命题是或真或假，而不会同时又真又假的陈述句。

判断要点：a 陈述句；b 或真或假，唯一真值；讲述：例：(1)地球是圆的；真的陈述句，是命题(2)2+3=5；真的陈述句，是命题(3)你知道命题逻辑吗？非陈述句，故非命题(4)3-x=5；陈述句,但真假随x的变化而变化，非命题(5)请安静！非陈述句，故非命题(6)火星表面的温度是800 C；现时不知真假的陈述句，但只能要么真要么假，故是命题(7)明天是晴天；尽管要到第二天才能得知其真假，但的确是要么真要么假，故是命题2(8) 我正在说谎；无法得知其真假，这是悖论注意到(4)不是命题，后续章节中会提到，这被称为谓词，命题函数或命题变项。

讲述：类似一般的事物，也有不同的命题，分成不同的类型。

板书：B) 分类：a 简单命题，通常用p,q,r,…,等表示命题变项，命题常项用1(T)，0(F)表示；b 复合命题，由简单命题和联结词构成；讲述：简单命题可以简单地用单个字母表示，但复合命题还包含了联结词，多个命题变项由联结词联结起来成为复合命题。

所以还需要考虑联结词的问题。

板书：二逻辑联结词讲述：首先最为简单的一种情况，就是日常语言中所说的“不”，这是对原有意思的的否定，所以称为否定式板书：1)否定式和否定联结词：命题p⌝p；符号⌝即为否定联结词。

第一节：命题符号化及联结词※引言命题逻辑是数理逻辑的基本组成部分，是谓词逻辑的基础，而数理逻辑是一门用数学方法研究推理过程的科学。

逻辑学主要研究各种论证，建立逻辑学的主要目的在于探索出一套完整的规则，按照这些规则就可以确定任何特定论证是否有效，这些规则通常称为推理规则。

在逻辑学中与其说注重的是论证本身，不如说注重的是论证形式，这样可以依据各项规则并使用机械方法，不难确定论证的有效性，但是，使用这种方法推理时，所遵循的规则一定不能具有二义性。

为表示任何成套规则或者理论，都需要为其配置一种语言。

所以，应制定一种形式语言，在这种形式语言中必须明确地和严格地定义好它的语义和语法，为了避免出现二义性，在形式语言种将使用一些符号，并给这些符号做出明确的定义，同时使用符号还有另外的含义：符号容易书写和处理。

※命题符号化及联结词数理逻辑研究的中心问题是推理，而推理的前提和结论都是表达判断的陈述句，所以，表达判断的陈述句构成了推理的基本单位。

【定义1】命题：能判断真假的陈述叫做命题注意：(1)命题的判断只有两种可能：正确的判断与错误的判断，前者称为命题的真值为真；后者称为命题的真值为假，(2)命题的真值通常使用大写英文字母T和F表示，或使用1和0表示(3)命题必须是具有唯一真值的陈述句【例题1】判断下列语句中哪些是命题(1)2是素数(2)雪是黑色的(3)532=+(4)明年十月一日是晴天(5)3 能被2整除(6)这朵花真好看呀！(7)明天下午有会吗？(8)请关上门！(9)5>+y x(10)地球外的星球上也有人其中：(1)(2)(3)(4)(5)(10)为命题【方法】(1)命题必须是陈述句，所以：非陈述句不是命题(2)命题必须有确定的真值，凡无确定真值的陈述句不是命题，特别注意：真值是否确定与我们是否知道它的真值是两码事(3)注意悖论：如：我正在说谎。

【定义2】原子命题：不能分解为更简单的陈述句叫做原子命题或简单命题【定义3】命题常项：对于简单命题如果它的真值是确定的，则：称其为命题常项或命题常元命题变项：真值可以变化的陈述句成为命题变项或命题变元，用小写的英文字母表示注意：命题变项不是命题【定义4】复合命题：由联结词、标点符号和原子命题复合构成的命题叫做复合命题【定义5】联结词类型(1)否定：设P为一个命题，P的否定是一个新的命题，记做：P如果P为T，则：P⌝为F；如果P为F，则：P⌝为T〖注意〗自然语言常用“非”、“不是”等(2)合取：两个命题P和Q的合取是一个复P∧合命题，记做：Q当且仅当P和Q同时为T时，QP∧的真值为T，否则为F〖注意〗自然语言常用“既……又……”、“不仅……而且……”、“虽然……但是……”等【例题2】将下列命题符号化(1)李平既聪明又用功(2)李平虽然聪明，但不用功(3)李平不但聪明，而且用功(4)李平不是不聪明，而是不用功〖解答〗用p：表示李平聪明，q：表示李平用功则：(1)(2)(3)(4)分别符号化为：∧⌝⌝⌝∧(∧)q∧qppqqpp⌝【练习】将下列命题符号化(1)苹果是红的与香蕉是黄的(2)他打开箱子，并拿出一件衣服(3)张小明和张小华是堂兄弟(4)4是偶数且是素数注意：(3)是简单命题(3)析取：两个命题P和Q的析取是一个复P∨合命题，记做：Q当且仅当P和Q同时为F时，QP∧的真值为F，否则为T〖注意〗自然语言常用“或”表示，注意或具有双义性，可以是兼容或，也可以是排斥或【例题3】将下列命题符号化(1)我选修英文课或数学课(2)灯泡有故障或开关有故障(3)通过电视看杂技或到剧场看这场杂技（异或）(4)小李或小张可以解答这个问题(4)条件：两个命题P和Q，其条件命题是P→一个复合命题，记做：Q当且仅当P的真值为T，且Q的真值为F时，QP→的真值为F，否则为T〖注意〗自然语言常用“只要……就……”、“……仅当……”、“只有……才……”、“如果……则……”等【例题4】将下列命题符号化(1)只要不下雨，我就骑车上班(2)只有不下雨，我才骑车上班(3)如果422=+，则：太阳从东方升起(4) 如果422≠+，则：太阳从东方升起(5)双条件（等价）：两个命题P和Q，其复P↔叫做等价命题合命题Q当且仅当与Q的真值相同时QP↔的真值为T，否则为F〖注意〗自然语言常用“当且仅当”等【例题5】将下列命题符号化3是奇数(1) 4+当且仅当22=(2) 422=+当且仅当3不是奇数(3) 422≠+当且仅当3是奇数(4) 422≠+当且仅当3不是奇数(5)两圆的面积相等当且仅当他们的半径相等(6)两角相等当且仅当它们是对顶角上述介绍的五种联结词成为逻辑联结词，在命题逻辑中，可用这些联结词将各种各样的复合命题符号化，其具体步骤是：(1)分析出各简单命题，将其符号化(2)使用合适的联结词，把简单命题逐个联结起来，组成复合命题的符号化表示【例题6】将下列命题符号化(1)小王是游泳冠军或百米赛冠军(2)小王现在宿舍或在图书馆(3)选小王或小李中的一个人当班长(4)如果我上街，我就去书店看看，除非我很累(5)小王是计算机系的学生，他生于1968年或1969年，他是三好学生〖解答〗(1) 用p：表示小王是游泳冠军，q：表示小王是百米冠军，命题可符号化为：qp∨(2) 用p：表示小王在宿舍，q：表示小王在图书馆，命题可以符号化为：qp∨(3) 用p：表示小王当班长，q：表示小李当班长，命题可以符号化为：⌝p∧∧⌝∨(q)q()p(4)用p：表示我上街，q：表示我去书店看看，r：表示我很累则：命题可以符号化为：)⌝(q→r→p (5) 用p：表示小王是计算机系的学生，q：表示小王生于1968年，r：表示小王生于1969年，s ：表示他是三好学生 则：命题可以符号化为：()p q r s ∧∨∧五种联结词符也称为逻辑运算符，它与普通的数的运算符一样，可以规定运算的优先级，规定：优先级的运算顺序是：↔→∨∧⌝，如果出现的联结词相同，又无括号时，按从左到右的顺序运算；如果有括号，先进行括号中的运算第二节：命题公式及分类 ※命题公式由联结词q p q p q p q p p ↔→∨∧⌝,,,,和多个命题常项可以组成更复杂的复合命题，如果在复合命题中，r q p ,,等不仅可以代表命题常项，也可以代表命题变项，这样组成的复合命题形式叫做命题公式 抽象的讲，命题公式是由命题常项、命题变项、联结词、括号等组成的符号串【定义1】合式公式：(1)单个命题常项或变项1,0,,,,,,,, i i i r q p r q p 是合式公式(2)如果A 是合式公式，则：)(A ⌝也是合式公式(3)如果B A ,是合式公式，则：也是合式公式(4)只有有限次使用(1)、(2)、(3)组成的符号串才是合式公式可以将合式公式称为命题公式，简称公式〖注意〗(1)为方便起见，规定：)(A ⌝，)(),(),(),(B A B A B A B A ↔→∨∧的外层括号可以省略不写(2)根据定义，可知：r q p r q p q p ↔∧→→∨⌝)(),(),(等是命题公式，但r q p r pq →∨⌝→),等不是命题公式一个含有命题变项的命题公式的真值是不确定的，只有对它的每个命题变项用指定的命题常项代替后，命题公式才变成命题，此时其真值唯一确定，由此引出解释或赋值的定义【定义2】解释或赋值设A 为一个命题公式，n p p p ,,,21 为出现在A中的所有的命题变项，给n p p p ,,,21 指定一组真值，称为对A 的一个解释或赋值。

日常生活和数学中所用的“一切的”，“所 有的”,“每一个”，“任意的”，“凡”，“都” 等词可统称为全称量词，将它们符号化为 “用x”, . y 等表示个体域里的所有个体;
用 xF ( x), yG( y)等分别表示个体域里所有个体 都有性质 F 和都有性质 G .
2 存在量词
日常生活和数学中所用的“存在”，“有一 个”，“有的”，“至少有一个” 等词统称为 存在量词，将它们都符号化为“”.
解: (a) 令 F(x): x2-3x+2=(x-1)(x-2)，G(x): x+5=3. 命题 (1) 的符号化形式为
xF(x)
(4.7)
命题 (2) 的符号化形式为
xG(x)
(4.8)
显然(1)为真命题；而(2)为假命题，因为N不含负数.
(b) 在D2内，(1)和(2)的符号化形式还是(4.7)式和 (4.8)式，(1)依然是真命题，而此时(2)也是真命题.
所以对任何人a， M(a)∧H(a) 均为假， 因而 x ( M(x)∧H(x) )为假， 所以(4.11)表示的命题为真 .
(4) 令 F(x): x 是在美国留学的学生， G(x): x 是亚洲人.
命题(4)符号化形式为
┐ x(F(x)→G(x))
这个命题也为真.
(4.12)
P65 4、解：（1）F(x): x是有理数；G(x)：x能表示成分数
解: (a) 令F(x): x 呼吸. G(x): x 用左手写字.
(1) xF(x)
(4.1)
(2) xG(x)
(4.2)
(b) D2中除了有人外，还有万物，因而在符号化 时，必须考虑将人分离出来.
令 M(x): 是人. 在D2中，(1),(2)可以分别重述如下:

解 当被问战士回答“对”，则逻辑学家开启所指的门从容离
去。当被问战士回答“否”，则逻辑学家开启另一门从容离去。
分析：如果被问者是诚实战士，他回答“对” 。则另 一 名战士是说谎战士，他回答“是”，那么，这扇门 不是死亡门。
如果被问者是诚实战士，他回答“否”。则另 一名是说谎战士，他回答“不是”，那么，这扇门是 死亡门。
说明:在数理逻辑中，即使p、q没有内在联系， 但仍有意义.
(5)等价式:p，q 为两命题，复合命题“p 当且仅当 q” 称作 p 与 q 的等价式，记作 p q，符号“ ”称作等价 联结词，p q 为真当且仅当 p 与 q 的真值相同。
Байду номын сангаас
p
q p q
0
0
1
0
1
0
1
0
0
1
1
1
例1.6 1）集合A中没有元素当且仅当集合A是空集。 2）当王刚心情愉快时，他唱歌；反之，当 他唱歌时，一定心情愉快。 3）三角形三边相等的充要条件是三个角相等。 4) 2+2=5的充要条件是太阳从西边升起。
罗素将集合分为两类，一类是集合 A 本身是 A 的一个
元素，即 A A；另一类是集合 A 本身不是 A 的一个
元素，即 A A 。构造一个集合 S：S={A|AA},问 S 是
不是它自己的一个元素。即 S S 还是 S S 。
原子命题： 称由简单陈述句构成的命题为简单命题
或原子命题，
命题符号化：用小写英文字母(或带下标)p,q，r，…， pi , qi , ri , ……表示命题，称为命题符号化．用数字 1（或 T）表示真，用 0(或 F)表示假，则任何命题的真值不是 1 就是 0，但决不可能既可以为 1 又可以为 0。

第1 章命题逻辑第1 章命题逻辑授课内容知识点1：命题、联结词及命题符号化知识点2：命题公式、真值表及公式分类知识点3：等价式与等价演算知识点4：对偶式与蕴涵式知识点5：范式第1 章命题逻辑授课内容知识点6：主析取范式与主合取范式知识点7：命题演算的推理理论知识点8：有效结论证明方法知识点9：命题演算推理实例解析知识点1：命题、联结词及命题符号化一问题的引入命题逻辑是研究由命题为基本单位构成的前提和结论之间的可推导关系。

那么，什么是命题？如何表示和构成？如何进行推理的？例如：已知：如果今天星期三，那么公鸡会下蛋。

今天是星期三。

问题：根据以上前提你能推出什么结论？二命题、联结词及命题符号化1 命题的概念定义1.1.1：能够判断真假的陈述句称作命题。

命题仅有两种可能的真值：真和假，且二者只能居其一。

真用1或T表示，假用0或F表示。

由于命题只有两种真值，所以称这种逻辑为二值逻辑。

例1.1.1 判断下列语句哪些是命题①-1是整数。

②地球是围绕月亮转的。

③3+5=8。

④木星的表面温度是20 F。

⑤不要讲话！⑥你吃饭了吗？⑦本命题是假的。

（他正在说谎。

等）解①-④都是命题，①和③的真值为真，②真值是假，④不知真和假，但真值是可以确定的。

⑤⑥都不是命题。

⑦无法确定它的真值，当它假时，它便真；当它真时，它便假。

这种断言叫悖论。

2 命题的分类与表示•命题分为两类，第一类是原子命题，它是由再也不能分解成更为简单的语句构成的命题，称为原子命题。

用英文字母P，Q，R，…或带下标Pi，Qi，Ri，…表示之。

例如，用P表示武汉是一座美丽的城市，记为P：武汉是一座美丽的城市。

冒号：代表表示的意思•第二类是复合命题，它由原子命题、命题联结词和圆括号组成。

3 联结词1.3.1 否定联结词﹁P定义1.1.2设P表示一个命题，由命题联结词⎤和命题P连接成⎤P，称⎤P为P的否定式复合命题，⎤P读“非P”。

称⎤为否定联结词。

⎤P是真当且仅当P为假；否定联结词“⎤”的定义可由表1-1表示。

说明： x yG(x, y) 和 x yG(x, y)表示的含义不同！
第 10 页
四、符号化
例2 在一阶逻辑中将下面命题符号化。
(1)人都爱美。
(2)有人用左手写字。
个体域分别为：
(a) D为人类集合 (b) D为全总个体域
解: (a)设F(x):x爱美，G(x):x用左手写字，则
(1) xF(x) (2) xG(x)
， L(x,y): x与y跑得同样快。 (5) ﹁ x y(F(x) G(y) H(x, y)) (6) ﹁ x y(F(x) F(y) L(x, y))
第 16 页
总结和作业
➢ 小结 ◆ 理解个体词、谓词、量词的含义 ◆ 掌握一阶逻辑命题的符号化
➢ 作业（做书上）
课本63-64页 4(1) (3), 5(1) (3)，6 (1) (3) (5)
第1 页
第四章 一阶逻辑基本概念
➢ 命题逻辑的局限性
在命题逻辑中，研究的基本单位是简单命题，对简单 命题不再进行分解，并且不考虑命题之间的内在联系和数 量关系。
➢ 一阶逻辑所研究的内容
为了克服命题逻辑的局限性，将简单命题再细分，分 析出个体词、谓词和量词，以期达到表达出个体与总体的 内在联系和数量关系。 ◆ §4.1一阶逻辑命题符号化 ◆ §4.2一阶逻辑公式及解释 ◆ §5.1一阶逻辑等值式与置换规则 ◆ §5.2一阶逻辑前束范式
第四章 一阶逻辑基本概念
➢ 苏格拉底三段论
◆ 所有的人都是要死的。 ◆ 苏格拉底是人。 ◆ 所以，苏格拉底是要死的。 试证明此推理。 解：令p:所有的人都是要死的,q:苏格拉底是人,r:苏格拉底 是要死的，则 前提：p，q 结论：r 推理的形式结构： p Ù q ® r

人，卻一毛錢也沒賺到！』算命仙摸著下巴說：「那就奇怪了，不過既然不準，錢就還給你吧 。」
當麥芽糖商人回去後，糕餅商人也怒氣衝天的跑進來。『今天我都沒賺到錢，把我的錢還 給我！』算命仙停頓了一下，問說：「那麼，是否有碰到來自東方的人呢？」糕餅商搔著頭說 ：『沒有耶，只碰到來自南方的人。』「那就對啦，我是說你如果碰到從東方來的人就會賺錢 ，可沒說碰到從南方來的人會賺錢啊。」糕餅商聽這話似乎有理，就回去了。
偽值表清楚的顯示只有在 3 的情形之下才會發生。所以，用「如果 p 就 q」的方法幫人家算命，總會有四分之三機率是準確的。因此，即使 承諾「如果算不準就退錢」，算命仙仍然可能賺到錢。因為，算不準 的機準只有四分之一。小心別上當哦！ • 大人常對小孩說：「如果你乖乖，我就給你糖吃。」不知道有沒 有小孩了解，即使不乖，還是可能有糖可吃這件事呢？
离散数学 第一章 命题逻辑
4
• 故事中的算命仙就是巧妙地運用了這種條件命題而賺到錢的。讓我們 來研究一下他是如何辦到的。
• 我們考慮“ P= 碰上來自東方的人，Q= 賺到錢 ”有四種情形會發 生：
1. 碰到來自東方的人，而賺到錢。 2. 碰到來自東方的人，但沒有賺到錢。 3. 沒有碰到來自東方的人，而賺到錢。 4. 沒有碰到來自東方的人，也沒賺到錢。 • 然而，算命仙算不準的情形即是「如果 p 就 q」為偽的情形。上面的真
4. 蕴含“→”
定义1-4 由命题P和Q利用“→”组成的复合命题，称为蕴含式复合
命题，记作“P→Q”（读作“如果P，则Q”）。
当P为真，Q为假时，P→Q为假，否则 P→Q为真。
P
Q
P→Q
0
0
1
0
1
1
1
0
0

如果写成 (PQ)∨(P R)，就表明两种作法都是假的时候，我说 的才是假话.这显然不对.
若写成(PQ) (P R)时，当P为F，Q为F时，即天没下雨而我没 上街，此时我说的是假话，但是表达式 (PQ) (P R) 的真值却是
“T” ，因为此时(P R)的真值是“T”.
4
二、复合命题的符号化(翻译) 有了命题演算的合式公式的概念,我们可以把自然语言
中的有些语句(复合命题),翻译成数理逻辑中的符号形式. 基本步骤如下:
1)首先要明确给定命题的含义. 2)对于复合命题，找联结词，用联结词断句，分解出各
个原子命题. 3)设原子命题符号，并用逻辑联结词联结原子命题符号，
构成给定命题的符号表达式.
5
例2 说离散数学无用且枯燥无味是不对的. P：离散数学是有用的. Q：离散数学是枯燥无味的. 该命题可写成： (P∧Q). 例3 如果小张与小王都不去，则小李去. P：小张去. Q：小王去. R：小李去. 该命题可写成： (P∧Q)R. 如果小张与小王不都去，则小李去. 该命题可写成： (P∧Q)R, 也可以写成： (P∨QP∧Q， PR， P∨Q∧R，PQ ∨S , (P W) Q)； 下面的式子才是合式公式：
(P∧Q)，(PR)，((P∨Q)∧R). 按照合式公式定义最外层括号必须写. 约定：为方便，最外层括号可以不写，上面的合式
公式可以写成： P∧Q，PR，(P∨Q)∧R.
命题公式及符号化
一、 命题公式
1.定义1-3.1 命题演算的合式公式
合式公式是由命题变元、命题常量、联结词和圆括号按 一定的逻辑关系联结起来的符号串.我们以如下递归的形 式来定义合式公式：
(1)单个命题变元是一个合式公式. (2)若A是合式公式，则┐A也是合式公式. (3)若A，B是合式公式，则(A∧B)，(A∨B)，(AB)，

命题符号化(1) 杭州不是中国的首都。

(2) 张三虽然学习努力但成绩并不优秀。

解 (1) 令P：杭州是中国的首都。

则命题“杭州不是中国的首都”符号化为：┐P(2) 令P：张三学习努力。

Q：张三成绩优秀。

则命题“张三虽然学习努力但成绩并不优秀。

”符号化为：P∧┐Q。

合取运算特点：只有参与运算的二命题全为真时，运算结果才为真，否则为假。

自然语言中的表示“并且”意思的联结词，如“既…又…”、“不但…而且…”、“虽然…但是…”、“一面…一面…”等都可以符号化为∧。

注意：不要见到“与”或“和”就使用联结词∧！下列命题符号化(1) 北京不仅是中国的首都而且是一个故都p：北京是中国的首都。

q：北京是一个故都。

p∧q：北京是中国的首都并且是一个故都。

（2）牛启飞和林妹妹是好朋友P:牛启飞和林妹妹是好朋友(3) 王晓既用功又聪明..王晓不仅聪明，而且用功 (4). (5) 王晓虽然聪明，但不用功. (6) 张辉与王丽都是三好生.(7) 张辉与王丽是同学：王晓聪明，则 p：王晓用功，q解令q ∧ (3) pq ∧ (4) p∧q.(5) p令 r : 张辉是三好学生，s :王丽是三好学生(6) r∧s.(7) 令 t : 张辉与王丽是同学，t 是简单命题 .设p,q为二命题，复合命题“p或q”称为p与q的析取式，记作p ∨ q，符号∨称为析取联结词。

将下列命题符号化(1) 2或4是素数.(2) 2或3是素数.(3) 4或6是素数.(4) 小元元只能拿一个苹果或一个梨.(5) 王晓红生于1975年或1976年.是素数, s: 6是素数, r: 4是素数, q: 3是素数 p: 2令解．.均为相容或则 (1), (2), (3)1, 1, 0. 它们的真值分别为∨s,: p分别符号化为∨r ,p∨q,r.而 (4),(5)为排斥或 u:小元元拿一个梨，小元元拿一个苹果，令t :(t∧∧u) ∨ (t 则 (4) 符号化为u).令v :王晓红生于1975年,w:王晓红生于1976年,则 (5) 符号化为w) w)(v∧∨(v∧。

解：这9个句子中，（7）～（9）都不是陈述句， 因而都不是命题。 （1）是真命题，（2）是假命题。 （3）的真值虽然现在还不能判断，到2100年就能 判断了，因而是命题。 （4）在十进制中为假，在二进制中为真，当确定 了进位制时其真值就确定了，因而是命题。 （5）是命题，真值视具体情况惟一确定（不是真 就是假）。 （6）是陈述句，但无法给出真假值。这种自相矛 盾的判断称为悖论，以后再讲。
1.2.2 合取联结词∧
定义1.2.2 设P,Q为二命题，复合命题“P并且Q”（或 “ P 与 Q” ）称为 P 与 Q 的合取式，记作 P∧Q ，符号 “∧” 称为合取联结词 . P属于二元 ∧Q为真当且仅当 P和Q同时为真 . 说明：1、“∧” (binary)运算符 . 2、联结词“∧”的定义真值表如下：
从上述例子可以看出，原命题与逆否命题意思相同, 即等价：
P Q Q P
逆命题与反命题意思相同。 这一点非常重要，在推理过程中，有时按原命题进 行推导比较困难，而用逆否命题却可收到事半功倍 的效果。
1.2.5 双条件联结词（等价联结词）
定义1.2.5 设P,Q为二命题，复合命题“P当且仅当Q” 称为P与Q的双条件命题，记作P iff Q或PQ，符号 称为双条件（等价）联结词。PQ为真当且仅当
Q:今天天下雨。
定义1-3 如果一个命题标识符代表任意未知命题，则 称该命题标识符为命题变元（命题变项）.如果一 个命题标识符代表一个确定的命题，则称之为命 题常元。
命题变元类似代数中的变量，命题常元类似
常量，但两者有着本质的区别。命题变元或常元
代表的是命题元素，而变量和常量代表的是一个
数值。
例如，x+y≥ 5 这是一个代数表达式，其中x和y是 变量，不是命题变元，但该表达式也可以作为一 个命题变元。假设代表该表达式的命题变元为z， 当变量x和y的值确定后，表达式成为一个命题常 元，命题变元z被该命题常元所取代成为命题，且 命题的真值随变量x和y不同取值而变化。 当用确定的命题代入命题变元时称为对命题 变元的代入。

12

（Ⅱ）形成规则
◦ （i）一个谓词符号F，后面跟有写在一对括号内、并用逗
点适当分开的n个个体词（n≥1），是原子公式。 ◦ （ii）如果A是公式，则A是公式。 ◦ （ iii ）如果 A 和 B 都是公式，则 A ∧ B ， A ∨ B ， AB ， AB是公式。 ◦ （iv）如果A是公式，则xA，xA是公式。 ◦ （v）只有按以上方式形成的符号串是公式。
（1）t是一个个体常项； （2）A是一个原子公式，x是其中的自由变项，t是任一个体词； （3）A含有量词，但自由变项x不在这些量词的辖域之内，t是任一 个体词； （4）A含有量词，且自由变项x在这些量词的辖域之内，则t必须是 与已量化变项不同的变项。否则，称为t对于公式A中的自由变项x代 入不自由。
33
◦ 全称量词引入规则＋：从A(x)推出xA(x)，只要能够确 保前提中的自由变项x是任意的。以下情况下的自由变项不 能确保是任意的，被称为“加标记变项”：
（i）给定前提中的自由变项；
（ii）根据假设引入规则所引入的假设中的自由变项；
（iii）从该前提或假设出发，根据QN的推演规则所得到的的那 些行中、与前提或假设中的自由变项相同的自由变项； （iv）给特指常项做下标的自由变项。对加标记变项，＋规则 不适用。

9

自然语言中性质命题的符号化
在论域为全域时，六种直言命题可以如下方式符号化：
◦ （1）全称的直言命题应符号化为一个全称蕴涵式。 SAP：x(S(x)→P(x))
SEP：x(S(x)→P(x))
◦ （2）特称的直言命题应符号化为存在合取式。 SIP：x(S(x)∧P(x))
20

谓词逻辑的树形图是命题逻辑树形图的扩充，命题 逻辑原有的关于联结词的九个画图规则仍然有效；

（1）所有的人都呼吸。 所有的个体都呼吸。 （2）有的人用左手写字。有的个体用左手写字。
所以个体域是全总个体域时，命题应转述为： （1）对于任意的个体，如果它是人，则它是要呼吸的。
（2）存在着个体，它是人并且用左手写字。
需要引进一种新的谓词（特性谓词）将人与其它事 物区分开来 令M（x）：x是人。
使用特性谓词M（x），所给命题就可以符号化为： （1）x（M（x）→F（x）） （2）x（M（x）∧ G（x））
命题可看成“存在在美国留学的学生不是亚洲 人”。
令F（x）：x是在美国留学的学生；
G（x）：x是亚洲人 命题符号化为：x（F（x）∧┐G（x）） 或者命题可看成“在美国留学的任意学生都是亚 洲人”的否定。 命题符号化为：┐x（F（x）→G（x））
2021
18
2021
19
例 使用多元谓词将下列命题符号化。 （1）兔子比乌龟跑得快。 （2）有的兔子比所有的乌龟跑得快。 （3）并不是所有的兔子都比乌龟跑的快。 （4）不存在跑的同样快的两只兔子。
解：本题未给出个体域，因而以全总个体域为个体域 令M（x）：x为人
（1）令F（x）：x长着黑头发
可将命题转述为：对所有个体而言，如果它是人， 那么它就长着黑头发。
命题符号化为：x（M（x）→F（x））
2021
16
（2）有的人登上过月球。 令G（x）：x登上过月球 可将命题转述为：存在着个体，它是人并且登上过
不带个体变项的谓词称为0元谓词。 例如：F（a），G（a，b），P（a1，a2，…，an） 都是0元谓词。
2021
8
例 将下面命题用0元谓词符号化。 （1）只有2是素数，4才是素数 （2）如果5大于4，则4大于6
命题的谓词符号化步骤： （a）找出谓词、个体词常项 （b）符号化谓词和个体词常项 （c）使用符号化了的谓词和个体词以及逻辑运算符

§4.2一阶逻辑公式及解释
14/26
非逻辑符号: 个体词常项符号, 函数符号和谓词符号 逻辑符号: 个体词变项符号, 量词符号, 联结词符号和括号与逗号 定义 设L是一个非逻辑符号, 由L生成的一阶语言L的字母表 包括下述符号如下:
非逻辑符号 (1) L中的个体常项符号: a, b, c, …; ai , bi , ci ,… , i≥1 (2) L中的函词符号: f, g, h, …; fi , gi , hi ,… , i≥1 (3) L中的谓词符号: F,G, H,…; Fi ,Gi , Hi ,…, i≥1 逻辑符号 (4) 个体变项符号: x, y, z, …; xi , yi , zi ,…, i≥1 (5) 量词符号: , . (6) 联结词符号: ┐,∧,∨, →, ↔. (7) 逗号与括号: , , ( ) .
练习 函数f(x)在x=a处极限为b 任给小正数ε, 则存在正数 δ, 使得 当0<|x-a|<δ时, |f(x)-b|<ε成立 任意ε>0, 存在δ>0, 使得 当0<|x-a|<δ时, |f(x)-b|<ε成立 ∀ε(ε>0→ ∃δ(δ>0∧ ∀x(|x-a|<δ→|f(x)-b|<ε)))
定义 在公式 xA 和 xA中, 称 x 为指导变元, A为相
应量词的辖域. 在x 和 x 的辖域中, x的所有出现都 称为约束出现, A中不是约束出现的其它变项都称为 自由出现.
谓词续
6/26
④不含个体变项的谓词称为0元谓词. 例如 F(a), G(a,b), P(a1,a2,…,an)等. 当F, G, P等为谓词常项时, 0元谓词即为命题. 因此, 命题可看作特殊的谓词. 例 用0元谓词将下列命题符号化, 并讨论它们的真值. (1) 只有当2是素数时, 4才是素数; (2) 如果5大于4, 则4大于6.

在深入探讨谓词逻辑以及如何使用它将概念和命题符号化之前，让我们先来了解一下什么是谓词逻辑。

谓词逻辑是一种数理逻辑系统，它通过谓词来描述命题中的主体和谓语之间的关系。

通过谓词逻辑，我们可以更准确地表达命题，并进行逻辑推理。

接下来，我们将按照从简到繁的方式来探讨如何使用谓词逻辑将概念和命题符号化的步骤。

一、理解谓词逻辑的基本概念在谓词逻辑中，谓词是描述一个或多个个体性质或关系的命题成分。

它由一个或多个变元（代表个体）以及逻辑联结词和量词构成。

在将概念和命题符号化的过程中，我们需要先理解谓词的基本概念，并学会如何用符号表示不同的谓词以及它们之间的关系。

二、将概念符号化的步骤1. 确定概念的要素：我们需要确定概念所涉及的要素和属性，以及它们之间的关系。

通过分析概念的内涵和外延，我们可以准确地描述概念所包含的内容。

2. 使用谓词符号化概念：一旦确定了概念的要素和属性，我们就可以使用谓词来符号化概念。

对于每个属性，我们可以引入相应的谓词，并用变元来表示个体，从而形成命题。

3. 建立命题关系：在将概念符号化的过程中，我们还需要建立命题之间的关系。

通过使用逻辑联结词（如“与”、“或”、“非”等），我们可以将多个命题进行组合，并得出更为复杂的命题。

三、将命题符号化的步骤1. 确定命题的要素：在将命题符号化之前，我们需要先确定命题所涉及的要素和关系。

通过分析命题的主体和谓语，我们可以准确地描述命题所表达的内容。

2. 使用谓词符号化命题：对于每个命题要素，我们可以引入相应的谓词，并用变元来表示个体，并进而用逻辑联结词构成命题符号。

3. 建立命题之间的逻辑关系：在将命题符号化的过程中，我们还需要建立命题之间的逻辑关系。

通过使用逻辑联结词和量词，我们可以对命题进行逻辑分析，并进行推理和论证。

总结回顾通过上述步骤，我们可以清晰地了解如何使用谓词逻辑将概念和命题符号化。

在这个过程中，我们需要先理解谓词逻辑的基本概念，然后分别对概念和命题进行符号化，并建立它们之间的逻辑关系。

数理逻辑中的命题符号化的几个值得注意的问题组长：学号：组员：学号：组员：学号：日期数理逻辑是离散数学的重要组成部分，也是计算机科学的基础之一。

数理逻辑要解决的一个主要问题就是如何用数学的方法来研究判断和推理的问题，而要想将逻辑推理的方法准确地应用到实际问题中去，并在相应的数理逻辑运算体系下进行正确的推理从而获得准确的结论，其首要前提就是对普通语言文字所描述的命题进行正确的符号化，也就是将现实的问题准确地翻译成数理逻辑体系下的数学语言，即是要解决好命题符号化的问题。

1深刻理解逻辑联结词的含义正确使用逻辑联结词，尤其是条件联结词在命题逻辑学中，对命题进行符号化时常用下列五个联结词：否定、合取、析取、条件、双条件等五个联结词。

只有在准确地理解逻辑联结词的含义的基础上，才能做到正确地使用逻辑联结词并将命题符号化。

所以将命题符号化的前提是要深刻地理解逻辑联结词的含义，上述五个逻辑联结词的含义具体如下：1．1否定：设P为一命题，则P的否定是一个新命题，记作P。

若P为真（T）时，﹃P为假（F）；若P为假（F）时，﹃P为真（T）。

﹃称作否定联结词。

它是日常语言中的“非”、“不是”、“并非”等词汇的逻辑抽象。

1．2合取：设P、Q是两个命题，P与Q的合取是一个复合命题，记作P∧Q。

当且仅当P、Q同时为真（T）时，P∧Q为真（T），在其他情况下，P∧Q的真值都为假（F）。

∧称作合取联结词，它是日常语言中的“并且”、“也”、“不但…而且”、“既…又…”等词汇的逻辑抽象。

1．3析取：设P、Q是两个命题，P与Q的析取是一个复合命题，记作P∨Q。

当且仅当P、Q同时为假（F）时，P∨Q的真值为假（F），在其他情况下，P∨Q的真值都为真（T）。

∨称作析取联结词，它是日常语言中的“或者”、“要么”等词汇的逻辑抽象。

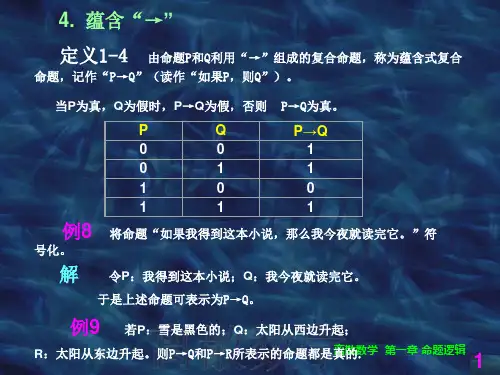
1．4条件：设P、Q是两个命题，其条件命题是一个复合命题，记作P→Q。

当且仅当P的真值为真（T），Q的真值为假（F）时，P →Q的真值为假（F），在其他情况下，P→Q的真值都为真（T）。

原子命题符号化及复合命题真假判断原子命题是逻辑学中最基本的命题，它不能再被分解为更小的命题。

原子命题可以用符号来表示，通常使用大写字母或者字母表中的其他字符来表示。

符号化是将自然语言中的命题转化为符号的过程。

在符号化的过程中，我们需要确定每个原子命题所代表的意义，以及它们之间的逻辑关系。

例如，我们可以用P来表示“今天是晴天”，用Q来表示“明天下雨”。

那么“今天是晴天并且明天下雨”可以用符号化的方式表示为P ∧ Q。

复合命题是由原子命题通过逻辑连接词（如并且、或者、非等）连接而成的命题。

通过对每个原子命题的真值赋值，我们可以判断复合命题的真值。

例如，对于复合命题P ∧ Q，如果P为真且Q为真，则整个命题为真；如果P 为真且Q为假，则整个命题为假。

下面是一个复杂的例子：
命题：如果明天下雨，那么我就不出门，除非我有雨伞。

符号化：用P表示“明天下雨”，用Q表示“我不出门”，用R表示“我有雨伞”。

那么命题可以表示为P → (Q ∧ R)。

真假判断：我们需要根据给定的条件判断每个原子命题的真值，然后根据逻辑连接词的真值表来判断复合命题的真值。

假设明天下雨为真，我不出门为真，我有雨伞为假。

根据逻辑连接词的真值表，我们可以得出P → (Q ∧ R) 的真值为真。

通过符号化和真假判断，我们可以更清晰地理解复杂命题中的逻辑关系。

这种方法不仅可以用于逻辑学的学习，还可以用于解决现实生活中的问题，如判断论证的有效性、分析法律文件等。

厦门大学数学科学学院命题及其符号化第1讲推理是由一系列的“命题”构成的。

推理“命题”“命题”“命题”前提结论能够判断真假（更确切地说，具有真假意义的）的陈述句。

即命题的判断结果。

真值只取两个值:真（用1表示）假（用0表示）真命题真值为真的命题。

假命题真值为假的命题。

命题命题的真值罗纳尔多是球星。

简单命题不能被分解成更简单的命题的陈述句。

简单命题的符号化用小写英文字母p,q,r,…或带有下标的小写英文字母p 1,p 2,p 3，…来表示。

例1.1复合命题由简单命题通过联结词联结而成的陈述句。

该假命题包含了两个简单命题，“如果…,则…”是联结词。

如果“3>2”,则“3=2”。

例1. 2定义1.1设p为命题，复合命题“非p”（或“p的否定”）称为p的否定式，记作⎤p，符号⎤称为否定联结词。

规定⎤p为真当且仅当p为假。

运算规则属于单目运算符p p 10 01定义1.2设p,q为二命题，复合命题“p并且q”（或“p与q”）称为p与q的合取式，记作p∧q，符号∧称为合取联结词。

规定p∧q为真当且仅当p和q 均为真。

pq p ∧q 000010100111类似求最小运算规则属于双目运算符定义1.3设p,q为二命题，复合命题“p或q”称为p与q的析取式，记作p∨q，符号∨称为析取联结词。

规定p∨q为假当且仅当p和q均为假。

运算规则属于双目运算符类似求最大p q p ∨q000011101111注意自然语言中的“或”“相容或”“排斥或”p ∨q(p ∨q )∧⎤( p ∧q )符号化为符号化为(p ∧⎤q) ∨(⎤p ∧q)定义1.4设p，q为二命题，复合命题“如果p，则q”称为p与q的蕴涵式，记作p→q，并称p为蕴涵式的前件，q为蕴涵式的后件，符号→称为蕴涵联结词。

规定p→q为假当且仅当p为真q为假。

运算规则属于双目运算符p q p q 001 011 100 111难点为什么规定前件为假时，不论后件真假与否，蕴含式都为真呢？其实我们平时也采用这种思维方式，譬如，说“如果太阳从西边出来，我就不姓张。