实验3模糊工具箱模糊推理

在线推理式模糊逻辑控制器设计实验报告学院：电力学院专业：自动化学号：姓名：时间：2013年11月16日一、实验目的利用Matlab软件实现模糊控制系统仿真实验，了解模糊控制的在线推理方法的基本原理及实现过程。

二、实验要求以matlab模糊工具箱中提供的一个水位模糊控制系统仿真的实例，定义语言变量的语言值，设置隶属度函数，根据提供的规则建立模糊逻辑控制器。

最后启动仿真，观察水位变化曲线。

三、实验步骤叙述在线推理模糊控制的仿真的主要步骤。

1）在matlab命令窗口输入：sltank，打开水位控制系统的simulink仿真模型图，如图；2）在matlab的命令窗口中，输入指令：fuzzy，便打开了模糊推理系统编辑器（FIS Editor），如图；3）利用FIS Editor编辑器的Edit/Add variable/input菜单，添加一条输入语言变量，并将两个输入语言和一个输出语言变量的名称分别定义为：level；rate；valve。

其中，level代表水位（三个语言值：低，高，正好），rate代表变化率（三个语言值：正，不变，负），valve代表阀门（五个语言变量：不变，迅速打开，迅速关闭，缓慢打开，缓慢关闭）；4）①利用FIS Editor编辑器的Edit/membership function菜单，打开隶属度函数编辑器，如下图，将输入语言变量level的取值范围（range）和显示范围（display range）设置为[-1，1]，隶属度函数类型（type）设置为高斯型函数（gaussmf），而所包含的三条曲线的名称（name）和参数（parameters）（[宽度中心点]）分别设置为：high,[0.3 -1];okay [0.3 0];low [0.3 1]。

其中high 、okay、low分别代表水位高、正好、低；②将输入语言变量rate的取值范围（range）和显示范围（display range）设置为[-0.1，0.1]，隶属度函数类型（type）设置为高斯型函数（gaussmf），而所包含的三条曲线的名称（name）和参数（parameters）（[宽度中心点]）分别设置为：negative,[0.03 -0.1];none [0.03 0];positive [0.03 0.1]。

控制理论与控制工程《智能控制基础》课程实验报告专业：控制理论和控制工程班级：双控研2016姓名：洪帅任课教师：马兆敏2016年12 月4 日第一部分：模糊控制实验一模糊控制的理论基础实验实验目的：1 练习matlab中隶属函数程序的编写，同时学习matlab数据的表达、格式、文件格式、存盘2 学习matlab中提供的典型隶属函数及参数改变对隶属度曲线的影响3 模糊矩阵合成仿真程序的学习4 模糊推理仿真程序实验内容（1）要求自己编程求非常老，很老，比较老，有点老的隶属度函数。

1隶属函数编程试验结果如图1-1图1-1隶属度函数曲线（2）完成思考题P80 2-2 写出W及V两个模糊集的隶属函数，并绘出四个仿真后的曲线。

仿真曲线见图1-2，图1-2隶属度函数曲线2 典型隶属函数仿真程序学习下列仿真程序，改变各函数中的参数，观察曲线的变化，并总结各种隶属函数中其参数变化是如何影响曲线形状变换的。

M=1 M=3M=3 M=4M=5 M=6图1-3 M 在1、2、3、4、5、6时的图形2 模糊矩阵合成仿真程序：学习P31例2-10，仿真程序如下，（1） 完成思考题P81 2-5，并对比手算结果。

完成思考题P81 2-4，并对比手算结果。

（2） 2-5：(1) Matlab 结果如下①②③P81 2-5手算结果：P=⎥⎦⎤⎢⎣⎡7.02.09.06.0 Q=⎥⎦⎤⎢⎣⎡4.01.07.05.0 R=⎥⎦⎤⎢⎣⎡7.07.03.02.0 S=⎥⎦⎤⎢⎣⎡5.06.02.01.0(PοQ)οR=⎥⎦⎤⎢⎣⎡4.04.06.06.0(PUQ)οS=⎥⎦⎤⎢⎣⎡5.06.05.06.0(PοS)U(QοS)=⎥⎦⎤⎢⎣⎡5.06.05.06.0总结：手算结果和MATLAB运行结果一致。

(2)（2）思考题P81 2-4 Matlab运行结果如下：P81 2-4题手算结果如下：()3020104.01104.02030++++-+-+-=eZEμ()30203.01013.0102030++++-+-+-=ePSμ()()3020104.03.0102030++++-+-+-=⋂eePSZEμμ()()30203.01011104.02030++++-+-+-=⋃eePSZEμμ总结：手算结果和MATLAB运行结果一致。

模糊推理方法模糊推理方法是一种基于模糊逻辑的推理方法，它不同于传统的二值逻辑推理，而是考虑了事物之间的不确定性和模糊性。

在现实生活中，我们经常面对各种模糊的问题，例如天气预报、医学诊断、金融风险评估等等，这些问题都存在一定的模糊性和不确定性。

而模糊推理方法正是为了解决这些模糊问题而被提出的。

模糊推理方法的核心是模糊集合理论，它将模糊性作为一个数学概念进行描述。

在模糊集合理论中，每个元素都可以具有一定的隶属度，表示该元素属于该模糊集合的程度。

通过模糊集合的隶属度，我们可以对事物进行模糊分类和模糊推理。

模糊推理方法主要包括模糊逻辑推理和模糊数学推理两种形式。

模糊逻辑推理是通过对模糊命题的模糊逻辑运算，推导出模糊结论的过程。

模糊数学推理则是利用模糊数学的方法，通过模糊关系的运算，得出模糊结论的过程。

在模糊推理方法中，常用的推理规则包括模糊蕴涵规则、模糊合取规则、模糊析取规则等。

这些推理规则可以根据具体的问题和需求进行选择和组合，以实现对模糊问题的推理和决策。

模糊推理方法的应用非常广泛。

在天气预报中，由于气象数据的不确定性和模糊性，传统的二值逻辑推理往往无法准确预测天气情况。

而模糊推理方法可以通过对多个气象数据的模糊运算，得出更准确的天气预报结果。

在医学诊断中，由于病情的复杂性和多样性，传统的二值逻辑推理往往无法全面考虑各种可能性。

而模糊推理方法可以通过对病情特征的模糊分类和模糊推理，提供更全面的医学诊断结果。

除了天气预报和医学诊断，模糊推理方法还广泛应用于金融风险评估、交通流量预测、工程管理等领域。

在金融风险评估中，由于金融市场的不确定性和复杂性，传统的二值逻辑推理往往无法准确评估风险。

而模糊推理方法可以通过对各种金融指标的模糊运算，得出更准确的风险评估结果。

在交通流量预测中，由于交通数据的不确定性和随机性，传统的二值逻辑推理往往无法准确预测交通流量。

而模糊推理方法可以通过对多个交通数据的模糊运算，得出更准确的交通流量预测结果。

§3.3 模糊推理系统系统是指两个以上彼此相互作用的对象所构成的具有某种功能的集体。

模糊推理系统又称为模糊系统，是以模糊集合理论和模糊推理等技术为基础，具有处理模糊信息能力的系统。

模糊推理系统以模糊理论为主要计算工具，可以实现复杂的非线性映射，而且其输入输出都是精确的数值，因此具有广阔的应用前景。

3.3.1 模糊推理系统的结构一、模糊推理系统的组成模糊推理是一种仿生行为的近似推理方法，主要用来解决带有模糊现象的复杂推理问题。

由于模糊现象普遍存在，因此，模糊推理系统被广泛使用。

目前，已经在自动控制，数据处理、决策分析及模式识别等领域得到成功应用。

从功能上来看，模糊推理系统主要由模糊化、模糊规则库、模糊推理方法及去模糊化几部分组成，其基本结构如图3.3.1所示。

图3.3.1模糊推理系统的功能结构二、模糊推理系统的工作过程为了满足实际信息处理需要，模糊系统的输入输出必须是精确的数值。

由图3.3.1看出，模糊推理系统的工作机理为：首先通过模糊化模块将输入的精确量进行模糊化处理，转换成给定论域上的模糊集合；然后激活规则库中对应的模糊规则，并且选用适当的模糊推理方法，根据已知模糊事实获得推理结果，最后将该模糊结果进行去模糊化处理，得到最终的精确输出量。

关于模糊推理方法，前面已经做了比较详细的介绍。

但是模糊推理系统对模糊规则库有何要求？如何将精确值转换成模糊集合，以及如何将模糊集合去模糊化，使之成为精确的数值？这些内容是设计模糊推理系统的基础，现在将详细阐述这方面的内容。

3.3.2 模糊化(Fuzzification)精确值进入模糊推理系统时，一般要将其模糊化成给定论域上的模糊集合。

可见，模糊化的实质是将给定输入*x转换成模糊集合*~A。

模糊化的原则是：①在精确值*x处模糊集合*~A的隶属度最大；②输入数据若噪声干扰时，模糊化结果就具有一定的抗干扰能力；③模糊化运算应尽可能简单。

下面介绍三种常用的模糊化方法。

如何使用Matlab进行模糊推理引言在现实生活中，我们往往需要处理不确定性和模糊性的问题。

而模糊推理作为一种处理模糊信息的方法，在人工智能和信息处理领域得到了广泛应用。

Matlab作为一个强大的数学建模和仿真工具，也提供了丰富的功能来进行模糊推理。

本文将介绍如何使用Matlab进行模糊推理的基本方法和技巧。

一、Matlab中的模糊逻辑工具箱Matlab提供了专门的工具箱来支持模糊逻辑的建模和推理。

用户可以使用这些工具箱中的函数和工具来构建模糊系统、进行模糊推理和进行系统性能评估。

在使用之前，需要先安装模糊逻辑工具箱，并通过调用相关函数将其加载到Matlab环境中。

二、模糊逻辑建模1. 变量和隶属函数的定义在进行模糊逻辑建模时，首先需要定义模糊变量和相应的隶属函数。

模糊变量表示模糊信息的输入或输出，而隶属函数则用来描述变量的模糊隶属度。

在Matlab中，可以通过调用相关函数来创建和定义模糊变量和隶属函数。

例如，使用fis工具箱中的newfis函数可以创建一个新的模糊系统对象，使用addvar 函数可以向模糊系统中添加新的模糊变量，使用addmf函数可以向模糊变量中添加新的隶属函数。

2. 模糊规则的定义模糊规则用来描述输入变量与输出变量之间的关系，其中包含了变量之间的模糊推理过程。

在Matlab中，可以使用addrule函数来定义和添加模糊规则。

该函数可以接受不同形式的输入，例如模糊规则的标准形式、模糊规则的表格形式等。

三、模糊推理1. 模糊推理的基本原理在进行模糊推理时，需要根据已有的输入变量和模糊规则来计算输出变量的模糊值。

在Matlab中，可以使用evalfis函数来进行模糊推理。

该函数接受输入变量、模糊规则和一些其他参数作为输入，返回输出变量的模糊值。

2. 基于模糊逻辑的决策制定通过模糊推理，我们可以根据已知的输入变量和模糊规则来计算输出变量的模糊值。

然而，模糊值通常需要转化为实际的决策结果。

实验一熟悉模糊工具箱一、目的和要求1.目的(1)通过本次实验，进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制器的设计过程。

(2)掌握MATLAB模糊逻辑工具箱的图形用户界面设计模糊控制器的过程。

2.要求（1）充分理解实验内容，并独立完成实验报告。

（2）实验报告要求：实验题目、实验具体内容、结果分析、收获或不足。

二、实验内容1、利用matlab中的模糊逻辑工具箱提供的图形用户界面（GUI）工具设计一个两输入、一输出的模糊控制器，控制器的要求如下：（1）设模糊控制器的输入变量为：误差E和误差变化EC，输出量为U。

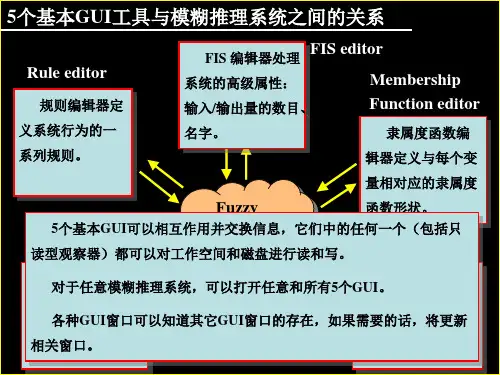
（2）隶属度函数：◆隶属度函数均为三角函数◆E、EC和U的模糊语言变量集均为{NB,NM,NS,ZO,PS,PM,PB}◆E和EC论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}◆U的论域为{-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}（3）控制规则表如下：表1 模糊控制表三．实验步骤模糊逻辑工具箱提供的图形用户界面（GUI）工具有五个：模糊推理系统（FIS）编辑器；隶属函数编辑器；模糊规则编辑器；模糊规则观察器；输出曲面观察器。

1.模糊控制器结构设计FIS处理系统有多少个输入变量，输出变量，名称是什么，模糊算子“与”(min，prod乘积，custom自定义)，“或”(max大，probor 概率统计方法，custom)，推理方法（min，prod，custom），聚类方法（max，probor，sum，custom），解模糊的方法（centroid 质心法，bisector中位线法，middle of maximum，largest of maximum，smallest of maximum）。

Matlab的FIS界面如图3所示。

图3 模糊推理系统（FIS）界面2.隶属函数编辑器：确定各个变量的论域和显示范围（左下角编辑区内），如图4所示。

实验报告课程名称智能控制学院自动化学院班级姓名学号日期2019.4.9基于mamdani 型模糊控制器线性系统的位置跟踪一、实验目的1.熟悉mamdani 模糊控制器的设计原理；2.掌握模糊控制器的设计步骤；3.熟悉模糊控制规则对控制系统效果的影响 ；4.熟悉模糊控制器设计的Matlab 命令；5.掌握用MATLAB 实现模糊控制系统仿真的方法。

二、设备及条件 计算机系统Matlab 仿真软件三、实验原理根据跟踪误差及其变化率，设计模糊控制器使得跟踪误差趋近于零。

四、设计要求 已知某一线性系统2400500s s+，根据误差及其变化率来设计模糊控制器，使得闭环系统的输出跟踪正弦信号0.5sin(10)t ，已知：误差及其变化率的范围初步定为[]33-，要求分为7个模糊集； 输出的范围初步定为[]4.5 4.5-，要求分为9个模糊集；设计隶属度函数误差变化划分表，控制电压变化划分表和模糊控制规则表，基于MATLAB 实现该控制器，并对控制效果进行仿真，根据仿真结果对模糊控制规则、控制信号范围、误差及其变化率进行调整。

五、实验环境I Simulink 介绍1.1 Simulink 简介Simulink 是MATLAB 中的一种可视化仿真工具， 是一种基于MATLAB 的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。

1.2 Simulink 优点Simulink 提供一个动态系统建模、仿真和综合分析的集成环境。

在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。

对各种时变系统，包括通讯、控制、信号处理、视频处理和图像处理系统，Simulink 提供了交互式图形化环境和可定制模块库来对其进行设计、仿真、执行和测试。

II模糊控制工具箱介绍2.1 模糊控制工具箱简介MATLAB模糊控制工具箱为模糊控制器的设计提供了一种非常便捷的途径，通过它我们不需要进行复杂的模糊化、模糊推理及反模糊化运算，只需要设定相应参数，就可以很快得到我们所需要的控制器，而且修改也非常方便。

模糊推理方法
模糊推理方法是一种基于非确定证据的推断方法，它是集合概念和统
计推理相结合的结果，由著名的模糊理论创始人洛洛·塔夫斯基在1965
年提出。

其基本思想是基于模糊集合的本质，建立了对普通语言的数学模型，使我们能够从有限的观测集合中提取出更多的有价值的信息，从而更
好地支持现有的决策。

模糊推理方法的主要过程可以分为三步：
（1）提出假设。

首先，在假设的基础上，需要把系统划分为若干假
设集，让假设集内的每一种情况都有一定权重，根据权重来控制假设的实现，以及概率对应权重的变化。

（2）分析和推断。

根据提出的假设和假设集，根据概率和统计原理，对系统事件进行分析推断，运用模糊变量和模糊模型，分析其内在规律，
从而推断出系统动态的变化情况。

（3）多模态决策。

最后，根据前两步推断出的结果，运用模糊语言，把推断出来的决策转换为多模态决策。

模糊推理方法，有三种重要的技术，分别为模糊规则，模糊数学和模
糊统计。

1.模糊规则：即把模糊规则作为系统推理过程的调控工具。

实验六模糊推理系统（FIS）的设计与仿真一、实验目的：1．认识MATLAB模糊逻辑工具箱的功能和特点；2．了解MATLAB模糊逻辑工具箱的五个图形化系统设计工具的功能；3．能够运用MATLAB模糊逻辑工具箱对模糊逻辑系统进行正确的参数设置；4．掌握基于Simulink的模糊逻辑系统模块的建立。

二、实验工具：MATLAB软件（6.1以上版本）。

三、实验内容及步骤：（一）PART A MATLAB模糊逻辑工具箱设计思想在MA TLAB中提供了Fuzzy Logic Toolbox（FIS，Fuzzy Inference System），主要有五个界面组成：（1）FIS Editor （模糊推理编译器）（2）Membership Function Editor （隶属度函数编辑器）（3）Rule Editor （模糊规则编辑器）（4）Rule Viewer （模糊规则浏览器）（5）Surface Viewer（模糊推理输入输出曲面视图）1. 模糊推理编译器（1）在MATLAB命令窗口中输入：fuzzy ，激活FIS Editor。

Fig. 1 MAMDANIFIS Editor用于建立模糊逻辑系统的整体框架，包括输入与输出数目、去模糊化方法等。

(2)MATLAB 提供两个逻辑推理MAMDANI 和SUGENO 方法。

Fig. 2 SUGENO窗口左下方的五种算法分别是：And Method ：“与”算法；Or Method ：“或”算法；Implication ：蕴涵算法；Aggregation：综合；Deffuzification: 清晰化。

(3) 编辑FIS维数：在添加变量时可Edit——Add Variable ——Output2. 隶属度编辑器双击任意输入与输出模块，打开如下Membership Function Editor：Fig. 3 Membership Function EditorType：隶属度函数类型；Range：集合论域的取值；Params：曲线的拐点。

模糊推理法傻瓜式教程模糊推理法是一种基于模糊逻辑和模糊集合理论的推理方法，其主要用于处理不确定性和模糊性问题。

模糊推理法是一种较为简单易懂的推理方法，适用于一些简单的实际问题。

下面是一个傻瓜式的模糊推理法教程，具体介绍了模糊推理法的基本原理和步骤。

一、基本原理模糊集合是指在一些取值范围内的每个元素都有一个隶属度，表示该元素与该集合的匹配程度。

隶属度可以用一个隶属函数来表示，该函数将取值范围中的每个元素映射到一个隶属度值。

二、步骤1.定义输入和输出变量：首先确定需要处理的问题的输入和输出变量，以及各个变量的取值范围。

2.定义模糊集合和隶属函数：对每个变量定义相应的模糊集合和隶属函数，选择合适的隶属函数类型，并确定各个隶属函数的参数。

3.确定规则集：根据问题的特点和经验知识，确定一组规则集。

每条规则包含一个条件和一个结论，条件和结论都是模糊集合。

4.模糊化输入：将实际输入的值映射到相应的模糊集合上，计算每个模糊集合的隶属度。

5.模糊推理：对每条规则，计算条件和实际输入的匹配程度，得到结论的隶属度。

6.合并输出：通过对所有规则的结论进行合并，得到最终的输出。

7.反模糊化：将模糊输出转化为实际的数值，可以使用一些常用的反模糊化方法，如最大隶属度法、面积法等。

8.输出结果：得到最终的输出结果，完成模糊推理过程。

三、例子现以车速为例，假设输入变量是车速，输出变量是制动距离，取值范围均为0到100。

1.定义模糊集合和隶属函数：假设车速和制动距离分别有三个模糊集合"低"、"中"和"高"，并分别定义对应的隶属函数。

2.确定规则集：假设有以下规则集：-如果车速是低，那么制动距离是近；-如果车速是中，那么制动距离是中等；-如果车速是高，那么制动距离是远。

3.模糊化输入：假设实际输入的车速是70，根据隶属函数计算车速的隶属度，分别为0.4、0.7和0.24.模糊推理：根据规则和条件的隶属度，计算每条规则的结论隶属度，分别为0.4、0.7和0.25.合并输出：将所有规则的结论隶属度进行合并，得到最终的输出。

1、命令窗口中输入fuzzy命令、得到以下界面2、edit--add variable 此时便有经典的E EC 输入，U输出系统3、输入输出变量的模糊化：即把输入输出的精确量转化为对应语言变量的模糊集合Edit--membership functions在上面的界面上edit-Add-mfs这个图表明的是添加隶属函数的个数为7.添加完后会出现比较乱的线实际上是可以直接删掉的Params填对应type的范围 range为总的范围此处的type指的是nb nm ns zero ps pm pb4、模糊推理决策算法设计：即根据模糊控制规则进行模糊推理，并决策出模糊输出量。

Edit--rules5、最后步骤为解模糊对输出模糊量的解模糊：模糊控制器的输出量是一个模糊集合，通过反模糊化方法判决出一个确切的精确量，凡模糊化方法很多，我们这里选取重心法。

然后Export to disk，即可得到一个.fis文件，这就是你所设计的模糊控制器最后得到的fis文件如下：说明：此文档就是为了说明步骤不代表控制真的就是这个样子的【附加总结类文档一篇，不需要的朋友可以下载后编辑删除，谢谢】2015年文化馆个人工作总结在XXXX年X月，本人从XXXX学院毕业，来到了实现我梦想的舞台--XX区文化馆工作。

在这里我用艰辛的努力，勤劳的付出，真诚而认真地工作态度认真的做好自身的每一项文化馆相关工作，取得了较为良好的工作业绩。

随着一场场活动的成功举办、一台台戏剧的成功出演，在这个带有着梦想和希望的舞台上，转眼之间我已在这里渡过了XX年的青春事业，我亦与舞台共同成长，逐步由一名青涩的毕业生，历练成为了今天的XXX。

梦想在于不断坚持，未来的旅途在于不断的前进，在这个承载着梦的舞台上，我持以坚定的信心和丰富的工作能力与工作经验，一步一步超前迈进着。

下面我将自身XX年来的工作能力情况总结如下：一、一专多能服务1、高端学识水平。

本人于XXXX年XX月毕业于XXXX大学XX专业。

模糊推理方法（总11页）本页仅作为文档页封面，使用时可以删几种典型的模糊推理方法根据模糊推理的定义可知，模糊推理的结论主要取决于模糊蕴含关系k(XY)及模糊关系与模糊集合之间的合成运算法则。

对于确定的模糊推理系统，模糊蕴含关系斤(X』)一般是确定的，而合成运算法则并不唯一。

根据合成运算法则的不同，模糊推理方法乂可分为Mamdani推理法、Larsen推理法、Zadeh推理法等等。

一、Mamdani模糊推理法Mamdani模糊推理法是最常用的一种推理方法,其模糊蕴涵关系定义简单，可以通过模糊集合兀和§的笛卡尔积(取小)求得，即“血(x, y) = “x (x)AjLt s(y)(3. 2. 1) 例3. 2.1已知模糊集合芯丄+ —+ —, 5 = —+ —+ 22 + 2d o求模糊集合久和g之间的模册兀2 尤3 >'1 >'2>3 >'3糊蕴含关系心(X』)。

解：根据Mamdani模糊蕴含关系的定义可知：■ ■1R M(XX)=A X S= 0.4 o[0.8 0.5 0.3 0.1]0.10.8 0.5 0.3 O.T=0.4 0.4 0.3 0.1o」o」o」0丄Mamdani将经典的极大一极小合成运算方法作为模糊关系与模糊集合的合成运算法则。

在此定义下，Mamdani模糊推理过程易于进行图形解释。

下面通过儿种具体情况来分析Mamdani模糊推理过程。

(i)具有单个前件的单一规则设才和兀论域X上的模糊集合，§是论域Y上的模糊集合，和方间的模糊关系是爲(X,y),有大前提(规则)：if A- is A then y is B小前提(事实)：A- is才结论：y is当(x,刃="x(x)A心(>')时，有0.85 80 100其中e = 乂［“子（兀）心仃（x ）］,称为久和丫的适配度。

在给定模糊集合才、久及§的情况下，Mamdani 模糊推理的结果亍如图3・2・1所示。