M02资_惯性矩和惯性积的平行移轴定理

第1节静矩和形心4.1静矩和形心任何受力构件的承载能力不仅与材料性能和加载方式有关.而口与构件截面的几何形状和尺寸有关.如：计算杆的拉伸与压缩变形时用到截面而积A ,计算圆轴扭转变形时用到横截面的极惯性矩I?等.A、1?等是从不同角度反映了截而的几何特性，因此称它们为截而图形的几何性质.4.1静矩和形心设有一任意截而图形如图4 一1所示，其面积为A .选収直角坐标系yoz ,在坐标为（y,z）处取一微小而积dA ,定义微而积dA乘以到y轴的距离z ,沿整个截面的积分，为图形对y轴的静矩S?,其数学表达式(4 -la )同理，图形对z轴的静矩为□4-1图41截面静矩与坐标轴的选取有关•它随坐标轴y、z的不同而不同.所以静矩的数值可能足正，也可能足负或定零.静矩的虽纲为长度的三次方.确定截面图形的形心位置（图4-1中C点）:A (4-2b)第1页共30页式中T、"为截而图形形心的坐标值.若把式（4-2）改写成心"•儿，為"•乙（4 3）性质：・若截面图形的静矩等于零，则此坐标轴必定通过截面的形心.・若坐标轴通过截而形心，则截而对此轴的静矩必为零.・山于截而图形的对称轴必定通过截而形心，故图形对其对称轴的静矩恒为零。

4 ）工程实际中，有些构件的截面形状比较复杂，将这些复杂的截面形状看成是山若干简单图形（如矩形、圆形等）组合g而成的.对于这样的组合截而图形，计算静矩（S»‘ r）与形心坐标（y*、z '）时，可用以下公式1-1 2-1式中A— y i , z i分别表示第，个简单图形的面积及其形心坐标值，n为组成组合图形的简单图形个数.即：组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和.组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积.组合截面图形有时还可以认为是山一种简单图形减去另一种简单图形所组成的.例4J己知T形截面尺寸如图4-2所示，试确定此截面的形心坐标值.i-1 i-1 (4-5)图4-2解：(1)选参考轴为y 轴，z 轴为对称轴,(2)将图形分成I 、口两个矩形，则= 20 x 100加朋 S 右=(10 + 140)^^34 = 2Q X 14%/,22 二注型(3)代入公式(4・5)20x100x150+20x140x70 20x100 + 20x140此=°4.2惯性矩、惯性积和惯性半径设任一截面图形(图4-3),其而积为A ・选取直角坐标系yoz ,在坐标为(y 、z)处取一微小面积dA ,定义此微2面积dA 乘以到坐标原点o 的距离的平方Q ,沿整个截面积分，为截而图形的极惯性矩I?.做而积dA 乘以到坐标轴y 的2距离的平方2 ,沿整个截而积分为截面图形对y 轴的惯性矩I 》•极惯性矩、惯性矩常简称极惯矩、惯矩.j.l ~2Z4数学表达式为打=f p^dA极惯性矩“俎（4-6）对y轴惯性矩图4-3山图4-3看到“ =y +Z 9所以有打=\A^dA= £cy2 +/）曲二必+加必即；? （4-8）式（4-8）说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。

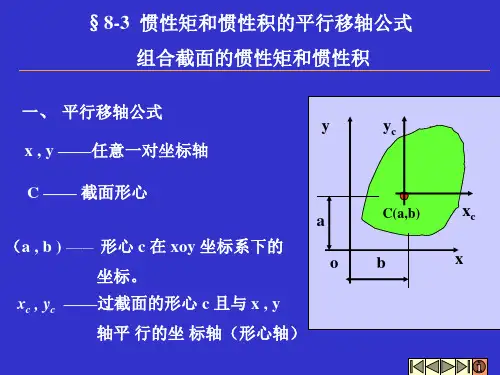
第6章 平面图形的几何性质6.3 惯性矩和惯性积的平行移轴公式 主轴和主惯性矩6.3.1 惯性矩和惯性积的平行移轴公式任一平面图形如图6.9所示，其面积为A ，形心为C ，坐标轴y c 和z c 为形心轴。

正交坐标轴y 、z 与形心轴y c 、z c 平行，两对平行轴之间的间距分别为a 和b 。

截面对y c 轴、z c 轴的惯性矩I y c、I z c 及惯性积I y z c c 为已知，现求图形对y 、z 轴的惯性矩和惯性积。

图中任一点在两坐标系下的坐标关系为=+z z a c =+y y b c由式（6.5）⎰⎰⎰⎰==+=++I z A z a A z A a z A a AAAAy c c c d ()d d 2d 2222其中⎰=z A I Ac y cd 2，⎰=A A Ad ，⎰=z A S Ac y cd 。

因y c 为形心轴，所以=S y c 0，于是可得同理 ⎭⎪=+⎪⎬=+⎪⎪=+⎫I I abA I I b A I I a A yz y z z z y y c c c 22c （6.9）上式即为惯性矩和惯性积的平行移轴公式（parallel-axis theorem ）。

因为a A 2和b A 2均为正，所以在所有相互平行的轴中，同一图形对形心轴的惯性矩最小。

在应用公式（6.9）时需注意，a 、b 是图形的形心C 在yOz 坐标下的坐标，有正、负之分。

同时，y c 、z c 轴一定是形心轴。

6.3.2 主轴和主惯性矩由式（6.6）可知，同一图形对不同的一对直角坐标轴的惯性积是不同的，若图形对某一对直角坐标轴的惯性积等于零，则该直角坐标轴称为主惯性轴，或简称为主轴（principal axes ）。

图形对主轴的惯性矩称为主惯性矩（principal moment of inertia ）。

通过图形形心的主轴称为形心主轴（centroidal axis ），图形对形心主轴的惯性矩称为形心主惯性矩（principal moment of inertia for an area ）。

I等． I等是从不同角度反映了截S，其数学表达式(4 -1a )(4-1b)(4 -2a )(4-2b)式中 y、 z 为截面图形形心的坐标值．若把式 (4-2) 改写成(4-3)性质：•若截面图形的静矩等于零，则此坐标轴必定通过截面的形心．•若坐标轴通过截面形心，则截面对此轴的静矩必为零．•由于截面图形的对称轴必定通过截面形心，故图形对其对称轴的静矩恒为零。

4 ）工程实际中，有些构件的截面形状比较复杂，将这些复杂的截面形状看成是由若干简单图形 ( 如矩形、圆形等 ) 组合而成的．对于这样的组合截面图形，计算静矩 (S) 与形心坐标 (y、 z ) 时，可用以下公式(4-4)(4-5)式中 A， y ， z 分别表示第个简单图形的面积及其形心坐标值， n 为组成组合图形的简单图形个数．即：组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和．组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积．组合截面图形有时还可以认为是由一种简单图形减去另一种简单图形所组成的．例 4-1 已知 T 形截面尺寸如图 4-2 所示，试确定此截面的形心坐标值．、两个矩形，则设任一截面图形 ( 图 4 — 3) ，其面积为 A ．选取直角坐标系 yoz ，在坐标为 (y 、 z) 处取一微小面积 dA ，定义此微面积 dA 乘以到坐标原点o的距离的平方，沿整个截面积分，为截面图形的极惯性矩 I．微面积 dA 乘以到坐标轴 y 的距离的平方，沿整个截面积分为截面图形对 y 轴的惯性矩 I．极惯性矩、惯性矩常简称极惯矩、惯矩．数学表达式为极惯性矩 (4-6)对 y 轴惯性矩 (4 -7a )同理，对 z 轴惯性矩 (4-7b)由图 4-3 看到所以有即(4-8) 式 (4 — 8) 说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。

在任一截面图形中 ( 图 4 —3) ，取微面积 dA 与它的坐标 z 、 y 值的乘积，沿整个截面积分，定义此积分为截面图形对 y 、z 轴的惯性积，简称惯积．表达式为(4-9)惯性矩、极惯性矩与惯性积的量纲均为长度的四次方． I,I,I恒为正值．而惯性积 I其值能为正，可能为负，也可能为零．若选取的坐标系中，有一轴是截面的对称轴，则截面图形对此轴的惯性积必等于零．当截面图形对某一对正交坐标轴的惯性积等于零时，称此对坐标轴为截面图形的主惯性轴．对主惯性轴的惯性矩称为主惯性矩．而通过图形形心的主惯性轴称为形心主惯性轴 ( 或称主形心惯轴 ) ．截面对形心主惯性轴的惯性矩称为形心主惯性矩 ( 或称主形心惯矩 ) ．例如，图 4-4 中若这对 yz 轴通过截面形心，则它们就是形心主惯性轴．对这两个轴的惯性矩即为形心主惯性矩．工程应用中 ( 如压杆稳定中 ) ，有时将惯性矩表示成截面面积与某一长度平方的乘积，即,或写成, （ 4-10 ）式中 i分别称为截面图形对 y 轴、 z 轴的惯性半径．其量纲为长度的一次方．例 4-2 已知矩形截面的尺寸 b,h( 图 4-5) ，试求它的形心主惯性矩．解：取形心主惯性轴 ( 即对称轴 )y,z ，及 dA=dy，代入公式 (I— 7a ,) 得同理：例 4-3 设圆的直径为 D( 图 4-6) ，试求图形对其形心轴的惯性矩及惯性半径值．解： (1) 求惯性矩因为图形对称， y,z 为对称轴，所以 I＝ I这是较简单的解法．本例也可取出图 4-6 上的微面积 dA ，按积分法来求得。

惯性矩是一个物理量，通常被用作描述一个物体抵抗扭动，扭转的能力。

惯性矩的国际单位为(m^4)。

工程构件典型截面几何性质的计算2.1面积矩1．面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。

定义：积分和分别定义为该图形对z轴和y轴的面积矩或静矩，用符号S z和S y，来表示，如式(2—2.1)(2—2.1)面积矩的数值可正、可负，也可为零。

面积矩的量纲是长度的三次方，其常用单位为m3或mm3。

2．面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成，如式(2—2.3)(2—2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。

图形形心相对于某一坐标距离愈远，对该轴的面积矩绝对值愈大。

图形对通过其形心的轴的面积矩等于零；反之，图形对某一轴的面积矩等于零，该轴一定通过图形形心。

3．组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。

如式(2—2.4)(2—2.4)式中，A和y i、z i分别代表各简单图形的面积和形心坐标。

组合平面图形的形心位置由式(2—2.5)确定。

(2—2.5)2.2极惯性矩、惯性矩和惯性积1．极惯性矩任意平面图形如图2-31所示，其面积为A。

定义：积分称为图形对O点的极惯性矩，用符号I P，表示，如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的，即同一图形对不同的点的极惯性矩一般是不同的。

极惯性矩恒为正，其量纲是长度的4次方，常用单位为m4或mm4。

(1)圆截面对其圆心的极惯性矩，如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩，如式(2—2.8)(2—2.8)式中，d/D为空心圆截面内、外径的比值。

2．惯性矩在如图6-1所示中，定义积分，如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。

惯性矩是对一定的轴而言的，同一图形对不同的轴的惯性矩一般不同。

惯性矩是一个物理量，通常被用作描述一个物体抵抗扭动，扭转的能力。

惯性矩的国际单位为(m^4)。

工程构件典型截面几何性质的计算2.1面积矩1．面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。

定义：积分和分别定义为该图形对z轴和y轴的面积矩或静矩，用符号S z和S y，来表示，如式(2—2.1)(2—2.1)面积矩的数值可正、可负，也可为零。

面积矩的量纲是长度的三次方，其常用单位为m3或mm3。

2．面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成，如式(2—2.3)(2—2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。

图形形心相对于某一坐标距离愈远，对该轴的面积矩绝对值愈大。

图形对通过其形心的轴的面积矩等于零；反之，图形对某一轴的面积矩等于零，该轴一定通过图形形心。

3．组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。

如式(2—2.4)(2—2.4)式中，A和y i、z i分别代表各简单图形的面积和形心坐标。

组合平面图形的形心位置由式(2—2.5)确定。

(2—2.5)2.2极惯性矩、惯性矩和惯性积1．极惯性矩任意平面图形如图2-31所示，其面积为A。

定义：积分称为图形对O点的极惯性矩，用符号I P，表示，如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的，即同一图形对不同的点的极惯性矩一般是不同的。

极惯性矩恒为正，其量纲是长度的4次方，常用单位为m4或mm4。

(1)圆截面对其圆心的极惯性矩，如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩，如式(2—2.8)(2—2.8)式中，d/D为空心圆截面内、外径的比值。

2．惯性矩在如图6-1所示中，定义积分，如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。

惯性矩是对一定的轴而言的，同一图形对不同的轴的惯性矩一般不同。

材料力学平行移轴公式
材料力学平行移轴公式是指，在研究杆件（也可以是板件、壳体、筏板等）的受力、变形及稳定性时，如果一个平行于某一轴线的受力系统在该轴线上的合力为零，则可以通过平移该受力系统，将其作用点移到该轴线上，不影响杆件的静力平衡和变形，即满足等效原理，从而用该轴线作为该杆件的平移轴线。

在材料力学中，平行移轴公式应用广泛，特别是在弹性力学的应用中很常见。

根据平行移轴公式，如果一个杆件受到的作用力在某一轴线上的合力为零，那么这个杆件就可以在该轴线上进行平移，移动的距离可以确定为受力系统到该轴线距离的乘积除以作用在某一点上的合力，即：
s = (M/V) * r
其中，s代表杆件平移的距离，M代表作用在轴线上的合力矩，V 代表轴线上的截面积，r代表受力系统到轴线的距离。

通过这个公式，可以比较方便地计算出杆件的平移距离。

需要注意的是，平移轴线要求在平移前后，杆件的受力状态和形状是不变的。

如果平移后，杆件的受力状态和形状发生了变化，就不能使用平移轴公式计算了。

总之，平行移轴公式在材料力学中具有重要的作用，特别是在弹性力学的应用中，可以方便地计算杆件的平移距离，为分析各种力学问题提供了有力的支持。

平移轴定理公式平移轴定理是一个在物理学和工程学中经常用到的重要定理，特别是在研究刚体的转动问题时。

先给您讲讲啥是平移轴定理。

简单来说，就是如果有一个刚体，我们知道它对于通过质心的轴的转动惯量，然后想要知道对于另一个与之平行但不通过质心的轴的转动惯量，那就可以用平移轴定理来计算。

公式是这样的：$I = I_{C} + md^2$ ，这里的$I$是对于不通过质心的轴的转动惯量，$I_{C}$是对于通过质心的轴的转动惯量，$m$是刚体的质量，$d$是两轴之间的垂直距离。

记得我之前教过一个班的学生，当时正在讲这个平移轴定理。

有个小家伙，特别活泼，上课总爱抢答问题，可一到这平移轴定理，他就懵圈了。

我就举了个例子，说咱们把教室的门想象成一个刚体，门轴就是通过质心的轴，那如果咱们在门的边上再安一个轴，这就相当于不通过质心的轴啦。

然后问大家，觉得对于这新轴的转动惯量会怎么变？这小家伙一下子来了精神，抢着说肯定变大。

我笑着问他为啥，他说感觉嘛。

我就接着引导他们一起思考，按照平移轴定理来算算。

最后算出结果，这小家伙恍然大悟，说原来这公式这么有用啊。

在实际生活中，平移轴定理也有很多应用呢。

比如说汽车的车轮，我们要研究车轮对于不同轴的转动情况，就可以用这个定理。

再比如一些机械零件的设计，工程师们就得考虑转动惯量的问题，这时候平移轴定理就能派上用场。

还有啊，咱们平时玩的陀螺，您想啊，如果陀螺的质量分布不均匀，要想知道它对于不同轴的转动特性，也能靠这个定理来帮忙分析。

总之，平移轴定理虽然看起来有点复杂，但只要理解了，掌握了，那就能在很多问题上给我们提供很大的帮助。

不管是解决物理难题，还是在实际的工程应用中，它都是一个非常实用的工具。

希望通过我今天的讲解，能让您对平移轴定理公式有更清楚的认识和理解。

以后再遇到相关的问题，就能够轻松应对啦！。

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点：(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形，取其单元如面积dA ，定义它对任意轴的一次矩为它对该轴的静矩，即 yydAdSx xdA dS y == x dA 整个图形对y 、z 轴的静矩分别为⎰⎰==A Ay ydA Sx xdA S （I-1） 0 A y 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0A S y x = ， AS x y = （I-2） 推论1 如果y 轴通过形心（即0=x ），则静矩0=y S ；同理，如果x 轴通过形心（即0=y ），则静矩0=Sx ；反之也成立。

推论2 如果x 、y 轴均为图形的对称轴，则其交点即为图形形心；如果y 轴为图形对称轴，则图形形心必在此轴上。

3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成，且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ；；，则图形对y 轴和x 轴的静矩分别为∑∑∑∑========n i n i ii xi x n i ii n i yi y y A S S x A S 1111S （I-3）截面图形的形心坐标为∑∑===n i i n i i iAx A x 11， ∑∑===n i in i i i A y A y 11 （I-4） 4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。

(2) 静矩有的单位为3m 。

(3) 静矩的数值可正可负，也可为零。

图形对任意形心轴的静矩必定为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。

(4) 若已知图形的形心坐标。

则可由式（I-1）求图形对坐标轴的静矩。

若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。

组合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静矩，然后由式（I-4）求出其形心坐标。