最新郑州小升初数学试卷

2024年郑州市二七区57中学小升初选拔数学试卷一.选择题(共6小题)1.一项工程，甲单独做10天完成，乙单独做15天完成．两人合作(▲)天可完成这项工程的56。

A.5B.6C.7D.82.比较分数9899、998999、99989999,发现(▲)。

A.9899最大B.998999最大C.99989999最大 D ．三个分数一样大3.自然数按一定的规律如下排列，从排列规律可知，99排在(▲)。

A.第2行第7列B.第2行第8列C.第2行第9列D.第2行第10列4.如图，同一直线上有A ，B ，C ，D 四点，已知线段DB 与AD 的长度之比为2∶3，AC 与CB 的长度之比为5∶2，CD=4cm ，那么AB=(▲)cm 。

A.2B.3C.4D.55.我们可以把a ×a ×a …×ａ(共n 个a 相乘)记为a n ，例如3×3×…×3(共6个3相乘)=729，现规定如下：如果正整数a ，n ，b 满足a n =b ，则记作n=a ○×b ，根据上述规定判断下列哪个是错误的？(▲) A.23×33=63B.2○×4=3○×9 CABDC.3○×3+3○×27=3○×81D.(3○×9)×(3○×3)=3○×27 6.小明由家去学校然后又按原路返回，去时每分钟行a 米，回来时每分钟行b 米，求小明来回的平均速度的正确算式是(▲) A.(a+b)÷2B.2÷(a+b)C.1÷(1a +1b )D.2÷(1a +1b)二.填空题(共6小题)7.如图，A 点与B 点分别是长方形长和宽的中点，阴影部分与空白部分的面积比是_____。

8.体育老师要购买50个足球，现有甲、乙、丙三个体育用品商店可以选择，三个商店足球的价格都是25元，但三个商店都有不同的优惠方式：甲店：买10个足球免费赠送2个，不足10个不赠送；乙店：每个足球优惠5元；丙店：购物满100元，返回25元。

2024年郑州市高新区朗悦实验中学小升初数学试卷(时间60分钟，满分80分)一、填空题(每题3分，共24分)1.甲数与乙数的比是7︰8，乙数是40，则甲数比乙数小____%。

2.把一个长4cm ，宽3cm 的长方形按5︰1放大，放大后的长方形的面积是____cm 2。

3.如果A ÷B=5(A ，B 为自然数)，那么A 和B 最大公因数是____。

4.张三读一本名人传记，第一天读了总页数的25，第二天读了总页数的12，还剩27页，这本名人传记共有____页。

5.如图，长方形的面积是6平方厘米，圆的面积是____平方厘米(π取3.14)。

6.有6个完全相同的小长方形纸片，每个小长方形的长是7cm ，宽是2cm ，将它们不重叠的放在长方形ABCD 中(如图)，阴影部分是没有被小长方形覆盖的部分，则长方形ABCD 的长和宽的比是____。

7.有A ，B 两组数，每组都按一定规律排列着，并且每组各有25个数，A 组数中前几个数是这样排列的：1，6，11，16，21…；B 组数中最后几个数是这样排列的：…105，110，115，120，125。

那么A ，B 两组数中所有数的和是____。

8.横截面为正方形的密闭长方体容器被一石块支起，如图为横截面示意图，容器内有一些水。

已知正方形的边长为5，长方体的长为10，如果将横截面所在的面作为DC底面把容器竖起来，水的深度为____。

二、解答题(本大题共56分) 9.计算题(每小题5分，共30分) (1)(83÷7－17×53)÷37(2)713－27+613-57(3)0.65×6.4－6.5×0.54 (4)4－0.7x =102 (5)1999÷199919992000+12001(6)335×3456+5555÷25288+654.3×3610.(8分)图1是一个三角形ABC ，沿直线MN 折叠后得到图2，图2中多边形AMNCFB ´E(直线MN 右侧部分图形)的面积是三角形ABC 面积的57，已知图2中阴影部分的面积和为15，将三角形ABC 的面积记作S △ABC ，若S △FNC －S △AME =S △EFB ，求四边形ABNF 的面积是多少？11.(8分)(1)用数对表示出三角形ABC 中两个顶点的位置：A(___，___)，C(___，___)。

河南省郑州市枫杨外国语学校小升初数学试卷一.填空（共6题，每题5分）1.（5分）现在是4点20分，再过分时针和分针第一次的夹角为30度.2.（5分）现有甲3千克纯酒精，乙2千克纯水，从甲取a千克倒入乙杯，搅拌均匀后，再从乙取a千克到甲杯，这时，甲的纯净水比乙的酒精多千克.3.（5分）一个圆柱侧面展开长18.宽12的长方形，圆柱的体积是（π取3）4.（5分）一个工程队18天修了三分之一，如果做了3天后，效率提高五分之一，一共要天完成一半.5.（5分）若自然数n使得作连式加法n+（n+1）+（n+2）时均不产生进位现象，便称n为“连绵数”，如因为12+13+14不产生进位现象，所以12是连绵数，但13+14+15产生进位现象，所以12是连绵数，则不超过200的连绵数有个.二.应用题（共6题，共55分）6.（7分）一个小孩拿40块糖说分给了9个人，每个人的糖都不一样.每人至少有一个，问成不成立.7.有一个商厦，进4万元的货，卖完之后，又进了8.8万元的货，进的货是第一次的两倍，并且每一次都比第一次贵4元，现在每件58元，卖完还剩150件时，打八折.问商厦一共赚了多少钱？8.两辆同一型号的汽车从同地同时同速沿一个方向出发，每年最多能带30桶汽油，每桶汽油使汽车前进60千米，每车都须返回出发点，两车可以找对方借油，为了使其中一辆车尽可能远离出发点，那么这辆汽车最远能离出发点多少千米？9.（10分）如图1，某容器由A.B.C三个长方体组成，其中A.B.C的底面积分别为25cm2.10cm2.5cm2，C的容积是容器容积的（容器各面的厚度忽略不计）.现在以速度v（单位:cm3/s）均匀地向容器注水，直至注满为止，图2是注水全过程中容器的水面高度h（单位:cm）与注水时间t（单位:s）的函数图象.问题:（1）在注水过程中，注满A所用的时间为s；（2）求A的高度h A及注水的速度V；（3）求所注满容器所需时间及容器的高度.10.如图，纸上画了四个大小一样的圆，圆心分别是A.B.C.D，直线m通过A.B，直线n通过C.D，用S表示一个圆的面积，如果四个圆在纸上盖住的总面积是5（S﹣1），直线m.n之间被圆盖住的面积是8，阴影部分的面积是S1.S2.S3满足关系式S3=S2=S1，求S.参考答案与试题解析一.填空（共6题，每题5分）1.（5分）现在是4点20分，再过7分时针和分针第一次的夹角为30度.【分析】分针每分钟=6°，时针每分钟走=0.5°，4点20分时，分针从数字12走到数字4，时针从数字4走了0.5°×20=10°，分针和分针第一次的夹角为30度时，分针要比时针多走30°+10°，根据追及问题即可解答.【解答】解:（30+10）÷（6﹣0.5）=40÷5.5=7（分）答:再过7分时针和分针第一次的夹角为30度.故答案为:7.2.（5分）现有甲3千克纯酒精，乙2千克纯水，从甲取a千克倒入乙杯，搅拌均匀后，再从乙取a千克到甲杯，这时，甲的纯净水比乙的酒精多0千克.【分析】由甲中取出a千克纯酒精倒入乙，算出此时乙杯中纯酒精的浓度，进而根据一个数乘分数的意义，用乘法求出这时从乙中取a千克混合液中水的质量，即为甲中水的质量，再求出a千克中纯酒精的质量，用a减去这个质量，即为乙中纯酒精的质量，然后进行比较，即可得出结论.【解答】解:从甲杯中取出a千克纯酒精到入乙杯搅匀后，乙杯中酒精的浓度为，则从乙杯中取出a千克混合液中水有a•=千克，即为这时甲杯中含有的水，而乙杯中纯酒精的含量为（a﹣a•）千克，因为a﹣a•=﹣=，所以甲杯中含有的水与乙杯中含有的纯酒精一样多，即这时甲杯中混入的纯净水比乙杯中的纯酒精多0千克；故答案为:0.3.（5分）一个圆柱侧面展开长18.宽12的长方形，圆柱的体积是324或216（π取3）【分析】根据题意，本题可分别把18.12作为圆柱的底面周长进行作答，可利用圆的周长公式计算出这个圆柱的底面半径是多少，然后再利用圆柱的体积=底面积×高进行计算圆柱的体积，列式解答即可得到答案.【解答】解:（1）假设圆柱的底面周长是18，那么圆柱的高为12，圆柱的底面半径为:18÷3÷2=3，圆柱的体积为:3×32×12=27×12，=324；（2）假设圆柱的底面周长是12，则圆柱的高为18，圆柱的底面半径为:12÷2÷3=2，圆柱的体积为:3×22×18，=12×18，=216；答:这个圆柱的体积可能是324或216.故答案为:324或216.4.（5分）一个工程队18天修了三分之一，如果做了3天后，效率提高五分之一，一共要23天完成一半.【分析】先根据工作效率=工作总量÷工作时间，求出工程队的工作效率，再依据分数乘法意义，求出效率提高五分之一后的工作效率，以及做3天后，完成的工作总量，最后根据工作时间=工作总量÷工作效率即可解答.【解答】解:（﹣18×3）÷[18×（1）]+3，=（）÷[]+3，=+3，=20+3，=23（天），答:一共要23天完成一半.故答案为:23.5.（5分）若自然数n使得作连式加法n+（n+1）+（n+2）时均不产生进位现象，便称n为“连绵数”，如因为12+13+14不产生进位现象，所以12是连绵数，但13+14+15产生进位现象，所以12是连绵数，则不超过200的连绵数有24个.【分析】首先根据题意求出个位数和十位数满足的条件，然后根据能构成“连绵数”的条件求出不超过100的“连绵数”的个数.【解答】解:根据题意个位数需要满足要求:∵n+（n+1）+（n+2）＜10，即N＜2.3，∴个位数可取0，1，2三个数，∵十位数需要满足:3n＜10，∴n＜3.3，∴十位可以取0，1，2，3四个数，小于200的连绵数共有3×4×2=24个.故答案为:24.二.应用题（共6题，共55分）6.（7分）一个小孩拿40块糖说分给了9个人，每个人的糖都不一样.每人至少有一个，问成不成立.【分析】假设最少的一个同学有一块，由于“每个人的糖都不一样.”，所以相邻的两个人的块数的差最小为1，也就是说，这9个人的块数最少为1～9的等差数列，那么至少需要的块数是:（1+9）×9÷2=45（块），与题干40块不符.【解答】解:根据分析可得，题设不成立.因为这9个人的块数最少为1～9的等差数列，所需块数:（1+9）×9÷2=45（块），45≠40，所以题设不成立.7.有一个商厦，进4万元的货，卖完之后，又进了8.8万元的货，进的货是第一次的两倍，并且每一次都比第一次贵4元，现在每件58元，卖完还剩150件时，打八折.问商厦一共赚了多少钱？【分析】如果第二次进和第一次同样的货要8.8÷2=4.4万元，又4.4﹣4=0.4万元=4000元，则第一次进货4000÷4=1000件，共进货2000+1000=3000件，又都定价58元，还有150件打8折，没打折部分卖的钱数是（3000﹣150）×58元，打折部分为150×58×0.8元，又总成本为4万元+8.8万元=12.8万元，即128000元，所以共赢利（3000﹣150）×58+150×58×0.8﹣128000=44260（元）.【解答】解:（8.8÷2）﹣4=4.4﹣4=0.4（万元）.0.4万元=4000元；4000÷4=1000（件），1000+1000×2=1000+2000=3000（件）.4万元+8.8万元=12.8万元，12.8万元=128000元，（3000﹣150）×58+150×58×0.8﹣128000=3850×58+6960﹣128000=223300+6960﹣128000=44260（元）.答:共赢利44260元.8.两辆同一型号的汽车从同地同时同速沿一个方向出发，每年最多能带30桶汽油，每桶汽油使汽车前进60千米，每车都须返回出发点，两车可以找对方借油，为了使其中一辆车尽可能远离出发点，那么这辆汽车最远能离出发点多少千米？【分析】甲车可以行驶到汽油用掉的时候，留汽油返程，给另一车加汽油，因为此时乙车也刚好用掉汽油的，所以乙车实际可用的汽油，所以它最远可达60×30÷2×千米.据此解答即可.【解答】解:甲车可以行驶到汽油用掉的时候，留汽油返程，给另一车加汽油，因为此时乙车也刚好用掉汽油的，所以乙车实际可用的汽油，乙车可以行驶:60×30÷2×=1800÷2×=900×=1200（千米）答:这辆汽车最远能离出发点1200千米.9.（10分）如图1，某容器由A.B.C三个长方体组成，其中A.B.C的底面积分别为25cm2.10cm2.5cm2，C的容积是容器容积的（容器各面的厚度忽略不计）.现在以速度v（单位:cm3/s）均匀地向容器注水，直至注满为止，图2是注水全过程中容器的水面高度h（单位:cm）与注水时间t（单位:s）的函数图象.问题:（1）在注水过程中，注满A所用的时间为10s；（2）求A的高度h A及注水的速度V；（3）求所注满容器所需时间及容器的高度.【分析】（1）看折线图可得答案；（2）从图中可以看出A和B的高度和是12厘米，就设注水的速度v；则注满时甲的高度加上乙的高度就是12厘米，列方程解得；（3）根据C的容积和总容积的关系求出C的容积，再求C的高度及注满C的时间，就可以求出注满容器所需时间及容器的高度.【解答】解:（1）看图象可知，注满A所用时间为10s，（2）从图中可以看出A和B的高度和是12cm，就设注水的速度vcm3；则注满时甲的高度加上乙的高度就是12cm，列方程得:+=12，20V+40V=600，60V=600，V=10，A的高度h A:10×V÷25=10×10÷25=4（cm），答:A的高度h4为4cm，注水的速度v是10cm3；（3）设C的容积为ycm3，则有，4y=10v+8v+y，将v=10代入计算得:4y﹣y=10×10+8×10+y﹣y，3y=180，y=60，那么容器C的高度为:60÷5=12（cm），故这个容器的高度是:12+12=24（cm），注满C的时间是:60÷v=60÷10=6（s），故注满这个容器的时间为:10+8+6=24（s）.答:注满容器所需时间是24s及容器的高度24cm.故答案为:10.10.如图，纸上画了四个大小一样的圆，圆心分别是A.B.C.D，直线m通过A.B，直线n通过C.D，用S表示一个圆的面积，如果四个圆在纸上盖住的总面积是5（S﹣1），直线m.n之间被圆盖住的面积是8，阴影部分的面积是S1.S2.S3满足关系式S3=S2=S1，求S.【分析】观察图形可以得到四个圆之间的位置关系，根据重叠部分的面积可以列出一个方程，然后与题目中S1，S2，S3的关系联立方程组，解方程组得到S的值.【解答】解:由题设可得:所以S1=①又因为2S﹣S1﹣S2﹣S3=8，即:2S﹣2S1=8 ②把①代入②消去S1得:2S﹣2×=86S﹣10+2S=248S=34S=.。

2024年河南省郑州实验中学小升初数学试卷一、选择题（每小题3分，共21分）1．（3分）定义新运算@，有a@b＝2ab+3b，那么5@6的计算结果是（）A．80B．78C．60D．702．（3分）一个长方体三个面的面积分别为6、12、18，这个长方体的体积是（）A．36B．42C．54D．723．（3分）某次知识竞赛共5道题，全班52人，答对一题得1分．已知全班共得181分．已知每人至少得1分，且得1分的有7人，得2分和得3分的人一样多，得5分的人有6人，则得4分的有（）人．A．25B．30C．31D．354．（3分）一列快车和一列慢车相向而行，快车的车长是270米，慢车的车长是360米，坐在快车上的人看见慢车驶过的时间是12秒，那么坐在慢车上的人看见快车驶过的时间是（）秒。

A．9B．10C．11D．125．（3分）某次小学生数学竞赛的满分为100分，小明和小光在竞赛中取得了优异成绩，成绩都不低于95分。

当小记者采访他们时，小明说：“我的名次、年龄和分数的乘积等于1261”，小光说：“我的名次、年龄和分数的乘积等于3135”。

那么小明和小光两人的平均分是（）分。

A．94B．98C．97D．966．（3分）如图所示，两个正方形重叠摆放后，这两个阴影部分的周长和是80厘米，它们的面积相差80平方厘米，那么这两个正方形面积和是（）平方厘米。

A．160B．208C．200D．2167．（3分）在如图的乘法算式中，两个乘数的和是（）A．244B．246C．254D．256二、填空题（每小题3分，共15分）8．（3分）如图，一只蚂蚁想从圆柱形水桶外侧的A点爬到内侧的B点寻找食物。

已知A点到桶口的距离AC＝20厘米，B点到桶口的距离BD＝16厘米，圆弧CD长15厘米。

蚂蚁爬行的最短路程是厘米。

9．（3分）如图中小三角形的边长都相等，那么小蚂蚁从A点沿三角形的边爬到B点的最短路线有条。

10．（3分）有一类四位数，除以5余2，除以7余5，除以11余10。

2023年河南省郑州市二七区小升初数学试卷一、巧思妙算1．（12分）直接写出下面各题的得数。

728﹣299＝0.24×50＝ 1.25×9×8＝（59+58）×72＝3.6×25%＝ 2.6﹣1.7＝0.77+0.33＝1−58+38=1÷0.125﹣8＝ 1.45﹣0.75＝0.13+78+0.87＝ 2.5×4÷2.5×4＝2．（12分）计算。

2.9÷8+1.1×18884÷34+17×21 1.25×3.2×0.2512：34=103．（2分）〇和□各代表一个数字，已知〇+〇+□+□+□＝51，〇+□＝21，求〇和□分别是多少。

二、数学万花筒。

4．（3分）人生如攀登。

在翻越一座高峰、踏上新的旅途之际，人们都需要稍作休整，回首过往、放眼未来，让人生之路张弛有度、行稳致远。

2023年的高考已经落幕，对于在学业道路上奋力攀登的青少年，高考既是高中学习生活的终点，也是大学学习生活的起点。

今年全国高考报名人数约为12914000人，比去年增加约980000人，再创历史新高。

其中河南省参加高考人数约为一百三十一万人。

位列各省排名第一。

（1）横线上的数读作，改写成以“万”做单位的数是。

（2）波浪线上的数写作。

5．（6分）一条德化衡，百年郑州史。

它是中原最大的商业集散中心二七商圈的中轴线。

承载着郑州人的精神记忆，是郑州近百年发展的历史缩影，这条街南起大同路，北至二七广场，全长600米，宽20米，就是这条又短又窄的街道，却聚集着众多名店，拥有约23个行业。

随着2020年7月德化街入选第二批全国步行街改造升级试点，郑州德化街正式迎来复兴改造。

以二七商圈区域城市复兴为主线，德化街围绕环境、产业、文化、智慧街区和品牌特色等方面实施新一轮改造升级，打通商圈复兴的“文脉”和“商脉”，建设现代时尚的国际化商业街区。

河南省郑州三中小升初数学试卷一.填空题（每题5分，共60分）1.（5分）（++）÷×=.2.（5分）设a.b为自然数，定义a※b如下:如果a≥b，定义a※b=a﹣b，如果a ＜b，则定义a※b=b﹣a.计算:（3※4）※9=.3.（5分）在所有的三位数中，能够被3整除的数共有个.4.（5分）三个连续自然数的积是2730，这三个数的和是.5.（5分）四个连续奇数，第一个数是第四个数的，那么四个数的和是.6.（5分）从A地到B地，甲车每5分钟行驶全程的10%，乙车每6分行驶全程的8%，乙车先出发，甲车后出发，但两车恰好同时到达B地.乙车比甲车早出发分.7.（5分）一段方钢，长2分米，横截面是正方形，把它锯成相等的两段后，表面积比原来增加8平方厘米，原来这个长方体方钢的表面积是平方厘米.8.（5分）一个等腰梯形中三条边的长分别是55厘米.25厘米.15厘米，并且它的下底是最长的一条边.那么，这个等腰梯形的一个腰长是厘米.9.（5分）a.b两数的和是11.5，如果把a的给b，那么b比a少2.9，原来b 比a少.10.（5分）长方形的长和宽的比是5:3，如果将长减少9厘米，宽增加7厘米，就变成一个正方形，原来长方形面积是平方厘米.11.（5分）去年光明小学的学生是红旗小学的，今年光明小学转入60名学生，红旗小学转出20名学生，现在光明小学的学生是红旗小学的，去年光明小学有学生人.二.应用题（写出主要的解答过程或推理过程，每题10分，共60分）12.（10分）果园里有苹果树.梨树一共800棵，其中苹果树占60%，后来又栽了一些苹果树，这样苹果树占总数的68%，后来又栽了多少棵苹果树？13.（10分）六年级学生120人在考试中语文.数学.外语三科及格百分比平均为85%，语文及格114人，外语及格100人，数学及格多少人？14.（10分）甲.乙共带86元钱，甲花去自己所带钱数的，乙花去16元，这时两人所剩钱数相等，求甲.乙原来各带了多少元钱？15.（10分）一辆车从甲地开往乙地.如果把车速减少10%，那么要比原定时间迟1小时到达，如果以原速行驶180千米，再把车速提高20%，那么可比原定时间早1小时到达.甲.乙两地之间的距离是多少千米？16.（10分）小明看一本故事书，小芳看一本科技书，故事书的页数是科技书的75%，小明每天看15页，小芳每天看18页.二人同时开始阅读，当小明看完故事书时，小芳还有24页没看.这两本书各有多少页？17.（10分）甲.乙两人分别从A.B两地同时出发，相向而行，乙的速度是甲的，两人相遇后继续前进，甲到达B地，乙到达A地立即返回，已知两人第二次相遇的地点距离第一次相遇的地点是3000米，求A.B两地的距离？参考答案与试题解析一.填空题（每题5分，共60分）1.（5分）（++）÷×=.【分析】根据数字特点，原式变为（++）××，进一步计算即可.【解答】解:（++）÷×，=（++）××，=（++）××，=×3××，=.故答案为:.2.（5分）设a.b为自然数，定义a※b如下:如果a≥b，定义a※b=a﹣b，如果a ＜b，则定义a※b=b﹣a.计算:（3※4）※9=8.【分析】根据“如果a≥b，定义a※b=a﹣b，如果a＜b，则定义a※b=b﹣a，”得出新的运算方法，再利用新的运算方法计算（3※4）※9的值即可.【解答】解:（3※4）※9，=（4﹣3）※9，=1※9，=9﹣1，=8；故答案为:8.3.（5分）在所有的三位数中，能够被3整除的数共有300个.【分析】最大的三位数是999，最小的三位数是100，共有（999﹣100+1）=900个三位数，求所有的三位数中，能够被3整除的数共有多少个，即求900中能被3整除的数共有多少个，也就是求900里面有几个3即可.【解答】解:最大的三位数是999，最小的三位数是100，共有（999﹣100+1）=900个三位数，900÷3=300（个）；答:在所有的三位数中，能够被3整除的数共有300个.故答案为:300.4.（5分）三个连续自然数的积是2730，这三个数的和是42.【分析】把2730分解质因数，从因数中找出3个连续的自然数，再把它们加起来即可.【解答】解:2730=2×3×5×7×13；2×7=14，3×5=15，所以这三个连续的自然数是13.14.15.13+14+15=42.答:这三个数的和是42.故答案为:42.5.（5分）四个连续奇数，第一个数是第四个数的，那么四个数的和是240.【分析】四个连续奇数第四个数比第一个要大6；把第四个数看成单位“1”，它的（1﹣）对应的数量是6，由此用除法求出这个数，进而求出其它的数，以及它们的和.【解答】解:6÷（1﹣），=6÷，=63；其它的三个数是:61，59，57；它们的和是:63+61+59+57，=（63+57）+（59+61），=120+120，=240；答:四个数的和是240.6.（5分）从A地到B地，甲车每5分钟行驶全程的10%，乙车每6分行驶全程的8%，乙车先出发，甲车后出发，但两车恰好同时到达B地.乙车比甲车早出发25分.【分析】已知甲每小时走全程的10%÷5=，乙每分钟走全程的8%÷6=.也就是说，甲走完全程要1÷=50（分），乙要1÷=75（分钟），乙想要与甲同时到达，要先走75﹣50=25（分钟）.【解答】解:甲走完全程要:1÷（10%÷5），=1÷，=50（分）；乙走完全程要:1÷（8%÷6），=1÷，=75（分钟）；乙车比甲车早出发:75﹣50=25（分钟）.答:乙车比甲车早出发25分钟.故答案为:25.7.（5分）一段方钢，长2分米，横截面是正方形，把它锯成相等的两段后，表面积比原来增加8平方厘米，原来这个长方体方钢的表面积是168平方厘米.【分析】根据题意可知，平均分成两段后表面积增加了两个底面积，那么每个底面积为（8÷2）平方厘米，再用分解因数的方法得到长方体方钢的底面正方形的边长，依此可求长方体方钢的侧面积，再用侧面积+2个底面积，即可得到这个长方体方钢的表面积.【解答】解:底面积为:8÷2=4（平方厘米），因为4=2×2，所以底面正方形的边长为2厘米，2分米=20厘米，这个长方体方钢的表面积为:2×4×20+4×2，=160+8，=168（平方厘米）.答:原来这个长方体方钢的表面积是168平方厘米.故答案为:168.8.（5分）一个等腰梯形中三条边的长分别是55厘米.25厘米.15厘米，并且它的下底是最长的一条边.那么，这个等腰梯形的一个腰长是25厘米.【分析】首先确定下底是55厘米，再分腰长为25厘米或15厘米两种情况讨论即可求解.【解答】解:①腰长为25厘米时:55+25×2+15=55+50+15=120厘米；②腰长为15厘米时，两底是55厘米.25厘米，无法构成等腰梯形，不符合题意.故答案为:25.9.（5分）a.b两数的和是11.5，如果把a的给b，那么b比a少2.9，原来b 比a少 4.5.【分析】把a看成单位“1”，它的就是a；把a的给b后，a还剩下（1﹣）a，b就是b+a，那么根据题意可以得出如下两个方程:a+b=11.5；（1﹣）a﹣（a+b）=2.9；根据代换的方法求出原来的a和b，进而求出它们的差.【解答】解:根据题意可以得出如下两个方程:a+b=11.5①；（1﹣）a﹣（a+b）=2.9②；由①可得:b=11.5﹣a③；由②可得:a﹣a﹣b=2.9，a﹣b=2.9④；把③带入④得:a﹣（11.5﹣a）=2.9，0.8a﹣11.5+a=2.9，1.8a=14.4，a=8；b=11.5﹣a=11.5﹣8=3.5；8﹣3.5=4.5；答:原来b比a少4.5.故答案为:4.5.10.（5分）长方形的长和宽的比是5:3，如果将长减少9厘米，宽增加7厘米，就变成一个正方形，原来长方形面积是960平方厘米.【分析】如果长减少9厘米，宽增加7厘米，正好变成一个正方形，说明长与宽的差是16厘米，又因为长和宽的比是5:3，也就是说如果长占5份，宽占3份，它们的差占2份，则一份长度为16÷2=8厘米，那么长方形的长为:8×5=40厘米，宽为:8×3=24厘米.根据长方形的面积公式:s=ab，把数据代入公式解答即可.【解答】解:先求出一份的长:（9+7）÷（5﹣3），=16÷2，=8（厘米），长是:8×5=40（厘米），宽是:8×3=24（厘米），原来的面积是:40×24=960（平方厘米）；答:原来长方形的面积是960平方厘米.故答案为:960.11.（5分）去年光明小学的学生是红旗小学的，今年光明小学转入60名学生，红旗小学转出20名学生，现在光明小学的学生是红旗小学的，去年光明小学有学生300人.【分析】我们运用方程进行解答，首先设去年光明小学有学生x人.由“今年光明小学转入60名学生，红旗小学转出20名学生，现在光明小学的学生是红旗小学的，”为等量关系列方程解答即可.【解答】解:设去年光明小学有学生x人.x+60=（x﹣20）×，x+60=x﹣15，x+60+15=x﹣15+15，x+75=x，x﹣x+75=x﹣x，x=75，x×4=75×4，x=300；答:去年光明小学有学生300人.故答案为:300.二.应用题（写出主要的解答过程或推理过程，每题10分，共60分）12.（10分）果园里有苹果树.梨树一共800棵，其中苹果树占60%，后来又栽了一些苹果树，这样苹果树占总数的68%，后来又栽了多少棵苹果树？【分析】苹果树.梨树一共800棵，其中苹果树占60%，则梨树占总数的1﹣60%，根据分数乘法的意义可知，梨树有800×（1﹣60%），又后来又栽了一些苹果树，这样苹果树占总数的68%，则此时梨树占总数的1﹣68%，根据分数除法的意义，此时共有果树800×（1﹣60%）÷（1﹣68%）棵，所以苹果树增加了800×（1﹣60%）÷（1﹣68%）﹣800棵.【解答】解:800×（1﹣60%）÷（1﹣68%）﹣800=800×40%÷32%﹣800，=1000﹣800，=200（棵）.答:后来又栽了200棵苹果树.13.（10分）六年级学生120人在考试中语文.数学.外语三科及格百分比平均为85%，语文及格114人，外语及格100人，数学及格多少人？【分析】因为语文.数学.外语三科及格百分比平均为85%，所以85%×3等于三科及格率的和，和减去语文减去外语的及格率得出数学及格率，再用六年级学生120人乘数学及格率得出数学及格人数.【解答】解:数学及格人数:120×（85%×3﹣114÷120﹣100÷120），=120×（2.55﹣0.95﹣），=120×（1.6﹣），=120×1.6﹣120×，=192﹣100，=92（人）.答:数学及格人92人.14.（10分）甲.乙共带86元钱，甲花去自己所带钱数的，乙花去16元，这时两人所剩钱数相等，求甲.乙原来各带了多少元钱？【分析】本题可列方程解答，设甲带了x元，则乙带了86﹣x元，甲花去自己所带钱数的，则还剩下（1﹣）x元，乙花去16元，则还剩下86﹣x﹣16元，此时这时两人所剩钱数相等，由此可是方程:（1﹣）x=86﹣x﹣16.【解答】解:设甲带了x元，则乙带了（86﹣x）元，可得方程:（1﹣）x=86﹣x﹣16.x=70﹣x，1x=70，x=45.86﹣45=41（元）.答:甲带了45元，乙带了41元.15.（10分）一辆车从甲地开往乙地.如果把车速减少10%，那么要比原定时间迟1小时到达，如果以原速行驶180千米，再把车速提高20%，那么可比原定时间早1小时到达.甲.乙两地之间的距离是多少千米？【分析】由题意知，原定时间是1÷10%×（1﹣10%）=9小时；如果速度提高20%行完全程，时间就会提前9﹣9÷（1+20%）=；因为只比原定时间早1小时，所以，提高速度的路程是1÷=；所以甲乙两地之间的距离是180÷（1﹣）=540千米.【解答】解:①原定时间:1÷10%×（1﹣10%）=9（小时）；②提高速度的路程:1÷[9﹣9÷（1+20%）]=；③180÷（1﹣）=540千米.答:甲.乙两地之间的距离是540千米.16.（10分）小明看一本故事书，小芳看一本科技书，故事书的页数是科技书的75%，小明每天看15页，小芳每天看18页.二人同时开始阅读，当小明看完故事书时，小芳还有24页没看.这两本书各有多少页？【分析】本题可列方程解答，设科技书有x页，则故事书有75%x页，小明每天看15页，小芳每天看18页，又当小明看完故事书时，小芳还有24页没看，由此可得方程=，解此方程后，即能求出两本书各有多少页.【解答】解:设科技书有x页，则故事书有75%x页，可得方程:=，（x﹣24）×5=6×75%x，5x﹣120=4.5x，0.5=120，x=240.240×75%=180（页）答:故事书有180页，科技书有240页.17.（10分）甲.乙两人分别从A.B 两地同时出发，相向而行，乙的速度是甲的，两人相遇后继续前进，甲到达B地，乙到达A地立即返回，已知两人第二次相遇的地点距离第一次相遇的地点是3000米，求A.B两地的距离？【分析】把两地间的路程看作单位“1”，当两人第二次相遇时，两人一共行驶了3个A.B 两地间的距离，根据时间一定路程和速度成正比，乙的速度是甲的，先求出两人行驶1个全程，甲和乙分别行驶的路程，进而求出行驶了3个A.B两地间的距离时，甲行驶的路程，再减去两地间的路程，也就是甲距B地的地点，最后求出3000米占总路程的分率，依据分数除法意义即可解答.【解答】解:2+3=5，3000÷[3﹣1﹣（1﹣）]，=3000÷[﹣1﹣]，=3000÷[]，=3000，=7500（米），答:A.B两地的距离7500米.第11页（共11页）。

2024年河南省郑州市金水区小升初数学试卷一、计算题（共22分）1．（4分）直接写出得数。

4.2﹣1.6＝ 3.5×2＝＝＝＝7.2÷0.09＝24×12.5%＝0.25：1.5＝2．（12分）计算下列各题，能简算的要简算。

4.83÷（7﹣2.4）＝1.25×0.5×323．（6分）解方程。

4（x+3.6）＝24.4二、填空题（共26分）4．（2分）2024年1至4月，中欧班列累计发送货物六十七万五千标箱，彰显着我国与班列沿线国家的经贸活力。

横线上的数写作，改写成用“万”作单位的数是万。

5．（2分）3.05公顷＝平方米75分＝时6．（4分）：24＝0.75＝＝%＝折7．（2分）比60千克多千克是千克；4.8千米比千米少40%。

8．（3分）数字2、7、6、0能组成个没有重复数字的两位数，其中组成的两位数中质数是，组成的的可能性大。

（填“奇数”或“偶数”）9．（3分）请在□里填上合适的数。

10．（1分）把87.5%、、0.8和0.869这四个数按从大到小的顺序排列。

排在第二位的数是。

11．（1分）刘奶奶把20000元按整存整取存入银行，存三年定期，年利率为2.35%，到期支取时，刘奶奶可得元利息。

12．（1分）一个精密仪器零件的高是4mm，画在图纸上的高是2dm，这幅图纸的比例尺是。

13．（2分）小学阶段很多知识之间有着密切联系。

如图，若A表示等腰三角形，则B可以表示等边三角形；若B表示方程。

则A可以表示；请你自己再举一个例子：。

14．（3分）如图，把一个圆柱切成若干等份，拼成一个近似的长方体，长方体的宽是6dm，高是5dm，长方体的长是dm，圆柱的侧面积是dm2，体积是dm3。

15．（2分）把边长为1厘米的正方形纸片，按下面的规律拼成长方形：用4个正方形拼成的长方形的周长是厘米，用n个正方形拼成的长方形的周长是厘米。

三、选择题（请将正确答案的序号填在括号里）（共16分）16．（2分）下面各数中，只读出一个零的是（）A．5001358B．3.008C．0.90%D．4239000317．（2分）如果a÷b＝10（a、b均为整数，且b≠0），那么a和b的最大公因数是（）A．a B．b C．ab D．1018．（2分）小明家在超市北偏东40°方向，那么超市在小明家（）方向。

河南省郑州经济技术开发区九龙中学2024年小升初数学综合练习卷一、选择题。

(选择正确答案的序号填在括号内。

每小题2分，共10分）1．17×78÷14＝（）A．12B．1718C．112D．12．一个圆柱体的体积和底面积，与一个圆锥体的体积和底面积都相等，圆柱体的高是圆锥体的（）。

A．13B．3 C．6 D．93．“一本书，读了16”，这句话里的单位“1”是（）。

A．已读的页数B．这本书的页数C．剩下的页数D．无法确定4．已知0.35×170=59.5,那么3.5×1.7的积是( )A．0.595 B．5.95 C．59.55．按1，中的规律接下来应填(）A．B．C．D．二、填空题。

(每小题2分，共28分）6．甲乙两数的的比是5:8，甲数比乙数少（______）％，乙数比甲数多（______）％．7．一个两位数，能同时被3和5整除，这个数如果是奇数，最大是______，如果是偶数，最小是______．8．如图，长方形ABCD的面积是100平方厘米，M在AD边上，且AM=AD，N在AB边上，且AN=BN．那么，阴影部分的面积等于_______平方厘米．9．一个三角形的三条边分别是3厘米，4厘米，5厘米，以4厘米的边为轴旋转一周，得到一个圆锥形，它的体积是________立方厘米。

10．把一个圆等分成若干个小扇形，用这些小扇形拼成了一个长方形。

已知长方形的周长比圆的周长多4厘米，长方形的宽是________厘米，长是________厘米。

11．已知a 、b 、c 、均为自然数，且各不相同，并且a+2c=，那么a+b+c 的最大值是（____）。

12．找规律把下列数中的最后一个填上214、319、5216、7325、11536、13849、171364、________。

13．平均每小时行102千米，全程大约有________千米。

14．如果3A=1.5B(A≠0)，那么A 与B 成（______）比例，A 与B 的最简整数比是（______）。

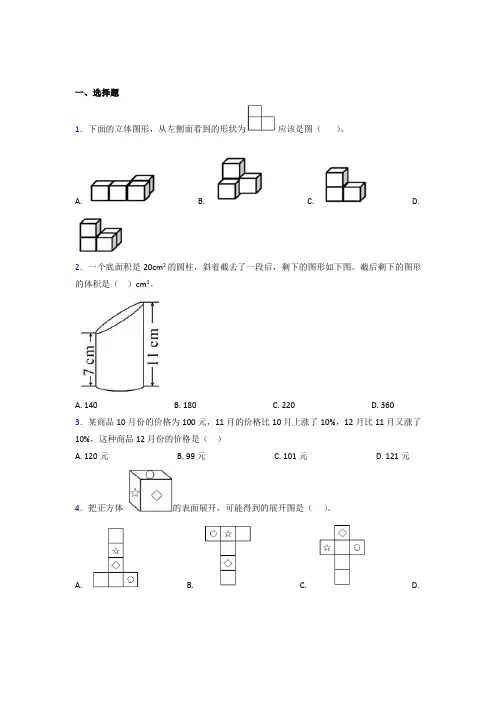
一、选择题1．下面的立体图形，从左侧面看到的形状为应该是图（）。

A. B. C. D.2．一个底面积是20cm2的圆柱，斜着截去了一段后，剩下的图形如下图。

截后剩下的图形的体积是（）cm3。

A. 140B. 180C. 220D. 3603．某商品10月份的价格为100元，11月的价格比10月上涨了10%，12月比11月又涨了10%，这种商品12月份的价格是（）A. 120元B. 99元C. 101元D. 121元4．把正方体的表面展开，可能得到的展开图是（）。

A. B. C. D.5．如图所示，小强在小林的（）方向上．A. 西偏南40°B. 东偏北50C. 北偏东50°D. 南偏西40°6．一桶油，第一次用了，第二次用了剩下的，那么（）A. 第一次用得多B. 第二次用得多C. 两次用得同样多D. 无法比较7．某项工程实际投资了80万元，比计划节约了20万元，实际投资比计划节约了（）A. 20% B. 25% C. 33% D. 60%8．将5：8的前项加上20，要使比值不变，后项应加上（）A. 15B. 20C. 32D. 409．笑笑在班级里进行了一项调查，并把调查结果制成如右图所示的统计图。

笑笑可能进行的调查内容是（）。

A. 你最喜欢什么宠物B. 你有几只宠物C. 你的宠物几岁了10．如图，以长方形的边a作底面周长，边b作高，分别可以围成一个长方体、正方体和圆形纸筒，再分别给它们别故一个底面。

这三个图形相比，容积最大的是（）。

A. 长方体B. 正方体C. 圆柱11．若一个四位数6□8△，既是2的倍数，又是3和5的倍数，则这个数最大是（）.A. 6980B. 6880C. 678012．大圆的半径6cm，小圆的半径3cm，大圆和小圆面积的比是（）。

A. 2：1B. 4：1C. 1：2二、填空题13．当一个圆柱的侧面展开图恰好是一个正方形时，这个圆柱的高是底面直径的________倍。

2024年郑州市第八中学小升初入学分班考试数学试卷(时间：60分钟；分值：100分)一、选择题(每小题3分，共24分)1.0.0…0(11个0)625÷0.0…0(12个0)25=(▲)。

A.25B.125C.1250D.2502.乐乐在计算25×(□+2)时，把算式抄成25×□+2，这样计算的结果与原来的正确答案相差(▲)。

A.50B.48C.25D.233.已知a=(1－12)－13，b=1－(12－13)，c=1－12－13，则(▲)。

A.a=c ，b=cB.a ≠c ，b=cC.a=c ，b ≠cD.a ≠c ，b ≠c4.下面4个数都是六位数，其中N 是比10小的自然数，S 是0，那么一定是3和5的倍数的是(▲)。

A.NNNSNNB.NSNSNSC.NSSNSSD.NSSNSN5.如图是无盖长方体盒子的表面展开图(重叠部分不计)，则盒子的容积为(▲)。

A.4B.6C.8D.126.把一些规格相同的杯子叠起来(如图)，4个杯子叠起来高20厘米，6个杯子叠起来高26厘米。

n 个杯子叠起来的高度可以用下面(▲)的关系式来表示。

A.6n－10B.3n+11C.6n－4D.3n+87.某商品原先的利润率为30%，为了促销，现降价30元销售，此时利润率下降为15%，那么这种商品的进价是(▲)。

A.300元B.200元C.150元D.130元8.现有若干防疫口罩，疫情防控人员计划将这些口罩分为两批，分别在两周内分发完毕。

第一周将第一批口罩数量按照1︰3︰4的比例分发给A，B，C三个小区且全部分完。

第二周先拿出第二批口罩数量的20%分发给社区工作人员，再将剩余口罩的1分发给A小区，则A小区两周收到的口罩数量与三个小区两周收到的口罩数量之和4的比为2︰9。

若B，C小区两周收到的口罩数量之比为3︰4，则B小区第二周收到的口罩数量与口罩总数量之比为(▲)。

A.8︰41B.9︰43C.8︰43D.9︰41二、填空题(每小题3分，共24分)9.在一本科幻书上，玛格内行星的人们使用migs，mags及mogs作为钱币单位，1mags=8migs，1mogs=6mags，则10mogs+6mags=_____migs。

2023年9月河南省郑州市小升初数学应用题自测练习卷三含答案解析学校:________ 姓名:________ 考号:________ 得分:________一、应用题(精选120题，每题1分。

一、审题：在开始解答前，应仔细阅读题目，理解题目意思、数量关系、问题是什么，以及需要几步解答；二、注意格式：正确使用算式、单位和答语；三、卷面要求：书写时应使用正楷，尽量避免连笔，字迹稍大，并注意排版，确保卷面整洁；四、π一律取值3.14。

)1.甲、乙两地相距225千米，一辆汽车从甲地开往乙地，每小时行45千米，到达乙地需要多少小时？（列出含有未知数x的算式，再解出来）2.一件衣服现在的售价是210元，比原价降低了3/10，这件衣服的原价是多少元？3.在献爱心捐款活动中，赤壁小学六年级学生捐款225元，比五年级多捐25%，五年级学生捐款多少元？4.甲、乙两辆汽车同时从相距425千米的两地相向而行，甲车每小时行40千米，比乙车每小时少5千米，几小时后两车在途中相遇？5.有54名工人，要把21桶油送到18千米外的工厂，两人抬一桶，大家轮流休息，问：平均每人抬几千米？6.一块梯形麦田，上底是48米，下底是52米，高是78米，平均每平方米产小麦0.45千克。

这块麦田共产小麦多少千克？7.有124吨水泥要用车从仓库运到商场，出租车场有两种车可以供出租：大卡车每次可运30吨，每次运费200元；小卡车每次可运4吨，每次运费90元。

请你设计一种最省钱的租车方案。

8.食堂买来24袋大米和32袋面粉，每袋大米重25千克，每袋面粉重20千克，大米和面粉一共买了多少千克？9.某工厂运来184吨煤，前8天平均每天用去15吨．剩下的预计4天用完，平均每天可用多少吨？10.五年级（1）班有45个同学，其中有23个女同学．男、女同学各占全班人数的几分之几？11.两地铁路长568千米，甲乙两列火车同时从两地相对开出，甲火车每小时行驶154千米，乙火车每小时行驶130千米，经过几小时两车相遇？（列方程解答）12.一个筑路队原计划20天修完一条路．实际每天比原计划多修45米，提前5天完成任务．原计划每天修路多少米？13.仓库里有一批货物，第一次运走14.58吨，第二次比第一次少运1.92吨．两次共运走多少吨？14.某服装工厂做一件上衣原来需要0.76米布，后来改进了技术，每件只需要0.684米布，原来做27件上衣用的布，现在可以多做多少件？15.建筑工地运来水泥74吨，运来的黄沙是水泥的3倍多12吨，运来黄沙多少吨？16.甲、乙、丙三人都以均匀的速度练习400米跑步，当甲到达终点，乙离终点80米，丙离终点160米，当乙到达终点时，丙离终点多少米？17.五年级同学参加植树活动，一班39人，共植树65棵；二班40人，共植树68棵；三班41人，共植树62棵．全级平均每人植树多少棵？18.红光饲养场养公鸡152只，母鸡624只，鸭子97只，问养鸡场养的鸡是鸭子的多少倍？19.体育用品商店迎春节促销．买1-4个，每个66元；买5-9个，每个64元；买10个以上，每个60元；我带了320元钱，最多能买多少个篮球？20.一箱色拉油4桶,每桶4升,买这样的一箱色拉油要128元。

2024年河南省郑州市中原区小升初数学试卷一、口算。

（0.5×8＝4分）1．（4分）口算。

2.08+7.2＝＝＝0.＝1.25×0.8＝3÷18＝＝＝二、填空。

（第1和第7小题，每题4分，其余每题2分，共18分。

）2．（4分）作为“中原粮仓”的河南省，2023年夏小麦总产量为三千五百四十九万七千三百吨，占全省粮食年产量的五成四。

（1）文中横线上的数写作，改写成用“万”作单位的数是万吨，保留整数约是万吨。

（2）文中画波浪线上的数改写成百分数是。

（3）如果某粮仓买入100吨小麦，记作+100吨，那么粮仓卖出200吨小麦吨。

3．（2分）根据如图前两个竖式，推算出第三个竖式的结果是。

4．（2分）学校种植园，宽是长的。

已知宽是3.6m，长是m。

在校园平面图上这块菜地宽6cm，校园平面图的比例尺是。

5．（2分）和谐小区2023年一共新增加了13辆电动清洁能源小汽车，至少有辆小汽车是在同一个月内购买的。

6．（2分）把一个底面半径是4dm,高是6dm的圆柱切拼成一个近似的长方体（如图），切拼后的长方体的长是dm，它的表面积比圆柱增加了dm2。

7．（2分）运动是保持健康的重要方式。

若把李老师今年1～5月每月跑步锻炼的平均次数记为0次，高于平均次数为正，低于平均次数为负，则李老师1～5月每月跑步锻炼的次数如图所示。

李老师这5个月跑步锻炼的平均次数是12次，则他1月跑步的次数为次，5月跑步的次数为次。

8．（4分）聪聪帮助妈妈一起干家务劳动，他的任务是清洗6个一模一样的杯子。

叠起来的杯子激发起了聪聪的学习兴趣，于是他拿起尺子开始探究。

（1）聪聪发现随着杯子数量的增加，叠起来杯子的整体高度也在不断增加，数据如表：杯子数量/个1234整体高度/cm11131517聪聪认为：叠起来杯子的整体高度与杯子的数量成正比例关系，你同意吗？写出判断理由：。

（2）如果叠起来5个杯子，整体高度是cm；n个杯子叠起来的整体高度是cm。

河南省郑州市枫杨外国语学校小升初数学试卷一.选择题（共8小题，每小题2分，满分16分）1.（2分）6.996保留两位小数是（）A.6.99B.7C.7.002.（2分）下面（）能化成有限小数.A. B. C.3.（2分）a为18，比b的2倍少4.则计算b的算式为（）A.（18+4）÷2B.18÷2+4C.18÷2﹣44.（2分）化简a﹣（b+c﹣d）=（）A.a﹣b+c﹣dB.a+b﹣c+dC.a﹣b﹣c+d5.（2分）将甲组人数拨给乙组，则甲乙两组人数相等.原来甲组人数比乙组人数多（）A. B. C.6.（2分）一项工程，计划5小时完成.实际4小时就完成了任务，工作效率提高了（）A. B. C.无法确定7.（2分）如图，平行四边形ABCD的底BC长是12厘米，线段FE长是4厘米，那么平行四边形中的阴影部分面积是（）平方厘米.A.24B.36C.48D.728.（2分）由5个小正方体搭成一个立体图形，从左面看形状是，从上面看形状是，共有（）种搭法.A.1B.2C.3D.4二.填空题（共10小题，每小题3分，满分30分）9.（3分）把4米长的绳子平均剪成5段，每段长是米，每段长占全长的.10.（3分）已知3x=2y，那么x:y=:.11.（3分）把3个棱长是4厘米的正方体木块粘合成一个长方体，这个长方体的体积是立方厘米，表面积比原来的3个小正方体表面积的和减少平方厘米.12.（3分）圆柱和圆锥的底面积比是4:3，高的比是2:5，它们的体积比是:.13.（3分）某化肥厂，今年一.二月份完成了第一季度生产任务的，二.三月份完成了第一季度生产任务的75%，二月份完成了第一季度生产任务的.14.（3分）将化成小数，小数点后第100位上的数字是.15.（3分）小明在计算有余数的除法时，把被除数472错看成427，结果商比原来小5，但余数恰巧相同.则该题的余数是.16.（3分）现有2克.3克.6克砝码各一个，那么在天平秤上能称出种不同重量的物体.17.（3分）有一个算式:≈1.37算式左边的□里却是整数，右边答案只写出了四舍五入的近似值，则算式□中的数依次分别是.18.（3分）某厂车队有3辆汽车给A.B.C.D.E五个车间组织循环运输.如图所示，标出的数是各车间所需装卸工人数.为了节省人力，让一部分装卸工跟车走，最少安排名装卸工保证各车间的需要.三.计算题（共3小题，满分16分）19.（4分）直接写出得数（1）30﹣19.0= （2）3.125+1=（3）1﹣0.94+0.06=（4）0.056×=20.（4分）求未知数x（1）1x+8×0.5=16（2）x:1=14:3.6.21.（8分）简算（1）1375+450÷18×25（2）（6﹣2）÷2（3）（3﹣112.5%+1）×1÷3（4）7÷0.24﹣2×0.875.四.面积体积计算22.（6分）一个零件，如图，求它的体积.（π取3）五.应用题23.（8分）紫荆花茶叶店运到一级茶和二级茶一批，其中二级茶的数量是一级茶的数量的，一级茶的买进价每千克24.8；二级茶的买进价是每千克16元，现在照买进价加价12.5%出售，当二级茶全部售完，一级茶剩下时，共盈利160元，那么，运到的一级茶有多少千克？24.（8分）快慢两车从甲乙两地相对开出，快车先行了全程的又11千米后，慢车才开出.相遇时，慢车行了全程的.已知快.慢两车速度比是5:4.甲乙两地相距多少千米？25.（8分）某校和某武警部队之间有一条公路，该校下午2点钟派车去接部队抗震救灾劳模来校作报告.往返需用1小时，这位劳模在下午1点钟便离开部队步行向学校走来，途中遇到接他的汽车，便立即上车驶往学校.在下午2点40分到达.汽车的速度是劳模步行速度的多少倍？参考答案与试题解析一.选择题（共8小题，每小题2分，满分16分）1.（2分）6.996保留两位小数是（）A.6.99B.7C.7.00【分析】6.996保留两位小数，要看小数点后面第三位数字是大于5还是小于5.因为6＞5，所以用四舍五入法可得6.996保留两位小数是7.00.【解答】解:6.996≈7.00.故选:C.2.（2分）下面（）能化成有限小数.A. B. C.【分析】如果一个最简分数的分母只含有质因数2或5，这个最简分数就能化成有限小数，否则就不能化成有限小数，由此判断即可.【解答】解:=，分母只含有质因数5，能；，分母含有质因数3，不能；=，分母含有质因数3，不能，.故选:A.3.（2分）a为18，比b的2倍少4.则计算b的算式为（）A.（18+4）÷2B.18÷2+4C.18÷2﹣4【分析】先用a加上4，就是b的2倍，然后再除以2就是b的值；据此解答.【解答】解:b可以表示为:（18+4）÷2.故选:A.4.（2分）化简a﹣（b+c﹣d）=（）A.a﹣b+c﹣dB.a+b﹣c+dC.a﹣b﹣c+d【分析】根据括号前面是减号，去掉括号变符号，据此先化简代数式，进而选择正确的选项.【解答】解:a﹣（b+c﹣d）=a﹣b﹣c+d.故选:C.5.（2分）将甲组人数拨给乙组，则甲乙两组人数相等.原来甲组人数比乙组人数多（）A. B. C.【分析】根据“将甲组人数拨给乙组，则甲乙两组人数相等”，可知把原来甲组人数看作5份数，拨给乙组1份数剩4份数，这是两组人数相等，说明乙组原来有4﹣1=3份数，进而求出原来甲组人数比乙组人数多的分率即可.【解答】解:原来甲组人数看作5份数，则现在甲组人数和乙组人数就是5﹣1=4份数，那么乙组人数原来有的份数:4﹣1=3份，则原来甲组人数比乙组人数多:（5﹣3）÷3=；答:原来甲组人数比乙组人数多.故选:B.6.（2分）一项工程，计划5小时完成.实际4小时就完成了任务，工作效率提高了（）A. B. C.无法确定【分析】把这项工程看作单位“1”，根据工作效率=工作量÷工作时间，分别求出计划和实际的工作效率，进而求出工作效率提高了几分之几.【解答】解:（）===，答:工作效率提高了.故选:B.7.（2分）如图，平行四边形ABCD的底BC长是12厘米，线段FE长是4厘米，那么平行四边形中的阴影部分面积是（）平方厘米.A.24B.36C.48D.72【分析】先求出三角形BFC的面积，因为两个空白三角形的面积相等，所以△GBC与△CAD的面积相等，都是平行四边形ABCD面积的一半，而△GFC是公共部分，所以△FAG与△CGD的面积之和与△FBC的面积相等，从而可以求出阴影部分的面积.【解答】解:因为△FAG与△CGD的面积之和与△FBC的面积相等，所以阴影部分的总面积是:12×4÷2×2，=48÷2×2，=48（平方厘米）.答:阴影部分的面积是48平方厘米.故选:C.8.（2分）由5个小正方体搭成一个立体图形，从左面看形状是，从上面看形状是，共有（）种搭法.A.1B.2C.3D.4【分析】从左面看有两层，上层有一个，下层有两排；从上面看，有两排，一排有两个，2×2+1=5，有两种搭法，满足5个小正方体搭成这个立体图形.如下图所示.上层的一个正方体可以在里排的左边或者右边.【解答】解:答案如图，答:共有2种搭法；故选:B.二.填空题（共10小题，每小题3分，满分30分）9.（3分）把4米长的绳子平均剪成5段，每段长是米，每段长占全长的.【分析】把4米长的绳子平均剪成5段，根据分数的意义，即将这根4米长的绳子当做单位“1”平均分成5份，则每段占全长的1÷5=，每段的长为:4×=（米）.【解答】解:每段占全长的:1÷5=，每段的长为:4×=（米）.故答案为:，.10.（3分）已知3x=2y，那么x:y=2:3.【分析】根据比例的基本性质“两内项之积等于两外项之积”，因此可以把3x看作比例的两外项乘积，2y看成比例的两内项乘积，然后转化成比例式.【解答】解:因为3x=2y，根据比例的基本性质得x:y=2:3.故答案为:2，3.11.（3分）把3个棱长是4厘米的正方体木块粘合成一个长方体，这个长方体的体积是192立方厘米，表面积比原来的3个小正方体表面积的和减少64平方厘米.【分析】合成后长方体的体积应是原来小正方体体积的3倍，表面在粘合处少了4个，减少的面积就是这四个面.【解答】解:体积:4×4×4×3，=64×3，=192（立方厘米）；减少的表面积:4×4×4=64（平方厘米）故答案为:192，64.12.（3分）圆柱和圆锥的底面积比是4:3，高的比是2:5，它们的体积比是8: 5.【分析】设圆柱的底面积为S，高为h，则圆柱的体积=Sh，圆锥的体积=×S ×h，用圆柱的体积除以圆锥的体积就能求得它们的体积比.【解答】解:设圆柱的底面积为S，高为h，则圆柱的体积=Sh，圆锥的体积=×S×h=Sh，体积比:Sh÷Sh=；答:它们的体积比是8:5.故答案为:8:5.13.（3分）某化肥厂，今年一.二月份完成了第一季度生产任务的，二.三月份完成了第一季度生产任务的75%，二月份完成了第一季度生产任务的.【分析】根据题意，把第一季度的生产任务看作单位“1”，已知一.二月份完成了第一季度生产任务的，二.三月份完成了第一季度生产任务的75%（），用75%﹣1即可求出二月份完成了第一季度生产任务的几分之几.由此解答.【解答】解:75%﹣1=1=1=1=；答:二月份完成了第一季度生产任务的.故答案为:.14.（3分）将化成小数，小数点后第100位上的数字是6.【分析】要求小数点后面第100位上的数字是多少，就要寻求简便的方法.因为=0.3636363636…小数部分第一位数字不再循环节之内，该循环节有2位数字，然后用100除以2，根据余数进行判断，因此该数字是6.【解答】解:=0.363636…100÷2=50，没有余数，因此，小数点后面第100位上的数字是6；故答案为:6.15.（3分）小明在计算有余数的除法时，把被除数472错看成427，结果商比原来小5，但余数恰巧相同.则该题的余数是4.【分析】根据被除数=除数×商+余数，本题在这两种除法计算中，除数与余数没变，假设除数是a，余数是r，则可列出两个等式，即可得解.【解答】解:在这两种除法计算中，除数与余数没变，只是商比原来小5.设除数是a，余数是r，则472=a×商+r，427=a×（商﹣5）+r，有472﹣427=a×5，a=（472﹣427）÷5=9；472÷9=52…4；所以余数r=4.故答案为:4.16.（3分）现有2克.3克.6克砝码各一个，那么在天平秤上能称出10种不同重量的物体.【分析】这道题没有限制砝码只能放在天平的同一秤盘上，因此天平两边的秤盘上都可以放砝码，尽管只有2克，3克，6克砝码各一个，但是如果天平一边是2克，另一边是3克，就可称出1克重的物体，如果它俩放在同一边又可称出5克重的物体；同理，2克与6克砝码可称出4克或8克重的物体；3克与6克砝码可称出3克或9克重的物体，其中3克重物体可以直接用3克砝码称出；用2克.3克和6克可称出7克，5克，1克，11克重的物体；所以用这三个砝码可称出1，2，3，4，5，6，7，8，9，11克共10种不同重量的物体.【解答】解:用2.3克的砝码可以但称出1克重和5克重的物体，2克与6克砝码可称出4克或8克重的物体；3克与6克砝码可称出3克或9克重的物体，其中3克重物体可以直接用3克砝码称出；用2克.3克和6克可称出7克，5克，1克，11克重的物体；所以用这三个砝码可称出1，2，3，4，5，6，7，8，9，11克共10种不同重量的物体.答:在天平秤上能称出10种不同重量的物体；故答案为:10.17.（3分）有一个算式:≈1.37算式左边的□里却是整数，右边答案只写出了四舍五入的近似值，则算式□中的数依次分别是1，3，3.【分析】因为算式的值为近似值，且其介于1.365和1.374之间，又因□里的数是整数，从而可推算□的值.【解答】解:≈1.37，所以1.365≤≤1.374，通分得1.365≤≤1.374，于是有150.15≤55×□+22×□+10×□≤151.14，由于□里的数是整数，所以，55×□+22×□+10×□=151，只有55×1+22×3+10×3=151，故□里数字依次填1，3，3.18.（3分）某厂车队有3辆汽车给A.B.C.D.E五个车间组织循环运输.如图所示，标出的数是各车间所需装卸工人数.为了节省人力，让一部分装卸工跟车走，最少安排21名装卸工保证各车间的需要.【分析】每个车间抽出3名装卸工，共抽出3×5=15人，每辆车上有3人，共需3×3=9人，这样可节约15﹣9=6（人）.这时A有3人，B有2人，C有4人，D 有0人，E有5人，再从A，B，C，E各抽出2人，每车上2人，这样又可省去2×4﹣2×3=2人.这样每辆车跟5人，共15人，A有1人，B有0人，C有2人，E有3人，D还是0人.共需装卸工:5×3+1+2+3=21（人）.【解答】解:每个车间抽出3名装卸工，共抽出3×5=15人，每辆车上有3人，共需3×3=9人，这样可节约15﹣9=6（人）.这时A有3人，B有2人，C有4人，D有0人，E有5人.再从A，B，C，E各抽出2人，每车上2人，这样又可省去2×4﹣2×3=2人.这样每辆车跟5人，共15人，A有1人，B有0人，C有2人，E有3人，D还是0人.共需装卸工:5×3+1+2+3=21（人）.答:最少安排21名装卸工保证各车间的需要.故答案为:21.三.计算题（共3小题，满分16分）19.（4分）直接写出得数（1）30﹣19.0=（2）3.125+1=（3）1﹣0.94+0.06=（4）0.056×=【分析】依据小数.分数四则运算计算方法解答.【解答】解:（1）30﹣19.0=10.9（2）3.125+1=4.25（3）1﹣0.94+0.06=0.12（4）0.056×=0.00820.（4分）求未知数x（1）1x+8×0.5=16（2）x:1=14:3.6.【分析】（1）先化简，再根据等式性质，方程两边同时减去4，再同时除以即可；（2）根据比例的性质得到 3.6x=1×14，化简后，再根据等式性质，方程两边同时除以3.6即可.【解答】解:（1）1x+8×0.5=161x+4=161x+4﹣4=16﹣41x÷=12÷x=9（2）x:1=14:3.63.6x=1×143.6x÷3.6=16÷3.6x=21.（8分）简算（1）1375+450÷18×25（2）（6﹣2）÷2（3）（3﹣112.5%+1）×1÷3（4）7÷0.24﹣2×0.875.【分析】（1）先算除法，再算乘法，最后算加法；（2）先算减法，再算除法；（3）先算括号里面的，再算乘法，最后算除法；（4）先算乘法和除法，再算减法.【解答】解:（1）1375+450÷18×25=1375+25×25=1375+625=2000；（2）（6﹣2）÷2=×=；（3）（3﹣112.5%+1）×1÷3=3×1÷3=××=；（4）7÷0.24﹣2×0.875=7.2÷0.24﹣×=30﹣2=28.四.面积体积计算22.（6分）一个零件，如图，求它的体积.（π取3）【分析】根据圆锥的体积公式:v=，长方体的体积公式:v=abh，把数据分别代入公式求出它们的体积和即可.【解答】解:×3×（12÷2）2×6+20×15×8=216+2400=2616（立方厘米），答:它的体积是2616立方厘米.五.应用题23.（8分）紫荆花茶叶店运到一级茶和二级茶一批，其中二级茶的数量是一级茶的数量的，一级茶的买进价每千克24.8；二级茶的买进价是每千克16元，现在照买进价加价12.5%出售，当二级茶全部售完，一级茶剩下时，共盈利160元，那么，运到的一级茶有多少千克？【分析】先分别求出两种茶各自每千克的盈利情况，再根据两种茶各自卖出部分的盈利等于盈利总额这个等量关系，即可列方程求解.【解答】解:设一级茶有x千克，则二级茶有x千克，一级茶每千克盈利24.8×12.5%=3.1（元）二级茶每千克盈利16×12.5%=2（元）由题意得:2×x+（1﹣）x×3.1=160x+x=160x=160x=.答:运到的一级茶有千克.24.（8分）快慢两车从甲乙两地相对开出，快车先行了全程的又11千米后，慢车才开出.相遇时，慢车行了全程的.已知快.慢两车速度比是5:4.甲乙两地相距多少千米？【分析】我们把全程的路程看作单位“1”已知慢车行驶了全程的，用全程的（1﹣）减去快车先行驶的与慢车相同时间内行驶的路程的和，再用1﹣减去得到的分率，就是11千米对应的分率；据此解答.【解答】解:11÷[（1﹣）﹣（4×5+）]，=11÷[﹣（）]，=11÷[]，=11÷，=11×，=70（千米）；答:甲乙两地相距70千米.25.（8分）某校和某武警部队之间有一条公路，该校下午2点钟派车去接部队抗震救灾劳模来校作报告.往返需用1小时，这位劳模在下午1点钟便离开部队步行向学校走来，途中遇到接他的汽车，便立即上车驶往学校.在下午2点40分到达.汽车的速度是劳模步行速度的多少倍？【分析】首先根据题意，可得这位劳模和接他的汽车在下午2点20分相遇，汽车提前60﹣40=20（分钟）到达，所以汽车从相遇点到部队需要20÷2=10（分钟），同样的路程，这位劳模走了2时20分﹣1时=1时20分=80分；然后根据速度×时间=路程，可得路程一定时，速度和时间成反比，求出汽车的速度是劳模步行速度的多少倍即可.【解答】解:根据分析，可得这位劳模和接他的汽车在下午2点20分相遇，（60﹣40）÷2=20÷2=10（分钟）2时20分﹣1时=1时20分=80分汽车的速度是劳模步行速度的:80÷10=8答:汽车的速度是劳模步行速度的8倍.。

2024年河南省郑州市中牟县小升初数学试卷一、填一填。

（每空1分，共26分）1．（3分）甲骨文是迄今为止中国发现年代最早的成熟文字系统，是商朝（公元前17世纪一公元前11世纪）的文化产物，距今约3600多年的历史，1899年在河南省安阳市殷墟首次发现。

据统计，中国共计出土甲骨十五万四千六百多片。

横线上的数写作，改写成用“万”作单位的数是万，省略“万”位后面的尾数约是万。

2．（4分）＝dm24t60kg＝t1.2时＝分5700cm3＝dm2＝L3．（3分）在一个比例中，两个内项的积是最小的质数，一个外项是5，则另一个外项是；16的因数有个，选取其中的四个组成比例是。

4．（2分）如果点C表示的数是，那么点B表示；如果点D表示的数是100，那么点A 表示。

5．（2分）国产大飞机C﹣919，国之重器。

在C﹣919的控制系统中有一个长5mm的精密机器零件，画在图纸上是25cm，这幅图的比例尺是；另一种精密零件长 4.2mm，画在这幅图上长。

6．（3分）把一个高6厘米的圆柱剪拼成一个近似的长方体（如图），表面积增加了24平方厘米。

这个圆柱的底面直径是厘米，这个圆柱的体积是立方厘米；如果把这个圆柱削成一个最大的圆锥，至少要削去立方厘米。

7．（2分）古诗“横看成岭侧成峰，远近高低各不同”，告诉我们要学会从多个角度思考和解决问题。

请你运用这种思维分析一下：如果一个几何体从前面看是，从上面看是，那么要搭成这样的几何体，至少需要个小正方体。

8．（4分）如图所示图象表示了香蕉、苹果的总价与数量之间的关系，看图回答问题。

（1）香蕉的总价和购买的数量成比例关系。

（填“正”或“反”）（2）从图象上看，单价更贵一些的水果是。

（填“香蕉”或“苹果”）（3）买3千克苹果要用元，20元可以买千克香蕉。

9．（3分）如图，摆1个六边形用6根小棒，摆2个六边形用11根小棒，……（1）照这样的规律摆下去，摆9个六边形用根小棒。

（2）用101根小棒可以摆个六边形。

2023年河南省郑州市小升初数学试卷一、按要求计算下面各题。

（每题0分）1．下面两个数是互素的是（ ）A．18和72B．4和6C．9和5D．22和33 2．2004年第一季度共有（ ）A．90天B．91天C．80天D．100天3．用5个同样的小正方体，摆出从正面看是的立体图形．下面摆法中，符合要求的是（ ）A．B．C．D．4．在①x+y＝12，②y＝2x，③＝y，④25%：y＝x：40中，表示x和y成反比例的式子有（ ）个．A．1B．2C．3D．45．如图中每个小正方形的面积是1cm2，估计阴影部分的面积约是（ ）A．24cm2B．32cm2C．40cm2D．45cm26．王老师把3000元存入银行，定期2年，年利率按2.25%计算，到期可得本金和税后利息共（ ）元．A．3000B．3108C．1087．圆柱的侧面展开不可能是（ ）A．长方形B．平行四边形C．梯形D．正方形8．苹苹家的客厅用方砖铺地，若用边长5dm的方砖，需要128块，如果改用边长是8dm的方砖，至少需要多少块？设至少需要x块，下列方程正确的是（ ）A．8x＝5×128B．8×8×x＝5×5×128C．8x＝5×5×1289．把一批书按2：3：4或2：4：5两种方案分给甲、乙、丙三个班，都可以将这批书正好分完，这批书可能有（ ）本．A．90B．99C．110D．18010．袋里有一些糖果，平均分给5个同学或者平均分给6个同学，都正好分完，袋里最少有（ ）个糖果。

A．30B．60C．11D．18二、认真阅读，组心填写。

（3分+6分+3分+2分+3分＝17分）11．（3分）2020年我国粮食总产量669490000吨，横线上的数读作 ，改写成以“万”为单位的数是 ，四舍五入到亿位是 。

12．（3分）在横线上填上合适的单位。

早上，丫丫和爸爸妈妈一起吃早餐，丫丫喝的豆浆比爸爸多100 。