03第三章-连接件强度的实用计算.
- 格式:doc
- 大小:610.00 KB
- 文档页数:11

连接件受力经验计算公式
1. 螺栓连接受力计算公式
- 轴向受力: F = π/4 * d^2 * σb
- 剪切受力: F = π/4 * d^2 * τ
其中, d为螺栓直径, σb为螺栓材料的抗拉强度, τ为螺栓材料的剪切强度。
2. 焊缝受力计算公式
- 焊缝长度受力: F = a * l * σw
- 焊缝面积受力: F = a * σw
其中, a为焊缝面积或长度, l为焊缝长度, σw为焊缝材料的极限强度。
3. 键连接受力计算公式
- 剪切受力: F = π/4 * d^2 * τ
- 压力受力: F = d * l * p
其中, d为键直径, l为键长度, τ为键材料的剪切强度, p为键与轴承的接触压力。
4. 铰链连接受力计算公式
- 剪切受力: F = π/4 * d^2 * τ
- 压力受力: F = d * b * p
其中, d为铰链直径, b为铰链宽度, τ为铰链材料的剪切强度, p为铰链与轴承的接触压力。
以上公式是基于理想工况下的简化计算方法,实际应用中还需考虑安全系数、应力集中等影响因素进行修正。
此外,对于复杂的连接形式,可能需要采用有限元分析等数值计算方法。

螺栓联接件强度计算
1.螺栓受力情况
螺栓受力情况见图1所示。
图1 螺栓受力图
1)横截面 11、 22上有作用力,象剪刀一样,试图把螺栓从该截面处剪开, 称F S为剪力(Shear force),引起切应力( Shear stress)。
2)杆段①、②、③受到被联接构件的挤压(Bearing),引起挤压应力(Bearing stress)。
2.失效形式
基于螺栓的受力,预测出螺栓可能的失效形式:
1)在截面 11,22处被剪断;
2)受挤压部分的半圆被“挤扁”(近似半椭圆)。
下图2中的螺栓产生了塑性变形,验证了此种情况。
图2 螺栓受挤压塑性变形
3.其他可能受力情况
1)没有受剪力作用;
2)同螺栓杆段①、②、③对应半圆孔受到螺栓挤压,有可能导致变形过大而失效(变成近似椭圆孔);
3)螺栓挤压,有可能把被联接构件端部豁开(一般将端部设计得充分长,抵御豁开力,因而对此不计算)。
4.强度计算
4.1剪切强度计算
1)剪力 F s = F/2
2)名义切应力
3)强度校核,否则需重新设计。
4.2挤压强度计算
挤压应力计算面积,实际挤压面在垂直挤压力方向上的投影。

联接设计以及强度计算在工程设计过程中,联接设计是非常重要的一环。
联接是指将两个或多个构件连接在一起,使其能够承受外部力和转动力矩。
联接设计的目的是确保连接的安全可靠,并满足预定的设计要求。
联接的设计考虑了多个方面,包括强度、刚度、耐久性、可维修性等。
其中,强度是联接设计中最重要的因素之一联接的强度计算涉及到强度和应力的概念。
强度是指材料可以承受的最大应力,通常以抗拉强度、抗压强度、抗剪强度等形式表示。
应力是指联接内部材料受到的力除以其所受面积的比值。
联接强度的计算需要考虑两个方面:联接部件的强度和联接方式的强度。
联接部件的强度计算涉及到材料的力学性能和几何参数。
首先,需要确定联接部件所使用的材料的力学性能,例如抗拉强度、屈服强度、弹性模量等。
其次,需要确定联接部件的几何参数,例如长度、直径、角度等。
然后,根据这些参数,可以利用相关的公式计算联接部件的强度。
例如,对于螺栓的抗拉强度计算,可以使用螺栓的截面面积乘以材料的屈服强度。
联接方式的强度计算涉及到连接方式的类型和载荷情况。
不同的连接方式有不同的强度计算方法。
例如,对于焊接连接,可以根据焊缝的长度、厚度和焊材的强度来计算其强度。
而对于螺栓连接,可以根据螺栓的直径、材料的强度和螺栓预紧力等参数来计算强度。
在进行联接设计时,还需要考虑到载荷情况。
载荷分为静载荷和动载荷,静载荷是指在联接上施加的静态力,动载荷是指在联接上施加的动态力。
静载荷可以通过等效静载荷的方法进行计算,动载荷可以通过动力学或者有限元分析等方法进行计算。
总之,联接设计以及强度计算是工程设计中非常重要的一部分。
通过合理的设计和准确的强度计算,可以确保联接的安全可靠,并满足设计要求。
因此,在工程设计中应重视联接设计的过程,保证设计结果的合理性和可靠性。

材料力学知到章节测试答案智慧树2023年最新山东科技大学第一章测试1.材料力学的研究方法与理论力学的研究方法完全相同。
参考答案:错2.内力只作用在杆件截面的形心处。
参考答案:错3.杆件某截面上的内力是该截面上应力的代数和。
参考答案:错4.确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
参考答案:对5.根据各向同性假设,可认为材料的弹性常数在各方向都相同。
参考答案:对6.根据均匀性假设,可认为构件的弹性常数在各点处都相同。
参考答案:对7.若物体各部分均无变形,则物体内各点的应变均为零。
参考答案:对8.外力就是构件所承受的载荷。
参考答案:错9.构件的强度、刚度和稳定性问题均与材料的力学性能有关。
参考答案:对10.可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
参考答案:对11.材料力学的研究对象为杆件。
参考答案:对12.题图所示直杆初始位置为ABC,作用力P后移至AB’C’,但右半段BCDE的形状不发生变化。
试分析哪一种答案正确。
参考答案:AB、BC两段都产生位移;13.根据各向同性假设,可认为构件的()沿各个方向相同。
参考答案:材料的弹性常数14.关于确定截面内力的截面法的适用范围,有下列说法正确的是()。
参考答案:不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况15.下列结论中是正确的是()。
参考答案:若物体各点均无位移,则该物体必定无变形16.以下结论中正确的是()。
参考答案:应力是内力的集度17.根据均匀性假设,可认为构件的下列各量中的哪个量在各点处都相同。
参考答案:材料的弹性常数18.材料力学的四个基本假设是()参考答案:连续性;各向同性;均匀性;小变形19.工程构件的基本类型是()参考答案:壳;板;杆件;块体20.下列描述正确的是()参考答案:应力是构件破坏的决定因素;应力是指内力的分布集度;应变是描述构件变形程度的量第二章测试1.因为轴力要按平衡条件求出,所以轴力的正负与坐标轴的指向一致。



材料力学一、课程的性质与设置目的和要求材料力学是由基础理论课向设计课程过渡的技术基础课。
该课程对后续专业课及工程应用都有深远的影响。
通过对材料力学课程的学习,要求学生对杆件的强度、刚度和稳定性问题具有明确的基本概念、必要的基础理论知识、比较熟练的计算能力、一定的分析能力和实验能力。
二、课程内容与考核目标本课程主要讲述杆件的强度、刚度和稳定性理论及其应用,包括四种基本变形与组合变形的应力和变形,强度和刚度计算,能量方法与超静定问题,压杆稳定,动载荷与交变应力。
第一章拉伸与压缩1.学习目的与要求:本章介绍杆件在拉伸或压缩时的应力和变形计算。
通过学习,要求能熟练绘制杆件的轴力图;能熟练进行杆件强度计算和变形计算。
2.课程内容:轴向拉、压的概念;外力、内力、应力、应变、变形、位移等概念;拉(压)杆的内力、内力图;应力和强度计算、材料的拉、压力学性能、杆件的变形计算;简单的超静定问题。
3.考核知识点:轴力、轴力图;轴向拉压时截面上的应力;轴向拉压时的变形、虎克定律;材料的力学性能(低碳钢、铸铁的拉伸试验的应力应变图;低碳钢和铸铁的压缩试验及两类材料的比较);轴向拉压的强度条件及强度计算;4.考核要求:能熟练运用截面法计算杆件的轴力,正确绘制轴力图;掌握杆件拉、压时的强度计算;掌握杆件的变形计算;了解材料的基本力学性能以及试件拉、压破坏时的现象和原因;掌握求解简单超静定问题的方法。
第二章剪切1.学习目的与要求:本章介绍连接件的实用计算。
通过学习,要求会计算简单的连接件的强度问题。
2.课程内容:剪切构件的受力和变形特点,连接处可能的破坏形式,剪切和挤压的实用计算。
3.考核知识点:剪切和挤压的概念,剪切和挤压的应力计算。
4.考核要求:了解剪切和挤压的概念,会计算简单的连接件的强度问题。
第三章扭转1.学习目的与要求:本章介绍杆件扭转时的应力和变形,通过学习,要求能熟练绘制杆件的扭矩图;掌握应力和变形的计算公式,能熟练进行轴类零件的强度和刚度计算2.课程内容:纯剪切概念、剪切胡克定律、切应力互等定理;功率、转速与外力偶矩的关系;扭矩和扭矩图、应力和变形的计算、强度条件和刚度条件;弹簧的应力和变形计算;简单扭转超静定问题的计算;非圆截面杆扭转的应力和变形简介。

第三章杆件的应力与强度计算一.基本要求1.拉伸与压缩变形1.1熟练掌握应力的计算,理解胡克定律。
1.2了解常用材料在拉伸和压缩时的机械性质及其测量方法。
1.3理解许用应力、安全系数和强度条件,熟练计算强度问题。
2.扭转变形2.1理解纯剪切的概念、切应力互等定理和剪切胡克定律。
2.2理解圆轴扭转时应力公式推导方法,并熟练计算扭转应力。
2.3理解圆轴扭转强度条件的建立方法,并熟练计算强度问题。
3.弯曲变形3.1理解弯曲正应力的概念及其公式推导方法,熟练掌握弯曲正应力及强度问题。
3.2理解弯曲切应力的概念及其公式推导方法,掌握简单截面梁弯曲切应力的计算及弯曲切应力强度条件。
4.剪切与挤压变形:了解剪切和挤压的概念,熟练掌握剪切和挤压的实用计算方法。
5.熟练掌握常用截面的形心、静矩、惯性矩的计算及平行移轴公式。
3.1 引言本章讨论了拉伸或压缩、扭转变形和弯曲变形的应力和强度计算,以及剪切和挤压的实用计算。
3.2 拉压杆的应力与应变一.轴向拉(压)杆横截面上的应力1)平面假设:变形前后横截面保持为平面,而且仍垂直于杆轴线,如图2-8所示。
根据平面假设得知,横截面上各点正应力σ相等,即正应力均匀分布于横截面上,σ等于常量。
2)由静力平衡条件确定σ的大小由于dN=σ⋅dA,所以积分得则式中:σ—横截面上的正应力FN—横截面上的轴力A—横截面面积此式对于过集中力作用点的横截面不适应。
3)正应力σ的正负号规定为:拉应力为正,压应力为负。
对于的变截面直杆,在考虑杆自重(密度ρ)时,有FN=⎰σdA=σA Aσ=FN Aσx=FNx Ax其中FN=P+ρAx⋅x若不考虑自重,则FNx=P对于等截面直杆,最大正应力发生在最大轴力处,也就是最易破坏处。
而对于变截面直杆,最大正应力的大小不但要考虑FNx,同时还要考虑Ax。
例1 起吊三角架,如图2-10所示,已知AB杆由2根截面面积为10.86cm的角钢制成,2P=130kN,α=30 。


第三章剪切与挤压同济大学航空航天与力学学院顾志荣一、教学目标与教学内容1、教学目标解决联接件的强度计算,要求掌握剪切与挤压的概念,熟练掌握剪切与挤压的使用计算方法。
2、教学内容(1) 剪切与挤压的概念及工程实例;(2) 剪切的实用计算;(3) 挤压的实用计算;(4) 连接件的实用强度计算。
二、重点与难点1、重点:全部教学内容。
2、难点:剪切面和挤压面的确定。
通过讲解和模型演示来解决。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
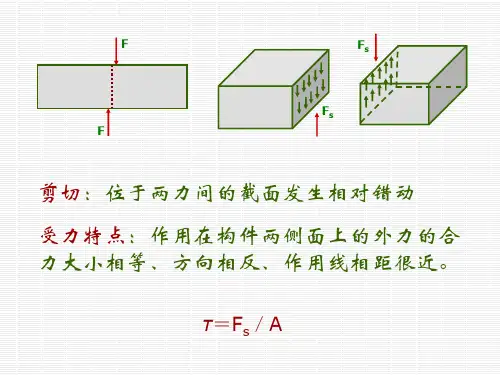
四、建议学时2学时五、实施学时六、讲课提纲一、铆钉的剪切强度计算1、剪切的概念⑴受力特点:(见图3-1,a)作用在垂直于构件两侧面上的外力的合力大小相等、方向相反,作用线相距很近。
(a) (b)图3-1⑵变形特点:(见图3-1,b)介于这两个作用力中间部分的截面,有发生相对错动的趋势。
这种变形形式称为剪切。
⑶剪切面:发生相对错动的截面称为剪切面(见图3-1,b:截面m-m)。
注意:剪切面总是与作用力平行,且居于相邻的一对外力作用线之间。
⑷单剪与双剪:只有一个剪切面的称为单剪(图3-2,b)有两个剪切面的称为双剪(图3-3,c)图3-3 2、剪切的实用计算⑴ 铆钉所受的外力F 1 指一个铆钉nF F P=1n 指铆钉的个数F P F P91PF =图3-4⑵ 铆钉剪切面上的内力F Q铆钉剪切面上的内力F Q 称为剪力。
单剪时: nF F F PQ ==1 双剪时: nF F F PQ 221==⑶ 剪切面上的名义剪应力τ ①何谓名义剪应力?τ在剪切面上各点的大小及分布规律很复杂,因为:a)铆钉的短跨弯曲;b)铆钉的冷却及螺帽的拧紧,使钉杆受拉; c)钢板孔壁与钉杆的互相挤压。
②τ的计算:QQ A F =τA Q —受剪面的面积③τ的单位:与σ一样:P a 、MP a ⑷剪切强度极限的测定图3-5①剪切试验装置根据联接件的的实际受剪情况,进行直接剪切实验来得到破坏荷载。