生存分析-cox 回归与sas应用总结

一、生存分析基本概念1、事件（Event）指研究中规定的生存研究的终点，在研究开始之前就已经制定好。

根据研究性质的不同，事件可以是患者的死亡、疾病的复发、仪器的故障，也可以是下岗工人的再就业等等。

2、生存时间(Survival time)指从某一起点到事件发生所经过的时间。

生存是一个广义的概念，不仅仅指医学中的存活，也可以是机器出故障前的正常运行时间，或者下岗工人再就业前的待业时间等等。

有的时候甚至不是通用意义上的时间，比如汽车在出故障前的行驶里程，也可以作为生存时间来考虑。

3、删失（Sensoring）指由于所关心的事件没有被观测到或者无法观测到，以至于生存时间无法记录的情况。

常由两种情况导致：（1）失访；（2）在研究终止时，所关心的事件还未发生。

4、生存函数（Survival distribution function）又叫累积生存率，表达式为S（t）=P(T>t),其中T为生存时间，该函数的意义是生存时间大于时间点t的概率。

t=0时S(t)=1，随着t的增加S(t)递减（严格的说是不增），1-S(t)为累积分布函数，表示生存时间T不超过t的概率。

二、生存分析的方法1、生存分析的主要目的是估计生存函数，常用的方法有Kaplan-Meier法和寿命表法。

对于分组数据，在不考虑其他混杂因素的情况下，可以用这两种方法对生存函数进行组间比较。

2、如果考虑其他影响生存时间分布的因素，可以使用Cox回归模型（也叫比例风险模型），利用数学模型拟合生存分布与影响因子之间的关系，评价影响因子对生存函数分布的影响程度。

这里的前体是影响因素的作用不随时间改变，如果不满足这个条件，则应使用含有时间依存协变量的Cox回归模型。

下面用一个例子来说明SPSS中Cox回归模型的操作方法。

例题要研究胰腺癌术中放疗对患者生存时间的影响，收集了下面所示的数据：操作步骤：SPSS变量视图菜单选择：点击进入Cox主对话框，如下，将time选入“时间”框，将代表删失的censor变量选入“状态”框，其余分析变量选入“协变量”框。

第十二章生存分析及COX回归在临床医学中, 对病人治疗效果的考查. 一方面可以看治疗结局的好坏，另一方面还可以通过治疗时间的长短来衡量。

例如某种疾病治愈的时间, 某癌症病人手术后的存活时间等, 把这类与时间有关的资料统称为生存资料。

生存资料一般通过随访收集，从某标准时刻(发病、手术或出院等)开始，按某种相等或不等时间间隔，对观察对象定期观察预定项目所得的资料，它的结局是死亡，治愈、复发、阳性等。

但在临床上，往往由于各种原因：(1)因迁移原因失去联系；(2)死于其他原因而造成失访；(3)预定终止结果迟迟不发生，致使在一定时期内，一部分病例得不到确切的生存期，但它们提供了其生存期长于观察期的信息，这种数据称为删失数据，也称截尾数据或终检值(censored data)，包含终检值的数据即为不完全数据。

处理这类数据的统计分析方法称为生存分析。

它包括三个方面的内容1）生存过程的描述，主要是生存率的估计；2）生存过程的比较；3）影响因素的分析。

§12.1 生存率的估计生存率估计常用的有两种方法乘积极限法和寿命表法。

1乘积极限法又称Kaplan-Meier 法适用于小样本资料。

基本思想：将生存时间由小到大依次排列，在每个死亡点上，计算其期初人数、死亡人数、死亡概率、生存概率和生存率。

CHISS实现：点击重复测量→生存分析→乘积极限法应用举例：例12-1某疗法治疗白血病后的存活月数为： 2+,13,7+,11+,6,1,11,3,17,7。

试估计其生存率。

带“＋”为存活终检值。

解步骤：1 进入数据模块此数据库已建立在CHISS\data文件夹中，文件名为：a9_0生存分析.DBF。

打开数据库点击数据→文件→打开数据库表找到文件名为：a9_0生存分析.DBF →确认2 进入统计模块进行统计计算点击重复测量→生存分析→乘积极限法时间变量： time 终检值指标：censor→确认3 进入结果模块查看结果点击结果乘积限估计法生存分析, 数据来自文件: C:\CHISS\Data\a9_0生存分析.DBF数据过滤条件：━━━━━━━━━━━━━━━━━━━秩观察死亡观察生存率次时间序号数生存率标准误(i) t(i) (j) n(i) S(j) Ss(j)───────────────────0 0 0 10 1.0000 ...1, 1 1 10 0.9000 0.09492, 2+ ... 9 ... ...3, 3 2 8 0.7875 0.13404, 6 3 7 0.6750 0.15515, 7 4 6 0.5625 0.16516, 7+ ... 5 ... ...7, 11 5 4 0.4219 0.17378, 11+ ... 3 ... ...9, 13 6 2 0.2109 0.172610, 17 7 1 0.0000 ...━━━━━━━━━━━━━━━━━━━注：删失数据为1。

利用“SAS”管探数学建模思想应用“SAS”（Survival Analysis System）是一款专门用于生存分析的软件，在医学、统计和生态等领域中得到广泛的应用。

本文将介绍如何利用“SAS”管探数学建模思想应用于生存分析领域。

一、生存分析的基本概念生存分析是研究时间相关性和其它因素对事件发生率的影响的一种方法，其中“事件”可以是死亡、复发、治疗失败等。

生存分析的核心是生存曲线和风险曲线。

生存曲线描述了时间和事件发生率之间的关系。

它可以通过在x轴上画时间，y轴上画累积事件发生率（1减去累积生存率）来得到。

生存曲线是逐渐下降的，表示随着时间的推移，事件发生率逐渐增加。

例如，某种癌症的生存曲线可能显示在第一个月之后有10%的病人离开了，第二个月有另外10%的病人离开了，以此类推。

二、SAS在生存分析中的应用在生存分析领域中，SAS提供了一系列统计命令，包括生存曲线和风险曲线的计算、模型拟合和预测等功能。

下面介绍几种在SAS中进行生存分析的方法。

1. Kaplan-Meier法Kaplan-Meier法是计算生存曲线的最常用方法之一。

它可以考虑在不同时间点的生存率不同的情况。

在SAS中，利用PROC LIFETEST命令可以计算Kaplan-Meier曲线，同时还可以进行组间比较。

2. Cox比例风险模型Cox比例风险模型是一种常用的生存分析模型，可以考虑影响生存时间的多个因素。

在SAS中，利用PROC PHREG命令可以拟合Cox比例风险模型，同时还可以进行组间比较和预测等功能。

3. Cox-Snell残差检验4. AUC值计算AUC（Area Under the Curve）值是评价模型预测能力的重要指标。

在生存分析中，可以利用AUC值来评估模型对事件随时间变化的预测能力。

在SAS中，利用PROC PHREG或PROC LIFETEST命令可以计算AUC值。

三、总结利用“SAS”管探数学建模思想应用于生存分析领域，可以进行生存曲线和风险曲线的计算、模型拟合和预测等功能。

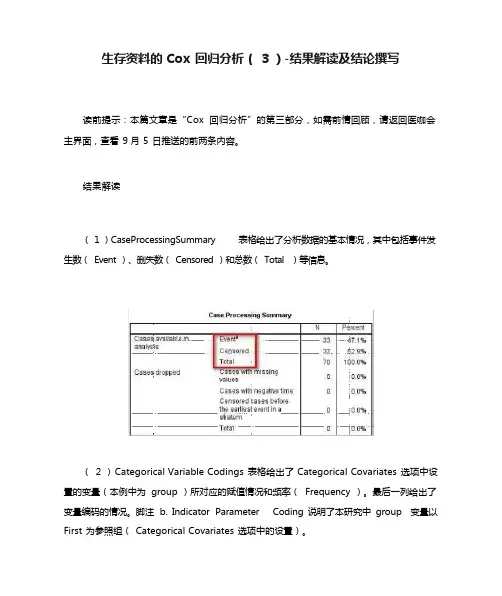
生存资料的Cox回归分析（3）-结果解读及结论撰写读前提示：本篇文章是“Cox回归分析”的第三部分，如需前情回顾，请返回医咖会主界面，查看 9 月 5 日推送的前两条内容。

结果解读（ 1 ）CaseProcessingSummary 表格给出了分析数据的基本情况，其中包括事件发生数（Event ）、删失数（Censored ）和总数（Total ）等信息。

（2 ）Categorical Variable Codings 表格给出了 Categorical Covariates 选项中设置的变量（本例中为group ）所对应的赋值情况和频率（Frequency ）。

最后一列给出了变量编码的情况。

脚注b. Indicator Parameter Coding 说明了本研究中group 变量以First 为参照组（Categorical Covariates 选项中的设置）。

（3 ）OmnibusTests of Model Coefficients 表格给出了模型中所有变量的回归系数全为0 的检验结果。

对于本例，①Score统计量为5.065, P=0.024 ；②对数似然比检验χ2 =5.399, P=0.020。

说明模型中至少有一个自变量的 HR 值不为1 ，模型整体检验有统计学意义。

（ 4 ）Variables in the Equation 表格给出了参数估计的结果。

结果显示最后筛选后的模型仅包含group 变量，①P =Sig.=0.029 说明治疗方式为影响肺癌患者预后的独立因素。

②相对危险度 HR=Exp(B)=0.410 ，说明使用新药的患者死亡风险为使用常规药物患者的 0.410 倍，③H R 的 95% 可信区间（ 95% CI ）为 0.184-0.914。

（ 5 ）生存曲线。

前述Plots 选项的设置要求输出按照不同药物分组的生存曲线。

新药组（赋值为 1 ，绿色线条）比常规药物组（赋值为0 ，蓝色线条）的生存率高。

cox回归模型的应用场景Cox回归模型的应用场景Cox回归模型是生存分析中一种常用的统计模型，主要用于探究事件发生时间与多个预测因素之间的关系。

该模型在医学、生物学、社会科学等领域具有广泛的应用。

本文将介绍Cox回归模型的应用场景，并通过实例说明其在实际问题中的应用。

一、医学领域在医学领域，Cox回归模型常用于研究患者的生存时间与各种预测因素之间的关系。

例如，研究某种疾病的患者在接受不同治疗方案后的生存情况，可以将患者的生存时间作为因变量，治疗方案、年龄、性别、病情严重程度等作为自变量，应用Cox回归模型进行分析。

通过分析结果，可以评估不同因素对患者生存时间的影响，并为医生制定个性化的治疗方案提供依据。

二、社会科学领域在社会科学研究中，Cox回归模型常用于研究人群中各种社会因素对事件发生时间的影响。

例如，研究员可以通过该模型分析员工的离职时间与薪资、工作满意度、晋升机会等因素之间的关系。

通过分析结果，可以了解不同因素对员工离职时间的影响程度，从而为企业提供人力资源管理的参考。

三、生物学领域在生物学研究中，Cox回归模型常用于研究生物实验中各种因素对生物体死亡时间的影响。

例如，研究员可以通过该模型分析实验组与对照组在给定药物的作用下的生存时间差异。

通过分析结果，可以评估药物对生物体生存时间的影响，为药物研发和治疗提供依据。

四、金融领域在金融领域，Cox回归模型常用于研究个人或企业的违约时间与各种因素之间的关系。

例如，研究员可以通过该模型分析借款人的违约时间与借款金额、信用评级、还款能力等因素之间的关系。

通过分析结果，可以了解不同因素对违约时间的影响程度，从而为银行和金融机构的风险管理提供参考。

总结起来，Cox回归模型在医学、社会科学、生物学和金融等领域都有广泛的应用。

通过该模型，研究人员可以探索事件发生时间与多个预测因素之间的关系，并为相关领域的决策提供科学依据。

然而，虽然Cox回归模型在实际应用中具有很大的优势，但也需要注意模型的前提假设和局限性，以保证分析结果的准确性和可靠性。

一、生存分析基本概念1、事件（Event）指研究中规定的生存研究的终点，在研究开始之前就已经制定好。

根据研究性质的不同，事件可以是患者的死亡、疾病的复发、仪器的故障，也可以是下岗工人的再就业等等。

2、生存时间(Survival time)指从某一起点到事件发生所经过的时间。

生存是一个广义的概念，不仅仅指医学中的存活，也可以是机器出故障前的正常运行时间，或者下岗工人再就业前的待业时间等等。

有的时候甚至不是通用意义上的时间，比如汽车在出故障前的行驶里程，也可以作为生存时间来考虑。

3、删失（Sensoring）指由于所关心的事件没有被观测到或者无法观测到，以至于生存时间无法记录的情况。

常由两种情况导致：（1）失访；（2）在研究终止时，所关心的事件还未发生。

4、生存函数（Survival distribution function）又叫累积生存率，表达式为S（t）=P(T>t),其中T为生存时间，该函数的意义是生存时间大于时间点t的概率。

t=0时S(t)=1，随着t的增加S(t)递减（严格的说是不增），1-S(t)为累积分布函数，表示生存时间T不超过t的概率。

二、生存分析的方法1、生存分析的主要目的是估计生存函数，常用的方法有Kaplan-Meier法和寿命表法。

对于分组数据，在不考虑其他混杂因素的情况下，可以用这两种方法对生存函数进行组间比较。

2、如果考虑其他影响生存时间分布的因素，可以使用Cox回归模型（也叫比例风险模型），利用数学模型拟合生存分布与影响因子之间的关系，评价影响因子对生存函数分布的影响程度。

这里的前体是影响因素的作用不随时间改变，如果不满足这个条件，则应使用含有时间依存协变量的Cox回归模型。

下面用一个例子来说明SPSS中Cox回归模型的操作方法。

例题要研究胰腺癌术中放疗对患者生存时间的影响，收集了下面所示的数据：操作步骤：SPSS变量视图菜单选择：点击进入Cox主对话框，如下，将time选入“时间”框，将代表删失的censor变量选入“状态”框，其余分析变量选入“协变量”框。

生存分析的c ox回归模型案例 --- spss作者:日期:一、生存分析基本概念1、事件(Ev en t)指研究中规定的生存研究的终点，在研究开始之前就已经制定好。

根据研究性质的不同，事件可以是患者的死亡、疾病的复发、仪器的故障，也可以是下岗工人的再就业等等。

2、生存时间(Surv i va 1 ti me指从某一起点到事件发生所经过的时间。

生存是一个广义的概念，不仅仅指医学中的存活，也可以是机器出故障前的正常运行时间，或者下岗工人再就业前的待业时间等等。

有的时候甚至不是通用意义上的时间，比如汽车在出故障前的行驶里程，也可以作为生存时间来考虑。

3、删失(Se n sor in g)指由于所关心的事件没有被观测到或者无法观测到，以至于生存时间无法记录的情况。

常由两种情况导致：(1)失访；(2)在研究终止时，所关心的事件还未发生。

4、生存函数(Sur vi val distribute n fun ct io n)又叫累积生存率，表达式为S( t )=P(T>t)，其中T为生存时间，该函数的意义是生存时间大于时间点t 的概率°t = 0时S(t )=1,随着t的增加S (t)递减(严格的说是不增)，1-S (t )为累积分布函数，表示生存时间T不超过t的概率。

?二、生存分析的方法1、生存分析的主要目的是估计生存函数，常用的方法有Kap 1 an-Meier法和寿命表法。

对于分组数据，在不考虑其他混杂因素的情况下，可以用这两种方法对生存函数进行组间比较。

2、如果考虑其他影响生存时间分布的因素，可以使用Cox回归模型(也叫比例风险模型)，利用数学模型拟合生存分布与影响因子之间的关系，评价影响因子对生存函数分布的影响程度。

这里的前体是影响因素的作用不随时间改变，如果不满足这个条件，则应使用含有时间依存协变量的Cox回归模型。

F面用一个例子来说明S P SS中Cox回归模型的操作方法。

例题要研究胰腺癌术中放疗对患者生存时间的影响，收集了下面所示的数据表M.J 験膈疼术申皴疔效杲硏愛数据的说碉旳E数值(N)8 0 手术吋的年龄 sex 数值(N) 8 0 性别trt bui ch数值㈣ 8 0数值㈣” 0数值㈣8有无甫中放疗□无朮中敵无3数值但)stage数值(N)8TFJIW 分期目II 朝｝…炉度量⑶足,名义(N) 昙右A^x(N) 雲右易名以N) 垂右di 序号Q) 言右 A «X[N) 尋石—品名0N)若右 =臺变址名 变值说明暫丘类申.分类童就的浦附『WTFK11馳者编号1 inw j 生存时闻⑴)ceitsrir跚矢2号类m 拓,f ：删矢叭T 术时的年龄连绩trt 处理组别的无术巾放疗) 2分类 m 无术中»Jr J ： ff 术中放疗M'l性別 2分类 S 男皿女L MII占位址2分娄th 騎赃头SLX 头部臥外 rh 程度W 序多分类 1: ultO >2 irhl 、3 = °：h2・4* «-h3P封无腹雎转将2分炎 U:无％ 1 J A 亠片1TMM 分类2分类3； III 期 J ： IX 期操作步骤：?SPSS 变量视图caserto 数值但) 8 0无_____ 无 8少度量⑶time 数值㈣ 8 1 生存时问(月)— 无—无 8度量⑸censor数值㈣8刪失m 死亡｝-无 8冨右— 曷 «X(N)范虞, 对齐名称卷数标签值列痕量标准胯脏头詔…无s 曉胆管檯润程厦8表M.J験膈疼术申皴疔效杲硏愛数据的说碉菜单选择:文件疋）履辑电）视團电）败握匸｝转弟折牲）直誚迴）團形迫）娈用程序世｝硏□世）琴助PZJ L-12' stage5cas&no123time2.41.710 11 12 13 14 15 16 17 18 101112141516U1819201.04.66410.S6 11 15S4.04.04.06.53 &£.96 2报告陆述颈计裁（D 上廊购値邂］一般线煙摸型1.9 广义线性摸型混合損型0》相关©回甘迟）对數线性摸型（Q 神经网络度呈⑶ 非参数检聽创预测（D生存函数程｝参重n轆应）缺尖M斩边… 雾重归園© 亘束抽肄丄＞|sex~ DQtri111Q°0|n園芽命a（L）...寸Kaplan4Jieier...Cox回归Q._|匕蛍依时协裘益⑼…点击进入C ox主对话框，如下，将ti me选入时间”框将代表删失的censo r变量选入状态”框，其余分析变量选入协变量”框。

一、生存分析基本概念1、事件（Event）指研究中规定的生存研究的终点，在研究开始之前就已经制定好。

根据研究性质的不同，事件可以是患者的死亡、疾病的复发、仪器的故障，也可以是下岗工人的再就业等等。

2、生存时间(Survival time)指从某一起点到事件发生所经过的时间。

生存是一个广义的概念，不仅仅指医学中的存活，也可以是机器出故障前的正常运行时间，或者下岗工人再就业前的待业时间等等。

有的时候甚至不是通用意义上的时间，比如汽车在出故障前的行驶里程，也可以作为生存时间来考虑。

3、删失（Sensoring）指由于所关心的事件没有被观测到或者无法观测到，以至于生存时间无法记录的情况。

常由两种情况导致：（1）失访；（2）在研究终止时，所关心的事件还未发生。

4、生存函数（Survival distribution function）又叫累积生存率，表达式为S（t）=P(T>t),其中T为生存时间，该函数的意义是生存时间大于时间点t的概率。

t=0时S(t)=1，随着t的增加S(t)递减（严格的说是不增），1-S(t)为累积分布函数，表示生存时间T不超过t的概率。

二、生存分析的方法1、生存分析的主要目的是估计生存函数，常用的方法有Kaplan-Meier法和寿命表法。

对于分组数据，在不考虑其他混杂因素的情况下，可以用这两种方法对生存函数进行组间比较。

2、如果考虑其他影响生存时间分布的因素，可以使用Cox回归模型（也叫比例风险模型），利用数学模型拟合生存分布与影响因子之间的关系，评价影响因子对生存函数分布的影响程度。

这里的前体是影响因素的作用不随时间改变，如果不满足这个条件，则应使用含有时间依存协变量的Cox回归模型。

下面用一个例子来说明SPSS中Cox回归模型的操作方法。

例题要研究胰腺癌术中放疗对患者生存时间的影响，收集了下面所示的数据：操作步骤：SPSS变量视图菜单选择：点击进入Cox主对话框，如下，将time选入“时间”框，将代表删失的censor变量选入“状态”框，其余分析变量选入“协变量”框。