第章角动量定理和刚体的转动题解

第1章质点的运动知识要点1.1 位移速度加速度1.2 圆周运动及其描述书后习题解析同步训练题同步训练题答案第2章牛顿运动定律知识要点2. 1 牛顿运动定律2.2 动量定理动能定理书后习题解析同步训练题同步训练题答案第3章运动的守恒定律知识要点3.1 保守力势能3.2 机械能守恒定律动量守恒定律书后习题解析同步训练题同步训练题答案第4章刚体的转动知识要点4.1 转动惯量转动动能定轴转动定律4.2 刚体的角动量角动量定理角动量守恒定律书后习题解析同步训练题同步训练题答案第5章相对论基础知识要点5.1 狭义相对论基本原理5.2 洛仑兹坐标变换书后习题解析同步训练题同步训练题答案第6章气体动理论知识要点6.1 理想气体6.2 麦克斯韦速率分布律6.3 玻尔兹曼分布律6.4 气体分子的平均碰撞次数及平均自由程书后习题解析同步训练题同步训练题答案第7章热力学基础知识要点7.1 热力学第一定律7.2 热力学第一定律对理想气体的应用7.3 循环过程7.4 热力学第二定律7.5 熵书后习题解析同步训练题同步训练题答案第8章真空中的静电场第9章导体和电介质中的静电场第10章恒定电流和恒定电场第11章真空中的恒定磁场第12章磁介质中的磁场第13章电磁感应和暂态过程第14章麦克斯韦方程组电磁场第15章机械振动和电磁振动第16章机械波和电磁波第17章波动光学第18章早期量子论和量子力学基础第19章激光和固体的量子理论第20章原子核物理和粒子物理简介。

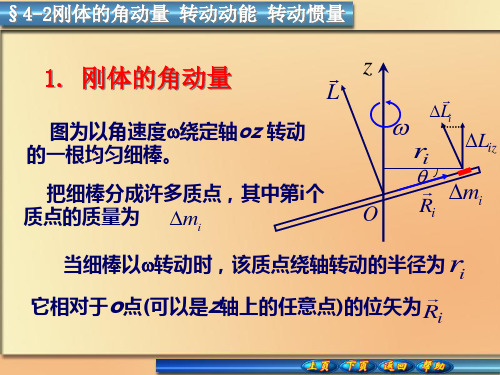
第四章 刚体的转动 问题4-1 以恒定角速度转动的飞轮上有两个点，一个点在飞轮的边缘，另一个点在转轴与边缘之间的一半处。

试问：在t ∆时间内，哪一个点运动的路程较长？哪一个点转过的角度较大？哪一个点具有较大的线速度、角速度、线加速度和角加速度？ 解 在一定时间内，处于边缘的点，运动的路程较长，线速度较大；它们转动的角度、角速度都相等；线加速度、角加速度都为零。

考虑飞轮上任一点P ，它随飞轮绕转轴转动，设角速度为ω，飞轮半径为r 。

在t ∆内，点P 运动的路程为P P l r t ω=∆，对于任意点的角速度ω恒定，所以离轴越远的点（P r 越大）运动的路程越长。

又因为点P 的线速度P P v r ω=，即离轴越远，线速度也越大。

同理，点P 转动的角度P t θω=∆，对于飞轮上任一个点绕轴转动的角速度ω都相等，即在相等的时间内，飞轮上的点转动的角度都相等。

又角速度ω恒定，即线加速度0P Pd a r dtω==，角加速度0P d dtωα==.4-2 如果一个刚体所受合外力为零，其合力矩是否也一定为零？如果刚体所受合外力矩为零，其合外力是否也一定为零？解 不一定。

如图（a ）轻杆（杆长为l ）在水平面内受力1F 与2F 大小相等方向相反，合力为零，但它们相对垂直平面内通过O 点的固定轴的力矩1M F l =不为零。

如图（b ），一小球在绳拉力作用下在水平面内绕固定轴作圆周运动，小球所受的合外力通过O 点，它所受的力矩为零。

4-3 有两个飞轮，一个是木制的，周围镶上铁制的轮缘，另一个是铁制的，周围镶上木制的轮缘，若这两个飞轮的半径相同，总质量相等，以相同的角速度绕通过飞轮中心的轴转动，哪一个飞轮的动能较大。

1F（a ） （b ）解 两飞轮的半径、质量都相同，但木制飞轮的质量重心靠近轮缘，其转动惯量要大于铁制轮缘。

飞轮的动能212k E J ω=，ω相同，转动惯量J 越大，动能越大。

即木制飞轮动能较大。

第五章 刚体的定轴转动一 选择题1. 一绕定轴转动的刚体，某时刻的角速度为ω，角加速度为α，则其转动加快的依据是：（ ）A. α > 0B. ω > 0，α > 0C. ω < 0，α > 0D. ω > 0，α < 0 解：答案是B 。

2. 用铅和铁两种金属制成两个均质圆盘，质量相等且具有相同的厚度，则它们对过盘心且垂直盘面的轴的转动惯量。

（ ）A. 相等；B. 铅盘的大；C. 铁盘的大；D. 无法确定谁大谁小 解：答案是C 。

简要提示：铅的密度大，所以其半径小，圆盘的转动惯量为：2/2Mr J =。

3. 一轻绳绕在半径为r 的重滑轮上，轮对轴的转动惯量为J ，一是以力F 向下拉绳使轮转动；二是以重量等于F 的重物挂在绳上使之转动，若两种情况使轮边缘获得的切向加速度分别为a 1和a 2，则有： （ ）A. a 1 = a 2B. a 1 > a 2C. a 1< a 2D. 无法确定 解：答案是B 。

简要提示：(1) 由定轴转动定律，1αJ Fr =和11αr a =，得：J Fr a /21= (2) 受力分析得：⎪⎩⎪⎨⎧===-2222ααr a J Tr ma T mg ，其中m 为重物的质量，T 为绳子的张力。

得：)/(222mr J Fr a +=，所以a 1 > a 2。

4. 一半径为R ，质量为m 的圆柱体，在切向力F 作用下由静止开始绕轴线作定轴转动，则在2秒内F 对柱体所作功为： （ ）A. 4 F 2/ mB. 2 F 2 / mC. F 2 / mD. F 2 / 2 m解：答案是A 。

简要提示：由定轴转动定律： α221MR FR =，得：mRFt 4212==∆αθ 所以：m F M W /42=∆=θ5. 一电唱机的转盘正以ω 0的角速度转动，其转动惯量为J 1，现将一转动惯量为J 2的唱片置于转盘上，则共同转动的角速度应为： （ ）A ．0211ωJ J J +B ．0121ωJ J J +C ．021ωJ JD ．012ωJ J解：答案是A 。

第5章 角动量守恒定律 刚体的转动5-1 质点的动量守恒与角动量守恒的条件各是什么，质点动量与角动量能否同时守恒？試说明之。

答：质点的动量守恒的条件是：当0F =时，p mv ==恒矢量。

质点的角动量守恒的条件是：当0M =时，即000,F r θπ⎧=⎪⎪=⎨⎪=⎪⎩时，L =恒矢量。

可见，当0F =时，质点动量与角动量能同时守恒。

5-2 质点在有心力场中的运动具有什么性质？答：质点在有心力场中运动时，0,0F M ≠=，则角动量守恒，即：当0M =时，L =恒矢量。

又因为有心力是保守力，则机械能守恒，即：当0ex in nc A A +=时，K P E E E =+=恒量。

5-3 人造地球卫星是沿着一个椭圆轨道运行的，地心O 是这一轨道的一个焦点。

卫星经过近地点和远地点时的速率一样吗？卫星在近地点和远地点时的速率与地心到卫星的距离有什么关系？答：卫星经过近地点和远地点时的速率不一样，由角动量守恒定律得：a ab b r mv r mv = a b b av r v r ∴= 可见，速率与距离成反比。

5-4 作匀速圆周运动的质点，对于圆周上某一定点，它的角动量是否守恒？对于通过圆心而与圆面垂直的轴上的任意一点，它的角动量是否守恒？对于哪一个定点，它的角动量守恒？答：作匀速圆周运动的质点，对于圆周上某一定点，它的角动量不守恒；对于通过圆心而与圆面垂直的轴上的任意一点，它的角动量不守恒；对于圆心定点，它的角动量守恒。

5-5 以初速度0v 将质量为m 的小球斜上抛，抛射角为θ，小球运动过程中，相对于抛射点的角动量如何变化？小球运动到轨道最高点时，相对于抛射点的角动量为多少？答：取抛射点为坐标原点，取平面直角坐标系Oxy ，y 轴正方向向上，则质点的运动方程和速度表达式为：020cos 1sin 2x v ty v t gt θθ=⎫⎪⎬=-⎪⎭ ， 00cos sin x y v v v v gt θθ=⎫⎬=-⎭ 对于抛射点的角动量：()()x y y x L r mv xi y j mv i mv j xmv k ymv k =⨯=+⨯+=- 将,,,x y x y v v 代入得：201cos 2L mgv t k θ=- 当小球到达最高点时，时刻为：0sin v t gθ=，代入上式得： 小球相对于抛射点的角动量为：320sin cos 2mv L k gθθ=-。

第4章 刚体的定轴转动 习题及答案1．刚体绕一定轴作匀变速转动，刚体上任一点是否有切向加速度？是否有法向加速度？切向和法向加速度的大小是否随时间变化？答：当刚体作匀变速转动时,角加速度β不变。

刚体上任一点都作匀变速圆周运动，因此该点速率在均匀变化，v l ω=，所以一定有切向加速度t a l β=，其大小不变。

又因该点速度的方向变化，所以一定有法向加速度2n a l ω=，由于角速度变化，所以法向加速度的大小也在变化。

2. 刚体绕定轴转动的转动定律和质点系的动量矩定理是什么关系？答：刚体是一个特殊的质点系，它应遵守质点系的动量矩定理，当刚体绕定轴Z 转动时，动量矩定理的形式为zz dL M dt=，z M 表示刚体对Z 轴的合外力矩，z L 表示刚体对Z 轴的动量矩。

()2z i i L m l I ωω==∑,其中()2i i I m l =∑，代表刚体对定轴的转动惯量，所以 ()z z dL d d M I I I dt dt dtωωβ====。

既 z M I β=。

所以刚体定轴转动的转动定律是质点系的动量矩定理在刚体绕定轴转动时的具体表现形式，及质点系的动量矩定理用于刚体时在刚体转轴方向的分量表达式。

3．两个半径相同的轮子，质量相同，但一个轮子的质量聚集在边缘附近，另一个轮子的质量分布比较均匀，试问：（1）如果它们的角动量相同，哪个轮子转得快？（2）如果它们的角速度相同，哪个轮子的角动量大？答：(1)由于L I ω=，而转动惯量与质量分布有关，半径、质量均相同的轮子，质量聚集在边缘附近的轮子的转动惯量大，故角速度小，转得慢，质量分布比较均匀的轮子转得快；（2）如果它们的角速度相同，则质量聚集在边缘附近的轮子角动量大。

4．一圆形台面可绕中心轴无摩擦地转动，有一玩具车相对台面由静止启动，绕轴作圆周运动，问平台如何运动？如小汽车突然刹车，此过程角动量是否守恒？动量是否守恒？能量是否守恒？答：玩具车相对台面由静止启动，绕轴作圆周运动时，平台将沿相反方向转动；小汽车突然刹车过程满足角动量守恒，而能量和动量均不守恒。