实际气体节流过程
- 格式:ppt
- 大小:206.00 KB
- 文档页数:22





焦耳一汤姆逊效应气体在节流反应过程里产生的温度变化,被称之为焦耳一汤姆逊作用(简称焦一汤作用)。
产生上述现象的根部原因,是由于气体的烩值,并不是简单的温度函数,同时也受到压强、气体性能的影响。
大部分气体在室温条件下,完成节流反应的时候,都会产生冷却作用,也就是通过节流设备之后的温度快速减小,上述温度改变就是正焦耳一汤姆逊作用。
只有很少数的气体在室温条件下,完成节流反应之后温度上升,这类温度改变就被称之为负焦耳一汤姆逊作用。
在相同温度条件下,焦耳一汤姆逊作用的正负性可以发生转化,这类温度就被称之为反转温度。
所有气体都具有自身独特的反转温度。
例如,空气,氮气和氧气的反转温度都比室温高。
节流过程节流过程是一类不可逆反应过程,在反应过程里,流体处于非平衡状态。
分析节流反应过程,就是研究从节流反应之前一直到节流反应之后,流体依次处于不同平衡状态的时候,所有指数经过反应过程产生的改变。
在绝热节流反应过程中,保持能量守恒。
这是因为在反应过程里,流体和外界没有产生热量传递,也没有能量的转化,假如维持流体在节流反应之后的高度、流速恒定,也就是没有重力势能以及运动势能的改变(或者改变非常小,基本忽略不计),那么节流反应之后,流体的烩h2和节流反应之前的烩hl保持一致,也就是h2=hl与此同时,由于绝热节流是一种不可逆的反应过程,节流后流体的嫡绝对增加,有s2>s1在气态流体通过绝热节流之后,体积会随着压强的减小而不断变大,但是液态流体的体积在节流反应前后,并不会产生显著地改变。
节流的温度效应在绝热节流反应前后,流体温度的改变被称之为节流反应的温度效应。
节流反应之后流体的实际温度快速减小,被称之为节流反应冷效应;节流反应之后流体的实际温度快速升高,被称之为节流反应热效应;节流反应前后流体的实际温度保持一致,被称之为节流反应零效应。
节流反应的温度效应和液体的类别,温度、压强都具有密切的联系。
绝热节流反应的温度效应可以采用绝热节流反应指数来表达。



实际气体绝热节流膨胀过程的△u在热力学中,气体的绝热节流膨胀过程是指气体从高压区域通过狭窄的孔口进入低压区域,过程中没有热量交换的现象。
在这个过程中,气体的内能发生变化,我们将其表示为△u。
本文将从理论和实际两个方面来探讨实际气体绝热节流膨胀过程的△u。
理论方面,根据绝热过程的定义,气体在绝热节流膨胀过程中,没有热量交换发生。
因此,气体的内能变化完全取决于气体的外界功。
根据热力学第一定律,内能变化△u等于外界对气体所做的功。
在绝热节流膨胀过程中,气体通过狭窄的孔口进入低压区域,气体分子受到孔口的限制而加速运动,从而使气体的动能增加,内能也随之增加。
因此,实际气体绝热节流膨胀过程的△u是正值。
实际方面,绝热节流膨胀过程广泛应用于工业生产中,例如气体喷嘴、气体涡轮等。
在这些应用中,气体通过狭窄的孔口进入低压区域,从而产生高速气流,用于推动机械设备或实现特定的工艺过程。
在实际应用中,我们可以通过测量气体的入口和出口参数来计算实际气体绝热节流膨胀过程的△u。
我们需要测量气体的入口压力和温度,以及出口压力。
根据理论方面的分析,气体的内能变化△u等于外界对气体所做的功。
在绝热节流膨胀过程中,外界对气体所做的功可以通过压力差来计算。
根据热力学第一定律,功等于压力差乘以气体的体积变化。
因此,△u等于压力差乘以气体的体积变化。
我们需要计算气体的体积变化。
在绝热节流膨胀过程中,气体通过狭窄的孔口进入低压区域,气体的体积发生变化。
根据理想气体状态方程,PV=nRT,气体的体积与物质的量成正比。
因此,我们可以通过测量气体的入口和出口物质的量来计算气体的体积变化。
我们可以将测得的压力差和体积变化代入△u的计算公式,从而得到实际气体绝热节流膨胀过程的△u值。
需要注意的是,在计算过程中,我们需要考虑气体的物性参数,如气体的摩尔质量、绝热指数等,以保证计算结果的准确性。
实际气体绝热节流膨胀过程的△u是正值,表示气体在绝热节流膨胀过程中内能的增加。

实际气体节流膨胀熵变在实际气体的世界里,节流膨胀听起来可能有点复杂,但其实就是气体在通过狭窄的地方时发生的一些奇妙变化。
想象一下,一个气球,刚打好的时候,里面的气体像小孩一样欢快地在里面蹦蹦跳跳。
可是,当你把气球的口捏住,突然放开,气体就像得了自由,快速地涌出来,这一瞬间,气体的温度和压力都发生了变化,甚至连周围的环境也感受到了一丝波动。
这就涉及到熵的概念。
听起来像是物理课上才会提到的词,但其实熵就像我们生活中的杂乱无章,越多的选择和状态,熵就越高。
节流膨胀的时候,气体分子从一个高压区域突然跃入一个低压区域,这个过程就像是开了个大门,分子们纷纷拥挤而出,快乐得不得了。
这种状态的变化,实际上就是在创造一种“混乱”,而这种混乱正是熵变的体现。
气体分子从原来的有序状态变得更加随机,真是“乱了阵脚”,这就是熵增的魅力所在。
在这个过程中,气体的温度也可能会下降。
比如说,你把喷雾罐里的气体喷出来,听到那“嘶”的一声,气体瞬间膨胀,温度立刻下降。
这就让人想起冰淇淋,夏天的时候你在阳光下舔着冰淇淋,感觉一阵清凉,这其实就是气体膨胀带来的那种“凉意”。
虽然说熵和温度有点难以捉摸,但可以理解成它们之间有种微妙的关系,像朋友一样,时而亲密,时而有点疏远。
在我们的日常生活中,节流膨胀现象其实无处不在。
你有没有注意到,冬天的时候,气体从暖气片出来,瞬间的热气让你觉得舒服极了。
然后它在空间中不断扩散,温度逐渐下降,这就像是气体的“旅行”,在不断的探索中,熵值也在悄悄地增加。
我们生活的每个细节都在悄悄影响着周围的环境,真是有趣。
想象一下,气体就像一群追求自由的小鸟,想要尽情飞翔,不愿意被拘束。
在节流膨胀的瞬间,它们打破了束缚,飞向更大的天空。
虽然说这过程有点复杂,但其实就是一种追求更高状态的表现,犹如我们人类的追求,追寻梦想,想要突破自己的极限。
这一切都和我们熟悉的物理定律紧密相连。
能量守恒、热力学定律,这些看似严肃的东西,其实也隐藏着生活的智慧。
节流工作原理
节流工作原理指的是通过控制流体流速来实现节流作用的工作原理。
在液体或气体传输过程中,通过简单的装置或设备来限制流体的流速和流量,从而达到节流的效果。
节流装置常见的有节流阀、节流孔、节流喉等。
它们的基本原理是通过缩小流体通道的断面积,增加流体流过该通道的阻力,从而降低流速和流量。
具体来说,当流体通过节流装置时,流体分子要通过狭窄的通道,导致流体速度加快,由于质量守恒,流体的压力随之降低。
这样通过改变节流装置的通道尺寸、长度或形状,可以实现对流速和流量的精确控制。
节流的物理原理包括伯努利原理、流体动能原理和公式伯努利方程。
伯努利原理指出,当流体在速度增加的地方压力就下降,流体在速度减小的地方压力上升。
而流体动能原理则指出,当流体通过狭窄通道时,由于断面积减小,流体速度增加,从而使其动能增大。
根据这些原理,通过调整节流装置的设计和工作参数,可以实现对流体的有效节流控制。
节流工作原理的应用广泛,在工业生产、流体控制系统、汽车制动系统等领域都有重要的应用。
通过精确控制流体的流速和流量,可以实现能量的调节、压力的稳定、流体的混合等目的,提高工作效率,保证系统的安全可靠性。
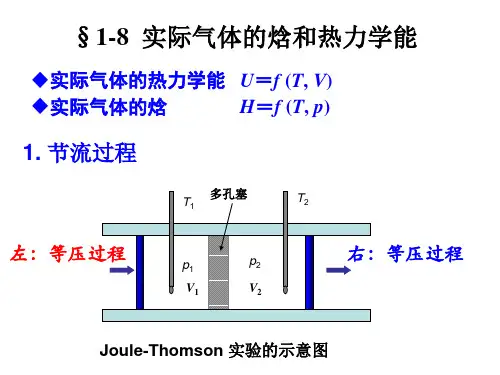
节流膨胀效应1. 实际气体的节流,通常把高压流体经管道中的小孔后压力显著降低的过程称为节流,如图1所示。
节流前的状态参数为p1、T1、U1,节流后的状态参数为P2、T2、U2。
图1节流过程(焦耳-汤姆逊效应)节流孔径越小,则局部阻力越大,节流前后的压力变化(P1-P2)也越大。
反之,就越小。
在实际工作中,为了便于调节,通常用调节阀代替固定节流孔。
从能量转换的观点看。
由于气体经过节流阀小孔时,流速大、时间短,来不及与外界进行热交换,因此节流过程可以近似看作绝热过程。
因为节流时有摩擦力损失,所以节流过程是不可逆的。
气体在节流时,既无能量输出,也无能量输入,所以气体节流前后的能量保持不变,即节流前后的焓值相等h1=h2。
这是节流过程的基本特点。
理想气体的焓值只是温度的函数,因而理想气体节流前后的温度是不变的。
而实际气体的焓值是温度和压力的函数,所以实际气体节流后的温度是发生变化的。
这种现象称做节流效应(焦耳-汤姆逊效应)。
它分为微分节流效应和积分节流效应。
微分节流效应是指气体节流时温度的变化(ΔT)与压力降(ΔP)所成比例关系,即ΔT=d hΔΔP或d h=(ΔT/ΔP)h(1-14)d h称为微分节流效应,即气流在节流时压力降为无限小时所发生的温度变化。
微分节流效应一般用实验方法求得,几种常用气体的微分节流效应如表所示。
对于空气及氧气,当接近于标准状态的温度范围及压力在100个大气压以下进行试验得到如下经验公式 d h=(a-bp)(273/T)2(1-15)空气 a=2.73×10-3, b=0.0895×10-6氧气 a=3.19×10-3, b=0.884×10-6表1-1几种常用气体在0℃及98kpa时的微分节流效应气体名称dh气体名称dh(℃/at)(10-3K/Pa)(℃/at)(10-3K/Pa)空气氧氮+0.27+0.31+0.26+2.75+0.31+2.65二氧化碳氢氦+1.30–0.03-0. 0596+13.26–3.06–6.082. 转换温度从表1-1中的数值可以看出,空气、氧气、氮等气体的d h 为正值,节流后温度降低;而氢、氦等气体的d h 却是负值的,节流后温度要上升。
气体的节流过程和绝热膨胀过程我们在上节利用麦氏关系将一些不能直接从实验中测得的物理量用物态方程和热容量表达出来。
在热力学中往往用偏倒数描述一个物理效应。
本节讨论气体的节流过程和绝热膨胀过程。
这两种过程都是获得低温的常用方法。
先讨论节流过程。
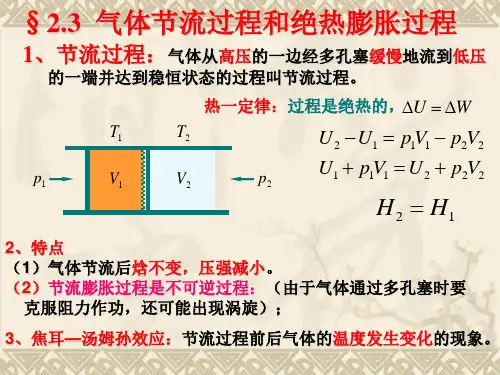
如图2.1所示,管子用不导热的材料包着,管子中间有一个多孔塞或节流阀。
现在用热力学理论对节流进行分析。
设在过程中有一定数量的气体通过了多孔塞。
在通过多孔塞前,其压强为p 1,体积为V 1,内能为U 1;通过多孔塞后,压强为p 2,体积为V 2,内能为U 2,在过程中外界对这部分气体所做的功是,因为过程是绝热的,根据热力学第一定律,有U 2-U 1=P 1V 1-P 2V 2即U 2+ P 2V 2= U 1+ P 1V 1或H 1=H 2 (2-3-1)这就是说,在节流过程前后,气体的焓值相等。
应该说明,节流过程是一个不可逆过程,对于气体在过程中所经历的非平衡态,焓是没有定义的。
式(2.3.1)指的是初态和终态的焓值相等。
现在讨论气体的绝热膨胀。
如果把过程近似地看作是准静态上,在准静态绝热过程中气体的熵保持不变。
由0)()(=∂∂+∂∂=dp pS T S dS T p 可得pS C VT p T α=∂∂)( (2.3.8) 式(2.3.8)给出在准静态绝热过程中气体的温度随压强的变化率。
上式右方是恒正的。
所以随者体积膨胀压强降低,气体的饿温度必然下降。
从能量的角度看,气体在绝热膨胀过程中减少其内能而对外作功,加以膨胀后其他分子见的平均距离增大,分子间的互相作用能量有所增加,因而使气体的温度下降。
气体的绝热膨胀过程也被用来使气体降温并液化。
我们将在进一步讨论节流过程和绝热膨胀过程获得低温的问题。