北师大数学七年级下册 第三章3.3 用图像表示的变量间关系 《板块专题20道—期中真题-培优拔高》

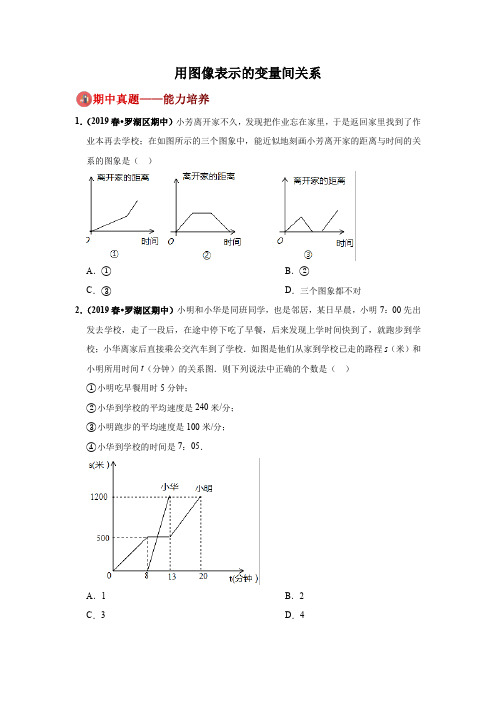
用图像表示的变量间关系1．（2019春•罗湖区期中）小芳离开家不久，发现把作业忘在家里，于是返回家里找到了作业本再去学校；在如图所示的三个图象中，能近似地刻画小芳离开家的距离与时间的关系的图象是（）A．①B．②C．③D．三个图象都不对2．（2019春•罗湖区期中）小明和小华是同班同学，也是邻居，某日早晨，小明7：00先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公交汽车到了学校．如图是他们从家到学校已走的路程s（米）和小明所用时间t（分钟）的关系图．则下列说法中正确的个数是（）①小明吃早餐用时5分钟；②小华到学校的平均速度是240米/分；③小明跑步的平均速度是100米/分；④小华到学校的时间是7：05．A．1B．2C．3D．43．（2019春•定安县期中）张老师从甲镇去乙村，一开始沿公路乘车，后来沿小路步行到达乙村，下列图中，横轴表示从甲镇出发后的时间，纵轴表示张老师与甲镇的距离，则较符合题意的图形是（）A．B．C．D．4．（2019春•成都期中）下列各图象所反映的是两个变量之间的关系，表示匀速运动的是（）A．①②B．②C．①③D．无法确定5．（2019春•建宁县期中）如图，正方形ABCD的边长为4，P为正方形边上一动点，它沿A→D→C→B→A的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映变量y与变量x的关系图象的是（）A．B．C．D．6．（2019春•灵石县期中）小明看到了一首诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还”，读完后，他想用图象描述这首诗的内容，如果用纵轴表示父亲与儿子行进中离家的距离，横轴表示父亲离家的时间，那么下列图象中大致符合这首诗含义的是（）A．B．C．D．7．（2019春•中山市校级期中）小亮家与姥姥家相距24km，小亮8：00从家出发，骑自行车去姥姥家．妈妈8：30从家出发，乘车沿相同路线去姥姥家．在同一直角坐标系中，小亮和妈妈的行进路程s（km）与时间t（h）的函数图象如图所示．根据图象得出下列结论，其中错误的是（）A．小亮骑自行车的平均速度是12 km/hB．妈妈比小亮提前0.5 h到达姥姥家C．妈妈在距家12 km处追上小亮D．9：30妈妈追上小亮8．（2019春•叙州区期中）周末，小李8时骑自行车从家里出发，到野外郊游，16时回到家里．他离家的距离s（千米）与时间t（时）之间的函数关系可以用图中的折线表示．现有如下信息：（1）小李到达离家最远的地方是14时；（2）小李第一次休息时间是10时；（3）11时到12时，小李骑了5千米；（4）返回时，小李的平均车速是10千米/时．其中，正确的信息有（）A．1个B．2个C．3个D．4个9．（2019秋•岑溪市期中）一辆客车从霍山开往合肥，设客车出发t（h）后与合肥的距离为S（km），则下列图象中能大致反映S与t之间的函数关系是（）A．B．C．D．10．（2019春•璧山区期中）小红骑自行车到离家为2千米书店买书，行驶了5分钟后，遇到一个同学因说话停留10分钟，继续骑了5分钟到书店．下图中的哪一个图象能大致描述她去书店过程中离书店的距离s（千米）与所用时间t（分）之间的关系（）A．B．C．D．11．（2019春•郫都区期中）小王周末骑电动车从家出发去商场买东西，当他骑了一段路时，想起要买一本书，于是原路返回到刚经过的新华书店，买到书后继续前往商场，如图是他离家的距离与时间的关系示意图，请根据图中提供的信息回答下列问题：（1）小王在新华书店停留了多长时间？（2）买到书后，小王从新华书店到商场的骑车速度是多少？12．（2019春•靖远县期中）张阳从家里跑步去体育场，在那里锻炼了一会儿后，又走到文具店去买笔，然后走回家，如图是张阳离家的距离与时间的关系图象．根据图象回答下列问题：（1）在这个变化过程中，自变量、因变量分别是、．（2）体育场离张阳家千米．（3）体育场离文具店千米．（4）张阳在文具店逗留了时间．（5）张阳从文具店到家的速度是．13．（2019春•槐荫区期中）已知动点P以2cm/s的速度沿图1所示的边框从B﹣C﹣D﹣E ﹣F﹣A的路径运动，记△ABP的面积为S（cm2），S与运动时间t（s）的关系如图2所示，若AB＝6cm，请回答下列问题：（1）图1中BC＝cm，CD＝cm，DE＝cm（2）求出图1中边框所围成图形的面积；（3）求图2中m、n的值；（4）分别求出当点P在线段BC和DE上运动时S与t的关系式，并写出t的取值范围．14．（2019秋•高州市期中）某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校．如图所示是小明从家到学校这一过程中所走的路程s（米）与时间t（分）之间的关系．（1）小明从家到学校的路程共米，从家出发到学校，小明共用了分钟；（2）小明修车用了多长时间？（3）小明修车以前和修车后的平均速度分别是多少？15．（2019春•长春期中）“珍重生命，注意安全！”同学们在上下学途中一定要注意骑车安全．小明骑单车上学，当他骑了一段时，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校，以下是他本次所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：（1）小明家到学校的路程是米．（2）小明在书店停留了分钟（3）本次上学途中，小明一共行驶了多少米？一共用了多少分钟？16．（2019春•济南期中）小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题：（1）小明家到学校的路程是米，小明在书店停留了分钟；（2）本次上学途中，小明一共行驶了米，一共用了分钟；（3）在整个上学的途中（哪个时间段）小明骑车速度最快，最快的速度是米/分；（4）小明出发多长时间离家1200米？17．（2019春•锦江区校级期中）如图①，在长方形ABCD中，AB＝10 cm，BC＝8 cm，点P从A出发，沿A、B、C、D路线运动，到D停止，点P的速度为每秒1 cm，a秒时点P的速度变为每秒bcm，图②是点P出发x秒后，△APD的面积S1（cm2）与y（秒）的函数关系图象：（1）根据图②中提供的信息，a＝，b＝，c＝．（2）点P出发后几秒，△APD的面积S1是长方形ABCD面积的四分之一？18．（2019春•邛崃市期中）如图反映的是小华从家里跑步去体育馆，在那里锻炼了一阵后又走到文具店去买笔，然后走回家，其中x表示时间，y表示小华离家的距离．根据图象回答下列问题：（1）小华在体育场锻炼了分钟；（2）体育场离文具店千米；（3）小华从家跑步到体育场、从文具店散步回家的速度分别是多少千米/分钟？19．（2019春•城关区校级期中）如图描述了一辆汽车在某一直路上的行驶过程，汽车离出发地的距离s（km）和行驶时间t（h）之间的关系，请根据图象回答下列问题：（1）汽车共行驶的路程是多少？（2）汽车在行驶途中停留了多长时间？（3）汽车在每个行驶过程中的速度分别是多少？（4）汽车到达离出发地最远的地方后返回，则返回用了多长时间？20．（2019春•雨城区校级期中）A、B两地相距50km，甲于某日骑自行车从A地出发驶往B 地，乙也于同日下午骑摩托车从A地出发驶往B地，在这个变化过程中，甲和乙所行驶的路程用变量s（km）表示，甲所用的时间用变量t（时）表示，图中折线OPQ和线段MN分别表示甲和乙所行驶的路程s与t的变化关系，请根据图象回答：（1）直接写出：甲出发后小时，乙才开始出发；（2）求乙行驶几小时后追上甲，此时两人距B地还有多少千米？（3）请分别求出甲、乙的行驶速度？。

3.3 用图象表示的变量间关系（1）教材与学情分析1、本节教材"温度的变化" 从学生所熟悉的情境人手，从图象中获取两变量之间的关系的信息，经历从数学的角度体会变量和变量之间相互依赖的关系，体会图象在表达两变量间变化关系的直观性，感受数学的应用价值。

本节教材能使学生初步感受函数思想，能更好地发展学生有条理地进行思考和表达的能力，为以后顺利过渡到函数学习打下基础。

2、学生通过观察现实生活，对用图象来反映两变量之间的关系有了一定的体验，积累有了一些生活的经验；具有初步的搜集信息的能力。

通过本节的学习，培养了学生的观察能力、思维表达能力等。

教学目标知识与技能目标：1、了解两个变量之间的对应关系，初步形成函数的思想．2、结合具体情境理解图象上的点所表示的意义．3、发展从图象中获得信息的能力及有条理地进行语言表达的能力．4、理解用数学的方法描述变量之间的关系，感受数学的价值．过程与方法目标：经历从图象中分析变量之间的关系的过程，进一步体会变量之间的关系，在具体情境中培养学生对变量之间关系的认识和语言描述的合理性，培养学生从图象中获取信息的广泛性和准确性．情感与态度目标：从解决大量实际问题和学生感兴趣的问题中提高学生用数学的意识，体验数学所蕴含的数学美．教学重点把实际问题转化为数学图象，再根据图象来研究实际问题，使学生获得对图象反映变量之间关系的体验．教学难点从图象中获得一些信息与在现实情景下用语言进行描述之间的等价转化；用图象法来反映两变量之间关系，解决自己身边的一些实际问题，根据图象的特点来研究实际问题．教学过程设计：教学过程教学内容同学们见过股市走势图吗？生活中还有哪些类似现象？你能看懂这些图象吗？本节课我们就来学习：用图象来表示一些量与量之间的关系上证指数271 3,02 T-2.81滋3.23%2.18%1.09%□%-1.03^-2.13^-3益玄&30 -10:30 -11:30 -14rDO 15:00下图是老师绘制的一张气温变化曲线图，直观形象地表达了温度随时间的变化而变化的情况，你能根据下图回答下列问题吗?温度/C(1)上午9时的温度是多少？12时呢？(2)这一天的最咼温度是多少？是在几时达到的？最低温度呢?(3)这一天的温差是多少？从最低温教师活动学生活动设计意图1、营造良好根据老师联系生活氛围，激发学提出的问实际创设生好奇心，引题，联想问题情导学生快速刖面学过境，激发进入状态. 的知识，学习兴2、启发引导积极思趣，调动学生思考分考，探求学生的积析，从多个角最佳方极性与主度展开联想. 案. 动性.1、让学生展1、学生根通过对层示自己的分据自己的层推进的析过程. 生活经验问题串的2、引导学生积极寻求形式逐步将新旧知识最佳表述引导学生联系起来，发方式. 获得图象现新问题，利2、学生展所传达的用所学知识示自己的信息，熟解决新问题，分析与解悉图象语引导学生进决过程. 言,培养行自主探究，3、在老师学生自主获得新知. 的引导下探索的意分组讨识和能论. 力，使学4、与同桌生在探索进行交的过程中流. 形成自己5、总结. 的观点，度到最高温度经过了多少时间?（4）在什么时间范围内温度在上升?在什么时间范围内温度在下降?（5）图中的A点表示的是什么？B点呢？就上述温度随时间变化而变化的图象特征，请同学们再想一想，我们还可以得出哪些看法？变量之间的关系还可以怎样表示？（学生分组讨论）教师小结：图象是我们表示变量之间关系的又一种方法，它的特点是非常直观。

七年级数学下册第三章变量之间的关系3.3.2用图象表示变量间的关系教案新版北师大版一. 教材分析本节课的主要内容是用图象表示变量间的关系。

通过本节课的学习，学生能够理解图象表示变量间关系的方法，并能够运用图象解决一些实际问题。

教材中给出了几种常见的图象表示方法，如线段图、折线图、饼图等，学生需要掌握这些图象的绘制方法和特点。

二. 学情分析学生在七年级上学期已经学习了图象的相关知识，对图象有一定的认识和理解。

但是，学生对图象表示变量间关系的方法和应用还不够熟练。

因此，在教学过程中，教师需要引导学生运用已有的知识去理解和掌握新的内容，并通过实际例子让学生感受图象在解决问题中的作用。

三. 教学目标1.理解图象表示变量间关系的方法，能够选择合适的图象表示问题。

2.掌握常见图象的绘制方法和特点，能够正确绘制图象。

3.能够运用图象解决一些实际问题，提高解决问题的能力。

四. 教学重难点1.重点：图象表示变量间关系的方法和应用。

2.难点：选择合适的图象表示问题，以及运用图象解决实际问题。

五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。

通过设置问题引导学生思考，通过案例让学生理解图象表示变量间关系的方法，通过小组合作学习让学生互相交流和讨论，提高学生的学习效果。

六. 教学准备1.准备一些实际问题，如温度和时间的关系、购买物品的价格和数量的关系等。

2.准备相应的图象模板或软件，如Excel、PPT等。

3.准备一些图象示例，如线段图、折线图、饼图等。

七. 教学过程1.导入（5分钟）教师通过展示一些实际问题，引导学生思考如何用图象表示变量间的关系。

例如，展示一张温度随时间变化的图象，让学生观察和描述图象中的信息。

2.呈现（10分钟）教师介绍常见的图象表示方法，如线段图、折线图、饼图等，并通过示例让学生理解这些图象的绘制方法和特点。

3.操练（10分钟）教师设置一些练习题，让学生运用所学知识绘制图象。

例如，给定一组数据，让学生选择合适的图象表示方法，并绘制出图象。

北师大版数学七年级下册目录
新版《数学七年级下册》目录：第一章整式的乘除
1．同底数幂的乘法 2．幂的乘方与积的乘方 3．同底数幂的除法 4．整式的乘法5．平方差公式 6．完全平方公式 7．整流器式的除法
第二章相交线与平行线
1．两条直线的位置关系 2．探索直线平行的条件 3．平行线的性质 4．用尺规作角第三章三角形
1．认识三角形 2．图形的全等
3．探索三角形全等的条件 4．用尺规作三角形 5．利用三角形全等测距离
第四章变量之间的关系
1．用表格表示的变量间关系 2．用关系式表示的变量间关系
3．用图像表示的变量间关系
第五章生活中的轴对称
1．轴对称现象 2．探索轴对称的性质 3．简单轴对称图形 4．利用轴对称进行设计第六章频率与概率
1．感受可能性 2．频率的稳定性 3 等可能事件的概率。

3.3（1）用图象表示的变量间关系学习目标1、经历从图象中分析变量之间关系的过程，进一步体会变量之间的关系。

2、结合具体情境，理解图象上的点所表示的意义。

3、能从图象中获取变量之间关系的信息，并能用语言进行描述温故知新1、我们知道，用表格或关系式可以表示变量间的关系:请根据自变量x与因变量的y的关系式2=-+，填表：248y x x2、假设圆柱的高是5厘米，当圆柱的底面半径由小到大变化时；圆柱的体积如何变化？（1）在这个变化中，自变量是______、因变量是__________（2）如果圆柱底面半径为r(厘米)，圆柱的体积v可以表示为 .（3）当r由1厘米变化到10厘米时，v由变化到 .自主探究：阅读课本p69-701.某地某天的温度变化情况如下图示，观察下表回答下列问题：（1）上午9时的温度是；12时的温度是 .（2）这一天时的温度最高，最高温度是；这一天时的温度最低，最低温度是 .（3）这一天的温差是，从最高温度到最低温度经过了小时（4）在什么时间范围内温度在上升？在什么时间范围内温度在下降？（5）图中的A点表示的是什么？_________________B点呢？（6）你能预测次日凌晨1时的温度吗？说说你的理由.小结：前图表示了温度随时间的变化而变化的情况，它是温度与时间之间关系的图象。

图象是我们表示变量之间关系的又一种方法，它的特点是___________。

图象表示变量之间的关系时，通常用水平方向的数轴（称为横轴）上的点表示_____________量，用竖直方向的数轴（称为纵轴）上的点表示______________。

议一议骆驼被称为“沙漠之舟”，它的体温随时间的变化而发生较大的变化。

（1）一天中，骆驼的体温的变化范围是什么？它的体温从最低上升到最高需要多少时间？（2）从16时到24时，骆驼的体温下降了多少？（3）在什么时间范围内骆驼的体温在上升？在什么时间范围内骆驼的体温在下降？（4）你能看出第二天8时骆驼的体温与第一天8时有什么关系吗？其他时刻呢？（5）A点表示的是什么？还有几时的温度与A点所表示的温度相同？（6）你还知道那些关于骆驼的趣事？随堂练习1、海水受日月的引力而产生潮汐现象，早晨海水上涨叫做潮，黄昏海水上涨叫做汐，合称潮汐。

3.3 用图像表示变量间的关系一.选择题1． 若y 与x 的关系式为306y x =-，当x ＝13时，y 的值为（ ） A ．5 B ．10 C ．4 D ．－4 2. 下列关于圆的面积S 与半径R 之间的关系式S 2R π=中，有关常量和变量的说法正确的是（ ）A ．S ，2R 是变量，π是常量B ．S ，π，R 是变量，2是常量C ．S ，R 是变量，π是常量D ．S ，R 是变量，π和2是常量3. 在关系式131y x =-中，自变量x 的取值范围是（ ） A ．13x < B ．13x ≠- C ．13x ≠ D ．13x >4．矩形的周长为18cm ，则它的面积S （2cm ）与它的一边长x （cm ）之间的关系式是（ ）A ．(9)(09)S x x x =-<<B ．(9)(09)S x x x =+<≤C ．(18)(09)S x x x =-<≤D ．(18)(09)S x x x =+<<5．如图，描述了安佶同学某日造成的一段生活过程：他早上从家里跑步去书店，在书店买了一本书后：马上就去早餐店吃早餐，吃完早餐后，立即散步走回家．图象中的平面直角坐标系中的x 表示时间，y 表示安佶离家的距离．请你认真研读这个图象，根据图象提供的信息，以下说法错误的是（ ）A ．安佶从家到新华书店的平均速度是10千米/分钟B ．安佶买书花了15分钟C ．安佶吃早餐花了20分钟D ．从早餐店到安佶家的1.5千米6．如图，某游客为爬上3千米的山顶看日出，先用1小时爬了2千米，休息0.5小时后，再用1小时爬上山顶，游客爬山所用时间t （小时）与山高h （千米）间的关系用图象表示是（ ）二.填空题7. 若球体体积为V ，半径为R ，则334R V π=．其中变量是_______、•_______，常量是________．8．如图中，每个图形都是若干个棋子围成的正方形图案，•图案的每条边（包括两个顶点）上都有n （n ≥2）个棋子，每个图案的棋子总数为S ，按图的排列规律推断S 与n 之间的关系可以用式子___________来表示．9. 油箱中有油30kg ，油从管道中匀速流出，1小时流完，•求油箱中剩余油量Q （kg ）与流出时间t （分钟）间的关系式为_______________，•自变量的范围是____________．当Q ＝10kg 时，t ＝__________（分钟）．10．星期日，小明同学从家中出发，步行去菜地里浇水，浇完后又去玉米地里除草，然后回到家里．如图是所用的时间与离家的距离的关系的图象，若菜地和玉米地的距离为a 千米，在玉米地里除草比在菜地里浇水多用的时间为b 分钟，则a= ，b= ．11. 如图所示，表示的是某航空公司托运行李的费用y （元）与托运行李的质量x （千克）的关系，由图中可知行李的质量只要不超过_________千克，•就可以免费托运．12．已知等腰三角形的周长为60，底边长为x，腰长为y，则y与x之间的关系式及自变量的取值范围为_______.三.解答题13.如图，这是反映爷爷每天晚饭后从家中出发去元宝山公园锻炼的时间与距离之间关系的一幅图．（1）如图反映的自变量、因变量分别是什么？（2）爷爷每天从公园返回用多长时间？（3）爷爷散步时最远离家多少米？（4）爷爷在公园锻炼多长时间？（5）计算爷爷离家后的20分钟内的平均速度．14. 心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间有如下关系：（其中0≤x≤30）提出概念所用时间（x） 2 5 7 10 12 13 14 17 20对概念的接受能力（y）47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55（1）上表中反映了哪两个变量之间的关系？（2）当提出概念所用时间是10分钟时，学生的接受能力是多少？（3）根据表格中的数据，你认为提出概念几分钟时，学生的接受能力最强；（4）从表中可知，当时间x在什么范围内，学生的接受能力逐步增强？当时间x在什么范围内，学生的接受能力逐步降低？15. 如图所示，正方形ABCD的边长为4 cm，E、F分别是BC、DC边上一动点，E、F同时从点C均以1 /cm s的速度分别向点B、点D运动，当点E与点B重合时，运动停止．设运动时间为x(s)，运动过程中△AEF的面积为y，请写出用x表示y的关系式，并写出自变量x的取值范围．参考答案一.选择题1. 【答案】C；【解析】130610643y=⨯-=-=.2. 【答案】C；【解析】π是圆周率，是一个常量.3. 【答案】C；【解析】要使式子有意义，需3x－1≠0.4. 【答案】A；【解析】矩形的另一边长为18292xx-=-，所以(9)(09)S x x x=-<<.5. 【答案】A；【解析】A、安佶从家到新华书店的平均速度是2.5÷15=千米/分钟，故A选项错误；B、由图象可得出安佶买书花了30﹣15=15（分钟），故B选项正确；C、由图象可得出安佶吃早餐花了65﹣45=20（分钟），故C选项正确；D、由函数图象可知，从早餐店到安佶家的1.5千米，故D选项正确．故选：A．6. 【答案】D；二.填空题7. 【答案】R 、V ；43π； 8. 【答案】44S n =-； 9. 【答案】t Q 5.030-=；600≤≤t ；40．【解析】油从油箱里流出的速度为30÷60=0.5/min kg ，所以关系式为t Q 5.030-=10.【答案】0.9km ；8min.【解析】由纵坐标看出家到菜地的距离是1.1千米，家到玉米地的距离是2千米，菜地和玉米地的距离为：2=1.1=0.9千米；由横坐标看出浇水时间为25﹣15=10（分钟），除草时间为55﹣38=18分钟，在玉米地里除草比在菜地里浇水多用的时间为18=10=8分钟，故答案为；0.9km ，8min ．11.【答案】20；【解析】由图象可知，在0＜x ＜20的范围内，y ＝0.12.【答案】130(030)2y x x =-<<； 【解析】2y ＋x ＝60，1302y x =-，由于2y ＞x 且x ＞0，所以030x <<. 二.解答题13.【解析】解：（1）由图象知，图形反映了距离和时间之间的函数关系；自变量是时间，因变量是路程．（2）爷爷没天从公园返回用了15分钟．（3）爷爷散步时最远离家900米．（4）爷爷在公园锻炼10分钟．（5）900÷20=45（米/分）．14.【解析】 解：（1）提出概念所用的时间x 和对概念接受能力y 两个变量；（2）当x =10时，y =59，所以时间是10分钟时，学生的接受能力是59．（3）当x =13时，y 的值最大是59.9，所以提出概念13分钟时，学生的接受能力最强．（4）由表中数据可知：当2＜x ＜13时，y 值逐渐增大，学生的接受能力逐步增强；当13＜x ＜20时，y 值逐渐减小，学生的接受能力逐步降低．15.【解析】解：ABE DAF CEF y S S S S ∆∆∆=---正方形ABCD2111222BC AB BE AD DF EF FC =---g g g 211144(4)4(4)222x x x x =-⨯⨯--⨯⨯--g 214(04)2x x x =-+≤≤．。