特殊四边形验收卷

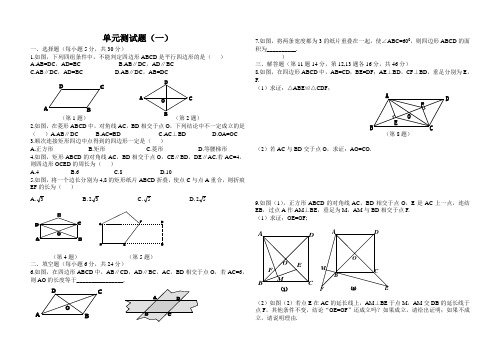
D C B A O DC BA O ED C B A FE DC B AD C B A O F ED C B A 单元测试题（一）一、选择题（每小题5分，共30分）1.如图，下列四组条件中，不能判定四边形ABCD 是平行四边形的是（ ） A.AB=DC ，AD=BC B.AB ∥DC ，AD ∥BC C.AB ∥DC ，AD=BC D.AB ∥DC ，AB=DC（第1题） （第2题）2.如图，在菱形ABCD 中，对角线AC ，BD 相交于点O ，下列结论中不一定成立的是（ ）A.AB ∥DC B.AC=BD C.AC ⊥BD D.OA=OC3.顺次连接矩形四边中点得到的四边形一定是（ ）A.正方形B.矩形C.菱形D.等腰梯形4.如图，矩形ABCD 的对角线AC ，BD 相交于点O ，CE ∥BD ，DE ∥AC.若AC=4，则四边形OCED 的周长为（ ）A.4B.6C.8D.105.如图，将一个边长分别为4,8的矩形纸片ABCD 折叠，使点C 与点A 重合，则折痕EF 的长为（ ）A.3B.32C.5D.52（第4题） （第5题） 二、填空题（每小题6分，共24分）6.如图，在四边形ABCD 中，AB ∥CD ，AD ∥BC ，AC ，BD 相交于点O ，若AC=6，则AO 的长度等于________________.7.如图，将两条宽度都为3的纸片重叠在一起，使∠ABC=600，则四边形ABCD 的面积为__________.）三、解答题（第11题14分，第12,13题各16分，共46分）8.如图，在四边形ABCD 中，AB=CD ，BE=DF ；AE ⊥BD ，CF ⊥BD ，垂足分别为E ，F.（1）求证：△ABE ≌△CDF ；（第8题）（2）若AC 与BD 交于点O ，求证：AO=CO.9.如图（1），正方形ABCD 的对角线AC ，BD 相交于点O ，E 是AC 上一点，连结EB ，过点A 作AM ⊥BE ，垂足为M ，AM 与BD 相交于点F. （1）求证：OE=OF;(1)O F MDCABE(2)OFMDCAB E（2）如图（2）若点E 在AC 的延长线上，AM ⊥BE 于点M ，AM 交DB 的延长线于点F ，其他条件不变，结论“OE=OF ”还成立吗？如果成立，请给出证明；如果不成立，请说明理由.O D CB A单元测试题（二） 一、选择题（每小题3分，共30分） 1，如图1，如果□ABCD 的对角线AC 、BD 相交于点O ，那么图中的全等三角形共有（ ） A.1对 B.2对 C.3对 D.4对 2，平行四边形的一边长是10cm ，那么这个平行四边形的两条对角线的长可以是（ ）A.4cm 和6cm B.6cm 和8cm C.8cm 和10cm D.10cm 和12cm3，在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的条件是( )A.AC ＝BD ，AB ＝CD ，AB ∥CDB.AD //BC ，∠A ＝∠CC.AO ＝BO ＝CO ＝DO ，AC ⊥BDD.AO ＝CO ，BO ＝DO ，AB ＝BC4，如图2，过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线，分别相交于E 、F 、G 、H 四点，则四边形EFGH 为（ ）A.平行四边形 B 、矩形 C 、菱形 D. 正方形5，如图3，大正方形中有2个小正方形，如果它们的面积分别是S 1、S 2，那么S 1、S 2的大小关系是（ ）A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定 6，如图5，将一个边长分别为4、8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF 的长是( )A ．3B ．23C ．5D ．25二、填空题（每题3分，共30分）7，已知菱形有一个锐角为60°，一条对角线长为6cm ，则其面积为＿＿＿cm 2.8，如图12，□ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，点A 正好落在CD 上的点F ，若△FDE 的周长为8，△FCB 的周长为22，则FC 的长为＿＿＿.三、解答题（共40分）9，如图16，已知四边形ABCD 是平行四边形，∠BCD 的平分线CF 交边AB 于F ，∠ADC 的平分线DG 交边AB 于G .（1）线段AF 与GB 相等吗？ （2）请你在已知条件的基础上再添加一个条件，使得△EFG 为等腰直角三角形,并说明理由.10，如图17，已知□ABCD 中，E 为AD 的中点，CE 的延长线交BA 的延长线于点E . （1）试说明线段CD 与F A 相等的理由； （2）若使∠F ＝∠BCF ，□ABCD 的边长之间还需再添加一个什么条件？请你补上这个条件，并说明你的理由(不要再增添辅助线). 11、如图，已知平行四边形ABCD 中，对角线AC BD ，交于点O ，E 是BD 延长线上的点，且ACE △是等边三角形． （1）求证：四边形ABCD 是菱形；（2）若2AED EAD ∠=∠，求证：四边形ABCD 是正方形．ECDBAOF ED C B A 图5D ABC E F 图12A B C DEF 图17 图16 图3 AD C B HE F G图2 O A B D C 图1。

5.3 四边形验收卷注意事项：本试卷满分100分，试题共23题，选择10道．填空6道、解答7道 .答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置． 答题时间：60分钟一、选择题（本大题共10小题，每小题2分，共20分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2023·河北邯郸·统考一模）根据图中所给的边长及角度，下列四边形中，一定可以判定为平行四边形的是（ ）．A ．B ．C ．D ．2．（2022秋·山东烟台·八年级统考期末）如图，将三角形纸片剪掉一角得四边形，设ABC V 与四边形BCDE 的外角和的度数分别为,a b ，则比较a 与b 的大小，结果正确的是（ ）A ．a b =B ．a b <C ．a b >D ．无法比较3．（2022秋·广西河池·八年级统考期末）已知一个n 边形的内角和是1800°，从它的一个顶点出发可以作m 条对角线，则m n +的值为（ ）A ．17B ．19C ．21D ．664．（2021·全国·八年级专题练习）如图，将ABC V 绕边AC 的中点O 顺时针旋转180°．嘉淇发现，旋转后的CDA V 与ABC V 构成平行四边形，并推理如下：小明为保证嘉淇的推理更严谨，想在方框中“∵=CB AD ，”和“∴四边形…”之间作补充，下列补充不正确的是（ ）点A ，C 分别转到了点C ，A 处，而点B 转到了点D 处．∵CB AD =，∴四边形ABCD 是平行四边形．A ．应补充：且DAC ACBÐ=ÐB ．应补充：且AB CD =C ．应补充：且//AB CD D ．应补充：且//AD CB5．（2023春·八年级课时练习）已知四边形ABCD 是平行四边形，下列结论中错误的有（ ）①当AB DC =时，它是菱形；②当AC BD ^时，它是菱形；③当90ABC Ð=°时，它是矩形；④当AC BD =时，它是正方形．A ．1个B ．2个C ．3个D ．4个6．（2023·河南商丘·校考一模）如图1，在矩形ABCD 中，点E 在边BC 上，连接AE ，点P 从点A 出发，沿折线A →E →C 以1cm /s 的速度匀速运动至点C ．图2是点P 运动时，ABP V 的面积()2cm y 随时间()s x 变化的函数图像，则a 的值为（ ）A ．40B ．10C ．24D ．207．（2023春·八年级单元测试）将图1中两个三角形按图2所示的方式摆放，其中四边形ABCD 为矩形，连接PQ ，甲、乙两人有如下结论：甲：若四边形ABCD 是边长为1的正方形，则四边形PQMN 必是正方形；乙：若四边形PQMN 为正方形，则四边形ABCD 必是边长为1的正方形．下列判断正确的是（ ）A ．甲正确，乙不正确B ．甲不正确，乙正确C ．甲、乙都不正确D ．甲、乙都正确8．（2022春·北京西城·八年级校考期中）如图，四边形ABCD 中，AC a =，BD b =，且AC BD ^，顺次连接四边形ABCD 各边中点，得到四边形1111D C B A ，再顺次连接四边形1111D C B A 各边中点，得到四边形2222A B C D ，¼，如此进行下去，得到四边形.n n n n A B C D 下列结论正确的有（ ）①四边形2222A B C D 是矩形；②四边形4444A B C D 是菱形；③四边形5555A B C D 的周长是4a b +；④四边形n n n n A B C D 的面积是12n ab +．A ．1个B ．2个C ．3个D ．4个9．（2023·江苏苏州·一模）如图，在矩形ABCD 中，动点M 从点A 出发沿边AD 向点D 匀速运动，动点N 从点B 出发沿边BC 向点C 匀速运动，连接MN ．动点M ，N 同时出发，点M 运动的速度为每秒1个单位长度，点N 运动的速度为每秒3个单位长度．当点N 到达点C 时，M ，N 两点同时停止运动．在运动过程中，将四边形MABN 沿MN 翻折，得到四边形MA B N ¢¢．若在某一时刻，点B 的对应点B ¢恰好与点D 重合，则A B B C 的值为（ ）A ．23B C D ．3410．（2022秋·广东深圳·九年级北大附中深圳南山分校校考期中）如图，正方形ABCD 的边长为4，点E 在AB边上，145BE DAM =Ð=°，，点F 在射线AM 上，且AF =，过点F 作AD 的平行线交BA 的延长线于点H CF ，与AD 相交于点G ，连接EC EG EF 、，．下列结论：①45EFG Ð=°；②AEG △的周长为8；③CEG AFG ∽V V ；④CEG V 的面积为6.8．其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个二、填空题（本大题共6小题，每小题3分，共18分）请把答案直接填写在横线上11．（2022秋·吉林长春·七年级吉林省第二实验学校校联考期中）足球表面为什么用正六边形和正五边形构成？因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角，而又不足一个周角．这样，由平面折叠而成的多面体充气后最终就呈现为球形．如图，在折叠前的平面上，拼接点处的缝隙∠AOB 的大小为 ______．12．（2023秋·河南新乡·八年级统考期末）如图所示，A B C D E F Ð+Ð+Ð+Ð+Ð+Ð=______度．13．（2023春·重庆沙坪坝·九年级重庆八中校考阶段练习）如图，在等腰直角ABC V 中，90ABC Ð=°；点E 和点D 分别是边AC 和AB 的中点，以点A 为圆心，AE 长为半径画弧，交AB 于点F ，以点D 为圆心，DE长为半径画弧，交AC 于点E ．若AB BC ==，则图中阴影部分的面积为___________．14．（2023春·湖南长沙·八年级长沙市长郡梅溪湖中学校考阶段练习）如图，菱形ABCD 的边长为4，E ，F 分别是AB ，AD 上的点，AC 与EF 相交于点G ，若1BE AF ==，120BAD Ð=°，则EF 的长为______．15．（2023·辽宁鞍山·统考一模）如图，矩形ABCD 中，P 为CD 边上一点()DP CP <，90APB Ð=°．将ADP △沿AP 翻折得到AD P ¢△、PD ¢的延长线交边AB 于点M ，过点B 作BN MP ∥交DC 于点N ，连接AC ，分别交PM ，PB 于点E ，F ．下面结论中：①连接DD ¢，则AP DD ¢=；②四边形PMBN 是菱形；③2AD DP PC =×；④若2AD DP =，则49EF AE =，正确的结论是________．16．（2023·安徽池州·校联考一模）如图，已知四边形ABCD 是正方形，AB =E 为对角线AC 上一动点，连接DE，过点E作EF DE^，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．（1）CE CG+=___________；（2）若四边形DEFG的面积为5，则CG=___________三、解答题（本大题共7小题，共62分．解答时应写出文字说明、证明过程或演算步骤）17．（2022春·江苏南京·八年级统考期末）四边形ABCD是平行四边形，点E是BC边的中点，请仅用无刻度的直尺按要求作图（不写作法，保留作图的痕迹）．(1)在图①中作出AD边的中点F；(2)在图②中作出AB的中点G．18．（2023·安徽·校联考一模）如图，矩形ABCD的两个顶点A，B都在反比例函数kyx=的图象上，AB经过原点O，对角线AC垂直于x轴．垂足为E，已知点A的坐标为()1,2．(1)求直线AB和反比例函数的解析式；(2)求矩形ABCD的面积．19．（2023春·湖南长沙·八年级长沙市长郡梅溪湖中学校考阶段练习）如图，已知E、F分别是ABCDY的边BC、AD上的点，且BE DF=．(1)求证：四边形AECF 是平行四边形；(2)在ABC V 中，若6AB =，8AC =，90BAC Ð=°，求BC 边上的高AG ．20．（2023·黑龙江哈尔滨·哈尔滨市萧红中学校考模拟预测）如图，矩形ABCD 的对角线AC 的垂直平分线EF 与AD 、AC 、BC 分别交于点E 、O 、F ．(1)求证：四边形AFCE 是菱形；(2)若5AB =，12BC =，6EF =，求：①BO 的长；②菱形AFCE 的面积．21．（2023春·黑龙江哈尔滨·九年级哈尔滨市第一一三中学校校考阶段练习）如图，菱形ABCD ，BE AD ^于点E ，BF CD ⊥于点F ，(1)如图1，求证：DE DF =；(2)如图2，若60BAD Ð=°，连接AC 分别交BE 、BF 于点G 、H ，在不添加辅助线的情况下，请你直接写出所有的钝角等腰三角形．22．（2023春·全国·八年级专题练习）如图，四边形ABCD 是正方形，点E 、F 分别在边BC AB 、上，点G 在边BA 的延长线上，且CE BF AG ==．(1)求证：①DE DG = ；②DE DG ^；(2)尺规作图：以线段DE DG 、为边作出正方形DEHG （保留作图痕迹不写作法和证明）；(3)连接（2）中的FH ，猜想四边形CEHF 的形状，并证明你的猜想；(4)当1CE CB n=时，求出方正方形正形ABCD H DE G S S 的值23．（2022秋·广东河源·九年级校考期末）如图，在菱形ABCD 中，对角线AC 与BD 交于点O ，且8AC =，6BD =，现有两动点M ，N 分别从A ，C 同时出发，点M 沿线段AB 向终点B 运动，点N 沿折线C D A --向终点A 运动，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t （秒）．(1)填空：AB = ；菱形ABCD 的面积S = ；菱形的高h = ．(2)若点M 的速度为每秒1个单位，点N 的速度为每秒2个单位，连接AN ，MN ．当0 2.5t <<时，是否存在t 的值，使AMN V 为等腰直角三角形？若存在，请求出t 的值；若不存在，请说明理由．(3)若点M 的速度为每秒1个单位，点N 的速度为每秒a 个单位（其中52a <），当4t =时在平面内存在点E 使得以A ，M ，N ，E 为顶点的四边形为菱形，请求出所有满足条件的a的值．。

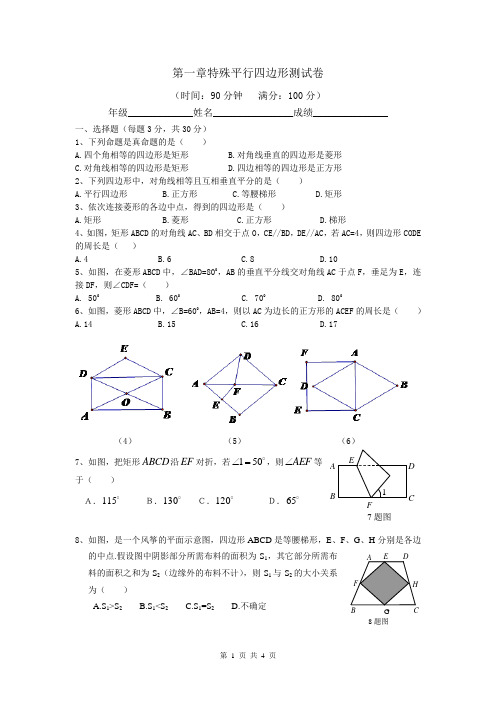
第一章特殊平行四边形测试卷（时间：90分钟满分：100分）年级_____________姓名________________成绩_______________一、选择题（每题3分，共30分）1、下列命题是真命题的是（）A.四个角相等的四边形是矩形B.对角线垂直的四边形是菱形C.对角线相等的四边形是矩形D.四边相等的四边形是正方形2、下列四边形中，对角线相等且互相垂直平分的是（）A.平行四边形B.正方形C.等腰梯形D.矩形3、依次连接菱形的各边中点，得到的四边形是（）A.矩形B.菱形C.正方形D.梯形4、如图，矩形ABCD的对角线AC、BD相交于点O，CE//BD，DE//AC，若AC=4，则四边形CODE 的周长是（）A.4B.6C.8D.105、如图，在菱形ABCD中，∠BAD=800，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF=（）A. 500B. 600C. 700D. 8006、如图，菱形ABCD中，∠B=600，AB=4，则以AC为边长的正方形的ACEF的周长是（）A.14B.15C.16D.17（4）（5）（6）7、如图，把矩形ABCD沿EF对折，若150∠= ，则AEF∠等于（）Ａ．115 Ｂ．130 Ｃ．120 Ｄ．658、如图，是一个风筝的平面示意图，四边形ABCD是等腰梯形，E、F、G、H分别是各边的中点.假设图中阴影部分所需布料的面积为S1，其它部分所需布料的面积之和为S2（边缘外的布料不计），则S1与S2的大小关系为（）A.S1>S2B.S1<S2C.S1=S2D.不确定AB CDEF17题图B G C8题图9、如图，把矩形纸条ABCD 沿EF GH ，同时折叠，B C ，两点恰好落在AD 边的P 点处，若90FPH =∠，8PF =，6PH =，则矩形ABCD 的边BC 长为（ ）Ａ．20 Ｂ．22 Ｃ．24 Ｄ．3010、如图将矩形纸片ABCD 沿AE 折叠，使点B 落在直角梯形AECD 的中位线FG 上，若则AE 的长为( )A.二、填空题（每题3分，共15分） 11、如图，已知正方形ABCD 的边长为1，连接AC 、BD ，CE 平分∠ACD 交BD 于点E ，则DE=_______ 12、如图，四边形ABCD 中，AB=BC，∠ABC=CDA=900，BE ⊥AD 于点E ，且四边形ABCD 面积是16，则BE=_____________.13、如图，点E 是正方形ABCD 内的一点，连接AE 、BE 、CE ，将△ABE 绕点B 顺时针旋转900到△CBE 、的位置，若AE=1，BE=2，CE=3，则∠BE 、C=___________（11） （12） （13）14、在直线l 上依次摆放着七个正方形(如图所示)。

特殊四边形测试题一、选择题1. 下列哪个选项不是特殊四边形的特点？A. 对角线互相平分B. 四边形的对角线垂直C. 四边形的对角线相等D. 四边形的对边相等2. 菱形的对角线具有以下哪个特点？A. 平行B. 垂直C. 相等D. 互相平分3. 矩形的对角线具有以下哪个特点？A. 平行B. 垂直C. 相等D. 互相垂直4. 梯形中，哪两个角相等？A. 相邻角B. 对角C. 同底角D. 没有角相等5. 以下哪个选项是平行四边形的判定条件？A. 对角线相等B. 对边相等C. 对角线互相垂直D. 对角线互相平分二、填空题6. 一个四边形的对角线互相垂直且平分，那么这个四边形是________。

7. 如果一个四边形的对边相等，且对角线互相平分，那么这个四边形是________。

8. 一个四边形的对角线相等，且对边平行，那么这个四边形是________。

9. 梯形中，如果有一个角是直角，那么这个梯形是________。

10. 如果一个四边形的一组对边平行，且另一组对边不平行，那么这个四边形是________。

三、简答题11. 描述矩形和正方形的相似之处和不同之处。

12. 解释为什么菱形的对角线互相垂直。

13. 根据题目给出的条件，如果一个四边形的对角线互相平分，且一边上的两个角都是直角，那么这个四边形是什么形状？四、计算题14. 已知一个平行四边形的两组对边长度分别为6cm和8cm，对角线长度分别为10cm和2x cm。

求x的值。

15. 如果一个梯形的上底长为5cm，下底长为10cm，且两底平行，求这个梯形的高，假设这个梯形是等腰梯形。

五、证明题16. 证明：如果一个四边形的对角线互相垂直且相等，那么这个四边形是正方形。

17. 证明：如果一个四边形的对角线互相平分，且一边上的两个角都是直角，那么这个四边形是矩形。

请注意，以上题目仅为示例，具体内容应根据实际教学大纲和学生水平进行调整。

特殊平行四边形测试题特殊平行四边形是指在平行四边形的基础上，具备某种特定性质的四边形。

它们在几何学中具有一定的研究价值和实际应用。

本文将介绍几道特殊平行四边形的测试题，并详细解答每道题目。

一、题目一已知平行四边形ABCD中，角A的度数是60°，角B的度数是120°，连结BD并延长交线段AC于点E。

请判断并证明四边形AEBD是否为一个特殊平行四边形。

解答：首先，连接AE。

由于平行四边形ABCD的对角线互相平分，所以有∠BED=∠BAC=60°。

然后，观察四边形AEBD。

由于∠BAD=∠BDA=180°-60°-120°=60°，而∠BED=60°，所以∠BAD=∠BED，即两对角相等。

最后，观察四边形AEBD的边长。

根据平行四边形性质，AB∥CD，AE∥BD，因此四边形AEBD为平行四边形。

综上所述，四边形AEBD满足特殊平行四边形的性质，即AEBD为一个特殊平行四边形。

二、题目二在平行四边形ABCD中，连结AC并延长交线段BD于点E，若∠BAC=50°，∠ACB=30°，请判断并证明四边形AEBD是否为一个特殊平行四边形。

解答：首先，连接AE。

由平行四边形的性质可知，∠BAD=∠BDA=180°-∠BAC-∠ACB=180°-50°-30°=100°。

然后，观察四边形AEBD。

由于∠BAC=50°，而∠BED=∠BAC=50°，因此∠BAC=∠BED，即两对角相等。

最后，观察四边形AEBD的边长。

根据平行四边形性质，AB∥CD，AE∥BD，因此四边形AEBD为平行四边形。

综上所述，四边形AEBD满足特殊平行四边形的性质，即AEBD为一个特殊平行四边形。

三、题目三在平行四边形ABCD中，连结AC并延长交线段BD于点E，若∠AEB=110°，请判断并证明四边形AEBD是否为一个特殊平行四边形。

特殊平行四边形测试卷一、选择题1、已知四边形ABCD ，以下有四个条件．（1）AB CD AB CD =∥， （2）AB AD AB BC ==， （3）A B C D ∠=∠∠=∠， （4）AB CD AD BC ∥，∥ 能判四边形ABCD 是平行四边形的有（ ）Ａ．1个 Ｂ．2个 Ｃ．3个 Ｄ．4个 2、菱形具有而一般平行四边形不具有的性质是（ ）A. 对角相等B. 对边相等C. 对角线互相垂直D. 对角线相等 3、 菱形的周长为100cm ，一条对角线长为14cm ，它的面积是（ ）A. 168cm 2B. 336cm 2C. 672cm 2D. 84cm 24、如图，矩形纸片ABCD 中，AB ＝6 cm ，BC ＝8 cm ，现将其沿AE 对折，使得点B 落在边AD 上的点B 1处，折痕与边BC 交于点E ，则CE 的长为( )A ．6 cmB ．4 cmC ．2 cmD ．1 cm 5、如图，菱形纸片ABCD 中，∠A ＝60°，折叠菱形纸片ABCD ，使点C 落在DP (P 为AB 中点)所在的直线上，得到经过点D 的折痕DE ，则∠DEC 的大小为( )A ．78°B ．75°C ．60°D ．45°6、若 ABCD 中，AB=10，BC=14,E 、F 分别为边BC 、AD 上的点，若四边形AECF 为正方形，则AE 的长为（ ）A. 7B. 4或10C. 5或9D.6或87、如图，在矩形ABCD 中，AB=3，AD=4，P 是AD 上的动点，PE ⊥AC 于E ，PF ⊥BD 于F ，则PE+PF 的值为（ ）A.2B.25 C.5 D.512（第4题） （第5题） （第7题）8、菱形的周长为20,两邻角的比为2∶1，则一组对边的距离为（ ） A.32B.332C.3 3D.5329、如图，四边形ABCD 是正方形，延长BC 至点E ，使CE ＝CA ，连结AE 交CD•_P _O _F _E _D _C _B _A于点F ，•则∠AFC 的度数是（ ）．（A ）150° （B ）125° （C ）135° （D ）112．5°10、如图，在菱形ABCD 中，∠B ＝60°，点E ，F 分别从点B ，D 同时以同样的速度沿边BC ，DC 向点C 运动.给出以下四个结论：① AE=AF ;② EF ∥BD ; ③ 当点E ，F 分别为边BC ，DC 的中点时，△AEF 是等边三角形；④ 当点E ，F 分别为边BC ，DC 的中点时，EF=3BE.上述结论正确的有（） A.1个 B.2个 C.3个 D.4个（第9题） （第10题）二．填空题 11、菱形的两条对角线分别是6 cm ，8 cm ，则菱形的边长为_____，面积为______． 12、如图所示，将直角△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ，添加一个条件_________，使四边形ABCD 为正方形．13、如图，已知点P 是正方形ABCD 对角线BD 上一点，且BP ＝BC ，则∠ACP 的度数是__ _度14、已知矩形ABCD ，AB ＝3 cm ，AD ＝4 cm ，过对角线BD 的中点O 作BD 的垂直平分线EF ，分别交AD ，BC 于点E ，F ，则AE 的长为__ _cm.（第12题） （第13题） （第14题）15、如图，菱形ABCD 的边长为4，过点A ，C 作对角线AC 的垂线，分别交CB 和AD 的延长线于点E ，F ，AE ＝3，则四边形AECF 的周长为__．16、如图，四边形ABCD 是正方形，△CDE 是等边三角形，则∠AED＝______，∠AEB＝______．17、如图，点O 是矩形ABCD 的中心，E 是AB 上的点，沿CE 折叠后，点B 恰好与点O 重合，若BC =3，则折痕CE 的长为 。

第一章 特殊平行四边形检测试卷一、选择题1. 不能判定四边形ABCD 为平行四边形的题设是（ ） （A ）AB 平行且等于CD 。

（B ）∠A=∠C ，∠B=∠D 。

（C ）AB=AD ，BC=CD 。

（D ）AB=CD ，AD=BC 。

2.矩形、菱形、正方形都具有的性质是 ( ) A.每一条对角线平分一组对角 B.对角线相等 C.对角线互相平分 D.对角线互相垂直3. 如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，若BD 、AC 的和为cm 18，CD ：DA=2：3，△AOB 的周长为cm 13,那么BC 的长是 （ ） A. cm 6 B. cm 9 C. cm 3 D. cm 124.在直角三角形ABC 中，∠ACB =︒90，∠B =︒60，AC =cm 3，则AB 边上的中线长为 （ ） A. cm 1 B. cm 2 C. cm5.1 D. cm 3 5. 下列说法错误的是（ ）A.一组对边平行且一组对角相等的四边形是平行四边形.B.每组邻边都相等的四边形是菱形.C.对角线互相垂直的平行四边形是正方形.D.四个角都相等的四边形是矩形. 6.下列命题中，真命题是 （ ）A ．两条对角线垂直的四边形是菱形B ．对角线垂直且相等的四边形是正方形C ．两条对角线相等的四边形是矩形D ．两条对角线相等的平行四边形是矩形 7．将两块能完全重合的两张等腰直角三角形纸片拼成下列图形：①平行四边形（不包括菱形、矩形、正方形）②矩形③正方形④等边三角形⑤等腰直角三角形 ( )A ．①③⑤B ．②③⑤C ．①②③D ．①③④⑤8.如图,已知菱形ABCD 与△ABE,其中D 在BE 上.若AB=17,BD=16,AE=25,则DE 的长度为 ( )A.8B.9C.11D.129. 如图在矩形ABCD 中,AB=10,BC=5,点E,F 分别在AB,CD 上,将矩形ABCD 沿EF 折叠,使点A,D 分别落在矩形ABCD 外部的点A 1,D 1处,则阴影部分图形的周长为 ( ) A.15B.20C.25D.3010．如图，菱形ABCD 中，对角线AC 、BD 相交于点O ，H 为AD 边中点，菱形ABCD 的周长为28，则OH 的长等于（ ）A. 3.5B. 4C. 7D. 1411．给出以下三个命题：①对角线相等的四边形是矩形；②对角线互相垂直的四边形是菱形；③对角线互相垂直的矩形是正方形；④菱形对角线的平方和等于边长平方的4倍，其中真命题的是（ ）A ．③B ．①②C ．②③D ．③④ 12.如图,正方形ABCD 中,AB=3,点E 在边CD 上,且CD=3DE.将△ADE 沿AE 对折至△AFE,延长EF 交边BC 于点G,连接AG,CF.下列结论: ①点G 是BC 的中点; ②FG=FC; ③∠GAE =︒45. 其中正确的是 ( )A.①②B.①③C.②③D.①②③ABCDO二、填空题：13.①等边三角形②菱形③平行四边形④矩形（5）正方形五个图形中,既是轴对称图形又是中心对称图形的是 (填写序号).14. 在Rt⊿ABC中，∠ACB =90°，∠A =30°，AC =32，则AB边上的中线为，高为15.菱形ABCD的边长为8cm，∠BAD=120°，则AC= ,BD= ,面积= 。

一、选择题1．菱形的一条对角线与它的边相等，则它的锐角等于（ ）A ．30°B ．45°C ．60°D ．75°2．如图，把矩形ABCD 沿EF 对折，若112,AEF ∠=︒则1∠等于（ ）A ．43B ．44C ．45︒D ．46︒3．如图，在平面直角坐标系中，将边长为a 的正方形OABC 绕点O 顺时针旋转45︒后得到正方形111OA B C ，依此方式连续旋转2021次得到正方形202120212021OA B C ，那么点2021A 的坐标是（ ）A ．22,22a a ⎛⎫ ⎪⎝⎭B ．22,22a a ⎛⎫- ⎪⎝⎭C ．22,22a a ⎛⎫-- ⎪⎝⎭D ．22,22a a ⎛⎫- ⎪⎝⎭ 4．如图所示，△ABC 是等边三角形，AQ=PQ ，PR=PS ，PR ⊥AB 于R ，PS ⊥AC 于S ，则四个结论正确的是( )①点 P 在∠A 的平分线上； ②AS=AR ； ③QP //AR ； ④△BRP ≌△QSP ．A ．全部正确B ．①②正确C ．①②③正确D ．①③正确5．如图，已知菱形OABC 的顶点()0,0O ，()2,0C 且60AOC ∠=︒，若菱形绕点O 逆时针旋转，每秒旋转45︒，则第2020秒时，菱形的对角线交点D 的坐标为（ ）A ．()3,3-B ．()1,3--C ．()2,3D ．33,22⎛⎫-- ⎪ ⎪⎝⎭6．如图，在矩形ABCD 中，23,4AB BC ==，E 为BC 的中点，连接,,,AE DE P Q 分别是,AE DE 上的点，且PE DQ =．设EPQ ∆的面积为y ，PE 的长为x ，则y 关于x 的函数关系式的图象大致是 （ ）A ．B ．C ．D ．7．如图，已知正方形ABCD 与正方形AEFG 的边长分别为4和1，若将正方形AEFG 绕点A 旋转，则在旋转过程中，点,C E 之间的最小距离为 （ ）A ．3B ．421-C ．321-D ．42 8．如图，将长方形纸片ABCD 沿AE 折叠，使点D 恰好落在BC 边上点F 处．若6AB =，10AD =，则EC 的长为（ ）A ．2B ．83C ．3D ．1039．如图，以△ABC 的三条边为边，分别向外作正方形，连接EF ，GH ，DJ ，如果△ABC 的面积为8，则图中阴影部分的面积为（ ）A ．28B ．24C ．20D ．1610．□ABCD 中，AC 、BD 是两条对角线，如果添加一个条件，可推出□ABCD 是菱形，那么这个条件可以是（ ）A ．AB=CDB ．AC=BDC ．AC ⊥BD D ．AB ⊥BD 11．如图所示，将矩形纸片ABCD 折叠，使点D 与点B 重合，点C 落在点C '处，折痕为EF ，若122EFC '∠=︒，那么ABE ∠的度数为（ ）A ．24︒B ．32︒C ．30D ．26︒12．如图，矩形ABCD 中，3AB =，4BC =，点E 是BC 边上一点，连接AE ，把B 沿AE 折叠，使点B 落在点'B 处，当'CEB ∆为直角三角形时，BE 的长为（ ）A ．3B ．32C ．2或3D ．3或32二、填空题13．如图，正方形ABCD 中，点E 在边AD 上，点F 在边CD 上，若BEF EBC ∠=∠，3AB AE =，则下列结论：①DF FC =；②AE DF EF +=；③45ABE CBF ∠+∠=︒；④::3:4:5DF DE EF =；其中结论正确的序号有_____．14．如图，将矩形ABCD 沿DE 折叠，使A 点落在BC 上的F 处，若∠EFB ＝60°，则∠CFD ＝_____．15．如图，在平面直角坐标系中，边长为1的正方形1111D C B A （记为第1个正方形）的顶点1A 与原点重合，点1B 在y 轴上，点1D 在x 轴上，点1C 在第一象限内，以1C 为顶点作等边122C A B ，使得点2A 落在x 轴上，22A B x ⊥轴，再以22A B 为边向右侧作正方形2222A B C D （记为第2个正方形），点2D 在x 轴上，以2C 为顶点作等边233C A B ，使得点3A 落在x 轴上，33A B x ⊥轴，若按照上述的规律继续作正方形，则第2021个正方形的边长为_________．16．如图，在△ABC 中，∠BAC =45°，AB=AC =4，P 为AB 边上一动点，以PA ，PC 为邻边作平行四边形PAQC ，则对角线PQ 的最小值为___________．17．如图，将一个装有水的杯子斜放在水平的桌面上，其截面可看作一个宽BC ＝6厘米的矩形．当水面触到杯口边缘时，水面宽度BE ＝12厘米，此时杯子的倾斜角α等于_____度．18．如图，矩形ABOC 的顶点B 、C 分别在x 轴、y 轴上，顶点A 在第一象限，点B 的坐标为（3，0），将线段OC 绕点O 顺时针旋转60°至线段OD ，若反比例函数k y x= （k ≠0）的图象进过A 、D 两点，则k 值为_____．19．如图，在矩形纸片ABCD 中，AD ＝3，将矩形纸片折叠，边AD 、边BC 与对角线BD 重合，点A 与点C 恰好落在同一点处，则矩形纸片ABCD 的周长是______．20．如图，正方形ABCD 的边长为6，点E ，F 分别是边AB ，CD 上的点，且60CFE ∠=︒．将四边形BCFE 沿EF 翻折，得到B C FE ''，点C '恰好落在AD 边上，B C ''交AB 于点G ，则GE 的长是_______．三、解答题21．如图，点D 是Rt ABC 斜边AB 的中点，过点B ，C 分别作//BE CD ，//CE BD ，连接DE ．（1）若60A ∠=︒，3AC =，求CD 的长；（2）求证：BC DE ⊥．22．如图，矩形EFGH 的顶点,E G 分别在菱形ABCD 的边,AD BC 上，顶点,F H 在菱形ABCD 的对角线BD 上．（1）求证：BG DE =；（2）若E 为AD 中点，5,12FG GH ==，求菱形ABCD 的周长；23．如图，E 是正方形ABCD 中CD 边上一点，以点A 为中心把ADE ∆顺时针旋转90︒．（1）在图中画出旋转后的图形；（2）若旋转后E 点的对应点记为M ，点F 在BC 上，且45EAF ︒∠=，连接EF ． ①求证：AMF AEF ∆≅∆；②若正方形的边长为6，35AE =，求EF ．24．如图，矩形ABCD 中，AB ＝6，BC ＝8，E 为BC 上一动点．将△ABE 沿AE 翻折后得到AFE ，延长AF 交CD 所在直线于点G ，设BE ＝x ．（1）若点G 在CD 边上，求x 的取值范围；（2）若x ＝5，求CG 的长．25．如图，正方形ABCD 的边AB 在数轴上，数轴上点A 表示的数为-1，正方形ABCD 的面积为16.（1）数轴上点B 表示的数为 ；（2）将正方形ABCD 沿数轴水平移动，移动后的正方形记为''''A B C D ，移动后的正方形''''A B C D 与原正方形ABCD 重叠部分的面积记为S.① 当S =4时，画出图形，并求出数轴上点'A 表示的数；② 设正方形ABCD 的移动速度为每秒2个单位长度，点E 为线段'AA 的中点，点F 在线段'BB上，且. 经过t秒后，点E，F所表示的数互为相反数，求出t的值.26．已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE＝∠CBP，BE＝BP．≌；.求证：（1）CPB AEB（2）PB⊥BE（3）请你连接PE，猜想线段PB与线段PE的数量关系，并说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】由菱形的性质可得这条对角线与菱形的两边组成等边三角形，从而求得锐角的度数等于60°．【详解】解：由菱形的性质得，菱形相邻的两边相等，则与这条对角线组成等边三角形，则它的锐角等于60°，故选C．【点睛】此题主要考查菱形的性质：四边相等．2．B解析：B【分析】根据矩形的对边平行，可得∠AEF+∠BFE=180°，继而求得∠BFE=68°，再利用折叠的性质和平角的定义求解即可．【详解】∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠AEF+∠BFE=180°，∵112AEF ∠=︒，∴∠BFE=68°，∴∠1=180°-2∠BFE=44°，故选B ．【点睛】本题考查了折叠问题，矩形的性质，平行线的性质，平角的定义，熟练掌握折叠的性质是解题的关键．3．C解析：C【分析】由正方形的性质和旋转的性质探究规律，利用规律解决问题即可．【详解】解：∵四边形OABC 是正方形，且OA=1，∴A （0，a ），∵将正方形OABC 绕点O 顺时针旋转45°后得到正方形OA 1B 1C 1，∴A 122)，A 2（a ，0），A 322)，A 4（0，-a ）…， 发现是8次一循环，∵2021÷8=252…5，∴点A 2021的坐标为22,22a ⎛⎫-- ⎪⎝⎭， 故选：C ．【点睛】本题考查了正方形的性质、旋转的性质、坐标与图形的变化、规律型：点的坐标等知识，解题的关键是学会从特殊到一般的探究规律的方法，属于中考常考题型．4．A解析：A【分析】因为△ABC 为等边三角形，根据已知条件可推出Rt △ARP ≌Rt △ASP ，则AR ＝AS ，故②正确，∠BAP ＝∠CAP ，所以AP 是等边三角形的顶角的平分线，故①正确，根据等腰三角形的三线合一的性质知，AP 也是BC 边上的高和中线，即点P 是BC 的中点，因为AQ ＝PQ ，所以点Q 是AC 的中点，所以PQ 是边AB 对的中位线，有PQ ∥AB ，故③正确，又可推出△BRP ≌△QSP ，故④正确．【详解】解：∵PR ⊥AB 于R ，PS ⊥AC 于S∴∠ARP ＝∠ASP ＝90°∵PR ＝PS ，AP ＝AP∴Rt △ARP ≌Rt △ASP∴AR ＝AS ，故②正确，∠BAP ＝∠CAP∴AP 是等边三角形的顶角的平分线，故①正确∴AP 是BC 边上的高和中线，即点P 是BC 的中点∵AQ ＝PQ∴点Q 是AC 的中点∴PQ 是边AB 对的中位线∴PQ ∥AB ，故③正确∵Q 是AC 的中点，∴QC=QP ，∵∠C=60°，∴△QPC 是等边三角形，∴PB=PC=PQ ，∵PR ＝PS ，∠BRP ＝∠QSP ＝90°，∴△BRP ≌△QSP ，故④正确∴全部正确．故选：A ．【点睛】本题利用了等边三角形的性质：三线合一，全等三角形的判定和性质，中位线的性质，熟练掌握上述性质和判定方法是解题的关键．5．D解析：D【分析】过A 作AE ⊥OC 于E ，由菱形OABC 的顶点()0,0O ，()2,0C 且60AOC ∠=︒，求出A（1D 为AC 中点，可求D （12458=360︒⨯︒，转8次回到原位置，菱形绕点O 逆时针旋转，每秒旋转45︒，则第2020秒时，2020445=45252+88⎛⎫︒⨯︒ ⎪⎝⎭，相当于旋转454=180︒⨯︒，菱形旋转180°。

特殊的四边形测试题一、选择题1. 下列四边形中，哪一个不是特殊的四边形？A. 平行四边形B. 矩形C. 菱形D. 任意四边形2. 特殊四边形中，哪一个的对角线相等？A. 平行四边形B. 矩形C. 菱形D. 梯形3. 以下哪个选项不是矩形的性质？A. 对边相等B. 四个角都是直角C. 对角线相等D. 对角线互相垂直4. 菱形的对角线性质是：A. 互相垂直B. 互相平行C. 相等D. 互相垂直且平分5. 下列哪个不是梯形的特点？A. 一组对边平行B. 另一组对边不平行C. 所有角都是直角D. 一组对边相等二、填空题6. 一个四边形的两组对边分别相等，且对角线相等，这个四边形是________。

7. 如果一个四边形的对角线互相垂直且平分，那么这个四边形是________。

8. 矩形的对角线性质是________。

9. 在特殊四边形中，只有________的对角线是互相垂直的。

10. 如果一个四边形的两组对边分别平行，那么这个四边形可能是________或________。

三、判断题11. 所有平行四边形的对角线都相等。

（对/错）12. 矩形的对角线将矩形分为两个相等的三角形。

（对/错）13. 菱形的对角线将菱形分为四个相等的直角三角形。

（对/错）14. 梯形的两组对边中，至少有一组是相等的。

（对/错）15. 所有特殊四边形的内角和都是360度。

（对/错）四、简答题16. 请简述矩形和正方形的共同性质。

17. 请解释为什么菱形的面积可以通过对角线的长度来计算。

18. 梯形的中位线定理是什么？请简述其内容。

19. 如果一个四边形的对角线互相垂直，那么这个四边形可能是哪种特殊四边形？20. 请描述如何通过已知的一组对边和对角线来确定一个四边形是否是平行四边形。

五、计算题21. 已知一个矩形的长为10厘米，宽为8厘米，求其对角线的长度。

22. 已知一个菱形的对角线长度分别为20厘米和16厘米，求其面积。

23. 如果一个梯形的上底为6厘米，下底为10厘米，高为4厘米，求其面积。

2019-2020学年八年级下学期期末考试高分直通车【人教版】专题2.4矩形、菱形、正方形学习质量检测卷班级：_________ 姓名：______________ 座号：__________ 分数：___________注意事项：本试卷共26题．其中选择10道，填空8道，解答8道。

答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级、座号填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2019秋•黄石期末）如图，在正方形ABCD的外侧，作等边三角形ADE，则∠BED为（）A．45°B．15°C．10°D．125°2．（2019春•洛南县期末）如图，在矩形ABCD中，对角线AC，BD交于点O，若∠COD＝50°，那么∠CAD的度数是（）A．20°B．25°C．30°D．40°3．（2019春•包河区期末）如图，在△ABC中，AE⊥BC于点E，BD⊥AC于点D；点F是AB的中点，连结DF，EF，设∠DFE＝x°，∠ACB＝y°，则（）A．y＝x B．y=−12x+90C．y＝﹣2x+180D．y＝﹣x+904．（2019秋•沈北新区期末）如图，在矩形COED中，点D的坐标是（1，3），则CE的长是（）A．3B．2√2C．√10D．45．（2019春•镇原县期末）直角三角形中，两直角边分别是12和5，则斜边上的中线长是（）A．34B．26C．8.5D．6.56．（2019秋•揭阳期末）如图，点P是矩形ABCD的边上一动点，矩形两边长AB、BC长分别为15和20，那么P到矩形两条对角线AC和BD的距离之和是（）A．6B．12C．24D．不能确定7．（2019春•滦南县期末）如图，在△ABC中，AB＝3，AC＝4，BC＝5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为（）A．1B．1.3C．1.2D．1.58．（2019春•河南期末）如图，在▱ABCD中，对角线AC⊥AB，O为AC的中点，经过点O的直线交AD于E交BC于F，连结AF、CE，现在添加一个适当的条件，使四边形AFCE是菱形，下列条件：①OE＝OA；②EF⊥AC；③E为AD中点，正确的个数有（）A ．0B ．1C ．2D ．39.（2019秋•东台市期末）用边长为1的正方形做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积为原正方形面积的（ ）A ．12B ．13C ．23D ．不能确定10．（2018春•随县期末）已知：如图，在正方形ABCD 外取一点E ，连接AE ，BE ，DE ，过点A 作AE 的垂线交DE 于点P ．若AE ＝AP ＝1，PB =√5．下列结论：①△APD ≌△AEB ；②点B 到直线AE 的距离为√62；③EB ⊥ED ；④S △APD +S △APB ＝1+√6．其中正确结论的序号是（ ）A ．①②③B ．①②④C ．②③④D ．①③④二、填空题（本大题共8小题，每小题3分，共24分）11．（2018春•西岗区期末）已知：正方形ABCD 中，对角线AC 、BD 相交于点O ，∠DBC 的平分线BF 交CD 于点E ，交AC 于点F ，OF ＝1，则AB ＝ ．12．（2018春•嘉兴期末）如图，菱形ABCD 和菱形BEFG 的边长分别是5和2，∠A ＝60°，连结DF ，则DF 的长为 ．13．（2018春•锦江区期末）如图，正方形ABCD 的边长AB ＝3，点E 、F 分别是CB ，DC 延长线上的点，连AF交CB于点G，若BE＝1，连接AE，且∠EAF＝45°，则AG长为．14．（2019春•滨海新区期末）如图，正方形ABCD的对角线AC、BD相交于点O，DE平分∠ODA交OA 于点E，若AB＝2+√2，则线段OE的长为．15．（2019春•内乡县期末）如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝°．16．（2019秋•莱山区期末）已知正方形ABCD的边长为4，点E，F分别在AD，DC上，AE＝DF＝1，BE 与AF相交于点G，点H为BF的中点，连接GH，则GH的长为．17．（2019秋•朝阳区校级期末）如图，在Rt△ABC中，∠BAC＝90°，且BA＝6，AC＝8，点D是斜边BC 上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为．18．（2019春•密山市期末）如图，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F．且AD交EF于O，则∠AOF＝度．三、解答题（本大题共8小题，满分66分）19．（2019春•玉田县期末）如图，菱形ABCD的对角线AC、BD相交于点O，BE∥AC，CE∥DB．求证：四边形OBEC是矩形．20．（2019春•潍坊期末）如图，△ABC中，∠ACB的平分线交AB于点D，作CD的垂直平分线，分别交AC、DC、BC于点E、G、F，连接DE、DF．（1）求证：四边形DFCE是菱形；（2）若∠ABC＝60°，∠ACB＝45°，BD＝2，试求BF的长．21．（2019春•邵东县期末）如图，已知菱形ABCD中，对角线ACBD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E．（1）求证：四边形CODE是矩形．（2）若AB＝5，AC＝6，求四边形CODE的周长．22．（2019秋•法库县期末）如图，菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上，连接CF．（1）求证：∠HEA＝∠CGF；（2）当AH＝DG时，求证：菱形EFGH为正方形．23．（2019春•洪江市期末）如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB 的角平分线于点E，交∠ACB的外角平分线于点F（1）求证：EO＝FO；（2）当点O运动到何处时，四边形CEAF是矩形？请证明你的结论．（3）在第（2）问的结论下，若AE＝3，EC＝4，AB＝12，BC＝13，请直接写出凹四边形ABCE的面积为．24．（2019秋•浦东新区期末）如图1，已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点．（1）求证：MN⊥DE．（2）连结DM，ME，猜想∠A与∠DME之间的关系，并证明猜想．（3）当∠A变为钝角时，如图2，上述（1）（2）中的结论是否都成立，若结论成立，直接回答，不需证明；若结论不成立，说明理由．25．（2018春•东阿县期末）四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）如图1，求证：矩形DEFG是正方形；（2）若AB＝2，CE=√2，求CG的长度；（3）当线段DE与正方形ABCD的某条边的夹角是30°时，直接写出∠EFC的度数．26．（2018秋•渭滨区期末）如图，在矩形ABCD中，AB＝8cm，BC＝16cm，点P从点D出发向点A运动，运动到点A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．（1）当t为何值时，四边形ABQP是矩形；（2）当t为何值时，四边形AQCP是菱形；（3）分别求出（2）中菱形AQCP的周长和面积．。