第四章 运输问题(Transportation Problem)

第四章 运输问题Chapter 4Transportation Problem§4.1 运输问题的定义设有同一种货物从m 个发地1，2，…，m 运往n 个收地1，2，…，n 。

第i 个发地的供应量（Supply ）为s i （s i ≥0），第j 个收地的需求量（Demand ）为d j （d j ≥0）。

每单位货物从发地i 运到收地j 的运价为c ij 。

求一个使总运费最小的运输方案。

我们假定从任一发地到任一收地都有道路通行。

如果总供应量等于总需求量，这样的运输问题称为供求平衡的运输问题。

我们先只考虑这一类问题。

图4.1.1是运输问题的网络表示形式。

运输问题也可以用线性规划表示。

设x ij 为从发地i 运往收地j 的运量，则总运费最小的线性规划问题如下页所示。

运输问题线性规划变量个数为nm 个，每个变量与运输网络的一条边对应，所有的变量都是非负的。

约束个数为m+n 个，全部为等式约束。

前m 个约束是发地的供应量约束，后n 个约束是收地的需求量约束。

运输问题约束的特点是约束左边所有的系数都是0或1，而且每一列中恰有两个系数是1，其他都是0。

运输问题是一种线性规划问题，当然可以用第一章中的单纯形法求解。

但由于它有特殊的结构，因而有特殊的算法。

在本章中，我们将在单纯形法原理的基础上，根据运输问题的特点，给出特殊的算法。

图4.1x x x x x x x x x d x x x d x x x d x x x s x x x s x x x s x x x .t .s x c x c x c x c x c x c x c x c x c z min mn2m 1m n22221n11211n mnn 2n122m 221211m 2111m mn2m 1m 2n222211n11211mn mn 2m 2m 1m 1m n 2n 222222121n 1n 112121111≥=++=++=++=++=+++=++=+++++++++++++=在运输问题线性规划模型中，令X =（x 11，x 12，…，x 1n ，x 21，x 22，…，x 2n ，……，x m1，x m2，…，x mn ）TC =（c 11，c 12，…，c 1n ，c 21，c 22，…，c 2n ，……，c m1，c m2，…，c mn ）T A =[a 11，a 12，…，a 1n ，a 21，a 22，…，a 2n ，……，a m1，a m2，…，a mn ]T=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎭⎪⎪⎬⎫⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡行行n m 111111111111111111b =（s 1，s 2，…，s m ，d 1，d 2，…，d n ）T则运输问题的线性规划可以写成：min z=C TX s.t. AX =b X ≥0其中A 矩阵的列向量a ij =e i +e m+je i 和e m+j 是m+n 维单位向量，元素1分别在在第i 个分量和第m+j 个分量的位置上。

运输问题运输问题（transportation problem）一般是研究把某种商品从若干个产地运至若干个销地而使总运费最小的一类问题。

然而从更广义上讲，运输问题是具有一定模型特征的线性规划问题。

它不仅可以用来求解商品的调运问题，还可以解决诸多非商品调运问题。

运输问题是一种特殊的线性规划问题，由于其技术系数矩阵具有特殊的结构，这就有可能找到比一般单纯形法更简便高效的求解方法，这正是单独研究运输问题的目的所在。

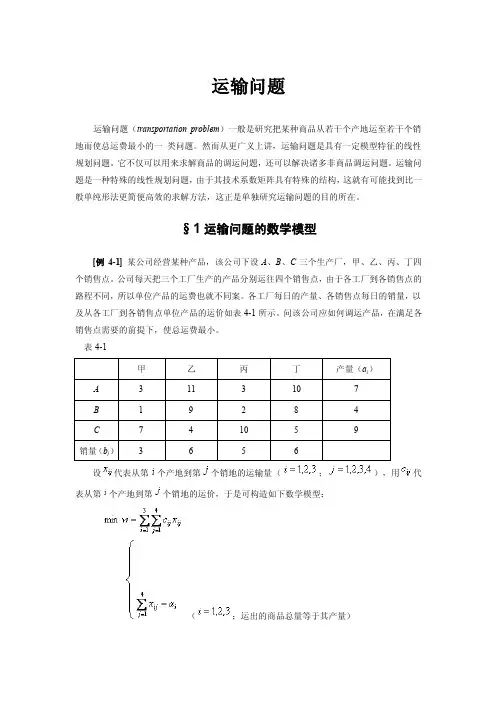
§1运输问题的数学模型[例4-1] 某公司经营某种产品，该公司下设A、B、C三个生产厂，甲、乙、丙、丁四个销售点。

公司每天把三个工厂生产的产品分别运往四个销售点，由于各工厂到各销售点的路程不同，所以单位产品的运费也就不同案。

各工厂每日的产量、各销售点每日的销量，以及从各工厂到各销售点单位产品的运价如表4-1所示。

问该公司应如何调运产品，在满足各销售点需要的前提下，使总运费最小。

表4-1设代表从第个产地到第个销地的运输量（；），用代表从第个产地到第个销地的运价，于是可构造如下数学模型：（；运出的商品总量等于其产量）（；运来的商品总量等于其销量）通过该引例的数学模型，我们可以得出运输问题是一种特殊的线性规划问题的结论，其特殊性就在于技术系数矩阵是由“1”和“0”两个元素构成的。

将该引例的数学模型做一般性推广，即可得到有个产地、个销地的运输问题的一般模型。

注意：在此仅限于探讨总产量等于总销量的产销平衡运输问题，而产销不平衡运输问题将在本章的后续内容中探讨。

（；运出的商品总量等于其产量）（；运来的商品总量等于其销量）供应约束确保从任何一个产地运出的商品等于其产量，需求约束保证运至任何一个销地的商品等于其需求。

除非负约束外，运输问题约束条件的个数是产地与销地的数量和，即；而决策变量个数是二者的积，即。

由于在这个约束条件中，隐含着一个总产量等于总销量的关系式，所以相互独立的约束条件的个数是个。

第四章 运输问题主要内容：1、运输问题及其数学模型； 2、表上作业法；3、运输问题的进一步讨论。

重点与难点：表上作业法的原理、求解步骤，产销不平衡运输问题的求解方法。

要 求：理解运输问题的基本概念及表上作业法的原理，掌握表上作业法确定初始可行解、最优解的判别与改进的方法。

§1 运输问题及其数学模型一、运输问题引例，设有m 个生产地iA ，可供应（产量）分别为m i a i ,,2,1, =;有n 个销地,j B 其需要量分别为n j b j ,,2,1, =。

已知从i A 到j B 运输单位物资的运价（单价）为ij c ，试问如何调运物资才能使总费用最小？设用ij x 表示从i A 到j B 的运量，可将这些数据汇总于下表：产销平衡表单价运价表第四章 运输问题 第39页注：有时将两表合二为一。

（1）若各产地的总产量等于各销地的总销量，即∑∑===nj j m i i ba 11，则称之为产销平衡的运输问题（或平衡运输问题）；（2）若所有产地的总产量不等于所有销地的总销量，即∑∑==≠n j j mi i ba 11，则称之为产销不平衡的运输问题（或不平衡的运输问题）；（3）若在运输途中，还存在中间转运点（转运点即是产地，又是销地），则称之为有转运的运输问题（或扩大的运输问题）。

二、平衡运输问题的数学模型在产销平衡的条件下，要求得总运费最小，可建立以下数学模型：∑∑===m i nj ij ij x c z 11min⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥====∑∑==0,,2,1,,2,11,1ij n j i ij j mi ij x m i a x n j b x 该运输问题也属于线性规划问题，包括： （1）n m ⨯个决策变量；（2）m+n 个约束条件；由于有∑∑===n j j mi iba 11，所以模型只有m+n –1个独立约束条件，基变量中含有m+n –1个变量；（3）系数矩阵的秩1)(-+≤n m A rank40（4）系数矩阵为n m n m ⋅⨯+)(阶矩阵，该系数矩阵中对应于变量ij x 的系数向量ij P ，其分量中除第i 个和第m +j 个为1以外，其余的都为零。

第四章运输问题本章主要介绍运输问题的及其特殊情形——指派问题的求解方法，其基本要求为：1.能用表上作业法求简单的运输问题的最优解2.会用匈牙利算法求标准指派问题的解。

．运输问题线性规划模型的特征请与课本（102 页）引例比较以下，看看模型的结构与形式是否一致，同时注意了解课本103 页下面的加工问题和运输问题的联系。

由上面的模型可以看出，运输问题显然是一个线性规划问题，因我们学过的单纯形法求解，但求解时对每一个等式必须加上一个人工变量（参考当约束条件方程为等式约束时求初始基本可行解的方法），这样将使一个很小规模的运输问题变得较为烦琐。

本章主要介绍的表上作业法求解运输问题，要比一般单纯形法简便得多。

三．表上作业法介绍表上作业法是一种迭代算法，也是从先求出初始基本可行解，然后用检验数判定是否最优解，若是就停止计算，否则就要对解进行调整、判定，直到求出最优解为止。

因为关于以上计算都可以在产销平衡表中进行，所以叫表上作业法。

第一节运输问题的线性规划模型我们在这里再给出一个实际的运输问题的模型。

例1.某公司经销甲产品，它下设有A i A2 A3三个加工厂, 每日产量分别为: A i—7 吨，A2 4吨，A3 ―― 9吨。

该公司把这些产品分别运往B l B2 B3 B4四个销售点，各销售点每日的销量为：B I3吨，B2——6吨, B3——5吨, B4——6 吨。

从各工厂到销售点的单位产品的运价为下表所示，问该公司应该如何调运产品，在满足各销售点需要量的前提下，使总运费最少?解：总产量为20吨，总需求量也为20吨，故产销平衡。

设：X ij表示有第个加工厂运往第个销售点的甲产品的数量（吨），则可得到该问题的设某种货物有m个产地A i, A2,…，A m,产量分别为a i, a2,…，a m个单位；另外有n个销地B i, B2,…，B n,销量分别为b i, b2,…，b n个单位,又假设产销是平衡的，即此外，还知道由产地A i向销地B j运输每单位货物的运价为C ij。