离散数学第三章PPT课件

离散数学
主讲教师
13.11.2020
1
第三章 集合的基本概念和运算
§3.1 集合的基本概念 §3.2 集合的基本运算 §3.3 集合中元素的计数
13.11.2020
离散数学
2
集合论 集合论是研究集合一般性质的数学分支,它的创 始人康托尔(G.Cantor ,1845－1918)。在现代数学中， 每个对象(如数，函数等)本质上都是集合，都可以用 某种集合来定义，数学的各个分支，本质上都是在研 究某一种对象集合的性质。集合论的特点是研究对象 的广泛性，它也是计算机科学与工程的基础理论和表 达工具，而且在程序设计，数据结构，形式语言，关 系数据库，操作系统等都有重要应用。本课程在第三， 四章中介绍集合论的内容。
如：
A∪B
E
A∩B
E
AB
E
~A
E
AB
E
13.11.2020
离散数学
15
二、文氏图 （Jahn Venn）
例4：用文氏图表示下面集合
13.11.2020
离散数学
16
二、文氏图 （Jahn Venn）
例5：用集合公式表示下面文氏图中的阴影部分
(1)A ∩ B ∩ C，
(2) (A∩B )∪(B∩C)∪(C∩A)
或A = B x(x A x B)
x(x A x B) x(x B x A)
13.11.2020
离散数学
8
四、集合之间的关系
3、真子集： B A。 BABABA BABA B=A
4、幂 集：集合A的全体子集构成的集合，记作P (A)。 符号化为 P (A) = { x | x A}
n 元集A的幂集P (A)含有2n个元素。

命题演算证明法的书写规范 (以下的X和Y代表集合公式) (1) 证XY
任取x， xX … xY (2) 证X=Y
方法一 分别证明 XY 和 YX 方法二 任取x，xX … xY
注意：在使用方法二的格式时，必须保证每步推理都是充分 必要的
27
第三章 集合
命题演算法
例3-3.2 证明A(AB) = A （吸收律）
元素a属于A，记作aA； 或者a不属于A，记作aA，也可以记作┓(aA)。
（4）任意性：集合的元素也可以是集合。 例：A={1，{2}，2，{3，4}，{6}} A=5，2A，{2}A，6A,{6}A
6
第三章 集合 例如：A={{a,b}，d，{{b}}}。可以用一种树形图来表示这种
隶属关系，该图分层构成，每一层上的结点都表示一个集 合，它的儿子就是它的元素。 集合的树型层次结构
32
第三章 集合
§3-3-3 笛卡儿积
定义3-3.2 两个元素a，b组成二元组，若它们有次序 之别，称为二元有序组，或称为有序对或序偶，记为<a， b>，称a为第一分量，b为第二分量；若它们无次序区分， 称为二元无序组，或称为无序对，记为（a，b）。
有序对具有如下性质。 （1）有序性：当x≠y时<x，y>≠<y，x>。 （2）<x，y>与<u，v>相等的充分必要条件是
A
B
11
第三章 集合
§3-2 集合之间的关系
§3-2-1 集合之间的关系 （1）相等关系： • 两集合A和B相等，当且仅当它们有相同的元素。 • 若A与B相等，记为A=B；否则，记为A≠B。 • 可形式化为：A=B(x)(xAxB)。
12
第三章 集合

17
例题
计算以下幂集：
，{}；{，{}}
解：
P()={} P({})={，{}} P({，{}})= {, {}，{{}},{，{}}}
18
3.3 集合的运算
集合的运算 并，交，补（绝对补），差（相对补－），和对称差等。
19
集合的并运算
• 定义3.3.1 设A，B为集合，由A和B的所有元素组成的集 合称为A与B的并集， 可表示为： AB={x|xAxB} 其文氏图：
其文氏图如下：
~E = ， ~ = E， ~（~A）= A A ~A = ， A ~A = E
27
德.摩根定律
• 定理3.3.5 设A，B为任意二个集合，则有： • （1） （AB）= A B • （2） （A B）= A B • 证明 设E为全集，显然有AE=A，AE=E成立。 • （1） （AB）= {x | xEx（AB）}= {x |
据的增加、删除、修改、排序，以及数据间关系的描述。
集合论在计算机语言、数据结构、编译原理、数据库与
知识库、形式语言及人工智能等许多领域得到广泛的应
用。
2
3.1 集合及其表示
• 集合是由一些对象聚集在一起构成的。 例如，全体整数 全体中国人 26个英文字母
• 构成集合的对象可以是各种类型的事物。 • 定义3.1.1 集合中的对象叫集合的元素，或成员。
• 集合中的元素可以具有共同性质，也可以表面上看起来不相干。
• 如{2，Tom，计算机，广州}
• 在集合论中，规定元素之间是彼此相异的，并且是没有次序关 系的。
例如，{3,4,5},{3,4,4,5,5},{5,3,4}都是同一个集合。
• 例如，A={3,4,5},

个男士和n个女士 【Example】一个组有 个男士和 个女士。如果把他们男 】一个组有n个男士和 个女士。 女相间地排成一排，有多少种方式？ 女相间地排成一排，有多少种方式？ Solution:
我们假设这一排列可以有不同性别的排头。 我们假设这一排列可以有不同性别的排头。 首先我们先考虑n个男士的排列， 首先我们先考虑 个男士的排列，所有的排列数 个男士的排列 P (n, n)=n! 同样的我们也可以得到n个女士的排列数也为 同样的我们也可以得到 个女士的排列数也为n!. 个女士的排列数也为 现在将n个男士与 个女士相间的排列 现在将 个男士与n个女士相间的排列，我们可以采取先将女士排 个男士与 个女士相间的排列， 列好，然后往其中进行男士的排列， 列好，然后往其中进行男士的排列，并存在男士作为排头或女士作 为排头的两种情况。 为排头的两种情况。 由乘积法则可以知道总的排列方式数为
单位有7位代表 单位有3位代表 【example】 A单位有 位代表，B单位有 位代表，排成一列 】 单位有 位代表， 单位有 位代表， 合影，要求B单位 人排在一起。 单位3人排在一起 合影，要求 单位 人排在一起。 a) 问有多少种不同的排列方案？ 问有多少种不同的排列方案？ b) 若B单位的 人不能相邻，且A单位的 人排在两端，问 单位的3人不能相邻 单位的2人排在两端 单位的 人不能相邻， 单位的 人排在两端， 有多少种不同的排列方案。 有多少种不同的排列方案。 Solution： a) 将B单位 个人的某一排列作为一个元素，参加 单位进行排列。 单位3 单位进行排列。 单位 个人的某一排列作为一个元素，参加A单位进行排列
Example 5 字母 字母ABCDEFGH有多少种排列包含串 有多少种排列包含串ABC？ 有多少种排列包含串 ？ Solution： 由于字母ABC必须成组出线，我们可以通过找6个对 必须成组出线，我们可以通过找 个对 由于字母 必须成组出线 和单个字母D、 、 、 和 的排列数得 象，即组ABC和单个字母 、E、F、G和H的排列数得 即组 和单个字母 到答案。 到答案。 由于这6个对象可以按任何次序出线， 由于这 个对象可以按任何次序出线，存在 个对象可以按任何次序出线 6！=6*5*4*3*2*1=720种ABCDEFGHZ字母的排列，其 ！ 字母的排列， 种 字母的排列 成组出现。 中ABC成组出现。 成组出现

rij=
1,如果aiRbj
0,如aiRbj
则称MR=［rij］矩阵是R的关系矩阵.

第3章 二元关系
例3.1-4
设A={a1,a2},B={b1,b2,b3},R={〈a1,b1〉,
〈a2,b1〉,〈a1,b3〉,〈a2,b2〉},则其关系矩阵为

第3章 二元关系
图 3.1―4

第3章 二元关系
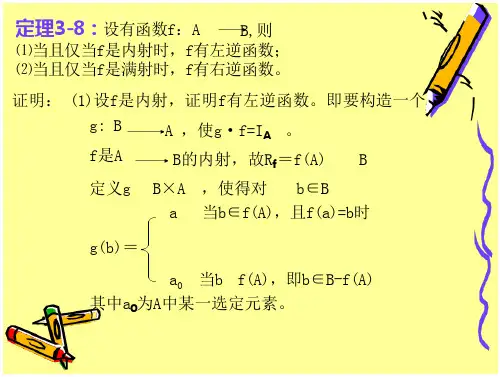
(2)如果对A中每一x,xRx,那么R是反自反的.即 A上的关系R是反自反的 x(x∈A→xRx)
例 如 ,A={1,2,3},R2={〈2,1〉,〈1,3〉,〈3,2〉} 是 反

第3章 二元关系
关系也可归纳地定义.自然数上的小于关系可定义
如下: (1) (基础)〈0,1〉∈＜
(2) (归纳)如果〈x,y〉∈＜,那么
(i)〈x,y+1〉∈＜ (ii)〈x+1,y+1〉∈＜ (3)(极小性)对一切x,y∈N,x＜y当且仅当〈x,y〉是 由有限次应用条款(1)和(2)构成。
1(真),当〈x1,x2,…,xn〉∈R时 0(假),当〈x1,x2,…,xn>∈R时

第3章 二元关系
当n=1时,R={〈x〉|P(x)}称为一元关系.它是一重组
集合,表示论述域上具有性质P的元素集合,其意义与 R={x|P(x)}相同,仅记法不同而已。 例如,设P(x)表示“x是质数”,论述域是N,则质数集 合可表示为 {〈x〉｜P(x)} 或 {x｜P(x)}
b1 b2
b3
a1 1
a2 1
0
1
1
0
即
1 0 1 MR 1 1 0

第3章 二元关系

⑵设f是满函数，要证f有右逆函数，即构造一个g:B A 使f·g=IB，则g为f的右逆函数。
证明：因为f是A B的满射，所以对 b∈B， a∈A使得f(a)=b。
构造g，对b∈B＝f(A）定义g(b)=a，其中a是满足f(a)=b的任意 一个确定的a。
这样g给B中每一个元素定义了唯一的象。
所以g:B A的 函数 对 b"∈B,记a " =g(b ")，则f·g(b ")=f(g(b "))=f(a ")=b" =IB(b " 所以f·g=IB，g是f的右逆 函数。
∴说这个小组有5个同学。
定义3-10：如果从集合Nm到A存在一个双射，则称集合A是
有限集，＃A＝m。＃Φ＝0，Φ也是有限集。不是有限集的 集
合称为无限集
有限集中最简单的一种是可数集。
定义3-11：如果从集合N到A存在一个双射，则称A是可 数集。记＃A＝§。“§ ”读作“阿列夫零”。有限集和可 数集总称为可计数集。如果集合A是无限的但不是可数的， 则称A是不可数集。
⒈n＝8时，可由一张3分和一张5分的邮票组合而成。则p(8)真。
⒉设n＝k时，p(k)真，即我们可以用3分和5分的邮票恰好组成k分 的邮费。那么n＝k+1时：
①若我们组成的k分邮费中至少有一张5分的邮票，那么 用2张三分的邮票去代替这张5分的邮票，我们就得到 k+1分的邮费。即p(k+1) 真。
②若k分的邮费全用3分的邮票组成，因此用两张5分的邮 票去代替三张3分的邮票就得到k+1的邮费。即p(k＋1)真 。
例1：Z(非负整数)是可数集
f:N Z f(x)=x-1 显然f是双射。
命题1：一个集合是可数集合的充要条件是它可以排成一个 无序列的形式。

《定义》 设A是集合，A的所有子集（作为元素）的集合 称为A的幂集。
(c)同一集合可以用多种不同的形式表示。 (d)集合也可作为某一集合的元素。
例：S={a,{1,2},p,{q}}
§1集合的概念和表示法
(3)三个特殊集合：空集、全集合、集合族 《定义》如果一个集合包含了所要讨论的每一个集合，
则称该集合为全集合，简称全集，用E表示。 E={x | p(x) ∨ p(x)} p(x)为任何谓词公式
§1集合的概念和表示法
注意：区分“”和“”的关系： “”关系是指集合和该集合中元素之间的关系。
例：S={a,{b},c} 则a S，{b}S，c S 而“”关系是指二个集合之间的关系。
例：S1={a, b} S2={a,b,1,2} 则S1 S2 若A不包含于B，则也可表示成AB 《定理》设E是全集，A是一个集合，则一定有
《定义》不拥有任何元素的集合称为空集（或称零集）， 用表示 ={x | p(x) ∧ p(x) }={ }
注意： ≠ {} 前者是空集，是没有元素的集合；后 者是以作为元素的集合。
§1集合的概念和表示法
《定义》集合中的元素均为集合，称这样的集合为集合 族。 例A={{a}，{b}，{c、d}}
2、集合之间的关系 《公理》给定二个集合A和B，当且仅当A和B具有同样
§1集合的概念和表示法
例：大于10的整数的集合：S1={x | x I ∧ x>10} 偶整数集合：S2={x | y (y I ∧ x=2y)} 有限个元素集合： S3={1,2,3,4,5}={x | x I ∧ (1 ≤ x ≤ 5) } S4={F,T}={x | x=T ∨ x=F} S5={1,4}={ x | (x²-5x+4=0) }

判断方法一：真值表法
真值表的最后一列全为1，所以（（p∨q）∧┐p） →q为重言式。因而推理正确。
判断方法二：等值演算法
（（p∨q）∧┐p）→q ⇔ （（p∧┐p）∨（q∧┐p））→q ⇔ （ q∧┐p ）→q ⇔ ┐q∨p∨q ⇔1
因为（（p∨q）∧┐p）→q为重言式，所 以推理正确。
判断方法三：主析取范式法
★ ★★
可见，如果能证明★★是重言式，则★也是重言式。 在★★中，原来的结论中的前件A已经变成前提了，称A为 附加前提。称这种将结论中的前件作为前提的证明方法为 附加前提法。
例：在自然推理系统P中构造下面推理的证明 如果小张和小王去看电影，则小李也去看电影。小
赵不去看电影或小张去看电影。小王去看电影。所 以，当小赵去看电影时，小李也去。
前提引入
② ┐s
前提引入
③ ┐p
①②拒取式（A→B）∧┐B⇒┐A
④ p∨q
B）∧┐B⇒A
⑥ q→r
前提引入
⑦r
⑤⑥假言推理（A→B）∧A⇒B
⑧ r∧（p∨q） ⑦④合取引入
（2）前提：┐p∨q，r∨┐q，r→s 结论：p→s
证明：
① ┐p∨q 前提引入
② p→q
①置换
（A→B）∧（C→D）∧（┐B∨┐D） ⇒（┐A∨┐C）
（12）合取引入规则：若证明的公式序列中出现过 A和B，则A∧B是A和B的有效结论。
推理规则（12个）
（1）前提引入规则 （2）结论引入规则（隐规则） （3）置换规则：等值置换 （4）假言推理规则：（A→B）∧A⇒B （5）附加规则：A⇒（A∨B） （6）化简规则：A∧B ⇒A （7）拒取式规则：（A→B）∧┐B⇒┐A （8）假言三段论规则：（A→B）∧（B→C）⇒（A→C） （9）析取三段论规则：（A∨B）∧┐B⇒A （10）构造性二难推理规则 （11）破坏性二难推理规则 （12）合取引入规则

以|P(A)|＝Cn0＋Cn1＋…＋Cnn＝2n。
定理3.6 设A和B是两个集合，则： (1)B∈P(A)BA。 (2)ABP(A)P(B)。 (3)P(A)＝P(B)A＝B。 (4)P(A)∈P(B)A∈B。 (5)P(A)∩P(B)＝P(A∩B)。 (6)P(A)∪P(B)P(A∪B)。
A∪B＝B。
反之，若A∪B＝B，因AA∪B，所以AB。 同理可证ABA∩B＝A。
定义3.7
设A和B为两个集合，所有属于A而不
属于B的元素组成的集合称为B对于A的补集
(Complement) ， 或 相 对 补 。 记 作 A － B ＝
{x|x∈A∧xB} 。 A － B 也 称 为 A 和 B 的 差 集
A的真子集，但A不是A的真子集。 注：∈与表示元素和集合的关系，而、与＝
表示集合和集合的关系。 例如，若A＝{0，1}，B＝{0，1，{0，1}}，则 AB且AB。
定理3.3 设A、B和C是三个集合，则
(1)(AA)。 (2)AB(BA)。 (3)AB∧BCAC。
证 仅证(2)和(3) 明 (2)AB x(x∈A→x∈B)∧x(x∈B∧xA)
例如，若A＝{0，{0}}，则P(A)A＝(P(A)－A)∪(A－ P(A))＝{，0，{{0}}，{0，{0}}}。
定理3.9 设A、B和C为三个集合，则： (1)AB＝BA。 (2)(AB)C＝A(BC)。 (3)A∩(BC)＝(A∩B)(A∩C)。
例1 设A和B为两个集合，且AB，则A∩CB∩C。
证 对任意的 x∈A∩C ，则有 x∈A 且 x∈C 。而 AB ， 明 由 x∈A 得 x∈B ，则 x∈B 且 x∈C ，从而 x∈B∩C 。所
以，A∩CB∩C。 例2 设A和B为两个集合，则ABA∪B＝BA∩B＝A。