叶片翼型,失速,升力计算

机翼升力计算公式机翼升力计算公式动力三角翼 2009-06-18 02:00 阅读463 评论0字号：大大中中小小机翼升力计算公式机翼升力计算公式升力L=1/2 *空气密度*速度的平方*机翼面积*机翼升力系数（N）机翼升力系数曲线如下注解：在小迎角时曲线斜率是常数。

在标识的1位置是抖振点，2位置是自动上仰点， 3位置是反横操纵和方向发散点，4位置是失速点。

对称机翼在0角时升力系数=0（由图）非对称一在机身水平时升力系数大于0，因此机身水平时也有升力滑翔比与升阻比升阻比是飞机飞行速度不同的情况下升力与阻力的比值，跟飞行速度成曲线关系，一般升阻比最大的一点对应的速度就是飞机的有利速度和有利迎角。

滑翔比是飞机下降单位距离所飞行的距离，滑翔比越大，飞机在离地面相同高度飞的距离越远，这是飞机固有的特性，一般不发生变化。

如果有两台飞行器，有着完全相同的气动外形，一台大量采用不锈钢材料的，另一台大量采用碳纤维材料，那么碳纤维材料的滑翔比肯定优于不锈钢材料的。

这个在SU-27和歼11-B身上就能体现出来，歼11-B应该拥有更大的滑翔比。

螺旋桨拉力计算公式（静态拉力估算）你的飞行器完成了，需要的拉力与发动机都计算好了，但螺旋桨需要多大规格呢？下面我们就列一个估算公式解决这个问题螺旋桨拉力计算公式：直径（米)×螺距(米）×浆宽度（米）×转速²（转/秒）×1大气压力（1标准大气压）×经验系数（0.25）=拉力（公斤）或者直径（厘米)×螺距(厘米）×浆宽度（厘米）×转速²（转/秒）×1大气压力（1标准大气压）×经验系数（0.00025）=拉力（克）前提是通用比例的浆，精度较好，大气压为1标准大气压，如果高原地区，要考虑大气压力的降低，如西藏，压力在0.6-0.7。

1000米以下基本可以取1。

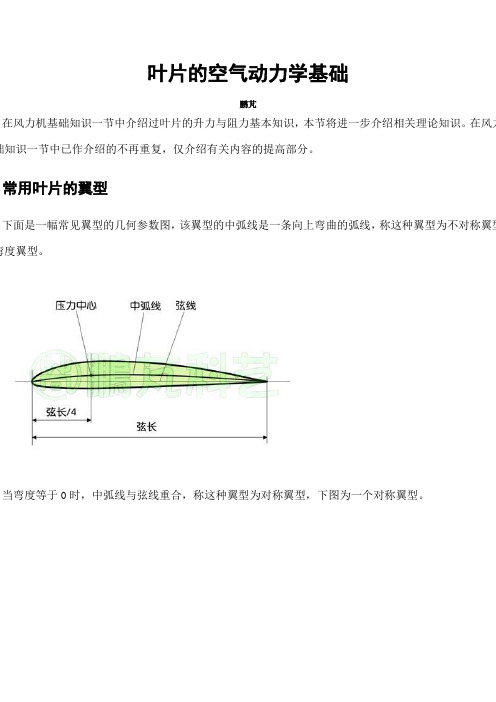
叶片的空气动力学基础鹏芃在风力机基础知识一节中介绍过叶片的升力与阻力基本知识，本节将进一步介绍相关理论知识。

在风力础知识一节中已作介绍的不再重复，仅介绍有关内容的提高部分。

常用叶片的翼型下面是一幅常见翼型的几何参数图，该翼型的中弧线是一条向上弯曲的弧线，称这种翼型为不对称翼型弯度翼型。

当弯度等于0时，中弧线与弦线重合，称这种翼型为对称翼型，下图为一个对称翼型。

下图是一个性能较好的低阻翼型，是带弯度翼型，在水平轴风力机中应用较多。

带弯度翼型的升力与失速下面为一个低阻翼型的气流动力图，翼型弦线与气流方向的夹角（攻角）为α，正常运行时气流附着翼面流过，靠近翼型上方的气流速度比下面的气流速度快，根据流体力学的伯努利原理，翼型受到一个上力Fl，当然翼型也会受到气流的阻力Fd。

这是正常的工作状态，有较大的升力且阻力很小。

但翼型并不是在任何情况下都能产生大的升力。

如果α大到一定程度，气体将不再附着翼型表面流过，在翼型上方气流会发生分离，翼型前缘后方会产生涡致阻力急剧上升升力下降，这种情况称为失速。

见下图翼型什么时候开始失速，下面是这种翼型的升力系数与阻力系数随攻角的变化曲线参考图，图中绿色的力曲线、棕色的是阻力曲线。

在曲线中可看出，攻角α在11度以下时升力随α增大而增大，当攻角α大度时进入失速状态，升力骤然下降，阻力大幅上升，在α等于45度时升力与阻力基本相等。

翼型开始失攻角α的值称为失速角。

大多数有弯度的薄翼型与该曲线所示特性相近。

在曲线图中看出翼型在攻角为0时依然有升力，这是因使攻角为0，翼型上方气流速度仍比下方快，故有升力，当攻角为一负值时，升力才为0，此时的攻角称升攻角或绝对零攻角。

翼型在失速前阻力是很小的，在近似计算中可忽略不计。

当攻角为0时，有弯度的翼型的压力中心在翼型的中部，随着攻角的增加（不大于失速角）压力中心向动到1/4弦长位置。

对称翼型的升力与失速对称翼型的升力与阻力等气动特性与有弯度翼型类似，但对称翼型在攻角为零时升力为零，因为此时翼面与下面气流速度相同。

翼载荷与失速速度、起飞速度的大致推算1、翼载荷与失速速度实际失速速度会随载荷的变化而改变。

1g失速速度（VS1g）和FAR失速速度（VSFAR），是指通过在翼型、机翼水平、起落架型态、飞机重量和重心位置一定的情况下经试飞得到，并作为该机型计算各种保护速度的标准。

它们在相应机型中都用VS来表示。

1g失速速度（VS1g）和FAR失速速度（VSFAR）分别是在载荷因子为1和小于1的条件下测得，也就是说实际飞行只有不但要严格满足测试此失速速度机体型态、重心位置、重量等要求，而且还必须严格保持平飞才不至于在此速度失速。

实际飞行状态和载荷因子、高度的改变会影响失速速度值。

* 载荷因子和平飞失速速度的关系：根据升力公式推得机动飞行失速速度V机动和同机型的平飞失速速度VS的关系为：V机动= √nyVSny：机翼载荷因子结论：不同飞行状态下的失速速度是平飞失速速度的√ny倍。

即飞机水平转弯或盘旋时，坡度增加、机翼载荷因子增加、对应实际飞行状态下的失速速度增加。

下表列出了盘旋转弯坡度、机翼载荷因子和平飞失速速度的对应关系转弯坡度0度15度25度30度40度45 度53度60度翼载荷因子 1 1.04 1 1 1.16 1.3 1.41 1.69 2平飞失速速度VS盘旋失速速度1VS 1.02VS 1.04VS 1.1VS 1.VS 1.2VS 1.3VS 1.4VS从上图看出，不同坡度导致不同翼载因子，又导致产生不同的失速速度。

为实际使用方便，为防止飞机机动失速，一般规定飞行中飞机的最小机动（选择）速度VLS,是目前情况下平飞失速速度VS的某一倍数。

如VLS=1.3VS意味着以此VLS速度飞行，当坡度达到50度时飞机开始接近失速。

2、翼载荷与起飞速度经过推导，最终公式为（海拔为0的情况下）：V = √（10X翼载荷) 其中，翼载荷单位为千克/平方米，速度单位为米/秒，用10做参数时，可以认为是失速速度。

V = √（12.3X翼载荷) 其中，翼载荷单位为千克/平方米，速度单位为米/秒，用12.3做参数时，可以认为是起飞速度。

1叶片产生升力的原因及失速原理
在二维低速流场中，气体的压力与速度存在下列关系，伯努利公式Po=P+PV。

／2
式中Po一为总压P为静压,PV/2动压叶片产生升力的原因是叶片上下翼面的形状不同，上翼面较突出而使得流过上翼面的空气流速加快，因而压力较低，下翼面较平缓而使得流过下翼面的空气流速较慢，故而压力较高，升力由此而产生。

失速产生的根本原因是由于边界层的分离。

所谓边界层是指气体绕翼面流动时，由于粘滞性的作用，在翼面附近一定范围内的气层其流速将小于主流区的流速，我们把这层流速小于主流区流速的气层称为边界层。

边界层分离是在翼面由突出变成平缓之后产生的，此时边界层内部的流动是减速扩压，在靠近壁面处的流体由于要克服相当大的摩擦阻力而消耗掉的动能较多，在这种双重的阻滞作用下，靠近壁面附近的流体的速度很快减小以至于停止前进，在正压强梯度的作用下，壁面附近的流体作逆向运行。

构成了倒流，因而形成了边界层的分离现象，分离使边界层急剧增厚，并形成一个旋涡区，气体的一部分机械能将在涡流运动中由于摩擦面不可逆转地变成流体的内能，造成很大的总压损失．
由于气流发生分离，流动失去翼型效应，与未分离时情况相比，翼型上侧气流速度下降，因而压力上升，上下表面压力差减小，因而升力下，降，叶片失速。

叶片的升力系数和阻力系数曲线叶片的升力系数和阻力系数曲线导语：本文将从叶片的升力系数和阻力系数曲线的基本概念入手，逐步深入探讨其原理、影响因素以及实际应用。

通过对这一主题的全面分析，读者将能够更好地理解叶片在空气中产生升力和阻力的机理，并在实践中灵活应用这些知识。

一、升力和阻力的基本概念升力和阻力是涉及到物体在流体中运动的基本力学特性。

在航空工程中，叶片是发动机、风力发电机以及其他旋转机械中的重要构件，其升力和阻力性能直接影响着设备的效率和稳定性。

1. 升力：叶片在空气中运动时，由于形状和角度的改变，周围流体对其产生了垂直于运动方向的力，即升力。

升力决定了叶片的承载能力和推进效率。

2. 阻力：与升力相对，阻力是叶片在运动过程中所受到的阻碍力，它可以视为对于运动方向的相反力。

阻力的大小与叶片的形状、表面状况以及运动速度等因素有关。

二、升力系数和阻力系数的计算与曲线为了更好地评估叶片的性能，我们需要引入升力系数和阻力系数这两个维度的指标。

通过归一化处理，我们可以将叶片的升力和阻力与流体速度、密度等因素消除，将其转化为与叶片本身特性相关的无量纲数值。

1. 升力系数（Cl）：升力系数是升力与流体动压乘积及叶片平面积的比值，即Cl = L / (0.5 * ρ * V^2 * A)。

其中L为升力力值，ρ为流体密度，V为叶片运动速度，A为叶片平面积。

2. 阻力系数（Cd）：阻力系数是阻力与流体动压乘积及叶片平面积的比值，即Cd = D / (0.5 * ρ * V^2 * A)。

其中D为阻力力值。

根据实验测量和理论计算，我们可以得到叶片在不同运动状态下的升力系数-阻力系数曲线。

通过绘制这样的曲线，我们可以清晰地了解叶片在不同条件下的性能表现。

三、升力系数和阻力系数曲线的特征升力系数和阻力系数曲线的形状和特征对叶片的设计和性能评估起着重要的作用。

以下是其中几个常见的特征：1. 攻角：攻角是指流体入射方向与叶片上法线之间的夹角。

1、雷诺数Re=pvb/μ（空气密度p-kg/m^3;标准状态下为1.226，与气流相对速度v-m/s，翼型弦长b-m，黏度μ=0.0000178）：雷诺数的大小决定该翼型所做机翼的性能，如边界层是湍流边界层还是层流边界层，普通翼型的极限雷诺数（边界层从层流变为湍流）大约是50000，雷诺数还决定了机翼的与来流迎角（攻角）范围，在不失速的情况下，同一翼型，同一表面粗糙程度，同展弦比，同平面形状的机翼，雷诺数越大，则不失速攻角的范围越大，《《重点！通过观察风洞实验所得曲线，在雷诺数大于50000的情况下，两翼型雷诺数相差几万但升力系数曲线基本重合，也就是说，模友在选择翼型时在雷诺数大于50000时，计算出最大雷诺数（v 取最大值），然后直接用最大雷诺数的那个翼型数据计算即可，不同的是雷诺数大的助力系数要小一些，由此结论还能得出雷诺数大于50000时，翼型升力性能与速度的改变和翼型弦长的大小关系微小，在航模上可忽略。

》》2、升力计算：Y=1/2V^2pSCl(升力Y-单位N，气流相对速度V-m/s，空气密度P-kg/^3;，S翼面积-m^2，Cl-翼型的升力系数）改公式计算的是翼型理想升力，即在展弦比为无穷大时，不受翼尖涡流影响时的升力，升力系数代翼型数据，设计航模时应该对其进行修改，后面会讲到。

3、阻力计算：D=1/2V^2PSCd（阻力D-单位N，Cd-阻力系数，其它与升力计算相同）实际情况下机翼的阻力为翼型理想阻力+涡流诱导阻力，该公式计算的是翼型理想阻力，阻力系数代翼型数据。

4、涡流诱导阻力：D=1/2V^2PSCdi，（D为诱导阻力，Cdi为诱导阻力系数——Cdi=Cl^2/3.142A,展弦比A后面再详细介绍，Cdi计算公式中升力系数用翼型数据），非圆形或梯形机翼须乘以修正系数（1.05-1.1）圆形或梯形部分越多修正系数越小。

5、展弦比：A=L^2/S（L翼展，S翼面积，计算比值时L与S用同一单位，L厘米则S 用cm^2）展弦比大则不失速迎角范围小，小则反之，因为小展弦比时翼尖涡流大产生抑制边界层与机翼分力的作用力大。

..飞机机翼升力的计算公式中C是升力系数，S是机翼的面积。

v是飞机的速度。

ρ是大气密度。

那么各个数据的单位是什么？Y=1/2ρCSv²等式两边的单位肯定相同的。

但是我要说，这个公式中各个量采用什么单位都是无所谓的，因为里面含有一个C（升力系数）的量，这个量的单位会随着别的量选用的单位而变化，来保证等式两边的单位是统一的。

等式两边的单位肯定相同的。

例如，各个物理量都采用国际单位制，即等式左边升力Y单位选用N，等式右边ρ选用kg/m³，S选用m²，V选用m/s。

那么C的单位就应该是n·s/kg（C绝对不是没有单位的，这点楼上两位说错了），这样才能保证左边运算结果的单位是N。

这个单位很奇怪，而且这个单位并没有什么物理意义，只是为了平衡等式两边的单位。

上面只是举了一个例子，而公式采用哪一套单位制都可以。

事实上，飞机领域都是西方国家占主导地位，他们采用的单位并不是国际单位制，而是英制单位，长度单位是英寸、英尺、英里等，面积单位可能就是平方英尺等，重量单位是磅，速度单位是英里/小时，等等。

而采用这一套单位，升力系数C 的单位又不同了，还是要平衡两边的单位。

而对于这个公式，我们没有必要追求他到底用什么单位，只要知道这个数量关系就可以了。

而如果你要应用这个公式的话，也是有难度的，因为C这个系数并不像普通公式里的系数一样固定不变，它是随着机翼迎角、机翼形状等因素而变化的，其值也应该由实验测量得出，而不能计算得出。

所以，除非做很严谨的科学研究，应用此公式的现实意义并不大。

Y=1/2ρCSv²C 没有单位.S m²V m/sρ kg/m³（标准状况为：1.297kg/m³）;.。