三视图练习题

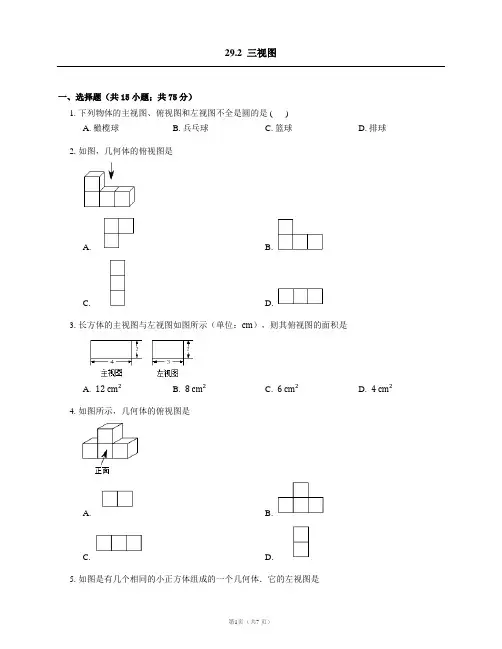
29.2 三视图一、选择题（共15小题；共75分）1. 下列物体的主视图、俯视图和左视图不全是圆的是 ( )A. 橄榄球B. 兵乓球C. 篮球D. 排球2. 如图，几何体的俯视图是A. B.C. D.3. 长方体的主视图与左视图如图所示（单位：cm），则其俯视图的面积是A. 12 cm2B. 8 cm2C. 6 cm2D. 4 cm24. 如图所示，几何体的俯视图是A. B.C. D.5. 如图是有几个相同的小正方体组成的一个几何体．它的左视图是A. B.C. D.6. 如图是由八个相同小正方体组成的几何体，则其主视图是A. B.C. D.7. 桌面上放着1个长方体和1个圆柱体，按下图所示的方式摆放在一起，其左视图是A. B. 与原题图不一样C. D.8. 下列几何体中，有一个几何体的俯视图的形状与其它三个不一样，这个几何体是 ( )A. B.C. D.9. 图中三视图所对应的直观图是A. B.C. D.10. 如图是常用的一种圆顶螺杆，它的俯视图正确的是A. B.C. D.11. 如图的几何体的三视图是A. B.C. D.12. 如图是由一些相同的小正方体搭成的几何体的三视图，则构成这个几何体的小正方体的个数为A. 4个B. 5个C. 6个D. 7个13. 一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是A. B.C. D.14. 一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为．A. 6B. 8C. 12D. 2415. 如图所示是某几何体的三视图，根据图中数据，求得该几何体的体积为A. 60πB. 70πC. 90πD. 160π二、填空题（共6小题；共30分）16. 一个几何体的主视图、俯视图和左视图都是大小相同的圆，则这个几何体是．17. 如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小正方体，王亮所搭几何体表面积为．18. 如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是．19. 由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数可能是．20. 用八个同样大小的小立方体粘成一个大立方体如图 1，得到的几何体的三视图如图 2 所示，若小明从八个小立方体中取走若干个，剩余小立方体保持原位置不动，并使得到的新几何体的三视图仍是图 2，则他取出的小立方体最多可以是个．21. 在桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，设组成这个几何体的小正方体的个数为n，则n的最小值为．三、解答题（共2小题；共26分）22. 如图所示的几何体是由12块棱长为1 cm的正方体堆积而成的．请求出它的表面积．23. 如图，四边形ABCD，将其绕CD所在直线旋转一周得到一个几何体，请画出这个几何体的从正面、左面、上面看到的形状图．答案第一部分1. A2. D3. A4. C5. B6. C7. C8. A9. C 10. B11. C 12. A 13. D 14. B 15. B第二部分16. 球体17. 19；4818. 619. 4或5或6或720. 421. 5第三部分22. (1) 由题意，得S=8×12×2+5×12×2+7×12×2=40．所以它的表面积为40 cm2．23. (1) 如图所示．。

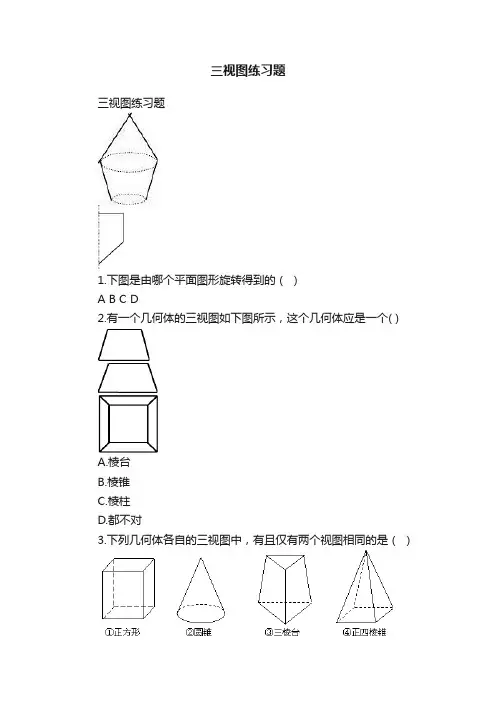
三视图练习题三视图练习题1.下图是由哪个平面图形旋转得到的（）A B C D2.有一个几何体的三视图如下图所示，这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对3.下列几何体各自的三视图中，有且仅有两个视图相同的是（）A ．①②B ．①③C ．①④D ．②④ 4.有一个几何体的三视图及其尺寸如下（单位：cm ），则该几何体的表面积和体积为( )A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cmππ D.以上都不正确5.如左图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h 随时间t变化的可能图象是（）侧视正视图俯视图6.正方体的截平面不可能是(1) 钝角三角形 (2) 直角三角形 (3) 菱形 (4) 正五边形 (5) 正六边形下述选项正确的是：（）(A) (1)(2)(5) (B) (1)(2)(4) (C) (2)(3)(4) (D) (3)(4)(5) 7.如图，在正方体ABCD —A1B1C1D1中，P 为BD1的中点，则△PAC 在该正方体各个面上的射影可能是（）A ．①④B ．②③C ．②④D ．①②8.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为（）俯视图侧视图正视图A.9.一空间几何体的三视图如图所示,则该几何体的体积为( ). A.2π+B. 4π+2π4π+10.如图，是几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）侧(左)视图正(主)视图俯视图A B C D1A 1B 1C 1D P① ③ ④ ②俯视图左视图主视图A ．5B ．6C ．7D ．811.如果一个几何体的三视图如图所示，其中正视图中ABC 是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧视图的面积为 ( )A ．23B ．32C ．12D ．612.用若干个棱长为1的正方体搭成一个几何体，其正视图、侧视图都是如右图形，对这个几何体，下列说法正确的是A ．这个几何体的体积一定是7 B ．这个几何体的体积一定是10C ．这个几何体的体积的最小值是6，最大值是10D ．这个几何体的体积的最小值是7，最大值是11 二、填空题13.如图，,E F 分别为正方体的面11A ADD 、面11B BCC的中心，则四边形E B F D1在该正方体的面上的射影可能是____________。

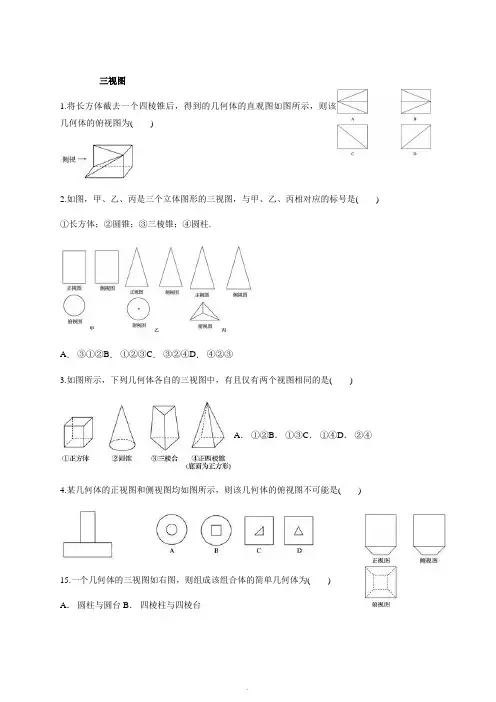
三视图1.将长方体截去一个四棱锥后，得到的几何体的直观图如图所示，则该几何体的俯视图为()2.如图，甲、乙、丙是三个立体图形的三视图，与甲、乙、丙相对应的标号是()①长方体；②圆锥；③三棱锥；④圆柱.A．③①②B．①②③C．③②④D．④②③3.如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④4.某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()15.一个几何体的三视图如右图，则组成该组合体的简单几何体为()A．圆柱与圆台B．四棱柱与四棱台C．圆柱与四棱台D．四棱柱与圆台5.一个长方体截去两个三棱锥，得到的几何体如图所示，则该几何体的三视图为()6.将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的侧视图为()7.如图所示为一个简单几何体的三视图，则其对应的几何体是()8.某几何体的直观图如图所示，下列给出的四个俯视图中正确的是()9.一个几何体的三视图如图所示，则该几何体的直观图可以是()10.如果用□表示1个立方体，用表示2个立方体叠加，用■表示3个立方体叠加，那么图中由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是()11.一个几何体的三视图如图所示，则该几何体的直观图可以是()A．B．C．D．12.下列三视图所对应的直观图是()A．B．C．D．13.下面的三视图对应的物体是()A．B．C．D．14.如图是哪一个物体的三视图()A．B．C．D．16.如图是一个物体的三视图，则此三视图所描述物体的直观图是()A．B．C．D．17.某几何体的三视图如图所示，则这个几何体的直观图是图中的()A．B．C．D．18.空间几何体的三视图如图所示，则此空间几何体的直观图为()A．B．C．D．19.某建筑物的三视图如图所示，则此建筑物结构的形状是()A．圆锥B．四棱柱C．从上往下分别是圆锥和四棱柱D．从上往下分别是圆锥和圆柱20.如图所示为一个简单几何体的三视图，则其对应的几何体是()A．B．C．D．21.已知一个几何体的三视图如图所示，则此几何体的组成为()A．上面为棱台，下面为棱柱B．上面为圆台，下面为棱柱C．上面为圆台，下面为圆柱D．上面为棱台，下面为圆柱22.如图所示为长方体木块堆成的几何体的三视图，此几何体共由________块木块堆成.23.已知某组合体的正视图与侧视图相同(其中AB＝AC，四边形BCDE为矩形)，则该组合体的俯视图可以是图中的________.(把你认为所有正确图象的序号都填上)24.若一个正三棱柱的三视图如图所示，则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.答案解析1.【答案】C【解析】俯视图从图形的上边向下边看，看到一个正方形的底面，在底面上有一条对角线，对角线是由左上角到右下角的线，故选C.2.【答案】D【解析】3.【答案】D【解析】在各自的三视图中①正方体的三个视图都相同；②圆锥有两个视图相同；③三棱台的三个视图都不同；④正四棱锥有两个视图相同.4.【答案】D【解析】根据几何体的三视图知识求解.由于该几何体的正视图和侧视图相同，且上部分是一个矩形，矩形中间无实线和虚线，因此俯视图不可能是D.5.【答案】C【解析】从该几何体可以看出，正视图是一个矩形内有一斜向上的对角线；俯视图是一个矩形内有一斜向下的对角线，没有斜向上的对角线，故排除B、D项；侧视图是一个矩形内有一斜向下的对角线，且都是实线，因为没有看不到的轮廓线，所以排除A项.6.【答案】B【解析】还原正方体后，将D1，D，A三点分别向正方体右侧面作垂线.D1A的射影为C1B，且为实线，B1C被遮挡应为虚线.7.【答案】A【解析】对于A，该几何体的三视图恰好与已知图形相符，故A符合题意；对于B，该几何体的正视图的矩形中，对角线应该是虚线，故不符合题意；对于C，该几何体的正视图的矩形中，对角线应该是从左上到右下的方向，故不符合题意；对于D，该几何体的侧视图的矩形中，对角线应该是虚线，故不符合题意.故选A.8.【答案】B【解析】几何体的俯视图，轮廓是矩形，几何体的上部的棱都是可以看见的线段，所以C，D不正确；几何体的上部中间的棱与正视图方向垂直，所以A不正确.故选B.9.【答案】D【解析】由俯视图是圆环可排除A，B，C，进一步将三视图还原为几何体，可得选项D.10.【答案】B【解析】结合已知条件易知B正确.11.【答案】D【解析】由俯视图可知，原几何体的上底面应该是圆面，由此排除选项A和选项C.而俯视图内部只有一个虚圆，所以排除B.故选D.12.【答案】C【解析】从俯视图可以看出直观图的下面部分为长方体，上面部分为圆柱，且与下面的长方体的顶面的两边相切，由侧视图可以看出上下部分高度相同．只有C满足这两点，故选C.13.【答案】D【解析】从俯视图可以看出直观图的下面部分为三个长方体，且三个长方体的宽度相同．只有D 满足这两点，故选D.14.【答案】C【解析】经分析可知，该物体应该是一个圆柱竖直放在一个长方体上，A中的不是一个圆柱，故排除．B中的圆柱直径小于长方体的宽．D项中上面不是一个圆柱体．故选C.15.【答案】B【解析】由已知中的三视图可得该几何体是一个组合体，由几何体上部的三视图均为矩形可知上部是四棱柱，由下部的三视图中有两个梯形可得下部为四棱台，故组成该组合体的简单几何体为四棱柱与四棱台，故选B.16.【答案】D【解析】正视图和侧视图相同，说明组合体上面是锥体，下面是正四棱柱或圆柱，由俯视图可知下面是圆柱．故选D.17.【答案】B【解析】由正视图可排除A，C选项；由侧视图可排除D选项，综合三视图可得，B选项正确．故选B.18.【答案】A【解析】由已知中三视图的上部分是锥体，是三棱锥，满足条件的正视图的选项是A与D，由侧视图可知，选项D不正确，由三视图可知该几何体下部分是一个四棱柱，选项都正确，故选A. 19.【答案】C【解析】由图可得该几何体是一个组合体，其上部的三视图有两个三角形，一个圆，故上部是一个圆锥，其下部的三视图均为矩形，故下部是一个四棱柱．故选C.20.【答案】A【解析】对于A，该几何体的三视图恰好与已知图形相符，故A符合题意；对于B，该几何体的正视图的矩形中，对角线应该是虚线，故不符合题意；对于C，该几何体的正视图的矩形中，对角线应该是从左上到右下的方向，故不符合题意；对于D，该几何体的侧视图的矩形中，对角线应该是虚线，故不符合题意．故选A.21.【答案】C【解析】结合图形分析知上为圆台，下为圆柱．故选C.22.【答案】4【解析】由三视图知，由4块木块组成.如图.23.【答案】①②③④【解析】由正视图和侧视图可知几何体为锥体和柱体的组合体.(1)若几何体为圆柱与圆锥的组合体，则俯视图为③；(2)若几何体为棱柱与圆锥的组合体，则俯视图为④；(3)若几何体为棱柱与棱锥的组合体，则俯视图为①；(4)若几何体为圆柱与棱锥的组合体，则俯视图为②.24.【答案】28√33【解析】25.【答案】三视图对应的几何体如下图所示.【解析】。

小学三视图练习题### 小学三视图练习题一、选择题1. 下列哪个选项是正确的主视图？A. 从物体的左侧观察得到的视图B. 从物体的右侧观察得到的视图C. 从物体的正面观察得到的视图D. 从物体的背面观察得到的视图2. 侧视图是从哪个方向观察物体得到的？A. 正面B. 背面C. 左侧D. 右侧3. 俯视图是从哪个方向观察物体得到的？A. 从物体的上方B. 从物体的下方C. 从物体的侧面D. 从物体的正面二、填空题4. 观察一个长方体的三视图，主视图显示的是长方体的______面和______面。

5. 当物体被放置在水平面上时，其______视图通常显示物体的底部。

三、判断题6. 三视图包括主视图、侧视图和俯视图。

（）7. 所有物体的主视图都是从物体的正面观察得到的。

（）四、简答题8. 请简述什么是三视图，并说明它们各自的特点。

五、绘图题9. 根据题目提供的长方体的三视图，绘制出该长方体的立体图。

六、应用题10. 假设你有一个正方体的盒子，其边长为10厘米。

请根据正方体的三视图，计算出正方体的体积。

七、实践题11. 请用纸板制作一个简单的立方体，并从三个不同的方向观察它，记录下你观察到的三视图。

八、分析题12. 观察一个圆柱体的三视图，分析并描述主视图、侧视图和俯视图所展示的圆柱体的特征。

九、综合题13. 假设你面前有一个由多个几何体组成的复杂物体，请尝试从三个不同的方向观察它，并绘制出相应的三视图。

十、创新题14. 设计一个简单的几何体，并为其绘制三视图。

在设计时，考虑如何通过三视图来最有效地传达该几何体的形状和尺寸。

请根据上述题目进行作答，注意审题并合理运用三视图的相关知识。

祝你练习愉快！。

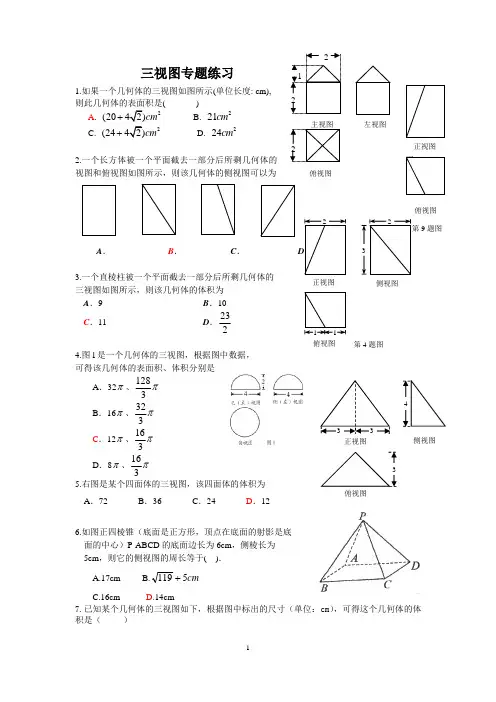
三视图专题练习1.如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是()A . 2(20cm + B. 221cm C. 2(24cm + D. 224cm2.一个长方体被一个平面截去一部分后所剩几何体的视图和俯视图如图所示，则该几何体的侧视图可以为A ．B ． C．3.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则该几何体的体积为 A ．9 B ．10 C ．11 D ．2324.图l 是一个几何体的三视图，根据图中数据， 可得该几何体的表面积、体积分别是A ．32π、1283π B ．16π、323π C ．12π、163πD ．8π、163π5.右图是某个四面体的三视图，该四面体的体积为 A ．72 B ．36 C ．24 D ．126.如图正四棱锥（底面是正方形，顶点在底面的射影是底 面的中心）P-ABCD 的底面边长为6cm ，侧棱长为 5cm ，则它的侧视图的周长等于( )．A.17cmB.cm 5119+C.16cmD.14cm7.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ ）1 1 正视图侧视图俯视图第4题图正视图俯视图9题图俯视图 左视图俯视图侧视图正视图图1Ａ．34000cm 3 Ｂ．38000cm 3Ｃ．32000cm Ｄ．34000cm 8.如右图，已知一个锥体的正（主）视图，侧（左）视图和 俯视图均为直角三角形，且面积分别为3，4，6，则该锥体的体积为A ．24B ．8C ．12D ．49.已知某个几何体的三视图如图2所示，根据图中标出的 尺寸（单位：cm ），则这个几何体的体积是( ). A. 38cm B . 312cm C. 324cm D. 372cm10.已知四棱锥P ABCD -的三视图如图1所示， 则四棱锥P ABCD -的四个侧面中面积最大的是 A ．3 B．C ．6 D ．811.若某一几何体的正视图与侧视图均为边长是1的正方形，且其体积为12，则该几何体的俯视图可以是（ ）12.如图所示，一个空间几何体的主视图和左视图都 是边长为1的正方形，俯视图是一个直径为1的圆， 那么这个几何体的全面积为A.4π B. 2π C.3πD.32π13.一个几何体的三视图如图所示，则该几何体的体积为（ ）A 、2B 、1C 、23D 、13第3题图主视图左视图俯视图正视图侧视图俯视图正(主)视图 侧(左)视图14.如图，网格纸上小正方形的边长为1则此几何体的体积为（） A.6 B 9 C.12D.1815.若一个几何体的三视图如图所示，则此几何体的体积为 A ．112B.5C.4 D . 9216.某几何体的正视图和侧视图均如图1所示， 则该几何体的俯视图不可能．．．是17.某几何体的三视图如图1所示，它的体积为A. 72πB. 48π C . 30π D. 24π18.已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是A.1cm 3B.2cm 3 C .3cm 3 D.6cm 319.某三棱锥的三视图如图所示，该三棱锥的表面积是（A ）28+B ）30+C ）56+D ）60+20.将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体， 则该几何体的左视图为 （ ）图1正视图 俯视图侧视图21.已知正三棱柱（侧棱与底面垂直，底面是正三角形）的高与底面边长均为2，其直观图和正(主)视图如下，则它的左(侧)视图的面积是 ．22.若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为__________．23.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积．．．等于24.某几何体的三视图如图所示，且该几何体的体积为3，则正视图中的x ＝＿＿＿＿25.已知某几何体的三视图如图所示，则该几何体的体积为____________.26.一个几何体的三视图如图所示，则该几何体的体积为_______________.27.一个几何体的三视图如图所示（单位：m ）,则该几何体的体 积 3m .28.某几何体的三视图如图所示，则该几何体的体积等于______。

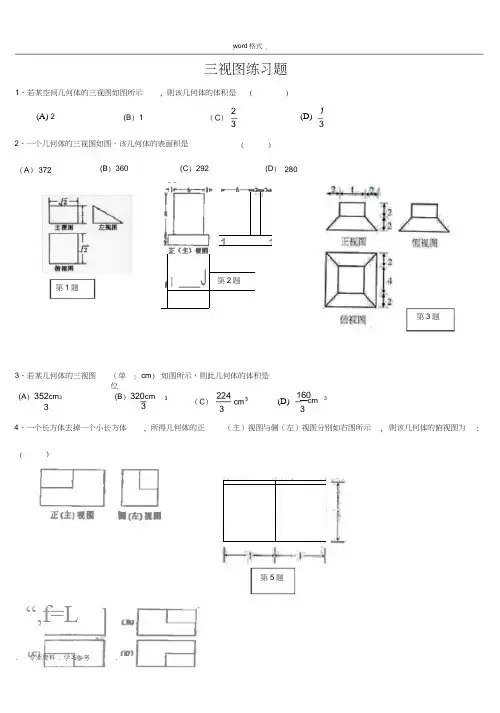
word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题（单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2（主）视图与侧（左）视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示，则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图，该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示，则其侧.面积等于（A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h=7、 一个几何体的三视图如图所示 ，则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图（也称主视图）是（）8、如图，网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形，)S 2a.俯视图正（主）视图侧（左）视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示，则该几何体的体积为（）.A.2 2.3B. 4 2 . 3侧（左）视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积（单位：c m2）为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。

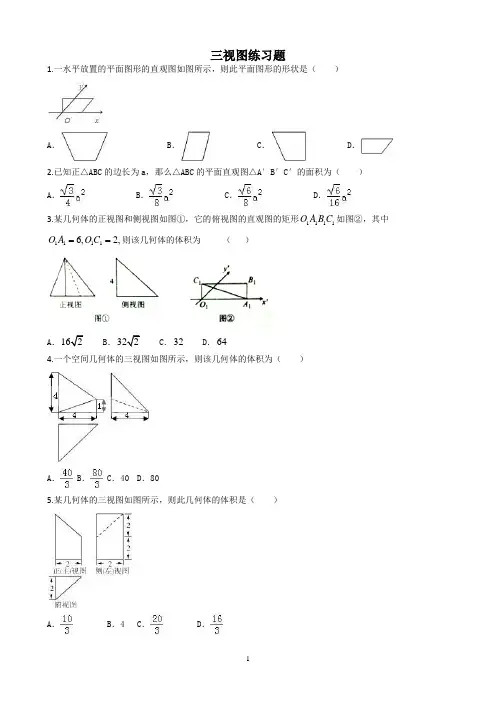
三视图练习题1.一水平放置的平面图形的直观图如图所示，则此平面图形的形状是（ ）A ．B ．C ．D ．2.已知正△ABC 的边长为a ，那么△ABC 的平面直观图△A′B′C′的面积为（ ）A ．B ．C ．D ．3.某几何体的正视图和侧视图如图①，它的俯视图的直观图的矩形1111O A B C 如图②，其中11116,2,O A O C ==则该几何体的体积为 （ ）A ．162B ．322C ．32D ．644.一个空间几何体的三视图如图所示，则该几何体的体积为（ ）A ．B ．C ．40D ．805.某几何体的三视图如图所示，则此几何体的体积是（ ）A ．B ．4C ．D ．6.一个几何体的三视图如图2所示(单位：cm)，则该几何体的体积是（A ）2333cm （B ）2233cm （C ）4763cm （D ）73cm7.在如图所示的空间直角坐标系O xyz 中，一个四面体的顶点坐标分别是（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为① ② ③ ④A ．①和② B．③和① C．③和④ D．④和② 8.如图为某几何体的三视图，则该几何体的表面积为（ ） A ．10+B ．10+C ．6+2+D ．6++9.多面体的三视图如图所示，则该多面体的表面积为（单位：cm ）（ ）A ．28+4B ．30+4C ．30+4D ．28+4xy． ． 1 1O ． ． ． ． z21 2 210.某四面体的三视图如图所示，该四面体四个面的面积中最大的是()A．8B．62C．10D．8211.某多面体的三视图如图所示，则该多面体各面的面积中最大的是（）A．1 B．C．D．12.如图，在正方体ABCD﹣A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P﹣BCD的正视图与侧视图的面积之比为（）A．1：1 B．2：1 C．2：3 D．3：213.三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（）A．2B．4C．D．16cm.14.某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是215.一个几何体的三视图如图所示，其中主视图、俯视图与左视图均是半径为2的圆，则这个几何体的表面积是．16.某空间几何体的三视图（单位：cm）如图所示，则其体积是cm3，其侧视图的面积是cm2．三视图练习图答案1.C2.D 解：∵正△ABC 的边长为a ，∴正△ABC 的高为，画到平面直观图△A′B′C′后，“高”变成原来的一半，且与底面夹角45度，∴△A′B′C′的高为=，∴△A′B′C′的面积S==．3.B4.A解：由三视图知：几何体为其中一个侧面在下面的四棱锥，如图：其中SA ⊥平面ABCD ，SA=4，底面ABCD 为直角梯形，且AD=4，BC=1，AB=4， ∴几何体的体积V=××4×4=． 5.C解：由已知中的三视图，可得该几何体是由三棱柱截得的，如图所示， 故体积V==，6.A该几何体是棱长为2的正方体1111ABCD A B C D -截去一个三棱锥1C B EF -后所得的多面体，其体积为1123222112323V =⨯⨯-⨯⨯⨯⨯=7.D 8.C解：由三视图可知：该几何体为一个四棱锥，如图所示，CD⊥底面PAD ，BA⊥底面PAD ，PA⊥AD，PA=AD=CD=2，AB=1．PC=2，PB=，BC=．∴S △PBC ==．该几何体的表面积S=++++=6+．9.A解：如图所示，由三视图可知：该几何体为三棱锥P﹣ABC．其中平面PAB⊥平面ABC，PB⊥AB，PB=AB=4，D为AB的中点，CD⊥AB，CD=4．∴该多面体的表面积S=+++=28+4．10.C【试题解析】因为如图为原几何体的直观图，面积中最大的是,故答案为：C11.C解：由三视图可知该几何体为底面为正方形的四棱锥P﹣ABCD，P在底面的投影E在DA的延长线上，且PE=AE=AD=CD=1，∴S△PAD==，S底面ABCD=1×1=1，PA==，PD==，PF==，∴S△PCD==，S△PAB==．S△PBC==．∴在四棱锥的五个面中，△PCD的面积最大．故选C．12.A 解：由题意可知，P 在主视图中的射影是在C 1D 1上，AB 在主视图中，在平面CDD 1C 1上的射影是CD ，P 的射影到CD 的距离是正方体的棱长； P 在左视图中，的射影是在B 1C 1上，在左视图中AC 在平面BCC 1B 1三度射影是BC ，P 的射影到BC 的距离是正方体的棱长， 所以三棱锥P ﹣ABC 的主视图与左视图的面积的比值为：：=1：1，故选：A13.B 解：由已知中的三视图可得SC⊥平面ABC ，且底面△ABC 为等腰三角形， 在△ABC 中AC=4，AC 边上的高为2，故BC=4， 在Rt△SBC 中，由SC=4，可得SB=4，14.π)2132(6++15.17π解：由三视图知：几何体是球体切去后余下的部分，∵球的半径为2，∴几何体的表面积S=（1﹣）×4π×22+π×22=17π． 故答案为：17π． 16.4,.解：∵根据三视图得出：该几何体是三棱锥，AB=2，BC=3，DB=5，CD=4， AB⊥面BCD ，BC⊥CD， ∴其体积：S △CBD ×AB==4，△BCD 边BD 的高为==侧视图的面积：×2=。

中考三视图练习题一、选择题1. 下列哪个选项是物体的主视图？A. 侧视图B. 俯视图C. 正视图D. 斜视图2. 在三视图中，下列哪个视图反映了物体的高度？A. 主视图B. 侧视图C. 俯视图D. 都不反映3. 下列哪个视图能够反映物体的长度和宽度？A. 主视图B. 侧视图C. 俯视图D. 都能反映二、填空题1. 三视图包括________、________和________。

2. 在主视图中，物体的长度和________可以清晰地表示出来。

3. 在侧视图中，物体的高度和________可以清晰地表示出来。

三、判断题1. 三视图中，主视图、侧视图和俯视图的长度比例相同。

（）2. 侧视图和俯视图的投影方向必须相互垂直。

（）3. 三视图中，主视图和俯视图的高度比例相同。

（）四、作图题物体形状：一个长方体，长为8cm，宽为6cm，高为4cm。

主视图：一个长方形，长为10cm，高为6cm。

侧视图：一个长方形，长为10cm，高为8cm。

俯视图：一个正方形，边长为5cm。

侧视图：一个长方形，长为7cm，高为5cm。

五、综合题1. 给出一个长方体，长为12cm，宽为8cm，高为6cm。

请分别画出其主视图、侧视图和俯视图。

2. 给出一个圆柱体，底面直径为10cm，高为15cm。

请分别画出其主视图、侧视图和俯视图。

3. 给出一个圆锥体，底面直径为8cm，高为12cm。

请分别画出其主视图、侧视图和俯视图。

六、应用题1. 一个物体的主视图是一个边长为6cm的正方形，侧视图是一个长方形，长为6cm，高为8cm。

请描述这个物体的可能形状，并画出其俯视图。

2. 一个物体的俯视图是一个直径为10cm的圆，侧视图是一个长方形，长为12cm，高为10cm。

请画出该物体的主视图，并推测物体的实际形状。

3. 一个物体的主视图和侧视图都是相同大小的正方形，边长为5cm。

请画出该物体的俯视图，并说明物体的可能形状。

七、分析题主视图：一个长方形，长为10cm，宽为6cm。

四年级数学三视图练习题三视图是在工程制图中常用的表示物体外观的方法，通过绘制物体的正视图、左视图和顶视图，可以清晰地展示物体的形状和结构。

对于四年级的学生来说，掌握三视图的绘制方法是非常重要的。

本文将介绍一些常见的四年级数学三视图练习题，帮助学生巩固相关知识。

练习题一：绘制物体的正视图和左视图请根据下面给出的物体的三视图图纸绘制物体的正视图和左视图。

（插入题目一的图纸图片）（插入题目一的答案图片）练习题二：根据三视图确定物体形状请根据下面给出的物体的三视图图纸，确定物体的形状并回答问题。

（插入题目二的图纸图片）问题一：物体的底面是什么形状？答：根据顶视图可以得知物体的底面是一个矩形。

问题二：物体的高度是多少？答：根据左视图可以测量得知物体的高度为5厘米。

练习题三：根据物体外部条件确定三视图请根据下面给出的物体的正视图和左视图，确定物体的外部条件并回答问题。

（插入题目三的正视图和左视图图片）问题一：物体的底面是否有孔洞？答：根据正视图可以看到物体底面有一个圆形孔洞。

问题二：物体的宽度是多少？答：根据左视图可以看到物体的宽度为6厘米。

练习题四：绘制物体的三视图请根据下面给出的物体的外部条件绘制物体的三视图。

物体的外部条件：底面是一个正方形，边长为3厘米；高度为4厘米。

（插入题目四的外部条件图片）（插入题目四的三视图答案图片）通过以上练习题，希望同学们能够掌握基本的三视图绘制方法，并能够根据给定的三视图进行问题的解答。

在实际生活中，工程制图和三视图的应用非常广泛，掌握这些知识对同学们的未来学习和职业发展都将有很大的帮助。

希望同学们能够认真练习，提高自己的数学素养。

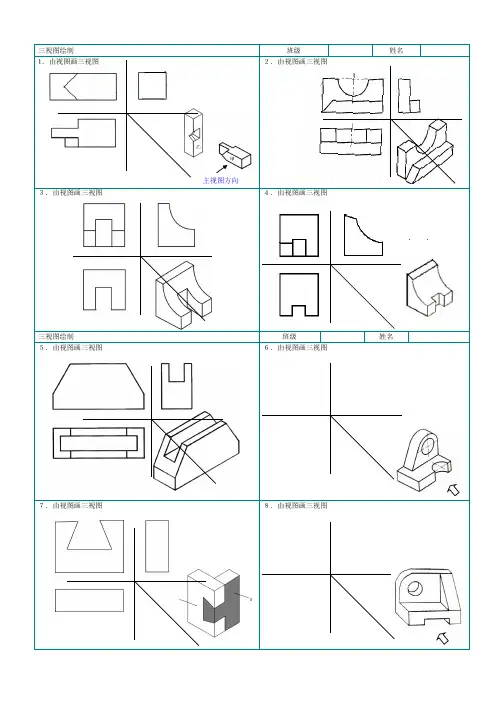
主视图方向３．由视图画三视图４．由视图画三视图三视图绘制班级姓名５．由视图画三视图６．由视图画三视图７．由视图画三视图８．由视图画三视图３．由视图画三视图４．由视图画三视图三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线3．添加所缺的三条线4．添加所缺的三条线5．添加所缺的三条线6．添加所缺的三条线7．添加所缺的三条线8．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线３．添加所缺的三条线４．添加所缺的三条线三视图绘制班级姓名５．添加所缺的三条线６．添加所缺的三条线７．添加所缺的三条线８．添加所缺的三条线。

三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为 。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

三视图练习题六年级在学习图学的过程中，三视图是一个非常重要的概念。

通过观察物体的正视图、侧视图和俯视图，我们可以更好地理解和描述物体的形状和结构。

本文将为六年级的学生提供一些三视图练习题，帮助他们加深对三视图的理解和运用。

练习题一：绘制三视图请你根据下面的描述，用适当比例绘制物体的三视图。

物体描述：这个物体是一个立方体，所有的边长都相等。

正视图上，你能看到正方形的轮廓，左上角有一个小正方形，表示开放的一面。

侧视图上，你能看到一个竖直方向的线段，表示物体的高度。

俯视图上，你能看到一个水平方向的线段，表示物体的宽度。

练习题二：识别物体下面是三个物体的正视图、侧视图和俯视图，请你根据给出的视图，识别物体的形状并写下对应的名称。

正视图：（图片描述）侧视图：（图片描述）（图片描述）练习题三：推测三视图下面是一个物体的正视图和侧视图，请你根据这两个视图，推测物体的俯视图，并画出来。

正视图：（图片描述）侧视图：（图片描述）练习题四：绘制三视图（进阶）请你使用适当比例，根据下面的描述绘制物体的三视图。

物体描述：这个物体是一个长方体，长边是短边的2倍。

正视图上，你能看到一个长方形的轮廓，短边朝向左侧。

侧视图上，你能看到一个竖直方向的线段，表示物体的高度。

俯视图上，你能看到一个水平方向的线段，表示物体的宽度。

练习题五：识别物体（进阶）下面是三个物体的三视图，请你根据给出的视图，识别物体的形状并写下对应的名称。

（图片描述）侧视图：（图片描述）俯视图：（图片描述）练习题六：推测三视图（进阶）下面是一个物体的正视图和俯视图，请你根据这两个视图，推测物体的侧视图，并画出来。

正视图：（图片描述）俯视图：（图片描述）以上是六年级的三视图练习题，希望对你们的学习有所帮助。

通过练习，相信你们能够更加熟练地观察和绘制物体的三视图，提高对图学的理解和运用能力。

加油！。

立体图形三视图练习一．操作题1．下面立体图形从上面、前面和左面看到的图形分别是什么？画一画。

2．动手实践，操作应用。

分别画出从正面、上面、左面看到的立体图形的形状。

3．分别画出下面三个物体从前面、上面和左面看到的图形。

4．把从正面、上面和左面看到的形状分别画出来。

5．在方格纸上画出从正面、左面和上面看到的图形。

6．下面的图形从上面，左面和正面看到的分别是什么形状？请画在方格纸上。

7．如图是由8个同样大小的正方体摆成的几何体，请在方格纸中画出从正面、左面和上面看到的图形。

8．画图题。

9．下列立体图形从上面、正面和左面看到的形状分别是什么？画一画。

10．在方格纸上画出从不同位置看到的图形。

11．在方格图中分别画出右边两个几何体从前面和左面看到的图形。

12．分别画出从前面、上面和左面看到的图形。

13．分别画出如图所示的立体图形从前面，左面和上面看到的形状。

14．分别画出从正面、上面、右面看到的立体图形的形状。

15．分别画出下面这个立体图形从正面、左面、上面看到的图形。

16．画出如图从前面、上面和左面看到的图形。

17．在方格纸上画出右上图从上面、左面和前面看到的平面图形。

18．下面的物体分别从正面、左面、上面看到的形状分别是什么？请你在方格纸上画出来。

19．动手实践，操作应用。

分别画出下图从正面、左面、上面看到的图形。

20．把下面的几何体从正面、上面、左面观察到的图形在方格纸上画出来。

21．在方格纸上分别画出下面物体从前面、上面、左面看到的图形。

22．分别画出下面立体图形从不同位置观察到的图形。

三视图作图试题及答案大全三视图作图是工程制图和设计领域中的一项基本技能，它要求学生能够根据物体的三个不同方向（通常是正视图、侧视图和俯视图）来理解和构建三维物体。

以下是一些三视图作图的试题及答案，供学生练习和参考。

试题 1题目：根据所给的正视图和侧视图，绘制出俯视图。

正视图：```AB| |CD```侧视图：```E/|FG D| |H CA B```答案：俯视图```EF| |GH```试题 2题目：根据所给的俯视图和侧视图，绘制出正视图。

俯视图：```12| |34```侧视图：```1/ |23 4\ |56```答案：正视图```56| |34```试题 3题目：根据所给的正视图和俯视图，绘制出侧视图。

正视图：```AB| |CD```俯视图：```AB| |CD| |EF```答案：侧视图```A/|BC D| |E F```试题 4题目：绘制一个长方体的三视图。

答案：- 正视图：```I/ |GH| |JK```- 侧视图：```I/ \GL\H\K```- 俯视图：```IG| |JH```试题 5题目：根据所给的俯视图和侧视图，绘制出正视图。

俯视图：```12| |34```侧视图：```1/ \2 3\ /4```答案：正视图```23| |14```请注意，这些试题和答案仅供参考，实际的三视图作图可能需要根据具体的物体形状和视角进行调整。

在实际应用中，三视图作图需要结合物体的实际尺寸和比例，以及可能的对称性和几何关系来进行绘制。

29.2 三视图一、单选题（共20题；共40分）1.如图，由五个完全相同的小正方体组合成一个立体图形，它的俯视图是（）A. B. C. D.2.如图，在长方体的数学课本上放有一个圆柱体，则它的主视图为（）A. B.C. D.3.如图是由5个小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是（）A. B. C. D.4.如图，一个由圆柱和长方体组成的几何体水平放置，它的俯视图是（）A. B. C. D.5.右边几何体的左视图是（）A. B. C. D.6.如图所示的工件，其俯视图是（）A. B. C. D.7.如图的几何体是由五个同样大小的正方体搭成的，其主视图是（）A. B. C. D.8.一个立体图形的三视图如图所示，则该立体图形是（）A. 圆柱B. 圆锥C. 长方体D. 球9.如图几何体是由6个大小完全一样的正方体组合而成的，它的俯视图是（）A. B. C. D.10.下列四个几何体:其中左视图与俯视图相同的几何体共有（）A. 1个B. 2个C. 3个D. 4个11.用4个完全相同的小正方体组成如图所示的立体图形，它的主视图是（）A. B. C. D.12.下列立体图形中，主视图是圆的是（）A. B. C. D.13.如图，水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒，俯视图是（）A. B. C. D.14.如图是由几个大小相同的小正方体搭成的几何体的俯视图，小正方形中的数字表示该位置上小正方体的个数，则该几何体的左视图是（）A. B. C. D.15.如图竖直放置的圆柱体的俯视图是（）A. 长方体B. 正方体C. 圆D. 等腰梯形16.如图，是由一个圆柱体和一个长方体组成的几何体，其俯视图是（）A. B. C. D.17.图中所示的几何体的左视图是（）A. B. C. D.18.下列几何体中，左视图与主视图不相同的只可能是（）A. B. C. D.19.桌面上放置的几何体中，主视图与左视图可能不同的是（）A. 圆柱B. 正方体C. 球D. 直立圆锥20.下列几何体中，俯视图是矩形的是（）A. B. C D.二、填空题（共20题；共27分）21.从正面看，从左面看，从上面看都一样的几何体可能是________。