§5.6 二次曲线方程的化简与分类

一般二次曲面方程的化简与分类研究[摘 要]本文通过对一般二次曲面方程进行化简与分类,化简成五类方程和17种标准形式.最后介绍了一般二次曲面方程分类与化简的应用.[关键词]二次曲面;分类;化简;应用１ 引言对于给定的二次曲面方程,通过特征方程可求出它所对应的主方向.由于二次曲面的每个特征根至少对应一个主方向,也就是说二次曲面至少有一个主径面,而二次曲面的主径面又是二次曲面的对称面,因而选取主径面作为新坐标面,或者选取主方向作为坐标轴方向,就成为化简二次曲面方程的主要方法.2 预备知识定义 2.1[3]果二次曲面的径面垂直于它所共轭的方向,那么这个径面就叫做二次曲面的主径面.显然主径面就是二次曲面的对称面.定义 2.2[4]二次曲面主径面的共轭方向（即垂直于主径面的方向）,或者二次曲面的奇向,叫做二次曲面的主方向.引理 2.1[5]二次曲面平行于非渐近方向的一族平行弦中点的轨迹是一个平面.其方程为1234(,,)(,,)(,,)(,,)0X Y Z x X Y Z y X Y Z z X Y Z φφφφ+++=. (1)注1：二次曲面沿非渐近方程::X Y Z 的所有平行弦中点所在的平面叫做平面共轭于非渐进方向::X Y Z 的径面,而平行弦叫做这个径面的共轭弦.注2：如果二次曲面的径面垂直于它所共轭的方向,那么这个径面就叫做二次曲面的主径面.实际上,主径面垂直于所平分的一组弦,是二次曲面的对称平面. 引理2.2 二次曲面的特征方程为1112131322231323330a a a a a a a a a λλλ--=- 即321230I I I λλλ-+-+=.其中λ是二次曲面的特征根.引理2.3 一般二次曲面的主方向方程组()()()1112131222231323330,0,0.a X a Y a Z a X a Y a Z a X a Y a Z λλλ-++=⎧⎪+-+=⎨⎪++-=⎩ 其中::X Y Z 是二次曲面(2)的非渐近方向.引理2.4 空间直角坐标变换设在空间给定了两个由标架{};;;o i j k 与{}'''';;;o i j k 决定的右手直角坐标系,前面一个叫做旧坐标系,后面的一个叫做新坐标系.它们之间的位置关系完全可由新坐标系的原点'o 在旧坐标系内的坐标,以及新坐标系的坐标矢量在旧坐标系内的分量所决定.2.4.1移轴设'o 在旧坐标系下的坐标为{}000,,x y z ,p 为空间任意一点,它在{};;;o i j k 与{}'''';;;o i j k 下的坐标分别是{},,x y z 与{}''',,x y z .其中移轴表换公式为'0'0'0x x x y y y z z z ⎧=+⎪=+⎨⎪=+⎩, 移轴公式为'0'0'x x x y y y z z z ⎧=-⎪=-⎨⎪=-⎩.转轴经过转轴变换后,新旧坐标轴间的交角如下表所示其中转轴变换公式为：'''123'''123'''123cos cos cos ,cos cos cos ,cos cos cos .x x y z y x y z z x y z αααβββγγγ⎧=++⎪=++⎨⎪=++⎩, 其中转轴逆变换公式为：'111'222'333cos cos cos ,cos cos cos ,cos cos cos .x x y z y x y z z x y z αβγαβγαβγ⎧=++⎪=++⎨⎪=++⎩ 3 二次曲面方程的化简定理 以三个主方向所建立的右手直角坐标系为新坐标系而作坐标轴的旋转，那么曲面方程222112233121323142434442222220a x a y a z a xy a xz a yz a x a y a z a +++++++++=.(2)在新坐标系中具有如下形式：''2''2''2'''''''112233142434442220a x a y a z a x a y a z a ++++++=. (3)证明 因为二次曲面至少有一个非奇主方向，以这个主方向作为新轴方向，以共轭于这个方向的主径面作为新坐标平面'0x =，建立直角坐标系''''o x y z -，设在这个新坐标系下，曲面的方程为''2''2''2'''''''''''''''112233121323142434442222220a x a y a z a x y a x z a y z a x a y a z a +++++++++=.在新坐标系下,曲面以'x 轴方向作为主方向1:0:0,代入式（1）,得与之共轭的主径面方程为'''''''111213140a x a y a z a +++=.那么这个方程表示坐标平面'0x =的充要条件是''''111213140,0a a a a ≠===.所以曲面在新坐标系下的方程为''2''2''2'''''''''11223323243444112220(0)a x a y a z a y z a y a z a a ++++++=≠.如果'230a =,那么有''2''2''2''''''11223324344411220(0)a x a y a z a y a z a a +++++=≠.如果'230a ≠,可在'''y o z 平面内,将y 轴与z 轴旋转一角度θ（保持x 轴不动）,并且适合''2233'23cot 22a a a θ-=,即经直角坐标变换'''''''''''''cos sin sin cos x x y y z z y z θθθθ⎧=⎪=-⎨⎪=+⎩, 就可使yz 项系数也等于零,从而得到''''2''''2''''2''''''''''''''112233142434442220a x a y a z a x a y a z a ++++++=.由定理可知,经过适当的坐标变换,二次曲面（2）总可以化为''2''2''2''''''''11223314243444112220(0)a x a y a z a x a y a z a a ++++++=≠.4 二次曲面方程的分类下面对(3)中系数的所有可能情形加以讨论.4.1 若'22a 和'33a 都不为零,作移轴变换'''''''24'22''''34'33x xa y y a a z z a ⎧⎪=⎪⎪⎪=-⎨⎪⎪⎪=-⎪⎩,则方程(3)可化为(I ) ''''2''''2''''2''112233440a x a y a z a +++= 4.2 若'22a 和'33a 中有一个为零,不妨假设'330a =,'220a ≠,则方程（3）化为 ''2''2''''''1122243444220a x a y a y a z a ++++=. (4) ① 若'340a ≠,作移轴变换'''''''24'22'''2'''224424''22342x x a y y a a a a z z a a ⎧⎪=⎪⎪⎪=-⎨⎪⎪-⎪=-⎪⎩, 则方程(4)化为(II ) '''2'''2''''11223420a x a y a z ++=② 若'340a =,作移轴变换'''''''24'22,x x a y y a ⎧=⎪⎨=-⎪⎩, 方程(4)化为(III ) '''2'''211220a x a y c ++=若'24a 和'34a 都为零,则方程（3）化为''2'''''11243444220a x a y a z a +++= (5)③ 若'24a 和'34a 不全部为零,因平面'''''243444220a y a z a ++=.与坐标平面'0x =垂直,则利用坐标变换''''''''''x x y ⎧=⎪⎨=⎪⎩使这个平面作为新坐标平面'0y =,此时方程（5）化为(IV ) '''2'''112420a x a y +=.④ ''24340a a ==,则方程（5）化为 (V ) '''2'11440a x a +=.综合以上的讨论,二次曲面方程（1）经过直角坐标变换总可以化为以下五种形式之一：(I ) 2220Ax By Cz D +++= （0ABC ≠）;(II ) 2220Ax By Pz ++= （0ABP ≠）; (III ) 220Ax By E ++= （0AB ≠）; (IV ) 220Ax QY += （0AQ ≠）; (V ) 20Ax R += （0A ≠）;这同中心分类是一致的.下面对二次曲面(1)的五种形式中的每一个就系数可能出现的情况作进一步的讨论,以便得出二次曲面的详细分类.5 二次曲面标准形式分类5.1 在方程(I )中, 若0D ≠,把方程(I )的两端除以D 并令222111,,,A B C D a D b D c=±=±=±其中正负号的选取使,,a b c 都是实数. ① 若,,A B C 同号,但与D 异号,则方程(I )化为2222220x y z a b c++=. (6)它表示椭球面.②,,,A B C D 都同号，则得22222x y z a b+=±. (7)它表示虚椭球面.③ 若,,A B C 中有两个同号,且D 与另一个同号,则得22222x y z a b-=±. (8)它表示单叶双曲面.④ 中有两个同号,且D 与这两个同号,则得22221x y a b+=. (9)它表示双叶双曲面.5.2 在方程(I )中,若0D =,在方程(I )中,令222111,,A B C a b c =±=±=±. ① 若,,A B C 中有两个同号,则方程(I )化为2222220x y z a b c+-=. (10) 它表示二次锥面.② 若,,A B C 同号,则得2222220x y z a b c++=. (11)它表示虚二次锥面由此可知,中心型二次曲面有且仅有六种. 5.3 在方程(II )中,令2211,A B P a P b=±=±. ① 若,A B 同号,则得22222x y z a b+=±. (12)它表示椭圆抛物面.② 若,A B 异号,则得22222x y z a b-=±. (13)它表示双曲抛物面.5.4 在方程(III )中,若0E ≠,令2211,A B E a E b=±=±. ① 若,A B 同号,且与E 异号,则得22221x y a b+=. (14) 它表示椭圆柱面.② 若,A B 同号,且与E 同号,则得22221x y a b+=-. (15) 它表示虚椭圆柱面.③ 若,A B 异号,则得22221x y a b-=±. (16)它表示双曲柱面.5.5 在方程(III )中,若0E =① 若,A B 异号,则得22220x y a b-=. (17) 它表示一对相交平面. ② 若,A B 同号,则得22220x y a b+=. (18) 它表示一对虚相交平面或z 轴.5.6 方程(IV )可以化为22x py =. (19) 它表示抛物柱面.5.7 在方程(V ) (ⅴ)中,若0R ≠① 若,A R 异号,则得220x a -=. (20) 它表示一对平行平面.② 若,A R 同号,则得220x a +=. (21) 它表示一对虚平行平面.5.8 在方程(V )中,若0R =,则得20x =. (22) 它表示一对重合平面.由上可知,非中心型二次曲面有且仅有11种.综上所述,一般二次曲面(2)经过坐标变换,总可以简化成十七种标准方程中的一种.6 二次曲面方程的化简与应用例1 化简二次曲面方程2225622666100x y z xy xz yz x y z ++--+-+-+=.解 二次曲面的矩阵为13133113115333310---⎛⎫ ⎪- ⎪ ⎪-- ⎪--⎝⎭, 1237,0,36I I I ===-,所以曲面的特征方程为327360λλ-+-=,即 (6)(3)(2)0λλλ--+=, 因此二次曲面的三特征根为6,3,2λ=-.(1) 与特征根6λ=对应的主方向::X Y Z 由方程组530,350,0X Y Z X Y Z X Y Z ---=⎧⎪--+=⎨⎪-+-=⎩决定,所以对应于特征根6λ=主方向为::X Y Z =311553::511335----------=8:8:161:1:2-=-, 与它共轭的主径面为20x y z -++=.(2) 与特征根3λ=对应的主方向::X Y Z 由方程组230,320,20X Y Z X Y Z X Y Z ---=⎧⎪--+=⎨⎪-++=⎩决定,所以对应于特征根3λ=的主方向为::X Y Z =311223::211332----------=5:5:(5)1:(1):1--=-, 与它共轭的主径面为30x y z -+-=.(3) 与特征根2λ=-对应的主方向为::X Y Z 由方程组330,330,70.X Y Z X Y Z X Y Z --=⎧⎪-++=⎨⎪-++=⎩决定,所以主方向为::X Y Z =311333::177111----=20:20:01:1:0=, 与它共轭的主径面为0x y +=.取这三主径面为新坐标平面作坐标变换,得变换公式为：'''x y z ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩解出,,x y z 得''''''''1,1,1,x x y z y x y z z x y ⎧=+++⎪⎪⎪=+-⎨⎪⎪=++⎪⎩代入原方程得曲面得简化方程为'2'2'263210x y z +-+=.曲面的标准方程为'2'2'21111632x y z +-=-. 这是一个双叶双曲面.例2 化简二次曲面方程22222342246230x y z xy xz yz x y z +++++-+-+=.解 因为1237,10,0I I I ===,所以曲面的特征方程为327100λλλ-+-=,特征根为 5,2,0λ=.非零特征根5λ=所对应的主方向由方程组320,230,20X Y Z X Y Z X Y Z -++=⎧⎪-+=⎨⎪+-=⎩决定,所以与5λ=所对应的主方向为::1:1:1X Y Z =,与这主方向共轭的主径面为0x y z ++=.非零特征根2λ=所对应的主方向由方程组20,20,0Y Z X Z X Y Z +=⎧⎪+=⎨⎪++=⎩决定,所以与2λ=所对应的主方向为::1:1:(2)X Y Z =-,与这主方向共轭的主径面为22430x y z +-+=.取上面的两个主径面分别作为新坐标系''''o x y z -的'''y o z 和'''x o z 坐标面,再任意取与这两主径面都垂直的平面,比如 0x y -+=,为'''x o y 坐标面,作坐标变换,得变换公式为'''x y z ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩解出,,x y z 得''''''''1,241,41,332x y z y x y z z x y ⎧=--⎪⎪⎪⎪=+-⎨⎪⎪=-+⎪⎪⎩代入原方程得'2'2'95204x y +++=, 所以'2'2'52040x y z +++=. 再作移轴''''''''',,40x x y y z z ⎧⎪=⎪⎪=⎨⎪⎪=-⎪⎩得曲面的简化方程为''2''2''520x y ++=.这是一个椭圆抛物面.7 小结二次曲面方程的化简二次曲线一样,它的关键是适当选取坐标系,如果所取的坐标系深红x ）是曲面的对称面,那么新方程里只含有这个对应坐标（例如x）的有一坐标面（例如0平平方项,曲面的方程就比较简单了,二次曲面的主径面就是它的对称面,因而选取主径面作为新坐标面,或者选取主方向为坐标轴的方向,就成为化简二次曲面方程的主要方法了.参考文献[1] 吕林根等.解析几何（第三版）[M].北京:高等教育出版社,2001.[2] 吴大任等.解析几何引论（第二版）[M].北京:高等教育出版社,1989.[3] 朱鼎勋.空间解析几何[M].上海:上海科学技术出版社,1986.[4] 李厚源.空间解析几何[M].山东:山东科学技术出版社,1983.[5] 南开大学编写组.空间解析几何引论[M]. 北京:高等教育出版社,1989.[6] 郑文晶.解析几何[M].哈尔滨:哈尔滨工业大学出版社,2008.6.[7] 崔冠之.唐宗李等编,空间解析几何.北京：中央民族学院出版社.1989.11[8] 华东师范大学数学系几何教研室,解析几何习题集, 华东师范大学出版社,1982.[9] (前苏联)A.B.波格列诺夫、姚志亭译,人民教育出版社,1982.[10] 陈绍菱、傅若男,空间解析几何习题试析,北京师范大学出版社,1984.Classification and Simpification of Generalquadric surface equationLei Song(Grade 06, Class 5, Major in Mathematics and Applied Mathematics, Department of Mathematics, Shaanxi University of Technology, Hanzhong, 723000, Shaanxi)Tutor: Sangang GuoAbstract:This article through carries on the simplification and the classification to the generalquadric equation, simplifies five class equations and 17 standard forms. Finally introduced the generaltwo tunesKey words:Quadratic surface; Classification; Simplification; Using。

本科毕业论文题目：二次曲线的方程化简、作图及分类学院：数学与计算机科学学院班级：数学与应用数学2007级5班姓名：曹振佐指导教师：李秀兰职称：教授完成日期： 2011 年 5 月 18 日二次曲线的方程化简、作图及分类摘要:本文给出二次曲线的几种化简方法,其中对合同变换法化简中心二次曲线作了一点探讨.从二次曲线的由不变量所表示的简化方程出发给出了二次曲线作图的一种新方法,从而弥补了通过计算不变量只知简化方程而无法在原坐标系下画出二次曲线图形的缺陷. 特别地我们利用了二次曲线的主直径为新坐标系作坐标变换来化简一般二次曲线的方程,从而使二次曲线的几何理论和代数理论自然地联系在一起,使得一般二次曲线的方程化简、作图以及根据二次曲线标准方程的度量分类也就比较简捷地一起完成了.关键词:坐标变换;不变量;主直径;主方向;合同交换目录1 引言 (4)2预备知识 (4)3 二次曲线的方程的化简 (5)3.1用坐标变换化简二次曲线 (5)3.1.1 化简缺少xy项的二次曲线 (5)3.1.1.1 利用坐标轴平移化简缺少xy项的二次曲线 (5)3.1.1.2 利用配方通过移轴化简缺少xy项的二次曲线 (6)3.1.2 利用转轴化简含有xy项的二次曲线 (6)3.1.3 一般二次曲线方程的化简 (7)3.1.3.1 中心曲线的化简 (7)3.1.3.2 非中心二次曲线的化简 (8)3.2通过主直径,主方向化简二次曲线 (8)3.2.1 中心曲线的化简 (9)3.2.2 无心曲线的化简 (9)3.2.3 线心曲线的化简 (10)3.3用不变量、半不变量化简二次曲线 (11)3.3.1 中心曲线的化简 (11)3.3.2 无心曲线的化简 (11)3.3.3 线心曲线的化简 (12)3.4正交变换化简二次曲线 (12)3.5合同变换法化简有心二次曲线 (13)4 二次曲线的方程的作图 (15)4.1中心二次曲线的作图方法 (15)4.2无心二次曲线的作图方法 (16)4.3线心二次曲线的作图方法 (18)5 二次曲线的方程分类 (18)5.1二次曲线的分类 (18)参考文献 (19)1 引言我们展开一般二次曲线的几何理论的研究,讨论一般二次曲线的渐近方向、中心、渐近线、切线、直径与主直径等重要概念与性质,也导出了二次曲线按不同角度的分类和作图.平面上的二次曲线的理论与空间的二次曲线的理论有着十分相识的地方.而平面的情况毕竟要比空间的情况简单得多,因此我们先对一般二次曲线的理论有了比较深入的了解后,再进一步学习空间的一般二次曲线的而理论将不会感到费力而它只是一种自然的推广.有二次曲线方程的系数构成的不变量321I I I ，，以及1K 完全可以画出二次曲线的形状大小,因此研究二次曲线的不变量也就成为解析几何的一个十分重要的中心问题.在这样的意义下,不变量也就最深刻地反映方程与曲线的关系,它也把我们对数形结合的问题提高到一个新的认识.2 预备知识在平面直角坐标系xy O -上,由二元一次方程022233231322212211=+++++a y a x a y a a x a )1(所表示的曲线,叫做二次曲线.我们讨论二次曲线的几何性质以及二次曲线方程的化简,最后对二次曲线进行分类和作图.为了方便起见,我们引进下面一些记号:33231322212211222),(a y a x a y a xy a x a y x F +++++≡ ,1312111),(a y a x a y x F ++≡ , 2322122),(a y a x a y x F ++≡ , 3323133),(a y a x a y x F ++≡ , 222122112),(y a xy a x a y x ++≡Φ , 这样我们容易验证,下面的恒等式成立),(),(),(),(321y x F y x yF y x xF y x F ++≡ ,)1(式也就可以写成),(),(),(),(321y x F y x yF y x xF y x F ++≡ . 我们把),(y x F 的系数所排成的矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=332313232212131211a a a a a a a a a A叫做二次曲线）（1的矩阵.），（y x Φ的系数所排成的矩阵 ⎥⎦⎤⎢⎣⎡=22121211*a a a aA 叫做），（y x Φ的矩阵.显然二次曲线)1(的矩阵A 的第一、第二与第三行（或列）的元素分别是),(),,(),,(321y x F y x F y x F 的系数.下面我们引用加个符号22111a a +=I ,221212112a a a a =I ,3323132322121312113a a a a a a a a a =I ,33232322331313111a a a a a a a a+=K .这里的1I 是矩阵*A 的主对角元素的和,2I 是矩阵*A 的行列式,3I 是矩阵A 的行列式.3 二次曲线的方程的化简 3.1 用坐标变换化简二次曲线 3.1.1 化简缺少xy 项的二次曲线3.1.1.1 利用坐标轴平移化简缺少xy 项的二次曲线方法 将坐标原点移至二次曲线的中心,在新方程中可以消去一次项.中心),(00y x 的坐标00,y x 由中心方程组⎩⎨⎧=++=++,0,0232212131211a y a x a a y a x a )2( 给出. 这样将变换公式 ⎪⎩⎪⎨⎧+=+=,,0'0'y y y x x x 代入原方程,即可化简原二次曲线. 例1 化简二次曲线方程01162422=+--+y x y x .解 二次曲线的系数矩阵 101048181A -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦. 因为 0440012≠==I ,所以 此曲线是中心二次曲线.由中心方程组)2(得⎩⎨⎧=-=-，084,01y x解 2,100==y x .可得 变换公式 ⎪⎩⎪⎨⎧+=+=，2,1''y y x x 代入原方程, 整理得 016422=-'+'y x .(椭圆) 3.1.1.2 利用配方通过移轴化简缺少xy 项的二次曲线例2 化简二次曲线方程010*********=++-+y x y x .解 将方程的左端配方,得: 036)2(9)5(422=-++-y x .令 ⎪⎩⎪⎨⎧+=-=,2,5''y y x x可得 变换公式 ⎪⎩⎪⎨⎧-=+=,2,5''y y x x 于是方程化为0369422=-'+'y x .(椭圆) 3.1.2 利用转轴化简含有xy 项的二次曲线方法 转轴化简二次曲线方程,只要是旋转适当的角度,就可使方程中的乘积项消去,而由公式12221122cot a a a -=α )3( 给出. 然后将变换公式 ⎪⎩⎪⎨⎧+=-=,cos sin ,sin cos ''''ααααy x y y x x 代入原方程. 例3 化简二次曲线方程080609241622=+++-y x y xy x .解 这里242,9,16122211-===a a a .由)3(得 247249162cot -=--=α,257)247(12472cos 2-=-+-=α, 542257122cos 1sin =+=-=αα, 532257122cos 1cos =-=+=αα, 所以 转轴公式为 ⎪⎪⎩⎪⎪⎨⎧+=+=-=-=),34(51cos sin ),43(51sin cos ''''''''y x y x y y x y x x αααα代入原方程,整理得'2'4x y -=.(抛物线) 3.1.3 一般二次曲线方程的化简 3.1.3.1 中心曲线的化简方法 一般采用先移轴后转轴较为简便. 例4 化简二次曲线方程021*******=+-++-y x y xy x .解 因为 0541232312≠-=--=I 即此曲线为中心曲线. 先移轴,由中心方程组得 ⎪⎪⎩⎪⎪⎨⎧=-+-=+-,0523,0523y x y x解得 ⎩⎨⎧=-=.2,200y x故移轴公式为 ⎪⎩⎪⎨⎧+=-=,2,2''y y x x 代入原方程,整理得0132'''2'=++-y y x x . )4(对方程)4(进行转轴 1,1,23,133'22'12'11'==-==a a a a .031122cot 12'22'11'=-=-=a a a α , 即 4πα=. 故转轴公式为 ⎪⎪⎩⎪⎪⎨⎧+=-=),(22),(22''''''''''y x y y x x 代入方程)4( 整理得最简方程为 0125212''2''=++-y x .(双曲线) 3.1.3.2 非中心二次曲线的化简方法 一般采用先转轴后移轴进行化简 例5 化简二次曲线方程0168222=+++-y y xy x .解 因为 01111112=-=--=I , 所以此曲线是非中心曲线.先进行转轴 02112cot =-=α , 即 4πα=. 故转轴公式为 ⎪⎪⎩⎪⎪⎨⎧+=-=),(22),(22''''y x y y x x 代入原方程,得 01624242''2'=++-y x y . )5( 对)5(进行移轴( 实质配方),得:)23(22)2('2'-=+x y .令 ⎪⎩⎪⎨⎧-=+=,23,2''''''x x y y 则变换公式为 ⎪⎩⎪⎨⎧+=-=,23,2''''''x x y y 则原方程化简为 ''2''22x y =.(抛物线) 3.2 通过主直径,主方向化简二次曲线方法 一坐标轴与二次曲线主方向平行,则化简后二次曲线方程中不含xy 项.3.2.1 中心曲线的化简方法 取它唯一一对相互垂直的主直径为坐标轴建立坐标系,即原点是曲线的中心.例6 化简二次曲线方程0122422=++++-y x y xy x .解 因为 2111=+=I , 0312212≠-=--=I ,所以 此曲线是中心曲线.其特征方程为0322=--λλ,因此两特征根为11-=λ, 32=λ.由11-=λ, 32=λ分别对应的两个主方向为1:1:11=Y X ,1:1:22-=Y X . 由两主方向决定的主直径分别为02=-+y x 和0=-y x 取二主直径为新坐标系轴, 得⎪⎪⎩⎪⎪⎨⎧--=-+=,2,22''y x y y x x 解得⎪⎪⎩⎪⎪⎨⎧++=+-=,1)(22,1)(22''''y x y y x x 代入原方程,化简得 132'2'=-y x .(双曲线)3.2.2 无心曲线的化简方法 取它的唯一的一个主直径为x 轴,过顶点垂直于主直径的直线为y 轴建立坐标系(顶点为坐标原点)例7 化简二次曲线方程0168222=+-+-x y xy x .解 这里0,4,1,1,12313221211=-==-==a a a a a .因为231322121211a a a a a a ≠= ,所以 此曲线是无心曲线. 因为 0,221==I I .其特征方程为022=-λλ,因此两特征根为0,221==λλ.对应于21=λ的非渐近主方向为1:1:11-=Y X .取主直径为 02=--y x 为新坐标系'x 轴,主直径与曲线的交点即顶点为)21,25(过顶点且以非渐近主方向11:Y X 为方向的直线方程为)25(21--=-x y 即03=-+y x .则变换公式为⎪⎪⎩⎪⎪⎨⎧---=-+=,22,23''y x y y x x 解得⎪⎪⎩⎪⎪⎨⎧++=+-=,21)(22,25)(22''''y x y y x x 代入原方程,整理得 '2'22x y =.(抛物线) 3.2.3 线心曲线的化简方法 取它的中心直线为x 轴,任取垂直它的直线为y 轴,建立坐标系. 例8 化简二次曲线方程0322222=--++-y x y xy x .解 因为,231322121211a a a a a a ==所以此曲线是线心曲线. 唯一的主直径为 01=+-y x .取主直径为新系的'x 轴,取任一垂直它的直线如0=+y x 为'y 轴,这时变换公式为⎪⎪⎩⎪⎪⎨⎧---=+=,21,2''y x y y x x 解得⎪⎪⎩⎪⎪⎨⎧++=--=,21)(22,21)(22''''y x y y x x 代入原方程,得22'±=y .(两条平行直线) 3.3 用不变量、半不变量化简二次曲线 3.3.1 中心曲线的化简方法 用不变量、半不变量化简中心曲线,它的最简形式为0232'22'1=++I I y x λλ 例9 化简二次曲线方程0121252522=--++y x y xy x .解 ,288,24,10321-===I I I 特征方程为024102=+-λλ.因此两特征根为.4,621==λλ可知最简形式为 024288462'2=-++y x‘. 即 1322'2'=+y x .(椭圆)3.3.2 无心曲线的化简方法 用不变量,半不变量化简无心曲线,它的最简形式为02'132'1=-±x I I y I . 例10 化简二次曲线方程048222=+-++x y xy x .解 因为 01644011411,01111,2321≠-=--====I I I . 它的最简形式为 0216222'=--±‘x y . 即 022'2'=±x y .(抛物线) 3.3.3 线心曲线的化简方法 用不变量、半不变量化简线心曲线,它的最简形式为:0112'1=+I K y I 例11 化简二次曲线方程0322222=-++++y x y xy x .解 这里,231322121211a a a a a a == 即此曲线是线心曲线. 831113111,211-=-+-==K I . 所以 它的最简形式为:02822'=-+y . 即 2'±=y .(两条平行的直线) 3.4 正交变换化简二次曲线方法 任意实二次型AX X x x ax x x f T i j i ijn ==∑∑==n1n1j 21),,( ,都可以用正交变换QY X =化为平方和2222211n n y y y f λλλ+++= . 这里),2,1(n i i =λ是A 的全部特征根.例12 化简二次曲线方程024241222=+-++y x y xy x .解 上式中所有二次项构成实二次型2212),(y xy x y x f ++=.它的系数矩阵⎥⎦⎤⎢⎣⎡=1661A .特征矩阵)5)(7(1661)(+-=----=A -E =λλλλλλf . 即 A 的特征根为 5,721-==λλ.当5,721-==λλ时,A 的特征向量分别为)1,1(),1,1(21-==αα单位化得)21,21(),21,21(21-==ββ.以21,ββ为列向量,作正交矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=21212121Q , 正交变换为 ⎪⎪⎩⎪⎪⎨⎧+=-=,2121,2121''''y x y y x x代入原方程,得 0857'2''=+-y y x .配方得 0516)45(572''=+--y x . 令⎪⎩⎪⎨⎧-==,45,''''''y y x x 则坐标交换为⎪⎪⎩⎪⎪⎨⎧--=+-=,5222121,5222121''''''''y x y y x x 得标准方程为516572''2''-=-y x .(双曲线)3.5 合同变换法化简有心二次曲线方法 对矩阵A 作合同变换,即⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡→⎥⎦⎤⎢⎣⎡333231232221131211321.........000000c c c c c c c c c d d d E A . 所作变换为⎪⎩⎪⎨⎧++=++=,,23'22'2113'12'11c y c x c y c y c x c x 这样)1(式就化简成0),(32'22'1=++≡d y d x d y x F例13 化简二次曲线方程021*******=+-++-y x y xy x .解 系数矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----=215551235231A . 因为451232312-=--=I ,所以 此曲线为中心曲线.10510031001555552500004242341555200152104225521333121001015222010012010010001001001001A E ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢--⎢⎥⎢⎥⎢⎥⎢-⎢⎥⎢⎥⎡⎤⎢⎥⎢=→→→⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎢⎥⎢⎥-⎢⎥⎢-⎢⎥⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎥⎢⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥⎥⎥⎥⎥. 这样经变换⎪⎩⎪⎨⎧+=-+=,2,223'''y y y x x 使原方程化为 01452'2'=+-y x .(双曲线) 检验 把变换⎪⎩⎪⎨⎧+=-+=,2,223'''y y y x x 代入原方程,并整理得01452'2'=+-y x . 经检验,此方法对中心曲线是成立的. 4 二次曲线的方程的作图 4.1 中心二次曲线的作图方法对中心二次曲线0),(:=y x F C 利用不变量可将其简化方程表为0232'22'1=++I I y x λλ. )6( 其中21,λλ是曲线C 的两特征根,且'',y x 轴分别沿1λ和2λ对应的主方向.因此x '轴关于原坐标系中x 轴的倾角α满足2212112111tan a a a a X Y -=-==λλα. 可见要从中心二次曲线C 的简化方程)6(作出其图形,只需以过C 的中心),(00'y x O 且与原坐标系中x 轴的倾角为α直线作为'x 轴,建立直角坐标系'''y x O -,然后在该坐标系下作出)6(所表示的曲线即可.例14 求二次曲线042226565:22=-+-+-y x y xy x C 的简化方程,并作出其图形.解 因为 不变量128,16,10321-===I I I . 所以解特征方程 016102=+-λλ. 即得曲线C 的两特征根,8,221==λλ且由823-=I I .得曲线的简化方程为 08822'2'=-+y x .即 142'2'=+y x (椭圆)另外通过解中心方程组⎪⎩⎪⎨⎧=++-=--,0253,02335y x y x 可得曲线的中心 )241,243('O . 过'O 作与x 轴的倾角41arctan πα==的直线 22--y x ,并以此作为'x 轴建立直角坐标系'''y x O -,且在该坐标系下作出方程142'2'=+y x (椭圆)所表示的曲线,如图1所示.4.2 对无心二次曲线0),(:C =y x F ,由于2211,a a 同号,不妨设它们均非负.利用不变量可将其简化方程为012'1312'=-±x I I I y 其中±号可任选, 这里不妨取-号, 即简化方程为 012'1312'=--x I I I y )7( 不难验证新坐标系的'x 轴是该二次曲线的对称轴(主直径),原点O '是曲线的顶点(主直径与曲线的交点).对任意点P ,若设其在旧、新坐标系的坐标为),(y x 和),(''y x ,则数),(y x F 与012'1312'=-±x I I I y 至多差一个正数倍,所以若主直径上某一点)0,(x P （或),0(y P ）的坐标使0)0,(<x F （或0),0(<y F ）则向量P O '便指向'x 轴的正向（因'x 轴正向上的点)0,(x P 使'1312'12x I I I y -±为负), 否则,便指向'x 轴的负向.可见要从简化方程)7(画出无心二次曲线0),(:C =y x F 的图形,只需先求出曲线的主直径和顶点),(00'y x O ,并选取主直径上一点)0,(x P （或),0(y P ）若0)0,(<x F （或0),0(<y F ）,则以O '作为原点,以向量P O '的正向作为'x 轴正向建立直角坐标系'''y x O -;若0)0,(>x F （或0),0(>y F ）则以O '作为原点,以向量O P '的正向作为'x 轴正向建立直角坐标系'''y x O -,并在该坐标系下作出方程)7(所表示的曲线即可.例15 求二次曲线0256102:22=+--+-y x y xy x C 的简化方程,并作出其图形. 解 对所给二次曲线0),(:=y x F C 由于231322121211a a a a a a ≠=. 所以 曲线是无心的.因为 曲线的不变量6402321-===I I I ，，,所以曲线的简化方程为 024'2'=-x y . )8(又曲线的主直径为01=--y x ,顶点为)1,2('O .取主直径上一点)0,1(P ,由于0)0,1(>F ,所以只需以'O 作为原点,以向量O P '的正向作为'x 轴正向建立直角坐标系'''y x O -并在该坐标系下作出方程)8(所表示的曲线即可,如图2所示.4.3 线心二次曲线的作图方法对线心二次曲线0),(:C =y x F 利用不变量可将其简化方程表为02112'=+I K y . （9）不难验证新坐标系的'x 轴是该二次曲线的对称轴（主直径）,所以若曲线的不变量01=K ,则要作出曲线的图形,只需作出主直径即可;若01<K ,只需作出与主直径0131211=++a y a x a 平行的二直线012211211131211=+-±++a a I K a y a x a 即可.例16 求二次曲线03222:22=--++-y x y xy x C 的简化方程,并作出其图形. 解 对所给二次曲线0),(:=y x F C 由于231322121211a a a a a a ==. 所以曲线是线心的.因为二次曲线的不变量802321-===I I I ，，,又曲线的主直径为01=+-y x ,所以只需在原坐标系下作出直线021=±+-y x ,即为要作的曲线的图形,如图3所示.5 5.1 二次曲线的分类通过适当地选取坐标系,二次曲线的方程总可以写成下面九中标准方程的一种形式:[1]12222=+by a x (椭圆)；[2]12222-=+by a x (虚椭圆)；[3]12222=-by a x (双曲线)；[4]02222=+b y a x (点或称两相交于实点的共轭虚直线)；[5]02222=-by a x (两相交直线)；[6]px y 22=(抛物线)； [7]22a y =(两条平行直线)； [8]22a y -=(两平行共轭虚直线)； [9]02=y (两重合直线)；参考文献:[1]吕林根,许子道.解析几何[M].第4版.北京:高等教育出版社,2006.[2]甘浪舟.利用不变量化简二次曲线方程的作图问题[J].安庆师范学院学报,2004,10(2):45-47.[3]吕林根.解析几何学习指导书[M]北京:高等教育出版社,2006.[4]廖民勋.二次曲线方程的化简及作图[J].广西师院学报(自然科学版),1997,14(2):76-81. [5]傅朝金.中心二次曲线化简的一种新方法及推广[J].湖北师范学院学报(自然科学版),2001,21(2):72-74.[6]苏婷.二次曲线方程化简[J].陕西师范大学继续教育学报,2006(23):247-249. [7]林梦雷.二次曲线方程的化简[J].漳州师范学院学报,1999,12(1):22-26.[8]席高文,刘晓君.二次曲线方程分类与化简的新方法[J].许昌师专学报,2001,20(20):6 -13. [9]Wen K T.Ways for the simplification of the Binary Curve Equation[J].Journal of Bijie Teachers College,1995,(2):66-71.[10] Qu J,Xi F Y.The simplification of the Binary Curve Equation by ParameterFunctions[J].High School Mathematics Teaching,1994,24-25.Second Curve Equation ReductionMapping And ClassificationAbstract:In this paper, we give the conic simplified methods, including several for contract transformation method for simplified center a bit conic are discussed . From the conic by not variable simplified equation said conic mapping is given a new method . Offsetting the knows only through calculating invariant simplified equation and can't in the original coordinate draw the second curve graphics defects. Specifically we use the quadratic curves for the new coordinate the Lord made diameter of coordinate transformation to the simplified general quadric curve equation. Thus the geometry of the conic theory and algebra theory naturally relates in together, generally makes the second curve equation according to the simplified, mapping and the metric standard equationconic classification also is briefly finish together.Key Words: Coordinate transformation; invarient; Lord diameter; Main directions; Contract exchange本科毕业论文题目：逼近法的相关研究学院：数学与计算机科学学院班级：数学与应用数学2007级5班姓名：晁燕萍指导教师：许芝卉职称：副教授完成日期： 2011 年 5 月 20 日逼近法的相关研究摘要：逼近法是在各个学科中应用极广泛的分析论证方法,本文就逼近法中最重要的几种方法加以论述,即二分逼近法、逐次逼近法和逐步逼近法,主要结合实例,介绍其分析论证的思想与方法.逼近法的应用和用法是非常广泛而多样的,最简明直观的是二分逼近法,它和实数连续性的配合运用,是分析论证微积分学中许多重要定理和基础问题的有力工具.逐次逼近法在各学科中也有广泛应用,本文就泛函分析中不动点的有关知识加以说明,此外,介绍了逐步逼近法在微分方程及其初等数论中的重要应用.关键词：逼近; 二分逼近; 逐次逼近; 逐步逼近目录1引言 (1)2二分逼近法 (1)1.2二分逼近法的典型证明方式 (1)2.2二分逼近法在数学分析中的应用 (2)3逐次逼近法以及在泛函分析中的应用 (3)4逐步逼近法 (5)1.4逐步逼近法在微分方程中的应用 (5)2.4一次同余式组的逐步逼近解法 (9)1.2.4用剩余定理求解的方法 (9)2.2.4逐步逼近法 (10)3.2.4两种解法计算量的比较 (12)参考文献 (13)1 引言逼近法是数学分析中贯穿全局的基本方法,它遵循着这样一个简朴实用的原则,以简御繁,以“已知”去研讨“未知”.作为一个分析论证方法,它是这个原则的具体化、数量化.譬如,任一个无理数,都可用有理数去无限逼近它,使误差可以到任意小.又如,数列{}n a 以A 为极限,其意即为用n a a a ,,,21 去逐步逼近常数A.再如,从几何上看定积分,曲边梯形的面积是通过一系列阶梯形逼近计算而得到的.可见,数学的研讨分析中普遍地渗透着逼近法的思想.不只如此,在泛函分析、微分方程和初等数论中也有非常广泛的应用, .以下主要就二分逼近法、逐次逼近法和逐步逼近法在不同学科中的应用加以论述.2 二分逼近法1.2 二分逼近法的典型证明方式二分逼近法在定理或问题分析论证中的思想是：欲找一个具有某一性质p 的实数,则可以从一个具有相应性质*P 的闭区间出发,逐次二等分,得到一个始终保持*P 的闭区间列,以这些闭区间的两个端点值分别形成左右两个夹逼数列,将具有性质p 的实数“夹逼”出来,而实数的连续性则确保了此数的存在,使这种逼近不至于“逼”空.现将二分逼近法典型证明方式说明于下1）确定一个闭区间使其具有某一性质*P .(*P 由性质p 决定)2）逐次二等分得到闭区间列[]{}m m B A ,,则所有的闭区间都具有性质*P ,且1221B B B A A A m m ≤≤≤≤≤≤≤≤(亦可写成：[][][][] ⊃⊃⊃⊃⊃m m B A B A B A B A ,,,,332211) 从而得到左右夹逼数列{}m A 与{}m B 满足：()021l i m l i m =-=-∞→∞→m m m m m m m A B A B 3）由实数的连续性得到实数k ,属于所有的闭区间,使k 满足：()i 具有性质p .这是由于k 属于所有的闭区间,被{}m A 与{}m B 左右夹逼,不妨形象的表示为：m m B k A ←→ ∞→m因而, k 的任意小的邻域内()εε+-k k ,都包含[]m m B A ,（m 足够大）,于是()εε+-k k ,具有*P ,故k 具有性质p .()ii k 是唯一的.事实上,若k 不唯一,设k k '≠,且满足m m B k A ←→,m m B k A ←'→,则对任何m , m m A k B k >'<,,得到m m A B k k -≤'-,而()0lim =-∞→m m m A B ,故k k '=,即k 唯一.2.2 二分逼近法在数学分析中的应用例1 设在[]b a ,上连续的单调递增函数()x f 满足:b b f a a f <>)(,)(,则存在),(b a c ∈,使()c c f =.证明 令11,B b A a ==,将[]11,B A 二等分,分点为211B A +, 若221111B A B A f +=⎪⎭⎫ ⎝⎛+,则命题结论成立. 若221111B A B A f +>⎪⎭⎫ ⎝⎛+,则取[]22111,,2B A B B A =⎥⎦⎤⎢⎣⎡+, 若221111B A B A f +<⎪⎭⎫ ⎝⎛+,则取[]22111,2,B A B A A =⎥⎦⎤⎢⎣⎡+. 逐次二等分区间,一般的对于区间[]m m B A ,,若22m m m m B A B A f +=⎪⎭⎫ ⎝⎛+,则命题结论成立; 否则,若22m m m m B A B A f +>⎪⎭⎫ ⎝⎛+,则取[]11,,2++=⎥⎦⎤⎢⎣⎡+m m m m m B A B B A , 若22m m m m B A B A f +<⎪⎭⎫ ⎝⎛+,则取[]11,2,++=⎥⎦⎤⎢⎣⎡+m m m m m B A B A A . 从而得到两个夹逼数列{}m A 与{}m B 满足：()i1221B B B A A A m m ≤≤≤≤≤≤≤≤且 ()0l i m=-∞→m m m A B()ii ()()m m m m B B f A A f <>,于是可知存在实数c ,使()∞→←→m B c A m m ,由于()x f 单增,所以()()()m m B f c f A f ≤≤,即:()()()m m m m B B f c f A f A <≤≤< 令()c c f m =∞→,上述证明中,所求的数c 具有的性质p :()c c f =,而构造的闭区间[]{}m m B A ,具有性 质*P ,则确定为()()m m m m B B f A A f <>,,从而得到夹逼数列{},m A {}m B 将c “逼出”.在不同问题的论证中性质p 与相应的*P 是具体的,在不同的情况下,必须紧扣实 际加以明确,这是正确应用二分逼近法成功论证的关键.二分逼近法是微积分学中许多基本定理证明的重要工具,是逼近法的最简明的形式之一,然而,逼近法的应用却更为广泛,在泛函分析,微分方程等数学分支中也都是一种有效的论证方法.下面通过介绍另一种逼近法来进一步体会这种方法的思想.3 逐次逼近法以及在泛函分析中的应用逐次逼近法,是从一个粗糙的近似解出发,使用某个固定公式逐次加工,使之逐步精确化以得到满足精度要求的近似解.例2 在完备度量空间中,压缩映射必有唯一不动点.证明 设()d X X ,=是完备的度量空间,T ：X →X 是压缩映射, 即对于任意X y x ∈,,不等式()()y x d Ty Tx d ,,θ≤成立,其中θ是满足不等式10<≤θ的常数.先证映射T 有不动点.构造X 中的序列{}n x .任取X x ∈0,并令()010201201,,,x T Tx x x T Tx T Tx x Tx x n n n =======- () 2,1=n , 我们证明{}n x 是X 中的基本点列,事实上,()()()()00101021,,,,Tx x d x x d Tx Tx d x x d θθ=≤=()()()()0022112132,,,,Tx x d x x d Tx Tx d x x d θθ≤≤=……… 一般地,可以证明()()001,,Tx x d x x d n n n θ≤+ () ,3,2,1=n于是,对自然数n 与k n +,由广义三角不等式得()()()()n n k n k n k n k n n k n x x d x x d x x d x x d ,,,,1211+-+-+-++++++≤()()0021,Tx x d n k n k n θθθ+++≤-+-+()00,1Tx x d kn n θθθ--=+ ()00,1Tx x d nθθ-≤对任何给定的0>ε,只有n 充分大,则()εθθ<-01,1x x d n因而{}n x 是柯西序列.又因X 是完备的,柯西序列{}n x 是收敛的, 即存在X x ∈,使x x n n =∞→lim ,再由于T 是压缩映射,必为连续映射, 于是.在n n Tx x =+1中,令∞→n ,得到x x T =即x 是不动点.再证唯一性.若x 不唯一,设不动点x x ≠',则x x T '=', 于是存在10<≤θ使()()()x x d x T x T d x x d '='=',,,θ则必有()0,='x x d ,故x x '=,则T 有唯一的不动点.上述证明中,为找出不动点,我们利用压缩映射在完备空间中构造了一个柯西序列去逼近极限点,并证明极限点即为不动点,从而完成了将不动点“逼出”的过程.4 逐步逼近法逐步逼近法也是逼近法中较为重要的一种论证方法,在各学科中都有广泛的应用.诸如在论证常微分方程解的存在唯一性定理、二项分布的一种新的计算方法、以及在初等数论中关于一次同余式组的解法都起到非常重要的作用.此外,逐步逼近法在破解技术难题------袁隆平科技创新方面起到了举足轻重的作用.1.4 逐步逼近法在微分方程中的应用在微分方程研究中,对于一阶或高阶的,显或隐的方程组的等各类方程,能求得精确解得并不多,因而方程的近似解又十分重要的实际意义的,而解的存在和唯一则是求近似解的前提和理论基础,且论证方法还提供了如何求近似解的途径.我们不妨以一阶微分方程解的存在唯一性定理的证明再次体会逼近法的思想.由于定理证明过程较长,我们以突出逼近法思想为重点来简叙其过程. 1） 现在先简单叙述一下运用逐步逼近法证明定理的主要思想. 首先证明求微分方程的初值问题的解等价于求积分方程()dx y x f y y xx ⎰+=0,0的连续解,再证明积分方程的解的存在唯一性.任取一个连续函数()x 0ϕ代入上面积分方程右端的y ,就得到函数()()()dx x x f y x xx ⎰+=0001,ϕϕ显然()x 1ϕ也是连续函数,如果()x 1ϕ=()x 0ϕ,那么()x 0ϕ就是积分方程的解,否则,我们又把()x 1ϕ代入积分方程右端的y ,得到()()()dx x x f y x xx ⎰+=0102,ϕϕ如果()x 2ϕ=()x 1ϕ,那么()x 1ϕ就是积分方程的解,否则,我们继续这个步骤,一般地,作函数()()()dx x x f y x xx n n ⎰-+=010,ϕϕ ()1这样就得到连续函数序列()()() ,,,,10x x x n ϕϕϕ如果()()x x n n ϕϕ=+1,那么()x n ϕ就是积分方程的解.如果始终不发生这种情况,我们可以证明上面的函数序列有一个极限函数()x ϕ,即()()x x n n ϕϕ=∞→lim存在,因而对()1式取极限时,就得到()()()dx x x f y x xx n n n n ⎰-∞→∞→+=010,lim lim ϕϕ()()dx x x f y xx n n ⎰-∞→+=010,lim ϕ()()dx x x f y xx ⎰+=0,0ϕ,即()()()dx x x f y x xx⎰+=0,0ϕϕ,这就是说,()x ϕ是积分方程的解.这种一步一步地求出方程的解的方法就称为逐步逼近法.2）一阶微分方程解的存在唯一性定理：设()b a f ,在R 上连续且满足利普希茨条件,则方程()y x f dxdy,= ()1 存在唯一解()x y ϕ=,定义于区间h x x ≤-0上,连续且满足初始条件()00y x =ϕ ()2这里()()y a f M Mba h Ry x ,max ,,min ,∈=⎪⎭⎫⎝⎛=证明 在区间h x x ≤-0上构造一个连续的函数序列(){}x n ϕ 以()x 0ϕ代入方程()1得 ()()x x f dxdy0,ϕ= ()3 则()()()dx x x f y x xx ⎰+=0001,ϕϕ是()3的且满足条件()2的解 再以()x 1ϕ代入方程()1得()()x x f dxdy1,ϕ= ()4则()()()dx x x f y x xx ⎰+=0102,ϕϕ是()4的且满足条件()2的解 一般地,继续这一步骤得到()()()dx x x f y x xx n n ⎰-+=010,ϕϕ是方程()()x x f dxdyn 1,-=ϕ 的且满足条件()2的解,从而得到函数序列(){}x n ϕ,可以证明该序列存在极限函数()x ϕ,从而有：()()()dx x x f y x xx ⎰+=0,0ϕϕ是()1的且满足条件()2的解.虽然我们对定理证明只给给予一个简单的叙述,但还是可以体会出逼近法思想在证明中所发挥的关键作用,然而逼近法的作用不仅仅是证明,它还提供了求近似解的途径.以下通过几个实例来体会逼近法在近似计算中的应用.例3 用皮卡逼近法求微分方程1=dxdy过点()1,1的解. 解 这里()1,1,1,00===y x y x f()()()⎰⎰+=+=-xx x n n d d f y x 11011,0ςςςϕςϕ ()1(),10=x ϕ代入()1 可得()x x =1ϕ()()x x 01ϕϕ≠,把()x 1ϕ代入()1可得 ()x x =2ϕ,故()()x x 12ϕϕ=,由逐步逼近法 ()x x =1ϕ是微分方程1=dxdy,过点()1,1的解. 例4 用皮卡逼近法求微分方程y dxdy=过点()1,0的解 解 这里()1,0,,00===y x y y x f()()()()⎰⎰--+=+=xn x x n n d d f y x 01101,0ςςϕςςϕςϕ ()1(),10=x ϕ代入()1 可得()x d x x+=+=⎰1101ςϕ()1!21)1(1202++=++=⎰x x d x xςςϕ()1!21!31)1!21(123203+++=+++=⎰x x x d x x ςςςϕ……由数学归纳法可得：()().1!11!11!11+++-+=-x x n x n x n n n ϕ显然()()x x n n ϕϕ≠+1 () ,3,2,1=n∑∞=0!n n n x 的n 项部分和函数为()x nϕ,可得幂级数∑∞=0!n n n x 的和函数是xe 在()+∞∞-,上 ()xn n e x =∴∞→ϕlim ()+∞<<∞-x由逐步逼近法有x e y = 是微分方程y dxdy=,过点()1,0的解. 例5 对于无法用初等积分法求通解的黎卡提方程22y x dxdy+=,我们可用逼近法求出满足初始条件()000=ϕ的近似解.解 ()00=x ϕ()()()33202021x dx x dx x x x xx==+=⎰⎰ϕϕ()()633)9()(730622122x x dx x x dx x x x xx+=+=+=⎰⎰ϕϕ ()()dxx x x x dx x x x xx⎰⎰+++=+=01410622223)396918929()(ϕϕ5953520792633151173x x x x +++=随着求解次数的增加,近似解()x n ϕ与真正解将越来越接近,因此在允许误差范围内可求出令人满意的解.上面我们结合不同数学分支中的实例,来体会逼近法的思想,尽管构造逼近序列的元素与方法各不相同,但其指导思想却是共同的,那就是用“已知的”、“简”的序列去逼近“未知的”“繁”的,从而达到我们的认识目的.正确领会逼近的思想,提高以逼近思想为指导的分析论证能力,将有助于我们深化对数学知识的认识,也将有助于我们提高数学分析运用能力和解决问题的能力.2.4 一次同余式组的逐步逼近解法用剩余定理求解一次同余式组是一种传统的方法,其缺点是兼容性差,计算量大.笔者将工程实践中的逐步逼近法引入传统的代数理论中,从而使一次同余式组的求解过程的兼容性大大增强,即一次同余式组增加几个条件时只需增加少量计算,而不必像对待一个新问题那样从头算起.设k m m m ,,,21 为两两互质的正整数,k b b b ,,,21 为整数.即求一次同余式组 1b x ≡ ()1mod m2b x ≡ ()2m o d m ()1k b x ≡ ()k mm o d的通解.它的最小正整数解,定义为一次同余式组()1的解.1.2.4 用剩余定理求解的方法令()k j m M M m M j j ki j ,2,1,1===∏=由于k m m m ,,,21 两两互质,故j M 与j m 也互质,故存在2个正整数j n 和()k j N j ,,2,1 =,满足1=+j j j j N M n m ()2 故j j j j j j j n m b b N M b -=从而有()∑∑∑+=-==+-+=kj i iiij j j jj i iiik i iiiNM b n m b bN M b N M b 1111于是j ki iiib NM b ≡∑=1()j m m o d对于任意整数l 有∏∑==+=ki i ki i i i m l N M b x 11()3此为式()1的通解.若∑==ki i i i N M b x 1()M m o d 为通解中的最小正整数解则为式()1的解,若同余式组()1增加了第1+k 个式子,则上述计算过程都需要重复计算,计算量较大.2.2.4 逐步逼近法)1 逐步逼近解法的构思设想一次同余式组i b x ≡ )(m o d i mk i ,,2,1 = 为k 个条件,称i b x ≡ ()i m m o d 为第i 个条件. 显然,对于任意整数1l ,111m l b x += ()4 满足第1个条件1b x ≡ )(m o d 1m逐步逼近法的构思是,选择适当的整数1l ,使式()4在满足第1个条件的同时满足第2个条件.如果存在一个整数1l 使式()4同时满足第1,第2个条件,则进一步假设211111m m l m l b x ++= ()5 对于任意整数2l ,显然式()5同时满足第1,第2个条件,只要适当选择整数2l ,使之再满足第3个条件,……,如此一步一步逼近,直至选择适当121,,,-k l l l ,使∏-=-++++=111212111k i i k m l m m l m l b x ()6满足所有k 个条件,则通解为∏∏=-=-+++++=ki ik i i k m l m l m m l m l b x 1111212111式中l 为任意整数.是()6如果为最小整数解,则为解.)2 逐步逼近解法的理论证明。

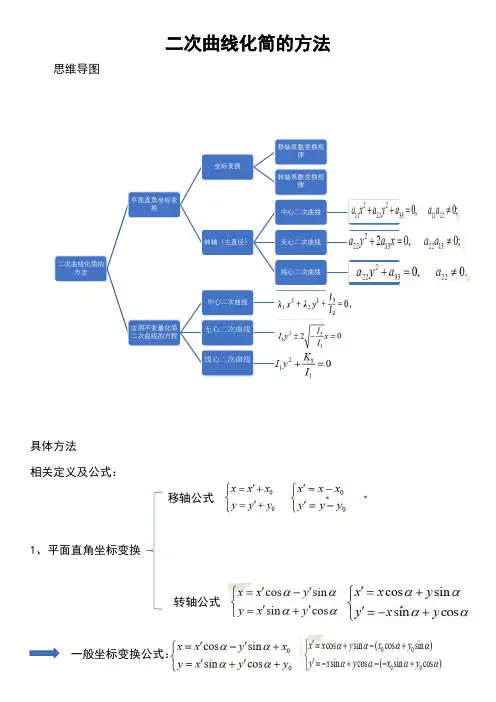
§5.6 二次曲线方程的化简与分类一、平面坐标变换1.移轴和转轴：如果平面内一点的旧坐标与新坐标分别为 (x, y)与(x', y')，则移轴公式为或式中(x0, y0)为新坐标系原点在旧坐标系里的坐标. 转轴公式为或式中α为坐标轴的旋转角. 前一公式为正变换公式，后一公式为逆变换公式. 注意两个变换的矩阵互为逆矩阵，因是正交变换，从而互为转置矩阵.2. 一般坐标变换公式为或3.设在直角坐标系里给定了两条相互垂直的直线l1：A1x＋B1y＋C1＝0,l2：A2x＋B2y＋C2＝0,其中A1A2＋B1B2＝0，如果取l1 为新坐标系中的横轴O'x'，而直线l2为纵轴O'y'，并设平面上任意点M的旧坐标与新坐标分别是 (x, y)与 (x'，y'), 则有其中正负号的选取应使第一式右端x的系数与第二式右端y的系数相等，即要使得这两项的系数是同号的.二、坐标变换对二次曲线方程系数的影响1．在移轴下，二次曲线F(x, y)≡a11x2 + 2a12xy+a22y2+2a13x+2a23y+a33=0的方程变为即新方程为这里因此，在移轴下，二次曲线方程系数的变化规律为：（1）二次项系数不变；（2）一次项系数变为 2F1(x0, y0)与 2F2(x0, y0)；（3）常数项变为F(x0, y0).从而当二次曲线有中心时，可作移轴，使原点与二次曲线的中心重合，则在新坐标系下二次曲线的新方程中一次项消失.2．在转轴下，二次曲线F(x, y)≡a11x2 + 2a12xy+a22y2+2a13x+2a23y+a33=0的方程变为即新方程为这里因此，在转轴下，二次曲线方程系数的变化规律为：（1）二次项系数一般要改变. 新方程的二次项系数仅与原方程的二次项系数及旋转角有关，而与一次项系数及常数项无关.（2）一次项系数一般要改变. 新方程的一次项系数仅与原方程的一次项系数及旋转角有关，而与二次项系数及常数项无关. 当原方程有一次项时，通过转轴不能完全消去一次项，当原方程无一次项时，通过转轴也不能产生一次项.（3）常数项不变. 从而当二次曲线方程中a12≠0时，选取旋转角α，使,则在新坐标系下二次曲线的新方程中xy项消失.三、二次曲线的方程化简1．利用坐标变换化简二次曲线的方程，在中心曲线时一般应先移轴后转轴；在非中心曲线时则一般应先转轴后移轴.例1．利用移轴与转轴, 化简下列二次曲线的方程，并画出它们的图形.（1）5x2＋4xy＋2y2－24x－12y＋18＝0；（2）x2＋2xy＋y2－4x＋y－1＝0；（3）5x2＋12xy－22x－12y－19＝0；（4）x2＋2xy＋y2＋2x＋2y＝0.解：（1）因为I2＝＝6≠0，所以曲线为中心曲线，由解得中心为(2, 1)，作移轴变换代入曲线原方程，整理得5x'2＋4x'y'＋2y'2－12＝0.由ctg2α＝，即,得 tgα＝－2，tgα＝.不妨取tgα＝，则由图5-1可得sinα＝，cosα＝,作转轴变换代入上述化简方程得6 x"2＋y"－12＝0.即.（如图5-2）.（2）因为I2＝＝0，故曲线为无心曲线，由ctg2α＝＝0,得α＝.作转轴变换代入原方程，整理得＝ 0,配方得＝0.作移轴变换得到 x"2＋y"＝0, 即 x"2＝－y". （如图5-3）.（3）因为I2＝＝－36≠0，所以曲线是中心曲线，由,得中心 (1, 1)，作移轴变换代入原方程，整理得5x'2＋12x'y'－36＝0.由ctg2α＝, 即,解得tg α＝－，tg α＝.不妨取tg α＝，则由图5-４可得sinα＝，cosα＝,作转轴变换代入上述方程整理得9 x"2－4y"2＝36,即.（如图5 – 5）.（４）因为I2＝＝0，故曲线为线心曲线，由ctg2α＝＝0,得α＝，作转轴变换代入原方程，整理得＝0, 配方：. 作移轴变换就有x"2＝, （如图5-6）.2. 利用转轴来消去二次曲线方程的xy项，其几何意义，就是把坐标轴旋转到与二次曲线的主方向平行的位置.如果二次曲线的特征根确定的主方向为，则由得，所以.因此通过转轴与移轴来化简二次曲线方程的方法，实际上就是把坐标轴变换到与二次曲线的主直径（即对称轴）重合的位置. 如果是中心曲线，坐标原点与曲线的中心重合；如果是无心曲线，坐标原点与曲线的顶点重合；如果是线心曲线，坐标原点可以与曲线的任何一个中心重合. 因此二次曲线方程的化简，也可以先求出二次曲线的主直径，以它作为新坐标轴，作坐标变换即可.例2. 以二次曲线的主直径为新坐标轴，化简下列方程，写出相应的坐标变换公式，并作出图形.（1）8x2＋4xy＋5y2＋8x－16y－16 ＝0；（2）x2－4xy－2y2＋10x＋4y ＝0；（3）4x2－4xy＋y2＋6x－8y＋3＝0；（4）4x2－4xy＋y2＋4x－2y＝0.解：（1）因为I1＝8＋5＝13，I2＝＝36≠0，故曲线为中心曲线，特征方程为λ2－13λ＋36＝0,解之得λ1＝4，λ2＝9，由它们确定的非渐近主方向分别为X1 : Y1＝－1:2，X2 : Y2＝2:1.由于F1(x, y)＝8x＋2y＋4，F2(x, y)＝2x＋5y－8，从而由λ1，λ2确定的主直径分别为x－2y＋5＝0, (x')2x＋y＝0, (y')得坐标变换公式为从而有正变换公式（注意此变换的系数矩阵就是上一变换矩阵的转置矩阵）代入原方程并整理得9 x'2＋4y'2－36＝0,即.同时 cosα＝，sinα＝，(x0, y0)＝(－1, 2)，由图6-7可得tgα＝，从而可确定α并作出图形，如图5-8.（２）因为I1＝1－2＝－1，I2＝＝－6 ≠0，故曲线为中心曲线，特征方程为λ2＋λ－6＝0.解之得λ1＝2，λ2＝－3，由它们确定的非渐近主方向分别为X1 : Y1＝－2: 1，X2 : Y2＝1: 2,由于F1(x, y)＝x－2y＋5，F2(x, y)＝－2x－2y＋2，从而由λ1，λ2确定的主直径分别为2x－y＋4＝0, (x')x＋2y－3＝0, (y')得坐标变换公式为从而有正变换公式代入原方程并整理得－3 x'2＋2y'2－1＝0.即－.同时sinα＝，cosα＝，(x0, y0)＝(－1, 2)，如图5—10.（3）因为I1＝4＋1＝5, I2＝＝0,,故曲线为无心曲线，特征方程为λ2－5λ＝0,解之得λ1＝5，λ2＝0，由λ1确定的非渐近主方向X1 : Y1＝－2: 1，由λ2确定的渐近主方向为X2 : Y2＝1: 2,由于F1(x, y)＝4x－2y＋3，F2(x, y)＝－2x＋y－4，，从而由λ1确定的唯一主直径为2x－y＋2＝0,将它取为O'x'轴，由解得曲线的顶点为，过它且垂直于2x－y＋2＝0的直线方程为x＋2y＋＝0,将它取为轴O 'y'，得坐标变换公式为，从而有正变换公式代入原方程并整理得5y' 2 －x'＝0.即y' 2 ＝x'.同时sinα＝，cosα＝，(x0, y0)＝, 如图5-12.（4）因为I1＝4＋1＝5, I2＝＝0, ，故曲线为线心曲线，特征方程为λ2－5λ＝ 0,解之得λ1＝5，λ2＝0，由λ1确定的非渐近主方向X1 : Y1＝－2: 1，由λ2确定的渐近主方向为X2 : Y2＝1: 2,由于F1(x, y)＝4x－2y＋2，F2(x, y)＝－2x＋y－1，从而由λ1确定的唯一主直径为2x－y＋1＝0,将它取为O'x'轴，过原点与它垂直的直线x＋2y＝0取为O'y'轴，得坐标变换公式为从而有正变换公式代入原方程并整理得5y' 2 －1＝0,即y' 2 ＝.同时 sinα＝，cosα＝，(x0, y0)＝,如图5-14.四、二次曲线的分类1.不论采用哪种方法化简方程，尽管所化简的曲线方程其形式可能不一致，但它们所刻划的几何图形相对于原坐标系而言是完全一致的.2.适当选取坐标系，二次曲线的方程总可以化成下列三个简化方程中的一个：(I) 中性心线： a11x2＋a22y2＋a33＝0，a11a22≠ 0；(II)无心曲线： a22y2＋2a13 x＝0，a22a13≠ 0；(III) 线心曲线： a22y2＋a33＝0，a22≠ 0.3.二次曲线以上三种简化方程总可以写成下面九种标准方程的一种形式：(I) 中性心线：[1] ＝ 1 (椭圆)；[2] ＝－1 (虚椭圆)；[3] ＝ 1 (双曲线)；[4] ＝ 0 (点或称两相交于实点的共轭虚直线)；[5] ＝ 0 (两相交直线)；(II) 无心曲线：[6] y2＝2px (抛物线)；(III) 线心曲线：[7] y2＝a2 (两平行直线)；[8] y2＝－a2 (两平行共轭虚直线)；[9] y2＝ 0 (两重合直线).例3. 试证中心二次曲线ax2＋2hxy＋ay2＝d的两条主直径为x2－y2＝0，曲线的两半轴的长分别是及.证明：因为曲线为中心曲线，所以I1＝a＋a＝2a，I2＝＝a2－h2 ≠ 0, a ≠±h,特征方程为λ2－2aλ＋(a2－h2)＝ 0,解之得λ1＝a＋h，λ2＝a－h，由它们确定的非渐近主方向分别为X1 : Y1＝1: 1，X2 : Y2＝－1: 1,由于F1(x, y)＝ax＋hy，F2(x, y)＝hx＋ay，从而由λ1，λ2确定的主直径分别为x＋y＝0, (y') x－y＝0, (x')即曲线的两条主直径为x2－y2＝0. 将它们分别取作O'y'轴与O'x'轴，得坐标变换公式为从而求得正变换公式代入曲线原方程整理得（依题意d ≠0）,即.所以两半轴长分别为和.例4. 已知≠0，且a1 a2＋b1 b2＝0，试求二次曲线(a1x＋b1y＋c1)2＋(a2x＋b2y＋c2)2＝1的标准方程与所用的坐标变换公式.解：因为a1 a2＋b1 b2＝0，所以直线a1x＋b1y＋c1＝0 与a2x＋b2y＋c2＝0互相垂直，分别取为O'y'轴与O'x'轴，得坐标变换公式为[其中a i, b i (i=1,2)不全为0]式中正负号的选取使得第一式中x的系数与第二式中y的系数相同，代入原方程得.由a1 a2＋b1 b2＝0 知λ≠ 0则a1＝λb2，b1＝－λa2，从而,注意到a2，b2不全为0，≠ 0, 代入得＝1,或令λ'=≠ 0，有＝1.作业题：1. 试证在任意转轴下，二次曲线新旧方程的一次项系数满足关系式.2. 利用坐标变换方法或主直径方法，化简下列二次曲线的方程，并画出它们的图形.(1) 2xy－4x－2y＋3＝0；(2) 5x2＋8xy＋5y2－18x－18y＋9＝0；(3) x2＋2xy＋y2－4x＋y－1＝0;(4) x2－3xy＋y2＋10x－10y+21＝0;(5) x2－xy＋y2＋2x－4y＝0；(6) x2+6xy＋y2＋6x+2y－1＝0；(7) x2－2xy＋y2＋2x－2y－3＝0；(8) x2+2xy＋y2＋2x＋y＝0.。

二次曲线的基本性质及方程式二次曲线是一类具有特定形状和性质的曲线，它的方程可以通过一些特定的形式描述。

本文将介绍二次曲线的基本性质以及常见的方程式。

一、二次曲线的基本性质1. 二次曲线的定义：二次曲线是平面上所有满足二次方程的点的集合。

其一般形式为Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0，其中A、B、C、D、E、F为常数，且A和C不能同时为0。

2. 二次曲线的对称性：二次曲线通常具有关于x轴、y轴或者原点的对称性。

当A=C且B=0时，二次曲线关于x轴对称；当A=0且B=C时，二次曲线关于y轴对称；当A=C且B≠0时，二次曲线关于原点对称。

3. 二次曲线的类型：根据方程中各项的系数，可以确定二次曲线的类型。

当B^2-4AC>0时，二次曲线为双曲线；当B^2-4AC=0时，二次曲线为抛物线；当B^2-4AC<0时，二次曲线为椭圆。

4. 二次曲线的焦点和准线：对于双曲线和抛物线，它们都有焦点和准线。

焦点是曲线上所有点到两个定点（称为焦点）的距离之和相等的点；准线是与曲线中所有点到直线的距离相等的直线。

而对于椭圆来说，它也有两个焦点，但没有准线。

二、二次曲线的方程式1. 双曲线的方程式：双曲线的一般方程为Ax^2 - Cy^2 = 1，其中A和C为正常数。

在此一般方程的基础上，双曲线还有一些常见的特殊形式，如横轴为主轴、纵轴为主轴的双曲线方程。

2. 抛物线的方程式：抛物线的一般方程为y = ax^2 + bx + c，其中a、b、c为常数。

抛物线还可以表达为以顶点为中心的顶点式方程或焦点为中心的焦点式方程。

3. 椭圆的方程式：椭圆的一般方程为(x-h)^2/a^2 + (y-k)^2/b^2 = 1，其中h、k分别为椭圆的中心在x轴和y轴上的坐标；a和b分别是椭圆的长半轴和短半轴。

椭圆的方程式还可以表达为标准方程或参数方程。

三、应用举例1. 双曲线的应用：双曲线在数学和物理中有广泛的应用。

山西师范大学现代文理学院（数计系）毕业论文论文题目：二次曲线方程的化简与应用学生姓名：刘彦雪学号： 1290110415专业：数学与应用数学班级： 1204班指导教师：范青龙二零一四年十一月四号目录摘要 (2)（一）、二次曲线的相关定义 (2)（二）、平面直角坐标变换 (3)2.1二次曲线方程的化简与分类 (3)2.2 利用系数的影响规律化简方程 ............................................... 错误!未定义书签。

（三）、应用举例.. (7)（四）、结束语 (10)参考文献 (11)二次曲线方程的化简与应用刘彦雪摘要二次曲线方程的化简是二次曲线理论的重要内容，是教学的一个难点，这方面的研究文献较多，分别总结出很多有效的方法。

文献给出了通过对二次曲线方程配方变形、直角坐标变换对二次曲线方程进行分类、化简;然后根据直线与二次曲线相交时参数t 的几何意义,确定二次曲线的标准方程.从而解决了利用坐标系的平移,旋转对二次曲线方程分类,化简时运算复杂或无法确定图形具体位置等问题.本论文首先对定义进行归纳总结，运用验证类比以及大量的举例对二次曲线化简作了说明，其次给出了一些方法和过程及证明，然后作出了归纳总结。

关键词 定义； 二次曲线； 平面直角坐标变换（一）、相关定义1.1.在平面上，由二元二次方程()22111222132333,2220F x y a x a xy a y a x a y a =+++++= 所表示的曲线,叫做二次曲线.1.2 有唯一中心的二次曲线叫做中心二次曲线;没有中心的二次曲线叫做无心二次曲线;有一条中心直线的二次曲线叫做线心二次曲线.无心二次曲线与线心二次曲线统称为非中心二次曲线.1.3 把一个点对于某一坐标系的坐标变换称为同一个点对于另一种坐标系的坐标,这种变换称为坐标变换.1.4 由曲线方程的系数给出的函数,如果在经过任意一个直角坐标变换后,它的函数值不变,就称这个函数是该曲线的一个正交不变量,简称不变量. 1.5 二次曲线的垂直于其共轭弦的直径叫做二次曲线的主直径。