二次曲线方程的化简与分类

2.8 二次曲线 二次曲面 归于二次型在中学阶段的数学学习中，遇到最多的也是很重要的问题要算是“二次”问题了。

如二次式、二次方程、二次函数、二次不等式、二次曲线：椭圆、双曲线、抛物线等，对这些“二次”，我们都作了详尽的讨论，而且还知道了球面方程也是二次的：x 2+y 2+z 2=r 2。

但是你类比了吗？归纳了吗？联想了吗？这些“二次”有什么联系？二次曲线就椭圆、双曲线、抛物线三种吗？除了球面外，还有其他的二次曲面吗？等等。

二次式、二次方程、二次函数、二次不等式的联系我们已经在学习中基本解决。

其中最基本的就是一元二次方程：ax 2+bx+c=0（a 、b 、c ∈R ，a ≠0），它可以配方、换元改写成ay 2+m=0，相当于作了一次平移变换x+ab2=y 。

于是可以根据a 、m 的符号来讨论该方程根，有也只有三种情况：两个实数根、一个重根、一对共轭虚根，对应于二次函数与x 轴的交点个数依次是2个、1个、0个。

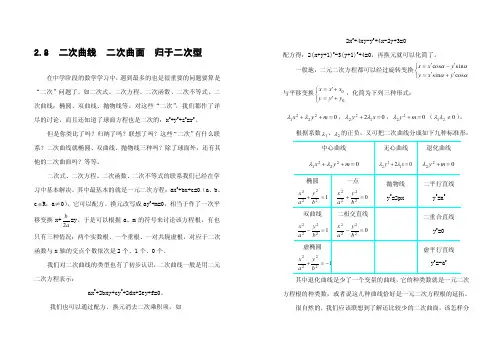
我们对二次曲线的类型也有了初步认识，二次曲线一般是用二元二次方程表示：ax 2+2bxy+cy 2+2dx+2ey+f=0。

我们也可以通过配方、换元消去二次乘积项，如2x 2+4xy-y 2+4x-2y+3=0配方得：2(x+y+1)2-3(y+1)2+4=0，再换元就可以化简了。

一般地，二元二次方程都可以经过旋转变换⎩⎨⎧'+'='-'=ααααcos sin sin cos y x y y x x 与平移变换⎩⎨⎧+'=+'=00y y y x x x ，化简为下列三种形式： 02221=++m y x λλ，02122=+x y λλ，022=+m y λ（021≠λλ）。

根据系数1λ、2λ的正负，又可把二次曲线分成如下九种标准形：其中退化曲线是少了一个变量的曲线，它的种类数就是一元二次方程根的种类数，或者说这几种曲线恰好是一元二次方程根的延拓。

口 ｌ ） ＋ ２ ｌ ｙ ｌ（ 。 ａ２ ＋ 口 ２ ） ＋ ｘ／ ２（ 。 Ｆ３ Ｘ ， ｏ （ ｏ Ｙ ）一 ０ ． （） ５
为论 述方 便 ， 我们 再 引进下 述记号
Ａ一 【 口
ｌ ２
Ｉ ｌ
ｎ ：
口 ｌ 口 ２ ｌ ＋ ２，
ｌ 口 ２ ２ ２ｆ
Ｉ ．
（ ２ ）
Ｆ２ ｏ Ｙ ） Ｆ３ ｏ Ｙ ）一 ０ （ ，ｏ ＋ （ ，ｏ ．
由于 （ ｏ Ｙ ） ｉ 的中心 ， Ｆｌ ，ｏ 一Ｏ Ｆ Ｘ ，ｏ为 Ｆ ＂ 故 （ 。Ｙ ） 且 ２
（） １
２ ｌ ＋ ２ ２Ｙ＋ 口 ３— ０ ａ３ ａ３ ３ ．
（。Ｙ） ． ，ｏ 一０ 于是 ， 程（ ） 方 １ 可化为
法， 即利 用转 轴 、 移 、 变 量或 参数 方 程等 进 行 平 不 化 简． 些方 法 有些计 算量较 大 ， 这 有些理论 较为 繁
杂， 有些 不利 于 画图 ， 些没 有对一般 的二 次 曲线 有
为 中心方 程 组 ． 时 ， 此 若 。 Ｙ ， ｏ满 足 中心 方 程 组 （ ） 则 （ ，ｏ 为二 次 曲线 ｒ 的 中心 ； （ 。 Ｙ ） ３， 勘 Ｙ） 若 ， ｏ 为 ｒ的中心 ， Ｘ ，ｏ 满 足 中心方程 组 （ ）¨ 则 ｏＹ ， ３ ｃ．
摘
要： 利用 高等代数 中矩 阵， 特征根， 特征向量， 以及解析几何 中二次 曲线 的有关理论 ， 通过两个定理 的证 明，
给出了一种化简一般 二次曲线的统一方法． 关■ 词 ： 特征根 ， 特征向量 ， 中心二次曲线 ， 非中心二次 曲线
中 圈分 类 号 ： １ ． ０２２ １ 文 献 标识 码 ： Ａ
口 ｌ 。 ２ ｌｘ ＋ 口２ Ｚ ｌ ＋ ａ２ｙ ２ｙ ＋

化简得
所求平面方程为
上一页
返回
解
§3.2 平面与点的相关位置
下一页
返回
上一页
下一页
返回
点到平面距离公式
上一页
下一页
返回
在第一个平面内任取一点，比如（0，0，1），
上一页
返回
定义
（通常取锐角）
两平面法向量之间的夹角称为两平面的夹角.
§3.3 两平面的相关位置
下一页
返回
按照两向量夹角余弦公式有
§1.5 标架与坐标
§1.7 两向量的数性积
§1.9 三向量的混合积
§1.8 两向量的矢性积
第二章 轨迹与方程
§2.1 平面曲线的方程
§2.2 曲面的方程
§2.4 空间曲线的方程
§2.3 母线平行与坐标轴的柱面方程
第三章 平面与空间直线
注意 空间曲面的参数方程的表达式不是惟一的.
抛物柱面
平面
抛物柱面方程：
平面方程：
三、母线平行与坐标轴的柱面方程
下一页
返回
从柱面方程看柱面的特征：
（其他类推）
实 例
椭圆柱面，
双曲柱面 ，
抛物柱面，
母线// 轴
母线// 轴
母线// 轴
上一页
下一页
返回
a
b
椭圆柱面
上一页
下一页
返回
y
平面的点法式方程
平面上的点都满足上方程，不在平面上的点都不满足上方程，上方程称为平面的方程，平面称为方程的图形．
其中法向量
已知点
上一页
下一页
返回
解
所求平面方程为
化简得
上一页
下一页

二次曲线- 二次曲线二次曲线- 正文也称圆锥曲线或圆锥截线，是直圆锥面的两腔被一平面所截而得的曲线。

当截面不通过锥面的顶点时，曲线可能是圆、椭圆、双曲线、抛物线。

当截面通过锥面的顶点时，曲线退缩成一点、一直线或二相交直线。

在截面上的直角坐标系(x,y)之下,这些曲线的方程是x,y 的二元二次方程：。

若截面不通过锥面的顶点，令截面与锥面轴线所成的角为θ,锥面的半顶角为α，则当时，所截曲线为圆；当时，截面与锥面的所有母线都相交,所截曲线为椭圆；当θ=α时，截面与锥面的一条母线平行，所截曲线为抛物线；当0≤θ<α时,截面与锥面的两条母线平行，所截曲线为双曲线。

焦点与准线如果圆锥曲线不是圆，则在圆锥曲线所在的平面上存在一定点和一定直线，使得圆锥曲线上任何一点到该定点和定直线的距离之比为常数，这个定点称为圆锥曲线的焦点，定直线称为圆锥曲线的准线。

为了得到焦点与准线，只需作一个球面内切于圆锥面并同时与圆锥曲线所在的平面σ相切。

设球面与平面σ相切于点F，球面与圆锥面相切于一个圆,这个圆所在的平面为ω，ω与σ相交于直线l，则点F，就是焦点，直线l就是准线（图1）。

二次曲线二次曲线这时,圆锥曲线上任意一点P到焦点F的距离｜PF｜与到准线l的距离｜PD｜之比为：。

其中θ,α都与P在曲线上的位置无关，所以是常数。

这个常数称为圆锥曲线的离心率，记为e。

当截线是椭圆时，e<1；当截线是双曲线时，e>1；当截线是抛物线时，e=1。

对于椭圆或双曲线，存在两个合于以上要求的球面，因此椭圆或双曲线都有两个焦点与两条准线。

每个焦点与其相应的准线都有上述性质。

抛物线只有一个焦点与一条准线。

若椭圆的两个焦点为F1,F2。

如图2所示的球面与圆锥面相切的圆为C1,C2。

这时对于椭圆上任意一点P，令通过P的母线OP（O为圆锥面的顶点）与C1、C2的交点分别为A、B。

则P 到F1的距离｜PF1｜与P到F2的距离｜PF2｜之和为｜PF1｜｜PF2｜=｜P A｜｜PB｜=｜AB｜。

第五章二次曲线的一般理论§ 5.1 二次曲线与直线的相关位置1. 求直线x-y-1=0与二次曲线2x2 xy y2 x 2y 1 0的交点.解：将y=x-1代入曲线方程,得2 22x x x 1 x 1 x 2 x 1 1 0,即0 0故直线在二次曲线上•2. 试决定k的值,使得(1) 直线x y 5 0与二次曲线x23x y k 0交于两不同实点；⑵直线x 1 kt与二次曲线x23y24xy y 0交于一点；y k t⑶直线x ky 1 0与二次曲线y22xy (k 1)y 1 0交于两个相互重合的实点x 1 t⑷已知直线与二次曲线2x2 4xy ky2 x 2y 0有两个共轭虚点，求ky 1 t的值解：(1). 将y=x+5代入二次曲线方程,得2x 2x k 5 02Q 2 4 k 5 04k 16 0k 4时，直线与二次曲线有两个不同的实交点•1 2 0(2).二次曲线的矩阵为 2 3 1/20 1/2 0且v X，丫k,1 •, X o, y o 1,kk 1,3时,原直线与二次曲线交于一个实点k 49时，直线与二次曲线有两个共轭虚交点。

24§ 5.2 二次曲线的渐进方向、中心、渐进线1. 求下列二次曲线的渐进方向，并指出曲线是属于何种类型的.1 x2 2xy y 2 3x y 0; 222 3x 4xy 2y 6x 2y 5 0;3 2xy 4x 2y 30.11 解:(1) Q X,Y X2 2XY Y 2 0时，X : Y1:1，同时 I ?0,11曲线有一个实渐进方向，是抛物型的k,1 k 2 4k 3 0,则 k 1 1,k 2 3,1)当 k . 1 时,F , X o y o X F 2 X o ，y o Y 0, 2).当 k 23时，F1X 0, y 0 X F 2X 0, y 0 Y1513 0,2(3). 二次曲线的矩阵为(1 11 (1 k)/20 k)/2 1解之, v X,Yk,1 , X o ,y o1 0,即―4k 1 1,k 25,2k0,即 k 2 6k 50,1)当 1时, X,Y k,1 2k 0, 2)当5时, 1,5 时, X,Y直线与二次曲线有二重合实交点.k,12k 0,(4).二次曲线的系数矩阵为22 1/21/ 2 1 01:( 1)取(X 0,y0)(“)，令V0,即[2(1k)(1)]2 (k 2)(3 k) 0 解得k24，且此时(1,1) 24( 1) k28282 Q X,Y 3X 2 4XY 2Y 2 0时,X :Y且i 23 2 2 o, 22曲线有两个共轭的虚渐进方向，是椭圆型的.•••曲线有两个渐进方向，是双曲型的•2. 判断下列二次曲线是中心曲线，无心曲线还是线心曲线1 1解：(1) QI 21 0 ,故为中心曲线；1 21 2 1 2 Q A24 1711 1有I 21 2 0,且 9113]2a 1324a 12a 22a 23曲线为无心曲线；an a 12 a 13 1 ,且有 一一 一 3,-312a 22 a 23•••曲线为线心曲线. 3. 求下列二次曲线的中心 2 21 5x 2xy 3y 2x 3y 6 0;2 22 2x 5xy 2y 6x 3y 5 0;3 9x 2 30xy 25y 2 8x 15y 0;2 24 4x 4xy y 4x 2y 0.X;Y 0:1 或 1:0,且 *〈0,5x y 1解1由解得x13 2 2 1 x 2xy 2y 22 2 x 4xy 4y223 9x 6xy y4x 6y 3 0; 2x 2y 1 0;6x 2y 0.••中心为3 (, 13 )28 282x5 y 3 0 2 由 2解得x 1, y 2 5 2y 3 x2 2--中心为1,2 J3an ai 2 3 a134 Q ———a i2 a225 ^23 15 '2曲线没有中心.曲线为线心曲线，中心直线方程为2x-y+仁0.y y 。

定理1.2.2 向量的加法满足下面的运算规律：
（1）交换律：
（2）结合律：
（3）
上一页
下一页
返回
O
A1
A2
A3
A4
An-1
An
这种求和的方法叫做多边形法则
上一页
下一页
返回
向量减法
上一页
下一页
返回
A
B
C
上一页
返回
例2 试用向量方法证明：对角线互相平分的四边形必是平行四边形.
证
上一页
下一页
返回
解
设
为直线上的点，
6、线段的定比分点坐标
上一页
下一页
返回
由题意知：
上一页
下一页
返回
定理1.5.4 已知两个非零向量
7、其它相关定理
则
共线的充要条件是
定理1.5.6 已知三个非零向量
，则
共面的充要条件是
上一页
返回
空间一点在轴上的投影(Projection)
§1.6 向量在轴上的射影
解
根据题意有
所求方程为
上一页
下一页
返回
根据题意有
化简得所求方程
解
上一页
下一页
返回
例4 方程 的图形是怎样的？
根据题意有
图形上不封顶，下封底．
解
以上方法称为截痕法.
上一页
下一页
返回
以上几例表明研究空间曲面有两个基本问题：
线为
的连
的中点
对边
一组
设四面体
证
e
e
e
AP
e
AD
e
AC
e

Ⅰ中心曲线 I2
a11 a21
a12 0 a22
Ⅱ非中心曲线 I2
a11 a21
a12 0 即 a11 a12
a22
a21 a22
ⅰ无心曲线： a11 a12 a13 a21 a22 a23
ⅱ线心曲线： a11 a12 a13 a21 a22 a23
3、二次曲线的渐进线 1、 定义（渐近线）：过中心具有渐进方向的直线叫做二次曲线的渐近线。
a22
a21 a22 a21 a22 a23
若 a11 a12 a13 无数多解，中心构成一条直线 a21 a22 a23
a11X a12Y a13 0 或 a21X a22Y a23 0 这条直线叫中心直线。
定义：有唯一中心的二次曲线叫做中心二次曲线，没有中心的二次曲线 叫无心二次曲线，有一条中心直线的二次曲线叫做线心二次曲线，无心 二次曲线与线心二次曲线统称为中心二，
X
:Y
为渐近方向，那么
FF12
( (
X X
,Y ,Y
) )
0 且 Q(X ,Y )
0
0
渐近线⑵与二次曲线⑴的交点由方程
Q( X ,Y )t2 2[ XF1(x , y ) YF2 (x , y )]t F (x , y ) 0 的根确定。当 F ( X ,Y ) 0 ，渐
因此二次曲线的渐进方向最多有两个，而非渐进方向有无数个。
⑶二次曲线按渐进方向分类 定义：没有实渐进方向的二次曲线叫做椭圆型的，有一个实渐进方向的二次 曲线叫做抛物型的，有两个实渐进方向的二次曲线叫做双曲型的。 因此二次曲线⑴按其渐进方向可以分为三种类型：即
ⅰ椭圆型曲线： I2 0
ⅱ抛物型曲线： I2 0
2、

＝（ｎｌａ２ ４－ａ；Ｏｘ；＋（ｂｌｂ２＋ｂ Ａ）《＋
（ａＩｂ２＋ａ２ｂ１）ＸＯＹｏ一
［（ａｌｂ２＋ａ２ｂ１）Ｙｏ＋２ａｌａ２名ｏ］名。一
［（ａＩｂ２＋ａ２ｂ１）茗ｏ＋２ｂＩｂ２Ｙｏ］Ｙｏ，
且口Ａ麟。算＋Ａ ｂｙｏｙ＝Ａ似：＋Ａ ６＿《．
从而，Ｏ；Ｘｏ髫＋ｂｙｏｙ＝鲋ｊ＋６扼．
这说明，点Ｍ（戈。，Ｙ。）关于双直线ＡＣ、
＼ ∥～ｙ ／ａ。＋２
Ｏ／
－ｘ
／
都成等角．证明：这
图６
样的折线只能位于
抛物线对称轴的一侧．
（第２２届全苏数学奥林匹克）
讲解：不妨设抛物线为Ｙ＝ａｘ２（ａ＞０）．
依次取折线上三个相邻的顶点Ａ；（并ｎａｘ；）
（ｉ＝ｎ，ｎ＋１，ｎ＋２，ｎＥ Ｎ）．
由抛物线在点Ａ。＋。处的切线方程（或求
导数）可知其斜率
ｋ七 ｌ２ｊ２：｝２－ａｋ＝ｘ＾忌Ａ＋ｎｌ一， ＋ｌ一Ａｎ．＋＋２．－－＝鼎掣叫＝凸Ｘ（ｎＸ＋ｎ２＋４＂Ｘ石ｎｎ＋＋Ｉ１）？）．
即５菇一７ｙ－鲁：ｏ．
所以，Ｑ也是ＭＮ的中点，即定点Ｑ平分 线段ＭＮ．
注：从曲线的含变化参数的方程（实际
上就是曲线系方程）求出曲线上的定点，是
证明曲线过定点的常规方法．由于本题中的
切点弦ＭＮ只依赖点Ｊｐ的位置，因此，使用切
点弦方程正是时机．证明点Ｑ平分线段ＭＮ
实际上是使用了同一法，同时也发挥了中点
弦方程的作用．
２００９年第８期
７
二次曲线中点弦、切线、切点弦及双切线方程
胡圣团
（湖南省澧县一中，４１５５００）
（本讲适合高中） １知识简介
记Ｇ（ｘ，Ｙ）＝Ａｘ２＋Ｂｘｙ＋Ｃｙ２＋Ｄｋ＋Ｅ｜ｙ＋Ｆ １．１二次曲线中点弦的方程

二次型与二次曲面-母线与坐标轴平行的柱面方程母线与坐标轴平行的柱面方程定义：直线L 在空间平行于固定方向运动，并且总和一条定曲线Γ相交所形成的曲面叫做柱面，直线L 叫做柱面的母线，定曲线Γ叫做柱面的准线。

()()(),0,0,0f x y z g y z x h z x y =----=----=----母线平行于轴的柱面母线平行于轴的柱面母线平行于轴的柱面绕坐标轴旋转的旋转面方程定义：曲线Γ绕一条固定直线L ，在空间旋转一周所成的曲面，称为旋转曲面，曲线Γ叫做母线，定直线L 叫做旋转轴。

定理 设Oxy 坐标面上一条曲线Γ的方程是()00≥=,y x,y f ，则以曲线Γ为母线，x 轴为旋转轴的旋转面方程为 ()022=+z y x,f 。

证明：在旋转面上任选一点P (x ,y ,z )，P 是由Γ上的点()0000,,y x P 绕x 轴旋转而得，则P 和P 0点坐标之间满足⎪⎩⎪⎨⎧=+=0220y z y x x 因为P 0在曲线Γ上，所以有()000=,y x f ，即()022=+z y x,f . 反之，若一点P (x ,y ,z )满足()022=+z y x,f ，则Oxy 坐标面上的点()0000,,y x P 满足方程()000=,y x f ，其中2200,z y y x x +==，因此点P 0在曲线Γ上，而点P 恰是由点P 0绕x 轴旋转而得，于是P (x ,y ,z )在该旋转面上，所以 ()022=+z y x,f 为所求旋转面的方程。

例：球面由⎩⎨⎧==+0222z r y x 绕x 轴旋转而得，所以球面方程为 ()222222222r z y x r z y x =++⇒=++例圆柱面由直线⎩⎨⎧==0x ry 绕z 轴旋转而成，所以圆柱面方程为 ()22222r y x r x y =+⇒=+ 例：⎩⎨⎧==02z x y 分别绕x 轴和y 轴的旋转面方程分别为 ()22222422222z x y z x y y x z y x z y x +=⇒+==+⇒=+轴：轴：空间曲线方程()()⎩⎨⎧==00x,y,z g x,y,z f 二次曲面的分类二次曲面：二次代数方程0222=+++d cz by ax 所代表的曲面。

２ 。
ｃ ｏ ｓ ２ ０ ：— ￣ ］ Ｉ ＋ ｃ ｔ ｇ — ２ ２ ８：
：
÷
…
－
乒 … － Ｊ 互 乒
Ｚ
等＋
．
巡一 等＋ 等
２ Ｃ
Ａ－Ｃ ２
将Ｓ ｉ ｎ ０ ， Ｃ ｏ ｓ ０ 代入 （ ３ ）
等．
— － — —
新横轴在原坐标系 中方程 为 ｙ－ ｂ＝ｋ （ ｘ－ ａ ）
基础教育 ２ ０ １ ４年 ２月 （ 上）
二元二次方程化简公式的推导
王 海 涵 （ 安徽省阜南实验 中学，安徽 阜南 ２ ３ ６ ３ ０ ０ ）
摘要 ：二元二 次方程是高 中 代 数的主要 内 容 ，本 文通过深入浅 出的推导，使 学习者有一个深刻的认识 ，从理念到方法都是值得推广的，使我们的学习效率更加
＋
Ｃ’ ＝ ｏ
令（ ３ ） 中的 Ｂ ０ ， 得ｃ ｔ ｇ２ ０＝— Ａ－ Ｃ
—
新横轴在原坐标 系中的方程为
ｙ—ｂ＝ Ａ－Ｃ
一
’
一
等 ｘ ｌ Ａ ｚ ＋ Ｂ ２ ＋ Ｃ ＝ － ２ Ａ Ｃ
： ！ ＝ ！ ： 里 ： ＝
Ｂ
压＋
Ｅ
＋Ｅ
为方便 计， 设８ ： Ａ ２ ＋ Ｂ ２＋ ｃ ２ — ２ Ａ ｃ 旋转 后新坐标 轴在 原坐标 系中 的方程 的斜 率为
！ ！
ｃ・ 一 Ａ＋Ｃ
４ Ａ Ｃ ） ＋（ Ａ ＋ Ｃ ）
。 ＋
当Ｂ － ４ Ａ Ｃ ￣０ 时，√ ≠Ａ ＋ ｃ
当Ｂ － ４ Ａ Ｃ ＝０时， ＿ Ａ ＋ ｃ 以下 分 四个 类 型 进行 讨 论 类型 （ 一） 当Ｂ 一 ４ Ａ Ｃ ￣０时，Ｂ ＞ ０

（ 南大学 数学 院 ， 封 ４５０ ） 河 开 ７ ０ ４
＋
Ａ
２
一
１ ２
ｎ
以
＿＿Ｊ
［ 摘 要 ］ 讨论 欧 氏 群 Ｅ（ ） 二 次 曲线 方 程 化 简 理 论 中 的 应 用 ．在 此 背 景 下 ，给 出 二 次 方 程 化 简 的 方 ２在
法 ；讨论 了 二 次 曲 线 方 程 的若 干 性 质 ．
一
（ ）（ 确 的 向 直 的 向 Ａ 定 方 ｘ：为 径 方 ． 。） ｙ
定义 １２】 设 ｌ 二 次 曲线 的一 条直 径 ， 果 它垂直 于 自己的共轭 弦 ， ｌ ．Ⅲ 为 如 则 称为 主直 径 ， 直径 主
［ 稿 日期 ］ ２ １ —３２ 收 ０ ００ —６
的方 向和垂 直 于主 直径 的方 向称 为 主方 向．
证 设 ｘ ： ｙ为 主直 径弦 的方 向 ，主直 径 方 向为 ｘ ： ，则 有 ｘ Ｙ 一 一Ｙ ： ． Ｙ ： ｘ 由命 题 １ １ ．，
Ｘ ：Ｙ 一 （ １Ｘ ＋ ａ ｚ 一 ｎ２ ２ｙ）：（ １Ｘ ＋ ａ２ 口ｌ １ ｙ）一 一 ｙ ：Ｘ ， 得
Ｘ
一
ｙ
一
“≠ ｏ． ～
ｌ８ Ｏ
大 学 数 学
第２ ８卷
定 Ⅲ如平上点 ， 足程 ｛三；： ｃ 为次线中． 义３ 果面一 ｃ， 方组 ： ：称 ， 二曲的心 ． ｚ满 则 ｚ ． ｙ
命题 １ ２ 二 次 曲线 的主直径 的共 轭方 向是 Ａ。 ． 的非 零特 征根对 应 的特征 向量 的方 向．
主 方 向 的 主 直 径 为 ｙ ｚ， 一 ＸＦ （ ） ０ 另 一 主 直 径 方 程 为 ＸＦ （ ， ＋ ｙ ｚ， 一 ０ Ｆ （ ） ， 一 ， － ） ｚ Ｆｚ ） ．当 然 （

二次曲线的理论及其应用文献综述文献综述二次曲线的理论及其应用一、前言部分在中学,我们就二次曲线的性质进行了简单的介绍,它在中学的教学里有很重要的地位,是中学平面解析几何中不可或缺的一部分,在本文中的一些定理的证明都利用到了二次曲线的基本性质。

可以这样说,二次曲线的其它性质都是建立正在他的基本性质之上。

所以我将对它进行一下总结,建立表格如下: 椭圆双曲线抛物线标准方程范围或对称性关于x轴或y轴对称关于原点中心对称关于x轴或y轴对称关于原点中心对称关于x轴顶点离心率渐近线无无准线焦点过曲线上点的切线方程二次曲线的定义:在欧式平面上,由一般二元二次方程(其中,,)表示的曲线,称为二次曲线,此方程称为二次曲线的方程。

定义 1.1:到两个定点的距离之和等于定长(定长大于两个定点间的距离)的动点的轨迹叫做椭圆。

它的方程为。

定义 1.2:到两个定点的距离的差的绝对值等于定长(定值小于两个定点间的距离)的动点的轨迹叫做双曲线。

它的方程为。

定义 1.3:到一个定点和一条直线的距离相等的动点轨迹叫做抛物线。

它的方程为文献综述介绍了二次曲线的定义,给出了二次曲线的分类,介绍了一些二次曲线的化简方法,以及对二次曲线的一些性质与特征的进一步讨论。

本文的目的是在原有知识体系的基础上加以整理和归纳,概括出二次曲线的性质与几何特征,并辅以典型的例题来论证方法的可行性,进而介绍了二次曲线方程的应用,使我们所学知识加以巩固和提高,起到“温故”而“知新”的作用。

二、主题部分公元前350年,古希腊梅纳克莫斯发现三种圆锥曲线,即现在所说的椭圆,双曲线,抛物线,并用开始编写几何学的历史。

古希腊的塞马力达斯开始解简单方程组。

半个世纪后,古希腊另一位数学家阿波罗尼斯又著《圆锥曲线论》.阿波罗尼斯的8卷《圆锥曲线论》以其几乎将圆锥曲线的全部性质网罗殆尽而永垂史册.可以这样说,在解析几何之前的所有研究圆锥曲线的著作中,没有一本达到像《圆锥曲线论》那样的对圆锥曲线研究得如此详尽的程度.但是,像古希腊所有的几何学一样,阿波罗尼斯的几何是一种静态的几何.它既不把曲线看作是一种动点的轨迹,更没有给它以一般的表示方法.这种局限性在16世纪前,并没有引起注意,因为实践没有向几何学提出可能引起麻烦的课题.16世纪以后的情况就不同了.哥白尼(Copernicus,1473-1543)提出日心说,伽利略(Galileo,1564-1642)由物体运动的研究,得出惯性定律和自由落体定律,这些都向几何学提出了用运动的观点来认识和处理圆锥曲线及其他几何曲线的课题.地球绕太阳运转的轨道是椭圆、物体斜抛运动的轨道是抛物线,这些远不是靠建立在用平面截圆锥而得到的椭圆和抛物线的概念所能把握的.几何学要能反映这类运动的轨道的性质,就必须从观点到方法来一个变革,创立起一种建立在运动观点上的几何学.17世纪解析几何的诞生创造了为二次曲线的研究创建了条件.作为点运动轨迹的二次曲线,在引进坐标的基础上显示出更明显的特征,它是二次方程的图形,即它又被命名为二次曲线。

《解析几何》课程教学大纲一、课程的性质、目的与任务通过本课程的教学，使学生掌握平面曲线、空间直线、平面、柱面、锥面、旋转曲面、二次曲面等的基本性质。

提高用代数方法解决几何问题的能力，为今后学习其它课程打下必要的基础，并能在较高理论水平的基础上处理中学数学的有关教学内容，以及生产、生活中的有关实际问题。

本课程是大学专科小学教育专业数学类必修的一门重要的专业课课程，通过本课程的教学，使学生系统掌握空间解析几何的基本知识和基本理论，正确地理解和使用向量；在掌握几何图形性质的同时，提高运用代数方法解决几何问题的能力和空间想象能力，能在较高理论水平的基础上处理中小学教学的有关问题。

二、课程教学内容和基础要求要求学生重点掌握空间解析几何的基本思想和基本方法；培养空间想象能力，逻辑思维能力以及运用现代各种数学方法处理几何问题的能力，运用几何结构，深入理解现行中学数学教材中的有关问题，并且具有应用几何知识解决实际问题的能力。

通过本课程的学习，为学好后续专业课程打下良好的基础。

第一章矢量与坐标教学目的：通过本章的教学,使学生掌握矢量的概念，矢量运算的定义、规律及几何意义，利用矢量的运算作为工具研究平面与空间的几何图形教学要求:理解矢量及与之有关诸概念,并能在具体问题中区分那些是矢量,那些是数量，掌握矢量的运算（矢量加（减）法）数与矢量乘法，两矢量的数性积，矢性积，混合积，二重矢性积等的定义与性质，注意与数的运算规律的异同之处，理解坐标系的建立，区分仿射坐标系与空间直角坐标系的区别，掌握在直角坐标系下，用坐标进行矢量的运算方法，会用矢量法进行有关的几何证明问题。

教学内容：§1.1矢量的概念§1.2矢量的加法§1.3数量乘矢量§1.4矢量的线性关系与矢量的分解§1.5标架与坐标§1.6矢量在轴上的射影§1.7两矢量的数性积§1.8两失量的矢性积§1.9三矢量的混合积§1.10三矢量的双重矢性积教学提示：由浅入深，采用启发式教学，并通过对比加深学生印象。

a12

a13
a22 a23
a23 a33
a24

a34

a14 a24 a34 a44
记
K1

a11 a14
a14 a22 a44 a24
a24 a33 a44 a34
a34 , a44
a11 a12 a14 a11 a13 a14 a22 a23 a24 K2 a12 a22 a24 a13 a33 a34 a23 a33 a34
为了以后讨论的方便，我们引进一些记号：
F (x, y, z) a11x2 a22 y2 a33 z2 2a12 xy 2a13 xz 2a23 yz 2a14 x 2a24 y 2a34 z a44 0
(x, y, z) a11x2 a22 y2 a33z2 2a12 xy 2a13 xz 2a23 yz
a11 a12
A1


a12

a13
a22 a23
a14 a24
a13 a23 a33 a34
a14
a24

a34

a44
a11
A


a12
a13
a12 a22 a23
a13
a23

a33
分别称为二次曲面F(x, y, z) 0和(x, y, z)的矩阵
表示虚椭球面
(3)
x2 y2 z2 a2 b2 c2 0
表示一点
(4)
x2 y2 z2 a2 b2 c2 1
单叶双曲面
(5)
x2 y2 z2 a2 b2 c2 1

题 过程 、解题 思 路 、解 题 方 法．还 需 对 涉 及 的 强学 生解决 问题 的能力 ，培养 学 生思 维能 力 ，
思想方法、有联系的问题进行反思等．具体可 特别是创新思维能力 ，提高数学教学质量都
反思 ：
起到重要作用 ，而且可以促进学生 良好 的数
（１）解题时运用 了哪些 思维方法？解法 学观念 的形成 ，提高学生的数学反思性学习
现 了多种 角度 的转 化 ，联 系 了多 个 知识 点 ，有 败 的教训 ？学 生 通 过 对 解题 思 维 的 反思 ，重
助于提高发散思维能力．各种方法的运用，分 新审查题意 ，更 正确、完整、深刻地理解 了题
别将代数 问题转化为了其它 问题 ，属于问题 目的条件 和结论 ，激 活 了学 生 的思 维 ，开 阔了
图 １
例 ２ 化简二次曲线方程 Ｘ －４ｘｙ－２ｙ
￣－２（４，８）ｆ １—１６：０， ＼ ／
＋ ｌＯｘ＋４ｙ＝Ｏ，并 画 出图形 ．
Ｉ１— ８＋ ５— １３， Ｉ ８ ２ Ｉ
一 ｌ ２ ５ Ｉ ６，
所 以曲线 的特征 方程 是
０— １３Ａ＋ ３６＝０，
解 得 １—９， ２－４． 将它们分别代人
转 换题 型．
思路 ，使学生思维的灵 活性在变换和化归的
３ 在 问题解 决后 进行 反思
训练 中得 到培养 和发 展．
这 里主 要指 解 题 后 的 反 思 ，这 是 一 项 很
总之 ，习题 课 是 数 学 教 学 的一 种 重 要 课
重要 的反思 ．主要包 括 检验 解题 结 果 、回顾 解 型 ，是新授课 的重要补充．它不仅能有效地增
ａ １１一 ａ １２

x = x ′ cosθ y′ sin θ y = x ′ sin θ + y′ cosθ
y O x y O x
第五章 二次型
§5.1 二次型及其矩阵表示
n元实二次型 f(x1, x2, …, xn) = a11x12+a22x22+…+annxn2 +…+a +2a12x1x2+2a13x1x3+…+2an-1,nxn-1xn +2a +2a +…+2a 1,n aij = aji Σ aijxixj
当方程是标准型时, 当方程是标准型时, 二次曲面用二次项的符号来进行分类 不太清楚,在化简成标准型时, 不太清楚,在化简成标准型时,为何总是得到同样数目的正项和负项
后来, 英国数学家西尔维斯特回答了这个问题: 后来, 英国数学家西尔维斯特回答了这个问题: 西尔维斯特回答了这个问题
给出了n个变数的二次型的惯性定律, 给出了n个变数的二次型的惯性定律, 但没有证明
1 1 其中y 其中y = 0 2 0 0 1 1/2 因而x 因而x = 0 1/2 0 0 1 1 x. 1 3/2 1/2 y. 1
第五章 二次型
§5.2 化二次型为标准形
例5. 用配方法化f =2x1x2+2x1x3 –6x2x3为标准形. 用配方法化f =2x +2x 为标准形. 并求所用的变换矩阵. 并求所用的变换矩阵. 分析: 若用前面正交变换的方法化f为标准形, 分析: 若用前面正交变换的方法化f为标准形, 非常麻烦. 非常麻烦. 因为 0 1 1 f(x1, x2, x3)的矩阵A = 1 0 3 , 的矩阵A 1 3 0
第五章 二次型