追击相遇问题分析方法

方法一：临界法 两车速度相同均为 v 时，设 所用时间为 t， 乙车的加速度 为 a2，则：v1－a1t＝v2－a2t v1＋v v2＋v ＝ v， t＝ t － x0 ， 2 2 解得：t＝2 s，a2＝6 m/s2
方法系列
巧解追及相遇问题的三种方法 试题
上页
下页
解析
即 t＝ 2 s 时刻，两车恰好未相撞，显然此后在停止运动前，甲 的速度始终大于乙的速度，故可避免相撞．满足题意的条件为 乙车的加速度至少为 6 m/s2. 方法二：函数法 1 甲运动的位移： x 甲＝ v1t－ a1t2， 2 1 乙运动的位移： x 乙＝ v2t－ a2t2 2 避免相撞的条件为：x 乙－ x 甲 <x0
方法系列
巧解追及相遇问题的三种方法 试题
上页
下页
解析
1 即 (a2－ a1)t2＋ (v1－ v2)t＋ x0>0 2 代入数据有： (a2－ 2)t2－ 16t＋ 16>0 不等式成立的条件是： Δ＝ 162－ 4×16(a2 － 2)<0 且 a2－ 2>0 解得： a2>6 m/s2 方法三：图象法 如图所示，当速度相同时，阴影面积Δx 表示两者位移之 差，若Δx≤x0，则不会相撞，由几何关系得：
巧解追及相遇问题的三种方法 试题
上页
下页
解析
【典例3】 如图所示，物体从高度相同、路径不同的光滑 斜面上静止滑下，物体通过两条路径的长度相等，通过C点 前后速度大小不变．问：物体沿哪一路径先到达最低点？
沿A→C→D路径先到达最低点
答案
方法系列
巧解追及相遇问题的三种方法 试题
上页
下页
解析
物体由A→B做初速度为零的匀加速 直线运动，到B点时速度大小为vt； 物体由A→C做初速度为零的匀加速 直线运动，加速度比AB段的加速度 大．由C→D做匀加速直线运动，初 速度大小等于AC段的末速度大小，加速度比AB段的加速度 小，由机械能守恒到D点时的速度大小也为vt.根据上述运动 过程，画出物体运动的v－t图象，如图所示，我们获得一个 新的信息，根据通过的路径长度相等知道两条图线与横轴所 围“面积”相等，所以沿A→C→D路径滑下用的时间较短，故 先到达最低点．

计算：根据图像信息，计算物体的运动时间、速度、加速度等物理量
验证：验证计算结果是否符合物理规律，如速度、加速度、时间等是否合理
物理模型法
● 追及相遇问题的定义：两个物体在同一直线上运动，一个物体追赶另一个物体，最终相遇的问题。 ● 物理模型法的基本步骤： a. 确定研究对象：确定追及相遇问题的两个物体。 b. 建立物理模型：根据题目要求，建立追及相遇问
碰撞问题
火车相撞：火车在行驶过程 中，两列火车发生碰撞
飞机相撞：飞机在飞行过程 中，两架飞机发生碰撞
汽车追尾：汽车在行驶过程 中，后车与前车发生碰撞
船舶碰撞：船舶在航行过程 中，两艘船舶发生碰撞
追及相遇问题的实例解 析
追及问题实例解析
实例1： 汽车追及 问题
实例2： 火车追及 问题
实例3： 飞机追及 问题
0 4
速度是描述物体运动过程的一个参数，通常用v表示
0 时间、距离和速度之间的关系是：s=vt，其中s是距 5 离，v是速度，t是时间
0 在追及相遇问题中，时间、距离和速度的关系容易混淆， 6 需要仔细分析题目中的条件，正确理解三者之间的关系。
对加速度和初速度的理解不够深入
加速度：物体速度的变化率，与速度方向无关
● 物理模型法的优缺点： a. 优点：能够直观地描述追及相遇问题，便于理解和求解。 b. 缺点：需要一定的物理知识，对于复杂的 追及相遇问题，可能需要多次尝试才能找到合适的物理模型。 • a. 优点：能够直观地描述追及相遇问题，便于理解和求解。 • b. 缺点：需要一定的物理知识，对于复杂的追及相遇问题，可能需要多次尝试才能找到合适的物理模型。
实例4： 船舶追及 问题
实例5： 跑步追及 问题
实例6： 自行车追 及问题

追及和相遇问题1．解答追及和相遇问题的三种方法情景分析法抓住“两物体能否同时到达空间某位置”这一关键，认真审题，挖掘题目中的隐含条件，建立一幅物体运动关系的情景图函数判断法设相遇时间为t，根据条件列方程，得到关于位移x与时间t的函数关系，由此判断两物体追及或相遇情况图像分析法将两个物体运动的速度—时间关系或位移—时间关系画在同一图像中，然后利用图像分析求解相关问题[典例]汽车A以v A＝4 m/s的速度向右做匀速直线运动，发现前方相距x0＝7 m处、以v B＝10 m/s的速度同向运动的汽车B正开始匀减速刹车直到静止后保持不动，其刹车的加速度大小a＝2 m/s2。

从此刻开始计时。

求：(1)A追上B前，A、B间的最远距离是多少？(2)经过多长时间A恰好追上B?[解题指导]汽车A和B的运动过程如图所示。

[解析] (1)当A 、B 两汽车速度相等时，两车间的距离最远，即v ＝v B －at ＝v A ，解得t ＝3 s此时汽车A 的位移x A ＝v A t ＝12 m汽车B 的位移x B ＝v B t －12at 2＝21 m 故最远距离Δx max ＝x B ＋x 0－x A ＝16 m 。

(2)汽车B 从开始减速直到静止经历的时间t 1＝v B a＝5 s 运动的位移x B ′＝v B 22a＝25 m 汽车A 在t 1时间内运动的位移x A ′＝v A t 1＝20 m此时相距Δx ＝x B ′＋x 0－x A ′＝12 m汽车A 需再运动的时间t 2＝Δx v A＝3 s 故A 追上B 所用时间t 总＝t 1＋t 2＝8 s 。

[答案] (1)16 m (2)8 s[延伸思考](1)若某同学应用关系式v B t －12at 2＋x 0＝v A t 解得经过t ＝7 s(另解舍去)时A 恰好追上B 。

这个结果合理吗？为什么？(2)若汽车A 以v A ＝4 m /s 的速度向左匀速运动，其后方相距x 0＝7 m 处，以v B ＝10 m/s 的速度同方向运动的汽车B 正向左开始匀减速刹车直到静止后保持不动，其刹车的加速度大小为a ＝2 m/s 2，则经过多长时间两车恰好相遇？提示：(1)这个结果不合理，因为汽车B 运动的时间最长为t ＝v B a＝5 s ＜7 s ，说明汽车A 追上B 时汽车B 已停止运动。

相撞？
见全品练习册，20页的13题
方法一：设：经过时间t，人与车速度相等，
因
人追不上车。人车间的最小距离为
方法二：设：经过时间t，人与车相距S，
则S= S0+S车 - S人=25 + 0.5 t2 - 6 t 令S=0，既假设人能追上车，0.5 t2 - 6 t+25=0 因b2-4ac = （-6）2 -4×0.5×25=-14＜0,方程无 解,故人追不上车 当t=人车间的最小距离为 s =25 + 0.5×62 - 6× 6=7m 时，s有最小值
追及与相遇问题
一、追及问题：二者速度相等时相距最远 （或者最近） 1、后面加速，前面匀速，二者相距x 。一定 能追上，二者速度相等时相距最远 。
2、后面匀速，前面从静止加速，二者相距x 。 不一定能追上，二者速度相等时相距最远近。
2 例6、车从静止开始以1m/s 的加
速度前进，车后相距s0为25m处， 某人同时开始以6m/s的速度匀速 追车，能否追上？若追不上，求 人、车间的最小距离。

《追及与相遇问题》知识清单一、追及问题追及问题是指两个物体在同一直线上运动，速度不同，后面的物体追赶前面的物体。

解决追及问题的关键在于找出两个物体之间的位移关系和速度关系。

1、速度小者追速度大者（1）类型一：两者速度相等时，若追者位移仍小于被追者位移，则永远追不上，此时二者间有最小距离。

例如，一辆慢车以速度 v1 行驶，后面一辆快车以速度 v2（v2 ＞ v1）追赶。

在某一时刻，两车速度相等，如果此时快车的位移小于慢车的位移，那么快车就追不上慢车，并且两者之间的距离会达到最小值。

（2）类型二：若速度相等时，追者位移恰好等于被追者位移，则刚好追上，也是二者相遇时避免碰撞的临界条件。

假设慢车先行驶了一段距离 s0，然后快车开始追赶。

当两车速度相等时，如果快车的位移刚好等于慢车的位移加上 s0，那么快车刚好追上慢车。

（3）类型三：若速度相等时，追者位移大于被追者位移，则会追上并超过被追者。

之后被追者还可能再次追上追者，二者速度相等时的距离最大。

比如，快车在速度相等时超过了慢车，但慢车可能会因为速度逐渐增大，在之后的某个时刻再次追上快车。

此时，两车速度相等时的距离是最大的。

2、速度大者追速度小者（1）当两者速度相等时，如果还没追上，那么就追不上了，此时二者间有最大距离。

例如，快车速度 v2 ，慢车速度 v1（v2 ＞ v1），在速度相等之前，两车的距离一直在拉大，当速度相等时，距离达到最大值。

如果此时还没追上，之后就再也追不上了。

（2）当追上时，两者的位移关系为追者位移等于被追者位移加上初始的距离。

假设慢车先出发，与快车相距 s0，当快车追上慢车时，快车的位移就等于慢车的位移加上 s0 。

二、相遇问题相遇问题是指两个物体从不同的地点出发，相向而行，在某一时刻相遇。

1、相向运动的相遇两物体相向运动，相遇时它们的位移之和等于两物体出发时的距离。

比如，A 物体从甲地以速度 v1 向乙地运动，B 物体从乙地以速度v2 向甲地运动，它们出发时相距 s ，经过时间 t 相遇，则有 v1t ＋ v2t＝ s 。

第10讲追及相遇问题的分析技巧【方法指导】一、追及问题(1)特点：两个物体在同一时刻到达同一位置。

(2)满足的位移关系：x2＝x0＋x1。

其中x0为开始追赶时两物体之间的距离，x1表示前面被追赶物体的位移，x2表示后面追赶物体的位移。

(3)临界条件：v1＝v2。

当两个物体的速度相等时，可能出现恰好追上、恰好避免相撞、相距最远、相距最近等临界问题。

二、相遇问题(1)特点：在同一时刻两物体处于同一位置。

(2)条件：同向运动的物体追上即相遇；相向运动的物体，各自发生的位移的绝对值之和等于开始时两物体之间的距离时即相遇。

三、处理“追及”“相遇”问题的三种方法(1)物理方法：通过对物理情和物理过程的分析，找到临界状态和临界条件，然后列出方程求解。

(2)数学方法：由于匀变速运动的位移表达式是时间t的一元二次方程，我们可利用判别式进行讨论：在追及问题的位移关系式中，若Δ>0，即有两个解，说明相遇两次；Δ＝0，有一个解，说明刚好追上或相遇；Δ<0，无解，说明不能够追上或相遇。

(3)图象法：对于定性分析的问题，可利用图象法分析，避开繁杂的计算，快速求解。

【对点题组】1. A与B两个质点向同一方向运动，A做初速度为零的匀加速直线运动，B做匀速直线运动．开始计时时，A、B位于同一位置，则当它们再次位于同一位置时()A．两质点速度相等B．A与B在这段时间内的平均速度相等C．A的瞬时速度是B的2倍D．A与B的位移相同2.在平直公路上，自行车与同方向行驶的一辆汽车在t＝0时同时经过某一个路标，它们位移x(m)随时间t(s)变化规律为：汽车为x＝10t－14t2(m)，自行车为x＝6t(m)，则下列说法正确的是()A．汽车做减速直线运动，自行车做匀速直线运动B ．不能确定汽车和自行车各做什么运动C ．开始经过路标后较短时间内自行车在前，汽车在后D ．当自行车追上汽车时，它们距路标96 m3. 甲、乙两车在公路上沿同一方向做直线运动，它们的v t -图象如下图所示。

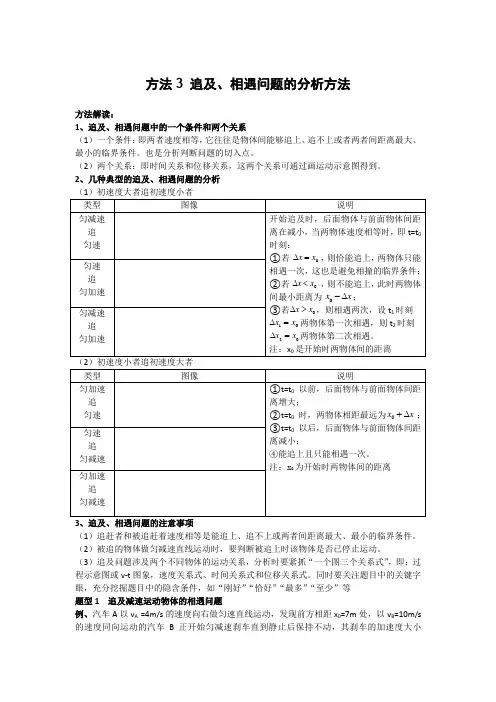
方法3 追及、相遇问题的分析方法方法解读：1、追及、相遇问题中的一个条件和两个关系（1）一个条件：即两者速度相等，它往往是物体间能够追上、追不上或者两者间距离最大、最小的临界条件。

也是分析判断问题的切入点。

（2）两个关系：即时间关系和位移关系，这两个关系可通过画运动示意图得到。

2、几种典型的追及、相遇问题的分析（1）初速度大者追初速度小者（1）追赶者和被追赶着速度相等是能追上、追不上或两者间距离最大、最小的临界条件。

（2）被追的物体做匀减速直线运动时，要判断被追上时该物体是否已停止运动。

（3）追及问题涉及两个不同物体的运动关系，分析时要紧抓“一个图三个关系式”，即：过程示意图或v-t图象，速度关系式、时间关系式和位移关系式。

同时要关注题目中的关键字眼，充分挖掘题目中的隐含条件，如“刚好”“恰好”“最多”“至少”等题型1 追及减速运动物体的相遇问题例、汽车A以v A =4m/s的速度向右做匀速直线运动，发现前方相距x0=7m处，以v B=10m/s 的速度同向运动的汽车B正开始匀减速刹车直到静止后保持不动，其刹车的加速度大小a=2m/s2. 从此刻开始计时，求：（1）A追上B前，A、B间的最远距离是多少?（2）经过多长时间A恰好能追上B?题型2 追及与相遇问题的多种解法例、在水平轨道上有两列火车A和B相距s，A车在后面做初速度为v0、加速度大小为2a 的匀减速直线运动，而B车同时做初速度为零、加速度为a的匀加速直线运动，两车运动方向相同。

要使两车不相撞，求A车的初速度v0满足什么条件。

题型3 追及、相遇中的极值与临界问题例、羚羊从静止开始奔跑，经过50m的距离能加速到最大速度25m/s,并能维持一段较长的时间。

猎豹从静止开始奔跑，经过60m的距离能加速到最大速度30m/s,但这个速度只能维持4.0s.设猎豹距离羚羊x时开始奔跑。

羚羊则从猎豹奔跑1.0s后才开始奔跑，假设羚羊和猎豹在加速阶段分别做匀加速运动且均沿同一直线。

2、当问题中的已知量为字母时，要注意解题思维的完整 性，同时还要注意“结论”成立的条件。
停下来的时间t2=v2/a2=20s,则B车先停下 来，要使两车不相碰 则有 使A、B不相碰应有
S ≧s1-s2=v1t-a1t12/2- (v2t-a2t22/2)=300m
点评：对于此类问题往往要分清不碰的条件，讨论前后物体谁
先停下，再找时间和位移关系求解。且用图象更能很好地帮助 解决问题。
反 思
变式1：若v1<v2，当相距S时， A车开始以加速度a做匀加速直线运动，问
A追上B前何时两车相距最远？最远距离多大？
分析：
A
v1 a
S
B V1=V2 a
v2
A
B
△S
v2
解答：当A车的速度达到V2时，两车相距最远，此过程中A车的
运动时间为：
最远距离
t=(V2-V1)2/a
△s=s+ v2t - (v1t+at2/2) = s+ (V2-V1)2/2a
分析： A
v1 a1 S
B
v2
a2
解答：
Ⅰ.A车停下来的时间为t1=v1/a1=40s，B车
停下来的时间t2=v2/a2=50s, 则有 V1-a1t=v2-a2t
设两车经历时间t时速度相等 得 t=33.3s
使A、B不相碰应有
S ≧s1-s2=v1t-a1t2/2- (v2t-a2t2/2)=166.7m
追及问题就是运动学中同一直线上两个运动物体的相 互追赶的问题
追及问题的特征：两个物体处于同一位置 追及问题的分析方法： 公式法 侧重运动过程分析和物理规律的运用 图象分析问题具有直观、简捷、物理意义明显 巧选参考系能使物体间的运动关系简单明了 运用二次函数的极值条件是物理学中常用的数学方法

考点一 追及相遇问题
方法一：物理分析法 假设再经t4时间两车第二次相遇(两车一直在运动)，由位移关系得vt4 － 12a2t42＝v0t4 解得t4＝15 s 赛车停下来的时间 t′＝av2＝440 s＝10 s 所以t4＝15 s不符合实际，两车第二次相遇时赛车已停止运动
考点一 追及相遇问题
设再经时间 t5 两车第二次相遇，应满足2va22＝v0t5，解得 t5＝20 s。 方法二：图像法 赛车和安全车的v－t图像如图。由图知t＝10 s， 赛车停下时，安全车的位移小于赛车的位移， 由v0t5＝2va22 ，得t5＝20 s。
考点二 图像中的追及相遇问题
当两车速度相等时，两车相距最远，由题图可知， 第 10 s 末时，两车速度相等，之间的距离最大。 0～10 s 内两车运动的位移分别为 x 甲′＝0＋2 6× 10 m＝30 m，x 乙′＝4＋2 6×10 m＝50 m，所以第 10 s 末两车相距 Δx′ ＝x 乙′－x 甲′＋x0＝45 m，故 C 错误；
返回
< 考点二 >
图像中的追及相遇问题
考点二 图像中的追及相遇问题
1.x－t图像、v－t图像中的追及相遇问题： (1)利用图像中斜率、面积、交点的含义进行定性分析或定量计算。 (2)有时将运动图像还原成物体的实际运动情况更便于理解。 2.利用v－t图像分析追及相遇问题：在有些追及相遇情景中可根据两个物 体的运动状态作出v－t图像，再通过图像分析计算得出结果，这样更直 观、简捷。 3.若为x－t图像，注意交点的意义，图像相交即代表两物体相遇；若为a －t图像，可转化为v－t图像进行分析。
考点二 图像中的追及相遇问题
例3 (多选)(2024·广东省四校联考)两车在不同的行车道上同向行驶，t＝ 0时刻，乙车在甲车前方25 m。两车速度—时间(v－t)图像分别为图中直 线甲和直线乙，交点坐标图中已标出，则 A.乙车的加速度是0.6 m/s2

追及与相遇问题追及相遇问题讨论追及、相遇问题的实质，就是分析两物体在相同时间内能否到达相同的空间位置．1．分析追及问题的方法技巧可概括为“一个临界条件”、“两个等量关系”．(1)一个临界条件——速度相等．它往往是物体间能否追上或(两者)距离最大、最小的临界条件，也是分析判断问题的切入点(2)两个等量关系：时间关系和位移关系，通过画草图找出两物体的位移关系是解题的突破口．2．能否追上的判断方法物体B追赶物体A：开始时，两个物体相距x0.若v A＝v B时，x A＋x0<x B，则能追上；若v A＝v B时，x A ＋x0＝x B，则恰好不相撞；若v A＝v B时，x A＋x0>x B，则不能追上．3．若被追赶的物体做匀减速直线运动，一定要注意判断追上前该物体是否已经停止运动．自行车以v 0＝6 m/s 的速度匀速驶来，从后边超过汽车，试问：(1)汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远？最远距离是多大？(2)当汽车与自行车距离最近时汽车的速度是多大？1、答案 (1)2 s 6 m (2)12 m/s解析 解法一 用临界条件求解(1)当汽车的速度为v 1＝v 0＝6 m/s 时，二者相距最远，所用时间为t 1＝v 1a＝2 s最远距离为Δx ＝v 0t 1－12at 21＝6 m. (2)两车距离最近时有v 0t 2＝12at 22 解得t 2＝4 s汽车的速度为v ＝at 2＝12 m/s.解法二 用图象法求解(1)汽车和自行车的v －t 图象如图所示，由图象可得t ＝2 s 时，二者相距最远．最远距离等于图中阴影部分的面积，即Δx ＝12×6×2 m ＝6 m. (2)两车距离最近时，即两个v －t 图线下方面积相等时，由图象得此时汽车的速度为v ＝` 12 m/s.2汽车以25 m /s 的速度匀速直线行驶，在它后面有一辆摩托车，当两车相距1 000 m 时，摩托车从静止起动做匀加速运动追赶汽车，摩托车的最大速度可达30 m /s ，若使摩托车在4 min 时刚好追上汽车．求：(1)摩托车做匀加速运动的加速度a.(2)摩托车追上汽车前两车相距最大距离x.2答案 (1)2.25 m /s 2 (2)1 138 m解析 (1)设汽车位移为x 1，摩托车位移为x 2摩托车的加速度为a ，摩托车达到最大速度所用时间为t ，则30 m /s ＝atx 1＝25×240 m ＝6 000 mx 2＝3022a ＋30(240－30a) 恰好追上的条件为x 2＝x 1＋1 000 m解得a ＝94m /s 2＝2.25 m /s 2 (2)摩托车与汽车速度相等时两车相距最远设此时刻为T ，最大距离为x max由运动学公式得25 m /s ＝aT解得T ＝1009 s 所以x max ＝1 000＋25T －aT 2210 2509m ＝1 138 m3 甲车以10 m/s 的速度在平直的公路上匀速行驶，乙车以4 m/s 的速度与甲车平行同向做匀速直线运动．甲车经过乙车旁边时开始以0.5 m/s 2的加速度刹车，从甲车刹车开始计时，求：(1)乙车在追上甲车前，两车相距的最大距离；(2)乙车追上甲车所用的时间．3解析 (1)当甲车速度减至等于乙车速度时两车的距离最大，设该减速过程所用时间为t ，则有v 乙＝v 甲－at ，解得t ＝12 s ，此时甲、乙间距离为v 甲t －12at 2－v 乙t ＝36 m (2)设甲车减速到零所需时间为t 1，则有t 1＝v 甲a＝20 s t 1时间内，x 甲＝v 甲2t 1＝102×20 m ＝100 m x 乙＝v 乙t 1＝4×20 m ＝80 m此后乙车运动时间t 2＝x 甲－x 乙v 乙＝204 s ＝5 s 故乙车追上甲车需t 1＋t 2＝25 s.4、(2011·江苏海安模拟)一辆值勤的警车停在公路边，当警员发现从他旁边以v ＝10 m /s 的速度匀速行驶的货车严重超载时，决定前去追赶，经过5.5 s 后警车发动起来，并以2.5 m /s 2的加速度做匀加速运动，但警车的行驶速度必须控制在90 km /h 以内．问：(1)警车在追赶货车的过程中，两车间的最大距离是多少？(2)判定警车在加速阶段能否追上货车．(要求通过计算说明)(3)警车发动后要多长时间才能追上货车？答案 (1)75 m (2)不能 (3)12 s4解析 (1)警车在追赶货车的过程中，当两车速度相等时，它们的距离最大，设警车发动后经过t 1时间两车的速度相等．则t 1＝102.5s ＝4 s x 货＝(5.5＋4)×10 m ＝95 mx 警＝12at 21＝12×2.5×42 m ＝20 m ；所以两车间的最大距离Δx ＝x 货－x 警＝75 m . (2)v m ＝90 km /h ＝25 m /s ，当警车刚达到最大速度时，运动时间t 2＝252.5s ＝10 s x 货′＝(5.5＋10)×10 m ＝155 mx 警′＝12at 22＝12×2.5×102 m ＝125 m 因为x 货′>x 警′，故此时警车尚未赶上货车．(3)警车刚达到最大速度时两车距离Δx ′＝x 货′－x 警′＝30 m ，警车达到最大速度后做匀速运动，设再经过Δt 时间后追赶上货车．则Δt ＝Δx ′v m －v＝2 s 所以警车发动后要经过t ＝t 2＋Δt ＝12 s 才能追上货车．【例1】一辆汽车在十字路口等汽车，当绿灯亮时汽车以3m/s2的加速度开始行驶，这时恰好一辆自行车以6m/s匀速驶来，从后面超过汽车（1）汽车从路口开动后，在追上自行车之前经过多少时间两车相距最远？距离是多少？（2）什么时候汽车能追上自行车，此时汽车的速度为多少？【例2】一列货车以28.8 km/h(8m/s)的速度在平直铁路上运行，由于调度失误，在后面600 m 处有一列快车以72 km/h(20m/s)的速度向它靠近。

《追及与相遇问题》知识清单一、追及问题追及问题是指两个物体在同一直线上运动时，速度快的物体追赶速度慢的物体的问题。

1、速度小者追速度大者（1）类型一：两者速度相等时，若追者位移仍小于被追者位移，则永远追不上，此时两者间有最小距离。

比如，一辆慢车在前面行驶，一辆快车在后面追赶。

当两车速度相等时，如果快车还没有追上慢车，那么之后就再也追不上了，而且此时两车的距离是最小的。

（2）类型二：两者速度相等时，若追者位移等于被追者位移，则恰好追上，也是两者相遇时避免碰撞的临界条件。

假设一个行人在前面走，后面有一辆摩托车以较快的速度追赶。

当摩托车的速度和行人的速度相等时，如果此时摩托车刚好追到行人，那么这就是恰好追上的情况。

（3）类型三：两者速度相等时，若追者位移大于被追者位移，则会追上并超过被追者，之后被追者还可能再次追上追者。

就像一辆汽车追赶一辆自行车，当汽车速度和自行车速度相等时，汽车已经超过了自行车。

但如果自行车继续前进，而汽车减速，自行车有可能又会追上来。

2、速度大者追速度小者（1）当两者速度相等时，若还没有追上，则永远追不上。

比如一辆快速行驶的跑车追赶一辆速度较慢的普通轿车，如果在跑车和轿车速度相等时，跑车还没追上轿车，那之后就追不上了。

（2）当两者速度相等时，两者间有最大距离。

例如，一只兔子在前跑，一只猎狗在后追。

当猎狗速度和兔子速度相等时，此时它们之间的距离是最大的。

二、相遇问题相遇问题是指两个物体相向运动，经过一段时间后在途中相遇。

1、相向运动的相遇两物体相向运动，相遇时它们走过的路程之和等于两物体初始位置之间的距离。

比如 A 地和 B 地相距 100 千米，一辆车从 A 地出发以 40 千米/小时的速度行驶，另一辆车从 B 地出发以 60 千米/小时的速度行驶，那么它们经过多长时间会相遇呢？这就是一个典型的相向运动的相遇问题，通过两者速度之和乘以时间等于总路程，可以计算出相遇时间。

2、同向运动的相遇这种情况通常发生在环形跑道上。

考点三：追及和相遇问题1.“追及”、“相遇”的特征“追及”的主要条件是：两个物体在追赶过程中处在同一位置。

两物体恰能“相遇”的临界条件是两物体处在同一位置时，两物体的速度恰好相同。

2.解“追及”、“相遇”问题的思路（1）根据对两物体的运动过程分析，画出物体运动示意图（2）根据两物体的运动性质，分别列出两个物体的位移方程，注意要将两物体的运动时间的关系反映在方程中（3）由运动示意图找出两物体位移间的关联方程（4）联立方程求解1. 分析“追及”、“相遇”问题时应注意的问题（1） 抓住一个条件：是两物体的速度满足的临界条件。

如两物体距离最大、最小，恰好追上或恰好追不上等；两个关系：是时间关系和位移关系。

（2） 若被追赶的物体做匀减速运动，注意在追上前，该物体是否已经停止运动2. 解决“追及”、“相遇”问题的方法（1） 数学方法：列出方程，利用二次函数求极值的方法求解（2） 物理方法：即通过对物理情景和物理过程的分析，找到临界状态和临界条件，然后列出方程求解习题21. 关于位移和路程的下列说法中，正确的是A. 物体沿直线朝某一方向运动时，通过的路程就是位移B. 几个运动物体有相同位移时，它们的路程也一定相同C. 几个运动物体通过的路径不等，但它们的位移可能相同D. 物体通过的路程不等于零，其位移也不等于零2. 如图是A 、B 两个物体做直线运动的速度图象，下列说法正确的是A. 物体A 做加速直线运动B. 物体B 做减速直线运动C. 物体A 的加速度为正值，B 的加速度为负值，所以A 的加速度大于B 的加速度D. 物体B 的速度变化比A 的速度变化快3. 甲、乙两车同时同向沿直线驶向某地。

甲在前一半时间内以速度1v 匀速运动，后一半时间内以速度2v 匀速运动；而乙车在前一半路程上以速度1v 匀速运动，后一半路程上以速度2v 匀速运动。

试问：哪辆车先到达目的地？4. 一物体做匀变速直线运动，某时刻速度的大小为4s m /，1 s 后速度的大小变为10s m /，在这1 s 内该物体的A. 速度变化的大小可能小于4s m /B. 速度变化的大小可能大于10s m /C. 加速度的大小可能小于4 2/s mD. 加速度的大小可能大于102/s m5. 天空有近似等高的浓云层，为了测量云层的高度，在水平地面上与观测者的距离为d ＝3.0km 处进行一次爆炸，观测者听到由空气直接传来的爆炸声和由云层反射来的爆炸声时间上相差t ＝6.0s.试估算云层下表面的高度。

追及、相遇问题一、问题实质讨论追及、相遇问题，其实质就是分析讨论两物体在同一时刻能否到达相同的空间位置。

二、关注两个关系和一个条件1.两个关系：时间关系和位移关系。

2.一个条件：两者的速度相等，它往往是物体间能否追上、追不上或(两者)距离最大、最小的临界条件，也是分析判断问题的切入点。

三、解决追及、相遇问题的思路和方法1.思路：（1）分析两物体的运动过程；（2）画运动示意图；（3）找两物体位移关系；找两物体速度关系；（4）列相关方程求解。

2.方法：（1）物理分析法：通过对物理情景和物理过程的分析，找到临界状态和临界条件，然后列出方程求解。

（2）数学解析法：因为在匀变速直线运动的位移表达式中有时间的二次方，我们可以列出方程，利用二次函数求极值的方法求解。

（3）图像法：利用v-t图像分析。

利用v-t图像的图线与时间轴所围成的面积表示物体对应的位移来判断两物体的位移差值，结合两物体的初位置间的距离来判断相遇的情况。

【典型例题】题型一、匀加速追匀速1.一辆汽车在十字路口等信号灯，当绿灯亮时汽车以3m/s2的加速度开始行驶。

恰在这时一辆自行车以6m/s的速度匀速驶来，从后边超过汽车。

试求：(1)汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远，此时距离是多少。

(2)什么时候汽车追上自行车，此时汽车的速度是多少。

题型二、匀减速追匀速1.火车A以v1=20m/s的速度匀速直线行驶，司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s的速度匀速行驶，A车立即做加速度大小为a的匀减速直线运动。

要使两车不相撞，a应满足什么条件？题型三、匀减速追匀减速1.有甲、乙两汽车正沿同一平直马路同向匀速行驶，甲车在前，乙车在后，若甲、乙两车均以15m/s的速度驶向路口，当两车快要到十字路口时，甲车司机看到黄灯闪烁(黄灯闪烁时间为3s)。

此时甲车车头距停车线L=30m，已知甲车紧急刹车时的加速度大小为5m/s2.(反应时间内视为匀速运动)请问：(1)要避免闯红灯，甲车司机的反应时间△t1不能超过多少？(2)乙车司机看到甲车刹车后也紧急刹车，乙车司机的反应时间△t2=0.4s，紧急刹车时的加速度大小为6m/s2，为保证两车在紧急刹车过程中不相撞，甲、乙两车刹车前的距离X0至少多大？练习题1.一辆汽车在十字路口等绿灯，当绿灯亮时汽车以3m/s2的加速度开使行驶，恰在这时一辆自行车在汽车后方相距20m的地方以6m/s的速度匀速行驶，则自行车能否追上汽车？若追不上，两车间的最小间距是多少？2.现检测汽车A的制动性能：以标准速度20m/s在平直公路上行驶时，制动后40s停下来.若A在平直公路上以20m/s的速度行驶时发现前方180m处有一货车B以6m/s 的速度同向匀速行驶，司机立即制动，能否发生撞车事故？3.为了安全，在公路上行驶的汽车之间应保持必要的距离．已知某高速公路的最高限速v＝120km／h．假设前方车辆突然停止，后车司机从发现这一情况，经操纵刹车，到汽车开始减速所经历的时间（即反应时间）t＝0.50s．刹车时汽车的加速度为a=4m／s2．该高速公路上汽车间的距离s至少应为多少？(取重力加速度g=10m／s2．)4.某地出现雾霾天气，能见度只有200m，即看不到200m以外的情况，A、B两辆汽车沿同一公路同向行驶，A车在前，速度v A=10m/s,B车在后，速度v B=30m/s，B车在距A车200m 处才发现前方的A车，这时B车立即以最大加速度a=0.8m/s2刹车，求：(1)B车撞上A车时的速度。

《追及与相遇问题》知识清单在我们的日常生活和物理学的学习中，追及与相遇问题是一个常见且重要的课题。

无论是在公路上的车辆行驶，还是在运动场上的运动员奔跑，都可能涉及到追及与相遇的情况。

理解和掌握这一问题，对于我们解决实际问题和提高物理思维能力都有着重要的意义。

一、追及问题追及问题，简单来说就是两个物体在同一直线上运动，速度快的物体追赶速度慢的物体。

1、速度小者追速度大者类型一：两者速度相等时，若还未追上，则永远追不上，此时两者距离有最小值。

比如，甲车以速度 v1 匀速行驶，乙车从静止开始以加速度 a 匀加速追赶甲车。

在乙车速度达到 v1 之前，两车的距离会越来越大；当乙车速度等于 v1 时，两车的距离达到最大值。

类型二：两者速度相等时，如果刚好追上，这是一个临界状态，也是相遇一次的情况。

假设甲车在前以速度 v1 匀速行驶，乙车在后以初速度 v0 匀加速追赶。

当乙车速度达到 v1 时，如果此时刚好追上甲车，那么这就是刚好追上的情况。

类型三：两者速度相等时，如果已经超过，那就会相遇两次。

还是上面的例子，若乙车速度达到 v1 时，已经超过甲车，之后甲车又可能反超乙车，从而形成两次相遇。

2、速度大者追速度小者两者速度相等时，如果还没追上，那么此时两者距离最小。

比如，甲车以较大速度 v1 匀速行驶，乙车以较小速度 v2 匀速行驶，甲车在后追赶乙车。

在甲车速度减小到 v2 之前，两车的距离会逐渐缩小；当甲车速度等于 v2 时，两车的距离达到最小值。

速度相等时如果已经追上，则会一直领先，不会再被追上。

二、相遇问题相遇问题是指两个物体从不同位置出发，相向而行，最终相遇。

1、相向运动的相遇两物体同时出发到相遇，所经历的时间相等，走过的路程之和等于两物体初始位置之间的距离。

例如，A 地的甲车以速度 v1 驶向 B 地，同时 B 地的乙车以速度 v2 驶向 A 地，经过时间 t 后两车相遇，那么就有 v1×t ＋ v2×t ＝两地点之间的距离。

13
解析：画出示意图，如图所示，甲追上乙时，x甲＝x0＋x
乙
，且t甲＝t乙(追及条件)，根据匀变速直线运动、匀速直线运
动的位移公式列出方程，即能解得正确的结果。
14
1 (1)设甲经过时间t追上乙，则有x甲＝ a甲t2，x乙＝v乙t，根 2 1 2 据追及条件，有 a甲t ＝x0＋v乙t，代入数值，解得t＝40s和t＝ 2 －20s(舍去) 这时甲的速度v甲＝a甲t＝0.5×40m/s＝20m/s 甲离出发点的位移 1 2 1 x甲＝ a甲t ＝ ×0.5×402m＝400m。 2 2
LC＝sA＋sB＝20m＋40m＝60m
26
(3)解①式得驾驶员的正常反应时间 s1 10 t＝ ＝ s＝0.9s v1 40 3.6 喝了酒的驾驶员的反应时间： t′＝t＋0.1s＝(0.9＋0.1)s＝1.0s 在反应时间内汽车行驶的距离： 72 s＝vt′＝ ×1.0m＝20m 3.6
27
v2 722 刹车距离：x＝ 2· x ＝ ×10m＝32.4m v1 1 402 停车距离：L＝s＋x＝(20＋32.4)m＝52.4>当甲的速度小于乙的速度时，甲、乙 之间的距离仍在继续增大；但当甲的速度大于乙的速度时， 甲、乙之间的距离便不断减小；当v甲＝v乙，甲、乙之间的距 v乙 5 离达到最大值。由a甲t＝v乙，得t＝ ＝ s＝10s。即甲在10s a甲 0.5 末离乙的距离最大。 1 2 xmax＝x0＋v乙t－ a甲t 2 1 ＝200m＋5×10m－ ×0.5×102m＝225m。 2
36
某同学求解过程如下：
2 2 由运动学知识有v2 － v ＝ 2 aL ，解得 v ＝ v 0 0－2aL。
代入数据后得到 v＝ 602－2×4.5×289m/s＝ 999m/s＝31.6m/s。 经检查，计算无误。该同学所得结论是否有错误或不完 善之处？若有，请予以改正或补充。

追及、相遇问题1．分析“追及”问题应注意的几点 (1)一定要抓住“一个条件，两个关系”：①“一个条件”是两物体的速度满足的临界条件，如两物体距离最大、最小，恰好追上或恰好追不上等．②“两个关系”是时间关系和位移关系．其中通过画草图找到两物体位移之间的数量关系，是解题的突破口．(2)若被追赶的物体做匀减速运动，一定要注意被追上前该物体是否已停止运动．(3)仔细审题，注意抓住题目中的关键字眼(如“刚好”、“恰好”、“最多”、“至少”等)，充分挖掘题目中的隐含条件．2．主要方法①临界条件法②图象法③数学法【典例4】一辆汽车在十字路口等待绿灯，当绿灯亮时汽车以a＝3 m/s2的加速度开始行驶，恰在这时一人骑自行车以v0＝6 m/s的速度匀速驶来，从后边超过汽车，试问：(1)汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远？最远距离是多大？(2)当汽车与自行车距离最近时汽车的速度是多大？解析方法一用临界条件求解v(1)当汽车的速度为v＝6 m/s时，二者相距最远，所用时间为t＝a＝2 s 1最远距离为Δx＝v0t－2at2＝6 m. 1(2)两车距离最近时有v0t′＝2at′2 解得t′＝4 s汽车的速度为v＝at′＝12 m/s.方法二用图象法求解(1)汽车和自行车的v -t图象如图所示，由图象可得t＝2 s时，二者相距最1远．最远距离等于图中阴影部分的面积，即Δx＝2×6×2 m＝6 m.(2)两车距离最近时，即两个v -t图线下方面积相等时，由图象得此时汽车的速度为 v＝12 m/s.方法三用数学方法求解1(1)由题意知自行车与汽车的位移之差为Δx＝v0t－2at2 －v0因二次项系数小于零，当t＝＝2 s时有最大值?1?2×?－2a???121最大值Δxm＝v0t－2at＝6×2 m－2×3×22m＝6 m. 1(2)当Δx＝v0t－2at2＝0时相遇得t＝4 s，汽车的速度为v＝at＝12 m/s. 答案 (1)2 s 6 m (2)12 m/s反思总结求解追及相遇问题的一般思路【跟踪短训】5．如图1－2－7所示，直线MN表示一条平直公路，甲、乙两辆汽车原来停在A、B 两处，A、B间的距离为85 m，现甲车先开始向右做匀加速直线运动，加速度a1＝2.5m/s2，甲车运动6.0 s时，乙车开始向右做匀加速直线运动，加速度a2＝5.0 m/s2，求两辆汽车相遇处距A处的距离．图1－2－71解析甲车运动6 s的位移为x0＝2a1t20＝45 m11此时甲车尚未追上乙车，设此后经过时间t与乙车相遇，则有2a1(t＋t0)2＝2a2t2＋85 m将上式代入数据并整理得：t2－12t＋32＝0 解得：t1＝4 s，t2＝8 st1、t2都有意义，t1＝4 s时，甲车追上乙车；t2＝8 s时，乙车追上甲车再次相遇1第一次相遇地点距A的距离：x1＝2a1(t1＋t0)2＝125 m 1第二次相遇地点距A的距离：x2＝2a1(t2＋t0)2＝245 m. 答案 125 m或245 m思想方法 2.思维转化法思维转化法：在运动学问题的解题过程中，若按正常解法求解有困难时，往往可以通过变换思维方式、转换研究对象，使解答过程简单明了．1．逆向思维法将匀减速直线运动直至速度变为零的过程转化为初速度为零的匀加速直线运动，利用运动学规律可以使问题巧解．【典例1】一物块(可看作质点)以一定的初速度从一光滑斜面底端A点上滑，最高可滑至C点，已知AB是BC的3倍，如图1－2－8所示，已知物块从A至B所需时间为t0，则它从B经C再回到B，需要的时间是( )．图1－2－8t0t0A．t0 B.4 C．2t0 D.2解析将物块从A到C的匀减速直线运动，运用逆向思维可看作从C到A的初速度为零的匀加速直线运动，根据初速度为零的匀加速直线运动规律，可知连续相邻相等的时间内位移之比为奇数比，而CB∶AB＝1∶3，正好符合奇数比，故tAB＝tBC＝t0，且从B到C 的时间等于从C到B的时间，故从B经C再回到B需要的时间是2t0，C对．答案 C即学即练1 做匀减速直线运动的物体经4 s后停止，若在第1 s内的位移是14 m，则最后1 s内的位移是( )．A．3.5 mB．2 m C．1 m D．0解析设加速度大小为a，则开始减速时的初速度大小为v0＝at＝4a，第1 s12内的位移是x1＝v0t1－2at21＝3.5a＝14 m，所以a＝4 m/s，物体最后1 s的位移是12x＝2at1＝2 m.本题也可以采用逆向思维的方法，把物体的运动看作是初速度为零的匀加速直线运动，其在连续相邻相等的时间内的位移之比是1∶3∶5∶7，已知第4 s内的位移是14 m，所以第1 s内的位移是2 m.答案 B 2．等效转化法“将多个物体的运动”转化为“一个物体的运动”．【典例2】屋檐每隔一定时间滴下一滴水，当第5滴正欲滴下时，第1滴刚好落到地面，而第3滴与第2滴分别位于高1 m的窗子的上、下沿，如图1－2－9所示，(g取10m/s2)问：图1－2－9(1)此屋檐离地面多高？(2)滴水的时间间隔是多少？解析如图所示，如果将这5滴水运动等效为一滴水的自由落体，并且将这一滴水运动的全过程分成时间相等的4段，设每段时间间隔为T，则这一滴水在0时刻、T末、2T 末、3T末、4T末所处的位置，分别对应图示第5滴水、第4滴水、第3滴水、第2滴水、第1滴水所处的位置，据此可作出解答．设屋檐离地面高为x，滴水间隔为T.则x＝16x0,5x0＝1 m 所以x＝3.2 m 1另有x＝2g(4T)2 解得T＝0.2 s答案 (1)3.2 m (2)0.2 s即学即练2 从斜面上某一位置，每隔0.1 s释放一个小球，在连续释放几颗小球后，对在斜面上滚动的小球拍下照片，如图1－2－10所示，测得xAB＝15 cm，xBC＝20 cm，求：图1－2－10(1)小球的加速度； (2)拍摄时B球的速度； (3)拍摄时xCD的大小；(4)A球上方滚动的小球还有几颗．xBC－xABΔx解析 (1)由a＝t2得小球的加速度a＝t2＝5 m/s2 (2)B点的速度等于AC段上的平均速度，即 xACvB＝2t＝1.75 m/s感谢您的阅读，祝您生活愉快。

《追及与相遇问题》知识清单在我们的日常生活和物理学的学习中，追及与相遇问题是一个常见且重要的课题。

理解和解决这类问题，不仅有助于我们应对各种实际场景，还能培养我们的逻辑思维和分析能力。

一、追及问题追及问题，简单来说就是两个物体在同一直线上运动，速度快的物体追赶速度慢的物体。

要解决追及问题，关键是要找出两个物体在运动过程中的位移关系、速度关系和时间关系。

1、速度小者追速度大者（1）两者速度相等时，如果还没有追上，那么此时两者之间的距离最大。

（2）如果在速度相等之前已经追上，那么追上时就是追及成功的时刻。

例如，甲车以 5m/s 的速度匀速行驶，乙车从静止开始以 2m/s²的加速度加速追赶甲车。

在乙车速度达到 5m/s 之前，两车的距离是不断增大的；当乙车速度达到 5m/s 时，两车的距离达到最大；之后乙车的速度大于甲车，距离开始逐渐减小，直到乙车追上甲车。

2、速度大者追速度小者（1）速度大者减速追赶速度小者时，在速度相等之前，如果两者的位移之差小于初始距离，那么就追不上；如果位移之差等于初始距离，恰好追上；如果位移之差大于初始距离，就会发生碰撞。

（2）速度大者匀速追赶速度小者时，如果两者的速度相等时，位移之差小于初始距离，那么就追不上。

比如，一辆速度为 15m/s 的汽车去追赶前方 80m 处速度为 5m/s 的自行车。

汽车以 1m/s²的加速度减速行驶，当汽车速度减到 5m/s 时，如果此时位移之差小于 80m，就追不上自行车。

二、相遇问题相遇问题可以分为相向运动的相遇和同向运动的相遇。

1、相向运动的相遇两个物体分别从两地相向而行，它们相遇时，走过的路程之和等于两地之间的距离。

假设 A、B 两地相距 1000 米，甲从 A 地以 3m/s 的速度出发，乙从B 地以 2m/s 的速度出发，经过一段时间 t 后，两人相遇。

则根据路程=速度×时间，可得到 3t ＋ 2t ＝ 1000，从而求出相遇时间 t。