当前位置：文档之家 › 离散数学函数

离散数学函数

  • 格式：ppt
  • 大小：1.32 MB
  • 文档页数：93

下载文档原格式

  / 93

合集下载

离散数学 第三章 函数

离散数学 第三章 函数


下面先规定几个标准集合的基数： 1) 空集的基数为0。 2) 设n为一自然数，Nn为从1到n的连贯的自然数集合， Nn={1,2,3,…,n}，Nn的基数为n，|Nn|=n 。 3) 设N为自然数的全体，N={1,2,3,…},N的基数为ℵ0(读成 阿列夫零， ℵ是希伯莱文的第一个字母)。 4) 设R为实数的全体，R的基数为ℵ ,|R|= ℵ 。 • • 以上四项规定，对于空集及Nn的基数，实际上就是集 合中元素的个数，关于ℵ0及ℵ，下面将予探讨。 有了标准基数之后，我们可以对各种集合测量其基数。 测量的手段是以双射函数为主体的等价关系一等势。 比如说，一个集合与N等势，那么这个集合的基数为 ℵ0 。
定理6 设A及B为两个可数集，那么A×B为一可数集。 定理 推论1 推论 设A1,A2,A3,…,An为n个可数集，那么 × A是可数集。
i=1 i n
定理7 (0,1)开区间上的实数不是可数集。 定理 定理8 设A为一集Y的函数，若f 是双射函数，则f 的逆关系 f –1是从Y到X的双射函数。 定理2 定理 设f 是从X到Y的函数，g 是从Y到Z的函数，则复合关 系f οg是从 X到Z的函数，将f ο g记为g ο f 。 定理3 定理 设f 是从X到Y的函数，g 是从Y到Z的函数。 1）若f 和g是满射函数，则g ο f 是满射函数； 2）若f 和g是单射函数，则g ο f 是单射函数； 3）若f 和g是双射函数，则g ο f 是双射函数。 定理4 定理 设f 是从X到Y的双射函数， f –1是f 的逆函数，则 1) (f –1) –1 = f 2) f –1 ο f = IX 3) f ο f –1 = IY
定义3 定义 设 |X|=n，P是从X到X的双射函数，称P为X上的置 换，称n为置换的阶。 • 在n个元素的集合中，不同的n阶置换的个数为n!。 • 通常用下面的方法表示置换。 x1 x2 x3 … xn P = p(x ) p(x ) p(x ) … p(x ) 1 2 3 n • 若∀xi∈X 有 p(xi) = xi ，则称P是恒等置换。 • P的逆函数P-1可表示为 p(x1) p(x2) p(x3) … p(xn) P-1 = x1 x2 x3 … xn • 置换的复合与关系的复合相同。 1 2 3 1 2 3 1 2 3 3 2 1 2 1 3 3 1 2
离散数学-----函数

离散数学-----函数


2019/12/13
11
计算机科学学院 刘芳
8.2 函数的性质
解 (1) f : R→R, f(x)= x2+2x1
在x=1取得极大值0. 既不是单射也不是满射的.
(2) f : Z+→R, f(x)=lnx
单调上升, 是单射的. 但不满射, ranf={ln1, ln2, …}.
(3) f : R→Z, f(x)= x
8.1 函数的定义
例3：
设A ＝ {1, 2, 3}, B ＝ {a, b}，则A到B共有多少个不
同的函数？分别列出来。
解：
f0={<1,a>,<2,a>,<3,a>} , f2={<1,a>,<2,b>,<3,a>} , f4={<1,b>,<2,a>,<3,a>},
f6={<1,b>,<2,b>,<3,a>} ,
BA＝{f | f : A→B}
思考：设|A|=m,|B|=n,则|BA|=？
2019/12/13
7
计算机科学学院 刘芳
8.1 函数的定义
解：
设：A={x1, x2, …,xm}, B={y1, y2, …,yn}, 则集合A到B的函数f形如：
f＝{<x1,□>， {<x2,□>，…… {<xm,□>} 对于每个□所在的 位置都可用B中的任何一个
2019/12/13
19
计算机科学学院 刘芳
8.4 函数的复合和反函数
定理8.1
设f, g是函数, 则f∘g也是函数, 且满足
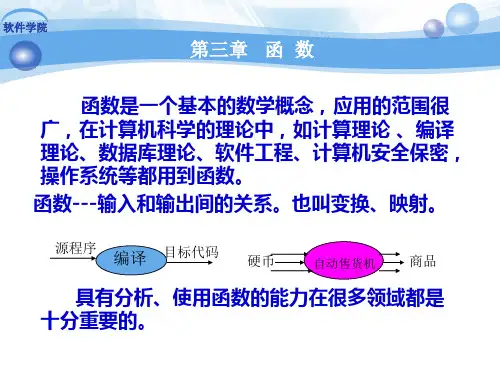
离散数学第3章 函数

离散数学第3章 函数

f:X Y 。 a 1。 。 b 2。 。 3。 c fC:Y X 。 1 a。 。 2 b。 。 3 c。
显然fC不是函数。可见如果一个函数不是双射的， 它的逆就不是函数。
软件学院
第三章 函 数 2.自变元与函数值(像源与映像) ：
f:XY, 如果<x,y>∈f,称x是自变元(像源)，称 y是x 的函数值(x的映像) 。
<x,y>∈f y=f(x) f:XY 3.定义域、值域 ：f:XY, f的定义域，记作Df 即
Df ={x|x∈X，y(y∈Y，<x,y>f)} =X

注意:这里把g写在f的左边了.所以叫左复合. g f :XZ,即 g f 是X到Z的函数.这样写是为了

照顾数学习惯: g f(x)=g(f(x))

复合函数的计算方法同复合关系的计算.
软件学院
复合函数
例1 f:XY, g:YZ X={1,2,3} Y={1,2,3,4,} Z={1,2,3,4,5,} f= {<1,2>,<2,4>,<3,1>} g={ <1,3>,<2,5>,<3,2>,<4,1> } g f={ <1,3>,<2,5>,<3,2>,<4,1> } {<1,2>,<2,4>,<3,1>} ={<1,5>,<2,1>,3,3>} g f g 用有向图复合: f X Z X Y X 。 1 。 。 。 1 。 1 1 1 。 2 。 2 。 。 2 。 2。 3 。 2 3 。 。 3。 4 。 4 3。 3 。 。 5 。 5
离散数学-第八章函数

离散数学-第八章函数


例8.5 对于以下各题给定的A,B和f，判断是否构成函 数f：A→B。如果是，说明 f：A→B是否为单射，满 射，双射的，并根据要求进行计算。 (1) A={1,2,3,4,5}, B={6,7,8,9,10}, f={<1,8>,<3,9>,<4,10>,<2,6>,<5,9>} 能构成函数f：A→B，但f：A→B既不是单射也不是 满射的。 (2) A,B同（1），f={<1,7>,<2,6>,<4,5>,<1,9>,<5,10>}
令f：A→B，使得f()=f0，f({1})=f1，f({2})=f2，f({3})=f3， f({1,2})=f4，f({1,3})=f5，f({2,3})=f6，f({1,2,3})=f7
(2) A=[0,1]，B=[1/4,1/2]
令f：[0,1]→[1/4,1/2]，f(x)=(x+1)/4. (3) A=Z，B=N 将Z中元素以下列顺序排列并与N中元素对应：
例8.1 设 F1={<x1,y1>,<x2,y2>,<x3,y2>} F2={<x1,y1>,<x1,y2>} 判断它们是否为函数。 解：F1是函数，F2不是函数。
因为对应于x1存在y1和y2满足x1F2y1和x1F2y2， 与函数定义矛盾。
F 是函数（映射） 对于x1，x2∈A， 如果x1=x2 ，一定有f(x1)＝f(x2)。即， 如果对于x1，x2∈A有f(x1) ≠f(x2)，则一定有x1≠x2
函数是集合，可以用集合相等来定义函数的相等
定义8.2 设F，G为函数，则 F=G F G∧G F 由以上定义可知，如果两个函数F和G相等，一 定满足下面两个条件： 1．domF=domG 2． x∈domF=domG都有F(x)=G(x)
离散数学第05章 函数

离散数学第05章 函数


g=f∩(CB)
则称g是f到C的缩小，记为f|c，即g为C到B 的函数：
g:CB
g(x)=f(x)
或
f|c(x)=f(x)
定义5.1.4 设f:CB，g:AB，且CA，
若g|c=f，则称g是f到A的扩大。
下面讨论由集合A和B，构成这样函数 f:AB会有多少呢？或者说，在AB的所有子 集中，是全部还是部分子集可以定义函数？令 BA表示这些函数的集合，即
定理5.3.1 设f:AB和g:BC是函数，通 过复合运算o，可以得到新的从A到C的函数， 记为gof，即对任意aA，有(gof)(x)=g(f(x))。
注意，函数是一种关系，今用斜体“o”表 示函数复合运算，记为gof，这是“左复合”， 它与关系的“右复合”fog次序正好相反，为区 分它们在同一公式中的出现，用粗体符号表示 关系复合fog，故有gof=fog。
BA={f|f:AB}
设 |A|=m ， |B|=n ， 则 |BA|=nm 。 这 是 因 为 对 每个自变元，它的函数值都有n种取法，故总共 有nm种从A到B的函数。
上面介绍一元函数，下面给出多元函数的 定义。
n 定义5.1.5 设A1,A2,···,An和B为集合，若f:
AiB 为 函 数 ， 则 称 f 为 n 元 函 数 。 在
f={<a,a>|xA} 则称f:AA为A上恒等函数，通常记为IA， 因为恒等关系即是恒等函数。 由定义可知，A上恒等函数IA是双射函数。
定义5.2.6 设A和B为集合，且AB，若函 数A:B{0,1}为
{xA(x)=
1 xA
0 否则
则称xA为集合A的特征函数。
特征函数建立了函数与集合的一一对应关 系。于是，可通过特征函数的计算来研究集合 上的命题。
离散数学第五章 函数

离散数学第五章 函数

f -1({0})={0, 1}, f -1({1})={2, 3}, f -1(Ø)= Ø
像与逆像: 映射的“提升”
设U和V是两个集合， f : U→V 是从U到V的一个函数， ρ(U)是U的幂集，ρ(V)是V的幂集。
像与逆像将从U到V的一个映射 f : U→V “提升” 为从U的幂集 ρ(U) 到V的幂集 ρ(V) 的映射
集合 A 在函数 f 下的 像 f (A)
U
f
V
A
f(A)
集合 B 在函数 f 下的 逆像 f -1(B)
U
f
V
-1
f (B)
B
例5.1.3 设 A={a, b, c, d, e} , B={1, 2, 3, 4} , φ: A→B, φ的定义如图所示。则
φ({a, b, c})={1, 2}
例：设 U={1,2,3,4}，V={1,2,…,16}，关系 f1={ <1,1>, <2,4>, <3,9>, <4,16> }， f2={ <1,1>, <2,3>, <4,4> }， f3={ <1,1>, <1,2>, <2,15>, <3,16>, <4,1> }，
试判断哪些是函数？
解：f1 是，且 f1(a)=a2。 f2 不是，因为f2(3)=? f3 不是，因为两个f3(1)。
n×n×…×n = nm
m
映射：递归定义
例5.1.8 (1) 阶乘 n! f: N→N, f(0)=1, f(n+1)=f(n)(n+1), n∈N。
（但需要检查，是否都有射，是否没有一射多）
离散数学 第3章 函数

离散数学 第3章 函数

集合的交，并运算 , :2X 2X 2X 是二元运算。
•关于运算，我们主要考虑其封闭性。 n元运算f的封闭性：对于任何n个元素x1 , x2 , , xn， x1 , x2 , , xnX f(x1 , x2 , , xn)X ，
或者 (x1 , x2 , , xn)Xn f(x1 , x2 , , xn)X 。
(8)偏函数(partial function)：部分有定义的函数。即 D(f)X （或者f -1(Y)X） 。
D(f) X D(f)X
2021/5/27
9
离散数学
例1.截痕函数(cross function)：f :X2XY ， f(x) = {x}Y 。
XY Y
{x}Y
Xx
例2.计算机是一个函数。即 计算机:输入空间输出空间；
2021/5/27
1
离散数学 第三章 函数
§1.函数的基本概念 §2.函数的复合
2021/5/27
2
离散数学
第三章 函数（function）
§1.函数基本概念
定义1.函数(映射(map)、变换(transformation))
函数是后者唯一的关系。即
f是由X到Y的函数，记为f :XY
f XY(xX)(yY)(zY)((x, y)f (x, z)f y=z)
f ={((x,y), z) : x, y , z 2X z= x y }
2021/5/27
13
离散数学
这里(x,y)是前者， z是后者；或者
f :2X 2X 2X ， f(x ,y) = z= x y ，
这里(x,y)是自变量， z是因变量； 因此 f = 。
例6.函数未必都有统一的表达式。不象连续函数那样大 多都有统一的表达式，离散函数大多都没有统一的表达 式。
离散数学函数概念

离散数学函数概念

离散数学函数概念1. 函数的概念在离散数学中，函数是一种非常重要的概念。

简单来说，函数就是一种将一个集合中的元素映射到另一个集合中的元素的规则。

具体地说，函数包括三个要素：定义域、值域和对应关系。

其中，定义域是函数的输入集合，值域是函数的输出集合，对应关系则是对定义域中的每个元素，函数规定相应的输出元素的一个映射关系。

函数通常用符号f表示，可以写成f：A→B，表示从定义域A到值域B的映射。

2. 性质和操作函数在离散数学中有许多重要的性质和操作，下面我们分别介绍一下。

2.1. 单射、满射和双射在定义域和值域中，函数有三种重要的映射状态：单射、满射和双射。

如果对于定义域中的任意两个不同的元素，它们映射到值域中的不同元素，那么这个函数就是单射。

如果对于值域中的任意元素，都有至少一个定义域中的元素映射到它，那么这个函数就是满射。

如果函数同时满足单射和满射的条件，那么它就是双射。

双射函数可以看作是一种一一对应的关系，它在离散数学中有着重要的应用。

2.2. 复合函数另一个重要的函数操作是「复合函数」。

复合函数是指在两个或多个函数之间进行合成的操作，即将一个函数的输出作为另一个函数的输入。

假设有函数f: A→B和函数g: B→C，那么它们的复合函数定义为g(f(x))，表示先将x代入函数f中得到f(x)，再将f(x)代入函数g中得到g(f(x))。

复合函数的应用在离散数学中非常广泛，是许多算法和数据结构的基础。

2.3. 逆函数逆函数是指在一个双射函数f的基础上，将定义域和值域交换位置得到的新函数。

逆函数通常用符号f-1表示，它的定义域和值域与原函数f完全相反，即f-1：B→A。

逆函数的作用是将一个函数的输入与输出交换位置，方便进行一些计算和处理。

3. 应用领域以及参考资料离散数学中的函数概念和相关操作在许多领域都有广泛的应用，如算法设计与分析、图形理论、密码学、计算机网络等。

对于一些计算机科学和工程学科的学生，掌握和理解离散数学中的函数概念和相关知识是非常重要的。

《离散数学》函数

《离散数学》函数


A
B
C
y=f(x)
z =g( y ) =( g◦f )( x )
x
29
函数的复合
例
– f ： → ，f (x) = x+1， – g ： → ，g(x) = 2x+1, – h ： → ，h(x) = x2+1, g ◦ f (x)=g(f(x)) =2f(x)+1 =2(x+1)+1=2x+3 f ◦ g(x)=f(g(x)) =g(x)+1 =2x+1+1=2x+2 h ◦ g ◦ f (x)=h(g(f(x))) = (2x+3)2+1
20
函数的性质
练习 – f： + → + ， – f(1) = 1，f(n) = n–1 (n>1)
– 单射? – 满射? – 双射?
21
函数的性质
对于有限集合上的函数，有如 下主要结果：
定理 假设 A 和 B 是两个有限集合
且满足 |A| = |B|，则函数 f : AB 是单射当且仅当 f 是满射。
第五章 函数
《离散数学及应用》
第五章 函数
§5.1 函数的定义 §5.2 函数的性质 §5.3 函数的复合 §5.4 逆函数 §5.5 计算机科学中的常用函数 *§5.6 双射函数及集合的势
2
函数
A 和 B 为非空集合 设 f 为 A 到 B 的二元关系, 若对于任意 xDom( f ) 都存在唯一的 yRan( f ) 使得 (x, y)f 成立，则称 f 为函数 (function)。 函 数 也 称 作 映 射 （ mapping ） 或 变 换 （transformation）
函数的概念 离散数学

函数的概念 离散数学


f(d)=2.
f是满射
设函数f :{a,b}→{2,4,6}为f(a)=2,f(b)=6.
f是入射
设f: R→R,f(x)=x3+2x2.
f是满Y 射
皮亚诺函数S: N → N,S(n)=n+1.
f是入射
设f: R →R,f(r)=r+3.
f既是满射又是入射
五. 双射
0
X
定义： 从X到Y的一个映射，若既是满射又是入射，则称这
f4 ＝{<a,1>, <b,0>, <c,0>} f5 ＝{<a,1>, <b,0>, <c,1>} f6 ＝{<a,1>, <b,1>, <c,0>} f7 ＝{<a,1>, <b,1>, <c,1>}
三. 满射
定义：对于X→f Y的映射中，如果ran f =Y，即Y的每一个元
素是X中一个或多个元素的象点，则称这个映射为满 射。 f:X→Y为满射,即对于任意y Y，存在x X使得f(x)＝y
四. 入射
定义：从X到Y的映射中，X中没有两个元素有相同的象，则
称这个映射为入射（一对一映射）。（也称单射）
f:X→Y为入射,即对于任意x1 , x2 X，
若x1 ≠ x2 ，有 f(x1)≠ f(x2)
例 设A={a,b,c,d},B={1,2,3},如果A→f B为： f(a)=1,f(b)=1,f(c)=3,
映射到Y的元
(3)<x,y>f 亦记作 y = f(x)；
素。所以函数
(4)记f(X)={f(x)|xX}。
又叫映射。
离散数学(函数)课件

离散数学(函数)课件


02
函数的运算
函数的加法
总结词
函数的加法是一种对应关系，表示将函数$f$和$g$的每一个输出值都加上一定的量。
详细描述
函数的加法是一种二元运算，表示将函数$f$和$g$的每一个输出值都加上一定的量。具体来说，如果函数$f$和 $g$的定义域分别为$D_f$和$D_g$，那么函数$f+g$的定义域为$D_{f+g} = D_f cap D_g$，对于任意$x in D_{f+g}$，有$(f+g)(x) = f(x) + g(x)$。
详细描述
幂函数的形式为 y=x^n，其中 n 是实数。当 n>0 时，幂函数是增函数；当 n<0 时，幂函数是减函数；当 n=0 时，幂函数值为 1。幂函数在离散数学中可 用于表示一些复杂的关系。
指数函数
总结词
指数函数是指数等于输入值的函数。
详细描述
指数函数的形式为 y=a^x，其中 a 是实数且 a>0，a≠1。当 a>1 时，指数函 数是增函数；当 0<a<1 时，指数函数是减函数。指数函数在离散数学中可用于 表示概率和统计中的分布情况。
函数的三要素包括定义域、值域和对应法则。
函数的表示方法
01
02
03
解析法
通过公式来表示函数，例 如y=f(x)。
表格法
通过表格的形式列出函数 的输入和输出值。
图象法
通过绘制函数图像来表示 函数。
函数的性质
单调性
函数在某个区间内单调增 加或单调减少。
有界性
函数在某个区间内有上界 和下界。
奇偶性
函数是否关于原点对称或 关于y轴对称。
函数的复合

离散数学第三章 函数

射函数。
第三章 函数
二、反函数
1、定义1：设f：AB是双射，则逆关系 f -1：BA
是从B到A的函数，称为 f 的反函数。
记 f -1 ：BA。 由定义可知：当函数 f：AB的反函数存在，若 f (x) = y，则f -1 (y) = x 且
f f 1 I A , f 1 f I B
f 0 ( x) x n 1 n f ( x ) f ( f ( x ))
第三章 函数
(2) 定理2： 设f: A→B,则 f。IB=IA。f=f
(3) 定理3：设有函数f：AB，g：BC
① 若f ，g是单射，则f g也是单射。
② 若f ，g是满射，则f g也是满射。
所以 f。g={(x, 4x 2+4x+2)}， g。f={(x, 2x 2+3)}
f。f={(x, 4x+3)}， g。g={(x, x 4+2x 2+2)}
第三章 函数
2、性质：
⑴ 定理1：设有函数f：AB，g：BC，h：
CD，则f ( g h) 和( f g ) h都是函数，且
③ 若f ，g是双射，则f g也是双射。
注：定理3的逆不成立。
第三章 函数
例3：设A={ 1, 2, 3 }, B={ a, b, c, d }, C={ x, y, z }
令 f = {(1, a), (2, b), (3, c)},
g = {(a , x), (b, y), (c, z), ( d, z)}
f ( g h) = ( f g ) h = f g h 证明： f。(g。h)(x) =(g。h) (f (x))=h (g (f (x)) =h((f。g) (x))=(f。g)。h (x)

离散型函数

离散型函数离散型函数是一种特殊的函数类型，其定义域是离散的，即只包含整数。

离散型函数在数学中有着广泛的应用，尤其在离散数学和计算机科学中，是非常重要的概念。

一、离散型函数的定义离散型函数是指定义域为整数集合的函数，其表达式可以写成f(x) = y，其中 x 和 y 都是整数。

例如，一个简单的离散型函数可以定义为 f(x) = x^2，其中 x 为整数。

当 x 取值为 -3、-2、-1、0、1、2、3 时，对应的函数值分别为 9、4、1、0、1、4、9。

二、离散型函数的性质1. 像的集合：离散型函数的像是整数集合，即所有可能的函数值都是整数。

2. 奇偶性：离散型函数可以是奇函数、偶函数或既不是奇函数也不是偶函数。

3. 周期性：离散型函数可以是周期函数，即存在一个正整数 k，使得对于所有整数 x，有 f(x+k) = f(x)。

4. 单调性：离散型函数可以是单调递增函数、单调递减函数或者既不是单调递增函数也不是单调递减函数。

5. 可逆性：离散型函数可以是可逆函数，即存在一个函数 g(y)，使得对于所有整数 x，有 g(f(x)) = x。

三、离散型函数的应用离散型函数在离散数学和计算机科学中有着广泛的应用，如下所示：1. 密码学：离散型函数是密码学中的重要概念，可以用于加密和解密数据。

2. 图论：离散型函数可以用于图论中的路径算法和最短路径算法。

3. 组合数学：离散型函数可以用于计算排列、组合和分组数。

4. 计算机科学：离散型函数可以用于计算机科学中的算法设计和数据结构。

四、离散型函数的例子1. 单位阶跃函数：单位阶跃函数是一种离散型函数，其定义为： $$u[n]=begin{cases}1,&ngeq00,&n<0end{cases}$$2. 斐波那契数列：斐波那契数列是一种离散型函数，其定义为：$$F_n=begin{cases}0,&n=01,&n=1F_{n-1}+F_{n-2},&n>1end{cases }$$3. 阶乘函数：阶乘函数是一种离散型函数，其定义为：$$n!=begin{cases}1,&n=0times(n-1)timescdotstimes2times1,&n>0end{cases}$$五、总结离散型函数是一种特殊的函数类型，其定义域是离散的，即只包含整数。

重庆大学《离散数学》课件-第4章函数

对于任意的 ∈ , ≠ ，因此 ∈ − 。 因为 = ，故有
∈ ( − )。由的任意性可知 − () ⊆ ( − )成立
4.2 逆函数和复合函数
▪ 例：定义一函数: → 如下：
1、 的定义域不是，而是的子集
2、 不满足函数定义：值的唯一性
所以 是一种二元关系，但不是函数
一个函数的逆函数存在的话，则此函
数一定是双射函数。
▪ 定理：设: X → 是一双射函数，那么 是Y → X的双射函数。
▪ 证明： （1）首先证明 :Y → X的函数。
因为是满射的，对任意的 ∈ 必有 < , >∈ ，且 = ，因此< , >∈
等函数。
定理：设函数: X → ，则 = ∘ = ∘
定理：如果函数: → 有逆函数 −1 : → ，则 −1 ∘ = ，且
∘ −1 =
例：令:{0,1,2} →{a,b,c},其定义如下图所示，求 −1 ∘ 和 ∘ −1
设: X → ，: → 是两个函数，则复合函数 ∘ 是一个从X到的
函数，对于每一个 ∈ 有 ∘ = (())。
例：设 = 1,2,3 , = , , = , ,
= < 1, >, < 2, >, < 3, > , = < , >, < , > , 求 ∘
， = 。又因为是入射，对每一个 ∈ 必有唯一的 ∈ ，使得<
, >∈ ，因此仅有唯一的 ∈ ，使得
< , >∈ 。因此 是一个函数。
（2）证 :Y → X满射的。
= =
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
分析
例8.5
例8.5 对于以下各题给定的A,B和 f，判断是否构成函数 f:A→B。如果是，说明 f:A→B是否为单射、满射和双射的， 并根据要求进行计算。 (1)A＝{1,2,3,4,5}，B＝{6,7,8,9,10}， f＝{<1,8>,<3,9>,<4,10>,<2,6>,<5,9>}
能构成f:A→B，
不能构成f:A→B，因为dom f＝{1,2,3,4}≠A。
(4)A＝B＝R，f(x)＝x 能构成f:A→B， 且 f 是双射的 。 (5)A＝B＝R+，f(x)＝x/(x2+1)（x∈R+ ） 能构成f:A→B， 但 f 既不是单射的也不是满射的。
因为该函数在 x＝1 取得极大值 f(1)＝1/2，函数不是单调 的，且ran f ≠R+。
f-1({0})＝{<n,n>|n∈N}
例8.6
例8.6 对于给定的集合A和B构造双射函数 f:A→B。 （1）A＝P({1,2,3}), B＝{0,1}{1,2,3}
（2）A＝[0,1], B＝[1/4,1/2] （3）A＝Z, B＝N
（4）A＝[/2,3/2], B＝[1,1]
例8.6的解答
＝{<a,0>,<b,0>,<c,0>}， {a,b} ＝{<a,1>,<b,1>,<c,0 >} {a} ＝{<a,1>,<b,0>,<c,0 >}
常用函数—自然映射
设R是A上的等价关系， 令
g：A→A/R
g(a)=[a]，a∈A
称g是从A到商集A/R的自然映射。
给定集合A和A上的等价关系R，就可以确定一个自然映射g ：A→A/R。
f 不是单射的，因为f(3)＝f(5)＝9, f 不是满射的，因为7ran f。 (2)A＝{1,2,3,4,5}，B＝{6,7,8,9,10}， f＝{<1,7>,<2,6>,<4,5>,<1,9>,<5,10>} 不能构成f:A→B，因为<1,7>∈f 且<1,9>∈f 。
例8.5
(3)A＝{1,2,3,4,5}，B＝{6,7,8,9,10}， f＝{<1,8>,<3,10>,<2,6>,<4,9>}
例8.5
(6)A＝B＝R×R，f (<x,y>)＝<x+y,x-y> 令L＝{<x,y>|x,y∈R∧y＝x+1}，计算 f(L)。
能构成 f:A→B，且 f 是双射的。
f(L)＝{<x+(x+1),x-(x+1)>|x∈R} ＝{<2x+1,-1>|x∈R}＝R×{-1} (7)A＝N×N，B＝N，f(<x,y>)＝|x2-y2| 计算f(N×{0}),f-1＝({0})。 能构成f:A→B， 但 f 既不是单射也不是满射的。 因为f(<1,1>)＝f(<2,2>)＝0，且2ran f。 f(N×{0})＝{n2-02|n∈N}＝{n2|n∈N}
3
c 4 c
3
4
单射
a b c 1 2 3 a b c d
不是函数
1 2 3 4 函数 a b c 1 2 3 满射
d
双射
4
d
例8.4
例8.4 判断下面函数是否为单射、满射、双射的，为什么? (1) f：R→R，f(x)= -x2+2x-1 (2) f：Z+→R，f(x)=ln x，Z+为正整数集 (3) f：R→Z，f(x)=x (4) f：R→R，f(x)=2x+1 (5) f：R+→R+，f(x)=(x2+1)/x，其中R+为正实数集。 实数集合上函数性质的判断方法 （1）f 在x=1取得极大值0。既不是单射也不是满射的。 （2）f 是单调上升的，是单射的，但不满射。ran f={ln1, ln2, …}。 （3）f 是满射的， 但不是单射的，例如f(1.5)=f(1.2)=1。 （4）f 是满射、单射、双射的，因为它是单调函数并且ran f=R。 （5）f 有极小值f(1)=2。 该函数既不是单射的，也不是满射的。
例如： f：N→N，f(x)＝2x是从N到N的函数， g：N→N，g(x)＝2也是从N到N的函数。
定义8.4 所有从A到B的函数的集合记作BA，读作“B上A”，
符号化表示为 BA＝{f | f：A→B} 。
例8.2
例8.2 设A＝{1,2,3}，B＝{a,b}，求BA。 解答 BA＝{ f0, f1, f2, f3, f4, f5, f6, f7} 。其中 f 0＝{<1,a>,<2,a>,<3,a>} f 4＝{<1,b>,<2,a>,<3,a6 设f:A→B， （1）若ran f＝B，则称f:A→B是满射(surjection)的。 （2）若y∈ran f 都存在唯一的x∈A使得f(x)＝y，则称 f:A→B是单射(injection)的。
（3）若f 既是满射又是单射的，则称f:A→B是双射(bijection) 的(一一映像(one-to-one mapping)) 。
说 明
是函数 不是函数
函数是特殊的二元关系。 函数的定义域为dom F，而不是它的真子集。 一个x只能对应唯一的y。
函数相等
定义8.2 设 F,G 为函数，则 F＝G FG∧GF 由定义可知，两个函数F和G相等, 一定满足下面两个条件： （1）dom F＝dom G
（2）x∈dom F＝dom G，都有 F(x)＝G(x)
f是单调递增的, 但不是严格单调递增的。
常用函数—特征函数
设A为集合，对于任意的AA，A的特征函数 A : A→{0,1}定义为 A (a) ＝ 1，a∈A 0， a∈AA
举例: A的每一个子集A都对应于一个特征函数，不同的子 集对应于不同的特征函数。
例如A＝{a,b,c}, 则有
例如A＝{1,2,3}，R＝{<1,2>,<2,1>}∪IA
g(1)＝g(2)＝{1,2}, g(3)＝{3}
不同的等价关系确定不同的自然映射，其中恒等关系所确定 的自然映射是双射， 而其他的自然映射一般来说只是满射。
中国地质大学本科生课程
离散数学
第8章 函数
本章说明
本章的主要内容
– 函数的定义 – 函数的性质
– 函数的逆
– 函数的合成
本章与后续各章的关系
–是代数系统的基础
本章内容
8.1 函数的定义与性质 8.2 函数的复合与反函数
8.3 一个电话系统的描述实例
本章小结
习题
作业
8.1 函数的定义与性质
定义8.1 设F为二元关系，若x∈dom F，都存在唯一的 y∈ran F 使xFy成立，则称F为函数(function)(或称作映射 (mapping))。 对于函数F，如果有 xFy，则记作y＝F(x)，并称y为F在x的 值。 举例 判断下列关系是否为函数 F1＝{<x1,y1>,<x2,y2>,<x3,y2>} F2＝{<x1,y1>,<x1,y2>}
说 明
注意区别函数的值和像两个不同的概念。 函数值f(x)∈B，而函数的像f(A1)B。
讨论
设 B1B，显然B1在 f 下的原像 f-1(B1)是A的子集。
设 A1A，那么 f(A1)B。
f(A1)的完全原像就是 f-1(f(A1))。 一般来说， f-1(f(A1))≠A1，但是A1 f-1(f(A1))。 例如函数 f:{1,2,3}→{0,1}，满足 f(1)＝f(2)＝0，f(3)＝1
（1）A＝P({1,2,3}), B＝{0,1}{1,2,3} A＝{,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}。 B＝{f0,f1,…,f7}, 其中 f0 ＝{<1,0>,<2,0>,<3,0>}, f2 ＝{<1,0>,<2,1>,<3,0>}, f4 ＝{<1,1>,<2,0>,<3,0>}, f6 ＝{<1,1>,<2,1>,<3,0>}, 令f: A→B, f() ＝ f0, f({3}) ＝ f3, f({1})＝f1, f({1,2})＝f4, f({2})＝f2, f({1,3})＝f5, f1 ＝{<1,0>,<2,0>,<3,1>}, f3 ＝{<1,0>,<2,1>,<3,1>}, f5 ＝{<1,1>,<2,0>,<3,1>}, f7 ＝{<1,1>,<2,1>,<3,1>}。
f 1＝{<1,a>,<2,a>,<3,b>}
f 2＝{<1,a>,<2,b>,<3,a>} f 3＝{<1,a>,<2,b>,<3,b>}
说 明
f 5＝{<1,b>,<2,a>,<3,b>}
f 6＝{<1,b>,<2,b>,<3,a>} f 7＝{<1,b>,<2,b>,<3,b>}
若|A|＝m，|B|＝n，且m,n>0，则|BA|＝nm。 当A或B至少有一个集合是空集时： A＝且B＝，则BA＝＝{}。 A＝且B≠，则BA＝B＝{}。 A≠且B＝，则BA＝A＝。