吉林省东北师大附中2015-2016学年高中数学 第三章 空间向量与立体几何 3.1-03 空间向量的数量积(1)教案

集合复习小结（2）课时：007课型：复习课10．数集M 满足条件，若a∈M，则1＋a 1－a∈M(a≠±1且a≠0)，已知3∈M，试把由此确定的集合M 的元素全部求出来．11．已知f(x)＝x 2－ax ＋b(a 、b∈R )，A ＝{x∈R |f(x)－x ＝0}，B ＝{x∈R |f(x)－ax＝0}，若A ＝{1，－3}，试用列举法表示集合B.课后检测解析：1．B 化简集合A ＝{0,1}，显然0∈A.2．B ∵x∈N ，且(8－x)∈N ，∴x＝0,1,2,3,4,5,6,7,8，共9个数．3．B ∵z＝x·y，x∈A，y∈B，∴z 的取值有：1×0＝0,1×2＝2,2×0＝0,2×2＝4，故A*B ＝{0,2,4}．∴集合A*B 的所有元素之和为0＋2＋4＝6.4．C 由题意得，a≠0，b≠0，所以a ＋b ＝0，a ＝－b.于是，{1,0，a}＝{0，－1，－a}．显然，a ＝－1，b ＝1，b －a ＝2.5．D 由3，52，73，94可得，31，52，73，94从中发现规律，关键要分清起始数并限定范围． 6．(1){－1,1} (2){0,3,4,5}(3){x|(x －2)(x －4)(x －6)(x －8)＝0}或{大于1小于9的偶数}等(4){x|x ＝1n，n≤4且n∈N *} 7．0或2 当x ＝1时，x 2＝1，这与集合中元素的互异性相矛盾，故x≠1；当x ＝2时，x 2＝4符合题意；当x ＝x 2时x ＝0或x ＝1(舍去)．综上可知x ＝0或2.8．{－1,3} 当ab<0时，y ＝a |a|＋b |b|＋ab |ab|＝－1； 当ab>0时，则a>0，b>0或a<0，b<0，若a>0，b>0，则有y ＝a |a|＋b |b|＋ab |ab|＝3； 若a<0，b<0，则有y ＝a |a|＋b |b|＋ab |ab|＝－1. 所以y ＝a |a|＋b |b|＋ab |ab|的所有值组成的集合元素共有两个元素－1和3，用列举法表示为{－1,3}．9．解：集合A 为单元素集，即方程ax 2＋2x ＋1＝0有唯一解或两个相等的实数解．由于此方程二次项的系数不确定，所以要对a 分类讨论．①a＝0时，x ＝－12； ②a≠0时，Δ＝4－4a ＝0，所以a ＝1，此时x ＝－1.10．解：∵a＝3∈M，∴1＋a 1－a ＝1＋31－3＝－2∈M. ∴1－21＋2＝－13∈M.∴1－131＋13＝12∈M. ∴1＋121－12＝3∈M. 再把3代入将重复上面的运算过程，由集合中元素的互异性可知M ＝{3，－2，－13，12}． 11．解：f(x)－x ＝0，即x 2－(a ＋1)x ＋b ＝0.∵A＝{1，－3}，∴由韦达定理，得⎩⎪⎨⎪⎧1＋(－3)＝a ＋1，1×(－3)＝b.∴⎩⎪⎨⎪⎧ a ＝－3，b ＝－3.∴f(x)＝x 2＋3x －3.f(x)－ax ＝0，亦即x 2＋6x －3＝0.∴B＝{x|x 2＋6x －3＝0}＝{－3－23，－3＋23}．点评：列举法和描述法是表示集合的两种常用方法．用列举法时要注意：元素间用逗号隔开；元素不重复；可不考虑元素间的顺序；若元素的个数较多需要省略时，必须把元素间的规律显示清楚后方可使用省略号．用描述法时要注意：写清元素的一般符号及取值范围；明确集合中元素的特征；不能出现未被说明的字母；准确使用“且”与“或”等．四．高考题小试牛刀1.（15年福建文科）若集合{}22M x x =-≤<，{}0,1,2N =，则M N 等于（ ）A ．{}0B ．{}1C ．{}0,1,2D {}0,1【答案】D考点：集合的运算．2.(15年新课标1文科)3.(15年新课标2理科) 已知集合A=｛-2，-1,0，1,2｝，B=｛x|（x-1）（x+2）＜0｝,则A∩B=（ ）（A ）｛--1,0｝ （B ）｛0,1｝ （C ）｛-1,0,1｝ （D ）｛,0,，1，2｝【答案】A 【解析】由已知得{}21B x x =-<<，故{}1,0A B =-，故选A4.(15年新课标2文科) 已知集合{}|12A x x =-<<,{}|03B x x =<<,则AB =（ ）A ．()1,3-B ．()1,0-C ．()0,2D ．()2,3【答案】A考点：集合运算.5.(15陕西文科) 集合2{|}M x x x ==，{|lg 0}N x x =≤，则M N =（ ） A ．[0,1] B ．(0,1] C ．[0,1) D ．(,1]-∞【答案】A考点：集合间的运算.6.(15年江苏) 已知集合{}3,2,1=A ，{}5,4,2=B ，则集合B A 中元素的个数为_______.【答案】5【解析】试题分析：{123}{245}{12345}5A B ==，，，，，，，，，个元素考点：集合运算7.【2014广东 理科卷】已知集合{1,0,1}M =-，{0,1,2}N =，则M N =(B)A.{1,0,1}-B.{1,0,1,2}-C.{1,0,2}-D.{0,1}8. 【2014高考北京理】已知集合A={x|},B={0,1,2},则AB=( )A{0}. B ．{0,1}. C ． {0,2}. D ．{0,1,2}.[答案C]【解析】：集合A={x|}={0,2},则AB={0,2},故选C ，考点：交集的运算，容易题。

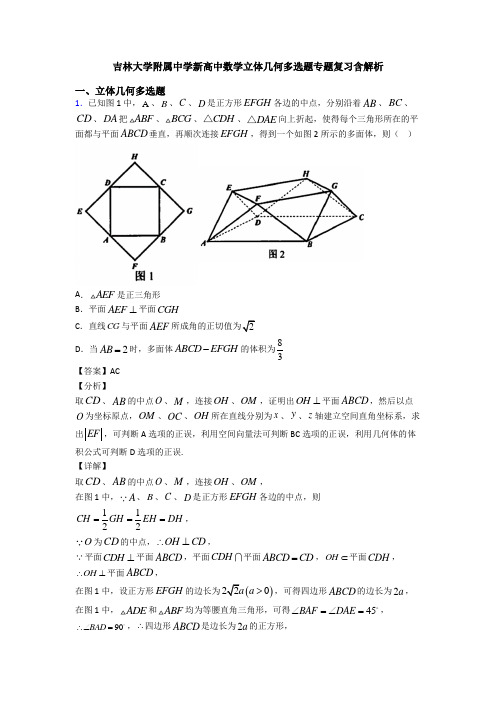
吉林大学附属中学新高中数学立体几何多选题专题复习含解析一、立体几何多选题1．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（ ）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83 【答案】AC【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误.【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===， O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ， 在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ， 在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=， 所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===， 所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由111100m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-， 设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-， 由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--， ()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG mCG m a CG m ⋅<>===⨯⋅， 设直线CG 与平面AEF 所成角为θ，则sin 6θ=，23cos 1sin θθ=-=， 所以，sin tan 2cos θθθ==，C 选项正确； 对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△， 因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误.故选：AC.【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin h lθ=（l 为斜线段长），进而可求得线面角； （3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.2．如图，一个结晶体的形状为平行六面体1111ABCD A B C D -，其中，以顶点A 为端点的三条棱长都等于1，且它们彼此的夹角都是60，下列说法中正确的是（ ）A ．()()2212AA AB AD AC ++= B ．1A 在底面ABCD 上的射影是线段BD 的中点C ．1AA 与平面ABCD 所成角大于45D ．1BD 与AC 6 【答案】AC【分析】对A ，分别计算()21++AA AB AD 和2AC ，进行判断；对B ，设BD 中点为O ，连接1A O ，假设1A 在底面ABCD 上的射影是线段BD 的中点，应得10⋅=O AB A ，计算10⋅≠O AB A ，即可判断1A 在底面ABCD 上的射影不是线段BD 的中点；对C ，计算11,,A A AC AC ，根据勾股定理逆定理判断得11⊥A A AC ，1AA 与平面ABCD 所成角为1A AC ∠，再计算1tan ∠A AC ；对D ，计算1,AC BD 以及1BD AC ⋅，再利用向量的夹角公式代入计算夹角的余弦值.【详解】对A ，由题意，11111cos602⋅=⋅=⋅=⨯⨯=AA AB AA AD AD AB ，所以()2222111112221113262++=+++⋅+⋅+⋅=+++⨯⨯=AA AB AD AA AB AD AA AB AB AD AA AD ，AC AB AD =+，所以()222221113=+=+⋅+=++=AC AB AD AB AB AD AD ， 所以()()22126++==AA AB AD AC ，故A 正确；对B ，设BD 中点为O ，连接1A O ，1111111222=+=+=++AO A A AO A A AC A A AD AB ，若1A 在底面ABCD 上的射影是线段BD 的中点，则1A O ⊥平面ABCD ，则应10⋅=O AB A ，又因为21111111111110222222224⎛⎫⋅=++⋅=-⋅+⋅+=-+⨯+=≠ ⎪⎝⎭O AB A A AD AB AB AA AB AD AB AB A ，故B 错误；对D ，11,BD AD AA AB AC AB AD =+-=+， 所以()()2211=2,=3=+-=+AD A B A AB AC AB AD D ()()2211111⋅=+-⋅+=⋅++⋅+⋅--⋅=AC AD AA AB AB AD AD AB AD AA AB AA AD AB AB AD BD，111cos ,2⋅<>===B ACD BD BD AC AC D 不正确；对C，112==AC BD ，在1A AC 中，111,===A A AC AC 22211+=A A AC AC ，所以11⊥A A AC ，所以1AA 与平面ABCD 所成角为1A AC ∠，又1tan 1∠=>A AC ，即145∠>A AC ，故C 正确；故选：AC【点睛】方法点睛：用向量方法解决立体几何问题，需要树立“基底”意识，利用基向量进行线性运算，要理解空间向量概念、性质、运算，注意和平面向量类比；同时对于立体几何中角的计算问题，往往可以利用空间向量法，利用向量的夹角公式求解.3．如图，已知四棱锥P ABCD -所有棱长均为4，点M 是侧棱PC 上的一个动点（不与点,P C 重合），若过点M 且垂直于PC 的截面将该四棱锥分成两部分，则下列结论正确的是（ ）A ．截面的形状可能为三角形、四边形、五边形B ．截面和底面ABCD 所成的锐二面角为4π C ．当1PM =时，截面的面积为52D ．当2PM =时，记被截面分成的两个几何体的体积分别为()1212,>V V V V ，则123=V V【答案】BCD【分析】点M 是侧棱PC 上的一个动点，根据其不同位置，对选项逐一进行判断即可.【详解】A 选项中，如图，连接BD ，当M 是PC 中点时，2MC =，由题意知三角形PDC 与三角形PBC 都是边长为4的正三角形，所以DM PC ⊥,BM BC ⊥，又DM ，BM 在面MBD 内，且相交，所以PC ⊥平面PBD ，三角形MBD 即为过点M 且垂直于PC 的截面，此时是三角形，点M 向下移动时，2MC <，如图，仍是三角形；若点M 由中点位置向上移动，2MC >，在平面PDC 内作EM PC ⊥，交PD 于E ，在平面PBC 内作FM PC ⊥交PB 于F ，平面MEF 交平面PAD 于EG ，交PAB 于FH ，即交平面ABCD 于GH ，则五边形MEGHF 即为过点M 且垂直于PC 的截面，此时是五边形； 故截面的形状可能为三角形、五边形，A 错误；B 选项中，因为截面总与PC 垂直，所以不同位置的截面均平行，截面与平面ABCD 所成的锐角为定值，不妨取M 是中点，连接AC ，BD ，MB ，MD ，设AC ，BD 交点是N ，连接PN ，由题意知，四边形ABCD 是边长为4的菱形，BD AC ⊥，因为MB =MD ，所以MN BD ⊥，故MNC ∠是截面与平面ABCD 所成的锐角，过点M 作MQ AC ⊥，垂足Q.在三角形PAC 中，MN =2，NQ=2，故在直角三角形MNQ 中，2cos 2NQ MNC MN ∠==，故4MNC π∠=，故B 正确；C 选项中，当PM =1时，M 是PC 中点，如图，五边形MEGHF 即为过点M 且垂直于PC 的截面，依题意，直角三角形PME 中，2cos PM PE EPM==∠，故E 为PD 的中点，同理，F 是PB 的中点，则EF 是三角形PBD 的中位线，1222EF BD ==，G ，H 分别在,AD AB 的中点上，证明如下，当G ，H ，也是中点时，1//,2GH BD GH BD =，有//,22GH EF GH EF ==，四边形EFHG 是平行四边形.依题意，三角形PAC 中4,42PA PC AC ===，故PA PC ⊥，故PC GE ⊥，易见，正四棱锥中BD ⊥平面PAC ，故BD PC ⊥，GH PC ∴⊥，因为 ,GE GH 均在平面EFHG 内，且相交，所以PC ⊥平面EFHG ，故此时平面EFHG 和平面MEF 即同一平面.又BD ⊥平面PAC ，有GH ⊥面平面PAC ，GH GM ⊥，根据对称性有GH GE ⊥，四边形EFHG 是矩形. 即五边形MEGHF 即为过点M 且垂直于PC 的截面，平面图如下:依题意，22GH EF ==2EG FG ==，三角形高为()()22321h =-=， 面积是122122⨯=，四边形面积是22242=，故截面面积是52 故C 正确；D 选项中，若PM =2，看B 选项中的图可知，21124M BCD P BCD P ABCD V V V V ---===，故剩余部分134P ABCD V V -= ，所以123=V V ，故D 正确.故选：BCD.【点睛】本题考查了棱锥的截面问题，考查了二面角、体积等计算问题，属于难题.4．已知正方体1111ABCD A B C D -的棱长为2，点O 为11A D 的中点，若以O 为球心，6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ，F ，G ，H ，则下列结论正确的是（ ）A ．11//A D 平面EFGHB ．1AC ⊥平面EFGHC ．11A B 与平面EFGH 所成的角的大小为45°D ．平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7【答案】ACD【分析】如图，计算可得,,,E F G H 分别为所在棱的中点，利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否，计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确，而几何体BHE CGF -为三棱柱，利用公式可求其体积，从而可判断D 正确与否.【详解】如图，连接OA ，则2115OA AA =+=，故棱1111,,,A A A D D D AD 与球面没有交点. 同理，棱111111,,A B B C C D 与球面没有交点.因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点. 因为正方体的棱长为2，而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ，F ，G ，H ，所以棱11,,,AB CD C C B B 与球面各有一个交点， 如图各记为,,,E F G H .因为OAE △为直角三角形，故22651AE OE OA -=-=，故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ，同理//GH BC ，故//EF GH ，故,,,E F G H 共面.由正方体1111ABCD A B C D -可得11//A D BC ，故11//A D EF因为11A D ⊄平面EFGH ，EF ⊂平面EFGH ，故11//A D 平面EFGH ，故A 正确.因为在直角三角1BA C 中，1A B =2BC = ，190A BC ∠=︒， 1A C 与BC 不垂直，故1A C 与GH 不垂直，故1A C ⊥平面EFGH 不成立，故B 错误. 由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ，而1A B ⊂平面11AA B B ， 所以1BC A B ⊥，所以1EF A B ⊥在正方形11AA B B 中，因为,E H 分别为1,AB BB 的中点，故1EH A B ⊥，因为EF EH E =，故1A B ⊥平面EFGH ，所以BEH ∠为直线AB 与平面EFGH 所成的角，而45BEH ∠=︒，故直线AB 与平面EFGH 所成的角为45︒，因为11//AB A B ，故11A B 与平面EFGH 所成的角的大小为45°.故C 正确.因为,,,E F G H 分别为所在棱的中点，故几何体BHE CGF -为三棱柱， 其体积为111212⨯⨯⨯=，而正方体的体积为8， 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7，故D 正确. 故选：ACD.【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算，注意根据球的半径确定哪些棱与球面有交点，本题属于中档题.5．（多选题）在四面体P ABC -中，以上说法正确的有（ ）A ．若1233AD AC AB =+，则可知3BC BD = B ．若Q 为△ABC 的重心，则111333PQ PA PB PC =++ C ．若0PA BC =，0PC AB =，则0PB AC =D ．若四面体P ABC -各棱长都为2，M N ，分别为,PA BC 的中点，则1MN =【答案】ABC【分析】作出四面体P ABC -直观图，在每个三角形中利用向量的线性运算可得.【详解】对于A ，1233AD AC AB =+，32AD AC AB ∴=+，22AD AB AC AD ∴-=- ， 2BD DC ∴=，3BD BD DC BC ∴=+=即3BD BC ∴=，故A 正确； 对于B ，Q 为△ABC 的重心，则0QA QB QC ++=，33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=即111333PQ PA PB PC ∴=++，故B 正确； 对于C ，若0PA BC =，0PC AB =，则0PA BC PC AB +=， ()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++= 0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+= 0CA BC PC AC ∴+=,0AC CB PC AC ∴+= ()0AC PC CB ∴+=，0AC PB ∴=，故C 正确；对于D ，111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+22211122222222222222222=++-⨯⨯⨯-⨯⨯⨯+⨯⨯⨯=2MN ∴=，故D 错误.故选：ABC 【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键． (2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量． (3)在立体几何中三角形法则、平行四边形法则仍然成立．6．如图四棱锥P ABCD -，平面PAD ⊥平面ABCD ，侧面PAD 是边长为26的正三角形，底面ABCD 为矩形，23CD =，点Q 是PD 的中点，则下列结论正确的是（ ）A ．CQ ⊥平面PADB ．PC 与平面AQC 所成角的余弦值为223C ．三棱锥B ACQ -的体积为62D ．四棱锥Q ABCD -外接球的内接正四面体的表面积为3【答案】BD 【分析】取AD 的中点O ，BC 的中点E ，连接,OE OP ，则由已知可得OP ⊥平面 ABCD ，而底面ABCD 为矩形，所以以O 为坐标原点，分别以,,OD OE OP 所在的直线为x 轴，y 轴 ，z 轴，建立空间直角坐标系，利用空间向量依次求解即可. 【详解】解：取AD 的中点O ，BC 的中点E ，连接,OE OP ， 因为三角形PAD 为等边三角形，所以OP AD ⊥, 因为平面PAD ⊥平面ABCD ，所以OP ⊥平面 ABCD ， 因为AD OE ⊥，所以,,OD OE OP 两两垂直，所以，如下图，以O 为坐标原点，分别以,,OD OE OP 所在的直线为x 轴，y 轴 ，z 轴， 建立空间直角坐标系，则(0,0,0),(6,0,0),(6,0,0)O D A ，(0,0,32),6,23,0),(6,23,0)P C B ，因为点Q是PD的中点，所以Q，平面PAD的一个法向量为(0,1,0)m =，6(2QC=-，显然m与QC不共线，所以CQ与平面PAD不垂直，所以A不正确；3632(6,23,32),(,0,),(26,2PC AQ AC=-==，设平面AQC的法向量为(,,)n x y z=，则362260n AQ x zn AC⎧⋅=+=⎪⎨⎪⋅=+=⎩，令=1x ，则y z==，所以(1,2,n=-，设PC与平面AQC所成角为θ，则21sin36n PCn PCθ⋅===，所以cos3θ=，所以B正确；三棱锥B ACQ-的体积为1132B ACQ Q ABC ABCV V S OP--==⋅1116322=⨯⨯⨯=，所以C不正确；设四棱锥Q ABCD-外接球的球心为)M a，则MQ MD=，所以222222a a⎛++-=++⎝⎭⎝⎭，解得0a=，即M为矩形ABCD对角线的交点，所以四棱锥Q ABCD-外接球的半径为3，设四棱锥Q ABCD-外接球的内接正四面体的棱长为x，将四面体拓展成正方体，其中正四面体棱为正方体面的对角线，x，所以22362x⎛⎫=⎪⎪⎝⎭，得224x=，所以正四面体的表面积为234243x ⨯=，所以D 正确. 故选：BD【点睛】此题考查线面垂直，线面角，棱锥的体积，棱锥的外接球等知识，综合性强，考查了计算能力，属于较难题.7．已知正四棱柱1111ABCD A B C D -的底面边长为2，侧棱11AA =，P 为上底面1111D C B A 上的动点，给出下列四个结论中正确结论为（ ）A ．若3PD =，则满足条件的P 点有且只有一个B ．若3PD =，则点P 的轨迹是一段圆弧C ．若PD ∥平面1ACB ，则DP 长的最小值为2D ．若PD ∥平面1ACB ，且3PD =，则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD 【分析】若3PD =，由于P 与1B 重合时3PD =，此时P 点唯一；()313PD =，，则12PD =P 的轨迹是一段圆弧；当P 为11A C 中点时，DP 有最小值为3=断C ；平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆，其半径为32=，可得D . 【详解】 如图：∵正四棱柱1111ABCD A B C D -的底面边长为2， ∴1122B D =，又侧棱11AA =， ∴()2212213DB =+=，则P 与1B 重合时3PD =，此时P 点唯一，故A 正确；∵()313PD =∈，，11DD =，则12PD =，即点P 的轨迹是一段圆弧，故B 正确； 连接1DA ，1DC ，可得平面11//A DC 平面1ACB ，则当P 为11A C 中点时，DP 有最小值为()22213+=，故C 错误；由C 知，平面BDP 即为平面11BDD B ，平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆，其半径为2221322122++=，面积为94π，故D 正确． 故选：ABD ． 【点睛】本题考查了立体几何综合，考查了学生空间想象，逻辑推理，转化划归，数学运算的能力，属于较难题.8．如图，1111ABCD A B C D -为正方体，下列结论中正确的是（ ）A ．11A C ⊥平面11BB D D B ．1BD ⊥平面1ACBC ．1BD 与底面11BCC B 2 D ．过点1A 与异面直线AD 与1CB 成60角的直线有2条 【答案】ABD【分析】由直线与平面垂直的判定判断A 与B ；求解1BD 与底面11BCC B 所成角的正切值判断C ；利用空间向量法可判断D ． 【详解】对于A 选项，如图，在正方体1111ABCD A B C D -中，1BB ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111BB A C ⊥， 由于四边形1111D C B A 为正方形，则1111AC B D ⊥， 1111BB B D B =，因此，11A C ⊥平面11BB D D ，故A 正确；对于B 选项，在正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ，1AC DD ∴⊥，因为四边形ABCD 为正方形，所以，AC BD ⊥，1D DD BD =，AC ∴⊥平面11BB D D ， 1BD ⊂平面11BB D D ，1AC BD ∴⊥，同理可得11BD B C ⊥，1ACB C C =，1BD ∴⊥平面1ACB ，故B 正确；对于C 选项，由11C D ⊥平面11BCC B ，得11C BD ∠为1BD 与平面11BCC B 所成角， 且111112tan 2C D C BD BC ∠==，故C 错误； 对于D 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，设正方体的棱长为1，则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ，()1,0,0DA =，()11,0,1CB =，设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =， 则221cos ,21DA m DA m DA my z ⋅<>===⋅++，1122111cos ,221CB m z CB m CB my z ⋅+<>===⋅⋅++， 整理可得2222341y z y z z ⎧+=⎨=++⎩，消去y 并整理得2210z z +-=，解得12z =-+或12z =--，由已知可得3z ≤，所以，12z =-+，可得22y =±， 因此，过点1A 与异面直线AD 与1CB 成60角的直线有2条，D 选项正确. 故选：ABD. 【点睛】方法点睛：证明线面垂直的方法： 一是线面垂直的判定定理； 二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．9．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点P 在线段B 1C 上运动，则（ ）A ．直线BD 1⊥平面A 1C 1DB ．三棱锥P ﹣A 1C 1D 的体积为定值C ．异面直线AP 与A 1D 所成角的取值范用是[45°，90°] D ．直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为63【答案】ABD 【分析】在A 中，推导出A 1C 1⊥BD 1，DC 1⊥BD 1，从而直线BD 1⊥平面A 1C 1D ；在B 中，由B 1C ∥平面 A 1C 1D ，得到P 到平面A 1C 1D 的距离为定值，再由△A 1C 1D 的面积是定值，从而三棱锥P﹣A1C1D的体积为定值；在C中，异面直线AP与A1D所成角的取值范用是[60°，90°]；在D 中，以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出直线C1P与平面A1C1D 所成角的正弦值的最大值为63．【详解】解：在A中，∵A1C1⊥B1D1，A1C1⊥BB1，B1D1∩BB1＝B1，∴A1C1⊥平面BB1D1，∴A1C1⊥BD1，同理，DC1⊥BD1，∵A1C1∩DC1＝C1，∴直线BD1⊥平面A1C1D，故A正确；在B中，∵A1D∥B1C，A1D⊂平面A1C1D，B1C⊄平面A1C1D，∴B1C∥平面A1C1D，∵点P在线段B1C上运动，∴P到平面A1C1D的距离为定值，又△A1C1D的面积是定值，∴三棱锥P﹣A1C1D的体积为定值，故B正确；在C中，异面直线AP与A1D所成角的取值范用是[60°，90°]，故C错误；在D中，以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1中棱长为1，P（a，1，a），则D（0，0，0），A1（1，0，1），C1（0，1，1），1DA＝（1，0，1），1DC＝（0，1，1），1C P＝（a，0，a﹣1），设平面A1C1D的法向量(),,n x y z=，则11n DA x zn DC y z⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x＝1，得1,1,1n，∴直线C1P与平面A1C1D所成角的正弦值为：11||||||C P nC P n⋅⋅＝22(1)3a a+-⋅＝21132()22a⋅-+，∴当a＝12时，直线C1P与平面A1C1D所成角的正弦值的最大值为6，故D正确．故选：ABD．【点睛】求直线与平面所成的角的一般步骤：（1）、①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解； （2）、用空间向量坐标公式求解.10．如图，已知P 为棱长为1的正方体对角线1BD 上的一点，且()()10,1BP BD λλ=，下面结论中正确结论的有（ ）A ．11A D C P ⊥；B ．当1A P PD +取最小值时，23λ=；C ．若()0,1λ∈，则7,312APC ππ⎛⎫∠∈⎪⎝⎭； D ．若P 为1BD 的中点，四棱锥11P AA D D -的外接球表面积为94π． 【答案】ABD 【分析】以D 为坐标原点建立如图空间直角坐标系，利用向量关系可判断ABC ；根据几何体外接球关系建立方程求出球半径即可判断D. 【详解】以D 为坐标原点建立如图空间直角坐标系，则()1,1,0B ，()10,0,1D ，设(),,P x y z ，()()10,1BP BD λλ=，1BP BD λ∴=，即()()1,1,1,1,1x y z λ--=--，则可解得()1,1,P λλλ--， 对A ，()()()111,0,1,0,0,0,0,1,1A D C ，()11,0,1A D ∴=--，()11,,1C P λλλ=---，则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=，则11A D C P ⊥，故A 正确；对B ，1A P PD +===则当23λ=时，1A P PD +取最小值，故B 正确； 对C ，()()1,0,0,0,1,0A C ，(),1,PA λλλ∴=--，()1,,PC λλλ=--，则222321cos 1321321PA PCAPC PA PC λλλλλλ⋅-∠===--+-+⋅，01λ<<，则2232123λλ≤-+<，则2111123212λλ-≤-<-+， 即11cos 22APC -≤∠<，则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦，故C 错误；对于D ，当P 为1BD 中点时，四棱锥11P AA D D -为正四棱锥，设平面11AA D D 的中心为O ，四棱锥11P AA D D -的外接球半径为R ，所以222122R R ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭，解得34R =， 故四棱锥11P AA D D -的外接球表面积为94π，所以D 正确. 故选：ABD. 【点睛】关键点睛：本题考查空间相关量的计算，解题的关键是建立空间直角坐标系，利用向量建立关系进行计算.。

一、知识梳理1．空间向量的概念向量：在空间，我们把具有大小和方向的量叫做向量。

如位移、速度、力等。

相等向量：长度相等且方向相同的向量叫做相等向量。

表示方法：用有向线段表示，并且同向且等长的有向线段表示同一向量或相等的向量。

说明：①由相等向量的概念可知，一个向量在空间平移到任何位置，仍与原来的向量相等，用同向且等长的有向线段表示；②平面向量仅限于研究同一平面内的平移，而空间向量研究的是空间的平移。

2．向量运算和运算率b a AB OA OBb a OB OA BA)(R a加法交换率：.a b b a加法结合率：).()(c b a c b a数乘分配率：.)(b a b a说明：①引导学生利用右图验证加法交换率，然后推广到首尾相接的若干向量之和；②向量加法的平行四边形法则在空间仍成立。

3．平行向量(共线向量)：如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量。

a 平行于b 记作a ∥b。

注意：当我们说a 、b 共线时，对应的有向线段所在直线可能是同一直线，也可能是平行直线；当我们说a 、b 平行时，也具有同样的意义。

共线向量定理：对空间任意两个向量a （a ≠）、b ，a ∥b 的充要条件是存在实数 使b ＝ a 注：⑴上述定理包含两个方面：①性质定理：若a ∥b （a ≠0），则有b ＝ a ，其中 是唯一确定的实数。

②判断定理：若存在唯一实数 ，使b ＝ a （a ≠0），则有a ∥b （若用此结论判断a 、b 所在直线平行，还需a （或b ）上有一点不在b （或a ）上）。

⑵对于确定的 和a ，b ＝ a 表示空间与a 平行或共线，长度为 | a |，当 >0时与a 同向，当 <0时与a反向的所有向量。

⑶若直线l ∥a ，l A ，P 为l 上任一点，O 为空间任一点，下面根据上述定理来推导的表达式。

推论：如果 l 为经过已知点A 且平行于已知非零向量a 的直线，那么对任一点O ，点P 在直线l 上的充要条件是存在实数t ，满足等式a t ①其中向量a 叫做直线l 的方向向量。

课题：空间向量与运算复习小结课时：10 课型：一、复习目标1．了解空间向量的概念；会建立坐标系，并用坐标来表示向量； 2．理解空间向量的坐标运算；会用向量工具求空间的角和距离. 二．知识梳理 1．求角：（1）直线和直线所成的角：求二直线上的向量的夹角或补角； （2）直线和平面所成的角：①找出射影，求线线角；②求出平面的法向量n ，直线的方向向量a，设线面角为θ,则|cos ,|||||||n asin n a n a θ⋅=<>=⋅.（3）二面角：①求平面角，或求分别在两个面内与棱垂直的两个向量的夹角（或补角）； ②求两个法向量的夹角（或补角）. 2．求距离（1）点M 到面的距离||cos d MN θ=（如图）就是斜线段MN 在法向量n方向上的正投影.由||||cos ||n NM n NM n d θ⋅=⋅⋅=⋅得距离公式：||||n NM d n ⋅=（2）线面距离、面面距离都是求一点到平面的距离；（3）异面直线的距离：求出与二直线都垂直的法向量n和连接两异面直线上两点的向量NM，再代上面距离公式.三、双基练习1．在空间直角坐标系中，已知点P （x ，y ，z ），下列叙述中正确的个数是 （ ） ①点P 关于x 轴对称点的坐标是P 1（x ，－y ，z ） ②点P 关于yOz 平面对称点的坐标是P 2（x ，－y ，－z ） ③点P 关于y 轴对称点的坐标是P 3（x ，－y ，z ） ④点P 关于原点对称的点的坐标是P 4（－x ，－y ，－z ）A.3B.2C.1D.0_ a_ nNMHθa nθ2． 直三棱柱A 1B 1C 1—ABC ，∠BCA =90°，D 1、F 1分别是A 1B 1、A 1C 1的中点，BC =CA =CC 1，则BD 1与AF 1所成角的余弦值是 （ ）A ．1030B . 21C ．1530 D ．10153．已知向量a =（1，1，0），b =（－1，0，2），且ka ＋b 与2a －b 互相垂直，则k= ___ 4． 已知A （3，2，1）、B （1，0，4），则线段AB 的中点坐标和长度分别是 ， .◆答案提示： 1. C ； 2. A ； 3. 57；4.（2，1，25），d AB =17四、典例题解析【例1】 【2015全国二卷19．（本题满分12分）】如图，长方体1111ABCD A B C D -中,=16AB ，=10BC ，18AA =，点E ，F 分别在11A B ，11C D 上，114A E D F ==．过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．（Ⅰ）在图中画出这个正方形（不必说出画法和理由）； （Ⅱ）求直线AF 与平面α所成角的正弦值． 19．（Ⅰ）详见解析；（Ⅱ）4515． 解析：（Ⅰ）交线围成的正方形EHGF 如图：（Ⅱ）作EM AB ⊥，垂足为M ，则14AM AE ==，18EM AA ==，因为EHGF 为正方形，所以10EH EF BC ===．于是226MH EH EM =-=，所以10AH =．以D为坐标原点，DA的方向为x 轴的正方向，建立如图所示的空间直角坐标系D xyz -，则(10,0,0)A ，(10,10,0)H ，(10,4,8)E ，(0,4,8)F ，(10,0,0)FE = ，(0,6,8)HE =-．设DD 1C 1A 1EFA BCB 1(,,)n x y z = 是平面E H G F 的法向量，则0,0,n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n = ．又(10,4,8)AF =- ，故45cos ,15n AF n AF n AF⋅<>==⋅ ．所以直线AF 与平面α所成角的正弦值为4515． 考点：1、直线和平面平行的性质；2、直线和平面所成的角．A 1AB 1BD 1DC 1CFE HGM【例2】（本小题满分13分）如图，在四棱柱1111A B C D A B C D -中，侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB =,12,5AC AA AD CD ====,且点M 和N 分别为11C D B D 和的中点.（Ⅰ）求证：//MN 平面ABCD ； （Ⅱ）求二面角11D AC B --的正弦值；（Ⅲ）设E 为棱11A B 上的点，若直线NE 和平面ABCD 所成角的正弦值为13，求线段1A E 的长.17．（Ⅰ）见解析； （Ⅱ）31010； （Ⅲ） 72-. 解析：如图，以A 为原点建立空间直角坐标系，依题意可得(0,0,0),(0,1,0),(2,0,0),(1,2,0)A B C D -，又因为,M N 分别为1B C 和1D D 的中点，得11,,1,(1,2,1)2M N ⎛⎫- ⎪⎝⎭.（Ⅰ）证明：依题意，可得(0,0,1)n = 为平面ABCD 的一个法向量，50,,02MN ⎛⎫=- ⎪⎝⎭ ，由此可得，0MN n ⋅=，又因为直线MN ⊄平面ABCD ，所以//MN 平面ABCD（Ⅱ）1(1,2,2),(2,0,0)AD AC =-= ，设1(,,)n x y z =为平面1ACD 的法向量，则 1110n AD n AC ⎧⋅=⎪⎨⋅=⎪⎩，即22020x y z x -+=⎧⎨=⎩，不妨设1z =，可得1(0,1,1)n = ， 设2(,,)n x y z = 为平面1ACB 的一个法向量，则21200n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩，又1(0,1,2)AB = ，得 2020y z x +=⎧⎨=⎩，不妨设1z =，可得2(0,2,1)n =-因此有12121210cos ,10n n n n n n ⋅==-⋅，于是12310sin ,10n n = ， 所以二面角11D AC B --的正弦值为31010. （Ⅲ）依题意，可设111A E A B λ=，其中[0,1]λ∈，则(0,,2)E λ，从而(1,2,1)NE λ=-+，又(0,0,1)n =为平面ABCD 的一个法向量，由已知得22211cos ,3(1)(2)1NE n NE n NE n λ⋅===⋅-+++，整理得2430λλ+-=， 又因为[0,1]λ∈，解得72λ=-，所以线段1A E 的长为72-.考点：直线和平面平行和垂直的判定与性质，二面角、直线与平面所成的角，空间向量的应用.五、提炼总结以为师1.求线线角、线面角、二面角的方法：2．求点面距离，线面距离、面面距离及异面直线的距离的方法：六、同步练习1.【2015高考】一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设BC 的中点为M ，GH 的中点为N .CB A DGE HFMEABCD（1）请将字母,,F G H 标记在正方体相应的顶点处（不需说明理由） （2）证明：直线//MN 平面BDH （3）求二面角A EG M --的余弦值. 18．（1）点F 、G 、H 的位置如图所示.MDCABEFH G（2）详见解析.（3）223解析：（1）点F 、G 、H 的位置如图所示.MDCABEFH G（2）连结BD ，设O 为BD 的中点.OMDCAB EFH GN因为M 、N 分别是BC 、GH 的中点，所以//OM CD ，且12OM CD =， //NH CD ，且12NH CD =，所以//,OM NH OM NH =，所以MNHO 是平行四边形，从而//MN OH ，又MN ⊄平面BDH ，OH ⊂平面BDH ，所以//MN 平面BDH . （3）连结AC ，过M 作MP AC ⊥于P.OM DCABEFH GP K N在正方形ABCD EFGH -中，//AC EG ，所以MP EG ⊥. 过P 作PK EG ⊥于K ，连结KM ，所以EG ⊥平面PKM ， 从而KM EG ⊥.所以PKM ∠是二面角A EG M --的平面角. 设2AD =，则1,2CM PK ==，在Rt CMP 中，2sin 452PM CM ==. 在Rt KMP 中，22322KM PK PM =+=.所以cos PK PKM KM ∠==223. 即二面角A EG M --的余弦值为223. 2.【2015山东】如图，在三棱台DEF ABC -中，2,,AB DE G H =分别为,AC BC 的中点.（Ⅰ）求证：//BD 平面FGH ；（Ⅱ）若CF ⊥平面ABC ，,AB BC CF DE ⊥= ，45BAC ∠=,求平面FGH 与平面ACFD 所成的角（锐角）的大小. 17．（Ⅰ）详见解析；（Ⅱ）60分析：（Ⅰ）思路一：连接,DG CD ，设CD GF O = ，连接OH ，先证明//OH BD ，从而由直线与平面平行的判定定理得//BD 平面HDF ；思路二：先证明平面 //FGH 平面 ABED ，再由平面与平面平行的定义得到//BD 平面HDF .（Ⅱ）思路一：连接,DG CD ，设CD GF O = ，连接OH ，证明,,GB GC GD 两两垂直, 以G 为坐标原点，建立如图所示的空间直角坐标系G xyz -，利用空量向量的夹角公式求解；思路二：作HM AC ⊥ 于点M ，作MN GF ⊥ 于点N ，连接NH ，证明MNH ∠ 即为所求的角，然后在三角形中求解. 解析：（Ⅰ）证法一：连接,DG CD ，设CD GF O = ，连接OH ， 在三棱台DEF ABC -中，2,AB DE G =为AC 的中点 可得//,DF GC DF GC = 所以四边形DFCG 为平行四边形 则O 为CD 的中点又H 为BC 的中点所以//OH BD 又OH ⊂平面,FGH BD ⊂/平面,FGH 所以//BD 平面FGH ．证法二：在三棱台DEF ABC -中，由2,BC EF H =为BC 的中点可得 //,,BH EF BH EF = 所以四边形BHFE 为平行四边形可得 //BE HF 在 ABC ∆中， G 为AC 的中点， H 为BC 的中点，所以 //GH AB 又 GH HF H = ，所以平面 //FGH 平面 ABED因为 BD ⊂平面 ABED 所以 //BD 平面FGH （Ⅱ）解法一：设2AB = ，则1CF = 在三棱台DEF ABC -中，G 为AC 的中点由12DF AC GC == ，可得四边形DGCF 为平行四边形，因此//DG CF 又FC ⊥平面ABC 所以DG ⊥平面ABC在ABC ∆中，由,45AB BC BAC ⊥∠=，G 是AC 中点，所以,AB BC GB GC =⊥ 因此,,GB GC GD 两两垂直,以G 为坐标原点，建立如图所示的空间直角坐标系G xyz -所以()()()()0,0,0,2,0,0,0,2,0,0,0,1G BC D可得()22,,0,0,2,122H F ⎛⎫⎪ ⎪⎝⎭ 故()22,,0,0,2,122GH GF ⎛⎫== ⎪ ⎪⎝⎭设(),,n x y z =是平面FGH 的一个法向量，则由0,0,n GH n GF ⎧⋅=⎪⎨⋅=⎪⎩ 可得020x y y z +=⎧⎪⎨+=⎪⎩ 可得平面FGH 的一个法向量()1,1,2n =-因为GB 是平面ACFD 的一个法向量，()2,0,0GB =所以21cos ,2||||22GB n GB n GB n ⋅<>===⋅所以平面与平面所成的解（锐角）的大小为60解法二：作HM AC ⊥ 于点M ，作MN GF ⊥ 于点N ，连接NH由FC ⊥ 平面ABC ，得HM FC ⊥ 又FC AC C = 所以HM ⊥平面ACFD 因此GF NH ⊥ 所以MNH ∠ 即为所求的角在BGC ∆ 中,12//,,22MH BG MH BG == 由GNM ∆∽GCF ∆ 可得,MN GM FC GF = 从而66MN = 由MH ⊥平面,ACFD MN ⊂平面ACFD 得,MH MN ⊥ 因此tan 3HMMNH MN∠== 所以60MNH ∠= 所以平面FGH 与平面ACFD 所成角（锐角）的大小为60 .。

吉林省东北师范大学附属中学2015春高中数学 2.1空间点、直线、平面之间的位置关系学案 理 新人教A 版必修2一、自主学习：自学35P -38P 回答：1。

平面的基本性质：（1）点和直线的基本性质：连接两点的线中， 最短；过两点 一条直线，并且 一条直线。

（2）平面的基本性质：1如果一条直线的 点在一个平面内，那么这条直线上的所有点 在 这个平面内。

这时我们就说 或 。

作用：2经过 同一直线的三点，有且只有 个平面。

也可以简单地说成： 的三点确定一个平面。

过不共线的三点A 、B 、C 的平面，通常记作： 。

作用：3 如果不重合的两个平面有 个公共点，那么它们有且只有 条过这个点的公共直线。

如果两个平面有一条公共直线，则称这两个平面 。

这条公共直线叫做着两个平面的 作用：注意：画两个相交平面时，，其中一个平面被另一个平面遮住的部分画成 线或 。

（3）平面的基本性质的推论：1经过一条直线和直线 的一点，有且只有 个平面。

02经过两条 直线，有且只有 个平面。

3经过两条 直线，有且只有 个平面。

三推论作用： （4）共面与异面直线：共面：空间中的几个点或几条直线，如果都在 ，我们就说它们共面。

共面的两条直线的位置关系有 和 两种。

异面直线：既 又 的直线叫异面直线。

判断两条直线为异面直线的方法：与一平面相交于一点的直线与这个平面内 的 直线是异面直线。

（5）符号语言：点A 在平面α内，记作 ；点A 不在平面α内，记作 。

直线l 在平面α内，记作 ；直线l 不在平面α内，记作 。

平面α与平面β相交于直线a , 记作 .直线l 和直线m 相交于点A ，记作 ，简记作： 。

基本性质01可以用集合语言描述为：如果点A α，点B α，那么直线AB α。

二、典型例题：例1. 已知三条直线a 、b 、c 两两相交但不共点，求证：a 、b 、c 共面。

例2.已知三条平行线a 、b 、c 都与直线d 相交. 求证:它们共面.例3.正方体1111D C B A ABCD -中,对角线C A 1与平面1BDC 交于AC O ,、BD 交于点M . 求证:点1C 、O 、M 共线.1B例4.已知三个平面α、β、γ两两相交,且α⋂β=c ,β⋂γ=a ,γ⋂α=b , 且直线a 和b 不平行.求证: a 、b 、c 三条直线必相交同一点.三、学生练习：38P 练习A 、B补充1。

课题：空间向量的数量积（1）课时：03 课型：新授课 教学目标：1．掌握空间向量夹角和模的概念及表示方法；2．掌握两个向量的数量积的计算方法，并能利用两个向量的数量积解决立体几何中的一些简单问题。

教学重、难点：空间数量积的计算方法、几何意义、立体几何问题的转化。

教具准备：与教材内容相关的资料。

教学设想：激发学生的学习热情，激发学生的求知欲，培养严谨的学习态度，培养积极进取的精神．教学过程学生探究过程：（一）复习：空间向量基本定理及其推论；（二）新课讲解：1．空间向量的夹角及其表示：已知两非零向量,a b rr ，在空间任取一点O ，作,OA a OB b ==u u u r u u u r r r ，则AOB ∠叫做向量a r 与b r 的夹角，记作,a b <>r r ；且规定0,a b π≤<>≤r r ，显然有,,a b b a <>=<>rr r r ；若,2a b π<>=rr ，则称a r 与b r 互相垂直，记作：a b ⊥r r ；2．向量的模：设OA a =u u u r r ，则有向线段OA u u u r 的长度叫做向量a r 的长度或模，记作：||a r ；3．向量的数量积：已知向量,a b r r ，则||||cos ,a b a b ⋅⋅<>r r r r 叫做,a b rr 的数量积，记作a b ⋅r r ，即a b ⋅=r r ||||cos ,a b a b ⋅⋅<>r rr r ．已知向量AB a =u u u r r 和轴l ，e r是l 上与l 同方向的单位向量，A CB A 'B 'e r作点在l 上的射影A '，作点在l 上的射影B '，则A B ''u u u u r 叫做向量AB u u u r 在轴l 上或在e r上的正射影；可以证明A B ''u u u u r 的长度||||cos ,||A B AB a e a e ''=<>=⋅u u u u r u u u r r r r r ．4．空间向量数量积的性质： （1）||cos ,a e a a e ⋅=<>r r r r r．（2）0a b a b ⊥⇔⋅=r rr r ．（3）2||a a a =⋅rr r．5．空间向量数量积运算律：（1）()()()a b a b a b λλλ⋅=⋅=⋅r r r r r r．（2）a b b a ⋅=⋅r r r r（交换律）．（3）()a b c a b a c ⋅+=⋅+⋅r r r r r r r（分配律）．（三）例题分析：例1．用向量方法证明：直线和平面垂直的判定定理。

吉林省东北师范大学附属中学2015届高考数学一轮复习空间几何体的结构、表面积与体积导学案文一、知识梳理：（必修2教材第2页-第7页；第23-第28页）1、空间几何体：（1）、多面体：（2）、旋转体：2、柱、锥、台、球的结构特征(1).棱柱：有两个面，其余各面都是，并且每相邻两个的公共边都相互平行，由这些面所围成的多面体叫做棱柱。

棱柱的性质：侧棱长都，侧面是。

(2)．棱锥：有一个面是，其余各面都是的三角形，由这些面所围成的多面体叫做棱锥。

底面是，顶点在的棱锥叫做正棱锥。

(3)．棱台：棱锥被所截，截面和底面之间的部分叫做棱台。

由正棱锥截得的棱台叫。

(4)．圆柱：以的一边所在直线为旋转轴，其余三边旋转所围成的旋转体叫做圆柱。

(5)．圆锥：以的所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥。

(6)．圆台：用圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台。

(7)．球：以的所在直线为旋转轴，旋转一周形成的旋转体叫做球。

球的性质：用一个平面去截一个球，截面是。

(8).组合体：由柱、锥、台、球等基本几何体组成的几何体叫组合体；3、多面体的表面积：多面体的表面积是各个面的面积之和，也就是展开图的面积4、旋转体的表面积公式：(1)圆柱的表面积公式：（r为底面半径，l为母线长）(2)圆锥的表面积公式：（r为底面半径，l为母线长）(3)圆台的表面积公式：（为上、下底面半径，l为母线长）(4)球的表面积公式：（R为球的半径）二、题型探究：空间几何体的结构例1：下列命题中正确的是（ D ）A.有两个面平行，其余各面都是四边形的几何体叫棱柱M A B D CO B.有两个面平行，其余各面都是平行四边形的几何体叫棱柱C.有一个面是多边形，其余各面都是三角形的几何体叫棱锥D.棱台各侧棱的延长线交于一点例2：下列几个命题中，①两个面平行且相似，其余各面都是梯形的多面体是棱台;②有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台;③各侧面都是正方形的四棱柱一定是正方体;④分别以矩形两条不等的边所在直线为旋转轴，将矩形旋转，所得到的两个圆柱是两个不同的圆柱.其中正确的有______个.（A ）A.1B.2C.3D.4解析:只有4对.探究二：柱、锥、台体的体积与表面积 例3：(2013闸北区) 如图，在四棱锥O-ABCD 中，底面ABCD 是边长为2的正方形，OA，OA=2，M 为OA 的中点．求四棱锥O-MCD 的体积；例4：求棱长为1的正四面体的棱切球与外接球的表面积和体积。

一、知识梳理：（必修2教材第11页-第18页） 1、 中心投影与平行投影：投影是光线通过不透明的物体,向选定的面投射,并在该面上得到图形的方法;平行投影的投影线是互相平行的，中心投影的投影线相交于一点. 2、三视图三视图是观测者从不同位置观察同一个几何体，画出的空间几何体的投影图形。

它具体包括：（1）正视图：物体前后方向投影所得到的投影图； 它能反映物体的高度和长度；（2）侧视图：物体左右方向投影所得到的投影图； 它能反映物体的高度和宽度； （3） 俯视图：物体上下方向投影所得到的投影图； 它能反映物体的长度和宽度；三视图的排列规则：主在前，俯在下，左在右画三视图的原则：主、左一样 ，主、俯一样 ，俯、左一样 。

3、直观图:斜二测画法①建立直角坐标系，在已知水平放置的平面图形中．．．．．取互相垂直的OX ，OY ，建立直角坐标系；②画出斜坐标系，在画直观图的纸．．．．．上（平面上）画出对应的O ’X ’,O ’Y ’,使'''X OY ∠=450（或1350），它们确定的平面表示水平平面；③画对应图形:在已知图形平行于y 轴的线段，在直观图中画成平行于x ‘轴，且长度保持不变；在已知图形平行于y 轴的线段，在直观图中画成平行于y ‘轴，且长度变为原来的一半； ④擦去辅助线:图画好后，要擦去y 轴、y 轴及为画图添加的辅助线（虚线）。

二、题型探究：探究一：空间几何体的三视图例1:一个几何体由几个相同的小正方体组合而成，它的主视图、左视图、俯视图如下图所示，则这个组合体包含的小正方体个数是 （ ）主视图 左视图 俯视图A 、7B 、6C 、5D 、4例2：已知ABC ∆的平面直观图'''C B A ∆是边长为a 的正三角形，那么原ABC ∆的面积为（ ） （A ）23a 2 （B ）243a （C ）226a （D ）26a例3.【北京2014】7.在空间直角坐标系Oxyz 中，已知()2,0,0A ，()2,2,0B ，()0,2,0C ，()1,1,2D ，若 1S ，2S ，3S 分别表示三棱锥D ABC -在xOy ，yOz ，zOx 坐标平面上的正投影图形的 面积，则（ ）（A ）123S S S == （B ）12S S =且 31S S ≠ （C ）13S S =且 32S S ≠ （D ）23S S =且 13S S ≠【解析】7. D 【命题意图】本小题主要考查了空间直角坐标系，正投影定义和图形面积的计算.如图所示：三棱锥D ABC -在xoy 平面上的正投影为OBC ∆，则12S =，设D 在yoz 平面上的正投影为2D ，棱锥D ABC -在yoz 平面上的正投影图形2D AC ∆，设D 在三、方法提升1、三视图是利用物体的三个正投影来表现空间几何体的方法，画几何体的三视图要注意：一个几何体的侧视图与正视图高度一样，俯视图与正视图长度一样，侧视图与俯视图宽度一样，侧视图在正视图的右边，俯视图在正视图的下边，能看见的轮廓线或棱用实线表示，不能看见的轮廓线或棱用虚线表示。

课题：2-1.3.4向量的数量积（2）课时：04课型：新授课教学目标：①向量的数量积运算②利用向量的数量积运算判定垂直、求模、求角教学重点：①向量的数量积运算②利用向量的数量积运算判定垂直、求模、求角教学方法：练习法，纠错法，归纳法教学过程：1.向量的数量积运算（1）、知识要点：1）定义：① 设<,a b r r >=θ,则a b =r r g （θ的范围为 ）②设11(,)a x y =r ，22(,)b x y =r 则a b =r r g。

注：①a b r r g不能写成ab r r ，或a b ⨯r r ②a b r r g 的结果为一个数值。

2）投影：b r 在a r 方向上的投影为 。

3）向量数量积运算律：①a b b a =r r r r g g ②()()()a b a b a b λλλ==r r r r r r g g g ③()a b c a c b c +=+r r r r r r r g g g注：①没有结合律()()a b c a b c =r r r r r r g g g g例题1讲练1、若a r ，b r ，c r 满足0a b c ++=r r r r ，且3,1,4a b c ===r r r ，则a b b c a c ++r r r r r r g g g = 。

2、已知2a b ==r r ，且a r 与b r 的夹角为3π，则a b +r r 在a r 上的投影为 。

向量数量积性质应用一）、知识要点：①0a b a b ⊥⇔=r r r r g（用于判定垂直问题）②a =r （用于求模运算问题） ③cos a b a bθ=r r g r r （用于求角运算问题） 例题2讲练1、已知2a =r ，3b =r ，且a r 与b r 的夹角为2π，32c a b =+r r r ，d ma b =-u r r r ，求当m 为何值时c d ⊥r u r2、已知1a =r ，1b =r ，323a b -=r r ，则3a b +=r r 。