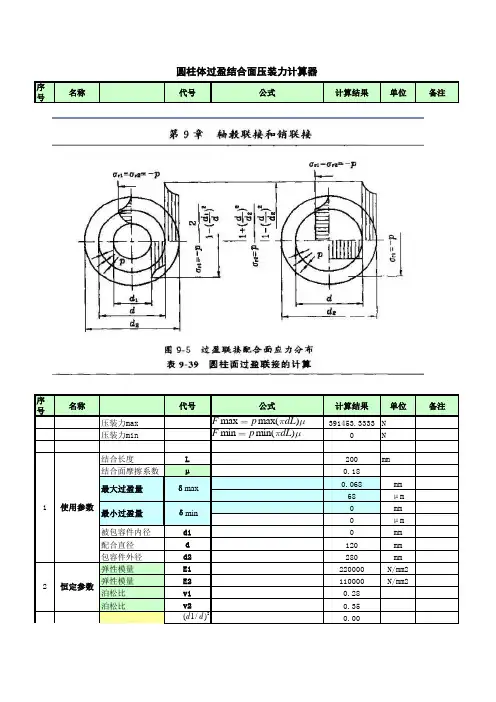
圆柱体常用量计算器
- 格式:xls
- 大小:9.50 KB
- 文档页数:1
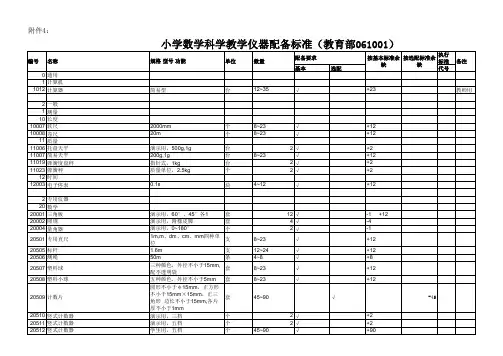

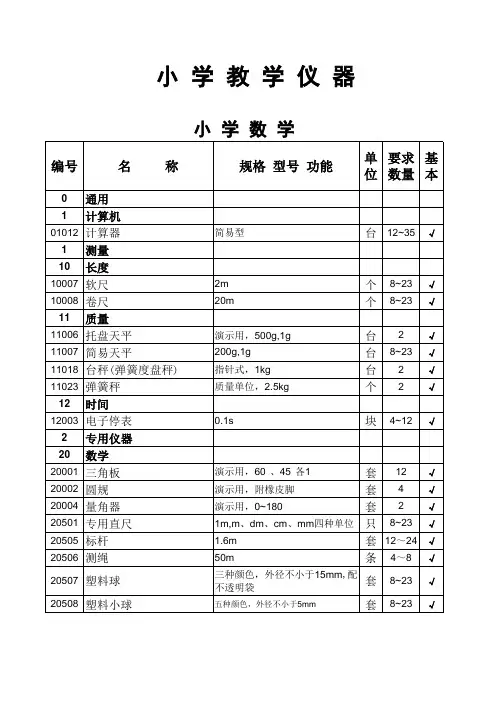
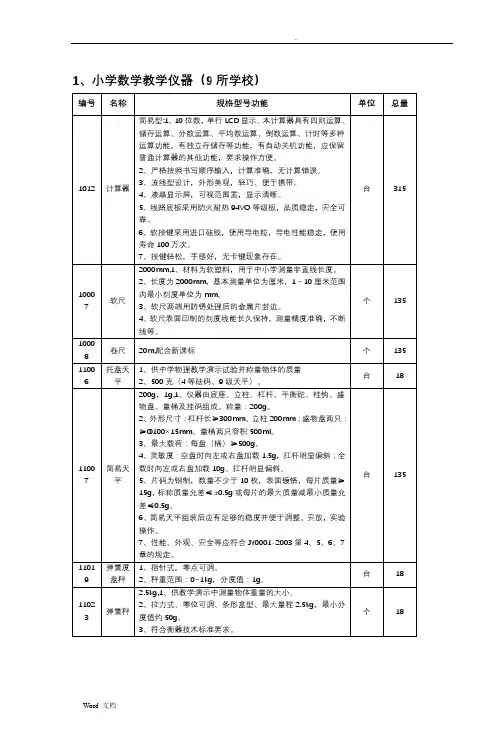
1、小学数学教学仪器(9所学校)
注:所有仪器设备按照设备编号规定的标准进行生产,符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定;按照9所学校进行包装,送到相应学校。
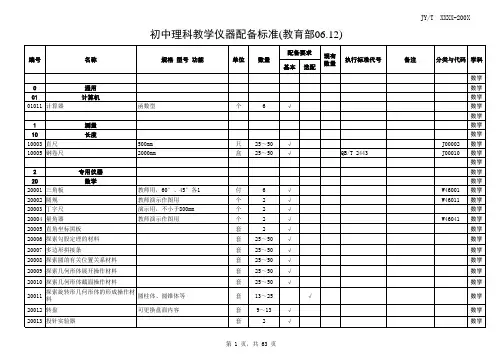
2、初中数学教学仪器(2所学校)
注:所有仪器设备按照设备编号规定的标准进行生产,符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定;按照2所学校进行包装,送到相应学校。
3、小学科学教学仪器(9所学校)
注:所有仪器设备按照设备编号规定的标准进行生产,符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定;按照9所学校进行包装,送到相应学校。
4、初中地理教学仪器(2所学校)
注:所有仪器设备按照设备编号规定的标准进行生产,符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定;按照9所学校进行包装,送到相应学校。
5、小学卫生器材(8所学校)
注:所有仪器设备按照设备编号规定的标准进行生产,符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定;按照8所学校进行包装,送到相应学校。
6、初中卫生器材(2所学校)
注:所有仪器设备按照设备编号规定的标准进行生产,符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定;按照9所学校进行包装,送到相应学校。
7、小学美术器材(9所学校)。

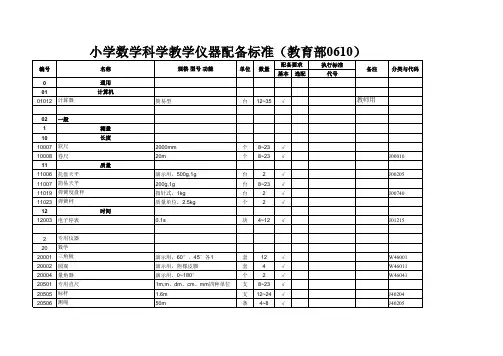
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)
小学数学科学教学仪器配备标准(教育部0610)。

圆柱纵截面体积计算圆柱是一个常见的几何体,它的纵截面体积是一个有趣的数学问题。
我们可以通过计算来得到圆柱的纵截面体积,而无需使用复杂的数学公式。
我们需要了解圆柱的结构。
圆柱有一个圆形的底面和一个平行于底面的顶面,这两个面之间由直线连接而成。
底面和顶面的半径相等,我们用r表示。
圆柱的高度用h表示。
我们可以将圆柱分成无数个纵截面,每个纵截面都是一个圆形。
如果我们将圆柱沿着高度方向切割成许多薄片,每个薄片的厚度非常小,那么每个薄片的纵截面都可以看作是一个圆形。
现在,我们来计算一个纵截面的体积。
假设我们取一个距离底面h1的纵截面,它的半径是r1。
由于纵截面是圆形,我们可以使用圆的面积公式来计算纵截面的面积,即πr1^2。
由于纵截面的厚度非常小,我们可以将整个圆柱看作是无数个纵截面的叠加。
每个纵截面的面积都是πr1^2,而纵截面的数量就是圆柱的高度h。
因此,整个圆柱的体积可以表示为Σ(πr1^2 * h1),其中Σ表示求和。
我们可以将Σ(πr1^2 * h1)简化为πΣ(r1^2 * h1)。
由于每个纵截面的半径和高度都可以不同,我们需要对每个纵截面进行求和。
通过将纵截面的半径和高度相乘,并将结果累加起来,我们可以得到整个圆柱的体积。
通过这种方法,我们可以计算任意形状的圆柱的纵截面体积,而无需使用复杂的数学公式。
这种计算方法简单直观,适用于各种实际问题,如容器的容积计算、建筑物的结构设计等。
当然,在实际计算中,我们可以使用计算器或计算机程序来快速得到结果。
通过这个简单的例子,我们可以看到数学在解决实际问题中的重要性。
数学不仅是一门学科,更是一种思维方式和工具,可以帮助我们理解和解决各种问题。
无论是计算圆柱的纵截面体积,还是解决更复杂的数学问题,数学的应用都离不开我们的思考和努力。
让我们一起探索数学的奥秘,感受数学的美妙吧!。

圆柱体的体积计算圆柱体是几何学中一个重要的二维形体,它具有两个平行且相等的圆底面,并由连接两底面的侧面组成。
在实际生活中,圆柱体的体积计算常常用于工程、建筑、制造等领域。
下面将介绍如何计算圆柱体的体积,以及相关的公式和实例。
一、圆柱体体积的公式圆柱体的体积(V)可以通过以下公式来计算:V = π * r^2 * h其中,π是一个常数,约等于3.14;r表示圆柱体底面的半径;h表示圆柱体的高度。
二、圆柱体体积计算的步骤下面以一个例子来演示如何计算圆柱体的体积。
例子:将半径为5cm,高度为12cm的圆柱体的体积计算出来。
1. 根据给定的数据,获得圆柱体的半径r和高度h。
半径r = 5cm高度h = 12cm2. 将半径r和高度h代入圆柱体体积的公式V = π * r^2 * h中。
V = 3.14 * 5^2 * 123. 进行计算,并得出结果。
V = 3.14 * 25 * 12≈ 942.48cm^3所以,半径为5cm,高度为12cm的圆柱体的体积约为942.48立方厘米。
三、圆柱体体积计算的注意事项在进行圆柱体体积计算时,需要注意以下几点:1. 确保半径和高度的单位一致。
如果半径使用的是厘米,那么高度也应使用厘米,以保证计算的准确性。
2. 在使用计算器计算过程中,应当注意保留足够的小数位数,以免影响最终结果的准确性。
最好将计算结果四舍五入至合适的位数。
3. 在实际应用中,如果需要进行大量的圆柱体体积计算,可以编写程序或使用电子表格软件来自动计算,提高工作效率和准确性。
四、其他常见形体的体积计算公式除了圆柱体,还有许多其他常见形体的体积计算公式,例如:1. 球的体积计算公式:V = (4/3) * π * r^3其中,r表示球的半径。
2. 正方体的体积计算公式:V = a^3其中,a表示正方体的边长。
3. 长方体的体积计算公式:V = l * w * h其中,l表示长方体的长度,w表示宽度,h表示高度。

浅谈大学物理实验数据的处理——管型圆柱体的体积计算随着科技的进步,物理实验在大学中占有越来越重要的地位。
大学物理实验数据的处理是大学物理实验中非常重要的一部分,可以使学生更好地理解物理实验中的本质。
其中,管型圆柱体的体积计算是比较常见的一种实验内容,可以帮助学生更好地理解空间几何的基本原理。
首先,要计算管型圆柱体的体积,首先要明确管型圆柱体的定义,它是一种长度大于宽度,侧面为圆柱面的几何图形。
管型圆柱体的体积可以由长度(L)、圆柱底面半径(r)和圆柱侧面半径(R)来计算。
根据计算公式,管型圆柱体的体积V =r^2L 。
了解完管型圆柱体的定义和体积计算公式后,就可以开始进行实验操作了。
在物理实验中,通常需要先量取此管型圆柱体的长度、底面半径和侧面半径。
根据上述计算公式,就可以得到管型圆柱体的体积了。
在物理实验中,学生需要注意一些实验操作的要求,以保证实验结果的准确性。
首先,学生在量取长度、底面半径和侧面半径时,需要注意操作过程的细节,以免量取错误。
其次,学生在计算体积时,可以使用计算器,以减少计算误差。
最后,在实验室中,学生应该注意实验环境的整洁,以及实验器材的延长使用寿命。
此外,学生还应该做好实验记录,有助于对实验结果进行正确的分析和比较。
总之,管型圆柱体的体积计算是物理实验中很常见的一种实验,
它不仅可以帮助学生更好地理解空间几何的基本原理,而且在实验中需要注意很多细节,使得学生能够得到准确的计算结果。
求圆柱的表面积教案教学目标:1. 理解圆柱的表面积概念。
2. 学会计算圆柱的表面积。
3. 能够应用表面积公式解决实际问题。
教学重点:1. 圆柱表面积的计算方法。
2. 应用表面积公式解决实际问题。
教学难点:1. 圆柱侧面积的计算。
2. 圆柱表面积公式的灵活运用。
教学准备:1. 圆柱模型。
2. 计算器。
3. 练习题。
教学过程:一、导入(5分钟)1. 引入圆柱的概念,引导学生观察圆柱的特征。
2. 提问:圆柱的表面积是什么意思?它包括哪些部分?二、新课讲解(15分钟)1. 讲解圆柱的表面积公式:圆柱的表面积=底面积×2+侧面积。
2. 解释底面积、侧面积的概念及计算方法。
3. 举例讲解如何计算圆柱的表面积。
三、课堂练习(10分钟)1. 让学生独立完成练习题,巩固圆柱表面积的计算方法。
2. 引导学生思考如何应用表面积公式解决实际问题。
四、课堂小结(5分钟)1. 回顾本节课所学内容,总结圆柱表面积的计算方法。
2. 强调圆柱表面积公式的灵活运用。
五、课后作业(课后自主完成)1. 完成练习题,巩固圆柱表面积的计算方法。
2. 尝试解决实际问题,如计算一个圆柱形杯子的表面积。
教学反思:本节课通过讲解和练习,使学生掌握了圆柱表面积的计算方法,并能应用到实际问题中。
在教学中,要注意引导学生观察圆柱的特征,理解底面积、侧面积的概念,从而更好地理解圆柱的表面积。
要加强课后作业的布置,让学生充分巩固所学知识。
六、案例分析(15分钟)1. 展示一个实际生活中的圆柱体物体,如圆柱形油桶、饮料瓶等。
2. 引导学生分析这个物体表面由哪些部分组成。
3. 让学生尝试计算这个圆柱体物体的表面积。
七、小组讨论(15分钟)1. 学生分组,每组选择一个圆柱体物体进行讨论。
2. 讨论如何测量和计算这个圆柱体物体的表面积。
3. 每组汇报讨论结果,分享计算方法和测量数据。
八、课堂练习(15分钟)1. 让学生独立完成练习题,巩固圆柱表面积的计算方法。
圆柱体封头体积计算公式圆柱体封头是一种将圆柱体的两个端面封闭的装置。
在工业领域中,圆柱体封头常用于制造容器和储存罐。
计算圆柱体封头的体积是制造这些装置的必要步骤之一,因此,了解圆柱体封头的计算公式是非常重要的。
以下为圆柱体封头体积计算公式的详细说明:1. 所需材料及工具计算圆柱体封头的体积需要以下材料和工具:- 表面积计算器- 圆柱体封头的半径- 圆柱体的高度2. 圆柱体封头的定义和类型圆柱体的封头分为以下几种类型:- 球形封头:以球的形状封闭圆柱的两端。
- 圆锥封头:以圆锥的形状封闭圆柱的一端。
- 空心封头:将两个封头组合在一起形成一个球形或圆柱形容器。
3. 圆柱体封头的计算公式计算圆柱体封头的体积需要使用以下公式:- 对于球形封头,体积=1/6πh(3a^2+h^2),其中h = 封头高度,a = 半径。
- 对于圆锥封头,体积=1/3πr^2h,其中r = 半径,h = 高度。
- 对于空心封头,体积=1/2πh(R^2-r^2),其中h = 高度,R = 更大半径,r = 更小半径。
4. 圆柱体封头计算公式的应用举例举例说明,我们现在需要计算一个直径为50cm、高度为30cm的球形封头的体积。
根据上面的公式,我们可以计算出该球形封头的体积为1.096立方米,这个结果可以用于制造一个球形容器。
5. 总结圆柱体封头的计算公式是制造圆柱体容器和储存罐的重要工具。
计算圆柱体封头的体积需要了解封头的类型、使用表面积计算器和输入圆柱体的高度和半径等参数。
通过正确地使用这些公式,可以计算出正确的体积结果,这对于制造这些容器和储存罐,以及其他工业应用是不可或缺的。