样本量估算

样本量估算公式
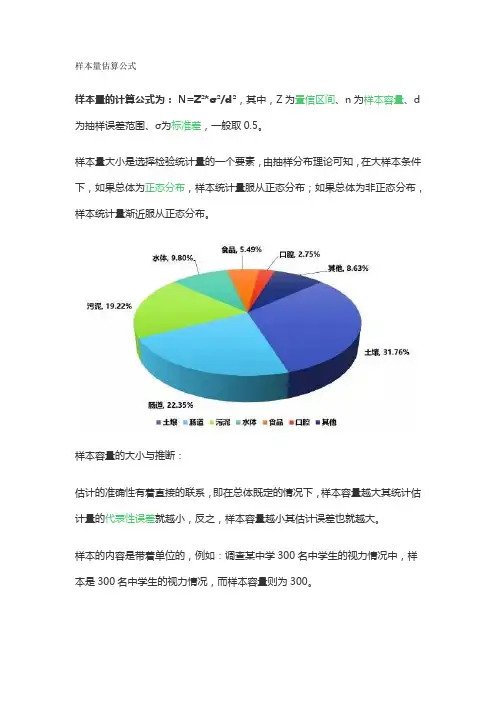
样本量的计算公式为： N=Z²*σ²/d²，其中，Z为置信区间、n为样本容量、d 为抽样误差范围、σ为标准差，一般取0.5。

样本量大小是选择检验统计量的一个要素，由抽样分布理论可知，在大样本条件下，如果总体为正态分布，样本统计量服从正态分布；如果总体为非正态分布，样本统计量渐近服从正态分布。

样本容量的大小与推断：
估计的准确性有着直接的联系，即在总体既定的情况下，样本容量越大其统计估计量的代表性误差就越小，反之，样本容量越小其估计误差也就越大。

样本的内容是带着单位的，例如：调查某中学300名中学生的视力情况中，样本是300名中学生的视力情况，而样本容量则为300。

样本容量的大小涉及到调研中所要包括的单元数，样本容量是对于研究的总体而言的，是在抽样调查中总体的一些抽样，比如：中国人的身高值为一个总体，随机取一百个人的身高，这一百个人的身高数据就是总体的一个样本，某一个样本中的个体的数量就是样本容量。

临床试验样本量的估算介绍临床试验样本量的估算是一个关键性的步骤，它决定了试验结果的可靠性和统计学上的显著性。

样本量的估算需要考虑多个因素，如预期效应大小、研究设计、统计分析方法以及可接受的错误率等。

本文将详细介绍临床试验样本量估算的基本原理和常用方法。

一、样本量估算的目的和原则样本量估算的主要目的是确保试验具有足够的统计功效，能够检测到预期效应的存在或差异的显著性。

同时，也需要避免过大的样本量，以减少资源的浪费和人体试验的风险。

样本量估算的原则如下：1.统计功效要求：根据研究者的预期效应大小，确定试验能够达到的最小统计功效要求。

通常，我们希望试验能够有80%的功效检测到预期效应。

2.显著性水平：选择统计学上的显著性水平，通常为α=0.053.效应大小的估计：根据已有的文献或专家经验，估计预期效应的大小。

4.变异性的估计：估计所研究的指标的标准差或方差。

5.实用性考虑：考虑到资源和时间的限制，选择可实现的最小样本量。

二、常用的样本量估算方法1.基于效应大小的样本量估算方法这种方法根据研究者希望检测到的最小效应大小来估算样本量。

常用的方法有两组均数差异的估算、比例差异的估算以及相关系数的估算。

对于两组均数差异的估算，可使用t检验或方差分析来进行样本量估算。

对于比例差异的估算，可使用Z检验来进行样本量估算。

对于相关系数的估算，可使用相关系数检验来进行样本量估算。

2.基于统计功效的样本量估算方法这种方法以试验的统计功效为基础，确定对于预期效应的检测，需要多大样本量。

常用的方法有功效检验和样本量递推法。

对于功效检验法，可以通过计算给定样本量下的样本估计效应大小，并判断是否满足统计功效要求。

对于样本量递推法，可以根据初步样本量估计和实际效应大小来修正样本量，直到满足统计功效要求。

3.基于生存分析的样本量估算方法这种方法适用于生存分析或生存率的研究。

常用的方法有Kaplan-Meier方法和Cox比例风险模型。

样本量估算是在研究设计和统计计划阶段的关键步骤，目的是确定为获得有效和可靠的统计结论所需的观察对象数量。

以下是样本量估算的基本步骤：
1. 确定研究目的和类型：首先需要明确研究的目的，例如描述性研究、因果研究、相关性研究等。

不同的研究类型会影响样本量计算的方法。

2. 确定效应大小：这是样本量估算的关键参数。

对于不同的研究类型和问题，所需的效应大小可能不同。

例如，在检验新药效果的研究中，可能需要较大的效应以证明新药的有效性。

3. 确定显著性水平和置信水平：显著性水平通常为0.05或0.01，表示当原假设为假时，拒绝原假设的错误概率。

置信水平通常为95%，表示样本统计量与总体参数之间的接近程度。

4. 选择适当的统计方法：根据研究目的和数据类型，选择适当的统计方法来确定样本量。

例如，在两独立样本均值比较的情境下，可以使用t检验或Mann-Whitney U检验等统计方法来计算样本量。

5. 进行样本量计算：根据上述参数和方法进行样本量计算。

这一步骤通常需要使用统计软件或在线工具来完成。

6. 考虑其他因素：在实际研究中，还需要考虑其他因素对样本量的影响，如预期的失访率、多中心研究的复杂性等。

7. 确定最终样本量：综合上述因素，确定最终的研究样本量。

对于多数研究而言，这个样本量需要是一个整数，所以可能需要通过调整来获得最接近的可用数值。

总之，样本量估算是一个复杂的过程，需要考虑多种因素。

在实践中，建议咨询统计学专家或使用专业的统计软件来帮助进行样本量估算。

统计学估算样本量一、样本量估算的基本概念在进行统计研究时，我们希望通过对样本的观察来推断总体的特征。

样本量的大小直接影响到我们对总体特征的估计精度和推断的准确性。

样本量估算是为了确定一个合适的样本容量，使得对总体参数的估计误差在一定范围内。

二、样本量估算的方法样本量的估算是根据研究目标、总体特征、假设检验的要求等因素综合考虑得出的。

常用的样本量估算方法有如下几种：1.常用的样本量估算方法之一是基于置信区间的方法。

在进行统计推断时，我们希望能够给出一个对总体参数的估计范围，即置信区间。

样本量的大小与置信区间的宽度有关，当我们希望估计的精度更高时，需要增加样本容量。

2.另一种常用的样本量估算方法是基于假设检验的方法。

在进行假设检验时，我们需要根据研究目标和假设的检测效应大小来确定样本量。

通常情况下，当我们希望检测到一个较小的效应时，需要增加样本容量。

3.此外，还有一些特殊的样本量估算方法，如基于方差分析、回归分析等。

这些方法根据具体的研究设计和分析方法来确定样本量。

三、样本量估算的注意事项在进行样本量估算时，需要注意以下几点：1.合理选择统计方法。

样本量估算方法的选择应根据研究目标和分析方法来决定，确保估算结果的准确性和可靠性。

2.注意样本的代表性。

样本应该尽可能代表总体的特征，避免出现样本选择偏差，否则样本量估算的结果可能不准确。

3.考虑实际可行性。

在进行样本量估算时，需要考虑实际可行性和研究资源的限制，避免过高或过低的样本容量。

4.定期进行样本量检查。

在实施研究过程中，应根据实际情况定期对样本量进行检查和调整，以确保研究结果的可靠性。

四、总结样本量的估算是统计学中重要的一部分，合理的样本量能够保证研究结果的可靠性和有效性。

在进行样本量估算时，需要根据研究目标、总体特征、假设检验的要求等因素综合考虑。

合理选择估算方法、注意样本的代表性、考虑实际可行性和定期进行样本量检查是进行样本量估算的关键要点。

临床试验样本量的估算临床试验的样本量估算是研究计划中非常重要的一个环节。

样本量的大小会直接影响到试验结果的可靠性和推广性。

本文将介绍一些常用的方法和考虑因素，来进行临床试验样本量的估算。

一、统计学方法1.样本量估算的原则样本量估算的基本原则是保证试验结果的统计学意义和实际应用的可行性，同时控制样本量的大小。

在样本量估算时需要考虑的主要因素包括：研究目的、效应大小、α水平、β水平、检验类型和预估结果的方差。

2.效应大小效应大小（Effect Size）指的是一种观察、试验或实验中的两组之间的差异，并且是研究中最重要的指标之一、效应大小的选择需要基于研究目标和研究领域的实际情况。

常用的效应大小指标包括：风险比、比值比、均值差异等。

3.α水平和β水平α水平和β水平是两种错误假设的概率。

α水平（Type I错误）是拒绝了一个真假设。

通常是将p值设置在0.05以下。

β水平（TypeII错误）是接受了一个错误的假设。

常见的β值是0.2、0.1、0.05和0.01、α和β的选择需要根据实际情况和研究目的进行权衡。

4.检验类型根据研究目的和数据类型的不同，可以选择不同的检验类型。

常见的检验类型包括：t检验、方差分析、卡方检验等。

不同的检验类型需要不同的样本量估算方法。

5.预估结果的方差预估结果的方差是样本量估算的另一个重要因素。

方差的预估可以通过先前的研究结果或者基于临床经验来估算。

二、样本量估算方法1.均值差异的样本量估算方法均值差异的样本量估算方法适用于需要比较两个或多个组之间平均值差异的研究。

常用的方法有：Z检验样本量估算、t检验样本量估算和方差分析样本量估算。

2.分类变量的样本量估算方法分类变量的样本量估算方法适用于比较不同组之间的比率、风险比、比值比等。

常用的方法有：卡方检验样本量估算和Fishers精确检验样本量估算等。

3.生存分析的样本量估算方法生存分析的样本量估算方法适用于评估治疗或干预措施对患者生存时间或复发时间的影响。

医学样本估算量计算公式在医学研究和临床实践中，样本估算量的计算是非常重要的。

正确的样本量可以保证研究结果的可靠性和代表性，从而为医学实践提供科学依据。

因此，研究者需要掌握样本估算量的计算方法，以确保研究的可信度和有效性。

样本估算量的计算涉及到多个因素，包括研究的目的、研究对象的特点、预期效应的大小等。

在医学研究中，常用的样本估算量计算公式包括以下几种：1. 二项分布样本量计算公式。

二项分布样本量计算公式适用于研究二分类变量的比较，比如治疗组与对照组的比较。

其计算公式为：n = (Zα/2 + Zβ)² (p1(1-p1) + p2(1-p2)) / (p1-p2)²。

其中，n为每组的样本量，Zα/2和Zβ分别为显著性水平和统计功效对应的Z 值，p1和p2分别为两组的事件发生率。

2. t检验样本量计算公式。

t检验样本量计算公式适用于研究连续变量的比较，比如两组平均数的比较。

其计算公式为：n = (Zα/2 + Zβ)² 2σ² / δ²。

其中，n为每组的样本量，Zα/2和Zβ分别为显著性水平和统计功效对应的Z 值，σ为总体标准差，δ为两组平均数的差异。

3. 相关性分析样本量计算公式。

相关性分析样本量计算公式适用于研究两个变量之间的相关性。

其计算公式为：n = (Zα/2 + Zβ)² 2(1-r²) / r²。

其中，n为样本量，Zα/2和Zβ分别为显著性水平和统计功效对应的Z值，r 为两个变量之间的相关系数。

以上是一些常用的样本估算量计算公式，研究者在进行样本量估算时可以根据研究的具体目的和设计选择合适的计算方法。

此外，还需要注意以下几点：1. 样本估算量的计算需要考虑到研究的实际可行性，包括研究时间、经费等因素。

2. 样本估算量的计算还需要考虑到研究的临床意义，以确保研究结果的实际应用性。

3. 在进行样本估算量计算时，还需要考虑到研究的预期效应大小，以确保研究结果的统计学意义。

样本量估算
样本量估算指的是在一项研究中需要招募多少参与者，以达到足够的统计学力量来回答研究问题。

样本量的大小取决于多个因素，包括研究的类型、目的、研究假设的大小、研究问题的类型和分析方法等。

在估算样本量时，需要考虑以下因素：
1. 样本的方差大小：当目标是检测两组之间的差异时，方差越大，则需要更大的样本量。

2. 置信度：样本量的大小受置信度的影响。

通常置信度为95%或99%。

3. 效应大小：一般来说，如果实际的效应大小增加，则需要更少的样本量。

4. 误差范围：需确定研究误差大小，通常用于指定结果估计值的置信区间。

假设在进行一项研究时，我们需要得出两组之间的差异，置信度为95%，实际的效应大小为0.5，研究误差范围为正负0.1。

基于这些条件，我们可以使用样本量计算公式来估算样本量：
n = 2 * (Z值 + Zβ值)^2 * σ^2 / Δ^2
其中，n表示要招募的样本量；Z值和Zβ值分别是计算置信度和功效所用的标准正态分布的值；Δ表示研究组之间的期望差异。

假设σ为0.5，则：
- 当期望的差异值为0.5时，n= 364
- 当期望的差异值为0.8时，n = 170
- 当期望的差异值为1.0时，n = 109
这意味着，为了达到95%的置信度和80%的功效，我们需要至少在每组招募109个参与者来完成我们的研究。

但是，样本量的大小仍然要考虑其它因素，如样本选择和可接受的误差范围。

因此，我们建议在设计研究时仔细考虑这些因素，在设置样本量时，结合实际情况和研究成本来做合理规划。

调查量表样本量的估算方法、技巧与实际应用在进行市场调查、社会科学研究或医学研究时，调查量表样本量的估算是一个至关重要的环节。

合理的样本量能够确保调查结果的代表性和可靠性，同时避免资源的浪费。

本文将详细介绍调查量表样本量的估算方法、技巧以及实际应用，帮助研究者更好地设计和实施调查。

一、调查量表样本量的估算方法1. 根据总体大小估算当总体大小（N）已知时，可以使用以下公式来估算样本量（n）：n = N ×(1 + Z^2 ×p ×(1-p))其中，Z是对应于所需置信水平（通常为95%）的标准正态分布的分位数，p是预期的响应比例（以小数形式），(1-p)是未响应的比例。

2. 根据总体比例估算当总体比例（p）未知时，可以使用以下公式来估算样本量：n = (Z^2 ×p ×(1-p)) / (E^2)其中，E是允许的误差范围（以小数形式），Z是标准正态分布的分位数，p是预期的响应比例。

3. 根据效应大小估算在医学研究中，样本量的估算通常基于效应大小（Δ）。

效应大小是指处理效应与控制效应之间的差异。

样本量可以通过以下公式估算：n = 2 ×(Z^2 + Δ^2) / (E^2)其中，Δ是效应大小，Z是标准正态分布的分位数，E是允许的误差范围。

二、调查量表样本量的估算技巧1. 考虑总体异质性在估算样本量时，需要考虑总体的异质性。

如果总体中各个单位的响应概率差异较大，需要增加样本量以确保结果的可靠性。

2. 适当增加样本量在调查设计中，适当增加样本量可以提高结果的精确度和可靠性。

但是，也要避免样本量过大，以免造成资源的浪费。

3. 考虑无响应率在调查中，可能会有一部分受访者不参与调查。

因此，在估算样本量时，需要考虑无响应率，并相应地增加样本量。

4. 使用专业软件现代统计软件（如SPSS、SAS、R等）提供了样本量估算的功能。

研究者可以使用这些软件来帮助估算样本量。

最低样本量的估算公式
在研究过程中，样本量的大小是非常重要的，因为合理的样本量大小可以增加研究结果的可靠性和有效性。

然而，确定样本量的大小并不是一件容易的事情。

有一些公式可以用来估算最低样本量的大小，这些公式可以根据研究的目的、研究设计和统计分析方法等因素进行调整。

最常用的估算公式是基于假设检验的方法。

在假设检验中，研究者会确定一个显著性水平，然后通过样本量的大小来确定研究结果是否具有统计学意义。

根据研究设计和统计分析方法的不同，有不同的估算公式。

最常用的公式是：
n = (Zα/2 + Zβ)2 × (p(1-p)/d2)
其中，n表示样本量的大小；Zα/2和Zβ表示显著性水平和功
效（1-β）的标准正态分位数；p表示研究样本中的预计成功率；d
表示预期的误差范围。

需要注意的是，这个公式是基于二元变量的假设检验，如果研究变量是定量变量或者是多元变量，需要使用不同的公式进行估算。

总之，估算最低样本量的大小是研究过程中一个非常重要的环节，需要研究者在设计研究时认真考虑。

选择合适的估算公式可以增加研究结果的可靠性和有效性。

- 1 -。

样本量的估算方法引言在实施研究项目时，样本量的估算是一个重要的步骤。

准确估算样本量对于确保研究结果的可靠性和有效性至关重要。

本文将介绍一些常用的样本量估算方法。

1. 常见的样本量估算方法1.1. 参数估计法参数估计法是一种常见的样本量估算方法，它基于对所研究总体参数的估计。

在使用参数估计法时，需确定研究中的主要参数，并通过合适的统计模型对其进行估计。

然后，根据所容忍的误差范围和置信水平，可以计算出所需的样本量。

1.2. 效应量估算法效应量估算法是另一种常用的样本量估算方法。

它关注的是待研究变量之间的差异大小。

研究的效应量越大，所需的样本量越小，反之亦然。

通过对已有文献中的效应量进行分析，可以得出对应于所研究效应量的样本量估算。

1.3. 推断力估算法推断力估算法是一种基于显著性检验的样本量估算方法。

它基于预先设定的显著性水平和所期望的统计效应大小，在保证所研究假设能够被充分检验的前提下，通过计算所需的样本量。

2. 样本量估算的重要性准确估算样本量对于研究的可靠性和有效性具有重要意义。

确保样本量足够可以提高研究结果的可靠性，避免假阳性或假阴性结果的出现。

同时，充分估算样本量可以避免资源的浪费，确保研究的高效性。

结论在实施研究项目时，样本量的估算是至关重要的一步。

参数估计法、效应量估算法和推断力估算法是常用的样本量估算方法。

准确估算样本量可以提高研究结果的可靠性和有效性，同时也可以避免资源的浪费。

因此，在研究设计之初，进行样本量估算是非常重要的。

1.单因素二水平设计定量资料的非劣效性检验时样本量的估算1.1计算公式：非劣效性检验应当采用单侧的检验水准α，假定允许的第二类错误概率不超过β，则非劣效性检验每组需要的样本含量为：22211)/()(2θδβα-+=--L S u u n （1-1）[1]2221）/（)(2δβαe s z z n n ⨯+== （1-2）[2] 1.2式中各参数代表的意义，n 为每组样本含量，α-1u 、β-1u 为单侧标准正态离差界值，S 为估计的共同标准差，L δ为非劣界值，且L δ＜0，θ 为试验组与对照组总体均值差值的估计值。

说明：单因素二水平设计定量资料的非劣效性检验时样本量的估算公式与上式完全类似，只需将非劣界值L δ（L δ＜0）替换成优效界值u δ（u δ＞0）即可。

1.3例题：某利尿新药拟进行Ⅱ期临床试验，与阳性药按1:1的比例安排例数，考察24h 新药利尿量（ml ）是否不差于阳性药。

根据以往的疗效和统计学的一般要求，取α=0.05，β=0.20，非劣效界值L δ=﹣60ml ，已知两组共同标准差S =180ml ，假定新药与阳性对照药总体利尿量的差值θ=﹣20ml ，问每组需要多少病例？将05.01-u =1.645，20.01-u =0.845，s=180，L δ=﹣60，θ=﹣20代入公式，得：22211)/()(2θδβα-+=--L S u u n =2（1.645+0.845）2×1802/（﹣60﹣（﹣20））2≈251.1，取n=252，即每组需要252例。

2.单因素二水平设计定性资料的非劣效性检验时样本含量的估算2.1计算公式：非劣效性检验应当采用单侧检验，检验水准为α，假定允许的第二类错误概率不超过β，试验组与对照组总体率的差值为C T ππθ-=（T π、C π未知时可用样本频率估计），两组的平均有效率为2/)(C T πππ+=，非劣界值为u δ＜0，则在两组样本含量相等的情况下，非劣效性检验每组需要的样本含量为：2211)/()1()(2θδππβα--+=--L u u n （2-1）[1]2合合221/）-1（)(2δβαp p z z n n +== （2-2）[2]说明：单因素二水平设计定性资料的优效性检验时样本含量的估计公式与式（2-1）完全类似，只需将非劣界值L δ（L δ＜0）替换成优效界值u δ（u δ＞0）即可。

医学研究中常见的样本量估算方法一、本文概述在医学研究中，样本量估算是一项至关重要的工作，它直接影响到研究结果的可靠性和有效性。

正确的样本量估算能够确保研究具有足够的统计效力，从而得出准确且可信的结论。

本文旨在深入探讨医学研究中常见的样本量估算方法，帮助研究人员在设计和实施研究时能够科学、合理地确定样本量，以提高研究的质量和效率。

文章将先对样本量估算的基本概念进行介绍，然后重点阐述几种常用的样本量估算方法，包括基于效应量、基于统计效力、基于预试验数据等方法。

文章还将讨论影响样本量估算的因素，如研究设计、目标总体、效应大小等，并提供一些实用的建议和指导，以帮助研究人员更好地进行样本量估算。

通过本文的学习，读者将能够掌握医学研究中样本量估算的基本方法和技巧，为成功开展医学研究奠定坚实的基础。

二、样本量估算的基本概念在医学研究中，样本量估算是一个至关重要的步骤，它决定了研究所需的数据量，进而影响到研究结果的准确性和可靠性。

样本量估算的基本概念主要包括以下几个方面：总体与样本：总体是指我们想要研究的全部观察对象的集合，而样本则是从总体中随机抽取的一部分观察对象。

样本量就是样本中所包含的观察对象的数量。

样本量的选择应当足以代表总体，并能够提供足够的信息来推断总体的特性。

效应量：效应量是指研究中预期的处理效应或差异的大小。

它可以是两组之间的均值差、比例差或其他任何形式的度量。

效应量的大小直接影响了样本量的需求，因为较大的效应量通常需要较小的样本量来检测。

误差与置信水平：在样本量估算中，我们通常会考虑到两类误差：一类是第一类错误（或称为α错误），即错误地拒绝了原假设（即实际上没有差异，但研究结果显示有差异）；另一类是第二类错误（或称为β错误），即错误地接受了原假设（即实际上有差异，但研究结果显示没有差异）。

样本量估算需要在这两类错误之间进行权衡，以确定一个合适的样本量。

置信水平也是影响样本量估算的一个重要因素，它表示我们对研究结果的信任程度。

三组样本量估算公式在统计学中，样本量是指用于研究和分析的观察单位的数量。

确定适当的样本量对于得出准确和可靠的研究结果至关重要。

样本量的选择要考虑到所需的可靠性、效应大小、显著性水平和统计功效等因素。

下面将介绍三种常见的样本量估算公式。

一、二项分布样本量估算公式：在二项分布中，有兴趣的事件发生的概率称为成功概率，而未发生的概率称为失败概率。

在一些研究中，我们想要估计成功概率的差异是否具有实际意义。

为了确定所需的样本量，可以使用以下公式：n=(Z^2*p*(1-p))/(d^2)其中，n是所需的样本量，Z是选择的显著性水平的Z值，p是预期的成功概率，d是所需的效应大小。

二、回归分析样本量估算公式：在回归分析中，我们研究自变量与因变量之间的关系。

为了确定所需的样本量，可以使用以下公式：n=(Z^2*σ^2)/(d^2*R^2)其中，n是所需的样本量，Z是所选显著性水平的Z值，σ是残差标准差，d是所需效应大小，R是自变量与因变量之间的相关系数。

三、t检验样本量估算公式：在t检验中，我们想要比较两个群体的均值是否有显著差异。

为了确定所需的样本量，可以使用以下公式：n=(2*(Z+T)^2*σ^2)/(d^2)其中，n是所需的样本量，Z是选择的显著性水平的Z值，T是选择的统计功效的T值，σ是总体标准差，d是所需效应大小。

在以上公式中，显著性水平（α）通常取0.05或0.01，统计功效（1-β）通常取0.8或0.9、所需效应大小是通过研究目的和实际问题来确定的。

综上所述，样本量的估算是统计研究中的一个重要步骤。

根据不同的统计方法和研究目的，可以选择适当的样本量估算公式来确定所需的样本量。

这些公式可以帮助研究者确定适当的样本量，确保研究结果的可靠性和有效性。