s z dz
P(1 2 )
E x 2 y 2
6.2
地基变形的弹性力学公式
地面上某点(x,y,0)处的沉降为:
P( 1 ) z 2 2( 1 ) S w 3 2E r r
第四章布氏解
任意(面)柔性荷载,地基沉降可由上两式按迭加原 理积分求得,如同计算附加应力,沉降叠加法 下面介绍圆形、矩形均布荷载下地基沉降计算式
6.2 地基变形的弹性力学公式
2.圆形荷载
半无限弹性体 均布柔性圆形荷载 荷载密度为p 荷载作用区半径为b,直径为B=2b 地基中任一点土竖向位移:
s
pb (1 ) z [ I 2 (1 ) I 1 ] E b
I1和I2 = 沉降影响数,与z/r 值和 z/b 值有关 E =地基土弹性模量,常用变形模量表示 z=0,地面沉降为:
第六章
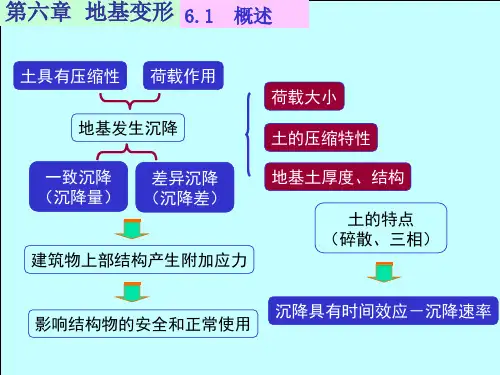
§ 6.1 概述
地基变形
§ 6.2 地基变形的弹性力学公式
§ 6.3 基础最终沉降量
§ 6.4 路基的沉降和位移*
§ 6.5 地基变形与时间的关系
1
§6 地基变形
概述
墨西哥某宫殿
问题: 沉降2.2米, 且左右两部分 存在明显的沉 降差。
地基:20多米厚的粘土
2
Kiss
由于沉降相互影响,两栋相邻的建筑物上部接触
p
S z H v H
e1
H
H/2 H/2
γH σc 2
γ,e1
σz=p z
e2
e
Vs 1 Vs 1
z v e e1 e2 1 e1 1 e1
c
侧限条件
压缩前