当前位置：文档之家 › 举例说明矩阵位移法

举例说明矩阵位移法

  • 格式：ppt
  • 大小：420.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

矩阵位移法的计算步骤及示例

矩阵位移法的计算步骤及示例

单元①②和③：
35
⎡ 500 0 0 − 500 0 0 ⎤
⎢ ⎢
0
12 24
0
− 12
24
⎥ ⎥
(1)
k
=
(2)
k
=
(3)
k
=
10
3
⎢ ⎢⎢−
0 500
24 0
64 0
0 − 24 32 ⎥
500 0
0
⎥ ⎥
⎢ 0 −12 − 24 0 12 − 24⎥
⎢ ⎢⎣ 0
24 32
0
− 24
⎥ 64 ⎥⎦
8-8 矩阵位移法的计算步骤及示例 1
矩阵位移法的计算步骤：（以后处理为例）
（1）对结点和单元进行编号，建立结构（整
体）坐标系和单元（局部）坐标系，并对结
点位移进行编号。
（2）计算各杆的单元刚度矩 k (e)、k (e) 。
（3）形成结构原始刚度矩阵K。
（4）计算固端力
F
(e) F
、等效结点荷载FE及综合
⎢⎣0.0 0.0 6.0 12.0⎥⎦
由于连续梁的单元刚度矩阵为非奇异矩阵， 由此组集而成的结构刚度矩阵K 也是非奇异 的，故无需再进行支座约束条件处理。
（4）计算固端力列阵及等效结点 15 荷载列阵。
②单元的固端力列阵
F (2) F
=
⎧ 300 ⎫ ⎩⎨− 300⎭⎬kN
⋅
m
等效结点荷载列阵：
k(3)
=
⎢ ⎢ ⎢
l(3) 2EI
⎢⎣ l ( 3 )
4
2EI l(3) 4EI l(3)
⎤ ⎥ ⎥ ⎥ ⎥⎦
3 4
（3）集成结构刚度矩阵K

结构力学十三讲矩阵位移法

结构力学十三讲矩阵位移法

-6EI l2
4EI l
4
§13-3 单元刚度矩阵(整体座标系)
一、单元座标转换矩阵 Y1
X1
X1
Y1
MM21
e
x
M2 X2
正交矩阵 [T]-1 =[T]T
e e
e T T e
v1
y e
X 2
Y2
Fⓔ T T F ⓔ
ee
F T F ee
座标转换矩阵
5
二、整体座标系中旳单元刚度矩阵
[k] e = [T]T k e [T]
(4)
(6)
00
(5)
y
单元 局部码总码
单元 局部码总码
（1） 1 （2） 2 （3） 3 （4） 0 （5） 0 （6） 4
1
2
3 0
0
4
（1） 1
1
（2） 2
2
（3） 3 （4） 0
3 0
（5） 0
0
（6） 0
0
18
1 2
[k] 1 = 3
0 0 4
1 2
[k] 2= 3
0 0 0
123004 101 102 103 104 105 106 201 202 203 204 205 206 301 302 303 304 305 306 401 402 403 404 405 406 501 502 503 504 505 506 601 602 603 604 605 606 123000 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66

结构力学基础矩阵位移法基本概念、计算程序和例题讲解

结构力学基础矩阵位移法基本概念、计算程序和例题讲解

例形成图示刚架可动结点劲度矩阵，E,I ,A为常数。
解： 1.编号，如图（b) 2.确定单元杆端自由度序号。
3.计算 kmi 4.计算单元转换矩阵
5.形成单元在整体坐标系中的劲度矩阵
6.根据单元杆端自由度序号叠加
二、可动结点劲度矩阵性质
1.对称方阵
反力互等定理
2.非奇异矩阵 考虑了约束条件，排除了刚体位移
7.求杆端力Fmi
8.求支座反力 支座反力由下式
计算，得
9.内力图
例2 求图2-21(a)所示平面刚架的内力,已知各杆 I 0.005m4
A0.05m2，E2106kNmA2B杆、CD杆杆
返回
§9—3 可动结点劲度矩阵
一、形成可动结点劲度矩阵的步骤
步骤： 1.对结构进行结点编号、单元标号、自由度编号： 2.确定单元杆端自由度序号（考虑约束条件）； 3.计算单元在局部坐标系中的劲度矩阵kmi 4.计算单元转换矩阵Ti 5.形成单元在整体坐标系中的劲度矩阵ki TiTkmiTi
6.按”对号入座”原则，将ki叠加到 k 中。
结构力学基础 矩阵位移法基本概念、计算程
序和例题讲解
§9-1 矩阵位移法基本概念 §9-2 单元劲度矩阵 §9-3 可动结点劲度矩阵 §9-4 可动结点等效荷载列阵 §9-5 单元杆端力和支座反力 §9-6 例题 §9-7 平面刚架计算程序
§9—1 矩阵位移法的基本概念
一、坐标系和符号规定 图示连续梁：
4.求 K
（1）计算机各单元的方向余弦和杆长：
（2）求 kmi
(3)求ki
单元（1）:Cx=0 Cy=1
杆长：l 同理：
（4）求 按照“对号入座“原则，由ki形成k哪
例如： 同理：

《结构力学》第十章矩阵位移法

《结构力学》第十章矩阵位移法

《结构力学》第十章矩阵位移法矩阵位移法是结构力学中的一种重要分析方法，通过将结构的受力分析转化为矩阵运算，可以有效地求解复杂结构的位移和应力分布。

本文将分为四个部分来介绍矩阵位移法的基本原理和应用。

第一部分将介绍矩阵位移法的基本原理。

矩阵位移法基于结构的受力平衡方程和变形条件，建立了适用于不同类型结构的一般形式的位移函数。

通过对这些位移函数进行适当组合，可以得到一个较为简化的位移矩阵方程。

这个方程可以通过矩阵运算求解，从而得到结构的位移和应力分布。

第二部分将介绍矩阵位移法的应用。

矩阵位移法可以用于求解各种类型的结构，包括梁、柱、框架等。

具体应用时，首先需要确定结构的边界条件和受力情况，然后根据结构的几何形状和材料性质，建立相应的位移函数。

之后，将位移函数按照一定的规则组合起来，建立一个位移矩阵方程。

通过解这个方程，可以得到结构的位移和应力分布。

第三部分将介绍矩阵位移法的优点。

相比于传统的力方法，矩阵位移法具有计算简单、准确性高、适用范围广等优点。

这是因为矩阵位移法可以通过矩阵运算将结构的受力分析转化为代数运算，减少了繁琐的计算过程，并且可以应用于各种不规则结构。

第四部分将介绍矩阵位移法的局限性。

矩阵位移法虽然具有很多优点，但也有一些限制。

首先，矩阵位移法对结构的刚度矩阵的求取较为复杂，需要通过精确和谐振数法等途径进行求解。

其次，矩阵位移法不能用于解决非线性和动力问题。

总结起来，矩阵位移法是一种重要的结构力学分析方法，通过将结构的受力分析转化为矩阵运算，可以有效地求解复杂结构的位移和应力分布。

它具有计算简单、准确性高、适用范围广等优点，但也有一些局限性。

因此，在实际应用中需要根据具体情况选择合适的方法。

同时，矩阵位移法的进一步研究和发展也是一个非常重要的方向。

结构力学应用-矩阵位移法

结构力学应用-矩阵位移法

3、集成总刚
（6）定位向量法：对号入座，同号相加 定位向量法：对号入座，
4．综合结点荷载
综合结点荷载 {F}={FD}+{FE} }――直接结点荷载 ①{FD}――直接结点荷载 }――等效结点荷载 ②{FE}――等效结点荷载 （7-1）局部坐标系单元固端力 （7-2）整体坐标系单元固端力 （7-3）单元等效结点荷载。 单元等效结点荷载。
等效原则： 等效原则： ——两种荷载对基本体系产生相同的结点位移。 两种荷载对基本体系产生相同的结点位移 ——两种荷载对基本体系产生相同的结点位移。
矩阵位移法的计算步骤及示例
矩阵位移法计算平面刚架 计算机计算――程序化） 程序化） （计算机计算 程序化
1. 编码、整理原始数据 编码、
（1）整体与局部坐标系 ） （2）结点位移编码 ） 单元编码 （3）原始数据： ）原始数据： E 、A i、I i、l i 定位向量{λ} 定位向量 e， αi（[ T ]） ]）
几点补充说明
1、结点位移分量编号，定位向量 、结点位移分量编号，
——引入支承条件：已知位移约束的方向，编码为零。 引入支承条件：已知位移约束的方向，编码为零。 引入支承条件
2、铰结点处理： 铰结点处理： 铰结点处理
铰结的各杆杆端的转角均为基本未知量 ——分别编码（统一单元，程序简单） 分别编码（统一单元，程序简单） 分别编码
矩阵位移法
矩阵位移法——基本原理与位移法相同 基本原理与位移法相同 矩阵位移法 *数学工具 —— 矩阵运算
1、矩阵知识 矩阵： （1）矩阵：A 方阵： 方阵： 阶方阵A相应的行列式 （2）行列式：n阶方阵 相应的行列式 ）行列式： 阶方阵 相应的行列式D 若D＝0，A为奇异矩阵 （3）矩阵运算 相等：加减：数乘： 相等：加减：数乘： l aik 乘法： 乘法：Cmn=Aml*Bln，则 cij =

结构力学之矩阵位移法

结构力学之矩阵位移法

第十二章 矩阵位移法【例12-1】 图 a 所示 连 续 梁 ，EI=常数，只 考 虑 杆 件 的 弯 曲 变 形 。

分别用位移法和矩阵位移法计算。

图12-1解：（1）位移法解∙基本未知量和基本结构的确定用位移法解的基本结构如图c 所示。

这里我们将结点1处的转角也作为基本未知数，这样本题仅一种基本单元，即两端固定梁。

∙位移法基本方程的建立⎪⎭⎪⎬⎫=+θ+θ+θ=+θ+θ+θ=+θ+θ+θ000333323213123232221211313212111P P P R K K K R K K K R K K K 将上式写成矩阵形式⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000321321333231232221131211P P P R R R K K K K K K K K K∙系数项和自由项 计算（须绘出单位弯矩图和荷载弯矩图）由图d ，结点力矩平衡条件∑=0M ，得 l EI K 411=，l EI K 221=，031=K由图e ，结点力矩平衡条件∑=0M ，得l EI K 212=，l EI l EI EI K 84422=+=，l EI K 232=由图f ，结点力矩平衡条件∑=0M ，得 013=K ，l EI K 223=，l EI l EI l EI K 84433=+=由图g ，结点力矩平衡条件∑=0M ，得1Pl R p -=，2Pl R P -=，03=P R将系数项和自由项代入位移法基本方程，得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0000118820282024321Pl l EI ∙解方程，得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ14114162321EI Pl ∙由叠加法绘弯矩图，如图h 所示。

（2）矩阵位移法解∙对单元和结点编号（图a ） 本题只考虑弯曲变形的影响，故连续梁每个结点只有一个角位移未知数。

结构力学第五版第十章矩阵位移法ppt课件

结构力学第五版第十章矩阵位移法ppt课件

k12
p3 k31 k32 k33 3
k112
简记为 P k---结构刚度方程
k21 k31
k 211 =1 k22
1
k
1 22
1
k32
2
k
2 21
k --结构刚度矩阵(总刚)
k11 k111 k21 k211
k31 0
k13 k121
k23 k33
=1
3
k12 k112 k22 k212 k121 k32 k221
1 2 3
6 3 P3
3 (P3 01 4 2 ) /(8 N ) 3 0
六.非结点荷载
(1).等效结点荷载
PE
PPEE12
PE3
PE1
PE 2
PE 3
---结构等效结点荷载
“等效”是指等效结点荷载引起的结点 位移与非结点荷载引起的结点位移相同
(2).等效结点荷载的计算
1
4
6/ 1.5
8
1.5 1 1
3
2
2
EI1 6 EI 2 24
4m 4m 12m
1
2
1
2
EI1 6
8m
34
3
2
3
1
2
k 2
4
24 4
/12
4 1 2 8 2 3
34
12
k
3
3 1.5
1.5 1 3
3
2
4
3 1.5 0 0
k 1.5 11
4
0
0 4 11 1.5
0
0
1.5
1 2
Fq
2
ql 2 /12 ql2 /12

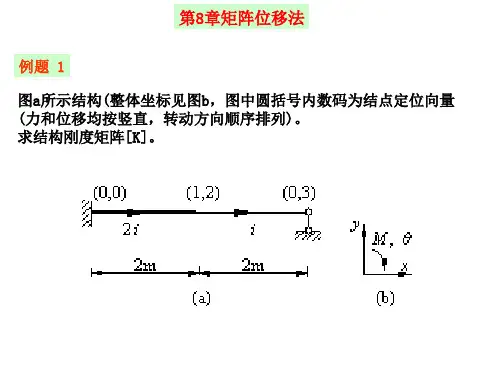
第8章矩阵位移法例题 结构力学

第8章矩阵位移法例题 结构力学

0
K
(2)
0
对
0 0.0142
称
0 0.060 0.3396
2.8285 0 0
2.8285
0 0.0142
0.060 0
0.0142
0
0.060
0.
1698
0
105
0.060
0.3396
4.列出整体坐标表示的单元刚度矩阵
单元（1）(3)的单元坐标和整体坐标一致，所以
4 0
0 4 0
l
1 ql
1 ql
2
2
p
1 pl 8
1 pl 8
l
l
2
2
1p
1p
2
2
第8章矩阵位移法
例题 2 （1）求各单元在局部坐标系中固端力向量
例题 2
第8章矩阵位移法
(2)将
转换成
单元①
单元②
例题 2
第8章矩阵位移法
(3)利用单元定位向量，将
中元素反号后叠加集成
第8章矩阵位移法
例题 3
图示桁架，已知结点位移列阵
0
0
0.04 0.12
0
0.04 0.12
K
(1)
K
(3)
0
0.48
0 4
0.12 0
0.24 0
105
对 称
0.04 0.12
0.48
单元（2）的单元坐标和整体坐标不一致，必须经过以下变换
第一种方法： 直接代入公式：
2 1 2i 2 BCx l2 Cy
(e)
K
1 2i (B l2 )CxC y
0
0
1
第8章矩阵位移法

矩阵位移法例题

矩阵位移法例题

3→4 0° 1
1
4×105
0.12×105
§10-7 矩阵位移法的计算步骤和示例
(3) 列出单元刚度矩阵 整体坐标表示的单元刚度矩阵公式
BC
2 x
12i l2
C
2 y
K (e)
B
12i l2
C
xC
y
BC
2 y
12i l2
Cx2
对称
6i l Cy 6i l Cx
4i
BC
2 x
12i l2
1 EA
49.64
0 49.64
kN
0
结果的正确性很容易从结 点2的平衡条件判断出来。
§10-7 矩阵位移法的计算步骤和示例
例 2： 平面刚架如图所示，各杆截面相同。A=0.24 m2,
E=1×107 kN/m2, I=0.0072 m4，试求各杆端力，并画出内
力图。
11
20kN/m
3 34
Δ 0 0 85.98 309 0 0T 1
EA (5) 求杆端力
F (e) K (e)T (e) Δ(e)
1 30℃
2
F2 F1
2
§10-7 矩阵位移法的计算步骤和示例
单元①的单元结点位移向量为
Δ(1) 0 0 85.98 309T 1
EA
单元①的杆端力为 F (1) K δ (1) (1) K T Δ (1) (1) (1)
3
1 30℃
2
F2 F1
2
原始总刚度矩阵为：
1
[K
]
K K
(1) ii
(1) ji
0
2
3
K (1) ij

《矩阵位移法》课件

《矩阵位移法》课件

实际工程案例分析
总结词
为了验证矩阵位移法的有效性，可以通过实际工程案例 进行分析。通过与实验结果的对比，可以评估方法的精 度和可靠性。
详细描述
选取具有代表性的实际工程案例，如高层建筑、大跨度 桥梁等，利用矩阵位移法进行计算，并将结果与实验数 据进行对比。通过对比分析，可以评估矩阵位移法的精 度和可靠性，为该方法在实际工程中的应用提供依据。 同时，也可以针对不同工程案例的特点，对矩阵位移法 进行优化和改进，提高其适用性和计算效率。
05
矩阵位移法的优缺点
优点
精确度高
矩阵位移法基于严格的数学推导，能 够精确地计算出结构的位移和内力， 尤其适用于复杂结构的分析。
适用性强
矩阵位移法可以处理多种类型的载荷 ，包括静载、动载以及温度载荷等， 适用范围广泛。
便于计算机化
矩阵位移法的计算过程可以通过计算 机程序实现，便于进行大规模的结构 分析。
多尺度方法
将矩阵位移法应用于多尺度问题 ，考虑不同尺度之间的相互作用 和影响，为复杂系统提供更准确 的模拟结果。
THANKS
感谢观看ts
目录
• 引言 • 矩阵位移法的基本概念 • 矩阵位移法的实施步骤 • 矩阵位移法的应用实例 • 矩阵位移法的优缺点 • 未来展望与研究方向
01
引言
什么是矩阵位移法
矩阵位移法是一种数值分析方法，用 于求解线性方程组和解决各种数值计 算问题。
它通过将原问题转化为矩阵形式，利 用矩阵运算来求解未知数，具有高效 、精确和灵活的特点。
并行计算
利用并行计算技术，将计算任务分解为多个子任务，同时运行在多 个处理器上，加快计算速度。
智能优化
结合人工智能和机器学习技术，自动调整算法参数，实现自适应优 化，提高算法的效率和稳定性。

结构力学(I)-结构静力分析篇6 矩阵位移法

结构力学(I)-结构静力分析篇6 矩阵位移法

用数字描述体系的位置，单元的属性。

10 / 105
第六章
例如
单元 FP
矩阵位移法
3(5,6)FP
2
1
2
2
结点
1
1(1,2) 单元方向 1
1
2(3,4)
2
1,2,3 ----结构结点编码（总码） (1,2,3) ----结点位移编码
1 2 ----杆端结点编码（局码）
1 2 ----单元编码

11 / 105

9 / 105
第六章
矩阵位移法
六、结构的离散化工作
将一个在荷载作用下的连续结构剖分成若干 个各自独立的单元，单元之间是由结点连接，用 此计算模型模拟原结构的受力和变形特性。 模型和原结构是有差别的，这个差别可以通 过单元的适当选取给予降低。 主要工作：单元的划分；体系的数字化。
直杆体系按自然选取杆件的汇交点、截面的 变化点、支撑点或荷载作用点作为结点，将结构 划分成一系列只在结点相连的单元集合。
EA l e
矩阵位移法
0
6 EI l2 4 EI l
0
12 EI l3 6 EI l2

EA l
0 12l EI 3 6lEI 2 0
12 EI l3 6 EI l2
0 0
EA l
0 12l EI 3
6 EI l2
0 6lEI 2
2 EI l
0 0
0 1 6 EI l2 2 2 EI 3 l 0 4 6lEI 5 2 4 EI 6 l
单元刚度方程
F k
e e
e

矩阵位移法

矩阵位移法

D1 = D2 = 0
； D5 = D6 = 0
则有修正后的总刚度矩阵：
-100 2 [K ] = 100 600
[k11 ] [k12 ] {F1} = {F2 } [k 21 ] [k 22 ]
{D1} {D 2 }
@
单元刚度矩阵的性质：①对称性；②奇异性； ③主对角元恒为正值
3、整体刚度矩阵
K ij ：单元仅发生第j个杆端单位位移时，在第
Y2 = QBA
写成矩阵表达式为：
4 EI 2 EI 6 EI q + q + -v ) ( v l 1 l 2 l2 1 2 2 EI 4 EI 6 EI q + q + -v ) ( M2 = v l 1 l 2 l2 1 2 6 EI 12 EI (v1 - v2 ) Y1 = (q1 +q 2 ) + l2 l2 6 EI 12 EI = q + q (v1 - v2 ) Y2 ( 1 2) l2 l2 M1 =
2
3
1 2
Hale Waihona Puke 3-1 50 1 50 50 300 -50 150 -1 -50 2 -100 -1 -50 = 50 150 -100 600 50 150 -1 50 1 50 -50 150 50 300
计入边界条件：因边界结点1和3 为固定端，故有：
0 12EI l3 6 EI - 2 l 0 12EI l3 6 EI - 2 l
@
0 6 EI l2 2 EI l 0 6 EI - 2 l 4 EI l
EA l 0 0

结构力学——矩阵位移法

结构力学——矩阵位移法
结构力学
学习内容
有限单元法的基本概念，结构离散化。 平面杆系结构的单元分析：局部坐标系下的单元刚度矩
阵和整体坐标系下的单元刚度矩阵。 平面杆系结构的整体分析：结构整体刚度矩阵和结构整
体刚度方程。 边界条件的处理，单元内力计算。 利用对称性简化位移法计算。 矩阵位移法的计算步骤和应用举例。
2
学习目的和要求
2、局部坐标系中的单元刚度矩阵
k
e
EA l
1 1
1
1
kk1211
k12 k22
刚度系数的物理意义： • 单元刚度矩阵是杆端力与杆端位移之物理关系； • 矩阵的阶数与杆端位移分量数相等； • kij 表示 uj 1 引起的杆端力Fi 的大小。
15
第二节 单元分析（局部坐标系下的单元分析 ）
5
第一节 矩阵位移法概述
结构力学传统方法与结构矩阵分析方法，二者同源而有别：
在原理上同源，在作法上有别
前者在“手算”的年代形成，后者则着眼于“电算”，计算手 段的不同，引起计算方法的差异。
与传统的力法、位移法相对应，在结构矩阵分析中也有矩阵力 法和矩阵位移过程程序化的优点而广为流传。
3、局部坐标系中的单元刚度矩阵性质
矩阵位移法的要点 ：
化整为零
集零为整
（离散化、单元分析） （结点力平衡、位移协调）
9
第一节 矩阵位移法概述
2、单元划分
将一个在荷载作用下的连续结构剖分成若干个各自独立 的单元，原结构可以看成是由各单元在连接点（称结点） 连接而成的体系——化整为零
在杆件结构矩阵分析中，一般 是把杆件的转折点、汇交点、 边界点、突变点或集中荷载作 用点等列为结点，结点之间的 杆件部分作为单元。
3

矩阵位移法过程

矩阵位移法过程

矩阵位移法过程嘿，朋友们！今天咱就来好好唠唠矩阵位移法这个神奇的玩意儿。

你想想啊，矩阵位移法就像是搭积木，一块一块地把整个结构给拼凑起来。

只不过这积木有点特别，是用数字和公式搭成的。

咱先说说这第一步，得确定结构的节点和单元吧。

这就好比是给要盖的房子先确定好柱子和梁的位置。

每个节点就像是一个关键点，单元呢就是连接这些关键点的部件。

然后呢，咱要给这些节点和单元编上号，就跟给小朋友分学号似的，可不能乱了套。

接下来，就得建立这些节点和单元的关系啦。

这就像是给每个积木块找到它该放的位置，它们之间的连接呀、力的传递呀，都得搞清楚。

这可不是个简单事儿，但咱得耐着性子慢慢来。

然后呢，咱要根据这些关系列出矩阵。

哎呀呀，这矩阵可就像个大表格，里面装满了各种数字和符号。

别被它吓着，其实它就是把那些复杂的关系用一种整齐的方式表现出来。

再说说这计算过程，就跟解谜题似的。

你得一步步地去推导、去计算，找到那个正确的答案。

有时候可能会遇到一些难题，就像走在路上碰到了一块大石头，但咱可不能退缩，得想法子把它挪开或者绕过去。

还有啊，这矩阵位移法还得考虑各种边界条件呢。

就好像盖房子得考虑地基稳不稳呀，周围环境怎么样呀。

这些边界条件可不能马虎，要不然整个结构可就不牢固啦。

咱在实际运用的时候，可得细心再细心。

一个小数字算错了，可能整个结果就全错啦。

这就跟下棋一样，一步错步步错。

总之呢，矩阵位移法虽然有点复杂，但它可是结构分析的得力助手呢！只要咱认真学，多练习，就一定能掌握它。

别害怕困难，别嫌麻烦，等你真正搞懂了它，你就会发现它的神奇之处啦！就像打开了一扇通往新世界的大门，让你看到结构背后的奥秘。

所以呀，加油吧朋友们，和矩阵位移法这个小伙伴好好相处，让它为我们的工程建设出一份力！原创不易，请尊重原创，谢谢!。

矩阵位移法

矩阵位移法
第十一章 矩 阵 位 移 法
一、单元的划分 矩阵位移法解题，首先将结构划分为若干个单元。同一个结构 单元的划分可多可少，但每个单元必须是等截面直杆。 单元的两端为结点，单元与单元间以结点相连。单元划分后， 需将单元和结点排序编码。 【例11－1】将图示结构划分为单元。 q
P D A B E C
q
P D B E C
K 13 K 23 K 33 K 43 K 53 K 63
K 14 K 24 K 34 K 44 K 54 K 64
K 15 K 25 K 35 K 45 K 55 K 65
K 16 K 26 K 36 K 46 K 56 K 66
e
同理可求得余下各列元素，即
0 0 0 sin cos 0
简写为：
T
e
0 ix 0 iy 0 i 0 jx 0 jy 1 j
cos sin 0 T 0 0 0
e
u i vi i u j v j j
e
K
e
K 11 K 21 K 31 K 41 K 51 K 61
K 12 K 22 K 32 K 42 K 52 K 62
K 13 K 23 K 33 K 43 K 53 K 63
K
e
EA 0 l 12EI 0 l3 6 EI 0 l2 EA 0 l 12EI 0 3 l 6 EI 0 l2
0 6 EI l2 4 EI l 0 6 EI 2 l 2 EI l
EA l 0 0 EA l 0 0

矩阵位移法基本原理

矩阵位移法基本原理
矩阵位移法
重 点：刚度方程 单元矩阵 组装过程 边界条件 难 点：刚度方程 组装过程 等效结点荷载
前 言：
超静定结构的方法：
力法、位移法 弯矩分配法、叠代法 剪力分配法
求解方程组
不需求解方程组
基本原理
实用计算 ---------另一种计算超静定结构的方法 适用计算机求解
矩阵位移法
矩阵位移法是以结构位移为基本未知 量，借助矩阵进行分析，并用计算机解决 各种杆系结构受力、变形等计算的方法。 理论基础：位移法 分析工具：矩阵 计算手段：计算机
式中，E为杆的弹模，A为截面积，L为杆长
在整个结构中，各杆的方向不同，所有的结点力与结点位移
都是两个方向。为了统一，补充两个y方向的力与两个位移，
即，Y i ，Yj ；v i ，v j （在图示坐标系下它们都是零）。 Yi y Y
Xi
j
Xj
这样，把上面的矩阵方 程扩写为：
vi
vj
x
ui
Xi Yi X j Y j EA L 0 EA L 0 0 0 0 0 EA L 0 EA L 0
vi
uj
vj
T
为整体坐标系下的单元位移向量 对杆端力向量也有这种转换关系，即
F T F
e e
e
F e X i
Yi X j Y j
T
整体坐标系下的单元结点力向量
单元坐标系下的单元刚度方程为：
F K D
e e
e
D T D
i
K
e
k11 k 21 k31 k 41
j
k12 k 22 k32 k 42

第四章 矩阵位移法

第四章 矩阵位移法

Ij,M j'i6 lE ij3 ij
Ii2 lE ij3 ij
Ii6 lE ij3 ij
Ij4 lE ij3 ij
I
j
4-2 矩阵位移法
规定
弯曲杆元e的节点位移列矩 阵
弯曲杆元e的杆端力向量
i
(e)


i j




zi


j

Txi cos N N Txyyjjico00s
sin sin
0 0
0 0
cos cos
ssi00ninN N TTxxyyijij
则xoy平面内平面刚架杆元的杆端力向量的坐标转换关系为：
Txi cos sin 0
012 1
x2y2w2
345 2
x3 y3w3
3 000
5
y 000
x5y5w5
4-4 编号约定与杆元定位向量
2、杆元定位向量
杆系结构节点的个个未知位移分量，按其编号的大小，依次排列起来成为一个向 量，这个向量称为结构节点未知位移向量。
w w y 11 x 2y 22x 4y 4
4-1 位移法
2.位移法中的符号规定与弯曲杆元刚度方程
位移法的符号规定： ① 杆端剪力与y轴正向一致为正； ② 杆挠度与y轴正向一致为正； ③ 杆端弯矩不论左右端一律规定顺时针为正。
由弯曲要素表可得固端弯矩与固端剪力为： M 21112 q1l2 2,N211 2q1l2
如何求弯曲杆元因杆端发生线位移和角位移而引起的杆端弯矩、剪力？
Ii1liE j2 3ij Ij6 lE ij3 ij
Ij,M j'i6 lE ij3 ij

举例说明矩阵位移法

举例说明矩阵位移法
FP A i1 l/2 l/2 (a) 两跨连续梁 M1 B q i2 l M2 C
单元编号 结点编号
qA =0 A=0
A M1 B q M2 C ①
qB B
B (b) 离散化 M1 ②
qC C
C
结点位移编号
i2 l
6 M2
/2
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
第二步，单元分析。
2
A =0
A
k
(2)
①
4i2 = B 2 2i
A
B
2i2 4i2②
B
C
C
C 第三步，整体分析。 i B l
A l/2 i1 l/2 (a) 两跨连续梁 FP M1 B q i2 l M2 C
=0 (b)A 离散化 ① B
②
C
M1 MBA B MBC
(b) 离散化 M1
M2 MCB C
分析结构的几何组成关系； 分析结构失稳时的临界荷载； 分析刚度变化对结构内力的影响； 选择适当的结构型式等等。
1
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
结构分析方法的发展：
与人类生产活动以及科学技术水平的发展有着密切的联系。
桁架结构分析理论与分析方法， 和钢结构的广泛应用有直接关系。 刚架结构的分析方法，与钢筋混凝土结构的大量出现有关。
F
(1) P (1)
=0
(1)
(2)
，
(1)
F
(2) P
=0
，则
=k
=k
(2)
(2)
(2)
为①、②两个单元的单元刚度方程。
k
(1)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

结构分析方法的发展：
与人类生产活动以及科学技术水平的发展有着密切的联系。
桁架结构分析理论与分析方法， 和钢结构的广泛应用有直接关系。 刚架结构的分析方法，与钢筋混凝土结构的大量出现有关。
计算机未广泛使用前，
迭代法、 D值法、
反弯点法、 分层法等等。
计算机广泛使用后， 结构矩阵分析方法、 有限元法等。
1 2 1 FP l ql 1 2 1 i1 4 4i2 22 i2 4= q BF l M 1 M BC 8 = 4i2q B 12 2i2qC ql M AB i1q i q A 1 B P= 12 8 1 M 2 4i2 1 C 2 2i2 q 2 1 ql M = 2 i q 4 i q ql M BA = 2i1q A 4i1q B FP l CB 2 B 2 C 12 12 8
C
a) 两跨连续梁
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
F
(1)
=k
(1)
(1)
(2)
F
(1) P
F
(2)
=k
(2)
(2)
F
(2) P
F (1)
F
为单元杆端力列阵。
(1) (2)
F
若
(1) P
为单元杆端位移列阵。
为非结点荷载引起的单元固端力列阵。
FP(2)
F
F
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
归纳起来，用矩阵位移法求解杆件结构的步骤为：
离散化
单元分析 整体分析 解方程组求结点位移
计算各单元杆端力
以下各节针对平面刚架结构作详细讨论
13
4i1 4i2 K = 2i2
第四步，解方程
2i2 4i2
K = F ，求 。
1 2 ql 2i2 q B 12 4i2 qC 1 ql 2 12
12
第五步，求杆端弯矩的最终值，并由此绘出原结 构的弯矩图。
A i1 B
FP
M1
q
M2
1 = 4i1q A 2i1q B FP l 8 1 = 2i1q A 4i1q B FP l 8 M
q
2
1 C FP l 4 i 2 i q 1 1 A 8 M AB l M l/2 = l/2 BA 2i1 4i1 q B 1F l P 8 (a) 两跨连续梁 i2
两跨连续梁
(c) 结点平衡MBA
B
(d) M 结点平衡 MCB BC
C
(c) 结点平衡
(d) 结点平
将结点B、C分别取出分析，如图(c)、(d)所示。
M BA M BC = M1
M CB = M 2
9
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
第三步，整体分析。
A i1
FP
M1 B l/2
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
第一节 概述
一、结构分析及其发展 结构分析，是指在一定的条件下计算结构的内力和位移； 还包括：
分析结构的几何组成关系； 分析结构失稳时的临界荷载； 分析刚度变化对结构内力的影响； 选择适当的结构型式等等。
1
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
F
(1) P (1)
=0
(1)
(2)
，
பைடு நூலகம்(1)
F
(2) P
=0
，则
=k
=k
(2)
(2)
(2)
为①、②两个单元的单元刚度方程。
k
(1)
、k
分别称为①、②两个单元的单元刚度矩阵。
8
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
k
(1)
M1
q
2
4i1 = 2i1
2i1 4i1 M
2
A =0
A
k
(2)
①
4i2 = B 2 2i
A
B
2i2 4i2②
B
C
C
C 第三步，整体分析。 i B l
A l/2 i1 l/2 (a) 两跨连续梁 FP M1 B q i2 l M2 C
=0 (b)A 离散化 ① B
②
C
M1 MBA B MBC
(b) 离散化 M1
M2 MCB C
2
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
二、结构矩阵分析方法
结构矩阵分析方法是以经典结构力学理论为基础、 以矩阵方法和线性代数作为其数学描述手段、以电子 计算机作为计算工具来实现结构分析的。 有：矩阵位移法、矩阵力法及矩阵混合法等。
矩阵位移法实际上是用矩阵形式表示的位移法分析过程。 矩阵力法则是以矩阵形式表示的力法分析过程。 矩阵混合法即为将矩阵位移法与矩阵力法结合起来
10
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
4i1 4i2 2i2
简记为：
1 2 1 FP l ql 2i2 q B M 1 8 12 = 4i2 qC M 2 1 ql 2 12
单元编号 结点编号
qA =0 A=0
A M1 B q M2 C ①
qB B
B (b) 离散化 M1 ②
qC C
C
结点位移编号
i2 l
6 M2
/2
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
第二步，单元分析。
建立单元杆端力与杆 端位移之间的关系。 ①单元
M AB M BA
M1 B
写成矩阵形式为：
M AB 4i1 M = BA 2i1 1 Fl 2i1 q A 8 P 4i1 q B 1Fl P 8
M BC 4i2 M = CB 2i2
q i2 l
M2 C
M BA M BC = M1
M CB = M 2l/2
1 2 (a) 两跨连续梁 1 (4i1 4i2 )qB 2i2qC FPl ql = M1 12 8
1 2 2i2q B 4i2qC ql = M 2 12
合并写成矩阵形式，有
K = FJ FE
K = F
T
结 构 刚 度 方 程
= q B q C
称为结构的结点位移列阵；
F 称为结构的综合结点荷载列阵 。 F = FJ FE
FJ 称为直接结点荷载列阵。FE 称为等效结点荷载列阵。
11
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
K称为结构刚度矩阵，在本例中
②单元
M BC = 4i2 M CB
M BC 4i2 A ① M = CB 2i2
qA =0 A=0
1 2 qC qB B ql C 2i2 q B 12 C B ② 4i2 qC 1 2
的一种分析方法。
3
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
本书中将主要介绍矩阵位移法。需要指 出，矩阵位移法用于分析杆件结构（亦称一 维结构）时，也可称为杆件结构有限元法， 所得结果为精确解。而对于分析二维结构 或三维实体结构的弹性力学有限元法来说， 所得结果为近似解。
4
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
三、 矩阵位移法分析杆件结构的步骤
举例说明：
FP A l/2 i1 l/2 (a) 两跨连续梁 M1 B q i2 l M2 C A
A=
求：各杆的杆端弯矩（亦称杆端力）。
5
结构分析中的有限元法
武汉理工大学出版社 出版社 科技分社
第一步，结构的离散化。
FP A i1 l/2 l/2 (a) 两跨连续梁 M1 B q i2 l M2 C
(b) 离散化
l/2
2 ql B 12 l 1 2 = 2i2q B 4i2qC ql 12
q i2 2i
2qC
C1
ql 12
(1) P
F
F
(1)
=k
(1)
(1) M1
F
F
M2
7
(2) MBA (2)
=k
B
(2) MBC
(2) M CB P