传热学3非稳态导热
- 格式:pptx
- 大小:1.30 MB
- 文档页数:94






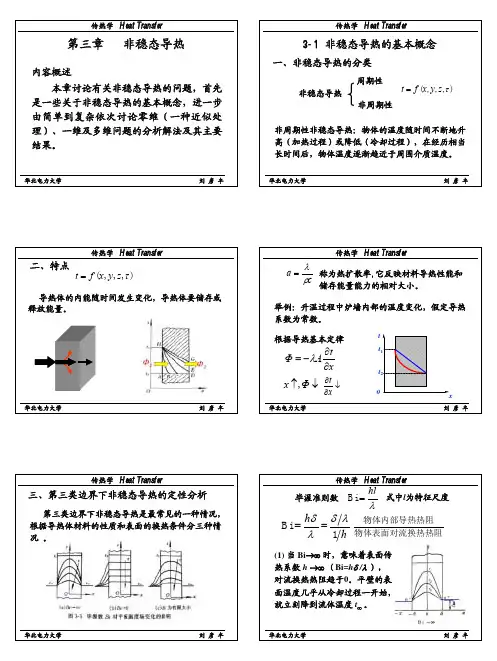



第三章非稳态导热Transient Conduction第五讲13.1 非稳态导热的基本概念一、非稳态导热的概念非稳态导热:物体内的各点温度随时间而变化的导热过程。
稳态导热:物体内各点温度随时间而温度不变的导热过程。
对于非稳态导热,物体内各点的热流密度随时间改变不?第五讲2二、应用背景•加热炉、连铸、连轧,加热时间和工件质量•改变材料的力学特性热处理(淬火、正火、回火);•机加工,零件的热应力、热变形;•微电子器件,瞬态、交变工作状态下的寿命、热应力;•热力设备的启动与停机;•表面处理、光盘的读写;•航天器的升空与降落过程;•子弹出膛时的升温过程;•。
第五讲3第五讲4工程上典型温度变化率的数量级第五讲6第五讲7第五讲8第五讲9无限大平板的初始温度为t 0。
τ= 0时刻,其左边温度突然上升为t 1并保持不变,右侧与温度为t 0的空气接触。
平板内温度变化过程?三、非稳态导热过程的特点第五讲10该阶段的温度变化规律是讨论的主要内容11二、非稳态导热问题作集总参数处理的条件•物体的尺寸比较小;•材料的热导率比较大;•表面传热系数比较小。
上述三条均为相对概念,并不能严格说明何时可以采用集总参数法。
那么应该用什么参数来作为判断准则呢?第五讲13第五讲16•Bi →∞导热热阻起决定作用,对流热阻极小,t w →t ∞, 第一类边界条件的瞬态问题•Bi →0 导热热阻极小,内部温度趋于一致•Bi 有限大小,内外热阻都起作用不同Bi数平板内温度变化(初温t 0、环境温度t ∞)第五讲24ρcV /hA 具有时间的量纲,称为时间常数τc.0/0.368θθ=用集总参数法分析时物体过余温度的变化曲线当τ=τc 时,第五讲26M :与物体的几何形状有关的常数平板:M=1圆柱:M=1/2球:M=1/3四、集中参数法的适用范围当Bi V <0.1M时,物体内各点间的过余温度的偏差将小于5%。
五、多集总系统由两个或两个以上子系统构成的系统(如两个接触良好的固体或盛在容器中的液体),集总参数法可以应用于其子系统。

传热学基本概念三维非稳态导热微分方程导热微分方程的基本形式是:\[\rho c \frac{{\partial T}}{{\partial t}} = \nabla \cdot (k \nabla T) + q\]其中,\(\rho\) 是介质的密度,\(c\) 是比热容,\(T\) 是温度,\(t\) 是时间,\(k\) 是导热系数,\(q\) 是单位体积内的热源。
这个方程描述了物质内部温度分布随时间的变化,以及热量在空间中的传递和变化。
对于三维非稳态导热问题,方程中的温度 \(T\)、密度\(\rho\)、比热容 \(c\)、导热系数 \(k\) 都可能是空间坐标 \(x\)、\(y\)、 \(z\) 和时间 \(t\) 的函数。
方程的实质是一个偏微分方程,描述了三维空间中温度分布随时间的变化规律。
在实际问题中,要解决三维非稳态导热问题的方程,需要满足一定的边界条件和初始条件。
边界条件指定了物体表面的温度、热流量或对流换热系数,初始条件指定了系统在初始时刻的温度分布和热能分布。
通过这些条件,可以得到方程的解析解或数值解,从而揭示物体内部温度变化的规律。
除了基本的三维非稳态导热微分方程外,传热学还涉及了许多重要的概念和原理,如热传导、热对流、热辐射等。
这些概念和原理不仅在工程领域有着重要的应用,而且在生活中也随处可见。
总结起来,对于三维非稳态导热微分方程及其相关的传热学概念,我们需要深入理解其基本原理和数学模型,掌握其解决方法和工程应用。
通过学习和研究,我们可以更好地理解和应用传热学知识,为解决工程和生活中的热传递问题提供理论和技术支持。
传热学是研究物体内部温度分布随时间的变化规律以及热量在空间中的传递和变化的学科,其理论和方法在工程热学、地球科学、生物医学工程和环境科学等领域有着广泛的应用。
三维非稳态导热微分方程是传热学中的基本方程之一,描述了物质内部温度分布随时间的变化规律。
在实际问题中,要解决三维非稳态导热问题需要满足一定的边界条件和初始条件,通过这些条件可以得到方程的解析解或数值解。