线性规划练习题

1.已知实数x,y满足2x 则2x y 2的最小值为（）xA. 1B. 3C. 4D. 62x 2.设关于x, y的不等式组0表示的平面区域内存在点P（x o, y o），满足X。

2y o2，贝y m的取值范围是() -)B.1 2(,3)C(,严3.已知a 0，x,y满足约束条件5，3)1x y 3，若zy a(x 2)2x y的最大值为1，则a()A.1B.!C .4 21D. 22x8x 4 .设x, y满足约束条件xyyy0,若目标函数z1-y(a 0,b 0)的最大值b为2，则 a b的最小值为（）A. 9B.25.当实数x,y满不等式组: y2x 00 时，恒有axy 2y 3成立，则实数a的取值范围是x 6.设实数x， y满足xy2 0,y2y 5 0,则z2 0,乂 -的取值范围是.x y2x y 1 0,7.设x,y满足约束条件x y 0,,若目标函数z ax by a 0,b 0的最大值x 0, y 0,为i，贝y丄4的最小值为__________ .a b8.已知方程x2ax 2b 0 (a R,b R),其一根在区间(0,1)内，另一根在区间(1,2) 内，则L2的取值范围为.a 1x y > 0,9.已知实数x, y满足条件x y > 0,则y x的最小值为二x < 1,10.若x,y满足条件y 2|x| 1，则z=x+3y的最大值为.y x 111.如图，直三棱柱ABC ABG的底面是边长为4正三角形，AA1 2、、6，M为A1B1的中点.(I)求证：AB MC ;(U)在棱CC1上是否存在点P，使得MC 平面ABP ?若存在，确定点P的位置；若不存在，说明理由.12.如图，在三棱锥P—ABC中，PA= PB= AB= 2，BC= 3，Z ABC= 90°平面PABL平面 ABC D E分别为AB AC中点.(1)求证：DE//平面PBC(2)求证：AB丄PE;(3)求二面角A— PB- E的大小.13.如图，已知四棱锥P- ABCD底面ABCD为边长为2对的菱形，PA!平面ABCD/ ABC=60，E，F分别是BC, PC的中点.(1)判定AE与PD是否垂直，并说明理由;(2)若PA=2求二面角E-AF- C的余弦值.14.如图，在四棱锥 P ABCD中，底面ABCD是正方形.点E是棱PC的中点，平面ABE 与棱PD交于点F .(I)求证：AB // EF ;(U)若PA AD，且平面PAD 平面ABCD，试证明AF 平面PCD ;(川)在(U)的条件下，线段PB上是否存在点M ,使得EM 平面PCD?(请说明理由) 15.如图，在长方体ABCD A I B I C I D i中，面BMD.N与棱CC i, AA i分别交于点M , N，且M,N 均为中点.(1)求证：AC// 面BMD i N;(2)若AD CD 2，DDi厶2'。

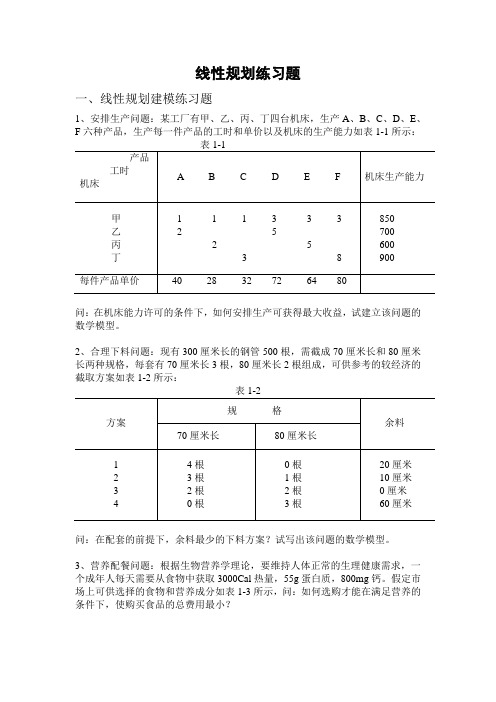
线性规划练习题一、线性规划建模练习题1、安排生产问题：某工厂有甲、乙、丙、丁四台机床，生产A、B、C、D、E、F六种产品，生产每一件产品的工时和单价以及机床的生产能力如表1-1所示：问：在机床能力许可的条件下，如何安排生产可获得最大收益，试建立该问题的数学模型。

2、合理下料问题：现有300厘米长的钢管500根，需截成70厘米长和80厘米长两种规格，每套有70厘米长3根，80厘米长2根组成，可供参考的较经济的截取方案如表1-2所示：问：在配套的前提下，余料最少的下料方案？试写出该问题的数学模型。

3、营养配餐问题：根据生物营养学理论，要维持人体正常的生理健康需求，一个成年人每天需要从食物中获取3000Cal热量，55g蛋白质，800mg钙。

假定市场上可供选择的食物和营养成分如表1-3所示，问：如何选购才能在满足营养的条件下，使购买食品的总费用最小？4、运输问题：某物流公司需要将A1、A2、A3三个工厂生产的一种产品运送到B1、B2、B3、B4四个销售点。

通过实地考察得到三个产地和四个销售点的产量、销量和单位运费等数据如表1-4所示，问：在产销平衡的条件下，求最小成本的配送方案？试建立该问题的数学模型。

1、min z=2x1+3x24x1+6x2>=6s.t 3x1+2x2>=4x1,x2>=02、max z=3x1+2x22x1+x2<=2s.t 3x1+4x2>=12x1,x2>=03、max z=10x1+5x23x1+4x2<=9s.t 5x1+2x2<=8x1,x2>=04、max z=5x1+6x22x1-x2>=2s.t -2x1+3x2<=2x1,x2>=0三、将下列线性规划问题化成标准形式：1、min z=-3x1+4x2-2x3+5x42、min z=2x1-2x2+3x34x1-x2+2x3-x4=-2 -x1+x2+x3=4s.t x1+x2-x3+2x4<=14 s.t -2x1+x2-x3<=6-2x1+3x2+x3-x4>=2 x1<=0,x2>=0,x3无约束x1,x2,x3>=0,x4无约束。

线性规划建模习题2.某医院昼夜24小时各时间段内需要的护士数量如下：2:00～6:00 10人；6:00～10:00 15人；10:00～14:00 25人；14:00～18:00 20人；18:00～22:00 18人；22:00～2:00 12人。

护士分别于2:00、6:00、10:00、14:00、18:00、22:00分六批上班，并连续工作8小时。

试确定：(a)该医院至少应设多少名护士，才能满足值班需要；(b)若医院可聘用合同工护士，上班时间同正式工护士。

若正式工护士报酬为10元/小时，合同工护士为15元/小时，问医院聘用正式工和合同工护士各多少人成本最低？3.某人有一笔30万元的资金，在今后三年内有以下投资项目：(1)三年内的每年年初均可投资，每年获利为投资额的20%，其本利可一起用于下一年投资；(2)只允许第一年年初投入，第二年年末可收回，本利合计为投资额的150%，但此类投资限额不超过15万元；(3)于三年内第二年初允许投资，可于第三年末收回，本利合计为投资额的160%，这类投资限额20万元；(4)于三年内的第三年初允许投资，一年收回，可获利40%，投资限额为10万元。

试为该人确定一个使第三年末本利和为最大的投资计划。

8.市场对I、II两种产品的需求量为：产品I在1～4月每月需10000件，5 ～9月每月30000件，10 ～12月每月需100000件；产品II在3 ～9月每月15000件，其他月每月50000件。

某厂生产这两种产品成本为：产品I在1 ～5月内生产每件5元，6 ～12月内生产每件4.5元；产品II 在1 ～5月内生产每件8元，6 ～12月内生产每件7元。

该厂每月生产两种产品能力总和不超过120000件。

产品I容积每件0.2立方米，产品II每件0.4立方米，而该厂仓库容积为15000立方米。

要求：(1)若占用本厂每月每立方米库容需1元，该厂应如何安排生产计划，才能在满足市场需求的前提下，确保生产加库存费用最低？(2)上述问题是否有可行解？(3)若该厂仓库不足时，可从外厂租借，租用外厂仓库时上述费用增加为1.5元，试问在满足市场需求情况下，该厂应如何安排生产，使总的生产加库存费用为最少？15.一个大的造纸公司下设10个造纸厂，供应1000个用户。

线性规划练习题一、选择题1. 线性规划问题中，目标函数的最优值是：A. 最大化B. 最小化C. 既可能最大化也可能最小化D. 不确定2. 下列哪个不是线性规划的基本假设？A. 目标函数是线性的B. 约束条件是线性的C. 约束条件是连续的D. 约束条件是不等式的3. 线性规划问题的图形解法中，可行域的边界条件是：A. 等式B. 不等式C. 既可能是等式也可能是不等式D. 无法确定4. 单纯形法是解决线性规划问题的哪种算法？A. 图形解法B. 枚举法C. 迭代法D. 直接法5. 以下哪个条件不是线性规划问题的基本假设？A. 目标函数是线性的B. 约束条件是线性的C. 目标函数和约束条件都是线性的D. 约束条件是确定的二、填空题6. 线性规划问题中，目标函数的最优解可能位于可行域的_________。

7. 单纯形法中，如果目标函数的系数在所有基变量上的系数都是_________，则该基可行解是最优解。

8. 线性规划问题中，如果目标函数是最大化问题，当可行域是无界的，则最优解是_________。

9. 线性规划问题中，如果约束条件中存在_________，则该问题可能没有可行解。

10. 单纯形法中，如果某一非基变量的系数在目标函数中为_________，则该变量在当前基可行解中为零。

三、简答题11. 解释线性规划问题中，为什么需要引入松弛变量？12. 描述单纯形法的基本步骤，并说明每一步的目的。

13. 线性规划问题中，如果目标函数是最大化问题，当可行域有界时，最优解可能出现在哪些位置？14. 解释线性规划问题中的对偶问题，并说明对偶问题与原问题之间的关系。

15. 什么是退化现象？在单纯形法中如何避免退化现象？四、计算题16. 考虑以下线性规划问题：Max Z = 3x + 4ys.t.2x + y ≤ 10x + 2y ≤ 8x, y ≥ 0求该问题的最优解，并给出最优值。

17. 假设你有一个生产问题，需要决定生产两种产品A和B的数量，以最大化利润。

作业1．第7题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.02．第8题下列不满足线性规划问题的典式要求的是（）。

A. 线性规划模型必须是标准形B. 基必须是单位矩阵。

C. 基变量可以出现在目标函数中D. 非基变量可以出现在目标函数中。

A.AB.BC.CD.D答案:C标准答案：C您的答案：题目分数：1.0此题得分：0.03．第13题A.AB.BC.CD.D答案:B标准答案：B 您的答案：题目分数：1.0 此题得分：0.04．第14题A.AB.BC.CD.D答案:D标准答案：D 您的答案：题目分数：1.0此题得分：0.05．第15题A.AB.BC.CD.D答案:A标准答案：A 您的答案：题目分数：1.0 此题得分：0.06．第16题A.AB.BC.CD.D答案:B标准答案：B 您的答案：题目分数：1.0 此题得分：0.07．第17题A.AB.BC.CD.D答案:A标准答案：A您的答案：题目分数：1.0此题得分：0.08．第18题若用二阶段法求没有可行解的线性规划问题，则在最后一张单纯表上（）。

A. 人工变量的检验数没有正数B. 人工变量的检验数没有负数C. 非基变量中有人工变量D. 基变量中有人工变量A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.09．第19题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.010．第20题若目标函数求极小值的线性规划问题没有最优解，则在最后一张单纯表上（）。

A. 对应非基变量的列上的系数没有正数B. 基变量的取值有负数C. 检验数没有负数D. 检验数为负的非基变量对应的列上的系数没有正数A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.011．第21题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0 此题得分：0.012．第26题A.AB.BC.CD.D答案:B标准答案：B您的答案：题目分数：1.0 此题得分：0.013．第28题A.AB.BC.CD.D答案:A标准答案：A您的答案：题目分数：1.0 此题得分：0.014．第33题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0 此题得分：0.015．第34题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0 此题得分：0.016．第35题A.AB.BC.CD.D答案:D标准答案：D您的答案：题目分数：1.0此题得分：0.017．第36题A.AB.BC.CD.D答案:A标准答案：A您的答案：题目分数：1.0此题得分：0.018．第46题检验有无迂回时，必须对（）进行。

1．目标函数z ＝4x ＋y ，将其看成直线方程时，z 的几何意义是( ) A ．该直线的截距 B ．该直线的纵截距 C ．该直线的横截距D ．该直线的纵截距的相反数解析：选B.把z ＝4x ＋y 变形为y ＝－4x ＋z ，则此方程为直线方程的斜截式，所以z 为该直线的纵截距．2．若x ≥0，y ≥0，且x ＋y ≤1，则z ＝x －y 的最大值为( ) A ．－1 B ．1 C ．2 D ．－2 答案：B3．若实数x 、y 满足⎩⎪⎨⎪⎧x ＋y －2≥0，x ≤4，y ≤5，则s ＝x ＋y 的最大值为________．解析：可行域如图所示，作直线y ＝－x ，当平移直线y ＝－x至点A 处时，s ＝x ＋y 取得最大值，即s max ＝4＋5＝9.答案：94．已知实数x 、y 满足⎩⎪⎨⎪⎧y ≤2x y ≥－2x .x ≤3(1)求不等式组表示的平面区域的面积；(2)若目标函数为z ＝x －2y ，求z 的最小值． 解：画出满足不等式组的可行域如图所示： (1)易求点A 、B 的坐标为：A (3,6)，B (3，－6)，所以三角形OAB 的面积为：S △OAB ＝12×12×3＝18.(2)目标函数化为：y ＝12x －z 2，画直线y ＝12x 及其平行线，当此直线经过A 时，－z2的值最大，z 的值最小，易求A 点坐标为(3,6)，所以，z 的最小值为3－2×6＝－9. 一、选择题1．z ＝x －y 在⎩⎪⎨⎪⎧2x －y ＋1≥0x －2y －1≤0x ＋y ≤1的线性约束条件下，取得最大值的可行解为( )A ．(0,1)B ．(－1，－1)C ．(1,0)D ．(12，12)解析：选C.可以验证这四个点均是可行解，当x ＝0，y ＝1时，z ＝－1；当x ＝－1，y ＝－1时，z ＝0；当x ＝1，y ＝0时，z ＝1；当x ＝12，y ＝12时，z ＝0.排除A ，B ，D.2．(2010年高考浙江卷)若实数x ，y 满足不等式组⎩⎪⎨⎪⎧x ＋3y －3≥0，2x －y －3≤0，x －y ＋1≥0，则x ＋y 的最大值为( )A ．9 B.157 C ．1D.715 解析：选A.画出可行域如图： 令z ＝x ＋y ，可变为y ＝－x ＋z ，作出目标函数线，平移目标函数线，显然过点A 时z 最大．由⎩⎪⎨⎪⎧2x －y －3＝0，x －y ＋1＝0，得A (4,5)，∴z max ＝4＋5＝9.3．在△ABC 中，三顶点分别为A (2,4)，B (－1,2)，C (1,0)，点P (x ，y )在△ABC 内部及其边界上运动，则m ＝y －x 的取值范围为( )A ．[1,3]B ．[－3,1]C ．[－1,3]D ．[－3，－1]解析：选C.直线m ＝y －x 的斜率k 1＝1≥k AB ＝23，且k 1＝1＜k AC ＝4，∴直线经过C 时m 最小，为－1， 经过B 时m 最大，为3. 4．已知点P (x ，y )在不等式组⎩⎪⎨⎪⎧x －2≤0y －1≤0x ＋2y －2≥0表示的平面区域内运动，则z ＝x－y 的取值范围是( )A ．[－2，－1]B ．[－2,1]C ．[－1,2]D ．[1,2]解析：选C.先画出满足约束条件的可行域，如图阴影部分， ∵z ＝x －y ，∴y ＝x －z .由图知截距－z 的范围为[－2，1]，∴z 的范围为[－1,2]．5．设动点坐标(x ，y )满足⎩⎨⎧?x －y ＋1??x ＋y －4?≥0，x ≥3，y ≥1.则x 2＋y 2的最小值为( )A. 5B.10C.172 D ．10解析：选D.画出不等式组所对应的平面区域，由图可知当x ＝3，y ＝1时，x 2＋y 2的最小值为10.6．(2009年高考四川卷)某企业生产甲、乙两种产品，已知生产每吨甲产品要用A 原料3吨、B 原料2吨；生产每吨乙产品要用A 原料1吨、B 原料3吨．销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元，该企业在一个生产周期内消耗A 原料不超过13吨、B 原料不超过18吨，那么该企业可获得的最大利润是( )A ．12万元B ．20万元C ．25万元D ．27万元解析：选D.设生产甲产品x 吨、乙产品y 吨，则获得的利润为z ＝5x ＋3y . 由题意得⎩⎪⎨⎪⎧x ≥0，y ≥0，3x ＋y ≤13，2x ＋3y ≤18，可行域如图阴影所示．由图可知当x 、y 在A 点取值时，z 取得最大值，此时x ＝3，y ＝4，z ＝5×3＋3×4＝27(万元)．二、填空题7．点P (x ，y )满足条件⎩⎨⎧0≤x ≤10≤y ≤1，y －x ≥12则P 点坐标为________时，z ＝4－2x ＋y取最大值________．解析：可行域如图所示，当y －2x 最大时，z 最大，此时直线y －2x ＝z 1，过点A (0,1)，(z 1)max ＝1，故当点P 的坐标为(0,1)时z ＝4－2x ＋y 取得最大值5.答案：(0,1) 58．已知点P (x ，y )满足条件⎩⎪⎨⎪⎧x ≥0y ≤x2x ＋y ＋k ≤0(k 为常数)，若x ＋3y 的最大值为8，则k ＝________.解析：作出可行域如图所示：作直线l 0∶x ＋3y ＝0，平移l 0知当l 0过点A 时，x ＋3y 最大，由于A 点坐标为(－k3，－k 3)．∴－k3－k ＝8，从而k ＝－6. 答案：－69．(2010年高考陕西卷)铁矿石A 和B 的含铁率a ，，冶炼每万吨铁矿石的CO 2的排放量b某冶炼厂至少要生产22(万吨)，则购买铁矿石的最少费用为________(百万元)．解析：设购买A 、B 两种铁矿石分别为x 万吨、y 万吨，购买铁矿石的费用为z 百万元，则z ＝3x ＋6y .由题意可得约束条件为⎩⎪⎨⎪⎧12x ＋710y ≥1.9，x ＋12y ≤2，x ≥0，y ≥0.作出可行域如图所示：由图可知，目标函数z ＝3x ＋6y 在点A (1,2)处取得最小值，z min ＝3×1＋6×2＝15 答案：15 三、解答题10．设z ＝2y －2x ＋4，式中x ，y 满足条件⎩⎪⎨⎪⎧0≤x ≤10≤y ≤22y －x ≥1，求z 的最大值和最小值．解：作出不等式组⎩⎪⎨⎪⎧0≤x ≤10≤y ≤22y －x ≥1的可行域(如图所示)．令t ＝2y －2x 则z ＝t ＋4.将t ＝2y －2x 变形得直线l ∶y ＝x ＋t2.则其与y ＝x 平行，平移直线l 时t 的值随直线l 的上移而增大，故当直线l 经过可行域上的点A 时，t 最大，z 最大；当直线l 经过可行域上的点B 时，t 最小，z 最小．∴z max ＝2×2－2×0＋4＝8， z min ＝2×1－2×1＋4＝4.11．已知实数x 、y 满足约束条件⎩⎪⎨⎪⎧x －ay －1≥02x ＋y ≥0x ≤1(a ∈R )，目标函数z ＝x ＋3y 只有当⎩⎨⎧x ＝1y ＝0时取得最大值，求a 的取值范围．解：直线x －ay －1＝0过定点(1,0)，画出区域⎩⎪⎨⎪⎧2x ＋y ≥0，x ≤1，让直线x －ay －1＝0绕着(1, 0)旋转得到不等式所表示的平面区域．平移直线x ＋3y ＝0，观察图象知必须使直线x －ay －1＝0的斜率1a ＞0才满足要求，故a ＞0.12．某家具厂有方木料90 m 3 ，五合板600 m 2，准备加工成书桌和书橱出售．已知生产每张书桌需要方木料0.1 m 3，五合板2 m 2；生产每个书橱需要方木料0.2 m 3，五合板1 m 2，出售一张方桌可获利润80元；出售一个书橱可获利润120元．(1)如果只安排生产方桌，可获利润多少？ (2)如果只安排生产书橱，可获利润多少？ (3)怎样安排生产可使所获利润最大？解：由题意可画表格如下：(1)设只生产书桌x 张，可获利润z 元， 则⎩⎪⎨⎪⎧ 0.1x ≤902x ≤600x ∈N *?⎩⎪⎨⎪⎧x ≤900x ≤300x ∈N *?x ≤300，x ∈N *.目标函数为z ＝80x .所以当x ＝300时，z max ＝80×300＝24000(元)，即如果只安排生产书桌，最多可生产300张书桌，获得利润24000元． (2)设只生产书橱y 个，可获利润z 元，则⎩⎪⎨⎪⎧ 0.2y ≤901·y ≤600y ∈N *?⎩⎪⎨⎪⎧y ≤450y ≤600y ∈N *?y ≤450，y ∈N *.目标函数为z ＝120y .所以当y ＝450时，z max ＝120×450＝54000(元)，即如果只安排生产书橱，最多可生产450个书橱，获得利润54000元． (3)设生产书桌x 张，书橱y 个，利润总额为z 元，则⎩⎪⎨⎪⎧0.1x ＋0.2y ≤902x ＋y ≤600x ≥0，x ∈N y ≥0，x ∈N ?⎩⎨⎧x ＋2y ≤900，2x ＋y ≤600，x ≥0，y ≥0，且x ∈N ，y ∈N .目标函数为z ＝ 80x ＋120y .在直角坐标平面内作出上面不等式组所表示的平面区域 ，即可行域(图略)． 作直线l ∶80x ＋120y ＝0，即直线l ∶2x ＋3y ＝0(图略)．把直线l 向右上方平移，当直线经过可行域上的直线x ＋2y ＝900,2x ＋y ＝600的交点时，此时z ＝80x ＋120y 取得最大值．由⎩⎪⎨⎪⎧x ＋2y ＝9002x ＋y ＝600解得交点的坐标为(100,400)．所以当x ＝100，y ＝400时，z max ＝80×100＋120×400＝56000(元)．因此，生产书桌100张，书橱400个，可使所获利润最大．。

一、思考题1． 什么是线性规划模型，在模型中各系数的经济意义是什么？ 2． 线性规划问题的一般形式有何特征？3． 建立一个实际问题的数学模型一般要几步？4． 两个变量的线性规划问题的图解法的一般步骤是什么？5． 求解线性规划问题时可能出现几种结果，那种结果反映建模时有错误？6． 什么是线性规划的标准型，如何把一个非标准形式的线性规划问题转化成标准形式。

7． 试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。

8． 试述单纯形法的计算步骤，如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。

9． 在什么样的情况下采用人工变量法，人工变量法包括哪两种解法？10．大M 法中，M 的作用是什么？对最小化问题，在目标函数中人工变量的系数取什么？最大化问题呢？ 11．什么是单纯形法的两阶段法？两阶段法的第一段是为了解决什么问题？在怎样的情况下，继续第二阶段？ 二、判断下列说法是否正确。

1． 线性规划问题的最优解一定在可行域的顶点达到。

2． 线性规划的可行解集是凸集。

3． 如果一个线性规划问题有两个不同的最优解，则它有无穷多个最优解。

4． 线性规划模型中增加一个约束条件，可行域的范围一般将缩小，减少一个约束条件，可行域的范围一般将扩大。

5． 线性规划问题的每一个基本解对应可行域的一个顶点。

6． 如果一个线性规划问题有可行解，那么它必有最优解。

7． 用单纯形法求解标准形式（求最小值）的线性规划问题时，与0>j σ对应的变量都可以被选作换入变量。

8． 单纯形法计算中，如不按最小非负比值原则选出换出变量，则在下一个解中至少有一个基变量的值是负的。

9． 单纯形法计算中，选取最大正检验数k σ对应的变量k x作为换入变量，可使目 标函数值得到最快的减少。

10． 一旦一个人工变量在迭代中变为非基变量后，该变量及相应列的数字可以从单纯形表中删除，而不影响计算结果。

高中数学线性规划各类习题精选7学校:___________姓名：___________班级：___________考号：___________一、单选题1．设x y ，满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩，则2x y -的最小值是（ ）A ．-4B ．127C ．0D ．6 2．定义,m a x {,},a a ba b b a b≥⎧=⎨<⎩，设实数x ，y 满足约束条件22x y ⎧≤⎪⎨≤⎪⎩，则m a x {4,3z x y x y=+-的取值范围是（ ） A ．[7,10]- B ．[8,10]- C ．[6,8]- D ．[7,8]-3．若x y ，满足约束条件221{21x y x y x y +≥≥-≤且向量()3,2a =， ()b x y =，，则•a b 的取值范围是（ ）A ．5,44⎡⎤⎢⎥⎣⎦B ．7,52⎡⎤⎢⎥⎣⎦C ．7,42⎡⎤⎢⎥⎣⎦D ．5,54⎡⎤⎢⎥⎣⎦4．实数x ，y 满足2x a y x x y ≥⎧⎪≥⎨⎪+≤⎩（1a <），且2z x y =+的最大值是最小值的4倍，则a的值是（ ） A ．211 B ．14 C ．12 D ．1125．已知变量x ，y 满足约束条件，则 的最大值为（ ）A ．B ．C ．1D ．26．设,x y 满足约束条件220840x y x y x y -+≥⎧⎪--≤⎪⎨≥⎪⎪≥⎩,若目标函数11(0,0)z x y a b a b =+>>的最大值为2，则a b +的最小值为（ ）A ．92B ．14C ．29D ．47．设y x ,满足不等式组⎪⎩⎪⎨⎧≥--≤--≤-+02301206y x y x y x ，若y ax z +=的最大值为42+a ，最小值为1+a ，则实数a 的取值范围为（ ）A ．]2,1[-B ．]1,2[-C ．]2,3[--D ．]1,3[-8．已知x ，y 满足，则使目标函数z=y ﹣x 取得最小值﹣4的最优解为（ ）A ．（2，﹣2）B ．（﹣4，0）C ．（4，0）D ．（7，3）9．已知变量y x ,满足以下条件：,,11y xx y R x y y ≤⎧⎪∈+≤⎨⎪≥-⎩，z ax y =+，若z 的最大值为3，则实数a 的值为（ ）A ．2或5B ．-4或2C ．2D ．5 10．不等式表示的平面区域（用阴影表示）是（ ）A ．B ．C ．D ．11．已知 是不等式组的表示的平面区域内的一点， ，为坐标原点，则的最大值（ ）A ．2B ．3C ．5D ．612．已知实数x ，y 满足条件若目标函数的最小值为5，其最大值为（ ）A ．10B ．12C ．14D ．1513．已知(),P x y 为区域22400y x x a -≤⎧≤≤⎨⎩内的任意一点，当该区域的面积为2时，2z x y=+的最大值是( )A ．5B ．0C ．2D ．14．若A 为不等式组表示的平面区域，则当从连续变化到时，动直线扫过A 中的那部分区域的面积为（ ）A ．34 B ．1 C ．74D ．2 15．过平面区域内一点 作圆 的两条切线，切点分别为，记 ，则当 最小时 的值为( ) A ．B ．C ．D ．16．若变量满足约束条件且的最大值为，最小值为，则的值是（ ） （A ）（B ）（C ）（D ）17．设变量x ，y 满足约束条件则目标函数z ＝3x －y 的最大值为（ ）A ．－4B ．0C ．D ．418．已知实数m ， n 满足不等式组，则关于x 的方程()23260x m n x mn -++=的两根之和的最大值和最小值分别是（ ）A ．7， 4-B ．8， 8-C ．4， 7-D ．6， 6-19．实数x ，y 满足不等式组则的取值范围是（ ）A ．B ．C ．D ．20．已知变量满足： 的最大值为（ ）A ．B ．C ．2D ．421．若y x ,满足⎪⎩⎪⎨⎧≥≤+≤-010x y x y x 则y x z 2+=的最大值为（ ）A ．0B ．1C ．23D ．2 22．若实数,x y 满足不等式组⎪⎩⎪⎨⎧≥+-≤--≥-+,01,032,033my x y x y x 且x y +的最大值为9，则实数m =（ ）A ．1B ．-1C ．2D ．-2 23．若两个正数b a ,满足24a b +<，则222-+=a b z 的取值范围是（ ）A ．{}|11z z -≤≤B ．{}|11z z -≥≥或z C ．{}|11z z -<< D ．{}|11z z ->>或z24．（题文）已知实数满足，若目标函数的最大值为，最小值为，则实数的取值范围是（ ）A ．B ．C ．D ．25．如果实数x ,y 满足约束条件⎪⎩⎪⎨⎧≤++≥+≥+-010101y x y y x ，则y x -2的最大值为（ ）A ．1B ．2C ．2-D ．3-26．如果实数,满足约束条件，则的最大值为（ ）A ．B ．C ．D ．27．设 ， 满足约束条件 ，若目标函数（ ）的最大值为 ，则的图象向右平移后的表达式为（ ）A ．B ．C ．D ．28．在平面直角坐标系中，不等式组20200x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩，表示的平面区域的面积是（ ）A．．4 C．．229．已知正数,x y 满足20350x y x y -≤⎧⎨-+≥⎩，则2z x y =--的最小值为（ ）A ．2B ．0C ．-2D ．-430．已知实数x 、y 满足，如果目标函数的最小值为－1，则实数m ＝（ ）． A ．6B ．5C ．4D ．331．设,x y 满足约束条件()0,230,,,230.x x y a y m x x y ≥⎧⎪+-≥=+⎨⎪+-≤⎩()1,2b =，且a ∥b ，则m 的最小值为（ ） A 、1 B 、2 C 、12 D 、1332．已知实数,x y 满足约束条件00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩，则11y z x -=+的取值范围是（ ）A ．11,3⎡⎤-⎢⎥⎣⎦B ．11,23⎡⎤-⎢⎥⎣⎦C ．1,2⎡⎫-+∞⎪⎢⎣⎭D ．1,12⎡⎫-⎪⎢⎣⎭33．设变量,x y 满足约束条件211y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则2x y +的最大值为（ ）A ．95 B ．25- C ．0 D ．5334．若实数x ，y 满足不等式024010x y x y x y +≥⎧⎪+-≤⎨⎪--≤⎩，且x y +的最大值为（ ）A ．1B ．2C ．3D ．435．已知实数满足：，，则的取值范围是A ．B ．C ．D ．36．若实数x ，y 满足不等式024010x y x y x my +≥⎧⎪+-≤⎨⎪--≤⎩，且x y +的最大值为3，则实数m =（ ）A ．-1B ．12C ．1D ．2 37．若点),(y x P 满足线性约束条件⎪⎩⎪⎨⎧≥≥+-≤-002303y y x y x ，点)3,3(A ，O 为坐标原点，则⋅的最大值为（ ）A ．0B ．3C ．-6D ．638．设变量,x y 满足约束条件⎪⎩⎪⎨⎧≤--≥-≥+3213y x y x y x ，则目标函数23z x y =+的最小值为（ ）A ．6B ．7C ．8D ．9 39．如果直线12:220,:840l x y l x y -+=--=与x 轴正半轴，y 轴正半轴围成的四边形封闭区域（含边界）中的点，使函数()0,0z abx y a b =+>>的最大值为8， 求a b +的最小值（ ）A 、4B 、3C 、2D 、040．设变量,x y 满足约束条件：3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，则目标函数1ax y z x ++=的取值范围是[3,5]，则a =（ ）A ．4B ．3C ．2D ．141．已知不等式组210210x y x x y -+≥⎧⎪≤⎨⎪+-≥⎩表示的平面区域为D ，若函数|1|y x m =-+的图象上存在区域D 上的点，则实数m 的取值范围是（ ） A ．1[0,]2 B ．1[2,]2- C ．3[1,]2- D ．[2,1]- 42．已知点集}0222|),{(22≤---+=y x y x y x M ，}022|),{(22≥+--=y x y x y x N ，则N M 所构成平面区域的面积为（ ）A ．πB ．π2C ．π3D ．π443．若实数x ，y 满足不等式组024010x y x y x my +≥⎧⎪+-≤⎨⎪--≤⎩，且x+y 的最大值为3，则实数m=（ ）A ．-1B ．12C ．1D ．2 44．若实数x ，y 满足不等式组，且x+y 的最大值为（ ）A ．1B ．2C ．3D ．445．设x ，y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ，若目标函数)0,0(>>+=b a by ax z 的值是最大值为12，则ba 32+的最小值为（ ） A ．38 B ．625 C ．311 D ．446．设O 是坐标原点，点A （-1，1），若点M （,x y ）为平面区域⎪⎩⎪⎨⎧≤≤≥+212y x y x 上的一个动点，则OA OM ⋅的取值范围为 （ ）A ．[]0,1-B ．[]1,0C ．[]2,0D ．[]2,1-47．已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥+≤112y x y x y ，则y x z +=3的最大值为（ ）A ．12B ．11C ．3D ．-1 48．在直角坐标系内，满足不等式的点的集合(用阴影表示)正确的是（ ）A ．B ．C ．D ．49．设x ，y 满足10x y y x y +≤⎧⎪≤⎨⎪≥⎩，则4z x y =+的最大值是（ ）A ．3B ．4C ．5D ．650． 若,x y 满足约束条件5315153x y y x x y +⎧⎪+⎨⎪-⎩≤≤≤，则35x y +的取值范围是（ ）A ．[13,15]-B ．[13,17]-C ．[11,15]-D ．[11,17]-51．设的最大值为（ ）A ．80B ．C ．25D ．52．已知0a >，不等式组00(2)x y y a x ≥⎧⎪≤⎨⎪≥-⎩表示的平面区域的面积为1，则a 的值为（ ）A ．14 B ．12C ．1D ．2 53．不等式2350x y --≥表示的平面区域是（ ）A ．B ．C ．D ．54．设x ，y 满足约束条件 ，若目标函数(0,0)z ax by a b =+>>的最大值为12，则的最小值为 （ ）． A ．4 B ． C ． D ．55．已知实数,x y 满足1000x y x y x +-≤⎧⎪-≤⎨⎪≥⎩，则2x y -的最大值为（A ）12-（B ）0 （C ）1 （D ）1256．若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥-+≤-≤-020102y x y x ，则目标函数y x t 2-=的最大值为（ ）A ． 1-B ．0C ．1D ．257．若实数x ，y 满足4024020+-⎧⎪--⎨⎪-+⎩x y x y x y ………，则目标函数23=+z x y 的最大值为（ ）A ．11B ．24C ．36D ．49⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x 23a b +3831162558．已知 ， 满足约束条件则目标函数 的最大值为（ ）A ．1B ．3C ．D ．59．已知实数,x y 满足不等式组2010220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩，，，则z x y =+的取值范围为（ ）A ．[]1,2-B ．[]13，C ．[]1,3-D ．[]2,460．设变量x ，y 满足约束条件00220x x y x y ≥⎧⎪-≥⎨⎪--≤⎩则z ＝3x －2y 的最大值为A ．4B ．2C ．0D ．661．已知实数x 、y 满足约束条件1,1,2 2.x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩则目标函数25y z x +-=的最大值为A ．3B ．4C ．3-D ．-1262．不在不等式623<+y x 所表示的平面区域内的点是（ ） A ．)0,0( B ．)1,1( C ．)2,0( D ．)0,2(二、填空题63．设不等式组2000x y x y +-≤⎧⎪≥⎨⎪≥⎩表示的平面区域为D ，在区域D 内随机取一点P ，则点P 落在圆221x y +=内的概率为 ．64．已知,x y 满足14210x x y x y ≥⎧⎪+≤⎨⎪--≤⎩，则2z x y =+的最大值为 ．65．已知方程220x ax b ++=(,)a R b R ∈∈，其一根在区间(0,1)内，另一根在区间(1,2)内，则31b a --的取值范围为 ． 66．设x ，y 满足， ，若 ，则m 的最大值为 ．67．设x ，y 满足约束条件则z ＝x ＋4y 的最大值为________．68．直线01-22=-+a y ax 与不等式组2040220x y x y x y -+-≤⎧⎪+-≤⎨⎪-+≤⎩表示的区域没有．．公共点，则a 的取值范围是 ．69．已知变量x ，y 满足⎪⎩⎪⎨⎧≥≤-+≤+-104034x y x y x ， xy y x 22+的取值范围为 ．70．设变量x ，y 满足则x ＋2y的最大值为 71．已知变量x 、y 满足约束条件 则的取值范围是 ．72．已知实数对（x ，y ）满足210x y x y ≤⎧⎪≥⎨⎪-≥⎩，则2x y +的最小值是 ．73．设变量y x ，满足约束条件⎪⎩⎪⎨⎧≤≥+≤-,2,2,1y y x y x 则目标函数22y x z +=的取值范围是 ．74．已知实数y x ,则 22222)(y x y y x +++的取值范围为 ． 75．若实数满足则的取值范围是 ．76．已知0m >，实数,x y 满足⎪⎩⎪⎨⎧≤+≥≥,,0,0m y x y x 若2z x y =+的最大值为2，则实数m =______．77．设2z x y =-+，实数,x y 满足2,{1, 2.x x y x y k ≤-≥-+≥若z 的最大值是0，则实数k =_______， z 的最小值是_______．78．给出平面区域如图所示，其中若使目标函数仅在点处取得最大值，则的取值范围是________．79．设实数x ，y 满足约束条件202x y y x -≥⎧⎪⎨≥-⎪⎩，则2z x y =+的最大值为 ． 80．设,x y 满足约束条件1{10 1x y x x y +≤+≥-≤，则目标函数2y z x =-的取值范围为___________． 81．设实数,x y 满足,102,1,x y y x x ≤⎧⎪≤-⎨⎪≥⎩向量2,x y m =-()a ，1,1=-()b ．若// a b ，则实数m 的最大值为 ．82．已知实数x ，y 满足220,220,130,x y x y x y --≥⎧⎪-+≤⎨⎪+-≤⎩则z xy =的最大值为 ．83．已知变量,x y 满足240{2 20x y x x y -+≥≤+-≥,则32x y x +++的取值范围是 ． 84．设x ，y 满足约束条件1210,0≤+⎧⎪≥-⎨⎪≥≥⎩y x y x x y ，若目标函数()0,0z abx y a b =+>>的最大值为35， 则a b +的最小值为 ．85．若x y ，满足约束条件1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩，，则2z x y =+的最大值为____________．86．若,x y 满足约束条件：1020,220,x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩，，则3x y +的最大值为___ ____．87．已知x 、y 满足，则 的最大值是___________ ．88．已知变量,x y 满足约束条件13,1,x y y x y +≥⎧⎪≤⎨⎪-≤⎩，若z kx y =+的最大值为5，且k 为负整数，则k =____________．89．已知不等式表示的平面区域为 ，若直线 与平面区域 有公共点，则 的范围是_________90．已知实数y x ,满足⎪⎩⎪⎨⎧≤≥+≥+-1002x y x y x 则y x z +=2的最小值为__________．91．若点（2，1）和（4，3）在直线230x y a -+= 的两侧，则a 的取值范围是____________．92．设变量x ，y 满足约束条件3{ 1 1x y x y y +≤-≥-≥，则2z x y =-的最小值为93．设变量y x ,满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩，则y x z 23+-=的最大值为 ．94．已知实数 满足，则的取值范围是__________．95．已知变量x ，y 满足约束条件22,24,41,x y x y x y +≥⎧⎪+≤⎨⎪-≥-⎩则目标函数33z x y =-+的最大值是 ．96．已知实数x ，y 满足约束条件则 的最大值等于______．97．设1,m >在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数5z x y =+的最大值为4，则m 的值为 ，目标函数y x z -=2的最小值为________．三、解答题98．画出不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 表示的平面区域99．（本小题12分）已知⎪⎩⎪⎨⎧≤--≥-+≥+-0520402y x y x y x ， 求（Ⅰ）12++=x y z 的取值范围; （Ⅱ）251022+-+=y y x z 的最小值．100．（本小题12分）已知y x ,满足不等式组⎪⎩⎪⎨⎧≤--≥-+≥+-0520402y x y x y x ，求（1）y x z 2+=的最大值；（2）251022+-+=y y x z 的最小值．参考答案1．A【解析】试题分析：作出x y ，满足约束条件下的平面区域，如图所示，由图当目标函数2z x y =-经过点(0,4)A 时取得最小值，且min 044z =-=-，故选A ．考点：简单的线性规划问题．2．A ．【解析】试题分析：若4320x y x y x y +≥-⇒+≥：4z x y =+，如下图所示，画出不等式组所表示的可行域，∴当2x y ==时，m a x 10z =，当2x =-，1y =时，m i n 7z =-；若432x y x y x y+<-⇒+<： 3z x y =-，画出不等式所表示的可行域，∴当2x =，2y =-时，max 8z =，当2x =-，1y =时，min 7z =-，综上，z 的取值范围是[7,10]-，故选A ．考点：线性规划的运用．3．D【解析】试题分析：∵向量()3,2a =， ()b x y =，，∴·32a b x y =+，设z=3x+2y ， 作出不等式组对于的平面区域如图：由z=3x+2y ，则322z y x =-+，平移直线322z y x =-+，由图象可知当直线322z y x =-+， 经过点B 时，直线322z y x =-+的截距最大，此时z 最大，由{ 21x yx y =-=，解得1{ 1x y ==，即B （1，1），此时zmax=3×1+2×1=5， 经过点A 时，直线322z y x =-+的截距最小，此时z 最小， 由{ 221x y x y =+=，解得14{ 14x y ==，即A 11,44⎛⎫ ⎪⎝⎭，此时zmin=3×14+2×14=54，则54≤z≤5 考点：简单线性规划4．B【解析】试题分析：在直角坐标系中作出可行域如下图所示，当目标函数y x z +=2经过可行域中的点)1,1(B 时有最大值3，当目标函数y x z +=2经过可行域中的点),(a a A 时有最小值a 3，由a 343⨯=得41=a ，故选B ．考点：线性规划．5．C【解析】试题分析：画出可行域如下图所示，由图可知，目标函数在点 取得最大值为 .考点：线性规划．6．A【解析】试题分析：作出可行域如图， ()2201,4840x y A x y -+=⎧⇒⎨--=⎩，当目标函数11(0,0)z x y a b a b=+>>过点()1,4A 时纵截距最大，此时z 最大．即()142,0,0a b a b+=>>．()1141419552222a b a b a b a b b a ⎛⎫⎛⎫⎛⎫∴+=++=++≥= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当且仅当4b a a b =，即322a b ==时取''''=．故选A ． 考点：1线性规划；2基本不等式．7．B【解析】试题分析：由z ax y =+得，y ax z =-+，直线y ax z =-+是斜率为,a y -轴上的截距为z 的直线，作出不等式组对应的平面区域如图：则()()1,1,2,4,A B z ax y =+的最大值为24a +，最小值为1a +∴直线z ax y =+过点B 时，取得最大值为24a +，经过点A 时取得最小值为1a +，若0a =，则y z =此时满足条件，若0a >则目标函数斜率0k a =-<，要使目标函数在A 处取得最小值，在B 处取得最大值，则目标函数的斜率满足1BC a k -≥=-，即01a <≤，若0a <，则目标函数斜率0k a =->要使目标函数在A 处取得最小值，在B 处取得最大值，则目标函数的斜率满足2AC a k -≤=，即20a -≤<，综上21a -≤≤；故选B ．考点：简单的线性规划8．C【解析】试题分析：由题意作出其平面区域将z=y-x 化为y=x+z ，z 相当于直线y=x+z 的纵截距，则由平面区域可知，使目标函数z=y-x 取得最小值-4的最优解为（4，0）；考点：简单线性规划问题9．B【解析】试题解析：当直线y ax z +=平移到点()1,1--B 时有最大值，此时应满足431-=⇒=--a a ；当直线y ax z +=平移到点()1,2-B 时有最大值，此时应满足2312=⇒=-a a ．考点：线性规划的应用．10．B【解析】试题分析：可用特殊值法．代入点可知满足不等式，故点所在区域即为所求．考点：二元一次不等式表示平面区域．11．D【解析】试题分析：由题意可知，，令目标函数 ，作出不等式组表示的平面区域，如图所示，由图知，当目标函数 经过点 时取得最大值，最大值为 ，故选D ．考点：简单的线性规划问题．12．A【解析】试题分析：依题意知，不等式表示的平面区域如图所示的三角型ABC 及其内部且A （2，2）、C （2，4-c ）．目标函数可看作是直线在y 轴上的截距，显然当直线过点C 时，截距最小及z 最小，所以解得，此时B （3，1），且直线过点B 时截距最大，即z 最大，最大值为．故选A ．考点：线性规划求最值．【方法点睛】线性规划求最值和值域问题的步骤：（1）先作出不等式组表示的平面区域；（2）将线性目标函数看作是动直线在y 轴上的截距；（3）结合图形看出截距的可能范围即目标函数z 的值域；（4）总结结果．另外，常考非线性目标函数的最值和值域问题，仍然是考查几何意义，利用数形结合求解．例如目标函数为可看作是可行域内的点（x ，y ）与点（0，0）两点间的距离的平方；可看作是可行域内的点（x ，y ）与原点（0，0）连线的斜率等等． 13．A 【解析】试题分析：由约束条件作出可行域，求出使可行域面积为2的a 值，化目标函数为直线方程的斜截式，数形结合可得最优解，求出最优解的坐标，代入目标函数得答案．2240{0y x x a-≤≤≤作出可行域如图, 由图可得22A a a B a a -（，），（，），1421122OAB S a a a B ∆=⨯⨯=∴=∴，，（，），目标函数可化为122z y x =-+，∴当122zy x =-+，过A 点时，z 最大，z=1+2×2=5，故选A ．考点：简单的线性规划14．C【解析】试题分析：如图，不等式组表示的平面区域是△AOB，动直线x+y=a（即y=-x+a）在y轴上的截距从-2变化到1．知△ADC是斜边为3的等腰直角三角形，△EOC是直角边为1等腰直角三角形，所以区域的面积13173112224 ADC EOCS S S∆∆=-=⨯⨯-⨯⨯=考点：二元一次不等式（组）与平面区域视频15．C【解析】试题分析：因为，所以在中，，因为，而函数在上是减函数，所以当最小时最大，因为为增函数则此时最大。

1习题2-1 判断下列说法是否正确：（1） 任何线性规划问题存在并具有惟一的对偶问题； （2） 对偶问题的对偶问题一定是原问题；（3） 根据对偶问题的性质，当原问题为无界解时，其对偶问题无可行解，反之，当对偶问题无可行解时，其原问题具有无界解；（4） 若线性规划的原问题有无穷多最优解，则其对偶问题也一定具有无穷多最优解；（5） 若线性规划问题中的b i ，c j 值同时发生变化，反映到最终单纯形表中，不会出现原问题与对偶问题均为非可行解的情况； （6） 应用对偶单纯形法计算时，若单纯形表中某一基变量x i <0，又x i 所在行的元素全部大于或等于零，则可以判断其对偶问题具有无界解。

（7） 若某种资源的影子价格等于k ，在其他条件不变的情况下，当该种资源增加5个单位时，相应的目标函数值将增大5k ；（8） 已知y i 为线性规划的对偶问题的最优解，若y i >0，说明在最优生产计划中第i 种资源已经完全耗尽；若y i =0，说明在最优生产计划中的第i 种资源一定有剩余。

2-2将下述线性规划问题化成标准形式。

⎪⎪⎩⎪⎪⎨⎧≥≥-++-≤+-+-=-+-+-+-=无约束43214321432143214321,0,,232142224.5243max )1(x x x x x x x x x x x x x x x x st x x x x z ()⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束321321321321,0,0624.322min 2x x x x x x x x x st x x x z 解：(1)令'''444x x x =-，增加松弛变量5x ，剩余变量6x ，则该问题的标准形式如下所示：'''12344'''12344'''123445'''123446'''1234456max 342554222214..232,,,,,,0z x x x x x x x x x x x x x x x x s t x x x x x x x x x x x x x =-+-+-⎧-+-+-=⎪+-+-+=⎪⎨-++-+-=⎪⎪≥⎩ (2)令'z z =-，'11x x =-，'''333x x x =-，增加松弛变量4x ，则该问题的标准形式如下所示：2'''''1233''''1233''''12334''''12334max 22334..26,,,,0z x x x x x x x x s t x x x x x x x x x x =+-+⎧++-=⎪+-++=⎨⎪≥⎩ 2-3分别用图解法和单纯形法求解下述线性规划问题，并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。

线性规划练习题含答案一、选择题1．已知不等式组2,1,0y x y kx x ≤-+⎧⎪≥+⎨⎪≥⎩所表示的平面区域为面积等于1的三角形，则实数k 的值为A ．－1 BD ．1 【答案】B【解析】略作出不等式组表示的可行域如右图所示阴影部分，由于AOB ∆的面积为2, AOC ∆的面积为1，所以当直线y=kx+1过点A （2，0），B （0，1故选B 。

2．定义()()max{,}a a b a b b a b ≥⎧⎪=⎨<⎪⎩，已知实数y x ,满足设{}m a x ,2z x y x y=+-，则z 的取值范围是 （ ） A【答案】D【解析】{},2,20max ,22,22,20x y x y x y x y x y z x y x y x y x y x y x y x y ++≥-+-≤⎧⎧=+-==⎨⎨-+<--->⎩⎩， 当z=x+y 时，对应的点落在直线x-2y=0z=2x-y 时，对应的点落在直线x-2y=0的右下3．若实数x ，y 满足⎪⎩⎪⎨⎧≤+≥≥,1234,0,0y x y x 则 ）A ．BCD【答案】DP(x,y)与点(-1,-3)连续的斜率，数形结3,,4PA k =应选D4．设,x y ∈R 且满足1230x x y y x ≥⎧⎪-+≥⎨⎪≥⎩，则2z x y =+的最小值等于 ( )A. 2B. 3C.5D. 9【答案】B【解析】解：因为设,x y ∈R 且满足满足1230x x y y x ≥⎧⎪-+≥⎨⎪≥⎩故其可行域为当直线Z=x+2y 过点（1，1）时，z=x+2y 取最小值3， 故选B5．若实数，满足条件则的最大值为（ ）（A ） （B ） （C ） （D ） 【答案】A【解析】作出如右图所示的可行域，当直线z=2x-y 过点A 时，Z 取得最大值.因为A(3,-3)，所以Z max =23(3)9⨯--=,故选A.x y 0,30,03,x y x y x +≥⎧⎪-+≥⎨⎪≤≤⎩2x y -9303-6．设变量x ，y 满足约束条件⎪⎩⎪⎨⎧≥+≤+≥-120y x a y x y x ，若目标函数z=2x+6y 的最小值为2，则a =A ．1B ．2C ．3D ．4 【答案】A【解析】解：由已知条件可以得到可行域，，要是目标函数的最小值为2，则需要满足直线过x 2y 1+=与x+y=a 的交点时取得。