当前位置：文档之家 › 第十一章 多重线性回归分析

第十一章 多重线性回归分析

  • 格式：doc
  • 大小：32.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第11章 多重线性回归分析2010

第11章 多重线性回归分析2010

22.5 21.5 28.5 26.0 35.0 20.0 23.0 24.8 23.3 27.0 26.0 28.0
2.00 2.40 3.00 1.00 2.80 1.45 1.50 1.50 0.90 0.65 1.83 2.00
资料来源：数据选自《卫生统计学》第 5 版（方积乾主编）人民卫生出版社
20.0 23.0 26.5 23.0 29.5 30.0 22.5 21.8 27.0 27.0 22.0 28.0
0.45 0.50 1.50 0.40 0.90 0.80 1.80 0.60 1.70 0.65 0.40 2.00
0.948 1.440 1.084 1.844 1.116 1.656 1.536 0.960 1.784 1.496 1.060 1.436
Xi Xi X Si
' i
标准化偏回归系数（standardized partial regression coefficient）
自变量筛选的统计学标准：
1. 残差平方和（ SS残差 ）缩小或确定系数（
R2 ）
增大;
2 MS R 2. 残差的均方（ 残差 ）缩小或调整确定系数（ ad）
增大;
偏回归系数的 t 检验与标准化偏回归系数 回归系数 0.116 0.004 -6.5510-6 -0.035 标准误 0.027 0.002 0.001 0.011
t
4.23 2.36 -0.01 -3.21
P
0.0005 0.0289 0.9925 0.005
标准化偏 回归系数 0.592 0.273 -0.001 -0.448
虑对数据进行变量变换 ；
3. 如果方差齐性的假定不成立，可以采用其它的

11-多重线性回归分析

11-多重线性回归分析

1个
1个
统计方法
简单线性相关
simple linear correlation
简单线性回归
simple linear regression
多重相关
multiple correlation
多重回归
multiple regression
典则相关
cononical correlation
多元回归
multivariate regression
量x 取值均为0时，y的平均估计值。
➢bi：变量xi的偏回归系数(partial regression coefficient)，
是总体参数βi 的估计值；指在方程中其它自变量固定 不变的情况下， xi 每增加或减少一个计量单位，反应 变量Y 平均变化 bi个单位。
Yˆ b0 b1X1 b2 X 2 ... bp X p
问题：对NO浓度的贡献，哪个因素作用的大一点， 哪个小一些？
回归系数的标准化：
1.自变量数据的标准化： 2.求标准化偏回归系数：
X
' i
Xi Xi Si
用标准化的数据进行回归模型的拟合，算出它的方程，
此时所获得的偏回归系数b’，叫~。
b’无单位，可用来比较各个自变量对反应变量的贡献大小
比较：
未标准化的回归系数（偏回归系数）：用来构建回归 方程，即方程中各自变量的斜率。
计值 Yˆ 之间的残差（样
本点到直线的垂直距离) 平方和达到最小。 .
两个自变量时回归平面示意图
通过SPSS等统计软件，拟合X1、X2 、X3 、X4关于空 气中NO浓度的多重线性回归方程，得：
Y 0.142 0.116X1 0.004X 2 6.55106 X3 0.035X 4

管理统计学习题参考答案第十一章

管理统计学习题参考答案第十一章

十一章1. 解：回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；在线性回归中，按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且自变量之间存在线性相关，则称为多元线性回归分析。

相关分析，相关分析是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度，是研究随机变量之间的相关关系的一种统计方法。

相关分析和回归分析是研究客观现象之间数量联系的重要统计方法。

既可以从描述统计的角度，也可以从推断统计的角度来说明。

所谓相关分析，就是用一个指标来表明现象间相互依存关系的密切程度。

所谓回归分析，就是根据相关关系的具体形态，选择一个合适的数学模型，来近似地表达变量间的平均变化关系。

它们具有共同的研究对象，在具体应用时，相关分析需要依靠回归分析来表明现象数量相关的具体形式，而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。

只有当变量之间存在着高度相关时，进行回归分析寻求其相关的具体形式才有意义。

由于相关分析不能指出变量间相互关系的具体形式，所以回归分析要对具有相关关系的变量之间的数量联系进行测定，从而为估算和预测提供了一个重要的方法。

在有关管理问题的定量分析中，推断统计加具有更加广泛的应用价值。

需要指出的是，相关分析和回归分析只是定量分析的手段。

通过相关与回归分析，虽然可以从数量上反映现象之间的联系形式及其密切程度，但是现象内在联系的判断和因果关系的确定，必须以有关学科的理论为指导，结合专业知识和实际经验进行分析研究，才能正确解决。

因此，在应用时要把定性分析和定量分析结合起来，在定性分析的基础上开展定量分析。

第十一章多重多元回归分析

第十一章多重多元回归分析

X1 11.5 9 7.9 9.1 11.6 13 11.6 10.7 11.1
X2 95.3 97.7 110.7 89 88 87.7 79.7 119.3 87.7
Y1 26.4 30.8 39.7 35.4 29.3 24.6 25.6 29.9 32.2
Y2 39.2 46.8 39.1 35.3 37 44.8 43.7 38.8 35.6
第十一章 多重多元回归分析
第一节 什么是多重多元回归分析
– 在工厂里研究产品的质量指标,而反映产品质量指标 有好几个，产品的质量指标可作为多个因变量；而 影响产品质量指标的因素也有多个，可作为自变量， 如何从数量上揭示这种相互依赖关系，又如何建立 它们的回归式以及预测预报就是一个多重多元回归 分析问题。
回归方程的检验：
即检验
这里，P=2，m2=m=2，N=9
在 所以，回归方程是显著的。
回归系数的检验 （1）检验
即检验
对
有无作用，在
之下，
表明
对
作用显著
（2）再检验
即检验 对
有无作用，在
之下，
表明
对
作用不显著
设
在 其中：
之下的剩余阵为：
且
独立，所以，
例：下表为某农学院育种研究室2002年品种区试的部分资料，其中x1为冬季分 蘖（单位：万），x2为株高（单位：厘米），y1为每穗粒数，y2为千粒重（单 位：克），进行y1、y2关于x1、x2的归归分析。
品种 小偃6号 7576/3矮790 68G(2)8 79190-1 9615_1 9615-13 73(36) 丰产3号 矮丰3号
称为回归方程
将数据写成矩阵的形式：
将n组数据带入到回归模型中：

11多元(重)线性回归精品PPT课件

11多元(重)线性回归精品PPT课件

编号
收缩压 年龄
(ID)
Y
X1
17
145
49
18
142
46
19
135
57
20
142
56
21
150
56
22
144
58
23
137
53
24
132
50
25
149
54
26
132
48
27
120
43
28
126
43
29
161
63
30
170
63
31
152
62
32
164
65
吸烟
X2
1 1 0 0 1 0 0 0 1 1 0 1 0 1 0 0
多元（重）线性回归
例子
人的体重与身高、胸围 血压值与年龄、性别、劳动强度、饮食习惯、
吸烟状况、家族史 糖尿病人的血糖与胰岛素、糖化血红蛋白、
血清总胆固醇、甘油三脂 射频治疗仪定向治疗脑肿瘤过程中，脑皮质
的毁损半径与辐射的温度、与照射的时间
32例40岁以上男性的年龄、吸烟、 体 重指数与收缩压
0.7967
Adj R-Sq （校正决定系数） 0.7749
Dependent Mean 应变量Y 的均值＝144.43750
剩余标准差（ Root MSE ）
S Y|12...p (YYˆ)2 /(np1)
SS残（np1） MS残 46.044886.78564
反映了回归方程的精度，其值越小说明回归效果越好
2. 逐步选择法
1. 前进法（forward selection） 2. 后退法（backward elimination） 3. 逐步回归法（stepwise regression）

多重线性回归分析方法

多重线性回归分析方法

多重线性回归分析方法多重线性回归分析是一种常用的统计方法，用于揭示自变量对因变量的影响。

它可以帮助我们理解多个自变量如何共同影响因变量，并通过建立一个数学模型来预测因变量的值。

本文将介绍多重线性回归分析的基本原理、步骤以及常见的模型评估方法。

一、基本原理多重线性回归分析是建立在线性回归模型的基础上的。

在简单线性回归模型中，只有一个自变量可以解释因变量的变化；而在多重线性回归模型中，有多个自变量同时对因变量产生影响。

其模型可表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中，Y代表因变量，X1, X2, ..., Xn代表自变量，β0, β1, β2, ..., βn代表回归系数，ε代表误差项。

二、分析步骤进行多重线性回归分析时，通常可以遵循以下步骤：1. 收集数据：首先，需要收集相关的自变量和因变量的数据，并确保数据的准确性和完整性。

2. 建立模型：根据收集到的数据，可以利用统计软件或编程工具建立多重线性回归模型。

确保选择合适的自变量，并对数据进行预处理，如去除异常值、处理缺失值等。

3. 模型拟合：利用最小二乘法或其他拟合方法，对模型进行拟合，找到最优的回归系数。

4. 模型评估：通过各种统计指标来评估模型的拟合效果，比如决定系数（R^2）、调整决定系数、F统计量等。

这些指标可以帮助我们判断模型的可靠性和解释力。

5. 解释结果：根据回归系数的正负和大小，以及显著性水平，解释不同自变量对因变量的影响。

同时，可以进行预测分析，根据模型的结果预测未来的因变量值。

三、模型评估方法在多重线性回归分析中，有多种方法可评估模型的拟合效果。

以下是几种常见的模型评估方法：1. 决定系数（R^2）：决定系数是用来衡量模型拟合数据的程度，取值范围为0到1。

其值越接近1，表示模型能够较好地解释数据的变异。

2. 调整决定系数：调整决定系数是在决定系数的基础上，考虑自变量的数量和样本量后进行修正。

管理统计学习题参考答案第十一章

管理统计学习题参考答案第十一章

一章1. 解：回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；在线性回归中，按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且自变量之间存在线性相关，则称为多元线性回归分析。

相关分析，相关分析是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度，是研究随机变量之间的相关关系的一种统计方法。

相关分析和回归分析是研究客观现象之间数量联系的重要统计方法。

既可以从描述统计的角度，也可以从推断统计的角度来说明。

所谓相关分析，就是用一个指标来表明现象间相互依存关系的密切程度。

所谓回归分析，就是根据相关关系的具体形态，选择一个合适的数学模型，来近似地表达变量间的平均变化关系。

它们具有共同的研究对象，在具体应用时，相关分析需要依靠回归分析来表明现象数量相关的具体形式，而回归分析则需要依靠相关分析来表明现象数量变化的相关程度。

只有当变量之间存在着高度相关时，进行回归分析寻求其相关的具体形式才有意义。

由于相关分析不能指出变量间相互关系的具体形式，所以回归分析要对具有相关关系的变量之间的数量联系进行测定，从而为估算和预测提供了一个重要的方法。

在有关管理问题的定量分析中，推断统计加具有更加广泛的应用价值。

需要指出的是，相关分析和回归分析只是定量分析的手段。

通过相关与回归分析，虽然可以从数量上反映现象之间的联系形式及其密切程度，但是现象内在联系的判断和因果关系的确定，必须以有关学科的理论为指导，结合专业知识和实际经验进行分析研究，才能正确解决。

因此，在应用时要把定性分析和定量分析结合起来，在定性分析的基础上开展定量分析。

多重线性回归分析

多重线性回归分析
32
三、分析步骤
• 2.5 模型拟合效果评价
• 2.5.1 决定系数(R2)
即复(全)相关系数的平方，其值等于因变量
观测值与预测值之间简单相关系数的平方。计算 公式为：
R =
2
l回归 l yy
l误差 = 1 l总
33
三、分析步骤
• 2.5 模型拟合效果评价
• 2.5.1 决定系数(R2)
R2取值介于0到1之间，其含义为自变量能够
2 C
其中，n为样本含量，p为模型中自变量个数。 决定系数相同时，自变量个数越多， Rc2越小。
37
三、分析步骤
• 2.5 模型拟合效果评价
• 2.5.3 AIC信息准则
该准则由日本学者赤池于1973年提出，广泛
应用于时间序列分析中自回归阶数的确定，多重 回归、广义线性回归中自变量的筛选以及非线性 回归模型的比较和选优。该统计量取值越小，反
24
三、分析步骤
• 2.4.2 后退法(BACKWARD)
从模型中包含全部自变量开始，计算留在回
归方程中的各个自变量所产生的F统计量和P值，
当P值小于sls(规定的从方程中踢除变量的临界水
准)则将此变量保留在方程中。
否则，从最大的P值所对应的自变量开始逐 一踢除，直到回归方程中没有变量可以被踢除时 为止。
变量之间的线性依存关系，称为多重线性回归分
析（multiple linear regression analysis）。
自变量是相互独立的连续型变量或分类变量。
4
一、方法简介
• 1.3 数据结构
表1 进行多重线性回归分析资料的数据结构 编号 1 2 ： X1 X11 X21 ： X2 X12 X22 ： … … … Xk X1k X2k ： Y Y1 Y2 ：

多重线性回归分析

多重线性回归分析
多重线性回归分析
例：由于改革开放政策，深圳特区中外来人口大幅度增加， 为了考察特区中外来人口对本地经济发展的贡献，深圳特 区统计局收集了所属的宝安县在1987年末18个镇的人口 与工农业总产值数据（见数据文件reg.sav）。此处把工 农业总产值当作因变量（W），而把外地及本地人口数当 作两个自变量（Z1，Z2）。 （有关统计方法的原理及计算参见孙尚拱，《医学多变 量统计与统计软件》，北京医科大学出版社，2000）
练习1
以下实例摘自 Hosmer, David W . (2000). Applied logistic regression . John Wiley, New York. 研究目的是考察与婴儿低出生体重有关的可能危险因素（当体重低于 2500g时，认为是低出生体重婴儿）。研究收集了189例妇女的数据，其中 59例分娩低出生体重婴儿，130例分娩正常体重婴儿（数据见文件 data1.sav）。
2.Logistic模型
g ( x) 0 1 x1 2 x2 .... i xi .... m xm
g(x)是对P的变换，称为logit变换：
P g ( x) ln 1 P
可以得到：
P exp[ g ( x)] 1 exp[ g ( x)]
Logistic回归分析
（一）Logistic回归分析的任务
影响因素分析 logistic回归常用于疾病的危险因素分析，logistic回归 分析可以提供一个重要的指标：OR。
（二）Logistic回归分析的基本原理
1.变量特点 因变量：二分类变量，若令因变量为y，则常用y＝1表 示“发病”，y＝0表示“不发病”（在病例对照研究中， 分别表示病例组和对照组）。 自变量：可以为分类变量，也可以为连续变量。

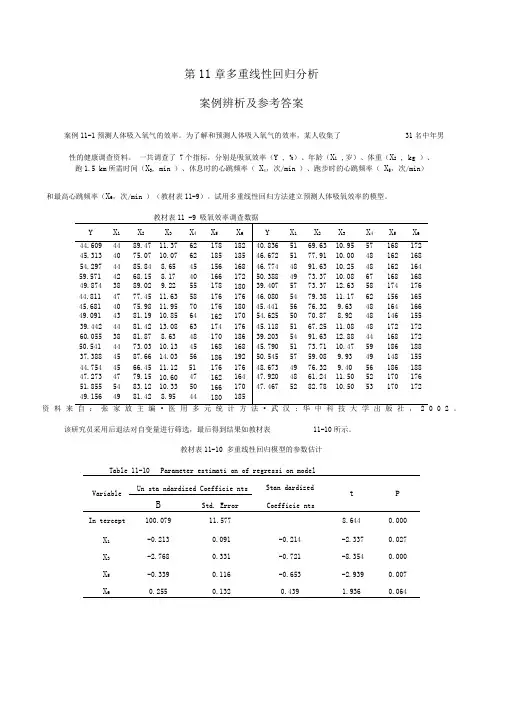
第11章多重线性回归分析案例辨析及参考答案

第11章多重线性回归分析案例辨析及参考答案

第11章多重线性回归分析案例辨析及参考答案案例11-1预测人体吸入氧气的效率。

为了解和预测人体吸入氧气的效率，某人收集了31名中年男性的健康调查资料。

一共调查了 7个指标，分别是吸氧效率（Y , %）、年龄（X1,岁）、体重（X2, kg ）、跑1.5 km所需时间（X3, min ）、休息时的心跳频率（X4，次/min ）、跑步时的心跳频率（X5，次/min）和最高心跳频率（X6，次/min ）（教材表11-9）。

试用多重线性回归方法建立预测人体吸氧效率的模型。

教材表11 -9 吸氧效率调查数据Y X1 X2X3 X4 X5 X6 Y X1 X2X3 X4 X5 X644.609 44 89.47 11.37 62 178 182 40.836 51 69.63 10.95 57 168 17245.313 40 75.07 10.07 62 185 185 46.672 51 77.91 10.00 48 162 16854.297 44 85.84 8.65 45 156 168 46.774 48 91.63 10.25 48 162 16459.571 42 68.15 8.17 40 166 172 50.388 49 73.37 10.08 67 168 16849.874 38 89.02 9.22 55 178 180 39.407 57 73.37 12.63 58 174 17644.811 47 77.45 11.63 58 176 176 46.080 54 79.38 11.17 62 156 16545.681 40 75.98 11.95 70 176 180 45.441 56 76.32 9.63 48 164 16649.091 43 81.19 10.85 64 162 170 54.625 50 70.87 8.92 48 146 15539.442 44 81.42 13.08 63 174 176 45.118 51 67.25 11.08 48 172 17260.055 38 81.87 8.63 48 170 186 39.203 54 91.63 12.88 44 168 17250.541 44 73.03 10.13 45 168 168 45.790 51 73.71 10.47 59 186 18837.388 45 87.66 14.03 56 186 192 50.545 57 59.08 9.93 49 148 15544.754 45 66.45 11.12 51 176 176 48.673 49 76.32 9.40 56 186 18847.273 47 79.15 10.60 47 162 164 47.920 48 61.24 11.50 52 170 17651.855 54 83.12 10.33 50 166 170 47.467 52 82.78 10.50 53 170 17249.156 49 81.42 8.95 44 180 185资料来自：张家放主编•医用多元统计方法•武汉:华中科技大学出版社，2002。

第11章 多重线性回归分析1

第11章 多重线性回归分析1

t= b =
Sb
S Y ⋅X /
b
∑ (X − X )2
两个结果一致：
t= F
10
多重线性回归分析的基本目的是用以上的一组 自变量（X1,X2,…，XP）的数值估计一个反应变
量（Y）及其变异性的统计分析方法。
多重线性回归的数学模型为: Y的平均数 = β0 + β1X1 + β2 X 2 + ⋅⋅⋅ + βP X P （11-1）
5
3. Cp统计量 C即Criterion，p为所选模型中变量的个数
由Mallows（1966）提出的Cp统计量近年来受 到了广泛的重视，其定义为:
CP
=
SS残，p MS残，全
+ （2 P +1）− n
（11-9）
模拟多个预测值，选择较小的Cp值，相应
的回归方程最优。详见下表。
31
32
结论：体重指数和瘦素每减少一个单位，脂联 素的平均水平改变1.08和0.75单位，从标准化回 归系数可看出瘦素对脂联素的影响较大。
此标准的缺陷？
每增加一个自变量，残差平方和总会减 少一些，决定系数总会增大，即使增加 无统计学意义的自变量，也会如此。
建议选用所有自变量进入进行分析比较。
29
2.残差均方（MS残）缩小或调整决定 系数（R2）增大
残差均方与残差平方和的关系式为:
MS残
=
n
SS残 − p −1
希望MS残愈小愈好，作为选择自变量的准则。 事实上，调整决定系数R2愈大愈好与MS残最小 化完全等价，分析见教材p198中段 。
33
二、自变量筛选的常用方法
α1：设为入选标准；α2设为剔除标准。

多重线性回归的主要原理

多重线性回归的主要原理

多重线性回归的主要原理多重线性回归是一种统计分析方法，用于研究多个自变量与一个因变量之间的关系。

该方法基于最小二乘法，在给定一组自变量的情况下，通过建立一个线性模型来估计因变量的值。

在多重线性回归中，变量可以分为两类：因变量和自变量。

因变量是我们希望预测或者解释的变量，而自变量是用来解释因变量的变量。

多重线性回归可以用以下方程表示：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中，Y表示因变量的值，X1、X2、...、Xn是自变量的值，β0、β1、β2、...、βn是对应的回归系数，ε是误差项。

回归系数表示自变量对因变量的影响程度，误差项表示模型无法解释的部分。

多重线性回归的主要原理是基于最小二乘法来求解回归系数。

最小二乘法的目标是最小化残差平方和，即找到一组回归系数，使得模型预测值与实际观测值之间的差异最小化。

具体而言，多重线性回归的求解过程可以分为以下几步：1. 数据准备：收集自变量和因变量的数据，并进行数据清洗和预处理，包括处理缺失值、异常值和离群值等。

2. 模型建立：根据问题背景和数据特点，确定多重线性回归模型的自变量和因变量，并设置回归方程。

3. 参数估计：使用最小二乘法对回归系数进行估计。

最小二乘法通过最小化实际观测值和模型预测值之间的残差平方和来确定回归系数。

具体计算方法是通过求解方程组来获取回归系数的值。

4. 模型拟合：将估计得到的回归系数代入回归方程，得到多重线性回归模型。

模型能够通过给定自变量值来预测因变量的值。

5. 模型评估：对多重线性回归模型进行评估，包括评价模型的拟合程度和回归系数的显著性等。

常用的指标有R方值、调整R方值和显著性检验等。

6. 模型应用：使用经过验证和评估的多重线性回归模型进行预测、推断和解释。

可以通过改变自变量的值来预测因变量的变化，并对因变量的影响进行解释。

多重线性回归有几个重要的假设前提需要满足。

首先，自变量和因变量之间应该存在线性关系。

11杨永利-多重线性回归与相关

11杨永利-多重线性回归与相关

一、多重线性回归模型拟合实例
【典型案例】
例17-5 为了研究影响肥胖者瘦素的主要危险因素， 某研究者调查了某医院肥胖门诊的500名肥胖就诊 者的瘦素、年龄、体重指数等因素，为了简化问题， 仅取自变量为年龄（X1，岁）、体重指数(X2， kg/m2)、总胆固醇(X3，mmol/L)、是否患糖尿病 （X4，患糖尿病为1，不患糖尿病为0）和是否患高 血压（X5，患高血压为1，不患高血压为0），应变 量为瘦素（Y，ng/ml）。为了说明的方便，这里仅 从500名肥胖就诊者中随机取30例，具体数据如表 17-11所示，分析肥胖者瘦素的主要影响因素。
ˆ y 0.175x1 0.513x2 0.116 x3 0.945x4 0.348x5 14.658
去掉无意义的变量
ˆ y 0.175x1 0.513x2 14.658
STEPWISE
决定系数越大，说明构建的回归方程越好。
STEPWISE
STEPWISE
先将贡献最大的变量进入方程，再将贡献次大的变量进 入方程……，直到所有有意义的变量都进入方程为止。
关于独立性的核查，可以通过计算 Durbin-Watson统计量来判断。该统计量 的取值一般在0-4之间，如果残差之间相 互独立，则取值在2左右，如果取值接近0 或4，则提示不满足独立性。
例17-5的模型假设诊断—正态性
提示残差满 足正态分布
如果残差不服从正态分布，可以对因变 量进行变量转换，如，取对数，使得因 变量近似服从正态分布。
Descriptives：提供一些变量描述，如有效例数、均数、标准差
等。
Collinearity diagnostics：给出一些用于共线性诊断的统计量，如
特征根（Eigenvalues）、方差膨胀因子(VIF)等。

多重线性回归分析.共155页文档

多重线性回归分析.共155页文档
。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
多重线性回归分析.
21、没有人陪你走一辈子，所以你要 适应孤 独，没 有人会 帮你一 辈子， 所以你 要奋斗 一生。 22、当眼泪流尽的时候，留下的应该 是坚强 。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之 首，因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿． 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ，它只 是让人 们的脚 放上一 段时间 ，以便 让别一 只脚能 够再往 上登。

第11章 多重线性回归精简

第11章 多重线性回归精简

2010-6-19
23
多重线性回归的小结
多重线性回归是简单线性回归的拓展，经常用 在筛选危险因素、控制混杂因素、分析交互作 用、预测与控制等。 基本步骤：单因素分析；逐步筛选变量；综合 单因素和多因素模型结果，当有矛盾时，结合 专业知识分析。
2010-6-19 24
1. 应用条件
（1）线性依存关系 应变量与自变量间具有线性依存 关系。 （2）正态性 应变量原则上是连续型可测正态变量， 其预测值与实际观测值的差值（即残差）服从正态 分布，当样本量较大时可以忽略正态性的要求。 （3）独立性 观察单位之间是独立的，即应变量的观 测值相互独立。
2010-6-19 27
思考与练习
1. 多重线性回归分析如何筛 选自变量？ 2.何谓共线性？它对资料分 析有何影响？ 3.如何评价方程的优劣？
？
2010-6-19
28
数据 设计方法
软件
SAS SPSS
？
结果
如何解释？
2010-6-19 29
2010-6-19
30
2010-6-19
9
矛盾出现了：对整体模型而言，获得R2＝0.9542 与整体F检验的概率为P＝0.0039的好结果；但 是，对于每一个偏回归系数而言，却没有一个偏 回归系数的效应具有统计学意义。 问题出在哪里？ 问题就出在X1，X2和X3存在共线性，以致回归系 数极不稳定，计算的结果并不是总体回归系数的 估计值，没有实际意义。
2010-6-19 13
对自变量较少的情况下可用逐步回归试一试？ 例3 按α=0.10水准，对上例8名学生数据进行肺活量
（Y）关于身高X1和体重X2与体重指数X3的逐步回归分 析。
2010-6-19
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、作业
教材P214 三。

二、自我练习
（一）教材P213 一。

（二）是非题
1．当一组资料的自变量为分类变量时，对这组资料不能做多重线性回归分析。

( )
2．若多重线性方程模型有意义．则各个偏回归系数也均有统计学意义。

〔)
3．回归模型变量的正确选择在根本上依赖于所研究问题本身的专业知识。

（）
4.从各自变量偏回归系数的大小．可以反映出各自变量对应变量单位变化贡献的大小。

( )
5.在多元回归中，若对某个自变量的值都增加一个常数，则相应的偏回归系数不变。

( )
（三）选择题
1. 多重线性回归分析中，共线性是指（），导致的某一自变量对Y的作用可以由其他自变量的线性函数表示。

A. 自变量相互之间存在高度相关关系
B. 因变量与各个自变量的相关系数相同
C. 因变量与自变量间有较高的复相关关系
D. 因变量与各个自变量之间的回归系数相同
2. 多重线性回归和Logistic 回归都可应用于（）。

A. 预测自变量
B. 预测因变量Y 取某个值的概率π
C. 预测风险函数h
D. 筛选影响因素（自变量）
3．在多重回归中，若对某个自变量的值都增加一个常数，则相应的偏回归系数：
A．不变
B．增加相同的常数
C．减少相同的常数
D．增加但数值不定
4．在多元回归中，若对某个自变量的值都乘以一个相同的常数k，则：
A．该偏回归系数不变
B．该偏回归系数变为原来的 1/k倍
C．所有偏回归系数均发生改变
D．该偏回归系数改变，但数值不定
5．作多重线性回归分析时，若降低进入的F 界值，则进入方程的变量一般会：
A．增多 B．减少 C．不变 D．可增多也可减少（四）筒答题
1.为什么要做多重线性回归分析？
2.多重线性模型中，标准化偏回归系数的解释意义是什么？
3.简述确定系数的定义及意义。

4.多重线性回归中自变量的筛选共有哪几种方法．请比较它们的优缺点？
5.何谓多重共线性，多重共线性对资料分析有何影响?。