201x版九年级数学上学期第三次周考试题

2019-2020年九年级9月第三周周考数学试题强春霞审题：聂晓岐一、选择题（每题6分，共30分）1、如右图,一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖,击中黑色区域的概率是 ( )A、 B、 C、 D、2、在一个不透明的口袋中装有除颜色外其余都相同的3个小球，其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后，记下颜色，再把它放回去。

摇匀后，第二次再从袋中摸出一个，那么两次都摸到黄色球的概率是（）A 、 B、 C、 D 、3、两个正四面体骰子的各面上分别标明数字1,2,3,4，如同时投掷这两个正四面体骰子，则着地的面所得的点数之和等于5的概率为（）A、 B、 C、 D、4、从—2，-1,2这三个数中任取两个不同的数作为点的坐标，该点在第四象限的概率是（）A 、 B、 C、 D、5、已知是方程的两个根，则的值为（）A 、 B、 2 C、 -2 D、二、填空题（每题6分，共30分）6、已知关于x的方程是一元二次方程,则m的值为：________。

7、在实数范围内定义一种运算“﹡”，其规则为a﹡b=a2-b2,根据这个规则，方程(x+2) ﹡5=0的解为。

8、小丽要在一幅长为80cm，宽为50cm的矩形风景画的四周外围镶上一条宽度相同的金色纸边制成一幅矩形挂图，使整幅挂图面积是5400cm2，设金色纸边的宽度为x cm，则x= 。

9、从1,2，—3，—4四个数中，随机抽取两个数相乘，积是正数的概率是10、一口袋中放有黑白两种颜色的球，其中黑色球6个和白色球若干，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共实验50次，其中有45次摸到白球，由此可估算其中白球有个。

西安远东一中初三年级数学第3周周考答题卡班级：姓名：总分：一、选择题（每小题6分，共30分）二、填空题（每题6分，共30分）．6、；7、；8、；9、 10、。

三、解答题 (每小题20分,共40分)11．某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，求该公司5, 6两个月营业额的月均增长率。

一、选择题（每题5分，共50分）1. 下列选项中，不是有理数的是（）A. 2.5B. -3C. $\sqrt{2}$D. $\frac{1}{3}$2. 已知 $a > b$，则下列不等式中正确的是（）A. $a^2 > b^2$B. $a + 1 > b + 1$C. $a - b < 0$D. $ab > 0$3. 下列函数中，是奇函数的是（）A. $f(x) = x^2$B. $f(x) = |x|$C. $f(x) = x^3$D. $f(x) = x^4$4. 若 $\sin A = \frac{1}{2}$，则 $A$ 的取值范围是（）A. $0 < A < \frac{\pi}{2}$B. $0 < A < \pi$C. $-\frac{\pi}{2} < A < \frac{\pi}{2}$D. $-\frac{\pi}{2} < A < \frac{3\pi}{2}$5. 下列等式中，正确的是（）A. $(a + b)^2 = a^2 + 2ab + b^2$B. $(a - b)^2 = a^2 - 2ab + b^2$C. $(a + b)^2 = a^2 - 2ab + b^2$D. $(a - b)^2 = a^2 + 2ab - b^2$6. 已知 $x^2 - 5x + 6 = 0$，则 $x$ 的值为（）A. 2 或 3B. 1 或 4C. 2 或 4D. 1 或 37. 下列图形中，是圆的是（）A. 正方形B. 等边三角形C. 梯形D. 圆形8. 若 $a^2 + b^2 = 25$，$a - b = 3$，则 $ab$ 的值为（）A. 4B. 6C. 8D. 109. 下列选项中，不是一次函数的是（）A. $y = 2x + 3$B. $y = -\frac{1}{2}x + 4$C. $y = \sqrt{x}$D. $y = 3$10. 若 $x + y = 5$，$x - y = 1$，则 $x$ 和 $y$ 的值分别是（）A. $x = 3, y = 2$B. $x = 2, y = 3$C. $x = 4, y = 1$D. $x = 1, y = 4$二、填空题（每题5分，共50分）11. $\frac{2}{3} - \frac{1}{4} = \frac{5}{12}$12. $(-2)^3 = -8$13. $x^2 - 5x + 6 = (x - 2)(x - 3)$14. $\sin 45^\circ = \frac{\sqrt{2}}{2}$15. $2^3 \times 3^2 = 72$16. $a^2 - b^2 = (a + b)(a - b)$17. $y = 2x - 3$ 的斜率为218. $x^2 + 2x + 1 = (x + 1)^2$19. 圆的面积公式为 $S = \pi r^2$20. 一元二次方程的解法有公式法和因式分解法三、解答题（每题10分，共30分）21. 解方程 $3x - 2 = 5$。

九年级上册第三次周清数学试卷(2)班级：________ 姓名：_________ 分数：_______一、单选题1．将抛物线21y x =-的图象先向左平移1个单位，再向上平移2个单位，得到的抛物线的解析式是（ ）A ．222=++y x xB ．222y x x =+-C ．()211y x =-+ D ．()213y x =-- 2．关于二次函数 ()231y x =--，以下说法错误的是（ ） A ．开口向上 B ．对称轴为直线3x =-C ．有最小值1-D ．与y 轴交点为()0,83．若二次函数2y ax =的图象经过()2,4P -，则该图象必经过点（ ） A ．()2,4 B ．()2,4-- C ．()4,2-- D ．()4,2- 4．已知二次函数2y ax bx c =++的图象如图所示，则点(),P c b 所在的象限是（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限5．已知点()13,A y -，()21,B y -，()32,C y 在函数22y x x b =--+的图象上，则1y 、2y 、3y 的大小关系为（ ）A ．132y y y <<B ．312y y y <<C ．321y y y <<D ．213y y y <<二、填空题6．将抛物线y=2x ²-4x+5向右平移2个单位长度，再向上平移3个单位长度，得到抛物线的解析式是 ．7．已知一元二次方程20ax bx c ++=有两个实数根11x =-，23x =，则二次函数2y ax bx c =++的对称轴是直线 ．8．抛物线2241y x x =--+的对称轴为直线 ．9．已知二次函数222y x x -=-+中，当14x -≤≤时，y 的最小值是 ． 10．用配方法将二次函数2=23y x x --化为()2y a x h k =-+的形式为 ．三、解答题11．已知二次函数243y x x =-+．(1)在所给的平面直角坐标系中画出它的图象；(2)0y >时，x 的取值范围是______；(3)若14x -<<，则y 的取值范围是______；(4)把所画的图象如何平移，可以得到函数2y x 的图象？请写出一种平移方案．12. 已知()()221315m m y m x m x +-=++--是y 关于x 的二次函数，求m 的值．13．已知抛物线的顶点坐标是(3,2)，且经过点(1,2)-．(1)求这条抛物线的解析式；(2)若点()()12,,,A m y B n y 都在该抛物线上，且3m n <<，则1y ____2y （填“>” “=”或“<”）．14．如图，已知抛物线21y x mx =-++经过点(1,4)．(1)求m 的值及此抛物线的顶点坐标．(2)试判断点()1,4P --是否在此函数图象上．15．已知二次函数23y ax bx =+-的图象经过点()1,4-和()1,0-．(1)求这个二次函数的表达式：(2)该函数有最大值还是有最小值？求出这个最值．16．已知函数()214y x =--+．(1)当x =____________时，抛物线有最大值，是____________．(2)当x ____________时，y 随x 的增大而增大．(3)该函数可以由函数2y x =-的图象经过怎样的平移得到？(4)该抛物线与x 轴交于点____________，与y 轴交于点____________．（写坐标）。

九年级数学综合测试卷（本试卷满分：100分，时间：100分钟）一、选择题（本大题共6小题，每小题３分，共18分每小题只有一个正确选项。

） 1.图中几何体的主视图是（ ）2．反比例函数y ＝kx的图象如图所示，则k 最有可能的值是（ ）14. 在同一坐标系中，反比例函数y =kx和一次函数y =kx +k 的图象大致是（ ）5.高4米的旗杆在水平地面上的影长5米,此时测得附近一个建筑物的影子长20米,则该建筑物的高是 ( )A ．16米B ．20米C ．24米D ．30米6．在同一直角坐标系中，若正比例函数y ＝2x 的图象与反比例函数y ＝42k+的图象没有交点，则实数k 的取值范围在数轴上表示为（ ）二、填空题（本大题共8个小题，每小题３分，共24分）7．九（1）班小丽、小华所在的数学兴趣小组有8个同学，小丽发现她和小华生日都在同一个月，于是小丽得出结论：8个人中有2个人生日在同一个月的概率 是1．小丽的判断 ．（填“对”与“错”） 8．如图,在□ABCD 中,AB ＝4cm , BC ＝7cm , ∠ABC 的平分线交AD 于点E , 交CD 于点F , 则DF ＝ cm .9．准备两张大小一样，分别画有不同图案的正方形纸片，把每张纸都对折、剪开，将四张纸片放在盒子里，然后混合，随意抽出两张正好能拼成原图的概率是 ． 10．如果点P 1（－1，y 1），P 2（1，y 2）和P 3（2，y 3）都在反比例函数1y x=-的图象上，那么y 1、y 2、y 3的大小关系为 ．11．某校有一个两层楼的餐厅，甲、乙、丙三名学生各自随机 选择其中的某个楼层的餐厅用餐，则甲、乙、丙三名学生在同 一个楼层餐厅用餐的概率为 ．12．如图,四边形ABCD 是一个等腰梯形,请直接在图中仅用直尺,准确地画出它的对称轴l ．， 15．电线杆上有一盏路灯O ，电线杆与三个等高的标杆整齐划一地排列在马路的一侧，AB 、CD 、EF 是三个标杆，相邻的两个标杆之间的距离都是2 m ， 已知AB 、CD 在灯光下的影长分别为BM ＝1. 6 m ，DN ＝0. 6m . （1）请画出路灯O 的位置和标杆EF 在路灯灯光下的影子。

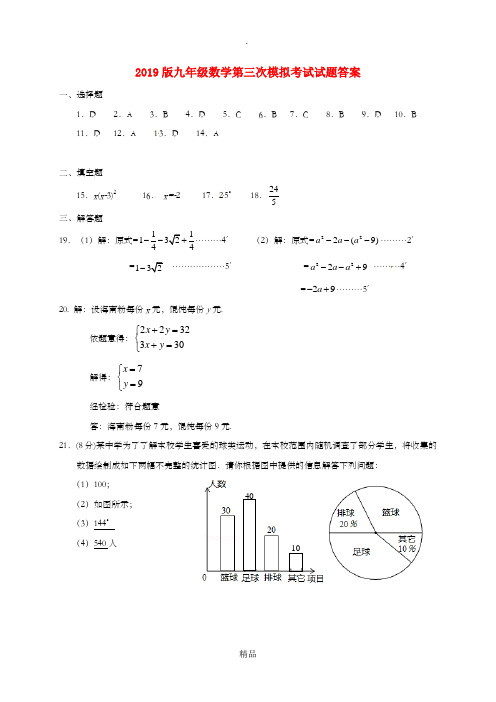
2019版九年级数学第三次模拟考试试题答案一、选择题1．D 2．A 3．B 4．D 5．C 6．B 7．C 8．B 9．D 10．B 11．D 12．A 13．D 14．A二、填空题15．x (x-3)2 16． x=-2 17．25° 18．245三、解答题19．（1）解：原式=1113244--+………4′ （2）解：原式=222(9)a a a ---………2′ =132- ………………5′ =2229a a a --+ ………4′=29a -+………5′20. 解：设海南粉每份x 元，馄饨每份y 元. 依题意得：2232330x y x y +=⎧⎨+=⎩解得：79x y =⎧⎨=⎩经检验：符合题意答：海南粉每份7元，馄饨每份9元.21．(8分)某中学为了了解本校学生喜爱的球类运动，在本校范围内随机调查了部分学生，将收集的数据绘制成如下两幅不完整的统计图．请你根据图中提供的信息解答下列问题： （1）100； （2）如图所示； （3）144° （4）540人401022.解：由题意可知：AB=500千米，∠ABC=40°过A点作AD⊥BC于点D，在Rt△ABD中，AD=AB·sin∠ABC=500×0.6428=321.4千米∵321.4>300∴三亚市不受这次台风的影响。

23.（1）证明；∵在矩形ABCD中，∠DCE=90°，F是斜边DE的中点，∴CF=DE=EF，∴∠FEC=∠FCE，∵∠BFC=90°，E为BC中点，∴EF=EC，∴CF=CE，在△BCF和△DEC 中，，∴△BCF≌△DEC（ASA）；（2）解：设CE=a，由BE=2CE，得：BE=2a，BC=3a，∵CF是Rt△DCE斜边上的中线，∴CF=DE，∵∠FEC=∠FCE，∠BFC=∠DCE=90°，∴△BCF∽△DEC，∴=，即：=，解得：ED2=6a2，由勾股定理得：DC===a，东南A（三亚）北西BC60°20°图8∴==；（3）解：过C′作C′H⊥AF于点H，连接CC′交EF于M，如图所示：∵CF是Rt△DCE斜边上的中线，∴FC=FE=FD，∴∠FEC=∠FCE，∵四边形ABCD是矩形，∴AD∥BC，AD=BC，∴∠ADF=∠CEF，∴∠ADF=∠BCF，在△ADF和△BCF中，，∴△ADF≌△BCF（SAS），∴∠AFD=∠BFC=90°，∵CH⊥AF，C′C⊥EF，∠HFE=∠C′HF=∠C′MF=90°，∴四边形C′MFH是矩形，∴FM=C′H=，设EM=x，则FC=FE=x+，在Rt△EMC和Rt△FMC中，由勾股定理得：CE2﹣EM2=CF2﹣FM2，∴12﹣x2=（x+）2﹣（）2，解得：x=，或x=﹣（舍去），∴EM=，FC=FE=+；由（2）得：，把CE=1，BE=n代入计算得：CF=，∴，解得：n=424．解：（1）∵抛物线与x 轴交于A （-1，0）、B （4，0）两点∴设抛物线的解析式为y =a （x +1）（x -4） ………………1′ 又∵抛物线与y 轴交于点C （0，3） ∴3=-4a解得：a=34-………………2′ ∴抛物线的解析式为3(1)(4)4y x x =-+-即：239344y x x =-++………………3′（2）当y=3时，120,3x x ==，∴D （3，3）由题意可知：在Rt △BCO 中：225BC OB OC =+=CP=t ，CP=52t ，则DP=3-t ， P （t ，3），Q （2t ，3-32t ），113()(3)222DPQ p q S PD y y t t =⋅-=-⋅配方得：23327()4216DPQ S t =--+∴当32t =时，DPQ S 有最大值2716（3）∵P （t ，3），Q （2t ，3-32t ），D （3，3）∴DP=3-t ，223()2PQ t t =+223(23)()2DQ t t =-+ ABCDPOQ图10ⅰ）以P 为顶角顶点时，PQ=PD3t =-解得： 143t --=(不符合题意舍去) 243t -+= ⅱ）以Q 为顶角顶点时， DQ = PQ即：=解得：31t =，43t =(不符合题意舍去)， ⅲ）以D 为顶角顶点时，DQ =D P即：3t =-解得：50t =(不符合题意舍去)， 687t =综上所述：当1t =或87t =或t =时，△DPQ 为等腰三角形 如有侵权请联系告知删除，感谢你们的配合！。

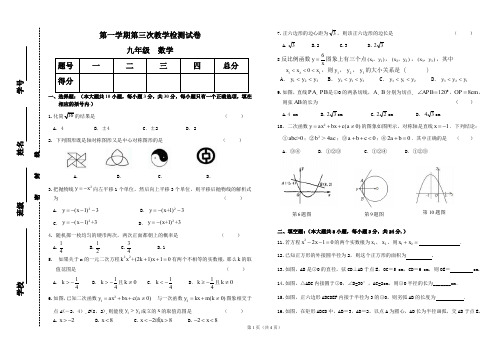
第一学期第三次教学检测试卷九年级 数学相应的括号内.） 1. （ ） A ．4 B ．±4 C ．±2 D ．2 2. 下列图形既是轴对称图形又是中心对称图形的是 （ ）A. B ． C ． D ．3.把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为 （ ） A ．2(1)3y x =--- B ．2(+1)3y x =-- C ．2(1)+3y x =-- D ．2(+1)+3y x =-5. 如果关于x 的一元二次方程+(21)10k x k x ++=有两个不相等的实数根，那么k 的取值范围是 （ ） A ．41->k B ．41->k 且0≠k C ．41-<k D ．41-≥k 且0≠k 6.如图，已知二次函数21(0)y ax bx c a=++≠ 与一次函数2(0)y kx m k =+≠图象相交于点A (－2，4）,B (8，2),则能使12y y >成立的x 的取值范围是 （ ）A.2x >- B.8x < C.28x x <->或 D.28x -<<7.正六边形的边心距为3，则该正六边形的边长是（ ）A.3B.2C.3D.328反比例函数xy 6=图象上有三个点)(11y x ，，)(22y x ，，)(33y x ，，其中3210x x x <<<，则1y ，2y ，3y 的大小关系是 ( )A ．321y y y <<B ．312y y y <<C ．213y y y <<D ．123y y y <<9.如图，直线PA ,PB 是⊙O 的两条切线，A ,B 分别为切点,120=∠APB ，cm OP 8=，则弦AB 的长为 ( ) A.4 cm B.32cm C.22cm D. 34cm10. 二次函数2(0)y ax bx c a =++≠的图象如图所示，对称轴是直线1x =-．下列结论：①c>0ab ；②2b ＞ac 4；③0<++c b a ；④02=+b a ．其中正确的是 （ ）A ．③④B ．①②③C ．①②④D ．①②③二、填空题:（本大题共8小题，每小题3分，共24分.）12.已知正方形的外接圆半径为2，则这个正方形的面积为 .13.如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，OC ＝5 cm ，CD ＝6 cm ，则OE ＝ cm. 14.如图，△ABC 内接圆于⊙O ，∠B=30°，AC=2cm ，则⊙O 半径的长为_______cm ． 15.如图，正六边形ABCDEF 内接于半径为3的⊙O ，则劣弧AB 的长度为 ． 16.如图，在矩形ABCD 中，AB ＝3，AD ＝2，以点A 为圆心，AD 长为半径画弧，交AB 于点E ， 第6题图 第9题图第10题图图中阴影部分的面积是 ．(结果保留π)17.在比例尺为1︰20000的地图上测得AB 两地间的图上距离为6cm ，则AB 两地间的实际距离为 ___________________m18.若双曲线y=(2m-1)22m x- 的图象在第一、三象限，则此函数的解析式为 .三、解答题(一):（本大题共5小题,共26分.解答应写出必要的文字说明、证明过程或演算步骤.）19.（4分）计算：(4－π)0＋|－2|－16×4－1＋12÷3；20.（4分)如图，在图中求作⊙P ，使⊙P 满足以线段MN 为弦且圆心P 到∠AOB 两边的距离相等．（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）21.(6分近视眼镜的度数y （度）与镜片焦距x （m ）成反比例．已知200度近视眼镜镜片的焦距为0.5m 。

外国语2021届九年级数学上学期第三次周考试题一、选择:〔每一小题6分，一共36分〕1．抛物线y=2〔x+3〕2+1的顶点坐标是〔〕A．〔3，1〕 B．〔3，﹣1〕C．〔﹣3，1〕D．〔﹣3，﹣1〕2．二次函数与y=kx2﹣8x+8的图象与x轴有交点，那么k的取值范围是〔〕A．k＜2 B．k＜2且k≠0 C．k≤2 D．k≤2且k≠03．假设(2，5)，(4，5)是抛物线y＝ax2＋bx＋c上的两个点，那么它的对称轴是( ) A．x＝1 B．x＝2 C．x＝3 D．x＝44.如图，在平面直角坐标系中，抛物线所表示的函数解析式为，那么以下结论正确的选项是〔〕A. B.＜0，＞0C.＜0，＜0D.＞0，＜04题图第5题图5．如图，抛物线y＝x2＋bx＋c与x轴交于点A，B，与y轴交于点C，∠OBC＝45°，那么以下各式成立的是( )A．b－c－1＝0 B．b＋c＋1＝0C．b－c＋1＝0 D．b＋c－1＝06．二次函数y＝ax2＋bx＋c(其中a>0，b>0，c<0)，关于这个二次函数的图象有如下说法：①图象的开口向上；②图象的顶点一定在第四象限；③图象与x轴的交点有一个在y轴的右侧．以上正确的说法的个数是( )A．0个 B．1个 C．2个 D．3个二填空〔每一小题6分，一共36分〕1.二次函数y ＝(k ＋1)x 2的图象如图，那么k 的取值范围为_____2．抛物线y ＝2x 2－4x ＋3绕坐标原点旋转180°所得的抛物线的表达式是 3.隧道的截面是抛物线形，且抛物线的解析式为y ＝－18x 2＋，一辆车高3 m ，宽4 m ，该车__ __ _通过该隧道．(填“能〞或者“不能〞)4.二次函数y=x 2-3x+2的图像与x 轴的交点坐标是 ,与y 轴的交点坐标为5．抛物线y ＝x 2－x －1与x 轴的交点为(m,0)，那么代数式m 2－m ＋2 011的值是__________．6. y ＝x 2-2x-2，假设，那么y 的取值范围是三简答题1．〔此题14分〕二次函数y=﹣x 2+2x+m ．〔1〕如图，二次函数的图象过点A 〔3，0〕，与y 轴交于点B ，直线AB 与这个二次函数图象的对称轴交于点P ，求点P 的坐标．〔2〕根据图象直接写出使一次函数值大于二次函数值的x 的取值范围．2.〔此题14分〕 杂技团进展杂技表演，演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处，其身体(看成一个点)的道路是抛物线y ＝－35x 2＋3x ＋1的一局部，如图 (1)求演员弹跳离地面的最大高度；(2)人梯高BC ＝米，在一次表演中，人梯到起跳点A 的程度间隔 是4米，问这次表演是否成功？说明理由．励志赠言经典语录精选句；挥动**，放飞梦想。

綦江长寿巴南三校联盟2021届九年级数学上学期第三次联考试题制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日〔考试时间是是：120分钟 总分：150分〕一、选择题：〔本大题12个小题，每一小题4分，一共48分〕在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个答案是正确的。

1. 抛物线4)3(2++-=x y 顶点坐标是〔 〕A. (3，4)B. (﹣3，4)C. (3，﹣4)D. (2，4) 2．下面的图形中既是轴对称图形又是中心对称图形的是〔 〕A ．B ．C ．D ．3. 一元二次方程0662=-+x x 配方后化为〔 〕A. 3)3(2=-xB. 15)3(2=-xC. 15)3(2=+xD. 3)3(2=+x 4. 如图，△ABC 是⊙O 的内接三角形，AC 是⊙O 的直径，∠C=50°，∠ABC 的平分线BD 交⊙O 于点D ，那么∠BAD 的度数是( )A ．45°B ．85°C ．90°D ．95°5. 假设关于x 的方程02)1(2)1(2=-++++k x k x k 有两个实数根，那么k 的取值范围在数轴上表示正确的选项是〔 〕 A.B.C.D.6. 一个布袋里装有6个只有颜色不同的球，其中2个红球，4个白球。

从布袋里任意摸出1个球，那么摸出的球是白球的概率为 ( )第4题图231-1O y xA ．21B ．51 C ．31D ．327. 抛物线)0(2>=a ax y 过A ),2(1y 、B ),1(2y -两点，那么以下关系式一定正确的选项是〔 〕A. 210y y >>B. 120y y >>C. 021>>y yD. 012>>y y 8. 如图，小明用如图的胶滚沿从左到右的方向将图案滚涂到墙上，以下给出的四个图形中，符合胶滚滚出的图案是〔 〕A. B. C. D.9. 某校进展体操队列训练，原有8行10列，后增加40人，使得队伍增加的行数、列数一样，你知道增加了多少行或者多少列吗？设增加了x 行或者列，那么列方程得〔 〕 A. (8﹣x) (10﹣x)=8×10﹣40 B. (8﹣x)(10﹣x)=8×10+40 C. (8+x)(10+x)=8×10﹣40 D. (8+x)(10+x)=8×10+40 10. 如图是二次函数)0(2≠++=a c bx ax y 的局部图象，那么不等式02>++c bx ax 的解集是〔 〕A. -1＜x ＜5B. x ＞5C. x ＜-1且x ＞5D. x ＜-1或者x ＞5 11. 在同一坐标系中一次函数y=ax-b 和二次函数bx ax y +=2的图象可能为〔 〕A. B. C. D.12. c bx ax y ++=2的图象如下图，其对称轴为直线x=-1，与x 轴的一个交点为〔1，0〕，与y 轴的交点在〔0，2〕与〔0，3〕之间〔不包含端点〕，那么以下结论正确的选项是〔 〕 A ．2a+b=0 B ． 3a+2c ＜0 C ． a+5b+2c ＞0 D ．321-<<-a第18题图第17题图第14题图二、填空题：〔本大题6个小题，每一小题4分，一共24分〕请将每个小题之答案直接填在答题卡〔卷〕．．．．．．中对应的标线上。

阜宁县实验初级中学2021届九年级数学上学期第三次阶段考试试题一、选择题〔本大题一一共8小题，每一小题3分，一共24分，在每一小题给出的四个选项里面，只有一个选项是正确的，请把答案写在答题纸相应的位置〕 1．数据﹣1，0，1，2，3的平均数是〔 ▲ 〕 A ．﹣1B ． 0C ． 1D ． 52．假设方程022=+-m x x 有两个不相等的实数根，那么m 的取值范围是〔 ▲ 〕 A ．1>mB ．1<mC.．1≤m D ．1≥m3．二次函数y =2〔x ﹣1〕2+3的图象的顶点坐标是〔 ▲ 〕 A ．〔1，3〕 B ．〔﹣1，3〕C ．〔1，﹣3〕D ．〔﹣1，﹣3〕4．假设⊙O 的半径为5cm ，点A 到圆心O 的间隔 为4cm ，那么点A 与⊙O 的位置关系〔 ▲ 〕A 在圆外 AA 在圆内5．盒子中装有2个红球和4个绿球,每个球除颜色外完全一样,从盒子中任意摸出一个球,是绿球的概率是〔 ▲ 〕A ．41B.31C.21 D.32 6．在二次函数y =-x 2+2x +1的图象中，假设y 随x 的增大而增大，那么x 的范围是〔 ▲ 〕 A. x<1B. x>1C. x<－1D. x>－1 7．如图，AB 为⊙O 的直径，点C 在⊙O 上,∠A =40°, 那么∠B 的度数为〔 ▲ 〕A ．20° B. 40° C. 60° D. 50°8．如图，是二次函数 y ＝ax 2＋bx ＋c 〔a ≠0〕的图像的一局部，给出 以下命题 ：①abc ＜0②b =2a ；③当-3<x<1时，ax 2+bx +c ＜0；CABO④)1)((-≠+<-m b am m b a ．其中正确的命题有〔 ▲ 〕 A ．1个 B.2个 C. 3个二、填空题〔本大题一一共10小题，每一小题3分，一共30分，把答案填写上在答题纸相应位置上〕9．当x = ▲ 时，二次函数x x y 22-=有最小值． 10．一元二次方程24x =x 的解是 ▲ ．11．母线长为2cm ，底面圆的半径为1cm 的圆锥的侧面积是 ▲ cm 2． 12．数据1，2，3，4，5的方差是 ▲ ．13．小红、小芳、小明在一起做游戏时需要确定做游戏的先后顺序，他们约定用“锤子、剪刀、布〞的方式确定.请问在一个回合中三个人都出“布〞的概率是 ▲ ． 14．三角形的三边分别为3cm 、4cm 、5cm ，那么这个三角形内切圆的半径是 ▲ ． 15．假如二次函数y=〔2k －1〕x 2－3x+1的图象开口向上，那么常数k 的取值范围是 ▲ ． 16．一只自由飞行的小鸟，将随意地落在如下图的方格地面上，每个小方格形状完全一样， 那么小鸟落在阴影方格地面上的概率是 ▲ ．17．如图，在坐标系中，二次函数y=ax 2+c 〔a≠0〕的图象过正方形ABOC•的三个顶点A ，B ，C ，那么ac 的值是 ▲ ．18．如图．Rt△ABC 内接于⊙O，BC 为直径， AB=4，AC=3, D 是AB 的中点，CD 与AB ． 的交点为E ，那么CEDE等于 ▲ ．三、解答题〔本大题一一共10题，10+9+9+9+9+9+9+10+11+11=96分，解容许写出必要的计算过程、推演步骤或者文字说明〕19．平行四边形ABCD 的两边AB 、AD 的长是关于x 的方程04122=-+-m mx x 的两个实数根. 〔1〕当m 为何值时，四边形ABCD 是菱形？求出这时菱形的边长； 〔2〕假设AB 的长为2，那么平行四边形的周长是多少20．二次函数223y x x =-++． 〔1〕求抛物线顶点M 的坐标；〔2〕设抛物线与x 轴交于A ，B 两点，与y 轴交于C 点，求A ，B ， C 的坐标〔点A 在点B 的左侧〕，并画出函数图象的大致示意图； 〔3〕根据图象，写出不等式2230x x -->的解集21．地震牵动着全国人民的心，某单位开展了“一方有难，八方支援〞赈灾捐款活动.第一天收到捐款10000元，第三天收到捐款12100元.〔1〕假如第二天、第三天收到捐款的增长率一样，求捐款增长率； 〔2〕按照〔1〕中收到捐款的增长速度，第四天该单位能收到多少捐款？22．如图，AB是⊙O的弦，OP⊥ OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．〔1〕求证：BC是⊙ O的切线；〔2〕假设⊙ O的半径为11,OP=1，求OC的长．23．某校为理解2021年八年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如下的表格，并绘制成如下图的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%．类别科普类教辅类文艺类其他册数〔本〕128 80 m 48〔1〕求表格中字母m的值及扇形统计图中“教辅类〞所对应的圆心角a的度数；〔2〕该校2021年八年级有500名学生，请你估计该年级学生一共借阅教辅类书籍约多少本？524．如图,在半径为、圆心角为45 º的扇形AOB内部作一个正方形CDEF，使点C在OA 上，点D、E在OB上，点F在AB上．〔1〕求正方形CDEF的边长；〔2〕求阴影局部的面积25．如下图，可以自由转动的转盘被3等分，指针落在每个扇形内的时机均等． 〔1〕现随机转动转盘一次，停顿后，指针指向数字1的概率为 ； 〔2〕小明和小华利用这个转盘做游戏，假设采用以下游戏规那么，你认为对双方公平吗？请用列表或者画树状图的方法说明理由．26．如图，半径为4的⊙O 与直线l 相切于点A ，点P 是直径AB 左侧半圆上的动点，过点P 作直线l 的垂线，垂足为C ，PC 与⊙O 交于点D ，连接PA 、PB ，设PC 的长为)84(<<x x . ⑴当5x =时，求弦PA 、PB 的长度；⑵当x 为何值时，CD PD ⋅的值最大？最大值是多少？27．某数学活动小组在一次活动中，对一个数学问题作如下探究：【问题发现】如图1，正方形ABCD 的四个顶点都在⊙O 上，假设点E 在弧AB 上，F 是DE 上的一点，且DF=BE ．试说明：△ADF≌△ABE；【变式探究】如图2，假设点E 在弧AD 上，过点A 作AM⊥BE，请说明线段BE 、DE 、AM 之间lPD CBOA满足等量关系：BE﹣DE=2AM；【解决问题】如图3，在正方形ABCD中，CD=2，假设点P满足PD=2，且∠BPD=90°，请直接写出点A到BP的间隔．28．如图，二次函数y=x2+bx+4与x轴交于点B〔4，0〕，与y轴交于点A，O为坐标原点，P 是二次函数y=x2+bx+4的图象上一个动点，点P的横坐标是m，且m＞4，过点P作PM⊥x轴，PM交直线AB于M．〔1〕求二次函数的解析式；〔2〕假设以AB为直径的⊙N恰好与直线PM相切，求此时点P的坐标；〔3〕在点P的运动过程中，△APM能否为等腰三角形？假设能，求出点M的坐标；假设不能,请说明理由．励志赠言经典语录精选句；挥动**，放飞梦想。

大池中学2021届九年级数学上学期第三次阶段考试试题时间是：100分钟 满分是：100分一. 选择题〔每一小题3分，一共30分〕1．在△ABC 中，∠C ＝90°，sinA ＝45，那么tanB ＝〔 〕 A ．43 B ．34 C ．35 D ．45y =x 2的图象向左平移2个单位，得到新的图象的二次函数表达式是〔 〕.A ．22y x =+ B ．2(2)y x =+ C ．2(2)y x =- D ．22y x =-x y 2=的图象与双曲线)0(≠=k xky 相交，那么当0x ＜ 时，该交点位于〔 〕 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限4.在围棋盒中有x 颗白色棋子和y 颗黑色棋子,从盒中随机取出一颗棋子,获得白色棋子的概率是2,如再往盒中放进3颗黑色棋子,获得白色棋子的概率变为14,那么原来盒里有白色棋子 〔 〕 颗颗颗颗5.抛物线221y x x =++的顶点坐标是〔 〕A. (0,-1)B. (-1,1)C. (-1,0)D.(1,0)6．如图，⊙O 的直径AB 的长为10，弦AC 长为6， ∠ACB 的平分线交⊙O 于D ，那么CD 长为〔 〕A. 7B. 72 第6题图C. 82D. 97. 抛物线c bx ax y ++=2图像如下图，那么一次函数24b ac bx y +--=与反比例函数a b c y x++=在同一坐标系内的图像大致为〔 〕.第7题图8．如图，⊙O 的半径为2，点A 的坐标为〔2，32〕，直线AB 为⊙O 的切线，B 为切点．那么B 点的坐标为〔 〕.A ． ⎪⎪⎭⎫⎝⎛-5823, B ． ()13,- C ． ⎪⎭⎫⎝⎛-5954, D ． ()31,-第8题图9．如图，边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D '''，那么它们的公一共局部的面积等于〔 〕.A．1 B．1-．12 D10．如图，梯形ABCO 的底边AO 在x 轴上，BC ∥AO ，AB ⊥AO ，过点C 的双曲线ky x= 交OB 于D ，且OD ：DB=1 ：2，假设△OBC 的面积等于3，那么k 的值 等于〔 〕A ． 2B ． 34C ． 245D ．无法确定 二、填空题〔每一小题3分，一共24分〕11．函数y =的自变量x 的取值范围是___________. 12．实数y x y x x y x +=-++则满足,033,2的最大值为 .C13．假设一个圆锥的侧面积是18π，侧面展开图是半圆，那么该圆锥的底面圆半径是___________．14．如图，ABC ∆内接于O ，90,B AB BC ∠==，D 是O 上与点B 关于圆心O 成中心对称的点，P 是BC 边上一点，连结AD DC AP 、、．8AB =， 2CP =，Q 是线段AP 上一动点，连结BQ 并延长交四边形ABCD 的一边于点R ，且满足AP BR =，那么BQQR的值是_______________． 第14题图15．有一个正十二面体，12个面上分别写有1~12这12个整数，投掷这个正十二面体一次，向上一面的数字是3的倍数或者4的倍数的概率是 ．16．如图，矩形ABCD 中，3AB =cm ，6AD =cm ，点E 为AB 边上的任意一点，四边形EFGB 也是矩形，且2EF =，那么AFC S =△ 2cm ．17. 如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD = 2，将腰CD 以D 为中心逆时针旋转90°至DE ，连接AE 、CE ，△ADE 的面积为3，那么BC 的长为 ．A DCEFGB第16题图第15题图18. 如图，扇形OAB ，∠AOB=90︒，⊙P 与OA 、OB 分别相切于点F 、E ，并且与弧AB 切于点C ，那么扇形OAB 的面积与⊙P 的面积比是 ．三、解答题:〔46分〕 19.〔1〕计算〔3分〕： (638)2〔2〕解方程〔3分〕：222(1)160x x x x +++-=．第17题图第18题图20．〔6分〕某中学数学兴趣小组在开展“保护环境，保护树木〞的活动中，利用课外时间是测量一棵古树的高，由于树的周围有水池，同学们在低于树基米的一平坝内(如图11)．测得树顶A的仰角∠ACB=60°，沿直线BC后退6米到点D，又测得树顶A的仰角∠ADB=45°．假设测角仪DE高米，求这棵树的高AM．(结果保存两位小数，3≈1.732)第20题图21. (9分) 如图，△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E，连结OE，CD=3，∠ACB=30°.〔1〕求证：DE是⊙O的切线；〔2〕分别求AB，OE的长；A Array22. 〔6分〕在毕业晚会上，同学们表演哪一类型的节目由自己摸球来决定.在一个不透明的口袋中，装有除标号外其它完全一样的A、B、C三个小球，表演节目前，先从袋中摸球一次〔摸球后又放回袋中〕，假如摸到的是A球，那么表演唱歌；假如摸到的是B球，那么表演跳舞；假如摸到的是C球，那么表演朗读.假设小明要表演两个节目，那么他表演的节目不是同一类型的概率是多少？23．〔9分〕如图，抛物线y = ax 2+ bx + 4与x 轴的两个交点分别为A 〔－4，0〕、B 〔2，0〕，与y 轴交于点C ，顶点为D ．E 〔1，2〕为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ．〔1〕求抛物线的函数解析式，并写出顶点D 的坐标；〔2〕假设点K 在x 轴上方的抛物线上运动，当K 运动到什么位置时，△EFK 的面积最大？并求出最大面积．24．〔10分〕如图，⊙O 的半径为1，点P 是⊙O 上一点，弦AB 垂直平分线段OP ，点D 是APB 上任一点〔与端点A 、B 不重合〕，DE ⊥AB 于点E ，以点D 为圆心、DE 长为半径作⊙D ，分别过点A 、B 作⊙D 的切线，两条切线相交于点C ． 〔1〕求弦AB 的长；〔2〕判断∠ACB 是否为定值，假设是，求出∠ACB 的大小；否那么，请说明理由； 〔3〕记△ABC 的面积为S ，假设2SDE ＝，求△ABC 的周长.大池中学2021-2021学年第一学期第三次阶段考试九年级数学试题参考答案一、选择题：〔3分×10=30分〕 B B C B C B D D D B 二、填空题:( 3分×8=24分)11． x 3≥ 12. 4 13. 3 14. 115.12 16. 9 17. 15 18. 34三、解答题:〔46分〕 19. (1)6(2) 经检验，1212,-3x x == 是原方程的解。