航空公司业绩统计数据相关回归计算题举例

航空公司培训考试试题及答案资料分析概念之基本增长“增长”是资料分析中最重要的概念，增长又分为增长量和增长率。

增长常用到的公式如下：【例题】2014年全年社会消费品零售总额237810亿元，比上年增长13.1%，扣除价格因素，实际增长11.5%。

按经营地统计，城镇消费品零售额205858亿元，增长12.9%;乡村消费品零售额31952亿元，增长14.6%。

按消费形态统计，商品零售额212241亿元，增长13.6%，餐饮收入额25569亿元，增长9.0%。

问题：2013年，城镇消费品零售额与乡村消费品零售额之差为()。

A.137810B.173906C.154456D.210158解析：【答案】C。

资料分析考点之年均增长例图 2005-2011年城镇职工基本医疗保险参保人数和享受待遇人数问题①：2005到2011年，平均每年新增城镇职工基本医疗保险参保者约为多少亿人?A.0.17B.0.19C.0.21D.0.23问题②：2005到2011年，城镇职工基本医疗保险参保者年均增长率为?A.11.2%B.19.4% 。

C.2.1%D.23%资料分析概念之进出口额对外贸易额就是一个国家在一定时期内的进口总额与出口总额之和。

贸易差额是指一个国家在一定时期内(通常为一年)出口总额与进口总额之间的差额。

贸易顺差，我国也称它为出超，表示一定时期的出口额大于进口额。

贸易逆差，我国也称它为入超、赤字，表示一定时期的出口额小于进口额。

贸易顺差=出口额-进口额，贸易逆差=进口额-出口额。

净出口额=出口额-进口额，数值可以是正数，也可以是负数。

正数表示顺差，负数表示逆差。

例《统计公报》显示，2012年全年货物进出口总额38668亿美元，比上年增长6.2%。

其中，出口20489亿美元，增长7.9%;进口18178亿美元，增长4.3%。

问题①：2012年，我国对外贸易顺差是多少亿美元?问题②：2011年，我国进出口贸易顺差是多少亿美元?解析：①解析：20489-18178;②解析：20489÷1.079-18178÷1.043。

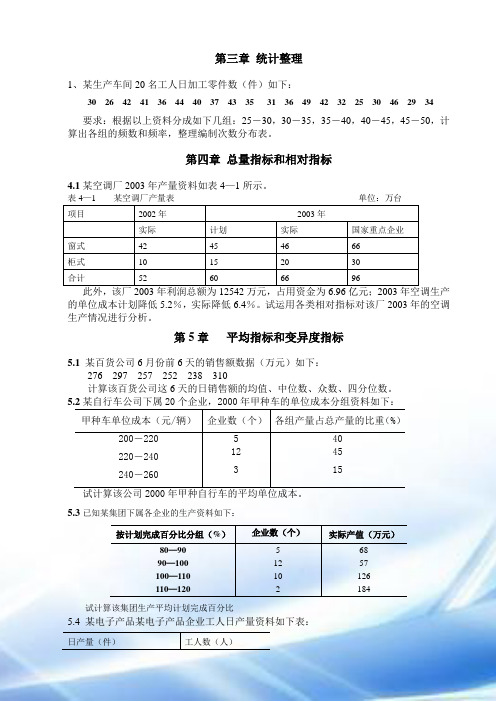
第三章统计整理1、某生产车间20名工人日加工零件数（件）如下：30 26 42 41 36 44 40 37 43 35 31 36 49 42 32 25 30 46 29 34要求：根据以上资料分成如下几组：25－30，30－35，35－40，40－45，45－50，计算出各组的频数和频率，整理编制次数分布表。

第四章总量指标和相对指标4.1某空调厂2003年产量资料如表4—1所示。

项目2002年2003年实际计划实际国家重点企业窗式42 45 46 66柜式10 15 20 30合计52 60 66 96的单位成本计划降低5.2％，实际降低6.4％。

试运用各类相对指标对该厂2003年的空调生产情况进行分析。

第5章平均指标和变异度指标5.1某百货公司6月份前6天的销售额数据（万元）如下：276 297 257 252 238 310计算该百货公司这6天的日销售额的均值、中位数、众数、四分位数。

5.2某自行车公司下属20个企业，2000年甲种车的单位成本分组资料如下：甲种车单位成本（元/辆）企业数（个）各组产量占总产量的比重（%）200－220 220－240 240－26051234045155.3已知某集团下属各企业的生产资料如下：按计划完成百分比分组（%）企业数（个）实际产值（万元）80—90 90—100 100—110 110—120 5121026857126184试计算该集团生产平均计划完成百分比5.4 某电子产品某电子产品企业工人日产量资料如下表：日产量（件）工人数（人）试根据表中资料计算工人日产量的平均数、中位数和众数，并判断该分布数列的分布状态。

5.5一位投资者持有一种股票，2001-2004年的收益率分别为 4.5%，2.1%，25.5%和1.9%。

要求计算该投资者在这4年内的平均收益率。

5.6 一种产品需要人工组装，现有两种可供选择的组装方法。

为检验哪种方法更好，随机抽取6名工人，让他们分别用两种方法组装，测试在相同的时间内组装的产品数量。

数据分析实战案例引言数据分析是一门十分重要且日益流行的技能。

无论是企业还是个人，都离不开数据的收集、处理和分析。

通过数据分析，我们能够揭示隐藏在海量数据中的规律和洞见，为决策和问题解决提供有力支持。

本文将介绍几个常见的数据分析实战案例，帮助读者理解数据分析的应用和意义。

案例一：销售数据分析问题背景一家电商公司想要提高其销售业绩，希望通过数据分析找出销售瓶颈并采取相应措施。

数据收集首先，需要收集电商公司的销售数据。

这些数据包括产品名称、销售数量、销售额、销售地区、销售时间等信息。

数据处理接下来，需要对收集到的数据进行处理。

可以使用Excel等工具进行数据清洗、去重和格式化，确保数据的准确性和一致性。

通过对销售数据进行统计和分析，可以揭示出一些有用的信息。

例如，可以计算不同产品的销售量和销售额，找出销售排名前列的产品；可以分析销售地区的数据，找出销售额较高的地区；可以分析销售时间的数据，找出销售旺季和淡季。

通过这些分析结果，可以为制定销售策略和优化供应链提供参考。

结果呈现最后，需要将数据分析的结果以可视化的方式呈现出来。

可以使用图表、表格、仪表盘等工具将数据呈现出来，使得决策者能够直观地了解销售情况和趋势，做出相应的决策。

案例二：用户行为数据分析问题背景一个社交媒体平台想要提升用户的活跃度，希望通过用户行为数据分析找出影响用户活跃度的因素。

数据收集首先，需要收集社交媒体平台的用户行为数据。

这些数据包括用户访问次数、停留时间、点击率、转发率等信息。

数据处理接下来，需要对收集到的数据进行处理。

可以使用Python等编程语言进行数据清洗、转换和计算，提取有用的特征和指标。

通过对用户行为数据进行统计和分析，可以发现一些有用的规律。

例如，可以分析用户访问次数和停留时间的数据，找出用户活跃度较高的群体；可以分析用户点击率和转发率的数据，找出用户喜欢的内容和关注的话题。

通过这些分析结果，可以为提升用户活跃度制定相应的策略和推荐个性化内容。

实验一：P60.3某百货公司连续40天的商品销售额如下表所示：根据表中的数据进行适当的分组，编制频数分布表，并绘制直方图。

操作步骤：1.打开数据文件。

2.选择数据菜单中的“排序”选项对数据按变量值升序排序。

3.选择“数据分析”对话框中“直方图”，跳出“直方图”对话框。

4.在“输入区域”对应编辑框输入学生成绩数据的引用。

5.在“接受区域”对应编辑框输入数据划分单元格的引用。

6.单击确定。

结果输出如下在图中显示的统计结果中，可以看见输出的内容分为两部分，一部分是数据表示形式，一部分是直方图形式。

在数据表部分，显示每个区间中的日销售额及累计百分率数值。

通过该统计结果，我们可以知道，日销售额有19个在49万~41万之间，13个在41万~33万之间，7个在33万~25万之间，1个在25万及以下。

实验二：P157，3实验内容：某大学生为了解学生每天上网的时间，在全校7500名同学中采取不重复抽样方法随机抽取36人，调查他们每天上网的时间，得到下面的数据（单位：小时）：求该校大学生平均上网时间的置信区间，置信水平分别为90％，95％和99％。

操作步骤：1.在excel中输入以上36人的平均上网时间。

2.运用计算公式计算出各指标。

3．以下为计算结果：（2.863481748，3.769851585），即我们有90%的把握认为学生每天上网的时间平均在2.863481748（小时）到3.769851585(小时)之间，；置信水平为95%时大学生平均上网时间的置信区间为（2.772141751，3.861191582），即我们有95%的把握认为学生每天上网的时间平均在2.772141751（小时）到3.861191582 (小时)之间；置信水平为99%时大学生平均上网时间的置信区间为（2.58607496，4.047258373），即我们有99%的把握认为学生每天上网的时间平均在2.58607496（小时）到4.047258373 (小时)之间。

第9章多元线性回归教材习题答案9.1 根据下面的数据用Excel进行回归，并对回归结果进行讨论，计算、时y 的预测值。

y x1x212 174 318 281 931 189 428 202 852 149 947 188 1238 215 522 150 1136 167 817 135 5详细答案：由Excel输出的回归结果如下：回归统计Multiple R 0.459234R Square 0.210896Adjusted R Square -0.01456标准误差13.34122观测值10方差分析df SS MS F Significance F回归分析 2 332.9837 166.4919 0.93541 0.436485残差7 1245.916 177.988总计9 1578.9Coefficients 标准误差t Stat P-value Lower 95% Upper 95%Intercept 25.0287 22.27863 1.12344 0.298298 -27.6519 77.70928X Variable 1 -0.04971 0.105992 -0.46904 0.653301 -0.30035 0.200918X Variable 2 1.928169 1.47216 1.309755 0.231624 -1.55294 5.409276得到的回证方程为：。

表示，在不变的条件下，每变化一个单位，y平均下降0.04971个单位；表示，在不变的条件下，每变化一个单位，y平均增加1.928169个单位。

判定系数，表示在因变量y的变差中能够被y与和之间的线性关系所解释的比例为21.09%。

由于这一比例很低，表明回归方程的拟合程度很差。

估计标准误差，预测误差也较大。

方差分析表显示，Significance F=0.436485>a=0.05，表明y与和之间的线性关系不显著。

请举出统计应用的几个例子：①用统计识别作者：对于存在争议的论文，通过统计量推出作者②用统计量得到一个重要发现：在不同海域鳗鱼脊椎骨数量变化不大，推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的③挑战者航天飞机失事预测请举出应用统计的几个领域：①在企业发展战略中的应用②在产品质量管理中的应用③在市场研究中的应用④在财务分析中的应用⑤在经济预测中的应用你怎么理解统计的研究内容：①统计学研究的基本内容包括统计对象、统计方法和统计规律。

②统计对象就是统计研究的课题，称谓统计总体。

③统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。

④统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。

举例说明分类变量、顺序变量和数值变量：①分类变量：表现为不同类别的变量称为分类变量，如“性别”表现为“男”或“女”，“企业所属的行业”表现为“制造业”、“零售业”、“旅游业”等，“学生所在的学院”可能是“商学院”、“法学院”等②顺序变量：如果类别有一定的顺序，这样的分类变量称为顺序变量，如考试成绩按等级分为优、良、中、及格、不及格，一个人对事物的态度分为赞成、中立、反对。

这里的“考试成绩等级”、“态度”等就是顺序变量。

③数值变量：可以用数字记录其观察结果，这样的变量称为数值变量，如“企业销售额”、“生活费支出”、“掷一枚骰子出现的点数”。

定性数据和定量数据的图示方法各有哪些：1、定性数据的图示：条形图、帕累托图、饼图、环形图2、定量数据的图示：①分组数据看分布：直方图②未分组数据看分布：茎叶图、箱线图、垂线图、误差图③两个变量间的关系：散点图④比较多个样本的相似性：雷达图和轮廓图直方图与条形图有何区别：①条形图中的每一个矩形表示一个类别，其宽度没有意义，而直方图的宽度则表示各组的组距。

②由于分组数据具有连续性，直方图的各矩形通常是连续排列，而条形图则是分开排列。

③条形图主要用于展示定性数据，而直方图则主要用于展示定量数据。

航空行业航班准点率的数据分析报告航空行业的发展与人们日常生活的出行需求密切相关。

航班准点率作为衡量航空公司运营效率与服务质量的重要指标之一，备受关注。

本文将通过对航空行业航班准点率的数据分析，深入探讨其影响因素，并对提高准点率提出建议。

一、航空行业航班准点率的定义与计算方法航班准点率指的是航班按照计划时间起飞或到达的比例。

常见的计算方法为，以航班实际起飞或到达的时间与计划起飞或到达时间之差的绝对值不超过15分钟的航班占总航班数量的百分比。

二、航班准点率的整体情况分析通过对航空行业航班准点率的数据进行统计与分析，我们可以得出以下结论：1. 年度准点率趋势：航空行业的年度准点率数据呈波动上升的趋势，但不同航空公司之间的准点率存在一定差距。

2. 月度准点率比较：在全年时间范围内，不同月份的航班准点率存在差异。

一般来说，节假日出行高峰期，航班准点率稍有下降。

三、航班准点率的影响因素分析航班准点率受到多种因素的影响，主要包括以下几个方面：1. 天气因素：恶劣的天气，如风暴、雾霾等，会导致飞行航速降低、机位拥堵等问题，从而影响航班准点率。

2. 航空交通管制：航空交通管制是为了保障空中交通的安全，但也可能因为流量控制、航路限制等，导致航班延误或取消。

3. 航空公司运营管理：航空公司的运营管理水平直接关系到航班的准点率。

优秀的调度和维护、高效的机组管理，都能提高航班的准点率。

4. 机场因素：机场的地理位置、跑道和停机位资源分配等，对航班准点率有一定影响。

四、提高航班准点率的建议针对航空行业航班准点率的问题，我们提出以下建议：1. 投资天气预报技术：通过提前获得天气信息，航空公司可以根据天气情况进行灵活的调度安排，降低天气因素对航班准点率的影响。

2. 强化航空交通管制协调：与相关部门和机构合作，加强航空交通管制的协调与信息共享，提高系统的整体效率。

3. 改善运营管理水平：航空公司应加强流程管理、技术支持和人员培训，提高调度和机组管理的水平，以提高航班准点率。

回归分析作业参考答案1 、数据文件“资产评估 1 ”提供了 35 家上市公司资产评估增值的数据。

num--- 公司序号pg---- 资产评估增值率gz---- 固定资产在总资产中所占比例fz---- 权益与负债比bc---- 总资产投资报酬率gm--- 公司资产规模（亿元）•建立关于资产评估增值率的四元线性回归方程，并通过统计分析、检验说明所得方程的有效性，解释各回归系数的经济含义。

•剔除 gz 变量，建立关于资产评估增值率的三元线性回归方程，与 a 中的模型相比较，那个更为实用有效，说明理由。

解：(1)、SPSS相关数据表如下：Model Summary(b)总资产投资报酬率b Dependent Variable: 资产评估增值率ANOVA(b)b Dependent Variable: 资产评估增值率Residuals Statistics(a)Minimum Maximum Mean Std. Deviation NPredicted Value -.084652 .494055 .172240 .1312429 35 Residual -.150002 .149380 .000000 .0739727 35Std. Predicted Value -1.957 2.452 .000 1.000 35Std. Residual -1.905 1.897 .000 .939 35a Dependent Variable: 资产评估增值率R为0.871，决定系数R2为0.759，校正决定系数为0.727。

拟合的回归模型F值为23.609，P值为0，所以拟合的模型是有统计意义的。

从系数的t检验可以看出，只有固定资产比重的相伴概率0.339>0.05，说明只有固定资产比重对资产评估增值率的影响是不显著的，其他自变量对固定资产增值的比率均有显著的影响。

线性回归方程为：pg=0.396+0.079gz+0.063fz+0.602bc-0.044gm表示，在权益与负债比、总资产投资报酬率和公司规模不变的条件下，固定资产比重每增加1个单位，资产评估增值率增加。

下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.(1)由折线图看出,可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明;(2)建立y 关于t 的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量. 参考数据：646.27,55.0)(,17.40,32.97127171≈=-==∑∑∑===i ii ii i iy y yt y参考公式：相关系数：.)()())((11221∑∑∑===----=ni ni iini i iy yt ty y t tr回归方程中斜率和截距的最小二乘估计公式：.ˆˆ,)())((ˆ121t b y at ty y t tbni ini i i-=---=∑∑==某互联网公司为了确定下一季的前期广告投入计划，收集了近6个月广告投入量x (单位：万元)和收益y (单位：万元)的数据如下表：月份 1 2 3 4 5 6 广告投入量 2 4 6 8 10 12 收益14.2120.3131.831.1837.8344.67他们分别用两种模型① y =bx +a ，② y =a e bx 分别进行拟合，得到相应回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值。

xy∑=61i ii yx∑=612i ix730 1464.24 364（1）根据残差图，比较模型①，②的拟合效果，应该选择哪个模型？并说明理由； （2）残差绝对值大于2的数据被认为是异常数据，需要剔除： （i ）剔除异常数据后求出（1）中所选模型的回归方程； （ii ）若广告投入量x =18时，该模型收益的预报值时多少？附：对于一组数据（x 1 , y 1）,（x 2 , y 2）, … ,（x n , y n ）,其回归直线a x b yˆˆˆ+=的斜率和截距的最小二乘估计分别为：.ˆˆ,)())((ˆ1221121x b y a x n xyx n yx x xy y x xbni ini i i ni ini i i-=--=---=∑∑∑∑====某公司为确定下一年度投人某种产品的宣传费，需了解年宣传费x (单位:千元)对年销售量y （单位：t ）和年利润z （单位:千元）的影响. 对近8年的年宣传费x i 和年销售量y i (i =1,2,..,8)数据作了初步处理，得到下面的散点图及一些统计量的值.xyw∑=-812)(i ix x∑=-812)(i iw w∑=--81))((i i iy y x x∑=--81))((i iiy yw w46.6 563 6.8289.8 1.61469108.8其中：i i x w =，.8181∑==i iw w(1)根据散点图判断，bx a y +=与x d c y +=哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据，建立y 关于x 的回归方程；(3) 已知这种产品的年利润z 与y x ,的关系为x y z -=2.0.根据(2)的结果回答下列问题： (i)年宣传费49=x 时，年销售量及年利润的预报值是多少? (ii)年宣传费x 为何值时，年利润的预报值最大?附：对于一组数据),(,,),(,),(2211n n v u v u v u ，其回归直线u v βα+=的斜率和截距的最小二乘估计分别为.ˆ,)())((ˆ121u v u uv v u uni ini i iβαβ-=---=∑∑==为了预测2018年双十一购物狂欢节成交额，建立了y 与时间变量t 的两个回归模型。