江西省重点中学第三章 相互作用——力综合测试卷(word含答案)

一、第三章相互作用——力易错题培优（难）1．如图所示，一固定的细直杆与水平面的夹角为α=15°，一个质量忽略不计的小轻环C套在直杆上，一根轻质细线的两端分别固定于直杆上的A、B两点，细线依次穿过小环甲、小轻环C和小环乙，且小环甲和小环乙分居在小轻环C的两侧．调节A、B间细线的长度，当系统处于静止状态时β=45°.不计一切摩擦．设小环甲的质量为m1，小环乙的质量为m2，则m1∶m2等于( )A．tan 15°B．tan 30°C．tan 60°D．tan 75°【答案】C【解析】试题分析：小球C为轻环，重力不计，受两边细线的拉力的合力与杆垂直，C环与乙环的连线与竖直方向的夹角为600，C环与甲环的连线与竖直方向的夹角为300，A点与甲环的连线与竖直方向的夹角为300，乙环与B点的连线与竖直方向的夹角为600，根据平衡条件，对甲环：，对乙环有：，得，故选C．【名师点睛】小球C为轻环，受两边细线的拉力的合力与杆垂直，可以根据平衡条件得到A段与竖直方向的夹角，然后分别对甲环和乙环进行受力分析，根据平衡条件并结合力的合成和分解列式求解．考点：共点力的平衡条件的应用、弹力．2．如图，A、B是两根竖直立在地上的木杆，轻绳的两端分别系在两杆上不等高的P、Q 两点，C为一质量不计的光滑滑轮，滑轮下挂一物体，下列说法正确的是（）A．将Q点缓慢上移，细绳中的弹力不变B．将P点缓慢上移，细绳中的弹力变小C．减小两木杆之间的距离，细绳中的弹力变大D．增大两木杆之间的距离，细绳中的弹力不变【答案】A【解析】【分析】【详解】设滑轮所受绳子拉力为T ，到左边木杆距离为x 1，到右边木杆距离为x 2，左侧细绳长度为L 1，右侧细绳长度为L 2，受力分析如图所示。

物体受力平衡，由平衡条件可知sin sin T T αθ=cos cos T T mg αθ+=解得αθ=，2cos mgT α=设两木杆之间的距离为d ，绳的总长为L ，由几何关系有11sin L x α= 22sin L x θ=由于αθ=，两式相加可得1212()sin L L x x α+=+可解得sin d Lα=AB ．上下移动P 或者Q ，因为两杆的宽度d 不变，绳子的长度L 也不变，故有α角度不变，由上面的分析2cos mgT α=可知细绳中的弹力不变，故A 正确，B 错误； C ．减小两木杆之间的距离，即d 变小，由sin dLα=可知，两侧绳与竖直方向夹角α减小，由2cos mgT α=可知，α减小，cos α增大，则细绳中弹力减小，故C 错误； D ．同理，增大两木杆之间的距离，即d 变大，α增大，cos α减小，则细绳中弹力增大，故D 错误。

一、第三章 相互作用——力易错题培优（难）1．如图，A 、B 是两根竖直立在地上的木杆，轻绳的两端分别系在两杆上不等高的P 、Q 两点，C 为一质量不计的光滑滑轮，滑轮下挂一物体，下列说法正确的是（ ）A ．将Q 点缓慢上移，细绳中的弹力不变B ．将P 点缓慢上移，细绳中的弹力变小C ．减小两木杆之间的距离，细绳中的弹力变大D ．增大两木杆之间的距离，细绳中的弹力不变 【答案】A 【解析】 【分析】 【详解】设滑轮所受绳子拉力为T ，到左边木杆距离为x 1，到右边木杆距离为x 2，左侧细绳长度为L 1，右侧细绳长度为L 2，受力分析如图所示。

物体受力平衡，由平衡条件可知sin sin T T αθ=cos cos T T mg αθ+=解得αθ=，2cos mgT α=设两木杆之间的距离为d ，绳的总长为L ，由几何关系有11sin L x α= 22sin L x θ=由于αθ=，两式相加可得1212()sin L L x x α+=+可解得sin d Lα=AB ．上下移动P 或者Q ，因为两杆的宽度d 不变，绳子的长度L 也不变，故有α角度不变，由上面的分析2cos mgT α=可知细绳中的弹力不变，故A 正确，B 错误； C ．减小两木杆之间的距离，即d 变小，由sin dLα=可知，两侧绳与竖直方向夹角α减小，由2cos mgT α=可知，α减小，cos α增大，则细绳中弹力减小，故C 错误； D ．同理，增大两木杆之间的距离，即d 变大，α增大，cos α减小，则细绳中弹力增大，故D 错误。

故选A 。

2．如图所示，水平直杆OP 右端固定于竖直墙上的O 点，长为2L m =的轻绳一端固定于直杆P 点，另一端固定于墙上O 点正下方的Q 点，OP 长为 1.2d m =，重为8N 的钩码由光滑挂钩挂在轻绳上处于静止状态，则轻绳的弹力大小为( )A ．10NB ．8NC ．6ND ．5N【答案】D 【解析】 【分析】根据几何关系得到两边绳子与竖直方向的夹角，再根据竖直方向的平衡条件列方程求解. 【详解】设挂钩所在处为N 点，延长PN 交墙于M 点，如图所示：同一条绳子拉力相等，根据对称性可知两边的绳子与竖直方向的夹角相等，设为α，则根据几何关系可知NQ =MN ，即PM 等于绳长；根据几何关系可得：1.2sin 0.62PO PM α===，则α=37°，根据平衡条件可得：2T cos α=mg ，解得：T =5N ，故D 正确，A 、B 、C 错误.故选D. 【点睛】 本题主要是考查了共点力的平衡问题，解答此类问题的一般步骤是：确定研究对象、进行受力分析、然后建立平衡方程进行解答.3．如图，倾角θ=30楔形物块A 静置在水平地面上，其斜面粗糙，斜面上有小物块B 。

一、第三章 相互作用——力易错题培优（难）1．如图所示，质量为M 的四分之一圆柱体放在粗糙水平地面上，质量为m 的正方体放在圆柱体和光滑墙壁之间，且不计圆柱体与正方体之间的摩擦，正方体与圆柱体的接触点的切线与右侧墙壁成θ角，圆柱体处于静止状态，则（ ）A ．地面对圆柱体的支持力大于（M ＋m ）gB ．地面对圆柱体的摩擦力为mg tan θC ．墙壁对正方体的弹力为tan mgθ D ．正方体对圆柱体的压力为cos mgθ【答案】C 【解析】 【分析】 【详解】CD ．以正方体为研究对象，受力分析，并运用合成法如图所示墙壁对正方体的弹力N 1=tan mgθ圆柱体对正方体的支持力为2sin mgN θ=根据牛顿第三定律，正方体对圆柱体的压力为sin mgθ。

选项C 正确，D 错误；AB ．以圆柱体和正方体整体为研究对象，地面对圆柱体的支持力N =(M ＋m ）g水平方向受力平衡，地面对圆柱体的摩擦力f =N 1=tan mgθ选项AB 错误。

故选C 。

2．如图，A 、B 是两根竖直立在地上的木杆，轻绳的两端分别系在两杆上不等高的P 、Q 两点，C 为一质量不计的光滑滑轮，滑轮下挂一物体，下列说法正确的是（ ）A ．将Q 点缓慢上移，细绳中的弹力不变B ．将P 点缓慢上移，细绳中的弹力变小C ．减小两木杆之间的距离，细绳中的弹力变大D ．增大两木杆之间的距离，细绳中的弹力不变 【答案】A 【解析】 【分析】 【详解】设滑轮所受绳子拉力为T ，到左边木杆距离为x 1，到右边木杆距离为x 2，左侧细绳长度为L 1，右侧细绳长度为L 2，受力分析如图所示。

物体受力平衡，由平衡条件可知sin sin T T αθ=cos cos T T mg αθ+=解得αθ=，2cos mgT α=设两木杆之间的距离为d ，绳的总长为L ，由几何关系有11sin L x α= 22sin L x θ=由于αθ=，两式相加可得1212()sin L L x x α+=+可解得sin d Lα=AB ．上下移动P 或者Q ，因为两杆的宽度d 不变，绳子的长度L 也不变，故有α角度不变，由上面的分析2cos mgT α=可知细绳中的弹力不变，故A 正确，B 错误； C ．减小两木杆之间的距离，即d 变小，由sin dLα=可知，两侧绳与竖直方向夹角α减小，由2cos mgT α=可知，α减小，cos α增大，则细绳中弹力减小，故C 错误； D ．同理，增大两木杆之间的距离，即d 变大，α增大，cos α减小，则细绳中弹力增大，故D 错误。

一、第三章 相互作用——力易错题培优（难）1．如图所示，斜面体置于粗糙水平地面上，斜面体上方水平固定一根光滑直杆，直杆上套有一个滑块．滑块连接一根细线，细线的另一端连接一个置于斜面上的光滑小球．最初斜面与小球都保持静止，现对滑块施加水平向右的外力使其缓慢向右滑动至A 点，如果整个过程斜面保持静止，小球未滑离斜面，滑块滑动到A 点时细线恰好平行于斜面，则下列说法正确的是（ ）A ．斜面对小球的支持力逐渐减小B ．细线对小球的拉力逐渐增大C ．滑块受到水平向右的外力逐渐增大D ．水平地面对斜面体的支持力保持不变 【答案】C 【解析】 【分析】 【详解】AB ．对小球受力分析可知，沿斜面方向cos sin T mg αθ=在垂直斜面方向sin cos N F T mg αθ+=（其中α是细线与斜面的夹角，θ为斜面的倾角），现对滑块施加水平向右的外力使其缓慢向右滑动至A 点，α变小，则细线对小球的拉力T 变小，斜面对小球的支持力N F 变大，故A B 错误；C ．对滑块受力分析可知，在水平方向则有sin cos()cos()sin (cos tan sin )cos mg F T mg θαθαθθθαθα+=+==-由于α变小，则有滑块受到水平向右的外力逐渐增大，故C 正确； D ．对斜面和小球为对象受力分析可知，在竖直方向则有sin()N mg Mg F T θα'+=++由于()αθ+变小，所以水平地面对斜面体的支持力逐渐增大，故D 错误。

故选C 。

2．内壁光滑的球体半径为R ，一长度小于直径的轻杆两端固定质量分别为m A 、m B 的小球A 、B 。

将轻秆置于球体内部后。

最终静止在图示位置不动，球心O 与轩在同一竖直平面内，过球心O 竖直向下的半径与杆的交点为M ，2ROM =。

下列判断正确的是（ ）A ．AB m m < B ．球体内壁对A 球的支持力A A 2N m g =C ．轻杆对B 球的支持力有可能小于B 球的重力D ．若增大m A ，θ角会增大【答案】B 【解析】 【分析】 【详解】A ．假设两球质量相等，则杆应处于水平位置，现A 位于B 的下方，可知m A ＞m B ．故A 错误；B ．以A 球为研究对象，A 球受到重力m A g 、球体内壁对A 球的支持力N A 、杆的压力F 。

一、第三章相互作用——力易错题培优（难）1．如图所示，O点有一个很小的光滑轻质圆环，一根轻绳AB穿过圆环，A端固定，B端悬挂一个重物。

另一根轻绳一端固定在C点，另一端系在圆环上，力F作用在圆环上。

圆环静止时，绳OC与绳OA水平，F与OA的夹角为45°。

现改变力F，圆环位置不变，且重物始终处于平衡状态，则下列说法中正确的是（）A．改变F方向时绳AB中拉力将改变B．当F沿逆时针旋转时，F先增大后减小C．当F沿顺时针旋转时，绳OC中的拉力先增大后减小D．F沿逆时转过的角度不能大于90°【答案】D【解析】【分析】【详解】A．因为重物始终处于平衡状态，所以AB绳子的拉力的大小与重物的重力大小相等，不变化，选项A错误；BC．对环受力分析，环受AO和BO两绳子的拉力，以及绳子CO和F的拉力；环的位置不变，则AB绳子的拉力不变，AO与BO的合力也不变，方向沿它们的角平分线，根据共点力平衡的特点可知，CO与F的合力与AO、BO的合力大小相等，方向相反；当力F的方向变化时，做出F与CO上的拉力的变化如图：由图可知，当沿逆时针族转时，F先减小后增大，绳OC的拉力减小；而当F沿顺时针旋转时，F逐渐增大，绳OC的拉力增大，选项BC错误；D．由于F与CO绳子的拉力的合力方向与水平方向之间的夹角是45°，可知F沿逆时转过的角度不能大于90°，选项D正确。

故选D。

2．如图所示，一轻质光滑定滑轮固定在倾斜木板上，质量分别为m 和2m 的物块A 、B ，通过不可伸长的轻绳跨过滑轮连接，A 、B 间的接触面和轻绳均与木板平行。

A 与B 间、B 与木板间的动摩擦因数均为μ，设最大静摩擦力等于滑动摩擦力。

当木板与水平面的夹角为45°时，物块A 、B 刚好要滑动，则μ的值为（ ）A ．13B ．14C ．15D ．16【答案】C【解析】【分析】【详解】当木板与水平面的夹角为45︒时，两物块刚好滑动，对A 物块受力分析如图沿斜面方向，A 、B 之间的滑动摩擦力1cos 45f N mg μμ==︒根据平衡条件可知sin 45cos45T mg mg μ=︒+︒对B 物块受力分析如图沿斜面方向，B 与斜面之间的滑动摩擦力23cos 45f N mg μμ='=⋅︒根据平衡条件可知2sin 45cos453cos45mg T mg mg μμ︒=+︒+⋅︒两式相加，可得2sin 45sin 45cos45cos453cos45mg mg mg mg mg μμμ︒=︒+︒+︒+⋅︒解得15μ=故选C 。

一、第三章 相互作用——力易错题培优（难）1．内壁光滑的球体半径为R ，一长度小于直径的轻杆两端固定质量分别为m A 、m B 的小球A 、B 。

将轻秆置于球体内部后。

最终静止在图示位置不动，球心O 与轩在同一竖直平面内，过球心O 竖直向下的半径与杆的交点为M ，2ROM =。

下列判断正确的是（ ）A ．AB m m < B ．球体内壁对A 球的支持力A A 2N m g =C ．轻杆对B 球的支持力有可能小于B 球的重力D ．若增大m A ，θ角会增大【答案】B 【解析】 【分析】 【详解】A ．假设两球质量相等，则杆应处于水平位置，现A 位于B 的下方，可知m A ＞m B ．故A 错误；B ．以A 球为研究对象，A 球受到重力m A g 、球体内壁对A 球的支持力N A 、杆的压力F 。

由平衡条件知，m A g 与F A 的合力与N A 等大、反向。

运用平行四边形定则作出力的合成图如图。

根据三角形相似得：A A N m gOA OM= 由OA ＝R ，OM 2R=，解得 N A ＝2m A g故B 正确；C ．以B 球为研究对象，分析其受力情况如图。

根据几何知识有 β＞α，则在图中，一定有 F B ＞m B g ，即轻杆对B 球的支持力一定大于B 球的重力，故C 错误；D ．若增大m A ，A 球下降，θ角会减小，故D 错误。

故选B 。

2．如图所示，固定倾斜直杆上套有一个质量为m 的小球和两根原长均为L 的轻弹簧，两根轻弹簧的一端与小球相连，另一端分别固定在杆上相距为2L 的A 、B 两点。

已知直杆与水平面的夹角为θ，两弹簧的劲度系数均为k =3sin mg L θ，小球在距B 点45L 的P 点处于静止状态，重力加速度为g 。

则小球在P 点处受到摩擦力为（ ）A ．sin 5mg f θ=，方向沿杆向下 B ．sin 5mg f θ=，方向沿杆向上 C ．sin 2mg f θ=，方向沿杆向下 D ．sin 2mg f θ=，方向沿杆向上 【答案】A 【解析】 【分析】 【详解】小球在P 点时两根弹簧的弹力大小相等，设为F ，根据胡克定律有45F k L L ⎛⎫=- ⎪⎝⎭设小球静止时受到的摩擦力大小为f ，方向沿杆向下，根据平衡条件有sin 2mg f F θ+=解得sin 5mg f θ=方向沿杆向下，选项A 正确，BCD 错误。

一、第三章 相互作用——力易错题培优（难）1．水平传感器可以测量器械摆放所处的水平角度，属于角度传感器的一种，其作用就是测量载体的水平度，又叫倾角传感器。

如图为一个简易模型，截面为内壁光滑的竖直放置的正三角形，内部有一个小球，其半径略小于内接圆半径，三角形各边有压力传感器，分别感受小球对三边压力的大小，根据压力的大小，信息处理单元能将各边与水平面间的夹角通过显示屏显示出来。

如果图中此时BC 边恰好处于水平状态，将其以C 为轴在竖直平面内顺时针缓慢转动，直到AC 边水平，则在转动过程中（ ）A ．当BC 边与AC 边所受压力大小相等时，AB 处于水平状态B ．球对AC 边的压力一直增大C ．球对BC 边的压力一直减小D ．BC 边所受压力不可能大于球的重力【答案】A【解析】【分析】 【详解】对正三角形内部的小球受力分析，如图所示由几何关系可知，随着角度θ从0°到120°增大过程中，角α与角θ之和保持不变，且α + θ = 120°，所以角β也保持不变，β = 60°，由平衡条件和正弦定理得()sin sin sin 120AC BC N N G βθθ==︒- 所以球对AC 边的压力23sin sin sin sin sin 60ACAC G G N N θθθβ'====︒ 球对BC 边的压力()()()23sin 120sin 120sin 120sin sin 60BC BC G G N N G θθθβ'==︒-=︒-=︒-︒ A ．当BC 边与AC 边所受压力大小相等时，即ACBC N N ''=，则θ = 60°，此时AB 处于水平状态，故A 正确；BC ．角度θ从0°到120°增大过程中，sin θ和()sin 120θ︒-都是先增大后减小，所以球对AC 边的压力和球对BC 边的压力都是先增大后减小，BC 错误；D ．当0 < θ < 60°时，BCN G '>，即BC 边所受压力有可能大于球的重力，故D 错误。

一、第三章相互作用——力易错题培优（难）1．如图所示，O点有一个很小的光滑轻质圆环，一根轻绳AB穿过圆环，A端固定，B端悬挂一个重物。

另一根轻绳一端固定在C点，另一端系在圆环上，力F作用在圆环上。

圆环静止时，绳OC与绳OA水平，F与OA的夹角为45°。

现改变力F，圆环位置不变，且重物始终处于平衡状态，则下列说法中正确的是（）A．改变F方向时绳AB中拉力将改变B．当F沿逆时针旋转时，F先增大后减小C．当F沿顺时针旋转时，绳OC中的拉力先增大后减小D．F沿逆时转过的角度不能大于90°【答案】D【解析】【分析】【详解】A．因为重物始终处于平衡状态，所以AB绳子的拉力的大小与重物的重力大小相等，不变化，选项A错误；BC．对环受力分析，环受AO和BO两绳子的拉力，以及绳子CO和F的拉力；环的位置不变，则AB绳子的拉力不变，AO与BO的合力也不变，方向沿它们的角平分线，根据共点力平衡的特点可知，CO与F的合力与AO、BO的合力大小相等，方向相反；当力F的方向变化时，做出F与CO上的拉力的变化如图：由图可知，当沿逆时针族转时，F先减小后增大，绳OC的拉力减小；而当F沿顺时针旋转时，F逐渐增大，绳OC的拉力增大，选项BC错误；D．由于F与CO绳子的拉力的合力方向与水平方向之间的夹角是45°，可知F沿逆时转过的角度不能大于90°，选项D正确。

故选D。

2．如图所示，一固定的细直杆与水平面的夹角为α=15°，一个质量忽略不计的小轻环C套在直杆上，一根轻质细线的两端分别固定于直杆上的A、B两点，细线依次穿过小环甲、小轻环C和小环乙，且小环甲和小环乙分居在小轻环C的两侧．调节A、B间细线的长度，当系统处于静止状态时β=45°.不计一切摩擦．设小环甲的质量为m1，小环乙的质量为m2，则m1∶m2等于( )A．tan 15°B．tan 30°C．tan 60°D．tan 75°【答案】C【解析】试题分析：小球C为轻环，重力不计，受两边细线的拉力的合力与杆垂直，C环与乙环的连线与竖直方向的夹角为600，C环与甲环的连线与竖直方向的夹角为300，A点与甲环的连线与竖直方向的夹角为300，乙环与B点的连线与竖直方向的夹角为600，根据平衡条件，对甲环：，对乙环有：，得，故选C．【名师点睛】小球C为轻环，受两边细线的拉力的合力与杆垂直，可以根据平衡条件得到A段与竖直方向的夹角，然后分别对甲环和乙环进行受力分析，根据平衡条件并结合力的合成和分解列式求解．考点：共点力的平衡条件的应用、弹力．3．如图所示，斜面体置于粗糙水平地面上，斜面体上方水平固定一根光滑直杆，直杆上套有一个滑块．滑块连接一根细线，细线的另一端连接一个置于斜面上的光滑小球．最初斜面与小球都保持静止，现对滑块施加水平向右的外力使其缓慢向右滑动至A点，如果整个过程斜面保持静止，小球未滑离斜面，滑块滑动到A点时细线恰好平行于斜面，则下列说法正确的是（）A．斜面对小球的支持力逐渐减小B．细线对小球的拉力逐渐增大C．滑块受到水平向右的外力逐渐增大D．水平地面对斜面体的支持力保持不变【答案】C【解析】【分析】【详解】AB ．对小球受力分析可知，沿斜面方向cos sin T mg αθ=在垂直斜面方向sin cos N F T mg αθ+=（其中α是细线与斜面的夹角，θ为斜面的倾角），现对滑块施加水平向右的外力使其缓慢向右滑动至A 点，α变小，则细线对小球的拉力T 变小，斜面对小球的支持力N F 变大，故A B 错误；C ．对滑块受力分析可知，在水平方向则有sin cos()cos()sin (cos tan sin )cos mg F T mg θαθαθθθαθα+=+==- 由于α变小，则有滑块受到水平向右的外力逐渐增大，故C 正确；D ．对斜面和小球为对象受力分析可知，在竖直方向则有sin()N mg Mg F T θα'+=++由于()αθ+变小，所以水平地面对斜面体的支持力逐渐增大，故D 错误。

一、第三章 相互作用——力易错题培优（难）1．如图所示，斜面体置于粗糙水平地面上，斜面体上方水平固定一根光滑直杆，直杆上套有一个滑块．滑块连接一根细线，细线的另一端连接一个置于斜面上的光滑小球．最初斜面与小球都保持静止，现对滑块施加水平向右的外力使其缓慢向右滑动至A 点，如果整个过程斜面保持静止，小球未滑离斜面，滑块滑动到A 点时细线恰好平行于斜面，则下列说法正确的是（ ）A ．斜面对小球的支持力逐渐减小B ．细线对小球的拉力逐渐增大C ．滑块受到水平向右的外力逐渐增大D ．水平地面对斜面体的支持力保持不变 【答案】C 【解析】 【分析】 【详解】AB ．对小球受力分析可知，沿斜面方向cos sin T mg αθ=在垂直斜面方向sin cos N F T mg αθ+=（其中α是细线与斜面的夹角，θ为斜面的倾角），现对滑块施加水平向右的外力使其缓慢向右滑动至A 点，α变小，则细线对小球的拉力T 变小，斜面对小球的支持力N F 变大，故A B 错误；C ．对滑块受力分析可知，在水平方向则有sin cos()cos()sin (cos tan sin )cos mg F T mg θαθαθθθαθα+=+==-由于α变小，则有滑块受到水平向右的外力逐渐增大，故C 正确； D ．对斜面和小球为对象受力分析可知，在竖直方向则有sin()N mg Mg F T θα'+=++由于()αθ+变小，所以水平地面对斜面体的支持力逐渐增大，故D 错误。

故选C 。

2．如图所示，固定倾斜直杆上套有一个质量为m 的小球和两根原长均为L 的轻弹簧，两根轻弹簧的一端与小球相连，另一端分别固定在杆上相距为2L 的A 、B 两点。

已知直杆与水平面的夹角为θ，两弹簧的劲度系数均为k =3sin mg L θ，小球在距B 点45L 的P 点处于静止状态，重力加速度为g 。

则小球在P 点处受到摩擦力为（ ）A ．sin 5mg f θ=，方向沿杆向下 B ．sin 5mg f θ=，方向沿杆向上 C ．sin 2mg f θ=，方向沿杆向下 D ．sin 2mg f θ=，方向沿杆向上 【答案】A 【解析】 【分析】 【详解】小球在P 点时两根弹簧的弹力大小相等，设为F ，根据胡克定律有45F k L L ⎛⎫=- ⎪⎝⎭设小球静止时受到的摩擦力大小为f ，方向沿杆向下，根据平衡条件有sin 2mg f F θ+=解得sin 5mg f θ=方向沿杆向下，选项A 正确，BCD 错误。

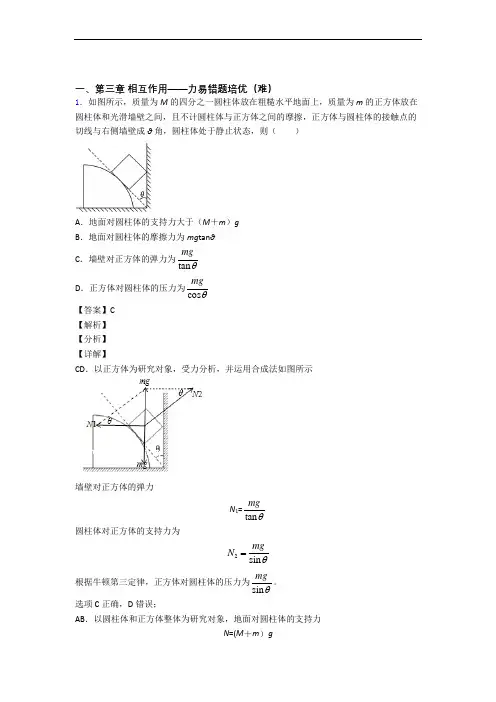
一、第三章 相互作用——力易错题培优（难） 1．如图所示，质量为M 的四分之一圆柱体放在粗糙水平地面上，质量为m 的正方体放在圆柱体和光滑墙壁之间，且不计圆柱体与正方体之间的摩擦，正方体与圆柱体的接触点的切线与右侧墙壁成θ角，圆柱体处于静止状态，则（ ）A ．地面对圆柱体的支持力大于（M ＋m ）gB ．地面对圆柱体的摩擦力为mg tan θC ．墙壁对正方体的弹力为tan mg θD ．正方体对圆柱体的压力为cos mg θ 【答案】C【解析】【分析】【详解】CD ．以正方体为研究对象，受力分析，并运用合成法如图所示墙壁对正方体的弹力N 1=tan mg θ圆柱体对正方体的支持力为 2sin mg N θ= 根据牛顿第三定律，正方体对圆柱体的压力为sin mg θ。

选项C 正确，D 错误；AB ．以圆柱体和正方体整体为研究对象，地面对圆柱体的支持力N =(M ＋m ）g水平方向受力平衡，地面对圆柱体的摩擦力f =N 1=tan mg θ选项AB 错误。

故选C 。

2．如图所示，物块A 放在直角三角形斜面体B 上面，B 放在弹簧上面并紧挨着竖直墙壁，初始时A 、B 静止。

现用力F 沿斜面向上推A ，但A 、B 仍未动，则施力F 后，下列说法正确的是（ ）A ．A 、B 之间的摩擦力一定变大B ．B 与墙之间可能没有摩擦力C ．B 与墙面间的弹力可能不变D ．B 与墙面间的弹力变大【答案】D【解析】【分析】【详解】 A ．对A 物体，开始受重力、B 对A 的支持力和静摩擦力平衡，当施加F 后，仍然处于静止，开始A 所受的静摩擦力大小为A sin m g θ，若A 2sin F m g θ=，则A 、B 之间的静摩擦力大小还是等于A sin m g θ，所以A 、B 之间的摩擦力可能不变，故A 错误；B ．对整体分析，因为AB 不动，弹簧的形变量不变，则弹簧的弹力不变，开始弹簧的弹力等于A 、B 的总重力，施加F 后，弹簧的弹力不变，总重力不变，根据平衡知，则B 与墙之间一定有摩擦力，摩擦力大小等于力F 在竖直方向的分力，方向竖直向下，故B 错误； CD ．以整体为研究对象，开始时B 与墙面的弹力为零，施加力F 后，B 与墙面的弹力变为F cos α，弹力增大，故C 错误，D 正确。