《立体几何》选择题及填空题.

高一数学必修第二册第八章《立体几何初步》单元练习题卷3（共22题）一、选择题（共10题）1.在空间四边形ABCD的边AB，BC，CD，DA上分别取E，F，G，H四点，若EF与HG交于点M，那么( )A．M一定在直线AC上B．M一定在直线BD上C．M可能在直线AC上，也可能在直线BD上D．M既不在直线AC上，也不在直线BD上2.关于“斜二测”画图法，下列说法不正确的是( )A．平行直线的斜二测图仍是平行直线B．斜二测图中，互相平行的任意两条线段的长度之比保持原比例不变C．正三角形的直观图一定为等腰三角形D．在画直观图时，由于坐标轴的选取不同，所得的直观图可能不同3.已知直线m，n与平面α，β，m⊥α，n⊥β，若α⊥β，则m，n的位置关系是( )A．平行B．垂直C．相交D．异面4.如图所示，正方体ABCD−A1B1C1D1的棱长为2，动点E，F在棱A1B1上，动点P，Q分别在棱AD，CD上，若EF=1，A1E=x，DQ=y，DP=z（x，y，z大于零），则四面体PQEF的体积( )A．与x，y，z都有关B．与x有关，与y，z无关C．与y有关，与x，z无关D．与z有关，与x，y无关5.在正方体中ABCD−A1B1C1D1中，E为棱CD的中点，则( )A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC6.一个四面体的所有棱长都为√2，四个顶点在同一球面上，则此球的表面积为( )A．3πB．4πC．3√3πD．6π7.正方体的内切球与其外接球的体积之比为( )A．1:√3B．1:3C．1:3√3D．1:98.《九章算术》中，称底面为矩形且有一侧棱垂直于底面的四棱锥为阳马，如图，某阳马的三视图如图所示，则该阳马的最长棱的长度为( )A．√2B．√3C．2D．2√29.已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积取最大值时，其高的值为( )A．3√3B．√3C．2√6D．2√310.若一个圆锥的轴截面（过圆锥顶点和底面直径的截面）是等边三角形，其面积为√3，则这个圆锥的体积为( )A．3πB．√3π3C．√3πD．√3π2二、填空题（共6题）11.已知正方体ABCD−A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M（如图），则四棱锥M−EFGH的体积为．12.如图，在正三棱柱ABC−A1B1C1中，已知AB=AA1=3，点P在棱CC1上，则三棱锥P−ABA1的体积为．13.正六棱柱的底面边长为4，高为6，则它的外接球（正六棱柱的顶点都在此球面上）的表面积为．14.正△ABC的斜二测画法的水平放置图形的直观图，若△AʹBʹCʹ的面积为√3，那么△ABC的面积为．15.正方体ABCD−A1B1C1D1中，若过A，C，B1三点的平面与底面A1B1C1D1的交线为l，则l与A1C1的位置关系是．16.如图所示，长方形ABCD−A1B1C1D1的体积为24，E为线段B1C上的一点，则棱锥A−DED1的体积为．三、解答题（共6题）17.如图，在正方体ABCD−A1B1C1D1中，P，Q分别是平面AA1D1D，平面A1B1C1D1的中心，证明：(1) D1Q∥平面C1DB；(2) 平面D1PQ∥平面C1DB．18.如图，在四棱锥P−ABCD中，底面ABCD是菱形，PB=PD．(1) 求证：平面APC⊥底面BPD；(2) 若PB⊥PD，∠DAB=60∘，AP=AB=2，求二面角A−PD−C的余弦值．19.如图，在△AOB中，∠AOB=90∘，AO=2，OB=1．△AOC可以通过△AOB以直线AO为轴旋转得到，且OB⊥OC，动点D在斜边AB上．(1) 求证：平面COD⊥平面AOB；(2) 当D为AB的中点时，求二面角B−CD−O的余弦值；(3) 求CD与平面AOB所成的角中最大角的正弦值．20.如图，在三棱柱ABC−A1B1C1中，四边形A1C1CA为菱形，∠B1A1A=∠C1A1A=60∘，AC=4，AB=2，平面ACC1A1⊥平面ABB1A1，Q在线段AC上移动，P为棱AA1的中点．(1) 若Q为线段AC的中点，H为BQ的中点，延长AH交BC于D，求证：AD∥平面B1PQ；(2) 若二面角B1−PQ−C1的平面角的余弦值为√13，求点P到平面BQB1的距离．1321.如图，AE⊥面ABCD，ABCD是正方形，AE=AB=2，F为BE的中点．求证：DE∥面ACF．22.阅读下面题目及其证明过程，在横线处填写适当的内容．如图，长方体ABCD−A1B1C1D1的底面ABCD是边长为1的正方形，点E，F分别为线段BD1，CC1的中点．（Ⅰ）求证：EF∥平面ABCD；（Ⅰ）当DD1=√2时，求证：DE⊥平面BFD1；证明：（Ⅰ）如图，连接AC，BD，设AC∩BD=O，连接OE．因为长方体ABCD−A1B1C1D1的底面ABCD是边长为1的正方形，所以BO=OD，又因为BE=ED1，DD1，所以OE∥DD1，OE=12因为F为线段CC1中点，DD1，所以CF∥DD1，CF=12所以CF∥OE，CF=OE．所以四边形OCFE为平行四边形．所以EF∥OC．又因为EF⊄平面ABCD，OC⊂平面ABCD，所以EF∥平面ABCD．（Ⅰ）因为F为线段CC1中点，所以BF=D1F，所以△D1FB是等腰三角形．因为E为BD1的中点，所以EF⊥BD1．因为BD⊥OC，EF∥OC，所以EF⊥BD．因为BD∩BD1=B，所以①．因为DE⊂平面BDD1，所以②．因为DD1=√2，所以DD1=BD，所以③．因为EF∩D1B=E，所以DE⊥平面BFD1．在上述证明过程中，（Ⅰ）的证明思路是：先证明“④”，再证明“⑤”．答案一、选择题（共10题）1. 【答案】A【解析】如图，因为EF∩HG=M，所以M∈EF，M∈HG，又EF⊂平面ABC，HG⊂平面ADC，故M∈平面ABC，M∈平面ADC，又平面ABC∩平面ADC=AC，所以M∈AC．故选A．【知识点】平面的概念与基本性质2. 【答案】C【解析】对于A，平行直线的斜二测图仍是平行直线，A正确；对于B，斜二测图中，互相平行的任意两条线段的长度之比保持原比例不变，B正确；对于C，正三角形的直观图不一定为等腰三角形，如图所示，所以C错误；对于D，画直观图时，由于坐标轴的选取不同，所得的直观图可能不同，D正确．【知识点】直观图3. 【答案】B【解析】m，n有可能相交或异面，但必定垂直．故答案选B．【知识点】直线与直线的位置关系4. 【答案】D【解析】设P点到平面A1B1CD的距离为ℎ，因为A1B1∥DC，所以Q到EF的距离为定值2√2，又因为EF=1，所以S△QEF=12×1×2√2=√2，因为V四面体PQEF =V三棱锥P−QEF=13S△QEF⋅ℎ=√23ℎ，即四面体的体积只与点P到平面A1B1CD的距离无关，所以四面体的体积与z有关，与x，y无关．【知识点】棱锥的表面积与体积5. 【答案】C【解析】画出正方体ABCD−A1B1C1D1，如图所示．对于选项A，连D1E，若A1E⊥DC1，又DC1⊥A1D1，所以DC1平面A1ED1，所以可得DC1⊥D1E，显然不成立，所以A不正确．对于选项B，连AE，若A1E⊥BD，又BD⊥AA1，所以DB⊥平面A1AE，故得BD⊥AE，显然不成立，所以B不正确．对于选项C，连AD1，则AD1∥BC1．连A1D，则得AD1⊥A1D，AD1⊥ED，所以AD1⊥平面A1DE，从而得AD1⊥A1E，所以A1E⊥BC1．所以C正确．对于选项D，连AE，若A1E⊥AC，又AC⊥AA1，所以AC⊥平面A1AE，故得AC⊥AE，显然不成立，所以D不正确．【知识点】空间中直线与直线的垂直6. 【答案】A【解析】联想只有正方体中有这么多相等的线段，所以构造一个正方体，则正方体的面对角线即为四面体的棱长，求得正方体的棱长为1，体对角线为√3，从而外接球的直径也为√3，所以此球的表面积为3π．【知识点】组合体、球的表面积与体积7. 【答案】C【解析】设正方体的棱长为a，则其内切球的半径为a2，所以V内=43π(a2)3−πa36，正方体的外接球的半径为√32a，所以V外=43π(√32a)3=3√3πa36，所以V内:V外=1:3√3．【知识点】球的表面积与体积8. 【答案】B【解析】根据题设条件可知三视图还原成的几何体为四棱锥，如图所示，其中PD=1，底面ABCD是边长为1的正方形，易知PB=√3，PA=PC=√2，故最长棱的长度为√3．【知识点】三视图、棱锥的结构特征9. 【答案】D【知识点】棱柱的表面积与体积10. 【答案】B【解析】设圆锥底面圆的半径为r，圆锥的高为ℎ，体积为V，则ℎ=√3r．因为12×2r×√3r=√3r2=√3，所以r=1，所以V=13πr2h=√33πr3=√3π3．【知识点】圆锥的表面积与体积二、填空题（共6题）11. 【答案】112【解析】连接AD1，CD1，B1A，B1C，AC，因为E，H分别为AD1，CD1的中点，所以EH∥AC，EH=12AC，因为 F ，G 分别为 B 1A ，B 1C 的中点， 所以 FG ∥AC ，FG =12AC ，所以 EH ∥FG ，EH =FG ， 所以四边形 EHGF 为平行四边形， 又 EG =HF ，EH =HG ， 所以四边形 EHGF 为正方形， 又点 M 到平面 EHGF 的距离为 12， 所以四棱锥 M −EFGH 的体积为 13×(√22)2×12=112．【知识点】棱锥的表面积与体积12. 【答案】9√34【解析】因为在正三棱柱 ABC −A 1B 1C 1 中，AB =AA 1=3，点 P 在棱 CC 1 上， 所以点 P 到平面 ABA 1 的距离即为 △ABC 的高， 即为 ℎ=√32−(32)2=3√32，S △ABA 1=12×3×3=92，三棱锥 P −ABA 1 的体积为：V =13×S △ABA 1×ℎ=13×92×3√32=9√34．【知识点】棱锥的表面积与体积13. 【答案】 100π【解析】依题意，该正六棱柱的外接球的球心应是上、下底面中心连线的中点， 所以其半径等于 √42+(62)2=5，其表面积等于 4π×25=100π．【知识点】球的表面积与体积14. 【答案】 2√6【知识点】直观图15. 【答案】 A 1C 1∥l【解析】因为 平面ABCD ∥平面A 1B 1C 1D 1，AC ⊂平面ABCD ， 所以 AC ∥平面A 1B 1C 1D 1，又平面 ACB 1 经过直线 AC 与平面 A 1B 1C 1D 1 相交于直线 l ， 所以 AC ∥l ， 又因为 A 1C 1∥AC ， 所以 A 1C 1∥l ．【知识点】直线与平面平行关系的性质、直线与平面平行关系的判定16. 【答案】4【解析】设AB=a，AD=b，AA1=c，则长方体的体积V ABCD−A1B1C1D1=abc=24，三棱锥A−DED1的体积V A−DED1=V E−ADD1=13S△ADD1⋅AB=13×12×AD×DD1×AB=16×bc⋅a=16×24=4.【知识点】棱锥的表面积与体积三、解答题（共6题）17. 【答案】(1) 由题可知D1Q∥DB．因为D1Q⊄平面C1DB，DB⊂平面C1DB，所以D1Q∥平面C1DB．(2) 由题可知D1P∥C1B．因为D1P⊄平面C1DB，C1B⊂平面C1DB，所以D1P∥平面C1DB．由（1）知，D1Q∥平面C1DB，又D1Q∩D1P=D1，所以平面D1PQ∥平面C1DB．【知识点】平面与平面平行关系的判定、直线与平面平行关系的判定18. 【答案】(1) 记AC∩BD=O，连接PO，因为底面 ABCD 是菱形，所以 BD ⊥AC ，O 是 BD ，AC 的中点， 因为 PB =PD ， 所以 PO ⊥BD ， 因为 AC ∩PO =O ， 所以 BD ⊥平面APC ， 又因为 BD ⊂平面BPD ，所以 平面APC ⊥平面BPD ．(2) 如图，以 O 为原点，OA ，OB ，OP 所在直线分别为 x ，y ，z 轴建立如图所示的空间坐标系， 则 A(√3,0,0)，D (0,−1,0)，P (0,0,1)，C(−√3,0,0,)，所以 DA ⃗⃗⃗⃗⃗ =(√3,1,0)，DP ⃗⃗⃗⃗⃗ =(0,1,1)，DC ⃗⃗⃗⃗⃗ =(−√3,1,0)， 设 n 1⃗⃗⃗⃗ =(x 1,y 1,z 1) 是平面 APD 的法向量，则 {DA ⃗⃗⃗⃗⃗ ⋅n 1⃗⃗⃗⃗ =0,DP ⃗⃗⃗⃗⃗ ⋅n 1⃗⃗⃗⃗ =0⇒{√3x 1+y 1=0,y 1+z 1=0, 令 y 1=−√3，得 n 1⃗⃗⃗⃗ =(1,−√3,√3)，同理可得平面 PCD 的法向量 n 2⃗⃗⃗⃗ =(1,√3,−√3)，所以 cos ⟨n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ ⟩=n1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ ∣∣n 1⃗⃗⃗⃗⃗ ∣∣⋅∣∣n2⃗⃗⃗⃗⃗ ∣∣=√3)×√3+(−√3)×√3√7×√7=−57，由图形可知二面角 A −PD −C 为钝二面角， 所以二面角 A −PD −C 的余弦值为 −57．【知识点】利用向量的坐标运算解决立体几何问题、平面与平面垂直关系的判定、二面角19. 【答案】(1) 在 △AOC 中，AO ⊥OC ， 因为 OB ⊥OC ，且 AO ∩OB =O ， 所以 OC ⊥平面AOB ， 又 OC ⊂平面COD ，所以 平面COD ⊥平面AOB ．(2) 如图建立空间直角坐标系 O −xyz ， 因为 D 为 AB 的中点，所以 O (0,0,0)，A (0,0,2)，B (0,1,0)，C (1,0,0)，D (0,12,1)，所以 OC ⃗⃗⃗⃗⃗ =(1,0,0)，OD ⃗⃗⃗⃗⃗⃗ =(0,12,1)，BC ⃗⃗⃗⃗⃗ =(1,−1,0)，BD⃗⃗⃗⃗⃗⃗ =(0,−12,1)， 设 n 1⃗⃗⃗⃗ =(x 1,y 1,z 1) 为平面 OCD 的法向量，所以 {n 1⃗⃗⃗⃗ ⋅OC ⃗⃗⃗⃗⃗ =0,n 1⃗⃗⃗⃗ ⋅OD ⃗⃗⃗⃗⃗⃗ =0, 即 {x 1=0,12y 1+z 1=0, 令 z 1=1，则 y 1=−2，所以 n 1⃗⃗⃗⃗ =(0,−2,1) 是平面 BCD 的一个法向量， 设 n 2⃗⃗⃗⃗ =(x 2,y 2,z 2) 为平面 OCD 的法向量， 所以 {n 2⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =0,n 2⃗⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0, 即 {x 2−y 2=0,−12y 2+z 2=0, 令 z 2=1，则 x 2=2，y 2=2，所以 n 2⃗⃗⃗⃗ =(2,2,1) 是平面 OCD 的一个法向量，所以 cos 〈n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ 〉=n 1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ ∣∣n 1⃗⃗⃗⃗⃗ ∣∣⋅∣∣n 2⃗⃗⃗⃗⃗ ∣∣=√02+(−2)2+12⋅√22+22+12=−√55， 所以二面角 B −CD −O 的余弦值为 √55． (3) 解法一：因为 OC ⊥平面AOB ，所以 ∠CDO 为 CD 与平面 AOB 所成的角， 因为 OC =1，所以点 O 到直线 AB 的距离最小时，∠CDO 的正弦值最大， 即当 OD ⊥AB 时，∠CDO 的正弦值最大， 此时 OD =2√55， 所以 CD =3√55， 所以 sin∠CDO =√53． 解法二：设 AD⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ (λ∈[0,1])， 所以 D (0,λ,2−2λ)．CD ⃗⃗⃗⃗⃗ =(−1,λ,2−2λ)，平面 AOB 的法向量 n ⃗ =(1,0,0)，所以 sinθ=∣∣n ⃗ ⋅CD⃗⃗⃗⃗⃗ ∣∣∣∣n ⃗ ∣∣∣∣CD⃗⃗⃗⃗⃗ ∣∣=√5λ2−8λ+5=√5(λ−45)2+95，所以当 λ=45 时，CD 与平面 AOB 所成的角最大，sinθ=√53． 【知识点】二面角、平面与平面垂直关系的判定、线面角20. 【答案】(1) 如图，取 BB 1 的中点 E ，连接 AE ，EH ． 因为 H 为 BQ 的中点， 所以 EH ∥B 1Q ．在平行四边形 AA 1B 1B 中，P ，E 分别为 AA 1，BB 1 的中点， 所以 AE ∥PB 1．又 EH ∩AE =E ，PB 1∩B 1Q =B 1， 所以 平面EHA ∥平面B 1QP ． 因为 AD ⊂平面EHA ， 所以 AD ∥平面B 1PQ ．(2) 如图，连接 PC 1，AC 1，因为四边形 A 1C 1CA 为菱形，∠C 1A 1A =60∘， 所以 AA 1=AC 1=A 1C 1=4， 即 △AC 1A 1 为等边三角形． 因为 P 为 AA 1 的中点， 所以 PC 1⊥AA 1．因为 平面ACC 1A 1⊥平面ABB 1A 1，平面ACC 1A 1∩平面ABB 1A 1=AA 1，PC 1⊂平面ACC 1A 1， 所以 PC 1⊥平面ABB 1A 1．在平面 ABB 1A 1 内过点 P 作 PR ⊥AA 1 交 BB 1 于 R ．以 PR ，PA 1，PC 1 所在直线分别为 x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系 Pxyz ，则 P (0,0,0)，A 1(0,2,0)，A (0,−2,0)，C 1(0,0,2√3)，C(0,−4,2√3)．设 AQ ⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ =λ(0,−2,2√3)，λ∈(0,1]（当 λ=0 时，平面 B 1PQ 即平面 ABB 1A 1，不符合题意），所以 Q(0,−2(λ+1),2√3λ)． 所以 PQ⃗⃗⃗⃗⃗ =(0,−2(λ+1),2√3λ)． 因为 A 1B 1=AB =2，∠B 1A 1A =60∘， 所以 B 1(√3,1,0)， 所以 PB 1⃗⃗⃗⃗⃗⃗⃗ =(√3,1,0)．设平面 PQB 1 的法向量为 m ⃗⃗ =(x,y,z )，则 {m ⃗⃗ ⋅PQ⃗⃗⃗⃗⃗ =0⃗ ,m ⃗⃗ ⋅PB 1⃗⃗⃗⃗⃗⃗⃗ =0⃗ ,所以 {−2(λ+1)y +2√3λz =0,√3x +y =0,令 x =1， 则 y =−√3，z =−λ+1λ，所以平面 PQB 1 的一个法向量为 m ⃗⃗ =(1,−√3,−λ+1λ)．设平面 AA 1C 1C 的法向量为 n ⃗ =(1,0,0)， 二面角 B 1−PQ −C 1 的平面角为 θ， 则cosθ=∣m⃗⃗⃗ ⋅n ⃗ ∣∣m⃗⃗⃗ ∣∣n ⃗ ∣=√1+3+(−λ)2=√1313.所以 λ=12 或 λ=−14（舍）， 所以 AQ⃗⃗⃗⃗⃗ =12AC ⃗⃗⃗⃗⃗ ， 所以 Q(0,−3,√3)， 又 B(√3,−3,0)，所以 QB⃗⃗⃗⃗⃗ =(√3,0,−√3)， 所以 ∣QB ⃗⃗⃗⃗⃗ ∣=√3+3=√6． 又 ∣B 1Q ⃗⃗⃗⃗⃗⃗⃗ ∣=√22， 所以 BQ 2+BB 12=B 1Q 2， 所以 ∠QBB 1=90∘．连接 BP ，设点 P 到平面 BQB 1 的距离为 ℎ， 则 13×12×4×√3×√3=13×12×4×√6⋅ℎ．所以 ℎ=√62， 即点 P 到平面 BQB 1 的距离为√62． 【知识点】直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题、二面角21. 【答案】连接 BD 交 AC 于 G ，连接 FG ．因为 F ，G 分别为 BE ，BD 的中点， 所以 FG ∥DE ，因为 FG ⫋平面ACF ，DE ⊄面ACF ， 所以 DE ∥面ACF ．【知识点】直线与平面平行关系的判定22. 【答案】① EF ⊥平面BDD 1② EF ⊥DE③ DE ⊥BD 1 ④线线平行 ⑤线面平行【知识点】直线与平面垂直关系的判定、直线与直线的位置关系、直线与平面平行关系的判定、直线与平面垂直关系的性质。

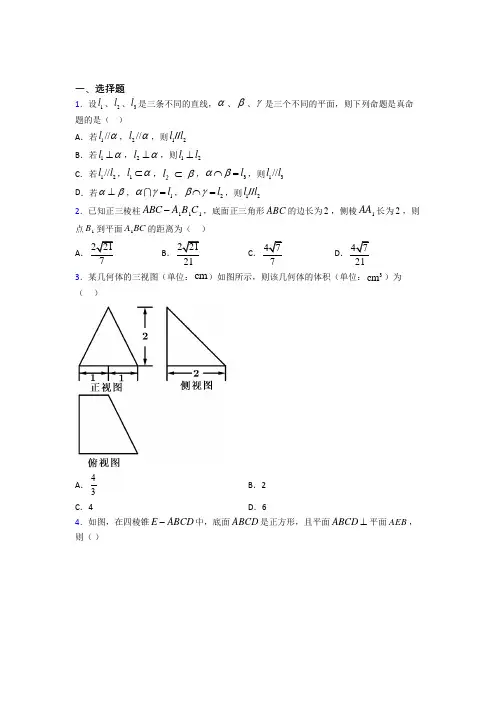
一、选择题1．设1l 、2l 、3l 是三条不同的直线，α、β、γ是三个不同的平面，则下列命题是真命题的是（ ）A ．若1//l α，2//l α，则12l l //B ．若1l α⊥，2l α⊥，则12l l ⊥C ．若12//l l ，1l α⊂，2l β⊂，3l αβ⋂=，则13//l lD ．若αβ⊥，1l αγ=，2l βγ⋂=，则12l l //2．已知正三棱柱111ABC A B C -，底面正三角形ABC 的边长为2，侧棱1AA 长为2，则点1B 到平面1A BC 的距离为（ ）A ．2217B ．22121 C ．47D ．473．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：3cm ）为（ ）A ．43B ．2C ．4D ．64．如图，在四棱锥E ABCD -中，底面ABCD 是正方形，且平面ABCD ⊥平面AEB ，则（ ）A ．DEC ∠可能为90︒B ．若AEB △是等边三角形，则DEC 也是等边三角形C ．若AEB △是等边三角形，则异面直线DE 和AB 所成角的余弦值为24D ．若AEB △是直角三角形，则BE⊥平面ADE5．如图所示，A ，B 为正方体的两个顶点，M ，N 为其所在棱的中点，则异面直线AB 与MN 所成角的大小为（ ）A ．30°B ．45°C ．60°D ．90°6．在长方体1111ABCD A BC D -中，2AB =，1AD =，12AA =，点E 为11C D 的中点，则二面角11B A B E --的余弦值为（ ） A ．3B ．3C 3D 37．《九章算术》是古代中国乃至东方的第一步自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（ ）A ．6π B ．4π C ．3πD ．2π 8．在正方体1111ABCD A BC D -中，M 是棱1CC 的中点．则下列说法正确的是（ ） A ．异面直线AM 与BC 所成角的余弦值为5B ．BDM 为等腰直角三角形C ．直线BM 与平面11BDD B 所成角的正弦值等于105D ．直线1AC 与平面BDM 相交9．一个几何体的三视图如图所示，则该几何体的体积为（ ）A ．4B ．8C ．12D ．1410．在三棱锥S ABC -中，SA ⊥底面ABC ，且22AB AC ==，30C ∠=，2SA =，则该三棱锥外接球的表面积为（ ） A ．20πB ．12πC ．8πD ．4π11．已知长方体1111ABCD A BC D -的顶点A ，B ，C ，D ，在球O 的表面上，顶点1A，1B ，1C ，1D ，在过球心O 的一个平面上，若6AB =，8AD =，14AA =，则球O 的表面积为（ ） A ．169πB ．161πC ．164πD ．265π12．已知直线a 、b 都不在平面α内，则下列命题错误的是（ ） A ．若//a b ，//a α，则//b α B ．若//a b ，a α⊥，则b α⊥ C ．若a b ⊥，//a α，则b α⊥D ．若a b ⊥，a α⊥，则//b α二、填空题13．若一个底面边长为6，侧棱长为6的正六棱柱的所有定点都在一个球的面上，则此球的体积是___________．14．已知正四棱锥的体积为18，侧棱与底面所成的角为45，则该正四棱锥外接球的表面积为___________.15．在正三棱锥O ABC -中，已知45AOB ∠=︒，记α为二面角--A OB C 的大小，cos =+m n α，其中m ，n 为整数，则以||n ，||m ，||m n +分别为长、宽、高的长方体的外接球直径为__________．16．已知一个圆锥内接于球O （圆锥的底面圆周及顶点均在同一球面上），圆锥的高是底面半径的3倍，圆锥的侧面积为910π，则球O 的表面积为________． 17．在三棱柱111ABC A B C -中侧棱垂直底面且底面是ABC 为等边三角形且12A A AB =，E 在棱1AA 上，112AE A A =，则异面直线1AC 与BE 所成角的余弦值___________.18．如图，矩形ABCD 中，2AB AD =，E 为边AB 的中点，将ADE 沿直线DE 翻折成1A DE △．若M 为线段1AC 的中点，则在ADE 翻折过程中，下面四个选项中正确的是______（填写所有的正确选项）（1）BM 是定值（2）点M 在某个球面上运动 （3）存在某个位置，使1DE AC ⊥ （4）存在某个位置，使//MB 平面1A DE 19．将半径为3，圆心角为23π的扇形围成一个圆锥，则该圆锥内切球的体积为________． 20．在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，且ABCD 为矩形，π2DPA ∠=，23AD =2AB =，PA PD =，则四棱锥P ABCD -的外接球的体积为________.三、解答题21．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为平行四边形，1,2AB BC ==，45ABC ∠=︒，AE PC ⊥垂足为E ．（Ⅰ）求证：平面AEB ⊥平面PCD ；（Ⅱ）若二面角B AE D --的大小为150︒，求侧棱PA 的长．22．在如图所示的几何体中，四边形BCED 为直角梯形，//DE CB ，BC EC ⊥，90AED ∠=︒.（1）证明：平面ABC ⊥平面ACE .（2）若P ，Q 分别是AE ，CD 的中点，证明：//PQ 平面ABC .23．在三棱锥A BCD -中，E 、F 分别为AD 、DC 的中点，且BA BD =，平面ABD ⊥平面ADC .（1）证明：//EF 平面ABC ； （2）证明：BE CD ⊥.24．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，,,AB AD AC CD PA AC ⊥⊥=，E 是PC 的中点．证明：（Ⅰ）CD AE ⊥； （Ⅱ）PD ⊥平面ABE ．25．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为梯形，//AD BC ，6BC =，2PA AD CD ===，E 是BC 上一点且23BE BC =，PB AE ⊥.（1）求证：AB ⊥平面PAE ； （2）求点C 到平面PDE 的距离.26．如图，在矩形ABCD 中，2AB AD =，M 为DC 的中点，将ADM △沿AM 折起使平面ADM ⊥平面ABCM .（1）求证：BM AD ⊥；（2）求直线DC 与平面DAB 所成角的正弦值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】利用已知条件判断1l 与2l 的位置关系，可判断AD 选项的正误；利用线面垂直的性质定理可判断B 选项的正误；利用线面平行的性质定理可判断C 选项的正误. 【详解】对于A 选项，若1//l α，2//l α，则1l 与2l 平行、相交或异面，A 选项错误； 对于B 选项，若1l α⊥，2l α⊥，由线面垂直的性质定理可得12//l l ，B 选项错误； 对于C 选项，12//l l ，1l α⊂，2l β⊂，α、β不重合，则1l β⊄，1//l β∴，1l α⊂，3l αβ⋂=，13//l l ∴，C 选项正确；对于D 选项，若αβ⊥，1l αγ=，2l βγ⋂=，则1l 与2l 相交或平行，D 选项错误.故选：C. 【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．2．A解析：A 【分析】根据题意，将点1B 到平面1A BC 的距离转化为点A 到平面1A BC 的距离，然后再利用等体积法11A A BC A ABC V V --=代入求解点A 到平面1A BC 的距离. 【详解】已知正三棱柱111ABC A B C -，底面正三角形ABC 的边长为2，侧棱1AA 长为2，所以可得11==A B AC 1A BC 为等腰三角形，所以1A BC 知，111--=B A BC A A BC V V ，所以点1B 到平面1A BC 的距离等于点A 到平面1A BC 的距离，所以11A A BC A ABC V V --=，又因为1122=⨯=A BC S △122ABCS =⨯=111233⨯⨯=⨯⨯A BC ABC S h S △△，即7h ==. 故选：A.【点睛】一般关于点到面的距离的计算，一是可以考虑通过空间向量的方法，写出点的坐标，计算平面的法向量，然后代入数量积的夹角公式计算即可，二是可以通过等体积法，通过换底换高代入利用体积相等计算.3．B解析：B【分析】根据三视图判断出几何体的结构，利用椎体体积公式计算出该几何体的体积.【详解】根据三视图可知，该几何体为如图所示四棱锥，该棱锥满足底面是直角梯形，且侧棱ED⊥平面ABCD，所以其体积为11(12)22232V=⨯⨯+⨯⨯=，故选：B.【点睛】方法点睛：该题考查的是有关根据几何体三视图求几何体体积的问题，解题方法如下：（1）首先根据题中所给的几何体的三视图还原几何体；（2）结合三视图，分析几何体的结构特征，利用体积公式求得结果.4．C解析：C 【分析】对A ，直角三角形的斜边大于直角边可判断；对B ，由>=EC EB DC 可判断；对C ，可得CDE ∠即异面直线DE 和AB 所成角，即可求出；对D ，EAB ∠（或EBA ∠）为直角时，BE 与平面ADE 不垂直. 【详解】对A ，由题意，若90DEC ∠=︒，则DC EC >，但EC BC CD >=，故A 不正确； 对B ，若AEB △是等边三角形，显然有>=EC EB DC ，所以DEC 不会是等边三角形，故B 不正确；对C ，若AEB △是等边三角形，设边长为2，则DE EC ==，//AB CD ，则CDE ∠即异面直线DE 和AB 所成角，易求cos4CDE ∠==，故C 正确； 对D ，当AEB △是以AEB ∠为直角的直角三角形时，BE ⊥平面ADE ，当AEB △是以EAB ∠（或EBA ∠）为直角的直角三角形时，BE 与平面ADE 不垂直，故D 不正确．故选：C. 【点睛】本题考查四棱锥的有关位置关系的判断，解题的关键是正确理解长度关系，正确理解位置关系的变化.5．C解析：C 【分析】由MN 与正方体的面对角线平行，可得异面直线所成的角，此角是正三角形的内角，由此可得． 【详解】作如图所示的辅助线，由于M ，N 为其所在棱的中点，所以//MN PQ ，又因为//AC PQ ，所以//AC MN ，所以CAB ∠即为异面直线AB 与MN 所成的角（或补角），易得AB AC BC ==，所以60CAB ∠=︒. 故选：C ．6．C解析：C 【分析】取11A B 的中点F ，过F 作1FG A B ⊥，垂足为G ，连EG ，可证EGF ∠为二面角11B A B E --的平面角，通过计算可得结果.【详解】取11A B 的中点F ，过F 作1FG A B ⊥，垂足为G ，连EG ，因为,E F 分别为1111,C D A B 的中点，所以11//EF A D ，在长方体1111ABCD A BC D -中，因为11A D ⊥平面11ABB A ，所以EF ⊥平面11ABB A ， 因为1A B ⊂平面11ABB A ，所以1EF A B ⊥，因为1FG A B ⊥，且FGEF F =，所以1A B ⊥平面EFG ，因为EG ⊂平面EFG ，所以1A B EG ⊥，所以EGF ∠为二面角11B A B E --的平面角， 因为12AB AA ==，所以14FA G π∠=，因为11A F =，所以12222FG A F ==， 在直角三角形EFG 中，221612EG EF FG =+=+=， 所以cos FG EGF EG ∠==2326=. 所以二面角11B A B E --3.故选：C 【点睛】关键点点睛：根据二面角的定义作出其中一个平面角是解题关键.7．D解析：D 【分析】过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，然后在CFG △中求解. 【详解】如下图所示，在平面ABFE 中，过点F 作//FG AE 交AB 于点G ，连接CG ， 则异面直线AE 与CF 所成角为CFG ∠或其补角，设1EF =，则3AB =，2BC CF AE ===，因为//EF AB ，//FG AE ，所以，四边形AEFG 为平行四边形， 所以，2FG AE ==，1AG =，2BG =， 由于2ABC π∠=，由勾股定理可得2222CG BC BG =+=所以，222CG CF FG =+，则2CFG π∠=.故选：D. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．8．C解析：C 【分析】A 通过平移，找出异面直线所成角，利用直角三角形求余弦即可. B.求出三角形的三边，通过勾股定理说明是不是直角三角形.C.求出点M 到面11BB D D 的距离，再求直线BM 与平面11BDD B 所成角的正弦.D.可通过线线平行证明线面平行. 【详解】 设正方体棱长为2A. 取1BB 的中点为N ，则//BC MN ，则AM 与BC 所成角为AMN ∠ 由BC ⊥面11ABB A ，故MN ⊥面11ABB A ，故MN AN ⊥，在Rt ANM △中，5tan 2AMN ∠=，故2cos 3AMN ∠=B. BDM 中，5BM =，22BD =，5DM =，不满足勾股定理，不是直角三角形C. AC BD ⊥，1AC BB ⊥，故AC ⊥面11BB D D ，1//CC 面11BB D D ，故M 到面11BB D D 的距离等于C 到面11BB D D 的距离，即为122d AC ==直线BM 与平面11BDD B 所成角为θ210sin 55d BM θ===直线BM 与平面11BDD B 所成角的正弦值等于10D.如图ACBD O =OM 为1ACC △的中位线，有1//OM AC故直线1AC 与平面BDM 平行故选：C 【点睛】本题考查了空间几何体的线面位置关系判定与证明：（1）对于异面直线的判定要熟记异面直线的概念：把既不平行也不相交的两条直线称为异面直线；（2）对于线面位置关系的判定中，熟记线面平行与垂直、面面平行与垂直的定理是关键.9．C解析：C 【分析】根据三视图还原得其几何体为四棱锥，根据题意代入锥体体积公式计算即可. 【详解】解：根据三视图还原得其几何体为四棱锥，图像如下：根据图形可得ABCD 是直角梯形，PA ⊥平面ABCD ，2,4,2,6AB CD PA AD ==== 所以11246212332P ABCD ABCD V S PA -+=⋅=⨯⨯⨯= 故选：C 【点睛】 识别三视图的步骤（1）弄清几何体的结构特征及具体形状、明确几何体的摆放位置；（2）根据三视图的有关定义和规则先确定正视图，再确定俯视图，最后确定侧视图； （3）被遮住的轮廓线应为虚线，若相邻两个物体的表面相交，表面的交线是它们的分界线；对于简单的组合体，要注意它们的组合方式，特别是它们的交线位置.10．A解析：A 【分析】利用正弦定理求出ABC 的外接圆直径2r ，利用公式()2222R r SA =+棱锥S ABC -的外接球直径，然后利用球体的表面积公式可求得结果. 【详解】如下图所示，设圆柱的底面半径为r ，母线长为h ，圆柱的外接球半径为R ，取圆柱的轴截面，则该圆柱的轴截面矩形的对角线的中点O 到圆柱底面圆上每个点的距离都等于R ，则O 为圆柱的外接球球心，由勾股定理可得()()22222r h R +=.本题中，SA ⊥平面ABC ，设ABC 的外接圆为圆1O ，可将三棱锥S ABC -内接于圆柱12O O ，如下图所示：设ABC 的外接圆直径为2r ，2SA h ==， 由正弦定理可得24sin ABr C==∠，，该三棱锥的外接球直径为2R ，则()222225R r h =+=.因此，三棱锥S ABC -的外接球的表面积为()224220R R πππ=⨯=.故选：A. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.11．C解析：C 【分析】把两个这样的长方体叠放在一起，构成一个长宽高分别为6，8，8的长方体，则球O 就是该长方体的外接球，根据长方体外接球的直径等于体对角线的长，求出直径，即可得出球的表面积. 【详解】 如下图所示：把两个这样的长方体叠放在一起，构成一个长宽高分别为6，8，8的长方体，则球O 就是该长方体的外接球，根据长方体的结构特征可得，其外接球直径等于体对角线的长， 所以球O 的半径R 满足2222688164R =++=， 所以球O 的表面积24164S R ππ==. 故选：C.【点睛】关键点点睛：本题主要考查几何体外接球的表面积，熟记长方体结构特征，其外接球的球心和半径与长方体的关系，以及球的表面积公式，是解决此类问题的关键.12．C解析：C 【分析】利用线面平行的性质和判定定理可判断A 选项的正误；由线面垂直的定义可判断B 选项的正误；根据已知条件判断b 与α的位置关系，可判断C 选项的正误；根据已知条件判断b 与α的位置关系，可判断D 选项的正误. 【详解】由于直线a 、b 都不在平面α内.在A 中，若//a α，过直线a 的平面β与α的交线m 与a 平行， 因为//a b ，可得//b m ，b α⊄，m α⊂，所以，//b α，A 选项正确；在B 中，若a α⊥，则a 垂直于平面α内所有直线，//a b ，则b 垂直于平面α内所有直线，故b α⊥，B 选项正确；在C 中，若a b ⊥，//a α，则b 与α相交或平行，C 选项错误； 在D 中，若a b ⊥，a α⊥，则//b α或b α⊂，b α⊄，//b α∴，D 选项正确.故选：C. 【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．二、填空题13．【分析】计算出正六棱柱的外接圆直径进而可求得外接球的半径利用球体体积公式即可计算出正六棱柱的外接球的体积【详解】如下图所示：圆柱的底面圆直径为母线长为则的中点到圆柱底面圆上每点的距离都相等则为圆柱外 解析：43π【分析】计算出正六棱柱的外接圆直径，进而可求得外接球的半径，利用球体体积公式即可计算出正六棱柱的外接球的体积. 【详解】 如下图所示：圆柱12O O 的底面圆直径为2r ，母线长为h ，则12O O 的中点O 到圆柱底面圆上每点的距离都相等，则O 为圆柱12O O 外接球的球心，设球O 的半径为R ，则()2222R r h =+可作出正六棱柱111111ABCDEF A BC D E F -的外接圆，可将正六棱柱111111ABCDEF A BC D E F -放在圆柱12O O 中，如下图所示：连接11O A 、11O B ，则11160AO B ∠=，且1111O A O B =，则111O A B △为等边三角形， 则圆1O 的半径为11116r O A A B ===正六棱柱111111ABCDEF A BC D E F -的侧棱长为6h = 设正六棱柱111111ABCDEF A BC D E F -的外接球的半径为R ，则()222223R r h =+=所以，3R 33443=4333V R πππ==⨯.故答案为：43π. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.14．【分析】作出图形计算出正四棱锥的高与底面边长设底面的中心为计算得出为正四棱锥的外接球球心可求得该正四棱锥的外接球半径即可得解【详解】如下图所示设正四棱锥的底面的中心为连接设正四棱锥的底面边长为则由于 解析：36π【分析】作出图形，计算出正四棱锥P ABCD -的高与底面边长，设底面ABCD 的中心为E ，计算得出E 为正四棱锥P ABCD -的外接球球心，可求得该正四棱锥的外接球半径，即可得解. 【详解】如下图所示，设正四棱锥P ABCD -的底面ABCD 的中心为E ，连接PE 、AC 、BD ，设正四棱锥P ABCD -的底面边长为a ，则2AC BD a ==，由于E 为正四棱锥P ABCD -的底面ABCD 的中心，则PE ⊥平面ABCD ， 由于正四棱锥P ABCD -的侧棱与底面所成的角为45，则45PAC PCA ∠=∠=， 所以，PAC △是以APC ∠为直角的等腰直角三角形， 同理可知，PBD △是以BPD ∠为直角的等腰直角三角形，E 为AC 的中点，122PE AC ==，2ABCD S a =正方形， 231122183326P ABCD ABCD V S PE a a a -=⋅=⨯⨯==正方形，解得32a =232PE a ==，由直角三角形的性质可得1122PE AC BD ==，即PE AE BE CE DE ====，所以，E 为正四棱锥P ABCD -外接球的球心，球E 的半径为3r PE ==，该球的表面积为2436r ππ=. 故答案为：36π. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.15．【分析】过作垂足为连接则为二面角的平面角即在中利用余弦定理结合为整数求出的值进而可得外接球直径【详解】如图过作垂足为连接则为二面角的平面角即不妨设因为所以所以所以在中因为为整数所以则设以为长宽高的长 6【分析】过A 作AH OB ⊥，垂足为H ，连接CH ，则AHC ∠为二面角--A OB C 的平面角，即∠=AHC α，在AHC 中，利用余弦定理结合m ，n 为整数，求出m ，n 的值，进而可得外接球直径． 【详解】如图，过A 作AH OB ⊥，垂足为H ，连接CH ，则AHC ∠为二面角--A OB C 的平面角，即∠=AHC α．不妨设2OC a =，因为45AOB ∠=︒，所以===CH a AH OH ，所以(21)=HB a ，所以22222(422)=+=-=BC HB HC a AC ．在AHC 中，222cos 2+-==⋅⋅HA HC AC HA HC α2222(422)212+--==+a a a m n a因为m ，n 为整数，所以1m =-，2n =，则||1m =，||2n =，||1m n +=． 设以||m ，||n ，||m n +为长、宽、高的长方体的外接球半径为R ， 则2222(2)||||||6=+++=R m n m n 6 6【点睛】关键点点睛：本题考查二面角的应用，考查几何体的外接球，考查解三角形，解决本题的关键点是利用定义法找出二面角的平面角，在AHC 中，利用余弦定理结合已知条件求出m ，n 的值，考查学生空间想象能力，考查计算能力，属于中档题．16．【分析】设圆锥的底面半径为球的半径为根据勾股定理可得根据圆锥的侧面积公式可得再根据球的表面积公式可得结果【详解】设圆锥的底面半径为球的半径为则圆锥的高为则球心到圆锥的底面的距离为根据勾股定理可得化简 解析：100π【分析】设圆锥的底面半径为r ，球O 的半径为R ，根据勾股定理可得53R r =，根据圆锥的侧面积公式可得3,5r R ==，再根据球的表面积公式可得结果. 【详解】设圆锥的底面半径为r ，球O 的半径为R ，则圆锥的高为3r ， 则球心O 到圆锥的底面的距离为3r R -，根据勾股定理可得()2223R r r R =+-，化简得53R r =，因为圆锥的高为3r ，母线长为()22310r r r +=， 所以圆锥的侧面积为21010r r r ππ⨯=，所以210910r ππ=，解得r =3，所以5353R =⨯=， 所以球O 的表面积为24425100R πππ=⨯=. 故答案为：100π 【点睛】关键点点睛：利用圆锥的侧面积公式和球的表面积公式求解是解题关键.17．【分析】取的中点连接可得所以或其补角即为异面直线与所成角在中求即可求解【详解】取的中点连接因为所以且所以或其补角即为异面直线与所成角设则所以因为是等边三角形所以因为平面平面所以所以在中因为异面直线所 解析：310【分析】取11AC 的中点1O ，连接1EO ，1AC ，可得11//EO AC ，所以1BEO ∠或其补角即为异面直线1AC 与BE 所成角，在1BEO 中，求1cos BEO ∠即可求解. 【详解】取11AC 的中点1O ，连接1EO ，11B O ，EB ，EC ，1BO ，1AC ， 因为112AE A A =，所以11//EO AC 且111=2EO AC ， 所以1BEO ∠或其补角即为异面直线1AC 与BE 所成角， 设1AB =，则12AA =， 所以2211115=12222EO AC =+=，112BE =+= 因为111A B C △是等边三角形，112AE A A =，所以21113122B O ⎛⎫=-= ⎪⎝⎭，因为1BB ⊥平面111A B C ，11B O ⊂平面111A B C ，所以 1BB ⊥11B O ，所以1BO === 在1BEO中，22211115192cos 2BE EO BO BEO BE EO +-+-∠===⨯， 因为异面直线所成的角为锐角或直角，所以异面直线1AC 与BE，故答案为：20【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．18．（1）（2）（4）【分析】首先取中点连结先判断（4）是否正确再根据平行关系以及等角定理和余弦定理判断（1）再判断（2）假设成立根据直线与平面垂直的性质及判定可得矛盾来判断（3）【详解】取中点连结则平解析：（1）（2）（4） 【分析】首先取CD 中点Q ，连结MQ ，BQ ，先判断（4）是否正确，再根据平行关系，以及等角定理和余弦定理判断（1），再判断（2），假设1DE AC ⊥成立,根据直线与平面垂直的性质及判定,可得11DA A E ⊥矛盾来判断（3）. 【详解】取CD 中点Q ，连结MQ ，BQ ，则1//MQ DA ，//BQ DE ，∴平面//MBQ 平面1A DE ，又MB ⊂平面MBQ ，//MB ∴平面1A DE ，故（4）正确；由1A DE MQB ∠=∠，112MQ A D ==定值，QB DE ==定值， 由余弦定理可得2222cos MB MQ QB MQ QB MQB =+-⋅⋅∠ 所以MB 是定值，故（1）正确；B 是定点，M ∴是在以B 为球心，MB 为半径的球面上，故（2）正确；145A DE ADE ∠=∠=，45CDE ∠=，且设1AD =，2AB =，则2DE CE ==若存在某个位置,使1DE AC ⊥,则因为222DE CE CD +=,即CE DE ⊥,因为1AC CE C =,则DE ⊥平面1ACE ,所以1DE A E ⊥,与11DA A E ⊥矛盾， 故（3）不正确.故答案为：（1）（2）（4） 【点睛】关键点点睛：本题考查线线，线面位置关系时，首先判断（4）是否正确，其他选项就迎刃而解，而判断线面平行时，可根据面面平行证明线面平行.19．【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径设内切球半径为r ﹐圆锥高为h 结合轴截面图形计算得最后计算体积即可【详解】解：设圆锥底面半径为R 则所以设内切球半径为r ﹐圆锥高为h 则如图是圆锥轴截面三 解析：23π【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径1R =，设内切球半径为r ﹐圆锥高为h ，结合轴截面图形计算得22r ，最后计算体积即可. 【详解】解：设圆锥底面半径为R ，则2233R ππ=⨯，所以1R =．设内切球半径为r ﹐圆锥高为h ，则9122h =-=， 如图，是圆锥轴截面三角形图， 所以3r Rh r =-，解得：22r ， 故34422233r V πππ==⨯=． 故答案为：23π【点睛】本题考查圆锥的侧面展开图，圆锥的内切球的体积，考查空间想象能力，是中档题.20．【分析】由矩形的边长可得底面外接圆的半径再由为等腰直角三角形可得其外接圆的半径又平面平面可得底面外接圆的圆心即为外接球的球心由题意可得外接球的半径进而求出外接球的体积【详解】解：取矩形的对角线的交点 解析：323π【分析】由矩形的边长可得底面外接圆的半径，再由PAD △为等腰直角三角形可得其外接圆的半径，又平面PAD ⊥平面ABCD 可得底面外接圆的圆心即为外接球的球心，由题意可得外接球的半径，进而求出外接球的体积． 【详解】解：取矩形的对角线的交点O 和AD 的中点E ，连接OE ，OP ，OE ， 则O 为矩形ABCD 的外接圆的圆心，而2DPA π∠=，23AD =2AB =，PA PD =，则//OE AB ，112OE AB ==， 132PE AD == 所以E 为PAD △的外接圆的圆心，因为平面PAD ⊥平面ABCD ， 所以O 为外接球的球心，OP 为外接球的半径，在POE △中，222222(3)14R OP PE OE ==+=+=，所以2R =， 所以外接球的体积343233V R ππ==， 故答案为：323π．【点睛】本题考查四棱锥的棱长与外接球的半径的关系及球的体积公式，属于中档题．三、解答题21．（Ⅰ）证明见解析；（Ⅱ2【分析】（Ⅰ）推导出AB AC ⊥，CD AC ⊥，PA CD ⊥，从而CD ⊥平面PAC ，进而CD AE ⊥，AE PC ⊥，由此能证明平面AEB ⊥平面PCD ．（Ⅱ）以A 为原点，以AB ，AC ，AP 所在射线分别为x ，y ，z 的正半轴，建立空间直角坐标系，利用向量法能求出侧棱PA 的长． 【详解】 证明：（Ⅰ）1,2,45AB BC ABC =∠=︒，AB AC ∴⊥又//AB CD ，CD AC ∴⊥， PA ⊥平面ABCD ，PA CD ∴⊥，又ACAP A =，,AC AP ⊂平面PAC ，CD平面PAC ，AE ⊂平面PAC ，CD AE ∴⊥，又AE PC ⊥，PC CD C =，,PC CD ⊂平面PCD ，AE ∴⊥平面PCD ，又AE ⊂平面AEB ，∴平面AEB ⊥平面PCD ．（Ⅱ）以A 为原点，以AB ，AC ，AP 所在射线分别为x ，y ，z 的正半轴，建立空间直角坐标系．设AP t =，则(0A ，0，0)，(1B ，0，0)，(0C ，1，0)，(1,10)D -，(0P ，0，)t ，AB PC ⊥，AE PC ⊥，PC ∴⊥平面ABE ，∴平面ABE 的一个法向量为(0,1,)n PC t ==-在Rt PAC △中，PA t =，211AC PC t =∴=+，又AE PC ⊥，21AE t =+，得222(0,,)11t tE t t ++设平面ADE 的一个法向量为(,,)m x y z =由m AD m AE ⎧⊥⎨⊥⎩，得222··0110t t y z t t x y ⎧+=⎪++⎨⎪-+=⎩，解得(1,1,)m t =- 二面角B AE D --的大小为150︒，∴222||3|cos ,||cos150|||||12m n m n m n t t 〈〉===︒=++， 解得2t =，故侧棱PA 的长为2．【点睛】本题考查了立体几何中的面面垂直的判定和二面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化，通过严密推理，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解. 22．（1）证明见解析；（2）证明见解析. 【分析】（1）由DE EC ⊥，AE DE ⊥，利用线面垂直的判定定理可得DE ⊥平面ACE ，再由。

2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．下列命题正确的是（ ）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行2．若3sin (0)52x x π=--<<，则tan x =_____________.二、填空题3．如图，有一圆柱形的开口容器（下表面密封），其轴截面是边长为2的正方形，P 是BC 中点，现有一只蚂蚁位于外壁A 处，内壁P 处有一米粒，则这只蚂蚁取得米粒所需经过的最短路程为 ．4．把半径为3cm ,中心角为π32的扇形卷成一个圆锥形容器，这个容器的容积为：__________．5．在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________（2013年高考上海卷（理））6．空间中可以确定一个平面的条件是 _．(填序号) ①两条直线； ②一点和一直线； ③一个三角形； ④三个点．7．设，，a b g 为两两不重合的平面,l ,m ,n 为两两不重合的直线,给出下列四个命题： ①若,,//,//,m n m n ⊂⊂a a b b 则//a b ； ②//,,l ⊂a b a 若则//l b ； ③,,,//,l m n l m ===若ab bg ga 则 //m n ; ④若⊥⊥a gb g ，，则//a b ； 则其中所有正确命题的序号是 ▲ ．8．如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥D D BB A 11-的体积为 cm 3.9．设正四棱锥的侧棱长为1，则其体积的最大值为 ▲ ．10．如图，在边长为a 的正方体ABCD-A 1B 1C 1D 1中，E 是棱AB 上一点，M 是棱D 1C 1上一点，则三棱锥M-DEC 的体积是 ▲11．给出下列命题：DABC1C1D 1A1BD C1A 1B 1C 1D .EBAM.（第6题图）（1）若直线a 在平面α外，则直线a 与平面α没有公共点；（2）两个平面平行的充分条件是其中一个平面内有无数条直线平行于另一个平面； （3）设a 、b 、c 是同一平面内三条不同的直线，若a ⊥b ，a ⊥c ，则b ∥c ; （4）垂直于同一平面的两个平面平行；（5）若,a b 为异面直线，则过不在,a b 上的任一点，可作一个平面与,a b 都平行． 上面命题中，真命题．．．的序号是 ．12．己知点E 、F 分别在正方体ABCD -A 1B 2C 3D 4的棱BB 1 、CC 1上，且B 1E =2EB, CF=2FC 1，则面AEF 与面ABC 所成的二面角的正切值等于 . (2011年高考全国卷理科16)13．如图，在三棱锥P ABC -中，PA ⊥平面ABC ，,AB BC PA AB BC ⊥==，则PB 与平面ABC 所成的角为_______，PC 与平面PAB 所成的角的正切值等于____________ CBAP14．在长方体1111ABCD A B C D -中，若13,4AB BC AA ===，求1A B 和1B C 所成角的余弦值。

高一数学必修第二册第八章《立体几何初步》单元练习题卷9（共22题）一、选择题（共10题）1.用斜二测画法作出一个三角形的直观图，则原三角形面积是直观图面积的( )A．12倍B．2√2倍C．2倍D．√24倍2.若长方体三个面的面积分别为√2，√3，√6，则长方体的体积等于( )A．√6B．6C．6√6D．363.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为( )A．9πB．22π3C．28π3D．34π34.在下列命题中：①存在一个平面与正方体的12条棱所成的角都相等；②存在一个平面与正方体的6个面所成较小的二面角都相等；③存在一条直线与正方体的12条棱所成的角都相等；④存在一条直线与正方体的6个面所成的角都相等．其中真命题的个数为( )A．1B．2C．3D．4 5.已知底面半径为1的圆锥侧面展开图是一个半圆，则该圆锥的体积是( )A．√33πB．2√33πC．√3πD．4√33π6.如图，正方体ABCD−A1B1C1D1的棱长为a，M，N分别为A1B和AC上的点，A1M=AN=√23a，则MN与平面BB1C1C的位置关系是( )A．相交但不垂直B．平行C．垂直D．不能确定7.体积为√3的三棱锥P−ABC的顶点都在球O的球面上，PA⊥平面ABC，PA=2，∠ABC= 120∘，则球O的体积的最小值为( )A．7√73πB．28√73πC．19√193πD．76√193π8.已知矩形ABCD中，AB=2，BC=1，F为线段CD上一动点（不含端点），现将△ADF沿直线AF进行翻折，在翻折过程中不可能成立的是( )A．存在某个位置，使直线AF与BD垂直B．存在某个位置，使直线AD与BF垂直C．存在某个位置，使直线CF与DA垂直D．存在某个位置，使直线AB与DF垂直9.如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则( )A．BM=EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM=EN，且直线BM，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线10.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A．14斛B．22斛C．36斛D．66斛二、填空题（共6题）11.若圆柱的轴截面为正方形，且此正方形面积为4，则该圆柱的体积为．12.设一个圆锥的侧面展开图是半径为2的半圆，则此圆锥的体积等于．13.若两条直线a，b无公共点，则两直线的位置关系是．14.棱长为1的正方体ABCD−A1B1C1D1及其内部一动点P，集合Q={P∣∣ PA∣ ≤1}，则集合Q构成的几何体表面积为．15.如图所示，已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成，则该多面体的体积是．16.在三棱椎P­−ABC中，底面ABC是等边三角形，侧面PAB是直角三角形，且PA=PB=2，PA⊥AC，则该三棱椎外接球的表面积为．三、解答题（共6题）17.已知圆柱的底面直径与高都等于球的直径．求证：(1) 球的表面积等于圆柱的侧面积；．(2) 球的表面积等于圆柱全面积的2318.侧面都是等腰直角三角形的正三棱锥，底面边长为a时，求该棱锥的表面积．19.已知四棱锥P−ABCD中，底面ABCD为等腰梯形，AD∥BC，PA=AD=AB=CD=1，BC=2，PB=PD=√2．(1) 证明：AC⊥平面PAB；(2) 过PA的平面交BC于点E，若平面PAE把四棱锥P−ABCD分成体积相等的两部分，求此时三棱锥E−PBD的体积．20.画出如图所示水平放置的直角梯形的直观图．21.如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD为正方形，F为对角线AC与BD的交点，E为棱PD的中点．(1) 证明：EF∥平面PBC；(2) 证明：AC⊥PB．22.如图，在正方体ABCD−A1B1C1D1中，点M，N，E，F分别是棱CD，AB，DD1，AA1上的点，若MN与EF交于点Q，求证：D，A，Q三点共线．答案一、选择题（共10题） 1. 【答案】B【解析】设原三角形的底边长为 a ，高为 ℎ，则直观图中底边长仍为 a ，高为 ℎ2⋅sin45∘=√2ℎ4，所以原三角形面积与直观图面积的比值为 12aℎ12a⋅√2ℎ4=√2=2√2，即原三角形面积是直观图面积的2√2 倍． 【知识点】直观图2. 【答案】A【解析】如图，设长方体 ABCD −A 1B 1C 1D 1 的侧面 AA 1B 的面积为 √2，侧面 AA 1D 的侧面积为 √3，侧面ABD 的侧面积为 √6．再设侧棱 AA 1=a ，AD =b ，AB =c ． 则 {ac =√2,ab =√3,bc =√6, 三式作积得：a 2b 2c 2=6．所以 abc =√6．所以长方体的体积等于 √6．【知识点】棱柱的表面积与体积3. 【答案】D【解析】根据几何体的三视图可得直观图为：该几何体为上面为一个半径为 2 的半球，下面为底面半径为 2，高为 3 的半圆柱体． 如图所示：故 V =12×π×22×3+23×π×23=34π3．【知识点】球的表面积与体积、由三视图还原空间几何体、圆柱的表面积与体积4. 【答案】D【解析】①存在一个平面AB1D1与正方体的12条棱所成的角都相等，故①正确；②存在一个平面AB1D1与正方体的6个面所成较小的二面角都相等，故②正确；③存在一条直线AC1与正方体的12条棱所成的角都相等，故③正确；④存在一条直线AC1与正方体的6个面所成的角都相等，故④正确．故选：D．【知识点】棱柱的结构特征5. 【答案】A【解析】设圆锥的母线长为l，则πl=2π×1，所以l=2，设圆锥的高为ℎ，所以ℎ=√22−1=√3，所以圆锥的体积V=13π⋅l2⋅√3=√3π3．【知识点】圆锥的表面积与体积6. 【答案】B【解析】如图，过点M作MP∥A1B1交BB1于点P，过点N作NQ∥AB交BC于点Q，连接PQ，因为A1M=AN=√23a，且A1B=AC=√2a，所以MP=23A1B1，NQ=23AB，所以四边形MNQP为平行四边形，所以MN∥PQ．又因为MN⊄平面BB1C1C，PQ⊂平面BB1C1C，所以MN∥平面BB1C1C．【知识点】直线与平面平行关系的判定7. 【答案】B【解析】因为V P−ABC=13S△ABC⋅PA=13×12×AB×BC×sin120∘×2=√3，所以AB⋅BC=6．因为PA⊥平面ABC，PA=2，所以O到平面ABC的距离为d=12PA=1．设△ABC的外接圆半径为r，球O的半径为R，R=√r2+d2=√r2+1．由余弦定理可知AC2=AB2+BC2−2AB⋅BC⋅cos120∘=AB2+BC2+6≥2AB⋅BC+6=18,当且仅当AB=BC=√6时取等号，所以AC≥3√2．由正弦定理可得2r=ACsin∠ABC ≥√2√32=2√6，所以r≥√6，所以R≥√7．所以当R=√7时，球O的体积取得最小值V=43πR3=28√7π3．【知识点】球的表面积与体积8. 【答案】C【解析】对于A，连接DB，作AF⊥BD于O，交DC与F（如图），此时DO⊥AF，BO⊥AF，将△ADF沿直线AF进行翻折过程中，AF⊥面DOB，可得AF⊥DB．对于B，因为AD⊥DF始终成立，要使直线AD与BF垂直，只需AD⊥DB即可，只需DB=√3即可，显然存在存在某个位置，使DB=√3，对于C，因为AD⊥DF始终成立，要使直线AD与CF垂直，只需AD⊥DC即可，根据勾股定理可得只需DC=2即可，显然不存在存在某个位置，使DC=2，对于D，如图∠DFA<90∘，在翻折过程中，一定存在某个位置使得DF⊥DC，即DF⊥AB．综上，在翻折过程中不可能成立的是C．【知识点】直线与直线的位置关系9. 【答案】B【解析】如图，连接BD，BE．因为N为正方形ABCD的中心，所以N∈BD．又因为M是ED的中点，所以M∈ED．所以M,N∈平面BED．所以由图知BM与EN相交，设ED=DC=a，则BD=√2a，EB=√2a．在△EBD中，由中线定理得EN2=14[2(ED2+EB2)−BD2]=a2，所以EN=a．又因为BM=√72a，所以BM≠EN．【知识点】直线与平面垂直关系的性质10. 【答案】B【解析】设圆锥底面的半径为R尺，由14×2πR=8得R=16π，从而米堆的体积V=1 4×13πR2×5=3203π（立方尺），因此堆放的米约有3203×1.62π≈22（斛）．【知识点】圆锥的表面积与体积二、填空题（共6题）11. 【答案】2π【解析】因为圆柱的轴截面是正方形，且面积为4，所以圆柱的底面半径r=1，高ℎ=2，所以圆柱的体积V=πr2h=π×12×2=2π．【知识点】圆柱的表面积与体积12. 【答案】√33π【解析】设圆锥的底面半径为r，则2πr=2π，所以r=1．所以圆锥的高ℎ=√22−12=√3．所以圆锥的体积V=13πr2h=√33π．【知识点】圆锥的表面积与体积13. 【答案】平行或异面【知识点】直线与直线的位置关系14. 【答案】5π4【知识点】球的表面积与体积15. 【答案】√26【解析】由题知该多面体为正四棱锥，底面边长为1，侧棱长为1，斜高为√32，连接顶点和底面中心即为高，可求得高为√22，所以体积V=13×1×1×√22=√26．【知识点】棱锥的表面积与体积16. 【答案】12π【解析】由于PA=PB，CA=CB，PA⊥AC，则PB⊥CB，因此取PC中点O，则有OP=OC=OA=OB，即O为三棱锥P−­ABC外接球球心，又由PA=PB=2，得AC=AB=2√2，所以PC=√22+(2√2)2=2√3，所以S=4π×(√3)2=12π．【知识点】球的表面积与体积三、解答题（共6题）17. 【答案】(1) 略．(2) 略．【知识点】圆柱的表面积与体积、球的表面积与体积18. 【答案】因为正三棱锥的侧面都是等腰直角三角形，所以侧棱长等于√22a，所以该棱锥的表面积S=√34a2+3×12×(√22a)2=3+√34a2．【知识点】棱锥的表面积与体积19. 【答案】(1) 在等腰梯形ABCD，AD∥BC，AD=AB=CD=1，BC=2，由题意得：∠ABC=60∘，在△ABC中，AC2=AB2+BC2−2AB⋅BCcos∠ABC=3，则有AB2+AC2=BC2，所以AC⊥AB，在△PAB中，因为PA=AB=1，PB=√2，所以PA⊥AB，同理，在△PAD中，所以PA⊥AD，所以AB∩AD=A，所以PA⊥平面ABCD，又因为PA⊥平面ABCDAC⊂平面ABCD}⇒PA⊥AC，即AC⊥ABAC⊥PAAB∩PA=A}⇒AC⊥平面PAB．(2) 在梯形ABCD中，设BE=a，所以V三棱锥P−ABE =12V四棱锥P−ABCD，所以S△ABE=12S梯形ABCD，所以12×AB×BEsin∠ABE=(BC+AD)×ℎ4，而ℎ=ABsin60∘=√32，所以a=32，所以V三棱锥E−PBD =V三棱锥P−BED=13S△BED⋅PA=13×12×32×√32×1=√38.故三棱锥E−PBD的体积为√38．【知识点】直线与平面垂直关系的判定、棱锥的表面积与体积20. 【答案】（1）在已知的直角梯形OBCD中，以底边OB所在直线为x轴，垂直于OB的腰OD所在直线为y轴建立平面直角坐标系．画相应的xʹ轴和yʹ轴，使∠xʹOʹyʹ=45∘，如图①②所示．（2）在xʹ轴上截取OʹBʹ=OB，在yʹ轴上截取OʹDʹ=12OD，过点Dʹ作xʹ轴的平行线l，在l上沿xʹ轴正方向取点Cʹ，使得DʹCʹ=DC．连接BʹCʹ，如图②．（3）所得四边形OʹBʹCʹDʹ就是直角梯形OBCD的直观图，如图③．【知识点】直观图21. 【答案】(1) 因为四边形ABCD是正方形，F为对角线AC与BD的交点，所以F是BD的中点，又E是PD的中点，所以EF∥PB，又EF⊄平面PBC，PB⊂平面PBC，所以EF∥平面PBC．(2) 因为四边形ABCD是正方形，所以AC⊥BD，因为PD⊥平面ABCD，AC⊂平面ABCD，所以AC⊥PD，又BD⊂平面PBD，PD⊂平面PBD，BD∩PD＝D，所以AC⊥平面PBD，又PB⊂平面PBD，所以AC⊥PB．【知识点】直线与平面平行关系的判定、直线与平面垂直关系的性质22. 【答案】因为MN∩EF=Q，所以Q∈直线MN，Q∈直线EF，又因为M∈直线CD，N∈直线AB，CD⊂平面ABCD，AB⊂平面ABCD，所以M,N∈平面ABCD，所以MN⊂平面ABCD，所以Q∈平面ABCD．同理，可得EF⊂平面ADD1A1，所以Q∈平面ADD1A1，又因为平面ABCD∩平面ADD1A1=AD，所以Q∈直线AD，即D，A，Q三点共线．【知识点】平面的概念与基本性质。

高一数学必修第二册第八章《立体几何初步》单元练习题卷7（共22题）一、选择题（共10题）1.如图，三棱柱A1B1C1−ABC中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则下列叙述正确的是( )A．CC1与B1E是异面直线B．AC⊥平面ABB1A1C．A1C1∥平面AB1ED．AE与B1C1为异面直线，且AE⊥B1C12.长方体的表面积为11，十二条棱长之和为24，则这个长方体的一条体对角线长为( )A．2√3B．√14C．5D．6．则3.如图，正方体ABCD−A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=12下列结论中正确的个数为( )① AC⊥BE；② EF∥平面ABCD；③三棱锥A−BEF的体积为定值；④ △AEF的面积与△BEF的面积相等．A．4B．3C．2D．14.已知三棱柱ABC−A1B1C1的底面为直角三角形，侧棱长为2，体积为1，若此三棱柱的顶点均在同一球面上，则该球半径的最小值为( )A．1B．2C．√6D．√625.下列几何体中是棱柱的有( )A．1个B．2个C．3个D．4个6.四条线段顺次首尾相连，它们最多可确定的平面个数有( )A．4B．3C．2D．17.空间四点A，B，C，D共面而不共线，那么这四点中( )A．必有三点共线B．必有三点不共线C．至少有三点共线D．不可能有三点共线8.若一个长方体的长、宽、高分别为√3，√2，1，则它的外接球的表面积为( )πB．5πC．6πD．24πA．329.若空间中n个不同的点两两距离都相等，则正整数n的取值( )A．至多等于3B．至多等于4C．等于5D．大于510.某三棱锥的三视图如图所示，则该三棱锥的体积是( )A．6B．8C．12D．24二、填空题（共6题）11.在棱长为2的正方体ABCD­−A1B1C1D1中，P是A1B1的中点，过点A1作与截面PBC1平行的截面，所得截面的面积是．12.在棱长为6的正方体ABCD−A1B1C1D1中，P，Q是直线DD1上的两个动点．如果PQ=2，那么三棱锥P−BCQ的体积等于．13.一条直线a上的3个点A，B，C到平面M的距离都为1，这条直线和平面的关系是．14.侧棱长为3，底面面积为8的正四棱柱的体对角线的长为．15.如图，A，B，C，D为空间四点，在△ABC中，AB=2，AC=BC=√2，等边三角形ADB以AB为轴运动，当平面ADB⊥平面ABC时，CD=．16.如图，点M为矩形ABCD的边BC的中点，AB=1，BC=2．将矩形ABCD绕直线AD旋转所得到的几何体体积记为V1，将△MCD绕直线CD旋转所得到的几何体体积记为V2，则V1V2的值为．三、解答题（共6题）17.如图，四棱锥S−ABCD中，△ABS是正三角形，四边形ABCD是菱形，点E是BS的中点．(1) 求证：SD∥平面ACE；(2) 若平面ABS⊥平面ABCD，AB=4，∠ABC=120∘，求三棱锥E−ASD的体积．18.如图，在长方体ABCD−A1B1C1D1中，AB=1，AD=2，E，F，Q分别为AD，AA1，BC的中点，求证：平面BEF∥平面A1DQ．19.如图，在四棱锥P−ABCD中，底面ABCD为菱形，∠BAD=60∘，Q为AD的中点，(1) 若PA=PD，求证：平面PQB⊥平面PAD；(2) 点M在线段PC上，PM=tPC，试确定实数t的值，使得PA∥平面MQB；(3) 在（2）的条件下，若平面PAD⊥平面ABCD，PA=AD=PD=2，求二面角M−BQ−C的大小．20.用符号表示下列语句，并画出图形．(1) 平面α与β相交于直线l，直线a与α，β分别相交于点A，B．(2) 点A，B在平面α内，直线a与平面α交于点C，点C不在直线AB上．AD=1，21.如图，四棱锥P−ABCD中，PA⊥CD，AD∥BC，∠ADC=∠PAD=90∘，BC=CD=12 PA=2√2，M为PD的中点．(1) 求证：PA⊥AB；(2) 求证：CM∥平面PAB；(3) 求直线CM与平面PAD所成的角．22.一个几何体，它的下面是一个圆柱，上面是一个圆锥，并且圆锥的底面与圆柱的上底面重合，圆柱的底面直径为3cm，高（两底面圆心连线的长度）为4cm，圆锥的高（顶点与底面圆心连线的长度）为3cm，画出此几何体的直观图．答案一、选择题（共10题）1. 【答案】D【知识点】直线与平面的位置关系、直线与直线的位置关系2. 【答案】C【解析】设长方体的长，宽，高分别为a，b，c，由题意可知，4(a+b+c)=24, ⋯⋯①2ab+2bc+2ac=11, ⋯⋯②联立①②可得a2+b2+c2=25，则这个长方体的一条体对角线长为5．【知识点】棱柱的结构特征3. 【答案】B【解析】①中AC⊥BE，由题意及图形知，AC⊥面DD1B1B，故可得出AC⊥BE，此命题正确；② EF∥平面ABCD，由正方体ABCD−A1B1C1D1的两个底面平行，EF在其一面上，故EF与平面ABCD无公共点，故有EF∥平面ABCD，此命题正确；③三棱锥A−BEF的体积为定值，由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B距离是定值，故可得三棱锥A−BEF的体积为定值，此命题正确；④由图形可以看出，B到线段EF的距离与A到EF的距离不相等，故△AEF的面积与△BEF的面积相等不正确．【知识点】棱锥的表面积与体积、直线与平面垂直关系的性质、直线与平面平行关系的判定4. 【答案】D【解析】因为三棱柱内接于球，所以棱柱各侧面均为平行四边形且内接于圆，所以棱柱的侧棱都垂直于底面，所以该三棱柱为直三棱柱．设底面三角形的两条直角边长为a，b，因为三棱柱ABC−A1B1C1的高为2，体积是1，所以12ab⋅2=1，即ab=1，将直三棱柱ABC−A1B1C1补成一个长方体，则直三棱柱ABC−A1B1C1与长方体有同一个外接球，所以球O的半径为√a2+b2+42≥√2ab+42=√62（当且仅当a=b=1时，等号成立）．【知识点】棱柱的结构特征、球的结构特征5. 【答案】C【解析】观察图形得：“有两个面互相平行，其余各面都是四边形，”的几何体有：①③⑤，只有它们是棱柱，共三个．【知识点】棱柱的结构特征6. 【答案】A【解析】首尾相连的四条线段每相邻两条确定一个平面，所以最多可以确定四个平面．【知识点】平面的概念与基本性质7. 【答案】B【解析】由题意，四点共面不共线分为图①和图②两种情况，只有选项B正确．【知识点】平面的概念与基本性质8. 【答案】C【知识点】球的表面积与体积、组合体9. 【答案】B【解析】由正四面体的定义可知n=4能满足条件．当n≥5时，可设其中三个点为A，B，C，由直线与平面垂直的性质及点到点的距离定义可知到A，B，C三点距离相等的点必在过△ABC 的重心且与平面ABC垂直的直线上，从而易知到A，B，C的距离等于正三角形ABC边长的点有两个，分别在平面ABC的两侧．此时可知这两点间的距离大于正三角形的边长，从而不可能有5个点满足条件．当然也不可能有多于5个的点满足条件．【知识点】空间线段的长度、直线与平面垂直关系的性质10. 【答案】B【知识点】由三视图还原空间几何体、棱锥的表面积与体积二、填空题（共6题）11. 【答案】2√6【解析】如图，取AB，C1D1的中点E，F，连接A1E，A1F，EF，则平面A1EF∥平面BPC1．在△A1EF中，A1F=A1E=√5，EF=2√2，S△A1EF =12×2√2×√(√5)2−(√2)2=√6，从而所得截面面积为2S△A1EF=2√6．【知识点】平面与平面平行关系的判定12. 【答案】12【解析】因为在棱长为6的正方体ABCD−A1B1C1D1中，P，Q是直线DD1上的两个动点，PQ=2，所以S△PQC=12×PQ×CD=12×2×6=6，所以三棱锥P−BCQ的体积：V P−BCQ=V B−PQC=13×S△PQC×BC=13×6×6=12．【知识点】棱锥的表面积与体积13. 【答案】平行【解析】假设直线a与平面α相交，则A，B，C三点中必有两个点在平面α同一侧，不妨设为A，B，过A，B分别作平面α的垂线，垂足为M，N，则AM∥BN，AM=BN．所以四边形AMNB是平行四边形，所以AB∥MN，又MN⊂α，AB⊄α，所以AB∥α，这与假设直线a与平面α相交矛盾，故假设错误，于是直线a与平面α平行．【知识点】直线与平面的位置关系14. 【答案】5【解析】正四棱柱的底面为正方形，设底面边长为a，侧棱长为b，则有a2=8，所以a=2√2，则四棱柱的体对角线为√a2+a2+b2=√8+8+9=5．故答案为：5．【知识点】棱柱的结构特征15. 【答案】2【解析】如图，取AB的中点E，连接DE，CE，因为△ADB是等边三角形，所以DE⊥AB．当平面ADB⊥平面ABC时，因为平面ADB∩平面ABC=AB，所以DE⊥平面ABC．又CE⊂平面ABC，所以DE⊥CE．由已知可得DE=√3，CE=1，在Rt△DEC中，CD=√DE2+CE2=2．【知识点】平面与平面垂直关系的性质16. 【答案】6【知识点】圆柱的表面积与体积三、解答题（共6题）17. 【答案】(1) 连接BD，设AC∩BD=O，连接OE，则点O是BD的中点．又因为E是BS的中点，所以SD∥OE，又因为SD⊄平面ACE，OE⊂平面ACE，所以SD∥平面ACE．(2) 因为四边形ABCD是菱形，且∠ABC=120∘，所以∠ABD=12∠ABC=60∘．又因为AB=AD，所以三角形ABD是正三角形．取AB的中点F，连接SF，则DF⊥AB，DF=2√3．又平面ABS⊥平面ABCD，DF⊂平面ABCD，平面ABS∩平面ABCD=AB，所以DF⊥平面ABS，即DF是四棱锥D−AES的一条高，而S△ASE=12SA⋅SE⋅sin∠ASE=2√3，所以V E−ADS=V D−AES=13S△ASE⋅DF=13×2√3×2√3=4.综上，三棱锥E−ASD的体积为4．【知识点】直线与平面平行关系的判定、棱锥的表面积与体积18. 【答案】因为E是AD的中点，Q是BC的中点，所以ED=BQ，ED∥BQ，所以四边形BEDQ是平行四边形，所以BE∥DQ，又因为BE⊄平面A1DQ，DQ⊂平面A1DQ，所以BE∥平面A1DQ，又因为F是A1A的中点，所以EF∥A1D,因为EF⊄平面A1DQ，A1D⊂平面A1DQ，所以EF∥平面A1DQ，因为BE∩EF=E，EF⊂平面BEF，BE⊂平面BEF，所以平面BEF∥平面A1DQ．【知识点】平面与平面平行关系的判定(1) 因为 PA =PD ，Q 为 AD 的中点，所以 PQ ⊥AD ．因为底面 ABCD 为菱形，∠BAD =60∘，所以 △ABD 为正三角形，所以 BQ ⊥AD ．又 BQ ∩PQ =Q ，所以 AD ⊥平面PQB ．又 AD ⊂平面PAD ，所以 平面PQB ⊥平面PAD ．(2) 当 t =13 时，PA ∥平面MQB ．下面证明：设 AC ∩BQ =N ，连接 MN ．因为 AQ ∥BC ，所以 AN NC =AQ BC =12．由 PM =13PC ，得 PM MC =12， 所以 AN NC =PM MC ，所以 PA ∥MN ．又 MN ⊂平面MQB ，PA ⊄平面MQB ，所以 PA ∥平面MQB ．(3) 由(1)，得 BQ ⊥AD ，PQ ⊥AD ．因为平面 PAD ⊥平面ABCD ，平面 PAD ∩平面ABCD =AD ，所以 PQ ⊥平面ABCD ．如图，建立空间直角坐标系，则 Q (0,0,0)，A (1,0,0)，B(0,√3,0)，C(−2,√3,0)，P(0,0,√3)，则 QB ⃗⃗⃗⃗⃗ =(0,√3,0), 且 QM ⃗⃗⃗⃗⃗⃗ =QP ⃗⃗⃗⃗⃗ +PM ⃗⃗⃗⃗⃗⃗ =QP ⃗⃗⃗⃗⃗ +13PC ⃗⃗⃗⃗⃗ =(−23,√33,2√33)． 设平面 MQB 的一个法向量为 n ⃗ =(x,y,z )．由 {n ⃗ ⋅QB ⃗⃗⃗⃗⃗ =0,n ⃗ ⋅QM ⃗⃗⃗⃗⃗⃗ =0, 得 {√3y =0,−2x 3+√3y 3+2√3z 3=0, 取 z =1，则 n ⃗ =(√3,0,1)．又因为平面 ABCD 的一个法向量为 m ⃗⃗ =(0,0,1)，所以 cos 〈m ⃗⃗ ,n ⃗ 〉=m ⃗⃗⃗ ⋅n ⃗ ∣m ⃗⃗⃗ ∣∣n ⃗ ∣=12， 于是，二面角 M −BQ −C 的大小为 π3．【知识点】直线与平面平行关系的判定、二面角、平面与平面垂直关系的判定、空间向量的应用(1) 用符号表示a∩β=l，a∩α=A，a∩β=B，如图．(2) 用符号表示A∈α，B∈α，a∩α=C，C∉AB，如图．【知识点】平面的概念与基本性质21. 【答案】(1) 因为∠PAD=90∘，所以PA⊥AD．又因为PA⊥CD，CD∩AD=D，所以PA⊥平面ABCD．又因为AB⊂平面ABCD，所以PA⊥AB．(2) 取PA中点N，连接MN，BN．因为M，N分别是PA，PD的中点，所以MN∥AD且MN=12AD，又因为BC∥AD且BC=12AD，所以MN∥BC且MN=BC，所以四边形MNBC是平行四边形，所以CM∥BN，又因为CM⊄平面PAB，BN⊂平面PAB，所以CM∥平面PAB．(3) 因为CD⊥PA，CD⊥AD，PA∩AD=A，所以CD⊥平面PAD．所以∠CMD为直线CM与平面PAD所成的角．在Rt△PAD中，因为PA=2√2，AD=2，所以PD=2√3，所以MD=√3．所以在Rt△CMD中，tan∠CMD=CDMD =√33．所以，直线CM与平面PAD所成的角为π6．【知识点】线面角、直线与平面垂直关系的判定、直线与平面平行关系的性质22. 【答案】（1）画轴．如图①所示，画x轴，z轴，使∠xOz=90∘．（2）画圆柱的下底面．在x轴上取A，B两点，使AB=3cm，且OA=OB，选择椭圆模板中适当的椭圆且过A，B两点，使它为圆柱的下底面．（3）在Oz上截取OOʹ=4cm，过点Oʹ作平行于Ox轴的Oʹxʹ轴，类似圆柱下底面的画法画出圆柱的上底面．（4）画圆锥的顶点．在Oz上截取点P，使POʹ=3cm．（5）成图．连接AʹA，BʹB，PAʹ，PBʹ，整理（去掉辅助线，将被遮挡部分改成虚线）得到此几何体的直观图，如图②所示．【知识点】直观图。

微专题七：立体几何选择填空多选题中档题一、单选题1．如图，在棱长为2的正方体1111ABCD A B C D -中，M 是11A B 的中点，点P 是侧面11CDD C 上的动点，且MP ∥截面1AB C ，则线段MP 长度的取值范围是（ ）.A ．[2,6]B ．[6,22]C ．[6,23]D ．[6,3]【答案】B 【分析】取CD 的中点为N,1CC 的中点为R,11B C 的中点为H,证明平面MNRH//平面1AB C ,MP ⊂平面MNRH ,线段MP 扫过的图形为MNR ∆,通过证明222MN NR MR =+,说明MRN ∠为直角,得线段MP 长度的取值范围为[],MR MN 即可得解. 【详解】取CD 的中点为N,1CC 的中点为R,11B C 的中点为H,作图如下:由图可知,11//,MB NC MB NC =,所以四边形1MNCB 为平行四边形, 所以1//MN B C ,因为1111//,//MH A C A C AC ,所以//MH AC , 因为1,MNMH M ACB C C ==, 故平面MNRH//平面1AB C ,因为MP ∥截面1AB C ,所以MP ⊂平面MNRH ,线段MP 扫过的图形为MNR ∆,由2AB =知,22,2MN NR ==,在1Rt MC R ∆中,22211MR C R C M =+,即()222156MR =+=,所以6MR =，所以222MN NR MR =+,即MRN ∠为直角,故线段MP 长度的取值范围为[],MR MN ,即6,22⎡⎤⎣⎦,故选:B【点睛】本题考查面面平行的判定定理与性质定理及空间两点间的距离;重点考查转化与化归的思想;属于难度大、抽象型试题.2．在正方体1111ABCD A B C D -中，E 是棱1CC 的中点，F 是侧面11BCC B 内的动点，且1A F 平面1D AE ，则1A F 与平面11BCC B 所成角的正切值t 构成的集合是（ ）A ．25|235t t B ．25|25t t C ．|223t t D ．|222t t【答案】D 【分析】为确定F 点位置，先找过1A 与平面1D AE 平行且与平面11B BCC 相交的平面，分别取111,B B B C 的中点,M N ，连接11,,A M MN A N ，可知平面1//A MN 平面1D AE ，故F 在线段MN 上，可知线面角为11A FB ∠，分析其正切值即可求出.【详解】设平面1AD E 与直线BC 交于点G ，连接,AG EG ，则G 为BC 的中点. 分别取111,B B B C 的中点,M N ，连接11,,A M MN A N ，则11//A M D E ， ∵1A M平面1D AE ，1D E ⊂平面1D AE ，∴1//A M 平面1D AE ，同理可得//MN 平面1D AE . ∵1,A M MN 是平面1A MN 内的两条相交直线， ∴平面1//A MN 平面1D AE ，且1//A F 平面1D AE ， 可得直线1A F ⊂平面1A MN ，即点F 是线段MN 上的动点.设直线1A F 与平面11BCC B 所成角为θ，运动点F 并加以观察，可得：当点F 与点M （或N ）重合时，1A F 与平面11BCC B 所成角等于11A MB ，此时所成角θ达到最小值，满足111tan 2A B B Mθ；当点F 与MN 中点重合时，1A F 与平面11BCC B 所成角达到最大值，此时111111tan 2222A B A B B FB M θ，∴1A F 与平面11BCC B 所成角的正切值t 构成的集合为|222t t ，故选D.【点睛】本题主要考查了面面平行的判定与性质，线面角，及线面角正切的最值问题，属于难题.3．如图，PO 是平面α的斜线，O 是斜足，PA α⊥于点A ，BC 是α内过点O 的直线．若POB ∠是锐角，则有（ ）．A ．POC COA ∠>∠B ．POA BOA ∠<∠C ．POC COA ∠<∠D ．POB AOB ∠<∠【答案】C 【解析】【分析】由三余弦定理可得POB AOB ∠>∠，即POC COA ∠<∠，再逐一检验A,B,D 选项即可得解. 【详解】解：由三余弦定理可得：cos cos cos POB POA AOB ∠=∠∠， 又,,POB POA AOB ∠∠∠为锐角，所以cos cos POB AOB ∠<∠， 所以POB AOB ∠>∠，所以POB AOB ππ-∠<-∠， 即POC COA ∠<∠，故C 正确，则选项A 错误， 同理POB AOB ∠>∠，则选项D 错误，又,POA BOA ∠∠大小无法确定，则不能比较大小，即选项B 错误， 故选C.【点睛】本题考查了三余弦定理，属中档题.4．如图，在棱长为2的正方体1111ABCD A B C D -中，,,E F G 分别是棱1,,AB BC CC 的中点，P 是底面ABCD 内一动点，若直线1D P 与平面EFG 不存在公共点，则三角形1PBB 的面积的最小值为A ．22B ．1C 2D ．2【答案】C 【分析】延展平面EFG ，可得截面EFGHOR ,其中H Q R 、、分别是所在棱的中点，可得1//D P 平面EFGHQR ,再证明平面1//D AC 平面EFGHQR ,可知P 在AC 上时，符合题意，从而得到P 与O 重合时三角形1PBB 的面积最小，进而可得结果. 【详解】延展平面EFG ，可得截面EFGHQR ,其中H Q R 、、分别是所在棱的中点， 直线1D P 与平面EFG 不存在公共点，所以1//D P 平面EFGHQR ,由中位线定理可得AC//EF ,EF 在平面EFGHQR 内，AC 在平面EFGHQR 外， 所以AC //平面EFGHQR ,因为1D P 与AC 在平面1D AC 内相交，所以平面1//D AC 平面EFGHQR ,所以P 在AC 上时，直线1D P 与平面EFG 不存在公共点， 因为B O 与AC 垂直，所以P 与O 重合时BP 最小， 此时，三角形1PBB 的面积最小，最小值为12222⨯⨯=，故选C.【点睛】 本题主要考查线面平行的判定定理、面面平行的判定定理，属于难题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面.5．已知ABC ∆是由具有公共直角边的两块直角三角板（Rt ACD ∆与Rt BCD ∆）组成的三角形，如左下图所示.其中，45,60CAD BCD ∠=∠=.现将Rt ACD ∆沿斜边AC 进行翻折成1D AC ∆（1D 不在平面ABC 上）.若,M N 分别为BC 和1BD 的中点，则在ACD ∆翻折过程中，下列命题不正确的是（ ）A ．在线段BD 上存在一定点E ，使得EN 的长度是定值B ．点N 在某个球面上运动C ．存在某个位置，使得直线1AD 与DM 所成角为60D ．对于任意位置，二面角1D AC B --始终大于二面角1D BC A -- 【答案】D 【分析】由题意，可得二面角1D AC B --和二面角1D BC A --有共同的平面角ABC ∠,且另一个面都过点1D ，过点1D 作平面ABC 的垂线，即可得到二面角1D AC B --和二面角1D BC A --的平面角，进而得大小关系即可. 【详解】不妨设1AD =，取AB 中点E ，易知E 落在线段BD 上，且11122EN AD ==, 所以点N 到点E 的距离始终为12，即点N 在以点E 为球心，半径为12的球面上运动， 因此A 、B 选项不正确；对于C 选项，作1//,AP DM AD 可以看成以AC 为轴线，以45为平面角的圆锥的母线，易知1AD 与AP 落在同一个轴截面上时，1PAD ∠ 取得最大值，则1PAD ∠的最大值为60，此时1D 落在平面ABC 上，所以160PAD ∠<，即1AD 与DM 所成的角始终小于60，所以C 选项不正确；对于D 选项，易知二面角1D AC B --为直二面角时，二面角1D AC B --始终大于二面角1D BC A --，当二面角1D AC B --为锐二面角时，如图所示作1D R ⊥平面ABC 与点R ，然后作,RO AC RS BC ⊥⊥分别交,AC BC 于,O S ，则二面角1D AC B --的平面角为1D OR ∠，二面角1D BC A --的平面角为1D SR ∠， 且1111tan ,tan D R D RD OR D SR OR SR∠=∠=，又因为OR SR <，所以11D OR D SR ∠>∠， 所以二面角1D AC B --始终大于二面角1D BC A --，故选D.【点睛】本题主要考查了空间几何体的结构特征，以及空间角的求解，其中解答中正确确定二面角的的平面角和异面直线所成的角是解答的关键，试题综合性强，难度大，属于难题，着重考查了空间想象能力，以及分析问题和解答问题的能力.6．如图，在棱长为1的正方体1111ABCD A B C D -中，点E F 、分别是棱BC ，1CC 的中点，P 是侧面11BCC B 内一点，若1A P //平面AEF ，则线段1A P 长度的取值范围是（ ）A ．325(,)42B ．325[,]42C ．5[1,]2D ．5[0,]2【答案】B 【解析】分析：先判断出点P 的位置，确定使得1A P 取得最大值和最小值时点P 的位置，然后再通过计算可求得线段1A P 长度的取值范围．详解：如下图所示，分别取棱111,BB B C 的中点M 、N ，连MN ，1BC ，∵,,,M N E F 分别为所在棱的中点，则11,MNBC EF BC ，∴MN ∥EF ，又MN ⊄平面AEF ，EF ⊂平面AEF ，∴MN ∥平面AEF ．∵11,AA NE AA NE =，∴四边形1AENA 为平行四边形，∴1A N AE ∥，又1A N ⊄平面AEF ，AE ⊂平面AEF ， ∴1A N ∥平面AEF ，又1A NMN N =，∴平面1A MN ∥平面AEF ．∵P 是侧面11BCC B 内一点，且1A P ∥平面AEF ，∴点P 必在线段MN 上．在11Rt A B M ∆中，2221111151()2A M AB B M ++．同理，在11Rt A B N ∆中，可得15A N =∴1A MN ∆为等腰三角形． 当点P 为MN 中点O 时，1A P MN ⊥，此时1A P 最短；点P 位于M 、N 处时，1A P 最长． ∵2222115232()()244AO A M OM =-=-=，115A M A N ==．∴线段1A P 长度的取值范围是325[,]42．故选B ．点睛：本题难度较大，解题时要借助几何图形判断得出使得1A P 取得最值时的点P 的位置，然后再根据勾股定理进行计算． 7．如图，正方体AC 1的棱长为1，过点A 作平面A 1BD 的垂线，垂足为点H ．则以下命题中，错误的命题是A ．点H 是△A 1BD 的垂心B ．AH 垂直平面CB 1D 1C ．AH 的延长线经过点C 1D ．直线AH 和BB 1所成角为45°【答案】D 【详解】因为三棱锥A －A 1BD 是正三棱锥，故顶点A 在底面的射影是底面的中心，A 正确；平面A 1BD ∥平面CB 1D 1，而AH 垂直于平面A 1BD ，所以AH 垂直于平面CB 1D 1，B 正确；根据对称性知C 正确，故选D.二、多选题8．如图，在四棱锥E ABCD -中，底面ABCD 是边长为2的正方形，CDE △是正三角形，M 为线段DE 的中点，点N 为底面ABCD 内的动点，则下列结论正确的是（ ）A ．若BC DE ⊥，则平面CDE ⊥平面ABCDB ．若BC DE ⊥，则直线EA 与平面ABCD 所成的角的正弦值为64C ．若直线BM 和EN 异面，则点N 不可能为底面ABCD 的中心D ．若平面CDE ⊥平面ABCD ，且点N 为底面ABCD 的中心，则BM EN = 【答案】ABC 【分析】根据面面垂直的判定，线面夹角的求解办法，以及异面直线的定义，结合面面垂直的性质，对每个选项进行逐一分析，即可容易判断选择.【详解】 ∵BC CD ⊥，BC DE ⊥，CDDE D =，,CD DE ⊂平面CDE ，∴BC ⊥平面CDE ，∵BC ⊂平面ABCD ，∴平面ABCD ⊥平面CDE ，A 项正确；设CD 的中点为F ，连接EF ､AF ，则EF CD ⊥.∵平面ABCD ⊥平面CDE ，平面ABCD 平面CDE CD =，EF ⊂平面CDE ∴EF ⊥平面ABCD ，设EA 与平面ABCD 所成的角为θ，则EAF θ=∠，223EF CE CF =-=，225AF AD FD =+=，2222AE EF AF =+=，则6sin 4EF AE θ==，B 项正确； 连接BD ，易知BM ⊂平面BDE ，由B ､M ､E 确定的面即为平面BDE ，当直线BM 和EN 异面时，若点N 为底面ABCD 的中心，则N BD ∈， 又E ∈平面BDE ，则EN 与BM 共面，矛盾，C 项正确；连接FN ，∵FN ⊂平面ABCD ，EF ⊥平面ABCD ，∴EF FN ⊥， ∵F ､N 分别为CD ､BD 的中点，则112FN BC ==， 又3EF=，故222EN EF FN =+=，227BM BC CM =+=，则BM EN ≠，D 项错误. 故选：ABC . 【点睛】本题综合考查面面垂直的判定以及性质、异面直线的定义、线面夹角的求解，属综合困难题.9．如图，正三棱柱11ABC A B C -中，11BC AB ⊥、点D 为AC 中点，点E 为四边形11BCC B 内（包含边界）的动点则以下结论正确的是（ ）A ．()1112DA A A B A BC =-+B ．若//DE 平面11ABB A ，则动点E 的轨迹的长度等于22AC C ．异面直线AD 与1BC 6D ．若点E 到平面11ACC AEB ，则动点E 的轨迹为抛物线的一部分 【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解，逐项判断，进而可得到本题答案. 【详解】解析：对于选项A ，()1112AD A A B A BC =-+，选项A 错误； 对于选项B ，过点D 作1AA 的平行线交11A C 于点1D ．以D 为坐标原点，1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz ．设棱柱底面边长为a ，侧棱长为b ，则002a A ⎛⎫ ⎪⎝⎭,,，00B ⎛⎫ ⎪ ⎪⎝⎭,，10B b ⎛⎫ ⎪ ⎪⎝⎭,，102a C b ⎛⎫- ⎪⎝⎭,,，所以12a BC b ⎛⎫=- ⎪ ⎪⎝⎭,,，12a AB b ⎛⎫=- ⎪ ⎪⎝⎭,． ∵11BC AB ⊥，∴110BC AB ⋅=，即22202a b ⎫⎛⎫--+=⎪ ⎪⎪⎝⎭⎝⎭，解得2b a =． 因为//DE 平面11ABB A ，则动点E的轨迹的长度等于1BB =．选项B 正确． 对于选项C ，在选项A 的基础上，002a A ⎛⎫⎪⎝⎭,,，00B ⎛⎫ ⎪ ⎪⎝⎭,，()0,0,0D ，1022a C a ⎛⎫- ⎪ ⎪⎝⎭,,，所以002a DA ⎛⎫= ⎪⎝⎭,,，12a BC ⎛⎫=- ⎪ ⎪⎝⎭，因为2111cos ,6||||a BC DA BC DA BC DA a ⎛⎫- ⎪⋅<>===-，所以异面直线1,BC DA所成角的余弦值为6，选项C 正确．对于选项D ，设点E 在底面ABC 的射影为1E ，作1EF 垂直于AC ，垂足为F ，若点E 到平面11ACC A 的，即有12E F EB =，又因为在1CE F ∆中，112E F E C =，得1EB E C =，其中1E C 等于点E 到直线1CC 的距离，故点E 满足抛物线的定义，另外点E 为四边形11BCC B 内（包含边界）的动点，所以动点E 的轨迹为抛物线的一部分,故D 正确.故选：BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题，其中涉及到抛物线定义的应用.三、填空题10．如图，正方体1111ABCD A B C D -的棱长为a ，动点P 在对角线1BD 上，过点P 作垂直于1BD 的平面γ，记这样得到的截面多边形（含三角形）的周长为y ，设BP x =，则当323[,]33x a a ∈时，函数()y f x =的值域为______． 【答案】{}32a【分析】 当323,33x a a ⎡⎤∈⎢⎥⎣⎦时，截面多边形是六边形HIJKLM ，利用相似比可知邻边长之和为定值即可得到结果. 【详解】当323,33x a a ⎡⎤∈⎢⎥⎣⎦时，截面多边形是六边形HIJKLM ，设11HI AC =111B I B C =λ，则1IJ B C =111C I B C =1﹣λ， ∴HI +2a ，∴截面六边形的周长为32a ；故答案为{}32a【点睛】本题考查了几何体中动点问题，截面周长问题,考查了空间想象力，属于中档题.11．如图，半径为R 的球O 的直径AB 垂直于平面α，垂足为B ，BCD 是平面α内边长为R 的正三角形，线段AC ，AD 分别与球面交于点M 、N ，则三棱锥A BMN -的体积是__________．【答案】38375R 【分析】 2AB R =，BC R =，5AC R =，BCD ∆是平面α内边长为R 的正三角形，ABC AMB ∆∽，45AM AC =，类似有45AN AD =，24()5A BMN AMN A BCD ABCV S V S -∆-∆==，由此能求出三棱锥A BMN -的体积． 【详解】 2AB R =，BC R =，5AC R =，半径为R 的球O 的直径AB 垂直于平面α，垂足为B ，BCD ∆是平面α内边长为R 的正三角形， 线段AC ，AD 分别与球面交于点M 、N ，BAM BAC ∴∠=∠，90AMB ABC ∠=∠=︒，ABC AMB ∴∆∆∽，∴AB AC AM AB =，455AM R ∴=， ∴45AM AC =，类似有45AN AD =， ∴2416()525A BMN AMN A BCD ABC V S V S -∆-∆===，∴三棱锥A BMN -的体积： 231613832253475A BMN V R R R -=⨯⨯⨯⨯=．故答案为：38375R ．【点睛】本题考查三棱锥的体积的求法，考查球、三棱锥的结构特征等基础知识，考查运算求解能力，是中档题． 12．如图，已知：在ABC 中，3CA CB ==，3AB =，点F 是BC 边上异于点B ，C 的一个动点，EF AB ⊥于点E ，现沿EF 将BEF 折起到PEF 的位置，使PE AC ⊥，则四棱锥P ACFE -的体积的最大值为________．2 过点D 作CD AB ⊥，由EF AB ⊥可知//EF CD ，进而证明PE ⊥平面ABC ，所以PE 为四棱锥P ACFE -的高，设BE PE x ==，通过题设条件分别求出BEF S 和ABC S 的表达式，进而得出ACFE S 四边形的表达式，记四棱锥P ACFE -的体积为(x)V ，由四棱锥的体积公式可得333()418V x x x =-（302x <<），然后利用导数求得(x)V 的最大值即可. 【详解】过点D 作CD AB ⊥，由EF AB ⊥可知//EF CD ，因为EF AB ⊥，所以翻折后PE EF ⊥，所以PE CD ⊥，又PE AC ⊥，AC CD D =，AC ，CD ⊂平面ABC ，所以PE ⊥平面ABC ，所以PE 为四棱锥P ACFE -的高， 因为3CA CB ==3AB =，CD AB ⊥，所以可得：()22223332CD AC AD ⎛⎫=-=-= ⎪⎝⎭ 设BE PE x ==，所以EF BE CD BD =332x =，即3EF x =， 所以2132BEF S BE EF x =⋅=△，又1332ABC S AB CD =⋅=△， 所以2333ACFE S x =四边形，记四棱锥P ACFE -的体积为(x)V ， 所以323334133()34618x V x x x x ⎛⎫=⋅⋅=- ⎪ ⎪⎝⎭-（302x <<），2()V x x '=，令()0V x '=可得x =或x =（舍去），所以当0,2x ⎛∈ ⎝⎭时，()0V x '>，()V x '单调递增；当322x ⎛⎫∈ ⎪ ⎪⎝⎭时，()0V x '<，()V x '单调递减，因此当2x =时，(x)V 取得最大值，最大值为24V ⎛= ⎝⎭.故答案为：4. 【点睛】本题考查棱锥体积的求法，考查利用导数研究函数的最值，考查逻辑思维能力和运算求解能力，属于中档题.。

人教A版高一数学必修第二册第八章《立体几何初步》章末练习题卷（共22题）一、选择题（共10题）1.分别在两个平面内的两条直线间的位置关系是( )A．异面B．平行C．相交D．以上都有可能2.下列说法正确的是( )A．相等的角在直观图中仍然相等B．相等的线段在直观图中仍然相等C．正方形的直观图是正方形D．若两条线段平行，则在直观图中对应的两条线段仍然平行3.截一个几何体，所得各截面都是圆面，则这个几何体一定是( )A．圆柱B．圆锥C．球D．圆台4.下列图形中不一定是平面图形的是( )A．三角形B．菱形C．梯形D．四边相等的四边形5.如图的简单组合体是由组合而成.A．棱柱、棱台B．棱柱、棱锥C．棱锥、棱台D．棱柱、棱柱6.如图所示，观察四个几何体，其中判断正确的是( )A．是棱台B．是圆台C．不是棱柱D．是棱锥7.下面是一些命题的叙述语（A，B表示点，a表示直线α，β表示平面），其中命题和叙述方法都正确的是( )A．若A∈α，B∈α，则AB∈αB．若a∈α，a∈β，则α∩β=aC．若A∈α，a⫋α，则A∈αD．若A∉a，a⫋α，则A∉α8.下列四个命题中真命题是( )A．同垂直于一直线的两条直线互相平行B．底面各边相等，侧面都是矩形的四棱柱是正四棱柱C．过空间任一点与两条异面直线都垂直的直线有且只有一条D．过球面上任意两点的大圆有且只有一个9.两个球的表面积之差为48π，它们的大圆周长之和为12π，则这两个球的半径之差为( )A．1B．2C．3D．410.用符号表示“点A在直线l上，l在平面α内”，正确的是( )A．A∈l，l∉αB．A⊂l，l⊄αC．A⊂l，l∈αD．A∈l，l⊂α二、填空题（共6题）11.几何体体积说明棱柱V棱柱=SℎS为棱柱的 ,ℎ为棱柱的 棱锥V棱锥=13SℎS为棱锥的 ,ℎ为棱锥的 棱台V棱台=13(Sʹ+√SʹS+S)ℎSʹ,S分别为棱台的 ,ℎ为棱台的 12.如果两个球的体积之比为8:27，那么两个球的表面积之比为．13.思考辨析 判断正误棱锥的体积等于底面面积与高之积．14.已知正三棱柱ABC−A1B1C1的各条棱长都相等，M是侧棱BB1的中点，N是棱AB的中点，则∠NMC1的大小是．15.思考辨析，判断正误．如果两条直线同时平行于第三条直线，那么这两条直线互相平行．16.思考辨析，判断正误在斜二测画法中，各条线段的长度都发生了改变．( )三、解答题（共6题）17.如图所示，梯形ABCD中，AD∥BC，且AD<BC，当梯形ABCD绕AD所在直线旋转一周时，其他各边旋转围成了一个几何体，试描述该几何体的结构特征．18.如图是长方体的表面展开图，在这个长方体中：(1) 直线DM与平面ABQP的位置关系是怎样的？(2) 平面DCMN与平面ERFG的位置关系是怎样的？(3) 线段BC的长度是点C到平面APQB的距离吗？19.有4条长为2的线段和2条长为a的线段，用这6条线段作为棱，构成一个三棱锥．问a为何值时，可构成一个最大体积的三棱锥，最大值为多少？20.根据图形用符号表示下列点、直线、平面之间的位置关系．(1) 点P与直线AB；(2) 点C与直线AB；(3) 点M与平面AC；(4) 点A1与平面AC；(5) 直线AB与直线BC；(6) 直线AB与平面AC；(7) 平面A1B与平面AC．21.应用面面平行判断定理应具备哪些条件？22.观察（1），（2），（3）三个图形，说明它们的位置关系有什么不同，并用字母表示各个平面．答案一、选择题（共10题）1. 【答案】D【解析】分别在两个平面的两条直线平行、相交、异面都可能，可将两条直线放在长方体里进行研究．【知识点】直线与直线的位置关系2. 【答案】D【解析】等腰三角形的两底角相等，但在直观图中不相等，故A错误；正方形的直观图是平行四边形，正方形的两邻边相等，但在直观图中不相等，故B，C错误．【知识点】直观图3. 【答案】C【解析】由球的结构特征知该几何体是球．【知识点】球的结构特征4. 【答案】C【知识点】平面的概念与基本性质5. 【答案】B【解析】该简单组合体的上面是一个棱锥，下面是一个棱柱．【知识点】组合体6. 【答案】D【解析】对A，侧棱延长线不交于一点，不符合棱台的定义，所以A错误；对B，上下两个面不平行，不符合圆台的定义，所以B错误；对C，将几何体竖直起来看，符合棱柱的定义，所以C错误；对D，符合棱锥的定义，正确．【知识点】棱台的结构特征、棱锥的结构特征、棱柱的结构特征7. 【答案】C【知识点】平面的概念与基本性质8. 【答案】C【知识点】棱柱的结构特征、直线与直线的位置关系、球的结构特征9. 【答案】B【解析】设两球半径分别为R1，R2，且R1>R2，则4π(R12−R22)=48π，2π(R1+R2)=12π，所以R1−R2=2．【知识点】球的表面积与体积10. 【答案】D【解析】点A在直线l上，表示为A∈l，l在平面α内，表示为l⊂α．【知识点】平面的概念与基本性质二、填空题（共6题）11. 【答案】底面积；高；底面积；高；上、下底面面积；高【知识点】棱锥的表面积与体积、棱柱的表面积与体积、棱台的表面积与体积12. 【答案】4:9【解析】因为V1:V2=8:27=R13:R23，所以R1:R2=2:3，所以S1:S2=R12:R22=4:9．【知识点】球的表面积与体积13. 【答案】×【知识点】棱锥的表面积与体积14. 【答案】90°【解析】通过计算可知NC12=NM2+MC12，故∠NMC1=90∘．如图．【知识点】棱柱的结构特征15. 【答案】√【知识点】空间中直线与直线平行16. 【答案】×【知识点】直观图三、解答题（共6题）17. 【答案】如图所示，旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体．【知识点】组合体18. 【答案】(1) 根据展开图还原长方体，其示意图如图所示， 则 直线DM ∥平面ABQP ．(2) 平面 DCMN 垂直于平面 ERFG ．(3) 线段 BC 的长度是点 C 到平面 APQB 的距离．【知识点】平面与平面的位置关系、点面距离（线面距离、点线距离、面面距离）、直线与平面的位置关系19. 【答案】构成三棱锥，这 6 条线段作为棱有两种摆放方式．（1）2 条长为 a 的线段放在同一个三角形中．如图所示，不妨设底面 BCD 是一个边长为 2 的正三角形．欲使体积达到最大，必有 BA ⊥底面BCD ，且 BA =2，AC =AD =a =2√2， 此时 V =13×√34×22×2=23√3．（2）2 条长为 a 的线段不在同一个三角形中，此时长为 a 的两条线段必处在三棱锥的对棱，不妨设 AD =BC =a ，BD =CD =AB =AC =2． 取 BC 中点 E ，连接 AE ，DE （见下图）．则 AE ⊥BC,DE ⊥BC ⇒BC ⊥平面AED ，V =13S △AED ⋅BC ， 在 △AED 中，AE =DE =√4−a 24，AD =a ，S △AED =12a √4−a 24−a 24=12a √4−a 22，所以 V =16a 2√4−a 22=16√a 2a 2(16−2a 2)⋅14，由均值不等式 a 2a 2(16−2a 2)≤(163)3， 等号当且仅当 a 2=163时成立，即 a =43√3， 所以此时 V max =16√(163)3⋅14=1627√3．【知识点】棱锥的表面积与体积20. 【答案】(1) 点P∈直线AB．(2) 点C∉直线AB．(3) 点M∈平面AC．(4) 点A1∉平面AC．(5) 直线AB∩直线BC=点B．(6) 直线AB⊂平面AC．(7) 平面A1B∩平面AC=直线AB．【知识点】点、线、面的位置关系、直线与平面的位置关系、平面与平面的位置关系、直线与直线的位置关系21. 【答案】①平面α内两条相交直线a，b，即a⊂α，b⊂α，a∩b=P．②两条相交直线a，b都与β平行，即a∥β，b∥β．【知识点】平面与平面平行关系的判定22. 【答案】图（1）表示两个相交的半平面；图（2）表示开口向里的两个相交的半平面；图（3）表示开口向外的两个相交的半平面．【知识点】平面的概念与基本性质。

高一数学必修第二册第八章《立体几何初步》单元练习题卷8（共22题）一、选择题（共10题）1.下列命题中正确的是( )A．三点确定一个平面B．垂直于同一直线的两条直线平行C．若直线l与平面α上的无数条直线都垂直，则直线l⊥αD．若a，b，c是三条直线，a∥b且与c都相交，则直线a，b，c共面2.紫砂壶是中国特有的手工制造陶土工艺品，其制作始于明朝正德年间．紫砂壶的壶型众多，经典的有西施壶、掇球壶、石瓢壶、潘壶等．其中，石瓢壶的壶体可以近似看成一个圆台（即圆锥用平行于底面的平面截去一个锥体得到的）．下图给出了一个石瓢壶的相关数据（单位：cm），那么该壶的容量约为( )A．100cm3B．200cm3C．300cm3D．400cm33.设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的( )A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件4.对于棱锥，下列叙述正确的是( )A．四棱锥共有四条棱B．五棱锥共有五个面C．六棱锥的顶点有六个D．任何棱锥都只有一个底面5.一个水平放置的平面图形的直观图是一个底角为45∘，腰和上底长均为1的等腰梯形，则该平面图形的面积等于( )A．12+√22B．1+√22C．1+√2D．2+√26.如图，是一个空间几何体的三视图，其主（正）视图是一个边长为2的正三角形，俯视图是一个斜边为2的等腰直角三角形，左（侧）视图是一个两直角边分别为√3和1的直角三角形，则此几何体的体积为( )A．√33B．1C．√32D．27.下列四个正方体中，A，B，C为正方体所在棱的中点，则能得出平面ABC∥平面DEF的是( )A．B．C．D．8.一个圆台上、下底面半径分别为r，R，高为ℎ，若其侧面积等于两底面面积之和，则下列关系正确的是( )A．2ℎ=1R+1rB．1ℎ=1R+1rC．1r=1R+1ℎD．2R=1r+1ℎ9.已知四棱锥M­−ABCD，MA⊥平面ABCD，AB⊥BC，∠BCD+∠BAD=180∘，MA=2，BC= 2√6，∠ABM=30∘．若四面体MACD的四个顶点都在同一个球面上，则该球的表面积为( ) A．20πB．22πC．40πD．44π10.某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值为( )A．2B．3C．32D．92二、填空题（共6题）11.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的表面积为．12.一个底面半径为2cm的圆柱形容器内盛有足量的水，能放入一个半径为2cm的实心铁球，沉入水底后，水未溢出容器，则水面升高了cm．13.已知圆柱的底面积为S，侧面展开图是一个正方形，那么这个圆柱的侧面积是．14.已知M，N是三棱锥P−ABC的棱AB，PC的中点，记三棱锥P−ABC的体积为V1，三棱锥N−MBC的体积为V2，则V2V1等于．15.如图，在正四棱柱ABCD−A1B1C1D1中，AB=3cm，AA1=√2cm，则三棱锥D1−A1BD的外接球的体积为．16.思考辨析，判断正误．异面直线所成角的大小与点O的位置无关，所以求解时，可根据需要合理选择该点．三、解答题（共6题）17.如图，在三棱柱ABC−A1B1C1中，侧面ABB1A1和BCC1B1都是正方形，平面ABB1A1⊥平面BCC1B1，D，E分别为BB1，AC的中点．(1) 求证：BE∥平面A1CD；(2) 求直线B1E与平面A1CD所成角的正弦值．18.如图，在四棱锥P−ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA=AB，AC与BD交于点O，E，F分别为AB，PC的中点．(1) 求证：平面PAD⊥平面PCD；(2) 求证：EF∥平面PAD；(3) 求证：AF⊥平面POD．19.如图，在直三棱柱ABC−A1B1C1中，CA=CB=1，∠BCA=90∘，AA1=2，M，N分别是棱AA1，A1B1的中点．(1) 求BM的长；(2) 求BA1与CB1所成角的余弦值；(3) 求证：BA1⊥C1N．20.用符号语言表示下列语句，并画出图形．(1) 三个平面α，β，γ相交于一点P，且平面α与平面β相交于PA，平面α与平面γ相交于PB，平面β与平面γ相交于PC;(2) 平面ABD与平面BDC相交于BD，平面ABC与平面ADC相交于AC．21.如图，在四棱锥P−ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，AB⊥AD，AB∥CD，CD=AD=2AB=2AP．(1) 求证：平面PCD⊥平面PAD；(2) 在侧棱PC上是否存在点E，使得BE∥平面PAD．若存在，确定点E的位置，并给出证明；若不存在，请说明理由．22.直三棱柱底面各边的比为17:10:9，侧棱长为16cm，全面积为1440cm2，求底面各边之长．答案一、选择题（共10题）1. 【答案】D【知识点】平面的概念与基本性质2. 【答案】B【知识点】圆锥的表面积与体积3. 【答案】A【解析】因为b⊥m，所以当α⊥β，则由面面垂直的性质可得a⊥b成立，若a⊥b，则α⊥β不一定成立，故“α⊥β”是“a⊥b”的充分不必要条件．【知识点】平面与平面垂直关系的性质4. 【答案】D【解析】对于A，四棱锥共有八条棱，故A错误；对于B，五棱锥共有六个面，故B错误；对于C，六棱锥的顶点只有一个，故C错误；对于D，根据棱锥的结构特征，知D正确．【知识点】棱锥的结构特征5. 【答案】D【解析】将直观图还原成平面图形如图所示，则平面图形是上底长为1，下底长为1+√2，高为2的直角梯形，其面积为2+√2．【知识点】直观图6. 【答案】A【知识点】棱锥的表面积与体积、由三视图还原空间几何体7. 【答案】B【解析】如图，在B中连接MN，PN，因为A，B，C为正方体所在棱的中点，所以AB∥MN，AC∥PN，因为MN∥DE，PN∥EF，所以AB∥DE，AC∥EF，因为AB∩AC=A，DE∩EF=E，AB,AC⊂平面ABC，DE,EF⊂平面DEF，所以平面ABC∥平面DEF．【知识点】平面与平面平行关系的判定8. 【答案】A【解析】设圆台的母线长为l，根据题意可得圆台的上底面面积为S上=πr2，圆台的下底面面积为S下=πR2，因为圆台的侧面面积等于两底面面积之和，所以侧面积S侧=π(r2+R2)=π(r+R)l，解之得l=r 2+R2r+R，因为l=√ℎ2+(R−r)2，所以r 2+R2r+R=√ℎ2+(R−r)2，所以(r 2+R2r+R )2=ℎ2+(R−r)2，所以2ℎ=1R+1r．【知识点】圆台的表面积与体积9. 【答案】C【解析】因为∠BCD+∠BAD=180∘，所以A，B，C，D四点共圆，∠ADC=∠ABC=90∘．由tan30∘=2AB，得AB=2√3，所以 AC =√(2√3)2+(2√6)2=6． 设 AC 的中点为 E ，MC 的中点为 O ， 因为 MA ⊥平面ABCD ，所以 OE ⊥平面ABCD ．易知点 O 为四面体 MACD 外接球的球心，所以 OC =√(62)2+(22)2=√10，S 球=4π⋅OC 2=40π． 故选C ．【知识点】球的表面积与体积10. 【答案】B【知识点】三视图、棱锥的表面积与体积二、填空题（共6题） 11. 【答案】 (32+√3)π【知识点】组合体、圆柱的表面积与体积12. 【答案】 83【知识点】圆柱的表面积与体积、球的表面积与体积13. 【答案】4πS【解析】设底面半径为 r ，由底面积 S =πr 2 得 r 2=S π，则 S 侧=(2πr )2=4π2r 2=4π2×Sπ=4πS ．【知识点】圆柱的表面积与体积14. 【答案】 14【解析】 M 是 AB 的中点，所以 S △ABC =2S △MBC ，N 是 PC 的中点，所以 ℎ1=2ℎ2，V2V 1=13S △MBC ⋅ℎ213S △ABC ⋅ℎ1=14．【知识点】棱锥的表面积与体积15. 【答案】20√53π cm 3【解析】因为正四棱柱底面为正方形，所以 AB =BC =3，且三棱锥的顶点为这正四棱柱 8 个当中的 4 个，所以两者的外接球为同一个， 设球的半径为 R ，则 2R =√9+9+2=√20=2√5， 所以 R =√5，所以球的体积为 V =43πR 3=43π×5√5=20√5π3cm 3．【知识点】组合体、球的表面积与体积16. 【答案】 √【知识点】异面直线所成的角三、解答题（共6题） 17. 【答案】(1) 取 A 1C 的中点 F ，连接 DF ，EF ． 因为 E ，F 分别为 AC ，A 1C 的中点， 所以 EF ∥AA 1，且 EF =12AA 1．因为四边形 ABB 1A 1 是正方形， 所以 BB 1∥AA 1，且 BB 1=AA 1， 所以 EF ∥BB 1 且 EF =12BB 1， 又因为 D 为 BB 1 的中点， 所以 EF ∥BD 且 EF =BD ， 所以四边形 EFDB 为平行四边形， 所以 BE ∥DF ，又 BE ⊄平面A 1CD ，DF ⊂平面A 1CD ，所以 BE ∥平面A 1CD ．(2) 由题意知 BA ，BC ，BB 1 两两垂直，以 B 为原点，BC ，BB 1，BA 所在直线分别为 x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，设 BA =BC =BB 1=2，则 B 1(0,2,0)，E (1,0,1)，C (2,0,0)，D (0,1,0)，A 1(0,2,2)．所以 B 1E ⃗⃗⃗⃗⃗⃗⃗ =(1,−2,1)，CD ⃗⃗⃗⃗⃗ =(−2,1,0)，A 1C ⃗⃗⃗⃗⃗⃗⃗ =(2,−2,−2)，设平面 A 1CD 的法向量为 m ⃗⃗ =(x,y,z )，则 {A 1C ⃗⃗⃗⃗⃗⃗⃗ ⋅m ⃗⃗ =0,CD ⃗⃗⃗⃗⃗ ⋅m ⃗⃗ =0,即 {2x −2y −2z =0,−2x +y =0,令 x =1，得 m ⃗⃗ =(1,2,−1)，设直线 B 1E 与平面 A 1CD 所成角为 θ，则 sinθ=∣∣cos⟨B 1E ⃗⃗⃗⃗⃗⃗⃗ ,m ⃗⃗ ⟩∣∣=∣∣∣B 1E ⃗⃗⃗⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ ∣∣B 1E ⃗⃗⃗⃗⃗⃗⃗⃗ ∣∣∣∣m⃗⃗⃗ ∣∣∣∣∣=∣∣√6×√6∣∣=23， 所以直线 B 1E 与平面 A 1CD 所成角的正弦值为 23．【知识点】线面角、直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题18. 【答案】(1) 因为 PA ⊥平面ABCD ， 所以 PA ⊥CD ．因为 CD ⊥AD ，AD ∩PA =A ， 所以 CD ⊥平面PAD ． 因为 CD ⊂平面PCD ，所以 平面PAD ⊥平面PCD ．(2) 取 PD 中点 G ，连接 FG ，AG ， 因为 F 为 PC 的中点所以 FG ∥CD ，且 FG =12CD ．因为 E 为 AB 的中点，底面 ABCD 为正方形， 所以 AE ∥CD ，且 AE =12CD ．所以 FG ∥AE ，且 FG =AE ． 所以四边形 AEFG 为平行四边形． 所以 EF ∥AG ．因为 EF ⊄平面PAD 且 AG ⊂平面PAD ， 所以 EF ∥平面PAD ．(3) 在正方形 ABCD 中，OD ⊥AC ， 因为 PA ⊥平面ABCD ， 所以 PA ⊥OD ． 因为 AC ∩PA =A ， 所以 OD ⊥平面PAC ． 所以 OD ⊥AF ．在 △PAC 中，设 PO 交 AF 于 H ． 因为 PA ⊥AC ，且 O ，F 分别为 AC ，PC 的中点， 所以 AF =FC ． 所以 ∠FAC =∠FCA ．设 PA =1，由已知 PA =AB ， 所以 AC =√2．所以 tan∠APO =tan∠ACP =√22． 所以 ∠APO =∠ACP ． 所以 ∠APO =∠ACP ，且 ∠AOP 为公共角，所以 △APO ∽△HAO ．所以 ∠AHO =90∘．所以 AF ⊥PO ．因为 PO ∩OD =O ，所以 AF ⊥平面POD ．【知识点】直线与平面平行关系的判定、平面与平面垂直关系的判定、直线与平面垂直关系的判定19. 【答案】(1) 根据题意，以 C 为坐标原点，分别以 CA ，CB ，CC 1 所在直线为 x 轴，y 轴，z 轴，建立空间直角坐标系 Cxyz ，如图，依题意得 B (0,1,0),M (1,0,1)，根据空间两点间的距离公式得，∣BM⃗⃗⃗⃗⃗⃗ ∣=√(1−0)2+(0−1)2+(1−0)2=√3． (2) 由（1）得，A 1(1,0,2)，B (0,1,0)，C (0,0,0)，B 1(0,1,2)，则 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,−1,2)，CB 1⃗⃗⃗⃗⃗⃗⃗ =(0,1,2)，所以 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅CB 1⃗⃗⃗⃗⃗⃗⃗ =3．又 ∣BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ∣=√6，∣CB 1⃗⃗⃗⃗⃗⃗⃗ ∣=√5，所以 cos 〈BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ,CB 1⃗⃗⃗⃗⃗⃗⃗ 〉=BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅CB 1⃗⃗⃗⃗⃗⃗⃗⃗ ∣BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ∣⋅∣CB 1⃗⃗⃗⃗⃗⃗⃗⃗ ∣=√3010． (3) 由（1）得，C 1(0,0,2)，N (12,12,2)，所以 C 1N ⃗⃗⃗⃗⃗⃗⃗ =(12,12,0)， 所以 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅C 1N ⃗⃗⃗⃗⃗⃗⃗ =12−12+0=0，所以 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⊥C 1N ⃗⃗⃗⃗⃗⃗⃗ ，即 BA 1⊥C 1N ．【知识点】利用向量的坐标运算解决立体几何问题、异面直线所成的角、空间中直线与直线的垂直、空间线段的长度20. 【答案】(1) 符号语言表示：α∩β∩γ=P ，α∩β=PA ，α∩γ=PB ，β∩γ=PC ．图形表示：如图(2) 符号语言表示：平面ABD ∩平面BDC =BD ，平面ABC ∩平面ADC =AC ．图形表示：如图【知识点】平面与平面的位置关系21. 【答案】(1) 因为PA⊥平面ABCD，CD⊂平面ABCD，所以PA⊥CD，又因为AB⊥AD，AB∥CD，所以CD⊥AD，又PA∩AD=A，PA⊂平面PAD，AD⊂平面PAD，所以CD⊥平面PAD，又CD⊂平面PCD，所以平面PCD⊥平面PAD．(2) 当点E是PC的中点时，BE∥平面PAD．证明如下：设PD的中点为F，连接EF，AF，则EF是△PCD的中位线，所以EF∥CD，EF=12CD，又AB∥CD，AB=12CD，所以EF∥AB，EF=AB，所以四边形ABEF为平行四边形，所以BE∥AF，又BE⊄平面PAD，AF⊂平面PAD，所以BE∥平面PAD．【知识点】平面与平面垂直关系的判定、直线与平面平行关系的性质22. 【答案】设底面边长为17k，10k，9k（k>0），cosα=(9k)2+(10k)2−(17k)22⋅9k⋅10k =−35，所以S底面=12⋅9k⋅10k⋅sinα=36k2，由题意，(17k+10k+9k)⋅16+2⋅36k2=1440，所以k=2，所以底面三条边长分别为34cm，20cm，18cm．【知识点】棱柱的表面积与体积。

一、选择题1．在底面为正方形的四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，PA AD ⊥，PA AD =，则异面直线PB 与AC 所成的角为（ ）A ．30B ．45︒C ．60︒D ．90︒2．已知正方体1111ABCD A BC D -，点,E F 分别是棱11B C ，11A D 的中点，则异面直线BE ，DF 所成角的余弦值为（ ）A ．5B ．35C ．45D ．25 3．正方体1111ABCD A BC D -的棱长为2，E 是1CC 的中点，则点1C 到平面EBD 的距离为（ ）A ．3B ．6C ．5D ．2234．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：3cm ）为（ ）A ．43B ．2C ．4D ．6 5．如图，圆锥的母线长为4，点M 为母线AB 的中点，从点M 处拉一条绳子，绕圆锥的侧面转一周达到B 点，这条绳子的长度最短值为25 ）A ．4πB ．5πC ．6πD ．8π6．一个几何体的三视图如图所示，则该几何体的外接球的表面积是（ ）A ．2πB ．3πC ．4πD ．16π7．已知一个正三棱锥的四个顶点都在一个球的球面上，且这个正三棱锥的所有棱长都为22 ）A ．4πB ．8πC ．12πD ．24π 8．在长方体1111ABCD A BC D -中，2AB =，1AD =，12AA =，点E 为11C D 的中点，则二面角11B A B E --的余弦值为（ ）A ．33-B ．3C ．33D ．329．三棱锥P ABC -中，6AB =，8AC =，90BAC ∠=︒，若52PA PB PC ===则点B 到平面PAC 的距离为（ ）A ．32B 3041C 1534D ．610．一个正方体的平面展开图及该正方体的直观图如图所示，在正方体中，设BC 的中点为M ，GH 的中点为N ，下列结论正确的是（ ）A ．//MN 平面ABEB ．//MN 平面ADEC ．//MN 平面BDHD ．//MN 平面CDE11．蹴鞠，又名蹴球，筑球等，蹴有用脚踢、踏的含义，鞠最早系外包皮革、内实含米糠的球．因而蹴鞠就是指古人以脚踢、踏皮球的活动，类似现在的足球运动．2006年5月20日，蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录．3D 打印属于快速成形技术的一种，它是一种以数字模型为基础，运用粉末状金属或塑料等可粘合材料，通过逐层堆叠积累的方式来构造物体的技术．过去常在模具制造、工业设计等领域被用于制造模型，现正用于一些产品的直接制造，特别是一些高价值应用（比如人体的髋关节、牙齿或飞机零部件等）．已知某蹴鞠的表面上有四个点A ．B ．C ．D ，满足任意两点间的直线距离为6cm ，现在利用3D 打印技术制作模型，该模型是由蹴鞠的内部挖去由ABCD 组成的几何体后剩下的部分，打印所用原材料的密度为31g/cm ，不考虑打印损耗，制作该模型所需原材料的质量约为（ ）（参考数据）π 3.14≈2 1.41≈3 1.73≈6 2.45≈．A ．101gB ．182gC ．519gD ．731g12．已知四面体ABCD ，AB ⊥平面BCD ，1AB BC CD BD ====，若该四面体的四个顶点都在球O 的表面上，则球O 的表面积为（ ）A ．73πB ．7πC ．712πD ．79π 二、填空题13．已知四棱锥P ABCD -的底面ABCD 为矩形，且所有顶点都在球O 的表面上，侧面PAB ⊥底面ABCD ，23PA PB ==，120APB ∠=︒，4=AD ，则球O 的表面积为_______.14．如图，圆柱的体积为16π，正方形ABCD 为该圆柱的轴截面，F 为AB 的中点，E 为母线BC 的中点，则异面直线AC ，EF 所成的角的余弦值为______．15．如图，在一个底面面积为4，侧棱长为10的正四棱锥P ABCD -中，大球1O 内切于该四棱锥，小球2O 与大球1O 及四棱锥的四个侧面相切，则小球2O 的体积为___________.16．一件刚出土的珍贵文物要在博物馆大厅中央展出，需要设计一个各面是玻璃平面的无底正四棱柱将其罩住，罩内充满保护文物的无色气体．已知文物近似于塔形（如图所示），高1.8米，体积0.5立方米，其底部是直径为0.9米的圆形，要求文物底部与玻璃罩底边至少间隔0.3米，文物顶部与玻璃罩上底面至少间隔0.2米，气体每立方米1000元，则气体费用最少为_________元．17．正四面体ABCD 棱长为2，AO ⊥平面BCD ，垂足为O ，设M 为线段AO 上一点，且90BMC ︒∠=则二面角M BC O --的余弦值为________．18．祖恒是我国南北朝时代的伟大科学家，他总结了刘徽的有关工作，提出来体积计算的原理“幂势既同，则积不容异”，称为祖恒原理，意思是底面处于同一平面上的两个同高的几何体，若在等高处 的截面面积始终相等，则它们的体积相等，利用这个原理求半球O 的体积时，需要构造一个几何体，该几何体的三视图如图所示，则该几何体的体积为_________________19．将半径为3，圆心角为23π的扇形围成一个圆锥，则该圆锥内切球的体积为________． 20．在一个密闭的容积为1的透明正方体容器内装有部分液体，如果任意转动该正方体，液面的形状都不可能是三角形，那么液体体积的取值范围是 ．三、解答题21．如图所示，已知在三棱锥A BPC -中，,AP PC AC BC ⊥⊥，M 为AB 的中点，D 为PB 的中点，且PMB △为正三角形．（Ⅰ）求证：//DM 平面APC ；（Ⅱ）求证：平面ABC ⊥平面APC ；（Ⅲ）若4,20BC AB ==，求三棱锥D BCM -的体积．22．如图，在直三棱柱111ABC A B C -中，底面ABC 为正三角形，1AB 与1A B 交于点O ，E ，F 是棱1CC 上的两点，且满足112EF CC =.（1）证明：//OF 平面ABE ；（2）当1CE C F =，且12AA AB =，求直线OF 与平面ABC 所成角的余弦值. 23．如图，在长方体1111ABCD A BC D -中，12AB BC AA ==，1O 是底面1111D C B A 的中心.（Ⅰ）求证：1//O B 平面1ACD ；（Ⅱ）求二面角1D AC D --的平面角的余弦值.24．在四棱台1111ABCD A BC D -中，1AA ⊥平面ABCD ，//AB CD ，90ACD ∠=︒，26BC AC ==，1CD =，1AM CC ⊥，垂足为M .（1）证明：平面ABM ⊥平面11CDD C ；（2）若二面角B AM D --正弦值为217，求直线AC 与平面11CDD C 所成角的余弦. 25．如图，已知三棱锥P ABC -﹐PC AB ⊥，ABC 是边长为23的正三角形，43PB =﹐60PBC ∠=，点F 为线段AP 的中点．（1）证明：PC ⊥平面ABC ；（2）求直线BF 与平面PAC 所成角的大小．26．如图，ABC 中，2AC BC AB ==，ABED 是边长为1的正方形，平面ABED ⊥平面ABC ，若G 、F 分别是EC 、BD 的中点．GF平面ABC；（1）求证：//（2）求证：AC⊥平面EBC．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】由已知可得PA⊥平面ABCD，底面ABCD为正方形，分别过P，D点作AD，AP的平行线交于M，连接CM，AM，因为PB∥CM，所以ACM就是异面直线PB与AC所成的角,再求解即可.【详解】由题意：底面ABCD为正方形，⊥，侧面PAD⊥底面ABCD，PA AD=，面PAD面ABCD ADPA⊥平面ABCD，分别过P，D点作AD，AP的平行线交于M，连接CM，AM，∵PM∥AD，AD∥BC，PM＝AD，AD＝BC．∴ PBCM 是平行四边形，∴ PB ∥CM ，所以∠ACM 就是异面直线PB 与AC 所成的角．设PA ＝AB ＝a ，在三角形ACM 中，2,2,2AM a AC a CM a ===，∴三角形ACM 是等边三角形．所以∠ACM 等于60°，即异面直线PB 与AC 所成的角为60°．故选：C.【点睛】思路点睛：先利用面面垂直得到PA ⊥平面ABCD ，分别过P ，D 点作AD ，AP 的平行线交于M ，连接CM ，AM ，得到∠ACM 就是异面直线PB 与AC 所成的角．2．B解析：B【分析】证明//BE AF ，得AFD ∠是异面直线BE ，DF 所成角或其补角，在三角形中求解即可．【详解】连接,AF EF ，∵,E F 分别是棱11B C ，11A D 的中点，∴//EF AB ，EF AB =， ∴ABEF 是平行四边形，∴//BE AF ，∴AFD ∠是异面直线BE ，DF 所成角或其补角， 设正方体的棱长为2，则111A F D F ==，22215AF DF ==+=，2223cos 25255AF DF AD AFD AF DF +-∠===⋅⨯⨯， 异面直线BE ，DF 所成角的余弦值为35． 故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角． 3．B 解析：B【分析】 利用等体积法11C EBD D C EB V V --=，设点1C 到平面EBD 的距离为d ，利用三棱锥的体积公式代入面积即求得d .【详解】如图，利用等体积法，11C EBD D C EB V V --=，设点1C 到平面EBD 的距离为d ，正方体1111ABCD A BC D -的棱长为2，故22,5BD BE ED ===，如图，2215232h ED BD ⎛⎫=-=- ⎪⎝⎭11223622EBD S BD h =⨯⨯=⨯= 又点D 到平面1C EB 的距离，即D 到平面11C CBB 的距离，为CD =2，111212EB C S =⨯⨯=， 由11C EBD D C EB V V --=得，1161233d =⨯⨯，故636d ==. 故选：B.【点睛】方法点睛：空间中求点到平面的距离的常见方法： （1）定义法：直接作垂线，求垂线段长；（2）等体积法：利用三棱锥换底求体积，结合两个面积和另一个高求未知高，即得距离； （3）向量法：过点的一个斜线段对应的向量a ，平面法向量n ，则a n d n⋅=.4．B解析：B 【分析】根据三视图判断出几何体的结构，利用椎体体积公式计算出该几何体的体积. 【详解】根据三视图可知，该几何体为如图所示四棱锥，该棱锥满足底面是直角梯形，且侧棱ED ⊥平面ABCD ， 所以其体积为11(12)22232V =⨯⨯+⨯⨯=， 故选：B. 【点睛】方法点睛：该题考查的是有关根据几何体三视图求几何体体积的问题，解题方法如下： （1）首先根据题中所给的几何体的三视图还原几何体；（2）结合三视图，分析几何体的结构特征，利用体积公式求得结果.5． B解析：B 【分析】根据圆锥侧面展开图是一个扇形，且线段25MB =. 【详解】设底面圆半径为r ， 由母线长4l，可知侧面展开图扇形的圆心角为22r rl ππα==，将圆锥侧面展开成一个扇形，从点M 拉一绳子围绕圆锥侧面转到点B ，最短距离为BM ； 如图，在ABM 中，25,2,4MB AM AB ===， 所以222AM AB MB +=, 所以2MAB π∠=,故22rππα==，解得1r =，所以圆锥的表面积为25S rl r πππ=+=, 故选：B 【点睛】关键点点睛：首先圆锥的侧面展开图为扇形，其圆心角为2rlπα=，其次从点M 拉一绳子围绕圆锥侧面转到点B ，绳子的最短距离即为展开图中线段MB 的长，解三角即可求解底面圆半径r ，利用圆锥表面积公式求解.6．C解析：C 【分析】由三视图还原出原几何体，确定其结构，再求出外接球的半径得球的表面积． 【详解】由三视图，知原几何体是一个四棱锥P ABCD -，如图，底面ABCD 是边长为1的正方形，PB ⊥底面ABCD ，由PB ⊥底面ABCD ，AD ⊂面ABCD ，得PB AD ⊥，又AD AB ⊥，AB PB B ⋂=，,AB PB ⊂平面PAB ，所以AD ⊥平面PAB ，而PA ⊂平面PAB ，所以AD PA ⊥，同理DC PC ⊥，同样由PB ⊥底面ABCD 得PB BD ⊥，所以PD 中点O 到四棱锥各顶点距离相等，即为其外接球球心，PD 为球直径，222222PD PB BD PA AD AB =+=++=，∴外接球半径为12ADr ==， 表面积为2414S ππ=⨯=． 故选：C ．【点睛】关键点点睛：本题考查由三视图还原几何体，考查棱锥的外接球表面积．解题关键是确定外接球的球心．棱锥的外接球球心在过各面外心（外接圆圆心）且与该面垂直的直线上．7．C解析：C 【分析】将正三棱锥补成一个正方体，计算出正方体的棱长，可得出正方体的体对角线长，即为外接球的直径，进而可求得这个球的表面积. 【详解】设该正三棱锥为A BCD -，将三棱锥A BCD -补成正方体AEBF GCHD -，如下图所示：则正方体AEBF GCHD -的棱长为22222⨯=，该正方体的体对角线长为23 所以，正三棱锥A BCD -的外接球直径为223R =3R 该球的表面积为2412S R ππ==. 故选：C. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.8．C解析：C 【分析】取11A B 的中点F ，过F 作1FG A B ⊥，垂足为G ，连EG ，可证EGF ∠为二面角11B A B E --的平面角，通过计算可得结果.【详解】取11A B 的中点F ，过F 作1FG A B ⊥，垂足为G ，连EG ，因为,E F 分别为1111,C D A B 的中点，所以11//EF A D ，在长方体1111ABCD A BC D -中，因为11A D ⊥平面11ABB A ，所以EF ⊥平面11ABB A ， 因为1A B ⊂平面11ABB A ，所以1EF A B ⊥，因为1FG A B ⊥，且FGEF F =，所以1A B ⊥平面EFG ，因为EG ⊂平面EFG ，所以1A B EG ⊥，所以EGF ∠为二面角11B A B E --的平面角， 因为12AB AA ==，所以14FA G π∠=，因为11A F =，所以12222FG A F ==， 在直角三角形EFG 中，221612EG EF FG =+=+=， 所以cos FGEGF EG ∠==2326=. 所以二面角11B A B E --3. 故选：C 【点睛】关键点点睛：根据二面角的定义作出其中一个平面角是解题关键.9．C解析：C【分析】取BC 中点为O ，连接OP ，OA ，根据题中条件，由线面垂直的判断定理，证明PO ⊥平面ABC ；求出三棱锥P ABC -的体积；以及PAC △的面积，设点B 到平面PAC 的距离为d ，根据等体积法，由P ABC B PAC V V --=，即可求出结果. 【详解】取BC 中点为O ，连接OP ，OA ，因为6AB =，8AC =，90BAC ∠=︒，所以226810BC =+=，则152AO BC ==； 又52PA PB PC ===222100PB PC BC +==，则PB BC ⊥，152PO BC ==， 所以22250PO OA PA +==，所以PO AO ⊥； 因为PB PC =，O 为BC 中点，所以PO BC ⊥，又BC AO O ⋂=，BC ⊂平面ABC ，AO ⊂平面ABC ，所以PO ⊥平面ABC ； 此时三棱锥P ABC -的体积为11168540332P ABC ABCV S PO -=⋅=⨯⨯⨯⨯=，因为在PAC △中，52PA PC ==8AC =，所以PAC △的面积为221843422PACAC SPA ⎛⎫=⨯-= ⎪⎝⎭设点B 到平面PAC 的距离为d ， 由P ABC B PAC V V --=可得1403PACS d =⋅，所以1534434d ==故选：C. 【点睛】 方法点睛：求解空间中点P 到面α的距离的常用方法：（1）等体积法：先设所求点到面的距离，根据几何体中的垂直关系，由同一几何体的不同的侧面（或底面）当作底，利用体积公式列出方程，即可求解；（2）空间向量法：先建立适当的空间直角坐标系，求出平面α的一个法向量m，以及平面α的一条斜线PA所对应的向量PA，则点P到面α的距离即为PA m dm⋅=.10．C解析：C【分析】根据题意，得到正方体的直观图及其各点的标记字母，取FH的中点O,连接ON,BO，可以证明MN‖BO,利用BO与平面ABE的关系可以判定MN与平面ABE的关系，进而对选择支A 作出判定；根据MN与平面BCF的关系，利用面面平行的性质可以判定MN与平面ADE的关系，进而对选择支B作出判定；利用线面平行的判定定理可以证明MN与平面BDE的平行关系，进而判定C；利用M,N在平面CDEF的两侧，可以判定MN与平面CDE的关系，进而对D作出判定.【详解】根据题意，得到正方体的直观图及其各点的标记字母如图所示，取FH的中点O,连接ON,BO，易知ON与BM平行且相等，∴四边形ONMB为平行四边形，∴MN‖BO,∵BO与平面ABE（即平面ABFE)相交，故MN与平面ABE相交，故A错误；∵平面ADE‖平面BCF,MN∩平面BCF=M,∴MN与平面ADE相交，故B错误；∵BO⊂平面BDHF,即BO‖平面BDH,MN‖BO,MN⊄平面BDHF,∴MN‖平面BDH,故C正确；显然M,N在平面CDEF的两侧，所以MN与平面CDEF相交，故D错误.故选：C.【点睛】本题考查从面面平行的判定与性质，涉及正方体的性质，面面平行，线面平行的性质，属于小综合题，关键是正确将正方体的表面展开图还原，得到正方体的直观图及其各顶点的标记字母，并利用平行四边形的判定与性质找到MN的平行线BO.11．B解析：B 【分析】由题意可知所需要材料的体积即为正四面体外接球体积与正四面体体积之差，求出正四面体体积、外接球体积，然后作差可得所需要材料的体积，再乘以原料密度可得结果. 【详解】由题意可知，几何体ABCD 是棱长为6cm 的正四面体， 所需要材料的体积即为正四面体外接球体积与正四面体体积之差，设正四面体的棱长为a ，则正四面体的高为2223632aa a ⎛⎫-⨯= ⎪ ⎪⎝⎭， 设正四面体外接球半径为R ，则222623()()332a R R a =-+⨯，解得R =6a ， 所以3D 打印的体积为：323346113662343223812V a a a a a ππ⎛⎫=-⋅⋅⋅=- ⎪ ⎪⎝⎭， 又336216a ==，所以276182207.71125.38182.331182V π=-≈-=≈， 故选：B 【点睛】关键点点睛：本题考查正四面体与正四面体的外接球，考查几何体的体积公式，解决本题的关键点是求出正四面体外接球体积与正四面体体积，考查学生空间想象能力和计算能力，属于中档题．12．A解析：A 【分析】本题首先可根据题意将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分，然后求出直三棱柱的外接球的半径，最后根据球的表面积计算公式即可得出结果. 【详解】因为AB ⊥平面BCD ，1AB BC CD BD ====，所以可将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分，如图所示：则四面体ABCD 的外接球即直三棱柱的外接球，因为底面三角形BCD 的外心到三角形BCD 的顶点的长度为22131323， 所以直三棱柱的外接球的半径221372312r， 则球O 的表面积2277π4π4π123S r ， 故选：A. 【点睛】关键点点睛：本题考查四面体的外接球的表面积的计算，能否将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分是解决本题的关键，考查直三棱柱的外接球的半径的计算，是中档题.二、填空题13．【分析】首先利用垂直关系和底面和侧面外接圆的圆心作出四棱锥外接球的球心再计算外接球的半径以及球的表面积【详解】连结交于点取中点连结并延长于点点是外接圆的圆心侧面底面侧面底面平面过点作平面侧面所以点是 解析：64π【分析】首先利用垂直关系和底面ABCD 和侧面ABCD 外接圆的圆心，作出四棱锥P ABCD -外接球的球心，再计算外接球的半径，以及球O 的表面积. 【详解】连结,AC BD ，交于点M ，取AB 中点N 连结AN ，MN ，并延长于点E ，点E 是PAB △外接圆的圆心，侧面PAB ⊥底面ABCD ，侧面PAB 底面ABCD AB =，MN AB ⊥MN ∴⊥平面PAB ，过点M 作MO ⊥平面ABCD ，//EO MN ，EO ∴⊥侧面PAB ，所以点O 是四棱锥P ABCD -外接球的球心，可知四边形MNEO 是矩形，右图，PA PB ==，120APB ∠=，2cos306AB PB ∴==， 点E 是PAB △外接圆的圆心，sin303PN PB ∴==，PBE △是等边三角形，PE =NE ∴==MO ∴=12MC AC ==223134R OC MO MC ∴==+=+=， ∴球O 的表面积2464S R ππ==故答案为：64π 【点睛】本题考查了球与几何体的综合问题，考查空间想象能力以及化归和计算能力，（1）当三棱锥的三条侧棱两两垂直时，并且侧棱长为,,a b c ，那么外接球的直径2222R a b c =++2）当有一条侧棱垂直于底面时，先找底面外接圆的圆心，过圆心做底面的垂线，球心在垂线上，根据垂直关系建立R 的方程.（3）而本题类型，需要过两个平面外接圆的圆心作面的垂线，垂线的交点就是球心.14．【分析】由圆柱体积求得底面半径母线长设底面圆心为可得为异面直线与所成的角（或其补角）在对应三角形中求解可得【详解】设圆柱底面半径为则母线长为由得设底面圆心为连接则所以为异面直线所成的角在中所以故答案 6【分析】由圆柱体积求得底面半径，母线长，设底面圆心为O ，可得OEF ∠为异面直线AC 与EF 所成的角（或其补角）．在对应三角形中求解可得． 【详解】设圆柱底面半径为r ，则母线长为2r ，由2216r r ππ⋅=得2r．设底面圆心为O ，连接OE ，OF ．则//OE AC ，所以OEF ∠为异面直线AC ，EF 所成的角．在Rt OEF △中，2OF =，22OE =23EF = 所以6cos OE OEF EF ∠==6．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．15．【分析】设为正方形的中心的中点为连接求出如图分别可求得大球与小球半径分别为和进而可得小球的体积【详解】解：由题中条件知底面四边形是边长为2的正方形设O 为正方形的中心的中点为M 连接则如图在截面中设N 为 2【分析】设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，求出OM ，PM ，PO ，如图，分别可求得大球1O 与小球2O 半径分别为22和24，进而可得小球的体积． 【详解】解：由题中条件知底面四边形ABCD 是边长为2的正方形.设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，则1OM =，221013PM PA AM -=-=，9122PO -=PMO 中，设N为球1O 与平面PAB 的切点，则N 在PM 上，且1O N PM ⊥，设球1O 的半径为R ，则1O N R =，∵1sin 3OM MPO PM ∠==，∴1113NO PO =，则13PO R =，11422PO PO OO R =+==∴22R =，设球1O 与球2O 相切于点Q ，则22PQ PO R R =-=，设球2O 的半径为r ，同理可得4PQ r =，∴22R r ==，故小球2O 的体积342324V r ππ==. 故答案为：224π．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.16．4000【分析】根据题意先求出正四棱柱的底面边长和高由体积公式求出正四棱柱的体积减去文物的体积可得罩内空气的体积进而求出所需的费用【详解】由题意可知文物底部是直径为09m 的圆形文物底部与玻璃罩底边至 解析：4000【分析】根据题意，先求出正四棱柱的底面边长和高，由体积公式求出正四棱柱的体积减去文物的体积可得罩内空气的体积，进而求出所需的费用.【详解】由题意可知，文物底部是直径为0.9 m 的圆形，文物底部与玻璃罩底边至少间隔0.3 m ， 所以由正方形与圆的位置关系可知：底面正方形的边长为0.9+2×0.3=1.5m ，由文物高1.8m ，文物顶部与玻璃置上底面至少间隔0.2m ，所以正四棱柱的高为1.8+0.2=2m .，则正四棱柱的体积为V =1.52×2=4.5m 3因为文物体积为0.5m 3,所以置内空气的体积为4.5-0.5 = 4 m 3,气体每立方米1000元,所以共需费用为4×1000=4000（元）【点睛】数学建模是高中数学六大核心素养之一，在高中数学中，应用题是常见考查形式： 求解应用性问题时，首先要弄清题意，分清条件和结论，抓住关键词和量，理顺数量关系，然后将文字语言转化成数学语言，建立相应的数学模型.17．【分析】连接延长交于则是中点可得是二面角的平面角求出可得结论【详解】由已知是中心连接延长交于则是中点连接则而∴平面平面∴∴是二面角的平面角由对称性又由平面平面得∴故答案为：【点睛】关键点点睛：本题考 解析：3 【分析】 连接DO 延长交BC 于E ，则E 是BC 中点，可得MEO ∠是二面角M BC O --的平面角．求出,ME OE 可得结论．【详解】由已知O 是BCD △中心，连接DO 延长交BC 于E ，则E 是BC 中点，连接AE ，则BC AE ⊥，BC DE ⊥，而AE DE E =，∴BC ⊥平面AED ，M E ⊂平面AED ，∴BC ME ⊥，∴MEO ∠是二面角M BC O --的平面角．2BC =，90BMC ︒∠=，由对称性2BM CM ==，112ME BC ==， 又113323323EO DE ==⨯⨯=， 由AO ⊥平面BCD ，EO ⊂平面BCD ，得AO EO ⊥， ∴3cos EO MEO ME ∠==． 故答案为：3．【点睛】关键点点睛：本题考查求二面角，解题关键是作出二面角的平面角．这可根据平面角的定义作出（并证明），然后在直角三角形中求角即得．注意一作二证三计算三个步骤． 18．【分析】根据给定的几何体的三视图得到该几何体为一个圆柱挖去一个圆锥得出圆柱的底面半径和高利用圆柱和圆锥的体积以及圆的公式即可求解【详解】解：根据给定的几何体的三视图可得该几何体表示一个圆柱挖去一个圆解析：23π 【分析】根据给定的几何体的三视图，得到该几何体为一个圆柱挖去一个圆锥，得出圆柱的底面半径和高，利用圆柱和圆锥的体积以及圆的公式，即可求解．【详解】解：根据给定的几何体的三视图，可得该几何体表示一个圆柱挖去一个圆锥， 且底面半径1，高为1的组合体，所以几何体的体积为：2221311113πππ⨯⨯⨯=⨯-⨯． 故答案为：23π.【点睛】 关键点点睛：本题考查了几何体的三视图及体积的计算，在由三视图还原为空间几何体的实际形状时，要根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线，求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应公式求解． 19．【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径设内切球半径为r ﹐圆锥高为h 结合轴截面图形计算得最后计算体积即可【详解】解：设圆锥底面半径为R 则所以设内切球半径为r ﹐圆锥高为h 则如图是圆锥轴截面三 解析：23π 【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径1R =，设内切球半径为r ﹐圆锥高为h ，结合轴截面图形计算得22r ，最后计算体积即可. 【详解】解：设圆锥底面半径为R ，则2233R ππ=⨯，所以1R =． 设内切球半径为r ﹐圆锥高为h ，则9122h =-=如图，是圆锥轴截面三角形图，所以3r R h r =-，解得：22r ，故3442223383r V πππ==⨯=． 故答案为：23π【点睛】本题考查圆锥的侧面展开图，圆锥的内切球的体积，考查空间想象能力，是中档题. 20．【详解】试题分析：如图正方体ABCD-EFGH 此时若要使液面不为三角形则液面必须高于平面EHD 且低于平面AFC 而当平面EHD 平行水平面放置时若满足上述条件则任意转动该正方体液面的形状都不可能是三角形解析：15,66⎛⎫ ⎪⎝⎭【详解】试题分析：如图，正方体ABCD-EFGH ，此时若要使液面不为三角形，则液面必须高于平面EHD ，且低于平面AFC ．而当平面EHD 平行水平面放置时，若满足上述条件，则任意转动该正方体，液面的形状都不可能是三角形．所以液体体积必须＞三棱柱G-EHD 的体积16，并且＜正方体ABCD-EFGH 体积-三棱柱B-AFC 体积15166-=考点：1．棱柱的结构特征；2．几何体的体积的求法三、解答题21．（1）见详解；（2）见详解；（3）107【分析】(1)先证DM AP ∥，可证//DM 平面APC .(2)先证AP ⊥平面PBC ，得⊥AP BC ，结合AC BC ⊥可证得BC ⊥平面APC .(3)等积转换，由D BCM M DBC V V --＝，可求得体积.【详解】证明：因为M 为AB 的中点，D 为PB 的中点，所以MD 是ABP △的中位线，MDAP . 又MD平面APC ，AP ⊂平面APC ， 所以MD平面APC . （2）证明：因为PMB △为正三角形，D 为PB 的中点，所以MD PB ⊥. 又MD AP ，所以AP PB ⊥.又因为AP PC ⊥，PBPC P ＝，所以AP ⊥平面PBC . 因为BC ⊂平面PBC ，所以⊥AP BC .又因为BC AC ⊥，AC AP A ⋂＝，所以BC ⊥平面APC .(3)因为AP ⊥平面PBC ，MD AP ，所以MD ⊥平面PBC ，即MD 是三棱锥M DBC -的高.因为20AB =，M 为AB 的中点，PMB △为正三角形， 所以310,53PB MB MD MB ==== 由BC ⊥平面APC ，可得BC PC ⊥， 在直角三角形PCB 中，由104PB BC ＝，＝，可得221PC ＝ 于是1114221221222BCD BCP S S ⨯⨯⨯=△△＝＝ 112215310733D BCM M DBC BCD V V S MD --⨯=△＝＝＝【点睛】关键点睛：三棱锥的体积直接求不便时，常采用等积转换的方法，选择易求的底面积和高。

立体几何基础A 组题一、选择题：1．下列命题中正确命题的个数是 （ ） ⑴ 三点确定一个平面⑵ 若点P 不在平面α内，A 、B 、C 三点都在平面α内，则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案：A2．已知异面直线a 和b 所成的角为︒50，P 为空间一定点，则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 （ ） A.1条 B.2条 C.3条 D.4条答案：B 3．已知直线⊥l 平面α，直线⊂m 平面β，下列四个命题中正确的是 （ ） (1) 若βα//，则m l ⊥ (2) 若βα⊥，则m l // (3) 若m l //，则βα⊥ (4) 若 m l ⊥，则βα//A.(3)与（4）B.（1）与（3）C.（2）与（4）D.（1）与（2）答案：B4．已知m 、n 为异面直线，⊂m 平面α，⊂n 平面β，l =βα ，则l （ ） A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案：B5．设集合A={直线}，B={平面}，B A C =，若A a ∈，B b ∈，C c ∈，则下列命题中的真命题是 （ ）A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案：A6．已知a 、b 为异面直线，点A 、B 在直线a 上，点C 、D 在直线b 上，且AC=AD ，BC=BD ，则直线a 、b 所成的角为 （ ） A. ︒90 B. ︒60 C. ︒45 D. ︒30答案：A7．下列四个命题中正确命题的个数是 （ ） 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形，各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案：D8．设M={正四棱柱}，N={长方体}，P={直四棱柱}，Q={正方体}，则这些集合之间关系是 （ ） A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案：B9．正四棱锥P —ABCD 中，高PO 的长是底面长的21，且它的体积等于334cm ，则棱AB 与侧面PCD 之间的距离是 （ ） A.cm 2 B. cm 2 C. cm 1 D.cm 22答案：A10．纬度为α的纬圈上有A 、B 两点，弧在纬圈上，弧AB 的长为απcos R （R 为球半径），则A 、B 两点间的球面距离为 （ ）A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案：D11．长方体三边的和为14，对角线长为8，那么 （ ） A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案：D12．正四棱锥P —ABCD 的所有棱长都相等，E 为PC 的中点，那么异面直线BE 与PA 所成角的余弦值等于（ ）A.21B. 22C. 32D. 33答案：D13．用一个过正四棱柱底面一边的平面去截正四棱柱，截面是 （ ）A.正方形B.矩形C.菱形D.一般平行四边形答案：B二、填空题：14．正方体1111D C B A ABCD -中，E 、F 、G 分别为AB 、BC 、CC 1的重点，则EF 与BG 所成角的余弦值为________________________答案：510 15．二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4，到棱a 的距离为24，则这个二面角的大小为__________________答案：︒︒16575或16.四边形ABCD 是边长为a 的菱形，︒=∠60BAD ，沿对角线BD 折成︒120的二面角A —BD —C 后，AC 与BD 的距离为_________________________答案：a 43 17．P 为︒120的二面角βα--a 内一点，P 到α、β的距离为10，则P 到棱a 的距离是_________________答案：3320 18．如图：正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角，则异面直线AD 与BF 所成角的余弦值是______________________答案：4219．已知三棱锥P —ABC 中，三侧棱PA 、PB 、PC 两两互相垂直，三侧面与底面所成二面角的大小分别为γβα,,，则=++γβα222cos cos cos _______________答案：1 20．若四面体各棱的长是1或2，且该四面体不是正四面体，则其体积的值是_____________（只需写出一个可能的值）。

立体几何考察试题及答案一、选择题1. 若直线l与平面α垂直，则直线l与平面α内任意直线的关系是（）。

A. 相交B. 平行C. 异面D. 垂直答案：D2. 已知一个正四面体的棱长为a，求其体积。

A. \( \frac{a^3 \sqrt{2}}{12} \)B. \( \frac{a^3 \sqrt{2}}{6} \)C. \( \frac{a^3 \sqrt{3}}{12} \)D. \( \frac{a^3 \sqrt{3}}{6} \)答案：C二、填空题1. 已知一个长方体的长、宽、高分别为a、b、c，则其对角线的长度为 \( \sqrt{a^2 + b^2 + c^2} \)。

2. 一个球的半径为r，则其表面积为 \( 4\pi r^2 \)。

三、解答题1. 已知一个圆锥的底面半径为r，高为h，求其体积。

解：圆锥的体积公式为 \( V = \frac{1}{3}\pi r^2 h \)。

答：圆锥的体积为 \( \frac{1}{3}\pi r^2 h \)。

2. 已知一个圆柱的底面半径为r，高为h，求其侧面积。

解：圆柱的侧面积公式为 \( A = 2\pi rh \)。

答：圆柱的侧面积为 \( 2\pi rh \)。

四、证明题1. 证明：若直线l与平面α内的两条直线m和n都垂直，则直线l与平面α垂直。

证明：设直线m和n在平面α内的交点为O，由于直线l与m、n都垂直，根据直线与平面垂直的判定定理，直线l与平面α垂直。

答：直线l与平面α垂直。

2. 证明：若两个平面α和β的交线为l，直线m在平面α内且与l平行，直线n在平面β内且与l平行，则直线m与直线n平行。

证明：设直线m与直线n的交点为P，由于m在平面α内且与l平行，n在平面β内且与l平行，根据平面与平面平行的性质，直线m与直线n平行。

答：直线m与直线n平行。

一、选择题1．设1l 、2l 、3l 是三条不同的直线，α、β、γ是三个不同的平面，则下列命题是真命题的是（ ）A ．若1//l α，2//l α，则12l l //B ．若1l α⊥，2l α⊥，则12l l ⊥C ．若12//l l ，1l α⊂，2l β⊂，3l αβ⋂=，则13//l lD ．若αβ⊥，1l αγ=，2l βγ⋂=，则12l l //2．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QAB QAC QBCPABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（ ）A ．42πB ．44πC ．48πD ．49π3．如图，正三棱柱111ABC A B C -的高为4，底面边长为43，D 是11B C 的中点，P 是线段1A D 上的动点，过BC 作截面AP α⊥于E ，则三棱锥P BCE -体积的最小值为（ ）A ．3B ．23C ．43D ．124．已知平面图形PABCD ，ABCD 为矩形，4AB =，是以P 为顶点的等腰直角三角形，如图所示，将PAD △沿着AD 翻折至P AD '△，当四棱锥P ABCD '-体积的最大值为163，此时四棱锥P ABCD '-外接球的表面积为（ ）A ．12πB ．16πC ．24πD ．32π5．已知E ，F 是四面体的棱AB ，CD 的中点，过EF 的平面与棱AD ，BC 分别相交于G ，H ，则（ ） A ．GH 平分EF ，BH AGHC GD = B ．EF 平分GH ，BH GDHC AG = C ．EF 平分GH ，BH AGHC GD= D ．GH 平分EF ，BH GDHC AG= 6．《九章算术》是古代中国乃至东方的第一步自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（ ）A ．6π B ．4π C ．3πD ．2π 7．正三棱柱111ABC A B C -各棱长均为1，M 为1CC 的中点，则点1B 到面1A BM 的距离为（ ） A 2B ．22C ．12D 38．已知四面体ABCD 中，二面角A BC D --的大小为60，且2AB =，4CD =，120CBD ∠=，则四面体ABCD 体积的最大值是（ ）A 43B 23C ．83D ．439．在四棱锥P -ABCD 中，//AD BC ，2AD BC =，E 为PD 中点，平面ABE 交PC 于F ，则PFFC=（ ） A ．1B ．32C ．2D ．310．已知四面体ABCD ，AB ⊥平面BCD ，1AB BC CD BD ====，若该四面体的四个顶点都在球O 的表面上，则球O 的表面积为（ ） A ．73π B ．7π C ．712π D ．79π 11．空间四边形PABC 的各边及对角线长度都相等，D 、E 、F 外别是AB 、BC 、CA 的中点，下列四个结论中不成立的是（ ） A ．//BC 平面PDF B ．DF ⊥平面PAE C ．平面PDE ⊥平面ABCD ．平面PAE ⊥平面ABC12．如果一个水平放置的平面图形的斜二测直观图是如图所示的直角梯形，其中2O A ''=，45B A O '''∠=,//B C O A ''''.则原平面图形的面积为（ ）A ．32B ．62C ．322D ．34二、填空题13．如图，已知直四棱柱1111ABCD A BC D -的所有棱长均相等，3BAD π∠=，E 是棱AB的中点，设平面α经过直线1A E ，且α平面111,B BCC l α=⋂平面112C CDD l =，若α⊥平面11A ACC ，则异面直线1l 与2l 所成的角的余弦值为_______．14．3ABCD 中，对角线3AC =ABC 沿AC 折起，使得二面角B AC D --的大小为2π，则三棱锥B ACD -外接球的体积是_________________．15．在正三棱锥P ABC -中，E ，F 分别为棱PA ，AB 上的点，3PE EA =，3BF FA =，且CE EF ⊥.若23PB =，则三棱锥P ABC -的外接球的体积为_________.16．点A 、B 、C 、D 在同一个球的球面上，3AB BC AC ===，若四面体ABCD 体积的最大值为3，则这个球的表面积为______. 17．三棱锥P ABC -的各顶点都在同一球面上，PC ⊥底面ABC ，若1PC AC ==，2AB =，且60BAC ∠=︒，给出如下命题：①ACB △是直角三角形；②此球的表面积等于11π； ③AC ⊥平面PBC ；④三棱锥A PBC -的体积为32. 其中正确命题的序号为______.（写出所有正确结论的序号）18．将底面直径为8，高为23的圆锥体石块打磨成一个圆柱，则该圆柱侧面积的最大值为______.19．在三棱锥P ABC -中，PA ⊥平面ABC ，60BAC ∠=︒，23AB AC ==，2PA =，则三棱锥P ABC -外接球的半径为____________.20．水平放置的ABC ∆的斜二测直观图如图所示,已知''4,''3B C A C ==,则ABC ∆中AB 边上的中线的长度为_______ .三、解答题21．如图，在四棱锥P ABCD -中，PAB △是等边三角形，CB ⊥平面,//PAB AD BC 且22PB BC AD F ===，为PC 中点．（1）求证：//DF 平面PAB ；（2）求直线AB 与平面PDC 所成角的正弦值．22．如图，四面体ABCD 中，O 是BD 的中点，点G 、E 分别在线段AO 和BC 上，2BE EC =，2AG GO =，2CA CB CD BD ====，2AB AD ==.（1）求证：//GE 平面ACD ； （2）求证：平面ABD ⊥平面BCD .23．如图，在正三棱柱111ABC A B C -中，若12AB BB =，AD DC =，试证明：（1）1//AB 平面1BC D ； （2）11AB BC ⊥.24．如图，圆柱的轴截面ABCD 是长方形，点E 是底面圆周上异于A ，B 的一点，AF DE ⊥，F 是垂足.（1）证明：AF DB ⊥；（2）若2AB =，3AD =，当三棱锥D ABE -体积最大时，求点C 到平面BDE 的距离. 25．在三棱锥P ABC -中，AE BC ⊥于点,E CF AB ⊥于点F ，且AE CF O ⋂=，若点P 在平面ABC 上的射影为点O ．（1）证明：AC PB ⊥；（2）若ABC 是正三角形，点,G H 分别为,PA PC 的中点．证明：四边形EFGH 是矩形．26．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为梯形，//AD BC ，6BC =，2PA AD CD ===，E 是BC 上一点且23BE BC =，PB AE ⊥.（1）求证：AB ⊥平面PAE ； （2）求点C 到平面PDE 的距离.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】利用已知条件判断1l 与2l 的位置关系，可判断AD 选项的正误；利用线面垂直的性质定理可判断B 选项的正误；利用线面平行的性质定理可判断C 选项的正误. 【详解】对于A 选项，若1//l α，2//l α，则1l 与2l 平行、相交或异面，A 选项错误； 对于B 选项，若1l α⊥，2l α⊥，由线面垂直的性质定理可得12//l l ，B 选项错误； 对于C 选项，12//l l ，1l α⊂，2l β⊂，α、β不重合，则1l β⊄，1//l β∴，1l α⊂，3l αβ⋂=，13//l l ∴，C 选项正确；对于D 选项，若αβ⊥，1l αγ=，2l βγ⋂=，则1l 与2l 相交或平行，D 选项错误.故选：C. 【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．2．D解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM =，再根据12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得到AB BC AC ==，然后根据22222213QA QB QC AB BC CA ++=++，ABCS =6,AB AQ ==，在AOQ△中，由222AO OQ AQ =+求解半径即可.【详解】 如图所示：作QM AB ⊥与M ，连接PM ， 因为PQ ⊥平面ABC ，所以PQ AB ⊥，又QM PQ Q ⋂=， 所以AB ⊥平面PQM ， 所以AB PM ⊥，所以112122QAB PAB AB QM S S AB PM ⨯⨯==⨯⨯△△, 2PM QM =,因为12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△， 由对称性得AB BC AC ==,又因为22222213QA QB QC AB BC CA ++=++，93ABCS=所以21sin 60932ABCSAB =⨯⨯= 解得6,23AB AQ ==所以3,23,3QM PM PQ ==， 设外接球的半径为r ，在AOQ △中，222AO OQ AQ =+，即()(222323r r =-+， 解得72r =， 所以外接球的表面积为2449S r ππ==， 即该球形容器的表面积的最小值为49π. 故选：D 【点睛】关键点点睛：本题关键是由12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..3．C解析：C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时，三棱锥P BCE -体积有最小值，建立坐标系求得当点E 的高为3时，问题得解. 【详解】以点O 为原点，,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系，如图所示：设点(),0,E x z ，依题意得()6,0,0A ，则()6,0,AE x z =- ，(),0,OE x z = 因为过BC 作截面AP α⊥于E ，所以AE OE ⊥则0AE OE ⋅=， 故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅=故选：C 【点睛】关键点点晴：本题的解题关键是将问题转化为求E ABC V -的最大值，通过建系求得三棱锥E ABC -的高的最大值即可.4．C解析：C 【分析】分析出当平面P AD '⊥平面ABCD 时，四棱锥P ABCD '-的体积取最大值，求出AD 、P A '的长，然后将四棱锥P ABCD '-补成长方体P AMD QBNC '-，计算出该长方体的体对角线长，即为外接球的直径，进而可求得外接球的表面积. 【详解】取AD 的中点E ，连接P E '，由于P AD '△是以P '为顶点的等腰直角三角形，则P E AD '⊥，设AD x =，则1122P E AD x '==， 设二面角P AD B '--的平面角为θ，则四棱锥P ABCD '-的高为1sin 2h x θ=， 当90θ=时，max 12h x =， 矩形ABCD 的面积为4S AB AD x =⋅=，2111216433233P ABCD V Sh x x x '-=≤⨯⨯==，解得22x =.将四棱锥P ABCD '-补成长方体P AMD QBNC '-， 所以，四棱锥P ABCD '-的外接球直径为22222226R P N P A P D P Q AD AB ''''==++=+=，则6R =，因此，四棱锥P ABCD '-的外接球的表面积为2424R ππ=.故选：C.【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.5．C解析：C 【分析】举特例舍去不正确选项，可得正确答案. 【详解】过EF 的平面为平面ABF 时，G 在A 点， H 在B 点， 所以0BH AGHC GD==，EF 平分GH ， 即BH AG HC GD=，所以舍去ABD ，选C 故选：C6．D解析：D 【分析】过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，然后在CFG △中求解. 【详解】如下图所示，在平面ABFE 中，过点F 作//FG AE 交AB 于点G ，连接CG ， 则异面直线AE 与CF 所成角为CFG ∠或其补角，设1EF =，则3AB =，2BC CF AE ===，因为//EF AB ，//FG AE ，所以，四边形AEFG 为平行四边形， 所以，2FG AE ==，1AG =，2BG =， 由于2ABC π∠=，由勾股定理可得2222CG BC BG =+=所以，222CG CF FG =+，则2CFG π∠=.故选：D. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．7．B解析：B 【分析】 连接11A N B AB =，根据已知条件先证明11B A A B ⊥、1⊥MN AB ，再通过线面垂直的判定定理证明1AB ⊥平面1A BM ，由此确定出1B N 的长度即为点1B 到面1A BM 的距离，最后完成求解. 【详解】连接1B A 交1A B 于N ，连接11,,,,MB MN MB MA MA ，如图所示：因为11A ABB 为正方形，所以11B A A B ⊥， 又因为22111115142MB MC C B =+=+=，2215142MA MC CA =+=+， 所以1MB MA =且N 为1AB 中点，则MN 为等腰三角形1AMB 的中垂线， ∴1⊥MN AB 且1MNA B N =，∴1AB ⊥平面1A BM ，∴1B N 就是点1B 到截面1A BM 的距离， 又因为1111211222B N AB ==+=，所以点1B 到截面1A BM 的距离为22， 故选：B. 【点睛】方法点睛：求解平面外一点A 到平面α的距离的方法：（1）几何方法：通过线面垂直的证明，找到A 在平面α内的投影点A '，则AA '即为A 到平面α的距离；（2）向量方法：①建立合适空间直角坐标系，在平面α内取一点B ；②求解出AB 和平面α的法向量n ；③根据AB n d n⋅=即可求解出点A 到平面α的距离.8．D解析：D 【分析】在BCD △中，利用余弦定理和基本不等式可得163BC BD⋅≤，由三角形的面积公式可得BCDS≤，由二面角A BC D --的大小为60，可得A 到平面BCD 的最大距离为2sin 603h ==ABCD 体积的最大值.【详解】在BCD △中，由余弦定理可得2222cos120CD BC BD BC BD =+-⋅22BC BD BC BD =++⋅因为222BC BD BC BD +≥，所以23CD BC BD ≥⋅， 所以163BC BD ⋅≤，当且仅当BC BD =时等号成立，1116sin120223BCDSBC BD =⋅≤⨯= 因为二面角A BC D --的大小为60，所以点A 到平面BCD的最大距离为2sin 603h == 所以114333A BCD BCDV S h -=⋅≤=， 所以四面体ABCD 体积的最大值是43， 故选：D 【点睛】关键点点睛：本题解题的关键点是利用余弦定理和基本不等式、三角形面积公式求出BCD S △最大值，再由二面角求出高的最大值. 9．C解析：C 【分析】首先通过延长直线,DC AB ，交于点G ，平面BAE 变为GAE ，连结PG ，EG 交于点F ，再根据三角形中线的性质，求PFFC的值. 【详解】延长,DC AB ，交于点G ，连结PG ，EG 交PC 于点F ，//AD BC ，且2AD BC =，可得点,B C 分别是,AG DG 的中点，又点E 是PD 的中点，PC ∴和GE 是△PGD 的中线，∴点F 是重心，得2PFFC=故选：C 【点睛】关键点点睛：本题的关键是找到PC 与平面BAE 的交点，即将平面BAE 转化为平面GAE 是关键.10．A解析：A 【分析】本题首先可根据题意将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分，然后求出直三棱柱的外接球的半径，最后根据球的表面积计算公式即可得出结果. 【详解】因为AB ⊥平面BCD ，1AB BC CD BD ====，所以可将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分，如图所示：则四面体ABCD 的外接球即直三棱柱的外接球，因为底面三角形BCD 的外心到三角形BCD 的顶点的长度为222131323，所以直三棱柱的外接球的半径221372312r， 则球O 的表面积2277π4π4π123S r ， 故选：A. 【点睛】关键点点睛：本题考查四面体的外接球的表面积的计算，能否将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分是解决本题的关键，考查直三棱柱的外接球的半径的计算，是中档题.11．C解析：C 【分析】由线面平行的判定定理可判断A ；由线面垂直的判定定理可判断B ；反证法可说明C ；由面面垂直的判定定理可判断D. 【详解】 对于A ，D ，F 外别是AB ，CA 的中点，//BC DF ∴，DF ⊂平面PDF ，∴//BC 平面PDF ，故A 正确，不符合题意；对于B ，各棱长相等，E 为BC 中点，,BC AE BC PE ∴⊥⊥，PEAE E =，BC ∴⊥平面PAE ，//BC DF ，∴DF ⊥平面PAE ，故B 正确，不符合题意；对于C ，假设平面PDE ⊥平面ABC ，设DE BF O ⋂=，连接PO ，则O 是DE 中点，PO DE ∴⊥，平面PDE 平面ABC DE =，PO ∴⊥平面ABC ，BF ⊂平面ABC ，PO BF ∴⊥，则PB PF =，与PB PF ≠矛盾，故C 错误，符合题意；对于D ，由B 选项DF ⊥平面PAE ， DF ⊂平面ABC ，∴平面PAE ⊥平面ABC ，故D 正确，不符合题意. 故选：C. 【点睛】本题考查线面关系和面面关系的判定，解题的关键是正确理解判断定理，正确理解垂直平行关系.12．A解析：A 【分析】作出原平面图形，然后求出面积即可． 【详解】45B A O '''∠=B O A '''=∠，则O A B '''△是等腰直角三角形，∴2A B OB '''==，又O C C B ''''⊥，45C O B '''∠=︒，∴1B C ''=， 在直角坐标系中作出原图形为：梯形OABC ，//OA BC ，2,1OA BC ==，高22OB = ∴其面积为1(21)22322S =+⨯= 故选：A 【点睛】方法点睛：本题考查斜二测法画平面图形直观图，求原图形的面积，可能通过还原出原平面图形求得面积，也可以通过直观图到原图形面积的关系求解：直观图面积为S '，原图形面积为S ，则4S S '=二、填空题13．【分析】取的中点连接证明平面平面平面即平面然后分别取的中点证明平面平面可得可得异面直线与所成的角即与所成的角由余弦定理可得答案【详解】由直四棱柱的所有棱长均相等所以是菱形连接且所以因为平面平面所以且 解析：910【分析】取AD 的中点F ，连接1A F ，证明平面1A EF ⊥平面11A ACC ，平面1A EF 即平面α，然后分别取1111BC DC 、的中点M N 、，证明平面1//A EF 平面MNC ，可得//CM 1l ，//CN 2l ，可得异面直线1l 与2l 所成的角即CM 与CN 所成的角，由余弦定理可得答案.【详解】由直四棱柱1111ABCD A BC D -的所有棱长均相等，3BAD π∠=，所以ABCD 是菱形，连接AC BD 、，1111AC B D 、，且ACBD O =，11111AC B D O ⋂=，所以BD AC ⊥，1111B D AC ⊥，因为1AA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以1AA BD ⊥，且1AA AC A =，所以BD ⊥平面11A ACC ，取AD 的中点F ，连接1A F ，连接EF 交AC 与G ，所以//EF BD ，且G 是AO 的中点，所以EF ⊥平面11A ACC ，所以平面1A EF ⊥平面11AACC ， 又1A E ⊂平面1A EF ，所以平面1A EF 即平面α， 分别取1111BC DC 、的中点M N 、，连接MN 交11AC 与H 点，H 即为11O C 的中点， 所以1A H GC =，且1//A H GC ，所以四边形1AHCG 是平行四边形，所以1//AG HC ， 1AG ⊄平面CMN ，CH ⊂平面CMN ，所以//A G 平面CMN ， 又因为11//////EF BD B D MN ，EF ⊄平面CMN ，MN ⊂平面CMN ， 所以//MN 平面CMN ，又1AG EF G =，所以平面1//A EF 平面MNC ，且平面11B C CB ⋂平面MNC MC =， 平面11D C CD平面MNC NC =，所以//CM 1l ，//CN 2l ，所以异面直线1l 与2l 所成的角即CM 与CN 所成的角，设2AB =， 则直四棱柱1111ABCD A BC D -的所有棱长均为2，由3BAD π∠=，所以112BD AB B D ===，11112MN D B ==， 且2211415CM CN CC C M ==+=+=，由余弦定理得222551922510CM CN MN MCN CM CN +-+-∠===⨯⨯.故答案为：910. 【点睛】本题考查了异面直线所成的角，关键点是作出平面α及找出异面直线所成的角，考查了学生分析问题、解决问题的能力及空间想象力.14．；【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析：556π； 【分析】分析菱形的特点，结合其翻折的程度，判断其外接球球心的位置，放到相应三角形中，利用勾股定理求得半径，利用球的体积公式求得外接球的体积. 【详解】根据题意，画出图形，3ABCD 中，对角线3AC = 所以ABC 和DBC △都是正三角形， 又因为二面角B AC D --的大小为2π， 所以分别从两个正三角形的中心做面的垂线，交于O ， 则O 是棱锥B ACD -外接球的球心，且11,2GD OG GE ===， 所以球的半径225R GD OG =+=， 所以其体积为3344555(3326V R ππ==⋅=， 故答案为：556π. 【点睛】思路点睛：该题考查的是有关几何体外接球的问题，解题思路如下： （1）根据题中所给的条件，判断菱形的特征，得到两个三角形的形状；（2）根据直二面角，得到两面垂直，近一倍可以确定其外接球的球心所在的位置； （3）利用勾股定理求得半径； （4）利用球的体积公式求得结果；（5）要熟知常见几何体的外接球的半径的求解方法.15．【分析】证明与垂直得线面垂直从而得正三棱锥的三条侧棱两两垂直结合正方体的性质得三条侧棱的平方和为外接球直径的平方求得球半径后可得球体积【详解】∵∴∴又∴取中点连接如图由于是正三棱锥∴而平面∴平面又平 解析：36π【分析】证明PB 与,CE AC 垂直得线面垂直，从而得正三棱锥的三条侧棱两两垂直，结合正方体的性质得三条侧棱的平方和为外接球直径的平方，求得球半径后可得球体积．【详解】∵3PE EA =，3BF FA =，∴AE AFAP AB=，∴//EF PB ，又CE EF ⊥，∴PB CE ⊥，取AC 中点D ，连接,PD BD ，如图，由于P ABC -是正三棱锥，∴,PD AC BD AC ⊥⊥，而PD BD D ⋂=，,PD BD ⊂平面PBD ，∴AC ⊥平面PBD ，又PB ⊂平面PBD ， ∴AC PB ⊥，∵ACCE C =，,AC CE ⊂平面PAC ，∴PB ⊥平面PAC ，而,PA PC ⊂平面PAC ，∴,PB PA PB PC ⊥⊥，同理正三棱锥中，PA PC ⊥． 设三棱锥P ABC -外接球半径为R ，则22222(2)3(23)R PA PB PC =++=⨯，3R =，球的体积为343363V ππ=⨯=． 故答案为：36π．【点睛】结论点睛：三棱锥的外接球问题，解题关键是找到外接球的球心，三棱锥的外接球球心在过各面外心且与该面垂直的直线上．当从同一顶点出发的三条棱两两垂直时，可以把三棱锥补成一个长方体，而长方体的对角线就是三棱锥外接球的直径．16．【分析】先由题意得到的面积以及外接圆的半径记的外接圆圆心为为使四面体体积最大只需与面垂直由此求出设球心为半径为根据为直角三角形由勾股定理列出等式求出球的半径即可得出结果【详解】根据题意知是一个等边三 解析：254π【分析】先由题意，得到ABC 的面积，以及ABC 外接圆的半径，记ABC 的外接圆圆心为Q ，为使四面体ABCD 体积最大，只需DQ 与面ABC 垂直，由此求出2DQ =，设球心为O ，半径为R ，根据AQO 为直角三角形，由勾股定理列出等式，求出球的半径，即可得出结果. 【详解】根据题意知，ABC 是一个等边三角形，其面积为()2213333322S ⎛⎫=-= ⎪ ⎪⎝⎭，ABC 外接圆的半径为1312sin 60r =⨯=，记ABC 的外接圆圆心为Q ，则1AQ r ==；由于底面积ABCS不变，高最大时体积最大，所以DQ 与面ABC 垂直时体积最大，最大值为133ABC S DQ ⋅=，2DQ ∴=， 设球心为O ，半径为R ，则在直角AQO 中，222OA AQ OQ =+， 即2221(2)R R =+-，54R ∴=， 则这个球的表面积为：2525444S ππ⎛⎫== ⎪⎝⎭. 故答案为：254π. 【点睛】 思路点睛：求解几何体与球外接问题时，一般需要先确定底面外接圆的圆心位置，求出底面外接圆的半径，根据球的性质，结合题中条件确定球心位置，求出球的半径，进而即可求解.17．①③【分析】①先求出再得到最后判断①正确；②先判断三棱锥的外接球就是以为顶点以棱的长方体的外接球再求半径最后求出球的表面积判断②错误；③先证明最后证明平面判断③正确；④直接求出三棱锥的体积判断④错误解析：①③. 【分析】①先求出3BC =，再得到222AB BC AC =+，最后判断①正确；②先判断三棱锥P ABC -的外接球就是以C 为顶点，以CA ，CB ，CP 棱的长方体的外接球，再求半径r ，最后求出球的表面积，判断②错误；③先证明AC PC ⊥，AC BC ⊥，⋂=PC CB C ,最后证明AC ⊥平面PBC ，判断③正确；④直接求出三棱锥A PBC -的体积，判断④错误. 【详解】解：①在ACB △，因为1AC =，2AB =，且60BAC ∠=︒， 所以2222cos 3BC AB AC AB AC BAC =+-⋅⋅∠=，则3BC =， 所以222AB BC AC =+，所以ACB △是直角三角形，故①正确； ②由（1）可知AC BC ⊥，又因为PC ⊥底面ABC ，所以三棱锥P ABC -的外接球就是以C 为顶点，以CA ，CB ，CP 棱的长方体的外接球，则2225r CA CB CP =++=，则此球的表面积等于245S r ππ==，故②错误； ③因为PC ⊥底面ABC ，所以AC PC ⊥，由（1）可知AC BC ⊥，⋂=PC CB C ,所以AC ⊥平面PBC ，故③正确； ④三棱锥A PBC -的体积113(13)132V =⨯⨯⨯⨯=，故④错误. 故答案为：①③. 【点睛】本题考查判断三角形是直角三角形、求三棱锥的外接球的表面积、求三棱锥的体积、线面垂直的证明，是中档题.18．【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h 底面半径为r 用r 表示h 从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥；设圆柱的高为h 底面半径为r 则解得；所以；当时取 解析：43π【分析】欲使圆柱侧面积最大，需使圆柱内接于圆锥，设圆柱的高为h ，底面半径为r ，用r 表示h ，从而求出圆柱侧面积的最大值. 【详解】欲使圆柱侧面积最大，需使圆柱内接于圆锥； 设圆柱的高为h ，底面半径为r ，4r =，解得2h =；所以()22242S rh r r r r ππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧； 当2r时，S 圆柱侧取得最大值为故答案为：. 【点睛】本题考查了求圆柱侧面积的最值，考查空间想象能力，将问题转化为函数求最值，属于中档题.19．【分析】先在等边三角形中求出外接圆半径从而可求该三棱锥的外接球的半径【详解】详解：因为所以为等边三角形所以等边外接圆的半径为如图三棱锥外接球球心为半径为设球心到平面的距离为外接圆圆心为连接则平面取中【分析】先在等边三角形ABC中求出BC =2r ，从而可求该三棱锥的外接球的半径. 【详解】详解：因为060AB AC BAC ==∠=，所以ABC 为等边三角形，所以BC =ABC 外接圆的半径为23r，如图，三棱锥P ABC -外接球球心为O ，半径为R ， 设球心O 到平面ABC 的距离为d ，ABC 外接圆圆心为'O ， 连接,','AO AO OO ，则'OO ⊥平面ABC ， 取PA 中点,D OP OA =，所以OD PA ⊥，又PA ⊥平面ABC ，所以//PA OO '，则四边形'ADOO 是矩形， 所以在PDO △和'OAO △中，由勾股定理可得()222222222R d R d ⎧=+⎪⎨=+-⎪⎩，解得：1,d R ==.【点睛】本题主要考查了三棱锥外接球的表面积，其中根据几何体的结构特征和球的性质，求得三棱锥的外接球的半径是解答的关键，着重考查了空间想象能力，以及推理与运算能力.20．【分析】首先根据直观图可知其平面图形为直角三角形且两条直线边长为长接下来利用勾股定理即可求出AB 的长然后利用直角三角形的性质进行解答即可【详解】把直观图还原成平面图形如图所示：得为直角三角形且两条直 解析：732【分析】首先根据直观图可知其平面图形为直角三角形，且两条直线边长为长3,8AC BC ==，接下来利用勾股定理即可求出AB 的长，然后利用直角三角形的性质进行解答即可. 【详解】把直观图还原成平面图形如图所示：得ABC ∆为直角三角形，且两条直角边的长3,8AC BC ==， 由勾股定理可得73AB = 故三角形AB 73 73 【点睛】本题是一道关于平面几何图形的直观图的题目，解答本题的关键是熟练掌握斜二测画法的相关知识.三、解答题21．（1）证明见解析；（2）24【分析】（1）取PB 边的中点E ，即可证明四边形AEFD 为平行四边形，再根据线面平行的判定定理即可证明；（2）取BC 边的中点G ，由//DG AB ，即可得到直线AB 与平面PDC 所成角即为DG 与平面PDC 所成角，再由等体积法求得22G PCD d -=，即可求得直线AB 与平面PDC 所成角的正弦值． 【详解】解：（1）如图所示：取PB 边的中点E ，连,AE FE ， 则三角形中位线可知：//EF BC 且12EF BC =， 由题可知：//AD BC 且12AD BC =， //AD EF ∴且AD EF =，即四边形AEFD 为平行四边形，//DF AE ∴又DF ⊄平面,PAB AE ⊂平面PAB ，故//DF 平面PAB ； （2）取BC 边的中点G ， 则//DG AB ，且2DG AB ==，直线AB 与平面PDC 所成角即为DG 与平面PDC 所成角， 又1CDGS=，且易得DC PD =,所以11223622CDPSPC DF =⋅=⨯⨯= 由等体积法，1113633P CDG G PCD G PCD V V d ---==⨯⨯=⨯⨯，得22G PCD d -=， DG ∴与平面PDC 所成角的正弦值为22224=， 故直线AB 与平面PDC 所成角的正弦值为24． 【点睛】关键点点睛：本题解题的关键是利用等体积法求出G 点到平面PCD 的距离. 22．（1）证明见解析；（2）证明见解析. 【分析】（1）先依题意得到G 为ABD △的重心，即得到21BG BE GM EC ==，证得//GE MC ，再利用线面平行的判定定理即证结论；（2）先在ABD △中，证得AO BD ⊥，求得1AO =，在BCD △中，求得3OC =，结合勾股定理证得AO OC ⊥，再利用线面垂直的判定定理证明AO ⊥平面BCD ，即证平面ABD ⊥平面BCD . 【详解】证明：（1）连接BG 并延长，交AD 于M ，连接MC ，在ABD △中，O 为BD 中点，G 在AO 上，2AG GO =， ∴G 为ABD △的重心∴21BG GM =， 又21BE EC =∴BG BEGM EC=∴//GE MC ， ∵GE ⊄平面ACD ，AC ⊂平面ACD ， ∴//GE 平面ACD ；（2）在ABD △中，O 为BD 中点，2BD =，2AB AD == ∴AO BD ⊥∴221AO AB BO -=，在BCD △中，2BC CD BD ===，O 为BD 中点，连接OC ，则3OC =又2CA =，∴222OA OC CA +=，∴AO OC ⊥ 由AO OC ⊥，AO BD ⊥，OC BD O =，,OC BD ⊂平面BCD ，得AO ⊥平面BCD ， 又AO ⊂平面ABD ， ∴平面ABD ⊥平面BCD . 【点睛】 思路点睛：证明线面平行时运用线面平行的判定定理证得，或者利用面面平行的性质证得；证明线面垂直时，运用其判定定理需要证明一条直线与相交的两条直线垂直，当题目条件中给出长度时可以采用勾股定理逆定理证得线线垂直，或者运用面面垂直的性质定理证得线面垂直．23．（1）证明见解析；（2）证明见解析. 【分析】（1）连接1BC 交1BC 于点E ，连接DE ，则E 为1BC 的中点，利用中位线的性质可得1//DE AB ，再利用线面平行的判定定理可证得结论成立；（2）取BC 中点F ，连接AF 、1B F ，证明出1BC ⊥平面1AB F ，进而可证得11AB BC ⊥.【详解】（1）连接1BC 交1BC 于点E ，连接DE ，在正三棱柱111ABC A B C -中，四边形11BB C C 为平行四边形，且11B C BC E =，则E为1BC 的中点， 又D 为AC 的中点，所以1//AB DE ,又1AB ⊄平面1BC D ，DE ⊂平面1BC D ，所以1//AB 平面1BC D ； （2）取BC 中点F ，连接AF 、1B F ，设11B FBC O =，在正三棱柱111ABC A B C -中，1BB ⊥平面ABC ，AF ⊂平面ABC ，1AF BB ∴⊥，ABC 为正三角形，且F 为BC 的中点，AF BC ∴⊥，1BB BC B =，AF ∴⊥平面11BB C C ，1BC ⊂平面11BB C C ，1AF BC ∴⊥，在侧面11BCC B中，1BC =，F 是BC的中点，11112BB BF BB B C ∴==， 又11190B BF BBC ∠=∠=，所以，111R t t BB R B C FB △△，111BFB B BC ∴∠=∠，所以，1111190BFB CBC B BC CBC ∠+∠=∠+∠=，90BOF ∴∠=，所以11BC B F ⊥，1AFB F F =，所以，1BC ⊥面1AB F ，因为1AB ⊂平面1AB F ，所以11BC AB ⊥.【点睛】方法点睛：证明线面垂直的方法： 一是线面垂直的判定定理； 二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等． 24．（1）证明见解析；（232211【分析】（1）根据题中条件，由线面垂直的判定定理，证明AF ⊥平面DEB ；即可推出AF DB ⊥；（2）先由题意，得到AEB △是等腰直角三角形时，三棱锥D ABE -体积最大，设点C 到平面EBD 的距离为h ，由C DBE E CBD V V --=，根据等体积法，即可求出结果. 【详解】（1） EB ⊂平面AEB ，DA EB ∴⊥， AB 是圆柱底面的直径，点E 在圆周上，AE EB ∴⊥，又AE DA A ⋂=，AE ⊂平面DAE ，DA ⊂平面DAE ，BE ∴⊥平面DAE ，AF ⊂平面DAE ，EB AF ∴⊥，又AF DE ⊥，且EB DE E =，EB ⊂平面DEB ，DE ⊂平面DEB ，AF ∴⊥平面DEB ，DB ⊂平面DEB ，AF DB ∴⊥；（2）13D AEB AEBV S DA -=⨯⨯，3DA =，。

《立体几何》（一）选择题：1．下列说法正确的是 ( ) （A ）两平面相交只有一个公共点 （B ）两两相交的三条直线共面 （C ）不共面的四点中，任何三点不共线 （D ）有三个公共点的两平面必重合 2．在空间，下列命题中正确的是 ( ) （A ）对边相等的四边形一定是平面图形 （B ）四边相等的四边形一定是平面图形（C ）有一组对边平行的四边形一定是平面图形 （D ）有一组对角相等的四边形一定是平面图形3．过空间一点作三条直线，则这三条直线确定的平面个数是 ( ) （A ）1个 （B ）2个 （C ）3个 （D ）1个或3个 4．空间不共线的四点，其中三点共线是这四点共面的 ( ) （A ）充分条件 （B ）必要条件 （C ）充要条件（D ）既非充分也非必要条件 5．下列说法正确的是 （ ） （A ）过三点确定一个平面 （B ）过一条直线和一个点确定一个平面 （C ）梯形、平行四边形都是平面图形（D ）四边形都是平面图形6．下列命题中正确的是 （ ） （A ）空间不同的三点确定一个平面（B ）空间两两相交的三条直线确定一个平面（C ）空间有三个角为直角的四边形一定是平面图形（D ）和同一条直线相交的三条平行直线一定在同一平面内7．“直线上有两点在平面内”是“这条直线在这个平面内”的 （ ） （A ）充分条件 （B ）必要条件 （C ）充要条件 （D ）既不充分又不必要 8．下列说法正确的是 （ ） （A ）四边形的对角线相交（B ）空间有任意四个角是直角的四边形一定是平面图形 （C ）两两相交的三条直线一定共面（D ）在空间的四点，若无三点共线，则这四点一定不共面。

9．不一定能确定一个平面的是 ( ) （A ）直线与直线外一点（B ）两条相交直线（C ）空间三点（D ）两条平行直线10．A 、B 、C 表示不同的点，a 、l 表示不同的直线，α、β表示不同的平面，下列推理不正确的是 （ ） ()A ααα⊂⇒∈∈∈∈l B l B A l A ,,,()B βα∈∈A A ,，AB B B =⇒∈∈βαβα ,直线 ()C αα∉⇒∈⊄A l A l ,()D α∈C B A ,,，β∈C B A ,,且C B A ,,不共线α⇒与β重合 （二）填空题：1．空间三条直线互相平行，但不共面，它们能确定 个平面；三条直线相交于一点，它们最多可确定 个平面。

高一数学必修第二册第八章《立体几何初步》单元练习题卷6（共22题）一、选择题（共10题）1.已知两个圆锥，底面重合在一起，其中一个圆锥顶点到底面的距离为2cm，另一个圆锥顶点到底面的距离为3cm，则其直观图中这两个顶点之间的距离为( )A．2cm B．3cm C．2.5cm D．5cm2.截一个几何体，所得各截面都是圆面，则这个几何体一定是( )A．圆柱B．圆锥C．球D．圆台3.下列说法中，正确的是( )A．棱柱的侧面可以是三角形B．若棱柱有两个侧面是矩形，则该棱柱的其他侧面也是矩形C．正方体的所有棱长都相等D．棱柱的所有棱长都相等4.若直线l不平行于平面α，且l⊄α，则( )A．α内的所有直线与l异面B．α内不存在与l平行的直线C．α与直线l至少有两个公共点D．α内的直线与l都相交5.一个建筑物上部为四棱锥，下部为长方体，且四棱锥的底面与长方体的上底面尺寸一样，已知长方体的长、宽、高分别为20m，5m，10m，四棱锥的高为8m，若按1:500的比例画出它的直观图，那么直观图中，长方体的长、宽、高和棱锥的高应分别为( )A．4cm,1cm,2cm,1.6cm B．4cm,0.5cm,2cm,0.8cmC．4cm,0.5cm,2cm,1.6cm D．2cm,0.5cm,1cm,0.8cm6.用一个平行于圆锥底面的平面截这个圆锥，截得的圆台上下底面半径之比为1:4，若截去的圆锥的母线长为3cm，则圆台的母线长为( )A．1cm B．3cm C．12cm D．9cm7.在空间内，可以确定一个平面的条件是( )A．三个点B．两条直线C．两两相交三条直线D．两两相交的三条直线且不交于同一点8.已知球的半径R=2，则这个球的体积为( )A．8π3B．32π3C．16πD．32π9.在正方体ABCD−A1B1C1D1中，E，F分别是线段BC，CD1的中点，则直线A1B与直线EF的位置关系是( )A．相交B．异面C．平行D．垂直10.利用斜二测画法画边长为1cm的正方形的直观图，可能是下面的( )A．B．C．D．二、填空题（共6题）11.空间不重合的两个平面的关系有．12.直线a∥b，c，d为不重合的两直线，且a∥c，b∥d，则c与d的位置关系是．13.用符号语言表示“点A在直线l上，l在平面α外”为．14.思考辨析，判断正误两个平面α，β有一个公共点A，就说α，β相交于A点，记作α∩β=A．( )15.16.一个正方体的顶点都在球面上，它的棱长为2cm，则球的表面积是cm2．三、解答题（共6题）17.(1) 直线与平面垂直的判定定理．(2) 思考：若把定理中的“两条相交直线”改为“两条直线”，直线与平面一定垂直吗？18.圆柱的侧面展开图是边长为6π和4π的矩形，求圆柱的全面积及体积．19.一个几何体按比例绘制的三视图如图所示（单位：m）．(1) 画出它的直观图（不要求写出画法）．(2) 求几何体的表面积和体积．20.如图，正四棱柱ABCD−A1B1C1D1的底面边长AB=2，若异面直线A1A与B1C所成角的大，求正四棱柱ABCD−A1B1C1D1的体积．小为arctan1221.如图所示，已知直角梯形ABCD，BC∥AD，∠ABC=90∘，AB=5cm，BC=16cm，AD=4cm．求：(1) 以AB所在直线为旋转轴旋转一周所得几何体的表面积；(2) 以BC所在直线为旋转轴旋转一周所得几何体的表面积．22.已知侧棱和底面边长都是3√2的正四棱锥ABCD−A1B1C1D1的8个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，则其外接球的半径是多少？答案一、选择题（共10题）1. 【答案】D【解析】由题意，圆锥顶点到底面的距离即圆锥的高，故两顶点间距离为2+3=5cm，在直观图中与z轴平行的线段长度不变，仍为5cm．【知识点】直观图2. 【答案】C【解析】由球的结构特征知该几何体是球．【知识点】球的结构特征3. 【答案】C【解析】棱柱的侧面都是平行四边形，选项A错误；其他侧面可能是平行四边形，选项B错误；棱柱的侧棱与底面边长并不一定相等，选项D错误；易知选项C正确．【知识点】棱柱的结构特征4. 【答案】B【解析】因为l⊄α，直线l不平行于平面α，所以直线l只能与平面α相交，于是直线l与平面α只有一个公共点，所以平面α内不存在与l平行的直线．【知识点】直线与直线的位置关系5. 【答案】C【解析】由比例尺可知长方体的长、宽、高和四棱锥的高分别为4cm，1cm，2cm和 1.6cm，再结合斜二测画法，可知直观图的相应尺寸应分别为4cm，0.5cm，2cm，1.6cm．【知识点】直观图6. 【答案】D【解析】如图，设圆锥的母线长为l，则33+l =14，解得：l=9，故选D．【知识点】圆锥的表面积与体积7. 【答案】D【解析】A.三个点，当三点共线时不能确定平面，排除；B.两条直线，当两条直线异面时不能确定平面，排除；C.两两相交的三条直线，当三条直线交于一点时不能确定平面，排除；D.两两相交的三条直线且不交于同一点，可以确定平面，正确；故选：D．【知识点】平面的概念与基本性质8. 【答案】B【知识点】球的表面积与体积9. 【答案】A【解析】由BC∥AD，AD∥A1D1知，BC∥A1D1，从而四边形A1BCD1是平行四边形，所以A1B∥CD1，又EF⊂平面A1BCD1，EF∩D1C=F，则A1B与EF相交．【知识点】直线与直线的位置关系10. 【答案】C【解析】正方形的直观图是平行四边形，且边长不相等．【知识点】直观图二、填空题（共6题）11. 【答案】两两垂直【知识点】平面与平面的位置关系12. 【答案】c∥d【知识点】直线与直线的位置关系13. 【答案】A∈l，l⊄α【知识点】直线与直线的位置关系14. 【答案】×【知识点】平面的概念与基本性质15. 【答案】平行；a∥b【知识点】平面与平面平行关系的性质16. 【答案】12π【解析】R=√3，S=4πR2=12π．【知识点】球的表面积与体积三、解答题（共6题）17. 【答案】(1) 两条相交直线；a∩b(2) 当这两条直线平行时，直线可与平面平行或相交或在平面内，但不一定垂直．【知识点】直线与平面垂直关系的判定18. 【答案】分情况讨论：（1）r=2，S全=24π2+8π，V=24π2；（2）r=3，S全=24π2+18π，V=36π2．【知识点】圆柱的表面积与体积19. 【答案】(1) 由三视图可知，该几何体由正方体和四棱柱组成，如图所示．(2) 表面积为2×2+32×1+√2×1+7×1×1+3×1=15+√2(m2)．由于正方体的体积为1×1×1=1，四棱柱的体积为2+32×1×1=52，所以几何体的体积为72(m3)．【知识点】直观图、三视图、棱柱的表面积与体积20. 【答案】因为A1A∥BB1，所以∠CB1B为A1A与B1C所成角，且tan∠CB1B=12．因为BC=2，所以BB1=4．所以V=Sℎ=16．【知识点】棱柱的表面积与体积21. 【答案】(1) 以AB所在直线为旋转轴旋转一周所得几何体是圆台，其上底面半径是4cm，下底面半径是16cm，母线DC=√52+(16−4)2=13(cm)，所以该几何体的表面积为π×(4+16)×13+π×42+π×162=532π(cm2)．(2) 以BC所在直线为旋转轴旋转一周所得几何体是圆柱和圆锥的组合体，如图所示．其中圆锥的高为16−4=12(cm)，由（1）可知圆锥的母线DC长为13cm，又圆柱的母线AD长为4cm，故该几何体的表面积为2π×5×4+π×52+π×5×13=130π(cm2)．【知识点】圆锥的表面积与体积、圆台的表面积与体积、圆柱的表面积与体积22. 【答案】依题意，得该正四棱锥底面对角线的长为3√2×√2=6，高为√(3√2)2−(12×6)2=3，因此底面中心到各顶点的距离均等于3，所以该正四棱锥的外接球的球心即为底面正方形的中心，其外接球的半径为3．【知识点】球的结构特征。

一、选择题1．如下图所示，在正方体1111ABCD A BC D -中，E 是平面11ADD A 的中心，M 、N 、F 分别是11B C 、1CC 、AB 的中点，则下列说法正确的是（ ）A ．12MN EF =，且MN 与EF 平行 B ．12MN EF ≠，且MN 与EF 平行 C ．12MN EF =，且MN 与EF 异面 D ．12MN EF ≠，且MN 与EF 异面 2．若圆锥的内切球（球面与圆锥的侧面以及底面都相切）的半径为1，当该圆锥体积取最小值时，该圆锥体积与其内切球体积比为（ ） A ．2：1B ．4：1C ．8：1D ．8：33．已知正方体1111ABCD A BC D -，E 、F 分别是正方形1111D C B A 和11ADD A 的中心，则EF 和BD 所成的角的大小是（ ） A ．30B ．45C ．60D ．904．在正方体1111ABCD A BC D -中，点,E F 分别是梭BC ，CD 的中点，则1A F 与1C E 所成角的余弦值为（ ） A 5B 25C 5D 255．已知正三棱柱111ABC A B C -，底面正三角形ABC 的边长为2，侧棱1AA 长为2，则点1B 到平面1A BC 的距离为（ ）A ．2217B ．22121 C 47 D 476．如图，四棱柱ABCD A B C D ''''-中，底面ABCD 为正方形，侧棱AA '⊥底面ABCD ，32AB =6AA '=，以D 为圆心，DC '为半径在侧面BCC B ''上画弧，当半径的端点完整地划过C E '时，半径扫过的轨迹形成的曲面面积为（ ）A ．96π B ．93π C ．96π D ．93π 7．已知三棱柱111ABC A B C -的所有顶点都在球O 的表面上，侧棱1AA ⊥底面111A B C ，底面111A B C △是正三角形，1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是23，则球O 的表面积是（ ） A ．28π3B ．14π3C ．56π3D ．7π 38．如图，正三棱柱111ABC A B C -的高为4，底面边长为43，D 是11B C 的中点，P 是线段1A D 上的动点，过BC 作截面AP α⊥于E ，则三棱锥P BCE -体积的最小值为（ ）A ．3B ．23C ．43D ．129．已知α、β是平面，m 、n 是直线，下列命题中不正确的是（ ） A ．若//m α，n αβ=，则//m n B ．若//m n ，m α⊥，则n α⊥ C ．若m α⊥，m β⊥，则//αβD ．若m α⊥，m β⊂，则αβ⊥10．如图，在矩形ABCD 中，1AB =，3BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥A BCD -正视图和俯视图如图，则三棱锥A BCD -中AC 长为（ ）A ．32B ．3C ．102D ．211．如图，正方形ABCD 的边长为4，点E ，F 分别是AB ，B C 的中点，将ADE ，EBF △，FCD 分别沿DE ，EF ，FD 折起，使得A ，B ，C 三点重合于点A '，若点G 及四面体A DEF '的四个顶点都在同一个球面上，则以FDE 为底面的三棱锥G -DEF 的高h 的最大值为（ ）A ．263+B ．463+C ．4263-D ．2263-12．空间四边形PABC 的各边及对角线长度都相等，D 、E 、F 外别是AB 、BC 、CA 的中点，下列四个结论中不成立的是（ ）A ．//BC 平面PDFB ．DF ⊥平面PAE C ．平面PDE ⊥平面ABC D ．平面PAE ⊥平面ABC二、填空题13．如图，在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，PAD △为等边三角形，四边形ABCD 为矩形，24AB AD ==，则四棱锥P ABCD -的外接球的表面积为________．14．如图，在一个底面面积为4，侧棱长为10的正四棱锥P ABCD -中，大球1O 内切于该四棱锥，小球2O 与大球1O 及四棱锥的四个侧面相切，则小球2O 的体积为___________.15．已知三棱锥A BCD -中，2AB CD ==，3AC BC AD BD ====，则三棱锥A BCD -的体积是____________．16．二面角a αβ--的大小为135A AE a E α︒∈⊥，，，为垂足，,B BF a F β∈⊥，为垂足，2,31AE BF EF P ===，，是棱上动点，则AP PB +的最小值为_______． 17．已知ABC 是等腰直角三角形，斜边2AB =，P 是平面ABC 外的一点，且满足PA PB PC ==，120APB ∠=︒，则三棱锥P ABC -外接球的表面积为________．18．在正三棱锥S ABC -中，23AB =，4SA =，E 、F 分别为AC 、SB 的中点，过点A 的平面α//平面SBC ，α平面=ABC l ，则异面直线l 和EF 所成角的余弦值为_________.19．如图，已知正四面体P ABC -的棱长为2，动点M 在四面体侧面PAC 上运动，并且总保持MB PA ⊥，则动点M 的轨迹的长度为__________.20．将半径为3，圆心角为23π的扇形围成一个圆锥，则该圆锥内切球的体积为________． 三、解答题21．如图所示，四棱锥P ABCD -的底面ABCD 是平行四边形，90DBA ∠=︒，2BA BD ==，10,,PA PD E F =分别是棱,AD PC 的中点.（1）证明：//EF 平面PAB ；（2）若二面角P AD B --为60︒，求点B 到平面PAD 的距离.22．如图，在正四棱柱1111ABCD A BC D -中，11,2AB AA ==，点E 为1CC 中点，点F 为1BD 中点．（1）求异面直线1BD 与1CC 的距离；（2）求直线1BD 与平面BDE 所成角的正弦值； （3）求点F 到平面BDE 的距离．23．如图，已知菱形ABCD 和菱形ACFE 所在的平面互相垂直，M 为BF 的中点．（1）求证：//DF 平面ACM ； （2）若2AB =，ABC CAE ∠=∠=π3，求三棱锥F BDE -的体积． 24．如图，该多面体由底面为正方形ABCD 的直四棱柱被截面AEFG 所截而成，其中正方形ABCD 的边长为4，H 是线段EF 上（不含端点）的动点，36==FC EB ．（1）证明：//GH 平面ABCD ； （2）求H 到平面AEC 的距离．25．如图，四棱锥P ABCD -的底面为正方形，PA ⊥底面ABCD ，E ，F ，H 分别为AB ，PC ，BC 的中点.（1）求证：DE ⊥平面PAH ；（2）若2PA AD ==，求直线PD 与平面PAH 所成线面角的正弦值.26．如图，四棱锥P ABCD -，底面ABCD 为矩形，PD ⊥面ABCD ，E 、F 分别为PA 、BC 的中点．（1）求证：//EF 面PCD ；（2）若2AB =，1AD PD ==，求三棱锥P BEF -的体积．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】设正方体1111ABCD A BC D -的棱长为2，利用正方体性质可求得2MN =3EF =知12MN EF ≠，再利用三角形中位线性质知1//MN B C ，从而//MN ED ，又EF 与ED 相交，可知MN 与EF 异面，即可选出答案.【详解】设正方体1111ABCD A BC D -的棱长为2，则22112MN MC C N =+=作E 点在平面ABCD 的投影点G ，即EG ⊥平面ABCD ，连接,EG GF ，在直角EGF △中，1EG =，222GF AG AF =+=2222123EF EG GF =+=+以12MN EF ≠，故排除A 、C 连接DE ，由E 是平面11ADD A 的中心，得112DE A D =又M N 、分别是11B C 、1CC 的中点，所以1//MN B C 又11//A D B C ，所以//MN ED ， 又EF ED E ⋂=，所以MN 与EF 异面 故选：D.【点睛】关键点睛：本题考查正方体中的线面关系，线线平行的关系，及判断异面直线，解题的关键是熟记正方体的性质，考查学生的逻辑推理能力，属于基础题.2．A解析：A 【分析】根据三角形相似得出圆锥的底面半径和高的关系，根据体积公式和基本不等式得出答案． 【详解】设圆锥的高为h ，底面半径为r ，则当球面与圆锥的侧面以及底面都相切时，轴截面如图，由~AOE ACF 可得：22(1)11h r --=，即22r h h =-， ∴圆锥的体积22148[(2)4]33(2)323h V r h h h h ππππ===-++--．当且仅当22h -=，即4h =时取等号．∴该圆锥体积的最小值为83π． 内切球体积为43π． 该圆锥体积与其内切球体积比2:1． 故选：A ．【点睛】方法点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”（即条件要求中字母为正数）、“定”（不等式的另一边必须为定值）、“等”（等号取得的条件）的条件才能应用，否则会出现错误.3．C解析：C 【分析】作出图形，连接1AD 、11B D 、1AB ，推导出1//EF AB ，11//BD B D ，可得出异面直线EF 和BD 所成的角为11AB D ∠，分析11AB D 的形状，即可得出结果. 【详解】如下图所示，连接1AD 、11B D 、1AB ，设正方体1111ABCD A BC D -的棱长为1，则11112AD AB B D ===， 所以，11AB D 为等边三角形，则1160AB D ∠=，因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心，则E 、F 分别是11B D 、1AD 的中点，所以，1//EF AB ，在正方体1111ABCD A BC D -中，11//BB DD 且11BB DD =， 所以，四边形11BB D D 为平行四边形，则11//BD B D ， 所以，异面直线EF 和BD 所成的角为1160AB D ∠=. 故选：C. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．4．D解析：D 【分析】延长DA 至G ，使AG CE =，可证11//AG C E ，得1GA F ∠是异面直线1A F 与1C E 所成的角（或其补角）．在1AGF △中，由余弦定理可得结论． 【详解】延长DA 至G ，使AG CE =，连接1,GE GA ,GF ，11,AC AC ， 又//AG CE 所以AGEC 是平行四边形，//,GE AC GE AC =， 又正方体中1111//,AC AC AC AC =， 所以1111//,AC DE AC DE =，所以11AC EG 是平行四边形，则11//AG C E ， 所以1GA F ∠是异面直线1A F 与1C E 所成的角（或其补角）． 设正方体棱长为2，在正方体中易得15AG =，10GF =，22222112(21)3A F AA AF =+=++=，1AGF △中，2221111125cos 2253AG A F GF GA F AG A F +-∠===⋅⨯⨯． 故选：D ．【点睛】方法点睛：本题考查空间向量法求异面直线所成的角，求异面直线所成角的方法： （1）定义法：根据定义作出异面直线所成的角并证明，然后解三角形得结论； （2）建立空间直角坐标系，由两异面直线的方向向量的夹角得异面直线所成的角．5．A解析：A 【分析】根据题意，将点1B 到平面1A BC 的距离转化为点A 到平面1A BC 的距离，然后再利用等体积法11A A BC A ABC V V --=代入求解点A 到平面1A BC 的距离.【详解】已知正三棱柱111ABC A B C -，底面正三角形ABC 的边长为2，侧棱1AA 长为2，所以可得1122==A B AC ，1A BC 为等腰三角形，所以1A BC 的高为7，由对称性可知，111--=B A BC A A BC V V ，所以点1B 到平面1A BC 的距离等于点A 到平面1A BC 的距离，所以11A A BC A ABC V V --=，又因为112772=⨯⨯=A BC S △，12332ABC S =⨯⨯=，所以111233⨯⨯=⨯⨯A BC ABC S h S △△，即2322177h ==. 故选：A.【点睛】一般关于点到面的距离的计算，一是可以考虑通过空间向量的方法，写出点的坐标，计算平面的法向量，然后代入数量积的夹角公式计算即可，二是可以通过等体积法，通过换底换高代入利用体积相等计算.6．A解析：A【分析】先确定曲面面积占以点D 为顶点，DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，利用圆锥的侧面积S rl π=即可得出结论. 【详解】由题意 6,32CE CC AA BC AB ''=====22361832BE CE CB -=-=45BCE ∠=， 45ECC '∠=， 所以曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，所以圆锥的侧面积 6S rl CC DC πππ'==⨯⨯=⨯⨯，所以曲面面积为18⨯=. 故选：A.【点睛】 方法点睛：本题考查曲面面积，考查圆锥的侧面积，确定曲面面积占以点D 为顶点，DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18是关键，考查系数的空间想象力. 7．A解析：A【分析】首先得到11AB A ∠是1AB 与底面111AB C 所成的角，再通过三棱柱的体积得到三棱柱的底面等边三角形的边长，最后通过球的半径，球心到底面距离，底面外接圆半径的关系计算．【详解】因为侧棱1AA ⊥底面111A B C ，则11AB A ∠是1AB 与底面111AB C 所成的角，则1145AB A ∠=︒． 故由11111tan tan 451AA AB A A B ∠=︒==，得111AA A B =．设111AA A B a ==，则111312ABC A B C V a a -=⨯==三棱柱， 解得2a =．所以球O 的半径R ==所以球O 的表面积2228π4π4π3S R ==⨯=．故选：A ．【点睛】解决球与其他几何体的切、接问题，关键在于仔细观察、分析，弄清相关元素的关系和数量关系，选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系)，达到空间问题平面化的目的． 8．C解析：C【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时，三棱锥P BCE -体积有最小值，建立坐标系求得当点E 的高为3时，问题得解.【详解】以点O 为原点，,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系，如图所示：设点(),0,E x z ，依题意得()6,0,0A ，则()6,0,AE x z =- ，(),0,OE x z =因为过BC 作截面AP α⊥于E ，所以AE OE ⊥则0AE OE ⋅=，故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABC V V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S -=-=⋅⋅=故选：C【点睛】 关键点点晴：本题的解题关键是将问题转化为求E ABC V -的最大值，通过建系求得三棱锥E ABC -的高的最大值即可.9．A解析：A【分析】根据已知条件判断直线m 、n 的位置关系，可判断A 选项的正误；利用线面垂直的性质可判断BC 选项的正误；利用面面垂直的判定定理可判断D 选项的正误.【详解】对于A 选项，若//m α，则直线m 与平面α内的直线平行或异面，由于n αβ=，则直线m 、n 平行或异面，A 选项错误；对于B 选项，若//m n ，m α⊥，则n α⊥，B 选项正确；对于C 选项，若m α⊥，m β⊥，则//αβ，C 选项正确；对于D 选项，若m α⊥，m β⊂，由面面垂直的判定定理可知αβ⊥，D 选项正确. 故选：A.【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．10．C解析：C【分析】先由正视图、俯视图及题意还原三棱锥，过A 作AM ⊥BD 于点M ,连结MC ，把AC 放在直角三角形AMC 中解AC .【详解】根据三棱锥A BCD -正视图和俯视图，还原后得到三棱锥的直观图如图示，由图可知：平面ABD ⊥平面CBD ，过A 作AM ⊥BD 于点M ,连结MC ,则AM ⊥平面CBD ，∴△MCA 为直角三角形.过C 作CN ⊥BD 于点N ,在直角三角形ABD 中，AB =1，AD 3∴222BD AB AD =+= 所以∠ABD=60°，∠ADB=30°，则在直角三角形ABM 中，AB =1，∠ABM=60°，∴13,22BM AM == 同理，在直角三角形CBD 中，13,22DN CN ==. ∴MN =BD -BM -DN =112122--=, ∴222237()122CM CN MN =+=+= 在直角三角形AMC 中，22227310()222AC CM AM ⎛⎫=+=+ ⎪ ⎪⎝⎭故选：C【点睛】(1)根据三视图画直观图，可以按下面步骤进行：①、首先看俯视图，根据俯视图画出几何体地面的直观图 ；②、观察正视图和侧视图找到几何体前、后、左、右的高度；③、画出整体，让后再根据三视图进行调整.(2)立体几何中求线段长度：①、把线段放在特殊三角形中，解三角形；②、用等体积法求线段.11．A解析：A【分析】先求出'A FDE -外接球的半径和外接圆的半径，再利用勾股定理求出外接球的球心到外接圆的圆心的距离，可得高h 的最大值.【详解】因为A ，B ，C 三点重合于点A '，原来A B C ∠∠∠、、都是直角，所以折起后三条棱'''A F A D A E 、、互相垂直，所以三棱锥'A FDE -可以看作一个长方体的一个角，它们有相同的外接球，外接球的直径就是长方体的体对角线，即为'2'2'22441626R AF AD AE =++=++6R =，2241625DE DF AD AE ==+=+=2222EF BE BF =+在DFE △中，22210cos 21022522DE EF DF DEF DE EF +-∠===⨯⨯⨯， 所以DEF ∠为锐角，所以2310sin 1cos 10DEF DEF ∠=-∠=， DEF 的外接圆的半径为5522sin 3310DF r DEF ===∠，则球心到DEF 2223R r -，以FDE 为底面的三棱锥G -DEF 的高h 的最大值为1R OO +263. 故选：A.【点睛】 本题考查了翻折问题和外接球的问题，关键点翻折前后量的变化及理解外接球和三棱锥的关系，考查了学生的空间想象力和计算能力.12．C解析：C【分析】由线面平行的判定定理可判断A ；由线面垂直的判定定理可判断B ；反证法可说明C ；由面面垂直的判定定理可判断D.【详解】对于A ，D ，F 外别是AB ，CA 的中点，//BC DF ∴，DF ⊂平面PDF ，∴//BC 平面PDF ，故A 正确，不符合题意；对于B ，各棱长相等，E 为BC 中点，,BC AE BC PE ∴⊥⊥，PE AE E =， BC ∴⊥平面PAE ，//BC DF ，∴DF ⊥平面PAE ，故B 正确，不符合题意；对于C ，假设平面PDE ⊥平面ABC ，设DE BF O ⋂=，连接PO ，则O 是DE 中点，PO DE ∴⊥，平面PDE 平面ABC DE =，PO ∴⊥平面ABC ，BF ⊂平面ABC ，PO BF ∴⊥，则PB PF =，与PB PF ≠矛盾，故C 错误，符合题意；对于D ，由B 选项DF ⊥平面PAE ， DF ⊂平面ABC ，∴平面PAE ⊥平面ABC ，故D 正确，不符合题意.故选：C.【点睛】本题考查线面关系和面面关系的判定，解题的关键是正确理解判断定理，正确理解垂直平行关系.二、填空题13．【分析】先根据面面垂直取平面的外接圆圆心G 平面的外接圆圆心H 分别过两点作对应平面的垂线找到交点为外接球球心再通过边长关系计算半径代入球的表面积公式即得结果【详解】如图取的中点的中点连在上取点使得取的 解析：643π 【分析】先根据面面垂直，取平面PAD 的外接圆圆心G ，平面ABCD 的外接圆圆心H ，分别过两点作对应平面的垂线，找到交点为外接球球心O ，再通过边长关系计算半径，代入球的表面积公式即得结果.【详解】如图，取AD 的中点E ，BC 的中点F ，连EF ，PE ，在PE 上取点G ，使得2PG GE =，取EF 的中点H ，分别过点G 、H 作平面PAD 、平面ABCD 的垂线，两垂线相交于点O ，显然点O 为四棱锥P ABCD -外接球的球心，由2AD =，4AB =，可得3PE =33GE OH ==，2222125AH AE EH +=+ 则半径22343(5)3r OA ⎛⎫==+= ⎪ ⎪⎝⎭故四棱锥P ABCD -外接球的表面积为2436443ππ⨯=⎝⎭． 故答案为：643π. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可. 14．【分析】设为正方形的中心的中点为连接求出如图分别可求得大球与小球半径分别为和进而可得小球的体积【详解】解：由题中条件知底面四边形是边长为2的正方形设O 为正方形的中心的中点为M 连接则如图在截面中设N 为 解析：224π 【分析】 设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，求出OM，PM ，PO ，如图，分别可求得大球1O 与小球2O 半径分别为22和24，进而可得小球的体积．【详解】 解：由题中条件知底面四边形ABCD 是边长为2的正方形.设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，则1OM =，221013PM PA AM =-=-=，9122PO =-=，如图，在截面PMO 中，设N 为球1O 与平面PAB 的切点，则N 在PM 上，且1O N PM ⊥，设球1O 的半径为R ，则1O N R =，∵1sin 3OM MPO PM ∠==，∴1113NO PO =，则13PO R =，11422PO PO OO R =+==，∴22R =，设球1O 与球2O 相切于点Q ，则22PQ PO R R =-=，设球2O 的半径为r ，同理可得4PQ r =，∴224R r ==，故小球2O 的体积342324V r ππ==. 故答案为：224π．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.15．【分析】取中点连接由条件可证明平面由此将三棱锥的体积表示为计算可得结果【详解】取中点连接如下图所示：因为所以平面平面所以平面又因为所以所以又因为故答案为：【点睛】关键点点睛：解答本题的关键是通过找的 解析：2 【分析】取AB 中点O ，连接,CO DO ，由条件可证明AB ⊥平面CDO ，由此将三棱锥A BCD -的体积表示为13CDO AB S⨯⨯，计算可得结果.【详解】取AB 中点O ，连接,CO DO ，如下图所示：因为AC BC AD BD ===，所以,AB CO AB DO ⊥⊥，CO DO O =，CO ⊂平面CDO ，DO ⊂平面CDO ，所以AB ⊥平面CDO ， 又因为3AC BC AD BD ====，2AB CD ==()2221032CO DO ⎛⎫==-= ⎪ ⎪⎝⎭， 所以22110221222CDO S ⎛⎫⎛⎫=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， 又因为1122133A BCD CDO V AB S -=⨯⨯==，故答案为：23. 【点睛】 关键点点睛：解答本题的关键是通过找AB 的中点，证明出线面垂直，从而将三棱锥的体积表示为13CDO AB S ⨯⨯，区别于常规的13⨯底面积⨯高的计算方法，本例实际可看成是两个三棱锥的体积之和. 16．【分析】首先将二面角展平根据两点距离线段最短求最小值【详解】如图将二面角沿棱展成平角连结根据两点之间线段最短可知就是的最小值以为邻边作矩形由可知三点共线则故答案为：【点睛】思路点睛：本题考查立体几何 解析：26【分析】首先将二面角展平，根据两点距离线段最短，求AP PB +最小值.【详解】如图，将二面角沿棱a 展成平角，连结AB ，根据两点之间线段最短，可知AB 就是AP PB +的最小值，以,AE EF 为邻边，作矩形AEFC ，由,CF a BF a ⊥⊥可知,,C F B 三点共线， 则()222213226AB AC BC =+=++= 26【点睛】思路点睛：本题考查立体几何中的折线段和的最小值，一般都是沿交线展成平面，利用折线段中，两点间距离最短求解，本题与二面角的大小无关.17．【分析】在平面的投影为的外心即中点设球半径为则解得答案【详解】故在平面的投影为的外心即中点故球心在直线上设球半径为则解得故故答案为：【点睛】本题考查了三棱锥的外接球问题意在考查学生的计算能力和空间想 解析：163π 【分析】P 在平面ABC 的投影为ABC 的外心，即AB 中点1O ，设球半径为R ，则()22211R CO R PO =+-，解得答案.【详解】PA PB PC ==，故P 在平面ABC 的投影为ABC 的外心，即AB 中点1O ，故球心O 在直线1PO 上，1112CO AB ==，113333PO BO ==， 设球半径为R ，则()22211R CO R PO =+-，解得233R =，故21643S R ππ==. 故答案为：163π.【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.18．【分析】取中点连结根据题意得故所以为异面直线和所成角再根据几何关系求得在中故进而得答案【详解】取中点连结依题意：所以所以为异面直线和所成角在正三棱锥中是中点所以又因为平面平面所以平面所以因为分别是的 解析：217【分析】取AB 、BC 中点D 、G ，连结DE 、DF 、GS 、GA ，根据题意得//l BC ，//DE BC ，故//lDE ，所以DEF ∠为异面直线l 和EF 所成角，再根据几何关系求得在Rt DEF ∆中，122DF SA ==，11322DE BC AB ===，227EF DE DF =+321cos 77DE DEF EF ∠===，进而得答案. 【详解】取AB 、BC 中点D 、G ，连结DE 、DF 、GS 、GA ，依题意：//l BC ，//DE BC ， 所以//l DE ，所以DEF ∠为异面直线l 和EF 所成角.在正三棱锥S ABC -中，G 是BC 中点，所以SG BC ⊥，AG BC ⊥， 又因为SG AG G ⋂=，SG ⊂平面SAG ，AG ⊂平面SAG ， 所以BC ⊥平面SAG ，所以BC SA ⊥. 因为F 、D 分别是SB 、AB 的中点， 所以//DF SA . 所以DEDF ⊥.Rt DEF ∆中，122DF SA ==，11322DE BC AB ===， 所以227EF DE DF +.所以321cos 7DE DEF EF ∠===. 故异面直线l 和EF 2121 【点睛】本题考查异面直线所成角的求解，考查空间思维能力与运算能力，是中档题.19．【分析】取PA 的中点E 连接EBEC 推出PA ⊥平面BCE 故点M 的轨迹为线段CE 解出即可【详解】取PA 的中点E 连接EBEC 因为几何体是正四面体P ﹣ABC 所以BE ⊥PAEC ⊥PAEB∩EC ＝E ∴PA ⊥平面解析：3【分析】取PA 的中点E ，连接EB ，EC ，推出PA ⊥平面BCE ，故点M 的轨迹为线段CE ，解出即可． 【详解】取PA 的中点E ，连接EB ，EC ，因为几何体是正四面体P ﹣ABC ，所以BE ⊥PA ，EC ⊥PA ，EB ∩EC ＝E ，∴PA ⊥平面BCE ，且动点M 在正四面体侧面PAC 上运动，总保持MB PA ⊥，∴点M 的轨迹为线段CE ，正四面体P ﹣ABC 的棱长为2，在等边三角形PAC 中求得CE ＝323⨯=. 故答案为：3【点睛】本题考查了正四面体的性质和线面垂直与线线垂直的判定，判断轨迹是解题的关键，属于中档题．20．【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径设内切球半径为r ﹐圆锥高为h 结合轴截面图形计算得最后计算体积即可【详解】解：设圆锥底面半径为R 则所以设内切球半径为r ﹐圆锥高为h 则如图是圆锥轴截面三 解析：23π 【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径1R =，设内切球半径为r ﹐圆锥高为h ，结合轴截面图形计算得2r ，最后计算体积即可. 【详解】解：设圆锥底面半径为R ，则2233R ππ=⨯，所以1R =． 设内切球半径为r ﹐圆锥高为h ，则9122h =-= 如图，是圆锥轴截面三角形图， 所以3r Rh r =-，解得：2r ， 故3442223383r V πππ==⨯=．故答案为：23π【点睛】本题考查圆锥的侧面展开图，圆锥的内切球的体积，考查空间想象能力，是中档题.三、解答题21．（1）证明见解析；（26 【分析】（1）取PB 中点M ，连接,MF AM ，证出四边形AMFE 为平行四边形，利用线面平行的判定定理即可证明.（2）连接,PE BE ，可得PEB ∠为二面角P AD B --的平面角，求出22PE =用余弦定理可得PB ，再利用面面垂直的判定定理证明平面PBE ⊥平面PDA ，点B 作BO PE ⊥交PE 于点O ，在PEB △中即可求解.【详解】解：（1）证明：取PB 中点M ，连接,MF AM ， 由F 为PC 中点，则//MF BC 且12MF BC =. 由已知有//,BC AD BC AD =，又由于E 为AD 中点，从而//,MF AE MF AE =， 故四边形AMFE 为平行四边形，所以//EF AM .又AM ⊂平面PAB ，而EF ⊂/平面PAB ，则//EF 平面PAB . （2）证明：连接,PE BE .由,PA PD BA BD ==，而E 为AD 中点， 所以,PE AD BE AD ⊥⊥，所以PEB ∠为二面角P AD B --的平面角，60PEB ∴∠=︒. 又2,90,22BA BD DBA AD ==∠=︒∴=∴在PAD △中，由10,22PA PD AD ===，可解得22PE =在Rt ABD △中，由22,AD E =为AD 的中点，可得122BE AD ==. ∴在PEB △中，2222cos PB PE EB PE EB PEB =+-⋅∠，2182222262PB ∴=+-⨯⨯⨯=， 2226,,PB PB EB PE PB EB ∴=∴+=∴⊥.又,,,PE AD BE AD PE BE E AD ⊥⊥⋂=∴⊥平面PBE ，AD ⊂平面PAD ，∴平面PBE ⊥平面PDA .过点B 作BO PE ⊥交PE 于点,O OB ∴⊥平面PDA .∴在PEB △中，OB PE PB EB ⋅=⋅， 从而62622PB EB OB PE ⋅⨯===. ∴点B 到平面PAD 的距离为6.【点睛】关键点点睛：本题考查了面面垂直的判定定理，求点到面的距离，解题的关键是求出6PB =，证出平面PBE ⊥平面PDA ，作出点到面的距离，考查了计算能力.22．（1）22；（2）23；（33 【分析】（1）取BD 中点G ，连接GC ，FG ，根据线面垂直的判定定理及性质，先证明EF 为1BD 与1CC 的公垂线，再由题中数据，计算出EF 的长，即可得出结果；（2）连接1ED ，由（1）得到EF ⊥平面1BDD ，设1D 到平面BDE 的距离为d ，根据等体积法，由11E DBD D DBE V V --=求出d ，记直线1BD 与平面BDE 所成角为θ，由1sin dBD θ=即可得出结果； （3）由（2）得到1D 到平面BDE 的距离d ，根据题中条件，得到F 到平面BDE 的距离为2d，即可得出结果. 【详解】（1）在正四棱柱1111ABCD A BC D -中，取BD 中点G ，连接GC ，FG ， ∵F ，G 分别为1,BD BD 的中点，∴1//FG D D 且112FG D D =， 又1//CE D D ，112CE D D =，所以//FG CE 且FG CE =，则四边形EFGC 为平行四边形，又CE ⊥平面ABCD ，CG ⊂平面ABCD ，∴CE CG ⊥， ∴四边形EFGC 为矩形，∴1EF CC ⊥， ∵11//D D C C ，∴1EF DD ⊥，又CG BD ⊥，//EF CG ，BD ⊂平面1BDD ，1D D ⊂平面1BDD ，1BD D D D ⋂=， ∴EF ⊥平面1BDD ，又1BD ⊂平面1BDD ，∴1EF BD ⊥， ∴EF 为1BD 与1CC 的公垂线，且1E CC ⊂，1F BD ⊂， ∴异面直线1BD 与1CC的距离为||2EF =． （2）在正四棱柱1111ABCD A BC D -中，连接1ED ，则11E DBD D DBE V V --=， 由（1）知EF ⊥平面1BDD ，设1D 到平面BDE 的距离为d ， ∵12AA =，1AB =，∴BD BE ED ===EF =1BD =∴1122DBD S==212DBES =⨯=从而1DBEDBD Sd SEF ⨯=⨯，∴d ==，记直线1BD 与平面BDE 所成角为θ，则1sin d BD θ===， ∴直线1BD 与平面BDE所成角的正弦值为3．（3）由（2）知，1D 到平面BDE 的距离23d =，∵F 是1BD 的中点，且B ∈平面BDE ，∴F 到平面BDE 的距离为32d =． 【点睛】 方法点睛：立体几何体中空间角的求法：（1）定义法：根据空间角（异面直线所成角、线面角、二面角）的定义，通过作辅助线，在几何体中作出空间角，再解对应三角形，即可得出结果；（2）空间向量的方法：建立适当的空间直角坐标系，求出直线的方向向量，平面的法向量，通过计算向量夹角（两直线的方法向量夹角、直线的方向向量与平面的法向量夹角、两平面的法向量夹角）的余弦值，来求空间角即可. 23．（1）证明见解析；（2）2. 【分析】（1）要证明线面平行，需先证明线线平行，（2）利用等体积转化2F BDE D OEF B OEF B OEF V V V V ----=+=三棱锥三棱锥三棱锥三棱锥，求三棱锥的体积.【详解】证明：（1）设AC 和BD 交于O ，连接OMM 和O 分别是BF 与BD 的中点，∴ //OM DF 又OM ⊂平面ACM ，DF ⊄平面ACM 所以 //DF 平面ACM（2）菱形ABCD ⊥菱形ACFE ，菱形ABCD菱形ACFE AC =又BD AC ⊥所以 BD ⊥面ACFE ，连接OE 和OF∴ D OEF B OEF V V --=三棱锥三棱锥∴ 2F BDE D OEF B OEF B OEF V V V V ----=+=三棱锥三棱锥三棱锥三棱锥又π3ABC CAE ∠=∠=， ∴2AC AB ==，3OB =132OEF ACEF S S ∆==菱形∴1•13OEF B OEF V OB S ∆-==三棱锥所以 22F BDE B OEF V V --==三棱锥三棱锥. 【点睛】方法点睛：本题考查了线面平行的判断定理，意在考查转化与化归和计算求解能力，不管是证明面面平行，还是证明线面平行，都需要证明线线平行，证明线线平行的几种常见形式，1.利用三角形中位线得到线线平行；2.构造平行四边形；3.构造面面平行. 24．（1）证明见解析；（26 【分析】（1）取BC 的中点M ，连接HM ，DM ．证明四边形DGHM 是平行四边形，可得线面平行；（2）由H 到平面AEC 的距离为F 到平面AEC 的距离的一半，先求出F 到平面AEC 的距离，用体积法可求得F 到平面AEC 的距离． 【详解】（1）证明：取BC 的中点M ，连接HM ，DM ．。