角动量和转动动能

引言：在经典力学中，圆周运动是一种常见的运动形式，它不仅在自然界中广泛存在，而且在工业、交通等领域中也有着重要的应用。

匀速圆周运动是圆周运动中最简单的一种，其动能和角动量的变化规律十分有趣，本文将重点分析并揭示这一规律。

一、匀速圆周运动的基本概念和公式匀速圆周运动是指保持恒定角速度的圆周运动，它的基本概念和公式如下：1.概念（1）圆周运动：一个物体沿着一个确定轨迹做圆周运动，称为圆周运动。

（2）角度：以圆心为顶点的两条射线所夹的角度称为圆心角，记为θ（单位为弧度）。

（3）圆周位移：一个物体在圆周上运动一周所经过的路程称为圆周位移，记为L（单位为米）。

（4）角速度：单位时间内圆心角的转动速度称为角速度，记为ω（单位为弧度/秒）。

2.公式（1）角速度的定义式：ω = Δθ / Δt（2）圆周位移的定义式：L = rθ（3）速度的公式：v = ωr（4）周期T的公式：T = 2π / ω（5）向心加速度a的公式：a = v² / r = ω²r二、匀速圆周运动的动能和角动量匀速圆周运动的动能和角动量是随时间而变化的，下面我们分别来分析它们的变化规律。

1.动能的变化规律圆周运动时，一个物体所具有的动能包括轨迹上的动能和转动动能两个部分，其中，轨迹上的动能与物体在圆周上匀速运动的速度有关，而转动动能则与物体沿圆周运动时顺时针方向自转的角速度相联系。

因此，动能的总量为：K = Kt + Kr = 1/2mv² + 1/2Iω²其中，Kt为轨迹上的动能，Kr为转动动能，m为物体的质量，v为其速度，I为物体的转动惯量，ω为其角速度。

由于匀速圆周运动中，物体的角速度和速度保持不变，在考虑一定的时间间隔内动能的变化时，可以得到以下结论：（1）轨迹上的动能Kt不变；（2）转动动能Kr随时间t而增加。

这一结论可以通过下面的分析予以证明。

（1）轨迹上的动能不变圆周运动时，一个物体的速度v为常量，因此，轨迹上的动能很容易计算，为Kt =1/2mv²。

转动动能定理、角动量守恒原理一，转动动能定理：1， 力矩的功设刚体在外力F 作用下发生角位移d φ 由功的定义：相应的元功为：ϕθϕθMd Frd ds F ds F dA o ==-⋅=⋅=sin )90cos(所以力矩的功为：⎰⎰==21ϕϕϕMd dA A2， 转动动能定理设M 为作用刚体上的合外力矩。

将转动定律应用于功的定义中：222121)(0ωωωωϕωϕβϕωωJ J d J d dt d J d J Md A -=====⎰⎰⎰⎰ 所以转动动能定理为：222121ωωϕJ J Md -=⎰ 说明，（1）⎰ϕMd 为合外力矩的功，是过程量221ωJ E K =为刚体在t 时刻的转动动能。

是时刻量。

（2）其中M 、J 、ω必须相对同一惯性系，同一转轴。

【例】：质量为m 长度为l 的匀质细棒，可绕端轴o 在铅垂铅垂面内自由摆动，求细棒自水平位置自由下摆到铅垂位置时的角速度。

解：取细棒为研究对象，视之为刚体。

细棒下摆到 任意θ位置时受外力有：重力mg ，端轴支持力N (对o 不成矩) 。

由功的定义：2cos 2)90sin(2900l mg d l mg d lmg Md o o ===-=⎰⎰⎰θθθθθ由转动动能定理：lgml J l mg 331210212222=∴⎪⎭⎫⎝⎛=-=ωωω二，角动量守恒定律设M 为作用于刚体的合外力矩，由定轴转动定律：dtdLdt J d dt d J J M ====)(ωωβ 所以，刚体定轴角动量定理为00L L dL Mdt LL tt -==⎰⎰特别当整个过程中合外力矩为零时，刚体的角动量守恒。

即刚体定轴转动角动量守恒定律为：常矢==L M 0说明：（1）刚体定轴角动量守恒条件是整个过程中合外力矩为零。

（2）守恒式各量（M 、J 、ω）均需是对同一惯性系中的同一转轴。

（3）⎩⎨⎧==都变，但乘积不变、都不变、ωωωJ J const I L（4）角动量守恒定律也是自然界基本定律之一。

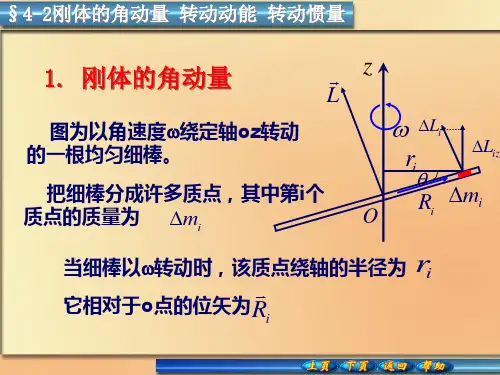
转动物体的动能与角动量研究物体的运动可以分为平动和转动两种形式。

平动是指物体整体平行移动，而转动则是物体绕固定轴线旋转。

在转动过程中，动能和角动量的变化与物体的质量、转动惯量、角速度等参数密切相关。

本文将就转动物体的动能和角动量进行研究。

一、转动物体的动能动能是描述物体运动状态的物理量，对于平动物体来说，动能等于质量乘以速度的平方再除以2，即 K = 1/2 mv^2。

然而，对于转动物体来说，情况略有不同。

首先，我们需要了解转动物体的转动惯量。

转动惯量是一个描述物体对转动运动的惯性的物理量，记作 I。

它依赖于物体的形状和质量分布。

对于直线轴对称的物体，转动惯量可以通过公式 I = mr^2 来计算，其中 m 为物体的质量，r 为参考轴线到质量元的距离。

在转动物体绕某一轴线旋转时，其动能的计算公式为K = 1/2 Iω^2，其中ω 为物体的角速度。

从这个公式可以看出，转动物体的动能与转动惯量和角速度的平方成正比。

转动物体的动能与平动物体的动能有一个非常重要的区别，即转动物体的动能是以转动轴上某一点为参考的。

这一点被称为旋转轴或转轴。

在计算动能时，必须选择一个合适的参考点作为旋转轴，否则将导致计算结果错误。

二、转动物体的角动量角动量是描述转动物体转动状态的物理量，记作 L。

它在数学上等于转动惯量与角速度的乘积，即L = Iω。

类似于动能，角动量也与旋转轴的选择有关，必须选择围绕转轴旋转的参考点作为计算基准。

与动能不同，角动量的大小和方向都是有意义的。

角动量的大小与物体质量、转动惯量和角速度的乘积有关。

当物体的转轴随着时间变化时，角动量的大小保持不变，这就是角动量守恒定律的内容之一。

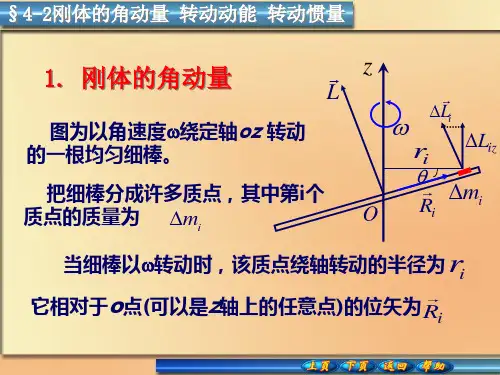
在对转动物体的角动量进行研究时，有一个重要的概念需要引入，即转动惯量矢量。

转动惯量矢量是一个描述转动物体转动惯量随转轴变化的物理量，记作I⃗。

转动惯量矢量的方向与转轴方向相同，并且其大小等于转动物体绕该转轴的转动惯量。

利用转动惯量矢量，可以方便地计算转动物体的角动量。

力学中的角动量与转动惯量公式整理角动量和转动惯量是力学中重要的物理量，在描述物体的旋转运动和转动惯量时起着关键作用。

本文将对角动量和转动惯量的概念进行解释，并整理总结了常见的角动量与转动惯量公式，以便更好地理解和应用于力学的相关问题。

一、角动量的概念和计算方法角动量是描述物体旋转运动的物理量，它与物体的质量、速度以及物体与旋转轴的距离有关。

角动量的计算公式为：L = I * ω其中，L表示角动量，I表示转动惯量，ω表示角速度。

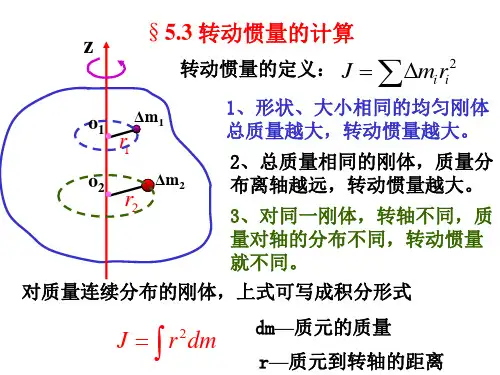
二、转动惯量的概念和计算方法转动惯量是描述物体抵抗转动的性质，它与物体的质量分布和旋转轴的位置有关。

转动惯量可以通过积分的方式计算得出，对于不同的物体和旋转轴位置需要使用不同的计算公式。

下面是一些常见物体的转动惯量公式：1. 点质量：对于一个质量为m的点质量，其转动惯量为：I = m * r^2其中，r表示点质量与旋转轴的距离。

2. 绕轴对称的刚体：对于一个绕轴对称的刚体，其转动惯量可以通过下面的公式计算：I = k * m * r^2其中，m表示刚体的质量，r表示质点到旋转轴的距离，k表示与旋转轴的相对位置有关的常数。

3. 绕轴的圆环：对于一个质量均匀分布在圆环上的物体，其转动惯量为：I = m * R^2其中，m表示圆环的质量，R表示圆环的半径。

4. 绕轴的圆盘：对于一个质量均匀分布的圆盘，其转动惯量为：I = (1/2) * m * R^2其中，m表示圆盘的质量，R表示圆盘的半径。

5. 绕轴的长杆：对于一个质量均匀分布的长杆，其转动惯量为：I = (1/12) * m * L^2其中，m表示长杆的质量，L表示长杆的长度。

三、常见角动量与转动惯量问题的应用角动量和转动惯量在力学中有着广泛的应用，下面举几个常见的例子：1. 转动惯量的变化对旋转运动的影响：转动惯量越大，物体的旋转惯性越大，对外力的抵抗力度越大，因此转动惯量的变化会影响物体的旋转速度和旋转动能的变化。

2. 旋转运动中角动量守恒定律：当物体在没有外力作用下绕某一轴旋转时，其角动量大小保持不变。