小学数学双向细目表
- 格式:doc
- 大小:47.50 KB
- 文档页数:1

数学试题双向细目表I. 整数与有理数A. 基本概念1. 整数的定义及性质2. 有理数的定义及性质B. 整数与有理数的运算1. 加法与减法2. 乘法与除法3. 混合运算C. 整数与有理数的应用1. 温度计算2. 货币兑换问题II. 代数表达式与方程式A. 代数表达式1. 变量与常数2. 四则运算3. 代数表达式化简B. 方程式1. 一元一次方程式2. 一元二次方程式3. 解方程应用题III. 几何A. 基本概念1. 点、线、面的定义2. 角的定义与性质B. 图形的性质与分类1. 三角形2. 四边形3. 圆与圆的构造C. 坐标系与向量1. 平面直角坐标系2. 向量的定义与运算IV. 概率与统计A. 概率1. 随机事件与样本空间2. 概率的计算3. 事件的复合与互斥B. 统计1. 数据的收集与整理2. 平均数与中位数3. 概率统计应用题V. 函数与图像A. 函数概念与性质1. 函数的定义2. 函数的图像与性质B. 常见函数类型1. 线性函数与非线性函数2. 幂函数与指数函数3. 对数函数与三角函数C. 函数的运算与应用1. 函数的加减与乘除2. 函数的复合与反函数VI. 三角函数A. 基本概念与性质1. 弧度与角度的换算2. 三角函数的定义B. 三角函数的图像与周期性1. 正弦函数与余弦函数2. 正切函数与余切函数C. 三角函数的应用1. 三角函数方程的解法2. 三角函数在几何中的应用VII. 数列与数学归纳法A. 数列的概念与性质1. 等差数列与等比数列2. 通项公式与求和公式B. 数学归纳法1. 数学归纳法的原理2. 数学归纳法的应用VIII. 解析几何A. 平面解析几何1. 平面直角坐标系2. 点、线、圆的方程B. 空间解析几何1. 空间直角坐标系2. 直线与平面的方程3. 空间图形的分类IX. 近似计算A. 有效数字与误差1. 有效数字的定义2. 误差的计算与表示B. 近似计算方法1. 数的四舍五入2. 数的科学记数法3. 近似计算的应用X. 排列组合与概率A. 排列与组合1. 排列的定义与计算2. 组合的定义与计算B. 概率统计1. 事件的概率计算2. 投掷与抽取问题的概率XI. 三角函数与复数A. 三角函数的复数表示1. 克莱布斯-戴维(C-D)公式2. 欧拉公式与复数表示B. 复数的运算与性质1. 复数的加减与乘除2. 复数的共轭与模XII. 微积分基础A. 导数的定义与性质1. 导数的定义2. 导数的性质与计算B. 函数的极值与应用1. 函数的极大值与极小值2. 函数的应用问题XIII. 平面向量A. 向量的概念与性质1. 向量的定义与表示2. 向量的性质与运算B. 向量的应用1. 向量的坐标表示2. 向量运算在几何中的应用XIV. 几何证明A. 平面几何证明1. 各种基本几何定理的证明2. 几何图形性质的证明B. 空间几何证明1. 空间几何定理的证明2. 空间图形性质的证明XV. 指数与对数函数A. 指数函数与对数函数的性质1. 指数函数的定义与性质2. 对数函数的定义与性质B. 指数与对数函数的应用1. 指数增长问题2. 对数衰减问题。
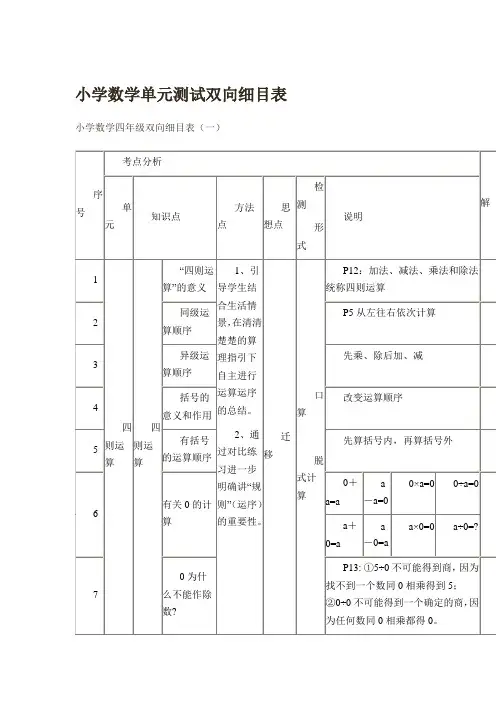
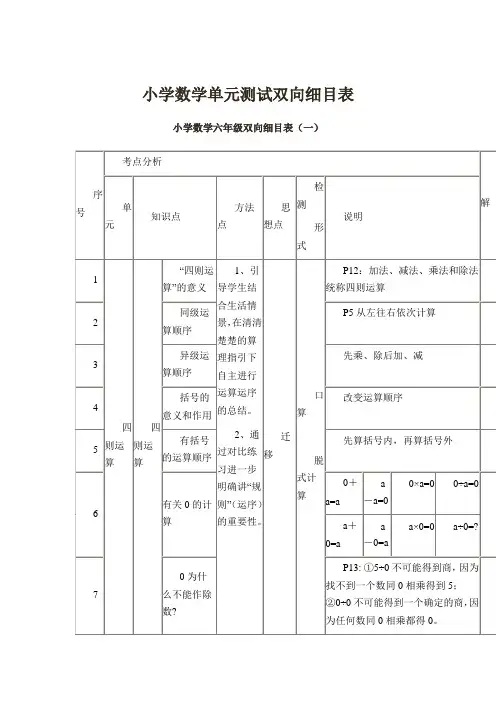
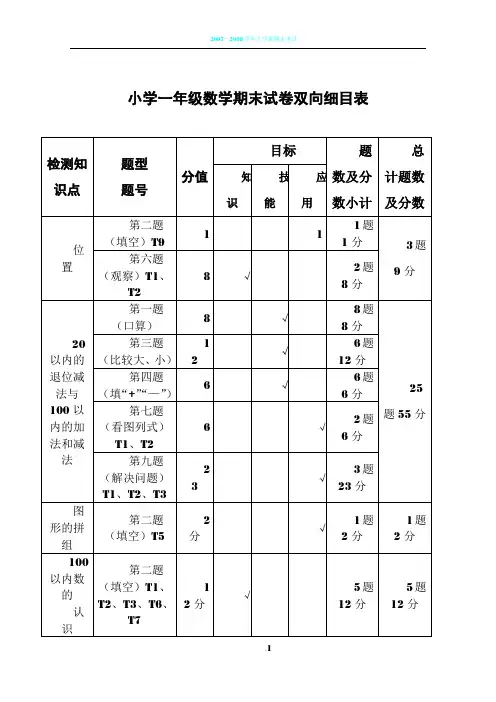



四年级数学上册第四单元.双向细目表在四年级的数学课程中,学生将接触到数学的另一个新领域——双向细目表。
这一概念不仅对学生的数学思维能力提出了更高的要求,而且也对他们的逻辑思维和数据分析能力提出了更高的要求。
本文将从深度和广度两个方面来探讨四年级数学上册第四单元的双向细目表。
一、什么是双向细目表?双向细目表是四年级数学上册第四单元的一个重要概念,它是一种表格形式,可以同时描述行和列上的数据。
在这种表格中,行和列上的数据可能是相关的,也可能是相互独立的。
通过双向细目表,学生可以更清晰地观察和比较不同方面的数据,从而更深入地理解数学概念。
在双向细目表中,行和列上的数据通常代表不同的变量或指标,学生可以根据自己的需要,选择不同的变量来构建双向细目表,以便更好地展现数据之间的关系。
通过观察和分析双向细目表,学生可以培养自己的数据分析能力和逻辑思维能力。
二、如何构建双向细目表?在构建双向细目表时,首先需要确定所需的变量或指标,然后将它们分别放置在表格的行和列上。
接下来,需要收集相关的数据,并将其填入表格中相应的位置。
在填充数据时,需要确保数据的准确性和完整性,以便后续的观察和分析。
在构建双向细目表时,需要注意以下几点:1. 行和列上的变量或指标应该具有一定的相关性,以便更好地展现数据之间的关系。
2. 数据的填充应该按照一定的规律和逻辑进行,以便观察和比较。
3. 表格的排版和格式应该清晰、简洁,便于观察和分析。
通过以上步骤,学生可以完成一个完整、准确的双向细目表,从而更好地理解其中的数学概念。
三、双向细目表的实际应用双向细目表不仅在数学课堂上有着重要的作用,而且在现实生活中也有着广泛的应用。
在经济学领域,双向细目表可以用来展现不同国家或地区的经济发展水平和相关指标;在市场营销领域,双向细目表可以用来展现不同产品或服务的销售情况和相关数据。
通过观察和分析双向细目表,人们可以更好地了解数据之间的关系和趋势,从而做出更准确的判断和决策。
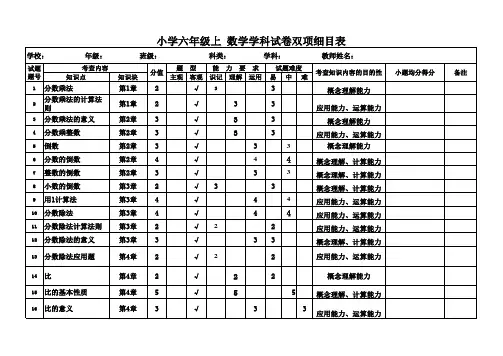
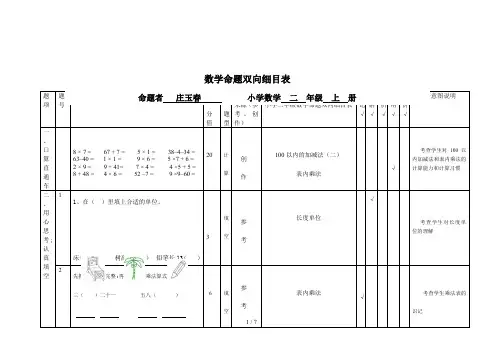
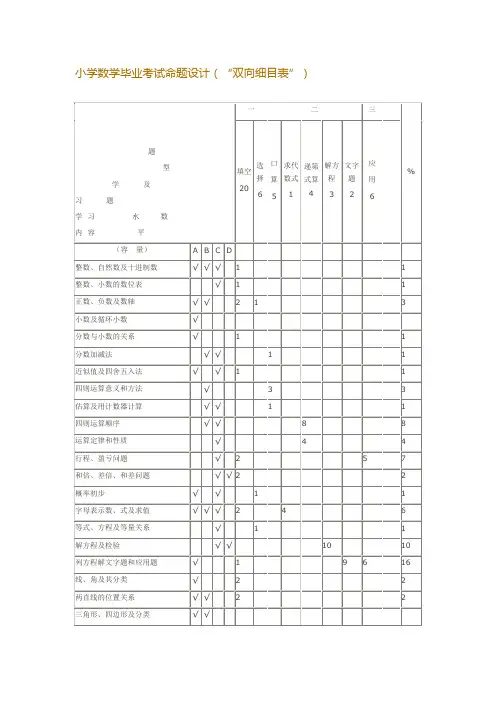
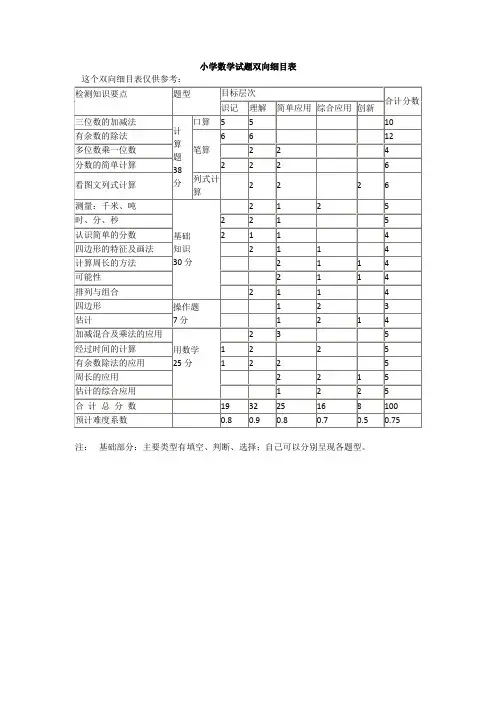
双向细目表是包括两个维度(双向)的表格,细目表也可以是多维的, 般用双向细目表。
较常见的有四种:
(1)反映测验内容与测验目标关系的双向细目表。
注:上表仅为试卷的一部分内容,不是一张完整的试卷双向细目表。
为选择题,二、为简答题,斜线上方的数字为小题号,括号内的数字是分值
(2)反映测验内容与测验目标、题型之间关系的双向细目表。
(3)反映题型与难度、测验目标之间关系的双向细目表。
难易度:A.较易 B.中等 C.较难 D.难度较大
认知度:1识记U理解川简单应用W综合运用(4)反映题型与难度、检内容之间关系的双向细目表
该表可以体现题型数量、难易度、测验内容的分配问题。
优点是试题取样代表性高,试题难易程度也可以作适当控制,表中数据容易分配。
局限性是未能反映测验目标。
小学数学第四单元测试双向细目表
➢该单元由五个小主题组成。
➢本张试卷的题型为:选择题、填空题、判断题、应用题。
➢选择题:15道。
每题2分,共30分
➢填空题:10道。
每题2分,共20分
➢应用题:5道,每题10分,共50分
【注】表中数字斜杠左边为题数,斜杠右边为分数。
如果按该表出试卷:
一、做到全覆盖。
二、重点在主题四和主题五(这两主题各出6道题,各占32分,比重最大)。
二、中等难度的题比重较大。
题数和所占分数都多于难题和容易的题。
三、难题和容易的题相比,容易的题所占分值少了一些,必要时可适当调整。
单元测验双向细目表
西桥小学邱萍
假定:
⌝该单元由五个小主题组成。
⌝本张试卷的题型为:选择题、辨析题、案例分析题。
其中:
⌝选择题:20道。
每题2分,共40分
⌝辨析题:5道。
每题4分,共20分
⌝案例分析题:2道,每题20分,共40分
【注】表中数字斜杠左边为题数,斜杠右边为分数。
题型
难度
如果按该表出试卷:
一、做到全覆盖。
二、重点在主题四和主题五(这两主题各出6道题,各占32分,比重最大)。
二、中等难度的题比重较大。
题数和所占分数都多于难题和容易的题。
三、难题和容易的题相比,容易的题所占分值少了一些,必要时可适当调整。