13、点线面角解析
- 格式:doc
- 大小:1023.00 KB
- 文档页数:32


解析数学中的平面几何点线和角度解析数学中的平面几何:点、线和角度平面几何是数学中的一个分支,研究平面内的点、线和角度之间的关系与性质。
在数学中,点和线是最基本的概念,而角度则是两条线之间的相对旋转程度。
本文将深入解析数学中的平面几何,探讨点、线和角度的定义、性质以及它们之间的关联。
一、点的定义和性质1. 点的定义:在平面几何中,点是最基本的几何对象,被视为没有长度、宽度和高度的位置。
点通常用大写字母表示,如A、B、C等。
2. 点的性质:a) 点没有大小或形状,只有位置。
b) 两个点之间只有两种关系,要么重合,要么不重合。
c) 一条直线上的所有点可以被视为是重合的。
d) 一条直线上的任意两点可以唯一确定一条直线。
二、线的定义和性质1. 线的定义:线是由无数个点按照一定次序排列而成的几何对象。
线通常用小写字母表示,如a、b、c等。
2. 线的性质:a) 线没有宽度,只有长度。
b) 一条线可以无限延伸,并且在平面上可以取任意位置。
c) 两条线可以平行(不相交)或相交于一点。
d) 三条或三条以上的线可以共面或不共面。
三、角度的定义和性质1. 角度的定义:角度是由两条射线共享端点而形成的几何对象。
角度通常用小写字母加“∠”表示,如∠ABC。
2. 角度的性质:a) 角度有大小,单位为度(°)或弧度(rad)。
b) 在平面几何中,角度通常被限制在0°到360°之间。
c) 角度的度量表示了两条射线之间的相对旋转程度。
d) 直角角度为90°,钝角大于90°,锐角小于90°。
四、点、线和角度的关联1. 点与线的关联:a) 一条线上的点可以被视为是重合的。
b) 两点可以确定一条唯一的线。
c) 三点可以共线或不共线。
2. 点与角度的关联:a) 一个点可以确定无数个角度,通过选择不同的端点射线。
b) 两个点和一个端点可以确定一个角度。
3. 线与角度的关联:a) 两条相交的线可形成四个不同的角度,分别是相交角、对顶角、内错角和外错角。

赏析插画中的点线面插画是一种通过点、线、面的组合来表现形象和情感的艺术形式。
在插画中,点、线、面的运用不仅仅是为了表现形象,更是为了传达情感和表达艺术家的个性。
本文将以赏析插画中的点、线、面为主题,探讨这三个元素在插画中的运用和表现。
点是插画中最基本的构成要素之一,它可以是一个孤立的小圆点,也可以是由线条交汇形成的小面。
在插画中,点的运用往往是为了突出画面的重点或者表现画面的细节。
比如在一幅插画中,一个小小的点可以成为一个人物的眼睛,通过眼睛的神情和眼神的交流,可以传达出人物的情感和内心世界。
另外,点的大小、形状和颜色也会对插画的氛围和情感产生影响。
比如在一幅插画中,用大面积的红色点来表现火焰,会让整个画面充满热烈和激情;而用小小的蓝色点来表现星空,则会让整个画面充满宁静和神秘。
线是插画中连接点和面的重要元素,它可以是直线、曲线、粗线、细线、实线、虚线等等。
在插画中,线的运用往往是为了表现物体的形态和轮廓。
比如在一幅插画中,线条的交错可以勾勒出一个人物的轮廓和动态,线条的粗细可以表现出物体的质感和力度,线条的曲直可以表现出物体的柔韧和刚强。
另外,线条的运用也可以传达出画家的个性和情感。
比如一些插画师喜欢用流畅的曲线来表现柔美和婉转,而一些插画师喜欢用粗犷的笔触来表现刚毅和豪放。
面是插画中最直观的表现形式,它可以是实体的、平面的、有质感的、无质感的。
在插画中,面的运用往往是为了表现画面的色彩和纹理。
比如在一幅插画中,用大面积的红色来表现火焰,用大面积的蓝色来表现海洋,用大面积的绿色来表现森林,都会让整个画面充满生机和活力。
另外,面的质感和纹理也会对插画的氛围和情感产生影响。
比如在一幅插画中,用粗糙的面来表现岩石,会让整个画面充满坚毅和坚定;用柔软的面来表现花瓣,会让整个画面充满温柔和娇媚。
综上所述,点、线、面是插画中不可或缺的三个构成要素,它们的运用和表现不仅仅是为了表现形象,更是为了传达情感和表达艺术家的个性。

初一下册几何点线面体,讲解点、线、面、体是几何学中的基本概念,它们之间的关系可以用来描述空间中的形状和结构。
●点:点是几何学中最基本的元素之一。
它没有大小,也没有方向。
在空间中,点的位置由其坐标确定。
通过在二维空间中放置一个点,可以形成一个有序数对,其中第一个数表示该点在x轴上的位置,第二个数表示该点在y轴上的位置。
在三维空间中,需要三个数来确定点的位置,即x、y和z坐标。
●线:线是由无数个点组成的集合。
在二维空间中,线是由所有有序数对组成的集合,其中第一个数是x坐标,第二个数是y坐标。
线有起点和终点,并且可以无限延伸。
在三维空间中,线是所有有序数对组成的集合,其中除了x和y坐标外,还有一个z坐标。
●面:面是由无数条线组成的集合。
在二维空间中,面是由所有有序数对组成的集合,其中第一个数是x坐标,第二个数是y坐标。
面有边界,并且可以无限延伸。
在三维空间中,面是由所有有序数对组成的集合,其中除了x和y坐标外,还有一个z坐标。
●体:体是由无数个面组成的集合。
在三维空间中,体是由所有有序数对组成的集合,其中除了x、y和z坐标外,还有一个表示高度的参数。
体有边界和内部空间。
●点、线、面、体的关系可以通过几何图形来演示。
例如,一个正方形可以由一个点、四条线和四个面组成。
通过将点移动到不同的位置,可以形成不同的几何图形。
总之,点、线、面、体是几何学中的基本概念,它们之间的关系可以用来描述空间中的形状和结构。
通过学习和理解这些概念和关系,我们可以更好地理解和掌握几何学的基础知识。

第一章丰富的图形世界1、几何图形从实物中抽象出来的各种图形,包括立体图形和平面图形。
2、点、线、面、体(1)几何图形的组成点:线和线相交的地方是点,它是几何图形中最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
3、生活中的立体图形圆柱柱生活中的立体图形球棱柱:三棱柱、四棱柱(长方体、正方体)、五棱柱、……(按名称分) 锥圆锥棱锥4、棱柱及其有关概念:棱:在棱柱中,任何相邻两个面的交线,都叫做棱。
侧棱:相邻两个侧面的交线叫做侧棱。
n棱柱有两个底面,n个侧面,共(n+2)个面;3n条棱,n条侧棱;2n个顶点。
5、正方体的平面展开图:11种6、截一个正方体:用一个平面去截一个正方体,截出的面可能是三角形,四边形,五边形,六边形。
7、三视图物体的三视图指主视图、俯视图、左视图。
主视图:从正面看到的图,叫做主视图。
左视图:从左面看到的图,叫做左视图。
俯视图:从上面看到的图,叫做俯视图。
第四章基本平面图形2(1)直线公理:经过两个点有且只有一条直线。
(两点确定一条直线。
)(2)过一点的直线有无数条。
(3)直线是是向两方面无限延伸的,无端点,不可度量,不能比较大小。
3、线段的性质(1)线段公理:两点之间的所有连线中,线段最短。
(两点之间线段最短。
)(2)两点之间的距离:两点之间线段的长度,叫做这两点之间的距离。
(3)线段的大小关系和它们的长度的大小关系是一致的。
4、线段的中点:点M把线段AB分成相等的两条相等的线段AM与BM,点M叫做线段AB的中点。
AM = BM =1/2AB (或AB=2AM=2BM)。
5、角:有公共端点的两条射线组成的图形叫做角,两条射线的公共端点叫做这个角的顶点,这两条射线叫做这个角的边。
或:角也可以看成是一条射线绕着它的端点旋转而成的。
6、角的表示角的表示方法有以下四种:①用数字表示单独的角,如∠1,∠2,∠3等。
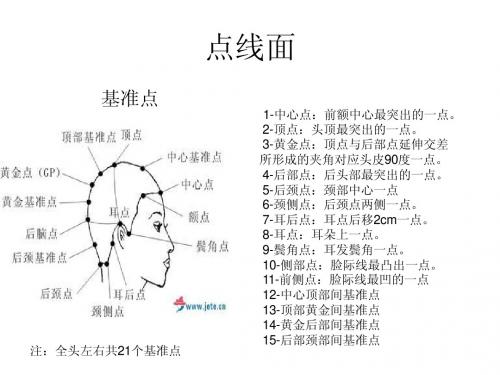
康定斯基《点线面》解析
康定斯基的《点线面》是一部非常重要的抽象艺术著作,它对于现代艺术的发展产生了深远的影响。
在这部著作中,康定斯基将点、线、面作为抽象艺术的基本元素,进行了深入的分析和探讨。
首先,康定斯基将点、线、面视为构成抽象艺术的基本元素。
他认为,这些元素可以构成复杂的画面,并表达出一种内在的和谐和秩序。
他强调,这些元素并不是简单的几何图形,而是具有深刻的象征意义和表现力的艺术形式。
其次,康定斯基认为,点、线、面在抽象艺术中具有不同的象征意义和表现力。
点可以代表具体和局部,也可以代表不确定和模糊;线可以代表方向和运动,也可以代表稳定和静止;面可以代表整体和广延,也可以代表多样性和变化。
这些元素的组合和相互作用,可以创造出丰富的视觉效果和情感表达。
最后,康定斯基认为,抽象艺术是一种独立于客观物象的艺术形式。
他认为,抽象艺术通过摆脱客观物象的束缚,可以更深入地探索艺术的本质和价值。
他认为,抽象艺术可以表达出人类内在的情感和心灵状态,以及宇宙的深层次规律和秩序。
综上所述,康定斯基的《点线面》是一部非常重要的抽象艺术著作,它对于现代艺术的发展产生了深远的影响。
在这部著作中,康定斯基将点、线、面作为抽象艺术的基本元素,进行了深入的分析和探讨。
他认为,这些元素可以构成复杂的画面,并表达出一种内在的和
谐和秩序。
同时,这些元素也具有深刻的象征意义和表现力,可以创造出丰富的视觉效果和情感表达。
他还认为,抽象艺术是一种独立于客观物象的艺术形式,可以更深入地探索艺术的本质和价值。
点线面三要素讲解点线面是空间中的三个基本要素,它们在视觉艺术、设计、建筑等领域都有着重要的作用。
在我们日常生活中,无论是在家里、在街道上还是在办公室里,点线面都无处不在,它们共同构成了我们所处的空间环境。
点是最基本的要素之一。
点是空间中最简单的形式,它没有长度、宽度和深度,只有位置。
然而,点的作用却是不可忽视的。
在设计中,点可以用来吸引注意力,突出重点。
在美术作品中,点可以用来表现光影效果,增加层次感。
在建筑中,点可以用来标识出入口、窗户等重要元素。
总之,点虽小,却有着不可替代的作用。
线也是空间中重要的要素之一。
线是由一系列相邻点连接而成的,它具有长度和方向,可以分为直线、曲线等不同形式。
线在设计中常被用来划分空间、界定形状、表达情感等。
在绘画中,线可以用来描绘轮廓、勾勒细节。
在建筑中,线可以用来连接各个部分、构成结构。
线的运用可以使作品更加有序、有节奏,增加视觉的动感和变化。
面是空间中最具体的要素之一。
面是由一系列相邻线围成的区域,具有长度、宽度和面积。
面可以是平面的,也可以是立体的,可以是规则的,也可以是不规则的。
在设计中,面可以用来填充空间、表现形状、传达信息。
在绘画中,面可以用来表现色彩、纹理、光影。
在建筑中,面可以用来构成建筑物的外观、内部空间。
面的大小、形状、颜色等因素会直接影响到空间的整体效果。
总的来说,点线面是空间中不可或缺的三个要素,它们共同构成了我们所处的环境。
点线面的合理运用可以使作品更加丰富多彩、生动有趣。
在设计、绘画、建筑等领域,艺术家们通过对点线面的处理,创造出无数令人赞叹的作品,为人们的生活增添了无尽的乐趣和惊喜。
让我们一起欣赏和感受点线面带来的魅力,享受艺术带来的美好。
点线角知识点总结一、点、线、面、体的定义及性质1. 点点是空间中不具大小的几何对象,为几何中最基本的元素。
点不占据任何空间,不具有长度、宽度和高度,只有位置。
点通常用大写字母表示,如A、B、C等。
2. 线线是由无限多个点连成的,没有宽度只有长度的几何对象。
线有直线和曲线之分,直线上的点是无限多的,而曲线的点数是有限的。
直线通常用小写字母表示,如l、m、n等。
3. 面面是由三条或三条以上的线段围成的几何对象,具有长度和宽度。
面有平面和曲面之分,平面包括平面图形和三维平面,而曲面则包括球面、圆锥面等。
平面通常用大写字母表示,如Δ、P、Q等。
4. 体体是由三个或三个以上的面围成的几何对象,具有长度、宽度和高度。
体包括立体图形和三维图形,如立方体、圆柱体等。
体通常用字母和数字表示,如A、B、C等。
二、点线角的关系1. 点与线点和线的关系是,点可以在直线上,也可以在曲线上。
直线是由无数个点连在一起形成的,点是构成线段和直线的基本要素。
2. 线与角线与角的关系是,两条线段或射线之间的夹角就是角。
角的大小用度量单位来表示,角的度数越大,夹角越大。
角是由两条射线或线段构成的。
3. 点与角角是由两条射线或线段的交点构成的,两个相交的射线或线段的交点就是角的顶点。
顶点以外的部分是角的两边,角的度数表示了两个射线或线段的夹角大小。
三、点线角的度量1. 点的度量在数学中,点是没有长度、宽度和高度的,因此无法用传统的长度单位来度量。
但是在平面直角坐标系和空间直角坐标系中,可以通过坐标来描述点的位置。
2. 线的度量线的度量可以用长度单位来度量,通常用米、厘米、毫米等长度单位来表示。
在数学中,线的长度是可以被测量和计算的。
3. 角的度量角的度量是用度数和弧度来表示的。
度数是最常见的角度度量单位,以°为符号表示,360°为一周。
弧度则是物理学和数学上使用的另一种角度度量单位,以弧长等于半径的圆心角为1弧度。
八年级数学点线面角知识点数学是一门让人爱恨交加的学科,其中点线面角的知识更是被认为是数学中最基础的知识点之一。
在八年级的数学学习中,点线面角的概念和相关公式也占据了很大一部分。
本文将会为大家详细介绍八年级数学中与点线面角相关的知识点及其应用。
一、点的概念与性质1. 点的定义点是空间中没有长度、面积和体积的物体,点也是几何学中最基本的元素,通常用一些字母表示,如 A、B 等。
2. 点的性质(1)点是没有长度、面积和体积的,只有位置,不能旋转、平移和对称。
(2)任何两点之间都是唯一的一条直线。
(3)同一个点的位置永远不变。
二、线的概念与性质1. 线的定义线是由无数个点组成的,具有长度但没有宽度和高度的物体,在几何学中也是基本的元素,通常用一些字母表示,如 AB、CD 等。
2. 线的性质(1)直线没有宽度,无法旋转、平移和对称。
(2)两点之间只有一条直线。
(3)一条直线可以延伸到无限远,也可以在无限远处相交。
三、面的概念与性质1. 面的定义面是由无数个点和线组成的,具有长度和宽度但没有高度的物体,在几何学中也是基本的元素,通常用一些字母表示,如ABC、DEF 等。
2. 面的性质(1)面有长度和宽度,但没有高度,不能旋转、平移和对称。
(2)一个面可以由无数个点和线组成。
(3)平面上的任意三个点不共线。
四、角的概念与性质1. 角的定义角是由两条射线所围成的空间区域,通常用一个字母表示,如∠A。
2. 角的性质(1)角的度数可以通过尺规作图或者解方程来求得。
(2)角的度数可以简单地表示为数学小学中学习的度数制度,但也可以表示为弧度制度。
(3)同一条直线上的角叫做邻角,邻角之和为 180 度;相对于同一个点的两个角叫做对角,它们之和为 360 度。
五、点线面角的应用1. 点线面角在图形计算中的应用(1)使用点线面角的概念和公式可以帮助我们计算图形的周长、面积和体积等。
(2)举例来说,我们可以使用平行四边形的面积公式 S=a×h (a 为底边长, h 为高),计算出一个平行四边形的面积。
点线面角一.选择题1.(2015•湖南株洲,第2题3分)已知∠α=35°,那么∠α的余角等于( )A.35°B.55°C.65°D.145°【试题分析】本题考点为互余两个角的性质理解:互余的两个角和为90°,从而解得。
答案为:B2.(2015湖南邵阳第5题3分)将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是()A.30°B.45°C. 60°D. 65°考点:平行线的性质..分析:先根据两角互余的性质求出∠3的度数,再由平行线的性质即可得出结论.解答:解:∵∠1+∠3=90°,∠1=30°,∴∠3=60°.∵直尺的两边互相平行,∴∠2=∠3=60°.故选C.点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.3.(2015•甘肃武威,第3题3分)若∠A=34°,则∠A的补角为()A . 56°B . 146°C . 156°D . 166°考点: 余角和补角.分析:根据互补的两角之和为180°,可得出答案.解答: 解:∵∠A =34°, ∴∠A 的补角=180°﹣34°=146°. 故选B . 点评: 本题考查了余角和补角的知识,解答本题的关键是掌握互补的两角之和为180°.4. (2015•浙江金华,第4题3分)已知35α∠=︒,则α∠的补角的度数是【 】A . 55°B . 65°C . 145°D . 165°【答案】C .【考点】补角的计算.【分析】根据“当两个角的度数和为180 °时,这两个角互为补角”的定义计算即可:∵35α∠=︒,∴α∠的补角的度数是18035145︒-︒=︒.故选C .5.(2015·黑龙江绥化,第5题 分)将一副三角尺按如图方式进行摆放 ,∠1、∠2不一定互补的是( )考点:余角和补角..分析:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角,据此分别判断出每个选项中∠1+∠2的度数和是不是180°,即可判断出它们是否一定互补.解答:解:如图1,,∵∠2+∠3=90°,∠3+∠4=90°,∴∠2=∠4,∵∠1+∠4=180°,∴∠1+∠2=180°,∴∠1、∠2互补.如图2,,∠2=∠3,∵∠1+∠3=180°,∴∠1+∠2=180°,∴∠1、∠2互补.如图3,,∵∠2=60°,∠1=30°+90°=120°,∴∠1+∠2=180°,∴∠1、∠2互补.如图4,,∵∠1=90°,∠2=60°,∴∠1+∠2=90°+60°=150°,∴∠1、∠2不互补.故选:D.点评:此题主要考查了余角和补角的性质和应用,要熟练掌握,解答此题的关键是要明确:等角的补角相等.等角的余角相等;并能分别判断出每个选项中的∠1+∠2的度数和是不是180°.6.(2015•山东聊城,第9题3分)图(1)是一个小正方体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是()A.梦B.水C.城D.美考点:专题:正方体相对两个面上的文字..分析:根据两个面相隔一个面是对面,再根据翻转的规律,可得答案.解答:解:第一次翻转梦在下面,第二次翻转中在下面,第三次翻转国在下面,第四次翻转城在下面,城与梦相对,故选:A.点评:本题考查了正方体相对两个面上的文字,两个面相隔一个面是对面,注意翻转的顺序确定每次翻转时下面是解题关键.7. (2015山东省德州市,8,3分)下列命题中,真命题的个数是()①若-1<x< -, 则-2<<-1;②若-1≤x≤2,则1≤x2≤4;③凸多边形的外角和为360°;④三角形中,若∠A+∠B=90°,则sinA=cosB.A. 4B. 3C. 2D.1【答案】B考点:解不等式;多边形的内角和;锐角三角函数间的关系.二、填空题1.(2015•江苏南京,第7题3分)一个角的度数是20°,则它的补角的度数为 .答案:解析:∵两角互补,和为180°,∴它的补角=180°-20°=160°.1. (2015•四川南充,第13题3分)如图,点D 在△ABC 边BC 的延长线上,CE 平分∠ACD ,∠A =80°,∠B =40°,则∠ACE 的大小是_____度.【答案】60考点:角平分线的性质、三角形外角的性质.2. (2015•浙江杭州,第14题4分)如图,点A ,C ,F ,B 在同一直线上,CD 平分∠ECB ,FG ∥CD ,若∠ECA 为α度,则∠GFB 为_________________________度(用关于α的代数式表示)【答案】902α-. 【考点】平角定义;平行的性质.【分析】∵ECA α∠=度,∴180ECB α∠=-度. ∵CD 平分∠ECB ,∴1809022DCB αα-∠==-度.第14题BAC EAC DGFB∵FG ∥CD ,∴902GFB DCB α∠=∠=-度.3. (2015·山东威海,第14 题3分)如图,直线a ∥b ,∠1=110°,∠2=55°,则∠3的度数为 55° .考点: 平行线的性质..分析: 要求∠3的度数,结合图形和已知条件,先求由两条平行线所构成的同位角或内错角,再利用三角形的外角的性质就可求解.解答: 解:如图:∵∠2=∠5=55°, 又∵a ∥b , ∴∠1=∠4=100°. ∵∠4=∠3+∠5, ∴∠3=110°﹣55°=55°, 故答案为:55°.点评: 本题考查了三角形的外角的性质和平行线的性质;三角形的外角的性质:三角形的外角等于和它不相邻的两个内角的和;平行线的性质:两直线平行,同位角相等.图形的展开与叠折一、选择题2.(2015•江苏无锡,第9题2分)如图的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是()A.B.C.D.考点:几何体的展开图.分析:根据正方体的表面展开图进行分析解答即可.解答:解:根据正方体的表面展开图,两条黑线在一列,故A错误,且两条相邻成直角,故B错误,间相隔一个正方形,故C错误,只有D选项符合条件,故选D点评:本题主要考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.2.(2015湖北荆州第8题3分)如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是()A.B.C.D.考点:剪纸问题.分析:根据题意直接动手操作得出即可.解答:解:找一张正方形的纸片,按上述顺序折叠、裁剪,然后展开后得到的图形如图所示:故选A.点评:本题考查了剪纸问题,难点在于根据折痕逐层展开,动手操作会更简便.3.(2015湖北鄂州第8题3分)如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF =()A.B.C.D.【答案】D.考点:翻折问题.4.(2015•四川资阳,第9题3分)如图5,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是A.13cm B.CD.考点:平面展开-最短路径问题..分析:将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.解答:解:如图:∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,图5此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,∴A′D=5cm,BD=12﹣3+AE=12cm,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B ===13(Cm).故选:A.点评:本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.5、(2015•四川自贡,第10题4分)如图,在矩形ABCD中,AB4AD6==,,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF'B D ‘,则'B D‘的最小值是()A. 2B.6C.2D.4 E B考点:矩形的性质、翻折(轴对称)、勾股定理、最值.分析:连接EA 后抓住△DEB 中两边一定,要使'DB 的长度最小即要使'DEB ∠最小(也就是使其角度为0°),此时点'B 落在DE 上, 此时''D B D E EB =-.略解:∵E 是AB 边的中点,AB 4= ∴1AE EB AB 22===∵四边形ABCD 矩形 ∴A 90∠=o∴在Rt △DAE 根据勾股定理可知:222DE AE AD =+又∵AD 6= ∴ED =根据翻折对称的性质可知'EB EB 2==∵△DEB 中两边一定,要使'DB 的长度最小即要使'DEB ∠最小(也就是使其角度为0°),此时点'B 落在DE 上(如图所示).∴''DB DE EB 2=-= ∴'DB 的长度最小值为2. 故选A6. (2015•绵阳第12题,3分)如图,D 是等边△ABC 边AB 上的一点,且AD :DB =1:2,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则CE :CF =( )E BA.B.C.D.考点:翻折变换(折叠问题)..分析:借助翻折变换的性质得到DE=CE;设AB=3k,CE=x,则AE=3k﹣x;根据余弦定理分别求出CE、CF的长即可解决问题.解答:解:设AD=k,则DB=2k;∵△ABC为等边三角形,∴AB=AC=3k,∠A=60°;设CE=x,则AE=3k﹣x;由题意知:EF⊥CD,且EF平分CD,∴CE=DE=x;由余弦定理得:DE2=AE2+AD2﹣2AE•AD•cos60°即x2=(3k﹣x)2+k2﹣2k(3k﹣x)cos60°,整理得:x=,同理可求:CF=,∴CE:CF=4:5.故选:B.点评:主要考查了翻折变换的性质及其应用问题;解题的关键是借助余弦定理分别求出CE、CF的长度(用含有k的代数式表示);对综合的分析问题解决问题的能力提出了较高的要求.7. (2015•浙江省台州市,第8题)如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能是()A.8cmB.C.5.5cmD.1cm8.(2015·贵州六盘水,第4题3分)如图2是正方体的一个平面展开图,原正方体上两个“我”字所在面的位置关系是()A.相对B.相邻C.相隔D.重合考点:专题:正方体相对两个面上的文字..分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.解答:解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“我”与“国”是相对面,“我”与“祖”是相对面,“爱”与“的”是相对面.故原正方体上两个“我”字所在面的位置关系是相邻.故选B .点评:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.9. (2015•浙江宁波,第10题4分)如图,将△ABC 沿着过AB 中点D 的直线折叠,使点A 落在BC 边上的A 1处,称为第1次操作,折痕DE 到BC 的距离记为1h ;还原纸片后,再将△ADE 沿着过AD 中点D 1的直线折叠,使点A 落在DE 边上的A 2处,称为第2次操作,折痕D 1E 1到BC 的距离记为2h ;按上述方法不断操作下去,经过第2015次操作后得到的折痕D 2014E 2014到BC 的距离记为2015h ,若1h =1,则2015h 的值为【 】A . 201521 B . 201421 C . 2015211- D . 2014212-【答案】D .【考点】探索规律题(图形的变化类);折叠对称的性质;三角形中位线定理.【分析】根据题意和折叠对称的性质,DE 是△ABC 的中位线,D 1E 1是△A D 1E 1的中位线,D 2E 2是△A 2D 2E 1的中位线,…∴21111122h =+=-,32211111222h =++=-,42331111112222h =+++=-,…20152201420141111112222h =+++⋅⋅⋅+=-.故选D .10.(2015•江苏泰州,第4题3分)一个几何体的表面展开图如图所示, 则这个几何体是A .四棱锥B .四棱柱C .三棱锥D .三棱柱【答案】A.【解析】试题分析:根据四棱锥的侧面展开图得出答案.试题解析:如图所示:这个几何体是四棱锥.故选A.考点:几何体的展开图.11. (2015•四川广安,第4题3分)在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面上标的字应是()A.全B.明C.城D.国考点:专题:正方体相对两个面上的文字..分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.解答:解:由正方体的展开图特点可得:与“文”字所在的面上标的字应是“城”.故选:C.点评:此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.12. (2015•浙江金华,第9题3分)以下四种沿AB折叠的方法中,不一定能判定纸带两条边线,互相平行的是【】A. 如图1,展开后,测得∠1=∠2B. 如图2,展开后,测得∠1=∠2,且∠3=∠4C. 如图3,测得∠1=∠2D. 如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD【答案】C.【考点】折叠问题;平行的判定;对顶角的性质;全等三角形的判定和性质.【分析】根据平行的判定逐一分析作出判断:A. 如图1,由∠1=∠2,根据“内错角相等,两直线平行”的判定可判定纸带两条边线,互相平行;B. 如图2,由∠1=∠2和∠3=∠4,根据平角定义可得∠1=∠2=∠3=∠4=90°,从而根据“内错角相等,两直线平行”或“同旁内角互补,两直线平行”的判定可判定纸带两条边线,互相平行;C. 如图3,由∠1=∠2不一定得到内错角相等或同位角相等或同旁内角互补,故不一定能判定纸带两条边线,互相平行;D. 如图4,由OA=OB,OC=OD,得到,从而得到,进而根据“内错角相等,两直线平行”的判定可判定纸带两条边线,互相平行.故选C.13. (2015•山东潍坊第11 题3分)如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是()A.cm2 B.cm2 C.cm2 D.cm2考点:二次函数的应用;展开图折叠成几何体;等边三角形的性质..分析:如图,由等边三角形的性质可以得出∠A=∠B=∠C=60°,由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK,根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO为矩形,且全等.连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°,设OD=x,则AO=2x,由勾股定理就可以求出AD= x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.解答:解:∵△ABC为等边三角形,∴∠A=∠B=∠C=60°,AB=BC=A C.∵筝形ADOK≌筝形BEPF≌筝形AGQH,∴AD=BE=BF=CG=CH=AK.∵折叠后是一个三棱柱,∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.∴∠ADO=∠AKO=90°.连结AO,在Rt△AOD和Rt△AOK中,,∴Rt△AOD≌Rt△AOK(HL).∴∠OAD=∠OAK=30°.设OD=x,则AO=2x,由勾股定理就可以求出AD= x,∴DE=6﹣2 x,∴纸盒侧面积=3x(6﹣2 x)=﹣6 x2+18x,=﹣6 (x﹣)2+ ,∴当x= 时,纸盒侧面积最大为.故选C.点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,矩形的面积公式的运用,二次函数的性质的运用,解答时表示出纸盒的侧面积是关键.二、填空题1. (2015•浙江嘉兴,第14题5分)如图,一张三角形纸片ABC,AB=AC=5.折叠该纸片使点A落在边BC的中点上,折痕经过AC上的点E,则线段AE的长为____▲____.考点:翻折变换(折叠问题)..分析:如图,D为BC的中点,AD⊥BC,因为折叠该纸片使点A落在BC的中点D上,所以折痕EF垂直平分AD,根据平行线等分线段定理,易知E是AC的中点,故AE=2.5.解答:解:如图所示,∵D为BC的中点,AB=AC,∴AD⊥BC,∵折叠该纸片使点A落在BC的中点D上,∴折痕EF垂直平分AD,∴E是AC的中点,∵AC=5∴AE=2.5.故答案为:2.5.点评:本题考查了折叠的性质,等腰三角形的性质以及平行线等分线段定理,意识到折痕EF垂直平分AD,是解决问题的关键.2. (2015•四川省内江市,第14题,5分)如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为.考点:翻折变换(折叠问题)..分析:先根据折叠的性质得DE=EF,CE=EF,AF=AD=2,BF=CB=3,则DC=2EF,AB=5,再作AH⊥BC于H,由于AD∥BC,∠B=90°,则可判断四边形ADCH为矩形,所以AH=DC=2EF,HB=BC﹣CH=BC﹣AD=1,然后在Rt△ABH中,利用勾股定理计算出AH=2,所以EF=.解答:解∵分别以AE,BE为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处,∴DE=EF,CE=EF,AF=AD=2,BF=CB=3,∴DC=2EF,AB=5,作AH⊥BC于H,∵AD∥BC,∠B=90°,∴四边形ADCH为矩形,∴AH=DC=2EF,HB=BC﹣CH=BC﹣AD=1,在Rt△ABH中,AH==2,∴EF=.故答案为:.点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.3. (2015•浙江滨州,第17题4分)如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为.【答案】(10,3)考点:折叠的性质,勾股定理4. (2015•浙江杭州,第16题4分)如图,在四边形纸片ABCD中,AB=BC,AD=CD,A Array∠A=∠C=90°,∠B=150°,将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为2的平行四边形,则CD=_______________________________第16题【答案】24+【考点】剪纸问题;多边形内角和定理;轴对称的性质;菱形、矩形的判定和性质;含30度角直角三角形的性质;相似三角形的判定和性质;分类思想和方程思想的应用.【分析】∵四边形纸片ABCD 中,∠A =∠C =90°,∠B =150°,∴∠C =30°.如答图,根据题意对折、裁剪、铺平后可有两种情况得到平行四边形:如答图1,剪痕BM 、BN ,过点N 作NH ⊥BM 于点H , 易证四边形BMDN 是菱形,且∠MBN =∠C =30°.设BN =DN =x ,则NH =12x .根据题意,得1222x x x ⋅=⇒=,∴BN =DN =2, NH =1.易证四边形BHNC 是矩形,∴BC =NH =1. ∴在Rt BCN ∆中,CN∴CD =2+如答图2,剪痕AE 、CE ,过点B 作BH ⊥CE 于点H ,易证四边形BAEC 是菱形,且∠BCH =30°.设BC =CE =x ,则BH =12x .根据题意,得1222x x x ⋅=⇒=,∴BC =CE =2, BH =1.在Rt BCH ∆中,CH ∴EH =2易证BCD EHB ∆∆∽,∴CD BCHB EH=,即1CD =∴224CD +==+.综上所述,CD =2+或4+5. (2015•四川省宜宾市,第15题,3分)如图, 一次函数的图象与x 轴、y 轴分别相交于点A 、B ,将△AOB 沿直线AB 翻折,得△ACB .若C (32,32),则该一次幽数的解析式为.y =+yxCBAO三、解答题1. (2015•浙江金华,第23题10分)图1,图2为同一长方体房间的示意图,图2为该长方体的表面展开图.(1)蜘蛛在顶点A'处①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD 爬行的最近路线A'GC和往墙面BB'C'C爬行的最近路线A'HC,试通过计算判断哪条路线更近?(2)在图3中,半径为10dm的⊙M与D'C'相切,圆心M到边CC'的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线。