第三章 词法分析与有穷自动机
- 格式:ppt
- 大小:2.54 MB
- 文档页数:77


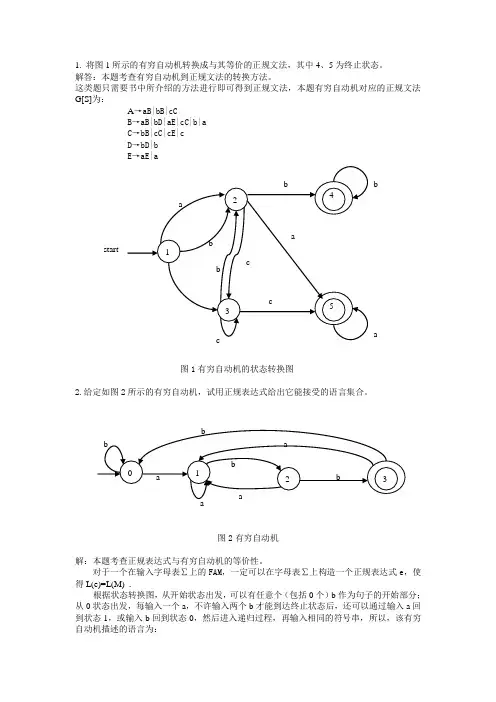
1. 将图1所示的有穷自动机转换成与其等价的正规文法,其中4、5为终止状态。
解答:本题考查有穷自动机到正规文法的转换方法。
这类题只需要书中所介绍的方法进行即可得到正规文法,本题有穷自动机对应的正规文法G[S]为:A →aB|bB|cCB →aB|bD|aE|cC|b|aC →bB|cC|cE|cD →bD|bE →aE|a图1有穷自动机的状态转换图2.给定如图2所示的有穷自动机,试用正规表达式给出它能接受的语言集合。
图2有穷自动机解:本题考查正规表达式与有穷自动机的等价性。
对于一个在输入字母表∑上的FAM ,一定可以在字母表∑上构造一个正规表达式e ,使得L(e)=L(M) .根据状态转换图,从开始状态出发,可以有任意个(包括0个)b 作为句子的开始部分;从0状态出发,每输入一个a ,不许输入两个b 才能到达终止状态后,还可以通过输入a 回到状态1,或输入b 回到状态0,然后进入递归过程,再输入相同的符号串,所以,该有穷自动机描述的语言为:startab(b*(aa*b)*b)*3. 构造下述正规表达式的DFA。
Xy*|yx*y|xyx解:本题考查由正规表达式构造有穷自动机的方法,本题可按照由正规表达式构造等价的NFA,NFA确定化,DFA最小化3步进行求解。
(1)根据题中所给的正规表达式得到相应的DFA如图3所示。
图3正规表达式Xy*|yx*y|xyx的DFA。
(2)依据该NFA采用子集法构造确定DFA其过程如表1(已换名)所示。
以所有包含NFA的终止状态Z的DFA状态作为终止状态,得到DFA相应的状态转换图如图4所示图4 DFA的状态转换图(3)对DFA进行最小化,过程如下:已知K={0,1,2,3,4,5,6}。
首先将K分成两个子集K1={0,2,3} (非终态集)K2={1,3,4,6} (终态集)在状态集合K1={0,2,3}中,因为{0}x={1}⊂K2{2,4}x={4}⊂K1所以状态0与状态2,4不等价,故K1可分割为K11={0} K12={2,4}在状态集合K12={2,4}中,因为有{2,4}x={4} {2,4}y={5}⊂K2所以,状态2和状态4等价。






